Türevlenebilirlik
Konu tekrarı için: Limit Tanımı | Süreklilik Tanımı | Türev Tanımı
Bir \( f \) fonksiyonunun bir açık aralıkta bulunan \( x = a \) noktasındaki türevini aşağıdaki limit ifadesi ile tanımladık.
\( f'(a) = \lim\limits_{h \to 0} {\dfrac{f(a + h) - f(a)}{h}} \)
Bir fonksiyon için belirli bir noktada yukarıdaki limit bir reel sayı olarak tanımlı ise fonksiyon bu noktada türevlenebilirdir, aksi takdirde türevlenebilir değildir.
Bir noktada limitin tanımlı olması o noktada soldan ve sağdan limitlerin tanımlı ve birbirine eşit olmasını gerektirdiği için, bir noktada türevin tanımlı olabilmesi için de o noktada soldan ve sağdan türevler tanımlı ve birbirine eşit olmalıdır.
\( L \in \mathbb{R} \) olmak üzere,
\( f'(a^-) \) ve \( f'(a^+) \) tanımlı ve \( f'(a^-) = f'(a^+) = L \) ise,
\( f \) fonksiyonu \( x = a \) noktasında türevlenebilirdir ve türev değeri soldan/sağdan türev değerine eşittir.
\( f'(a) = L \)
Buna göre bir noktada türevin tanımlı olması, bu noktanın soldan ve sağdan türevlerindeki limit ifadelerinin aynı reel sayı eğim değerine yaklaşması anlamına gelir.
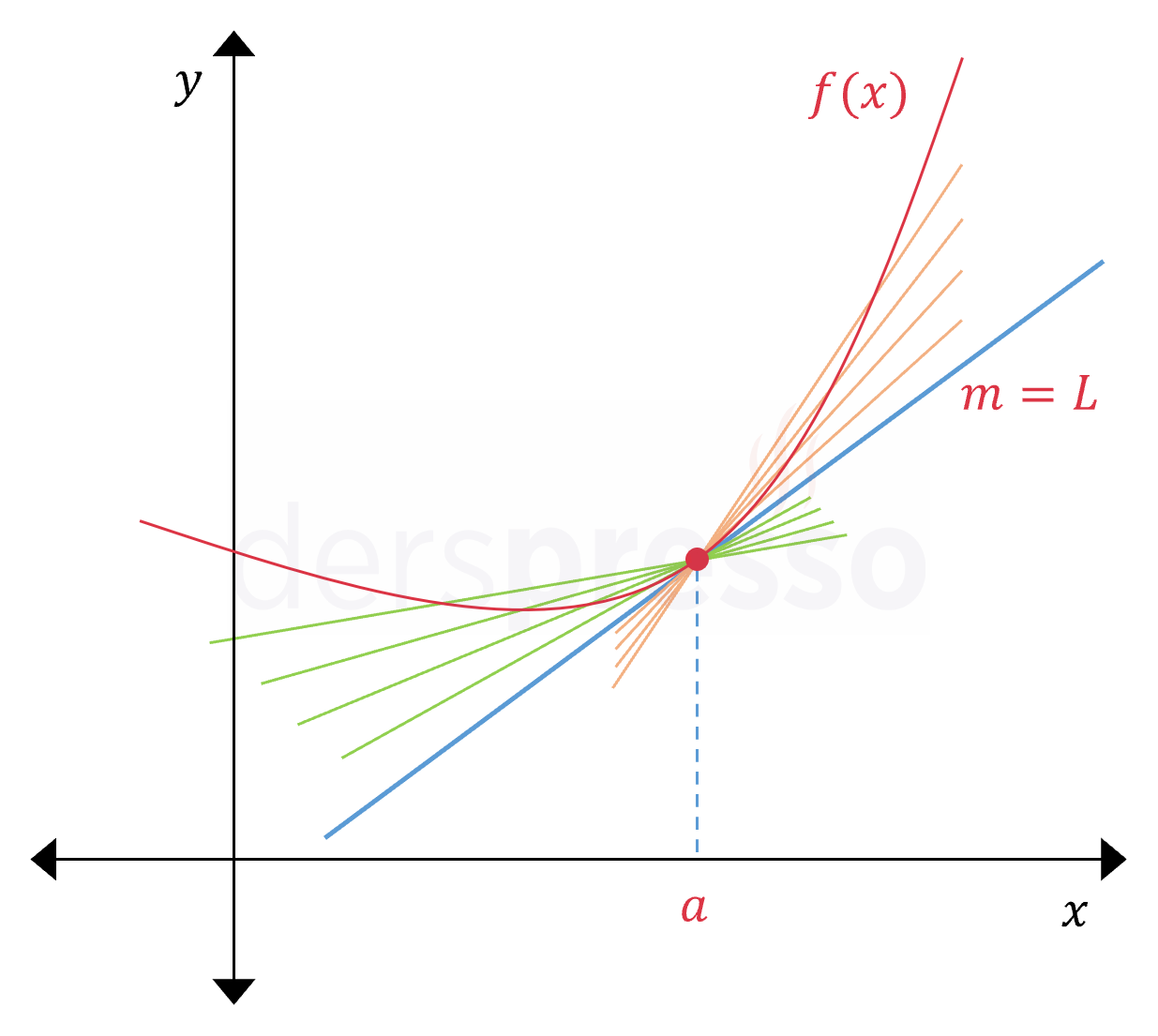
Bir fonksiyonun bir noktadaki soldan ve sağdan türevlerinden en az biri reel sayı olarak tanımlı değilse ya da bu iki türev değeri birbirine eşit değilse fonksiyon bu noktada türevlenebilir değildir.
Bir fonksiyonun bir noktada türevlenebilir olması aynı zamanda fonksiyona bu noktada tek bir teğet çizilebilmesi anlamına gelir.
\( f(x) = \begin{cases} x^2 & x \le 3 \\ 4x - 3 & x \gt 3 \end{cases} \)
fonksiyonunun \( x = 3 \) noktasında soldan ve sağdan türevlenebilirliğini inceleyelim.
Fonksiyon grafiği aşağıdaki gibidir.
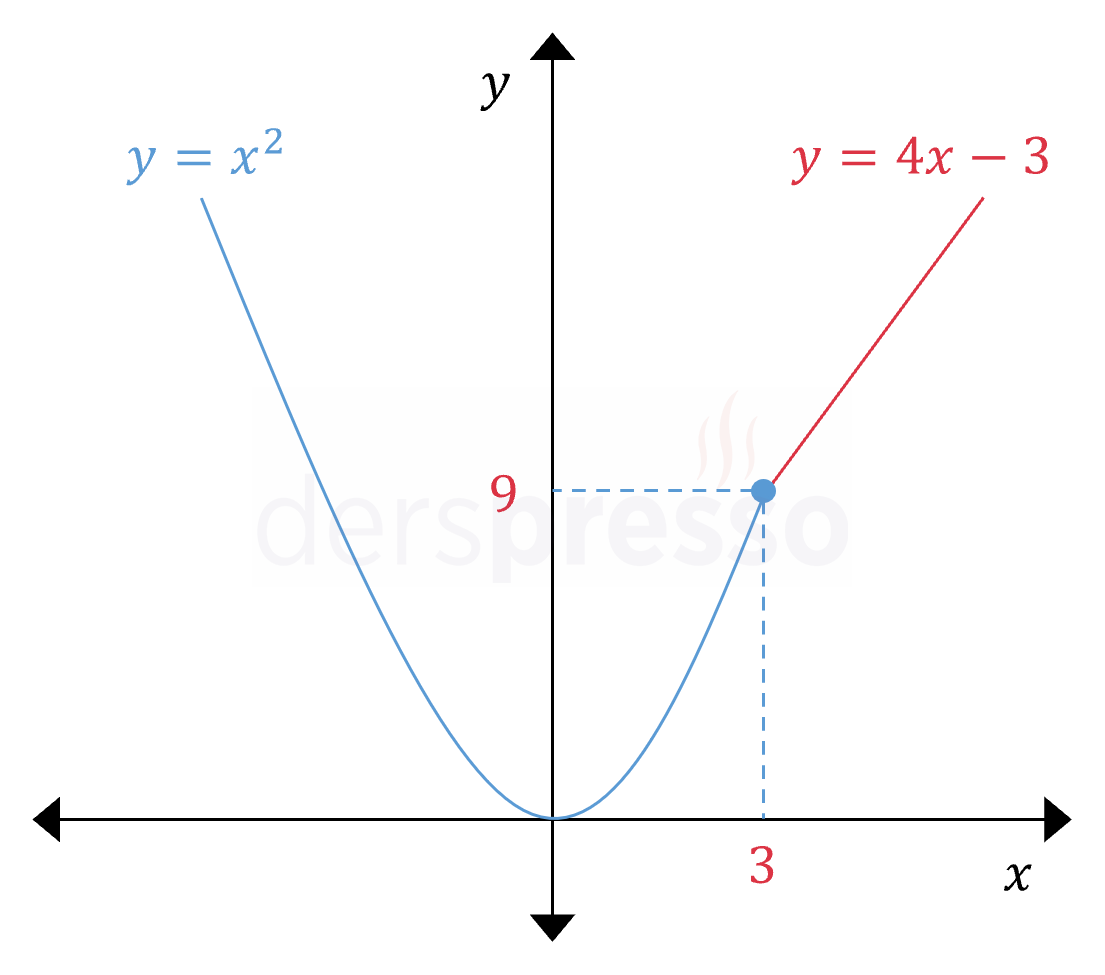
Soldan türevi bulalım.
\( f'(3^-) = \lim\limits_{h \to 0^-} {\dfrac{f(3 + h) - f(3)}{h}} \)
\( = \lim\limits_{h \to 0^-} {\dfrac{(3 + h)^2 - 3^2}{h}} \)
\( = \lim\limits_{h \to 0^-} {\dfrac{9 + 6h + h^2 - 9}{h}} \)
\( = \lim\limits_{h \to 0^-} (6 + h) = 6 \)
Sağdan türevi bulalım.
\( f'(3^+) = \lim\limits_{h \to 0^+} {\dfrac{f(3 + h) - f(3)}{h}} \)
Burada dikkat etmemiz gereken nokta, sağdan yaklaşırken \( f(3) \) değeri için kullanmamız gereken fonksiyon tanımı \( 4x - 3 \) değil, bu noktada geçerli olan \( x^2 \) tanımıdır.
\( = \lim\limits_{h \to 0^+} {\dfrac{(4(3 + h) - 3) - 3^2}{h}} \)
\( = \lim\limits_{h \to 0^+} {\dfrac{12 + 4h - 3 - 9}{h}} \)
\( = \lim\limits_{h \to 0^+} {4} = 4 \)
Buna göre bu noktada soldan ve sağdan türevler birer reel sayı olarak tanımlıdır, ancak türev değerleri birbirine eşit değildir.
\( f'(3^-) \ne f'(3^+) \)
Dolayısıyla fonksiyonun bu noktada türevi tanımlı değildir, bir diğer ifadeyle fonksiyon bu noktada türevlenebilir değildir.
Soldan ve sağdan türevlerin eşit olmadığı, fonksiyon grafiğinde \( x = 3 \) noktasının solunda ve sağında eğimlerin birbirine eşit olmamasından da görülebilir.
\( f(x) = \begin{cases} x & x \le 0 \\ x + 2 & x \gt 0 \end{cases} \)
fonksiyonunun \( x = 0 \) noktasında soldan ve sağdan türevlenebilirliğini inceleyelim.
Fonksiyon grafiği aşağıdaki gibidir.

Soldan türevi bulalım.
\( f'(0^-) = \lim\limits_{h \to 0^-} {\dfrac{f(0 + h) - f(0)}{h}} \)
\( = \lim\limits_{h \to 0^-} {\dfrac{(0 + h) - 0}{h}} \)
\( = \lim\limits_{h \to 0^-} {1} = 1 \)
Sağdan türevi bulalım.
\( f'(0^+) = \lim\limits_{h \to 0^+} {\dfrac{f(0 + h) - f(0)}{h}} \)
Burada dikkat etmemiz gereken nokta, sağdan yaklaşırken \( f(0) \) değeri için kullanmamız gereken fonksiyon tanımı \( x + 2 \) değil, bu noktada geçerli olan \( x \) tanımıdır.
\( = \lim\limits_{h \to 0^+} {\dfrac{((0 + h) + 2) - 0}{h}} \)
\( = \lim\limits_{h \to 0^+} {\dfrac{h + 2}{h}} = \infty \)
Sağdan limit bir reel sayı olarak tanımlı olmadığı için bu noktada sağdan türev tanımlı değildir.
Buna göre fonksiyon bu noktada soldan türevlenebilirdir, ancak sağdan türevlenebilir değildir.
Dolayısıyla fonksiyonun bu noktada türevi tanımlı değildir, bir diğer ifadeyle fonksiyon bu noktada türevlenebilir değildir.
Türevlenebilirlik ve Süreklilik
Bir fonksiyonun belirli bir noktada limitli/sürekli/türevlenebilir olma durumları arasındaki ilişki aşağıdaki gibidir.

Buna göre:
- Fonksiyon bir noktada türevlenebilir ise bu noktada sürekli ve limitlidir.
- Fonksiyon bir noktada sürekli ise bu noktada limitlidir.
- Aynı ilişki ters yönde her zaman doğru olmayabilir, yani fonksiyon bir noktada limitli ise bu noktada sürekli veya türevli olabilir ya da olmayabilir.
- Benzer şekilde, fonksiyon bir noktada sürekli ise bu noktada türevli olabilir ya da olmayabilir.
Bu ilişkinin bir sonucu olarak, bir fonksiyon bir noktada türevlenebilir ise o noktada süreklidir.
Bir fonksiyon bir noktada türevlenebilir ise o noktada süreklidir.
Karşıt ters ifadeyle, bir fonksiyon bir noktada sürekli değilse o noktada türevlenebilir değildir.
İSPATI GÖSTER
\( f \) fonksiyonu \( x = a \) noktasında türevlenebilir ise türev değeri aşağıdaki limit değerine eşittir.
\( f'(a) = \lim\limits_{x \to a} \dfrac{f(x) - f(a)}{x - a} \)
\( f \) fonksiyonunun \( x = a \) noktasında sürekli olma koşulu ise bu noktadaki limit değerinin tanımlı ve bu noktadaki fonksiyon değerine eşit olmasıdır.
\( \lim\limits_{x \to a} f(x) = f(a) \)
\( f \) fonksiyonunun \( x = a \) noktasında türevlenebilir olduğunu varsayalım.
Aşağıdaki limit ifadesini tanımlayalım.
\( \lim\limits_{x \to a} (f(x) - f(a)) \)
İfadenin pay ve paydasını \( x - a \) ile çarpalım.
\( = \lim\limits_{x \to a} [(x - a) \cdot \dfrac{f(x) - f(a)}{x - a}] \)
Limit çarpma kuralına göre iki fonksiyonun çarpımının limiti fonksiyonların limitlerinin çarpımına eşittir. Bu kuralı kullanabilmemiz için gerekli olan iki fonksiyonun limitinin ayrı ayrı tanımlı olması koşulunu aşağıda göstereceğiz.
\( = \lim\limits_{x \to a} (x - a) \cdot \lim\limits_{x \to a} \dfrac{f(x) - f(a)}{x - a} \)
İkinci çarpan fonksiyonun \( a \) noktasındaki türevinin tanımıdır. Fonksiyonun \( a \) noktasında türevlenebilir olduğunu varsaydığımız için bu limit tanımlıdır ve bu noktadaki türev değerine eşittir.
\( = \lim\limits_{x \to a} (x - a) \cdot f'(a) \)
Birinci çarpan doğrusal bir fonksiyondur ve limit değerini doğrudan yerine koyma yöntemi ile sıfır olarak buluruz.
\( = (a - a) \cdot f'(a) \)
\( = 0 \cdot f'(a) = 0 \)
Buna göre tanımladığımız limit ifadesi sıfıra eşittir.
\( \lim\limits_{x \to a} (f(x) - f(a)) = 0 \)
Eşitliğin solundaki limit ifadesinin ikinci terimi sabit bir değer olduğu için limit dışına çıkarabiliriz.
\( \lim\limits_{x \to a} f(x) - f(a) = 0 \)
Sabit değeri eşitliğin sağ tarafına alalım.
\( \lim\limits_{x \to a} f(x) = f(a) \)
Elde ettiğimiz eşitlik \( x = a \) noktasındaki sürekliliğin tanımıdır. Dolayısıyla bir fonksiyon bir noktada türevlenebilir ise o noktada süreklidir.
Bir fonksiyonun bir noktadaki tek taraflı türevlenebilirliği ve sürekliliği arasındaki ilişki aşağıdaki gibidir.
- Bir fonksiyon bir noktada soldan türevlenebilir ise o noktada soldan süreklidir. Karşıt ters ifadeyle, fonksiyon bir noktada soldan sürekli değilse o noktada soldan türevlenebilir değildir.
- Bir fonksiyon bir noktada sağdan türevlenebilir ise o noktada sağdan süreklidir. Karşıt ters ifadeyle, fonksiyon bir noktada sağdan sürekli değilse o noktada sağdan türevlenebilir değildir.
Buna göre aşağıdaki şekildeki üç fonksiyonun \( x = a \) noktasındaki türevlilik ve süreklilik durumları ile ilgili olarak; \( f \) hem soldan hem sağdan türevli ve sürekli, \( g \) sadece soldan türevli ve sürekli, \( h \) ise ne soldan ne de sağdan türevli ve süreklidir.

Uç Noktalarda Türevlenebilirlik
\( [a, b] \) kapalı aralığında tanımlı bir fonksiyonun uç noktalarındaki türevlenebilirlik için fonksiyonun sadece tanımlı olduğu yönlerdeki türevlenebilirliğe, yani \( x = a \) noktasında sağdan, \( x = b \) noktasında ise soldan türevlenebilirliğe bakmamız yeterlidir.
\( f: [a, b] \to \mathbb{R} \) olmak üzere, \( f \) fonksiyonu:
\( x = a \) noktasında sağdan türevlenebilir ise bu noktada türevlidir.
\( f'(a) = f'(a^+) \)
\( x = b \) noktasında soldan türevlenebilir ise bu noktada türevlidir.
\( f'(b) = f'(b^-) \)
Buna göre \( [a, b] \) aralığında tanımlı aşağıdaki \( f \) fonksiyonu \( x = a \) noktasında türevlenebilir iken \( x = b \) noktasında türevlenebilir değildir. Dikkat edilirse, uç noktalardaki türevlilik tek yönlü türevliliğe bağlı olduğu için \( x = a \) noktası için "sağdan türevli" ifadesine ek olarak, bir yön belirtmeden "türevli" ifadesi de kullanılabilir.
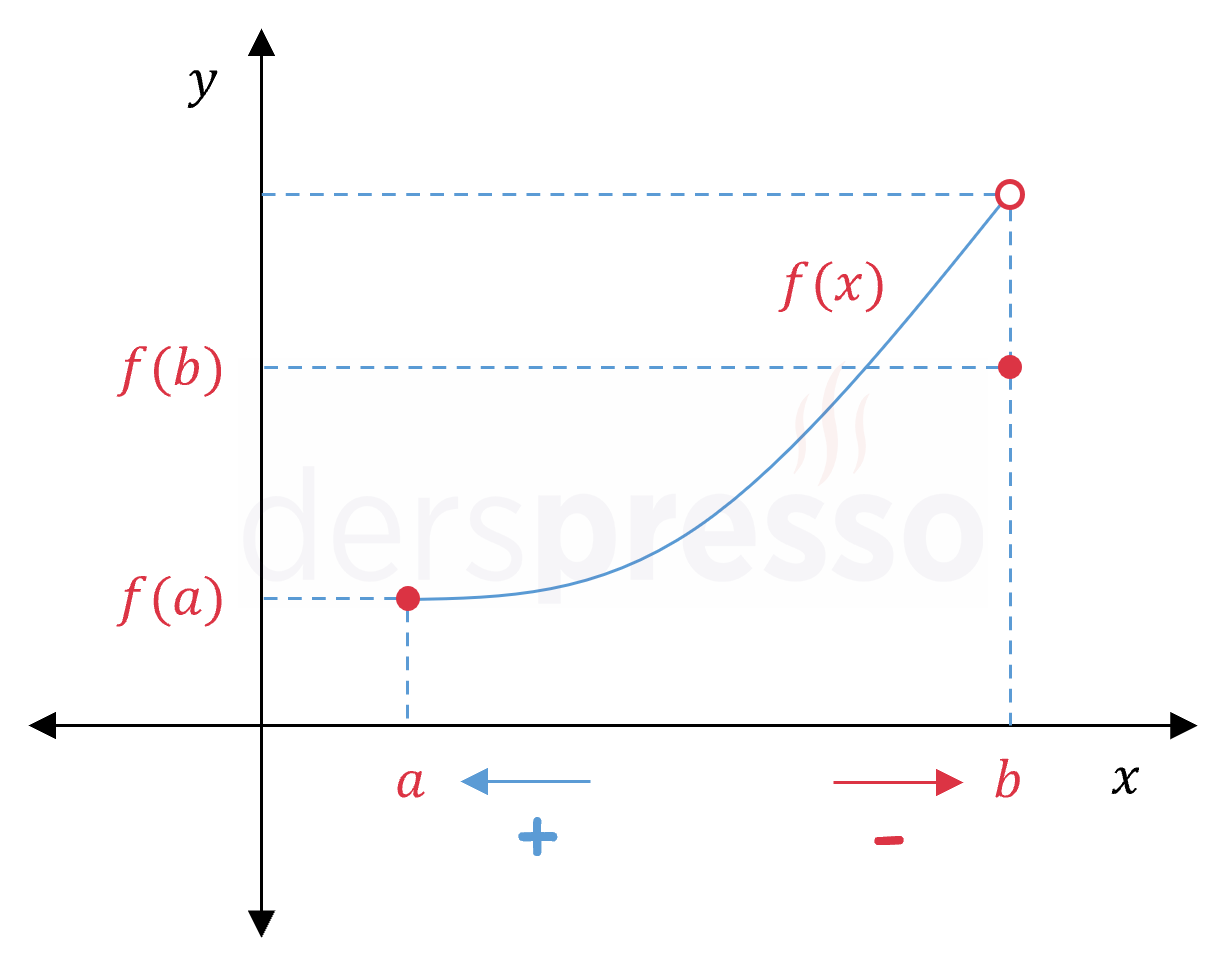
Bir Aralıkta Türevlenebilirlik
Yukarıda bahsettiğimiz iç ve uç noktalardaki türevlenebilirlik tanımları bir aralıktaki türevlenebilirliğe aşağıdaki şekilde uyarlanabilir.
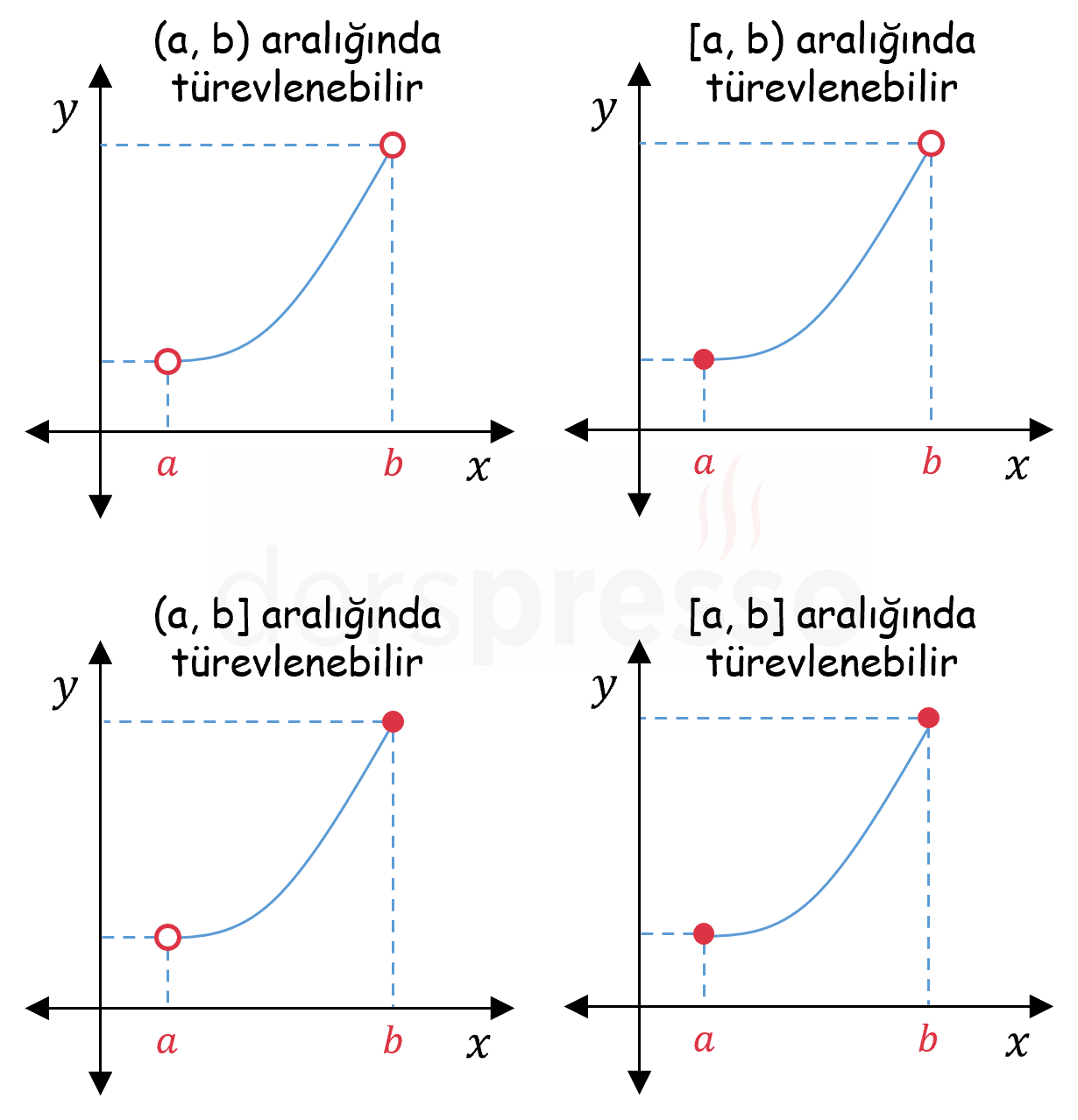
Buna göre \( f \) fonksiyonu:
- \( (a, b) \) aralığındaki tüm noktalarda türevlenebilir ise \( (a, b) \) açık aralığında türevlenebilirdir.
- \( (a, b) \) aralığına ek olarak \( a \) noktasında sağdan türevlenebilir ise \( [a, b) \) yarı açık aralığında türevlenebilirdir.
- \( (a, b) \) aralığına ek olarak \( b \) noktasında soldan türevlenebilir ise \( (a, b] \) yarı açık aralığında türevlenebilirdir.
- \( (a, b) \) aralığına ek olarak \( a \) noktasında sağdan, \( b \) noktasında soldan türevlenebilir ise \( [a, b] \) kapalı aralığında türevlenebilirdir.
Bir fonksiyonun soldan ve sağdan türevlerine iki sebeple ihtiyaç duyulabilir.
- Parçalı fonksiyonların sınır ve mutlak değer fonksiyonlarının kritik noktalarında türevlenebilirliğini bulmak için soldan ve sağdan türev değerleri ayrı ayrı bulunmalı ve eşitliği gösterilmelidir.
- Bir aralığın uç noktalarında sadece tek taraflı türev hesaplanabilir. Örneğin bir \( [a, b] \) kapalı aralığının \( a \) noktasında sadece sağdan, \( b \) noktasında sadece soldan türeve bakılır.
Temel Fonksiyonların Türevlenebilirliği
Fonksiyonlar konusunda incelediğimiz aşağıdaki fonksiyonlar en geniş tanım kümelerinde sürekli ve türevlenebilirdir.
Sürekli olup türevlenebilir olmayan temel fonksiyonlara örnek olarak \( f(x) = \abs{x} \) mutlak değer fonksiyonu verilebilir.
| Fonksiyon | Denklem | En Geniş Tanım Kümesi |
|---|---|---|
| Sabit fonksiyon | \( f(x) = c \) | Tüm reel sayılar |
| Doğrusal fonksiyon | \( f(x) = mx + c \) | Tüm reel sayılar |
| Kuvvet fonksiyonu | \( f(x) = x^n \) | Tüm reel sayılar |
| Köklü fonksiyon (çift dereceli) | \( f(x) = \sqrt[2n]{x} \) | \( [0, \infty) \) |
| Köklü fonksiyon (tek dereceli) | \( f(x) = \sqrt[2n + 1]{x} \) | Tüm reel sayılar |
| Polinom fonksiyonu | \( f(x) = a_nx^n + \ldots + a_0 \) | Tüm reel sayılar |
| Rasyonel fonksiyon | \( f(x) = \dfrac{g(x)}{h(x)} \) | Paydayı sıfır yapan reel kökler dışında tüm reel sayılar |
| Sinüs fonksiyonu | \( f(x) = \sin{x} \) | Tüm reel sayılar |
| Kosinüs fonksiyonu | \( f(x) = \cos{x} \) | Tüm reel sayılar |
| Tanjant fonksiyonu | \( f(x) = \tan{x} \) | \( \{ \ldots, \frac{\pi}{2}, \frac{3\pi}{2}, \ldots \} \) dışında tüm reel sayılar |
| Kotanjant fonksiyonu | \( f(x) = \cot{x} \) | \( \{ \ldots, 0, \pi, \ldots \} \) dışında tüm reel sayılar |
| Sekant fonksiyonu | \( f(x) = \sec{x} \) | \( \{ \ldots, \frac{\pi}{2}, \frac{3\pi}{2}, \ldots \} \) dışında tüm reel sayılar |
| Kosekant fonksiyonu | \( f(x) = \csc{x} \) | \( \{ \ldots, 0, \pi, \ldots \} \) dışında tüm reel sayılar |
| Üstel fonksiyon | \( f(x) = a^x \) | Tüm reel sayılar |
| Logaritma fonksiyonu | \( f(x) = \log_a{x} \) | \( (0, \infty) \) |
\( g(x) = \begin{cases} x^3 + ax^2 + 4bx - 5 & x \le -1 \\ -x^2 + bx - 3a & x \gt -1 \end{cases} \)
fonksiyonu her noktada türevlenebilir olduğuna göre, \( a \cdot b \) çarpımı kaçtır?
Çözümü GösterVerilen parçalı fonksiyonun iki aralıktaki tanımı da birer polinom fonksiyonudur. Polinom fonksiyonları tüm reel sayılarda sürekli ve türevlenebilirdir.
Parçalı fonksiyonun her noktada türevlenebilir olması için, geçiş noktası olan \( x = -1 \) noktasında da sürekli olmalıdır.
Fonksiyonun \( x = -1 \) noktasındaki soldan limiti:
\( \lim\limits_{x \to -1^-} g(x) = \lim\limits_{x \to -1^-} (x^3 + ax^2 + 4bx - 5) \)
\( = (-1)^3 + a(-1)^2 + 4b(-1) - 5 \)
\( = a - 4b - 6 \)
Fonksiyonun \( x = -1 \) noktasındaki sağdan limiti:
\( \lim\limits_{x \to -1^+} g(x) = \lim\limits_{x \to -1^+} (-x^2 + bx - 3a) \)
\( = -(-1)^2 + b(-1) - 3a \)
\( = -3a - b - 1 \)
\( x = -1 \) noktasındaki fonksiyon değeri:
\( g(-1) = a - 4b - 6 \)
Fonksiyonun bu noktada sürekli olması için soldan ve sağdan limit değerleri ve fonksiyon değeri bu noktada tanımlı ve birbirine eşit olmalıdır.
\( a - 4b - 6 = -3a - b - 1 \)
\( 4a - 3b = 5 \)
Fonksiyon bu noktada türevlenebilir olduğuna göre soldan ve sağdan türevler tanımlı ve birbirine eşit olmalıdır.
Fonksiyonun türev fonksiyonunu bulalım.
\( g'(x) = \begin{cases} 3x^2 + 2ax + 4b & x \le -1 \\ -2x + b & x \gt -1 \end{cases} \)
Fonksiyonun \( x = -1 \) noktasındaki soldan türevi:
\( g'(-1^-) = 3(-1)^2 + 2a(-1) + 4b \)
\( = -2a + 4b + 3 \)
Fonksiyonun \( x = -1 \) noktasındaki sağdan türevi:
\( g'(-1^+) = -2(-1) + b \)
\( = b + 2 \)
Fonksiyonun bu noktada türevlenebilir olması için soldan ve sağdan türev değerleri tanımlı ve birbirine eşit olmalıdır.
\( -2a + 4b + 3 = b + 2 \)
\( -2a + 3b = -1 \)
Elde ettiğimiz iki bilinmeyenli iki denklemi ortak çözdüğümüzde aşağıdaki değerleri buluruz.
\( a = 2, \quad b = 1 \)
\( a \cdot b = 2 \cdot 1 = 2 \) bulunur.
Aşağıdaki fonksiyonların \( x = 0 \) noktasındaki türevlenebilirliklerini inceleyin.
(a) \( f(x) = \cos{\abs{4x}} \)
(b) \( g(x) = 3\abs{-x^3} \)
(c) \( h(x) = \abs{\frac{1}{x}} \)
Çözümü Göster(a) seçeneği:
Fonksiyonu parçalı fonksiyon şeklinde yazalım.
\( 4x \) ifadesi \( x \lt 0 \) aralığında negatif olduğu için mutlak değerden negatif işaretli, \( x \ge 0 \) aralığında sıfır ya da pozitif olduğu için olduğu gibi çıkar.
\( f(x) = \begin{cases} \cos(-4x) = \cos(4x) & x \lt 0 \\ \cos(4x) & x \ge 0 \end{cases} \)
\( = \cos(4x) \)
Kosinüs fonksiyonu tüm reel sayılarda sürekli ve türevlenebilirdir.
(b) seçeneği:
Fonksiyonu parçalı fonksiyon şeklinde yazalım.
\( -x^3 \) ifadesi \( x \lt 0 \) aralığında pozitif olduğu için mutlak değerden olduğu gibi, \( x \ge 0 \) aralığında sıfır ya da negatif olduğu için negatif işaretli çıkar.
\( g(x) = \begin{cases} 3(-x^3) = -3x^3 & x \lt 0 \\ 3(x^3) = 3x^3 & x \ge 0 \end{cases} \)
Fonksiyonun \( x = 0 \) noktasındaki sürekliliğini inceleyelim.
\( \lim\limits_{x \to 0^-} g(x) = \lim\limits_{x \to 0^-} (-3x^3) = 0 \)
\( \lim\limits_{x \to 0^+} g(x) = \lim\limits_{x \to 0^+} (3x^3) = 0 \)
\( g(0) = 3(0)^3 = 0 \)
Soldan ve sağdan limit değerleri ve fonksiyon değeri tanımlı ve birbirine eşit olduğu için fonksiyon \( x = 0 \) noktasında süreklidir.
Fonksiyonun türev fonksiyonunu bulalım.
\( g'(x) = \begin{cases} -9x^2 & x \lt 0 \\ 9x^2 & x \ge 0 \end{cases} \)
Fonksiyonun \( x = 0 \) noktasındaki türevlenebilirliğini inceleyelim.
\( g'(0^-) = -9(0)^2 = 0 \)
\( g'(0^+) = 9(0)^2 = 0 \)
Soldan ve sağdan türev değerleri tanımlı ve birbirine eşit olduğu için fonksiyon \( x = 0 \) noktasında türevlenebilirdir.
(c) seçeneği:
Fonksiyon \( x = 0 \) noktasında tanımsız olduğu için süreksizdir, dolayısıyla türevlenebilir değildir.
\( f(x) = \dfrac{x^7 + x^6 + x^{-5}}{\sqrt[3]{x} + \sqrt{x} - 12} \) fonksiyonunun \( x = 64 \) noktasındaki türev değerini bulunuz.
Çözümü GösterBu tip türevi çok işlem gerektirebilecek fonksiyonlarda ilk önce fonksiyonun istenen noktada türevlenebilir olup olmadığını kontrol edebiliriz.
Fonksiyonda \( x = 64 \) koyduğumuzda paydanın sıfır olduğunu, dolayısıyla fonksiyonun bu noktada tanımsız olduğunu görürüz.
\( \sqrt[3]{64} + \sqrt{64} - 12 = 0 \)
Fonksiyon bu noktada tanımsız olduğu için türevi de tanımsızdır.
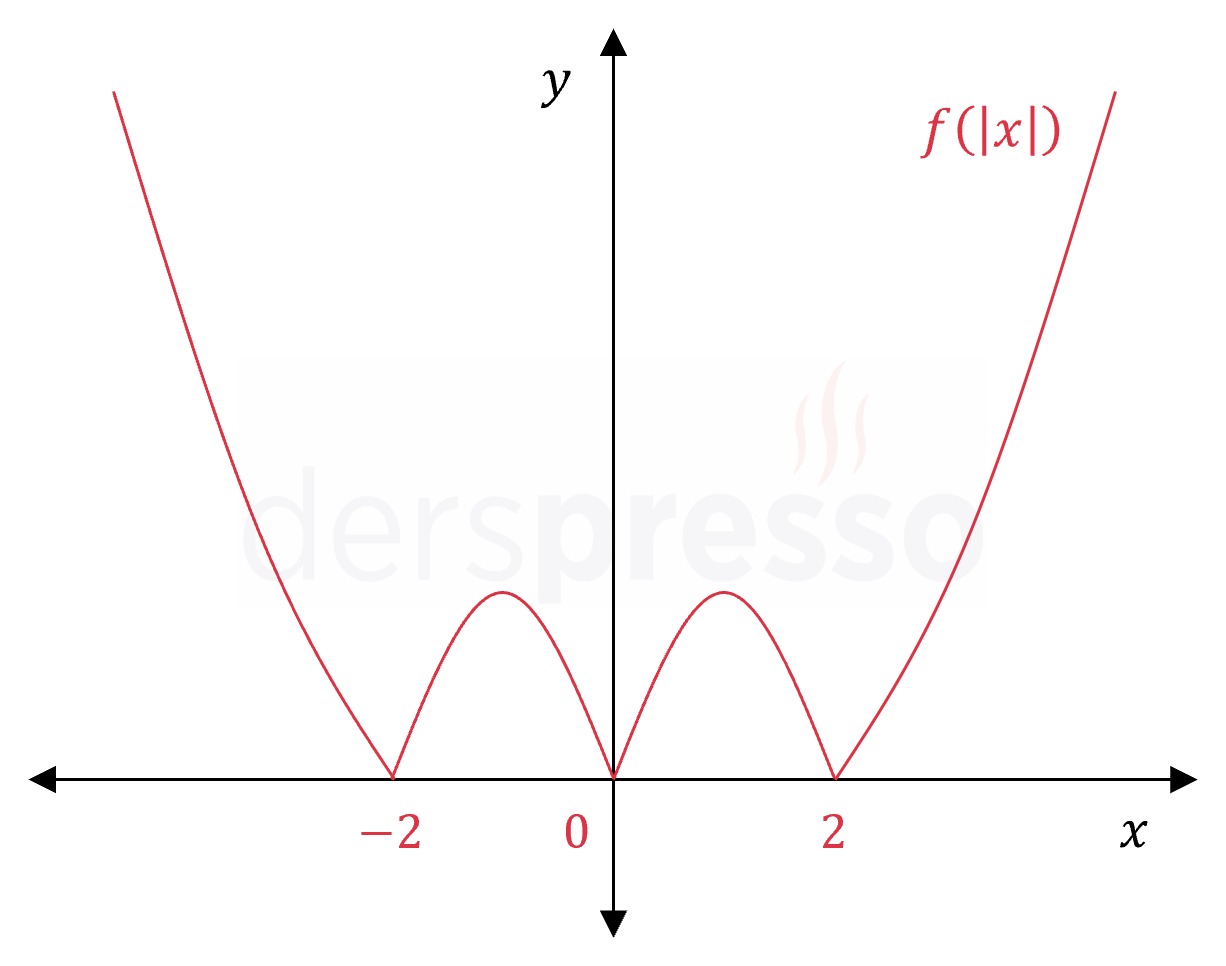
\( f(x) = \abs{x^2 - 2x} \) fonksiyonu veriliyor.
\( f(\abs{x}) \) fonksiyonunun \( x = 0 \) ve \( x = 2 \) noktalarındaki sürekliliğini ve türevlenebilirliğini inceleyin.
Çözümü Göster\( f(x) = \abs{x^2 - 2x} = \abs{x(x - 2)} \)
Fonksiyonu parçalı fonksiyon şeklinde yazalım.
\( x(x - 2) \) ifadesi \( 0 \lt x \lt 2 \) aralığında negatif olduğu için mutlak değerden negatif işaretli, diğer aralıklarda sıfır ya da pozitif olduğu için olduğu gibi çıkar.
\( f(x) = \begin{cases} x^2 - 2x & x \le 0 \\ -x^2 + 2x & 0 \lt x \lt 2 \\ x^2 - 2x & x \ge 2 \end{cases} \)
\( f(\abs{x}) \) fonksiyonunu bulmak için \( f(x) \) tanımında \( x \) yerine \( \abs{x} \) yazalım.
\( f(\abs{x}) = \begin{cases} \abs{x}^2 - 2\abs{x} & \abs{x} \le 0 \\ -\abs{x}^2 + 2\abs{x} & 0 \lt \abs{x} \lt 2 \\ \abs{x}^2 - 2\abs{x} & \abs{x} \ge 2 \end{cases} \)
Mutlak değerli bir ifade negatif olamaz, dolayısıyla parçalı fonksiyonun birinci aralığını tanımdan çıkarabiliriz. \( x = 0 \) değerinde birinci ve ikinci aralık aynı sıfır değerini verdiği için bu değeri ikinci aralığa dahil edebiliriz.
\( f(\abs{x}) = \begin{cases} -\abs{x}^2 + 2\abs{x} & 0 \le \abs{x} \lt 2 \\ \abs{x}^2 - 2\abs{x} & \abs{x} \ge 2 \end{cases} \)
\( 0 \le \abs{x} \lt 2 \) aralığını \( x \) işaretine göre iki aralığa bölelim.
\( -2 \lt x \lt 0 \) ve \( 0 \le x \lt 2 \)
\( -2 \lt x \lt 0 \) ise \( -\abs{x^2} + 2\abs{x} = -x^2 - 2x \)
\( 0 \le x \lt 2 \) ise \( -\abs{x^2} + 2\abs{x} = -x^2 + 2x \)
\( \abs{x} \ge 2 \) aralığını \( x \) işaretine göre iki aralığa bölelim.
\( x \ge 2 \) ve \( x \le -2 \)
\( x \ge 2 \) ise \( \abs{x}^2 - 2\abs{x} = x^2 - 2x \)
\( x \le -2 \) ise \( \abs{x}^2 - 2\abs{x} = x^2 + 2x \)
Buna göre \( f(\abs{x}) \) fonksiyonunun tanımı aşağıdaki gibi olur.
\( f(\abs{x}) = \begin{cases} x^2 + 2x & x \le -2 \\ -x^2 - 2x & -2 \lt x \lt 0 \\ -x^2 + 2x & 0 \le x \lt 2 \\ x^2 - 2x & x \ge 2 \end{cases} \)
Fonksiyonun \( x = 0 \) noktasındaki sürekliliğini inceleyelim.
\( \lim\limits_{x \to 0^-} f(\abs{x}) = \lim\limits_{x \to 0^-} (-x^2 - 2x) = 0 \)
\( \lim\limits_{x \to 0^+} f(\abs{x}) = \lim\limits_{x \to 0^+} (-x^2 + 2x) = 0 \)
\( f(\abs{0}) = -0^2 + 2(0) = 0 \)
Soldan ve sağdan limit değerleri ve fonksiyon değeri tanımlı ve birbirine eşit olduğu için fonksiyon \( x = 0 \) noktasında süreklidir.
Fonksiyonun \( x = 2 \) noktasındaki sürekliliğini inceleyelim.
\( \lim\limits_{x \to 2^-} f(\abs{x}) = \lim\limits_{x \to 2^-} (-x^2 + 2x) = 0 \)
\( \lim\limits_{x \to 2^+} f(\abs{x}) = \lim\limits_{x \to 2^+} (x^2 - 2x) = 0 \)
\( f(\abs{2}) = 2^2 - 2(2) = 0 \)
Soldan ve sağdan limit değerleri ve fonksiyon değeri tanımlı ve birbirine eşit olduğu için fonksiyon \( x = 2 \) noktasında süreklidir.
Fonksiyonun türev fonksiyonunu bulalım.
\( f'(\abs{x}) = \begin{cases} 2x + 2 & x \le -2 \\ -2x - 2 & -2 \lt x \lt 0 \\ -2x + 2 & 0 \le x \lt 2 \\ 2x - 2 & x \ge 2 \end{cases} \)
Fonksiyonun \( x = 0 \) noktasındaki türevlenebilirliğini inceleyelim.
\( f'(0^-) = -2(0) - 2 = -2 \)
\( f'(0^+) = -2(0) + 2 = 2 \)
Fonksiyon \( x = 0 \) noktasında sürekli olsa da, soldan ve sağdan türev değerleri birbirine eşit olmadığı için bu noktada türevlenebilir değildir.
Fonksiyonun \( x = 2 \) noktasındaki türevlenebilirliğini inceleyelim.
\( f'(2^-) = -2(2) + 2 = -2 \)
\( f'(2^+) = 2(2) - 2 = 2 \)
Fonksiyon \( x = 2 \) noktasında sürekli olsa da, soldan ve sağdan türev değerleri birbirine eşit olmadığı için bu noktada türevlenebilir değildir.
\( f(\abs{x}) \) fonksiyonunun bu iki noktadaki sürekliliği ve türevlenebilirliği aşağıdaki grafik üzerinde de incelenebilir.