Fonksiyon Grafikleri
Bir fonksiyonun birinci ve ikinci türevi fonksiyonun grafiği ve davranışı hakkında önemli bilgiler verir. Bu fonksiyonların en temel yorumu aşağıdaki şekilde özetlenebilir.
| Fonksiyon | Grafik Yorumu |
|---|---|
\( f(x) \) |
Tanım kümesindeki her \( x \) için \( y \) değişkeninin değeri |
\( f'(x) \) |
\( f(x) \) grafiğine belirli bir \( x \) noktasında çizilen teğet doğrunun eğimi ve \( f(x) \) grafiğinin bu noktadaki yönü \( f'(x) \gt 0 \) olduğu aralıkta \( f(x) \) artandır. \( f'(x) \lt 0 \) olduğu aralıkta \( f(x) \) azalandır. \( f'(x) = 0 \) olduğu aralıkta \( f(x) \) sabittir. |
\( f''(x) \) |
\( f'(x) \) grafiğine belirli bir \( x \) noktasında çizilen teğet doğrunun eğimi ve \( f(x) \) grafiğinin bu noktada hangi yönde kıvrıldığı \( f''(x) \gt 0 \) olduğu aralıkta \( f(x) \) eğimi artandır. \( f''(x) \lt 0 \) olduğu aralıkta \( f(x) \) eğimi azalandır. \( f''(x) = 0 \) olduğu aralıkta \( f(x) \) eğimi sabittir. |
Bu bölümde önce fonksiyon grafikleri ile ilgili bazı önemli kavramları inceleyeceğiz, daha sonra bu kavramları ve türev fonksiyonlarını kullanarak grafiklerle ilgili daha detaylı yorumlar yapmaya çalışacağız.
Birinci Türev ve Grafiğin Yönü
Yaptığımız türev tanımına göre; bir fonksiyonun birinci türevinin belirli bir noktadaki değeri, fonksiyonun grafiğine o noktada çizilen teğet doğrunun eğimine eşittir. Dolayısıyla, birinci türevin belirli bir aralıktaki işareti fonksiyonun grafiğinin o aralıktaki yönünü (sabit, artan ya da azalan olmasını) belirler.
Sabit Aralık
Bir fonksiyonun belirli bir aralıkta birinci türevi sıfır ise grafiği bu aralıkta sabittir.
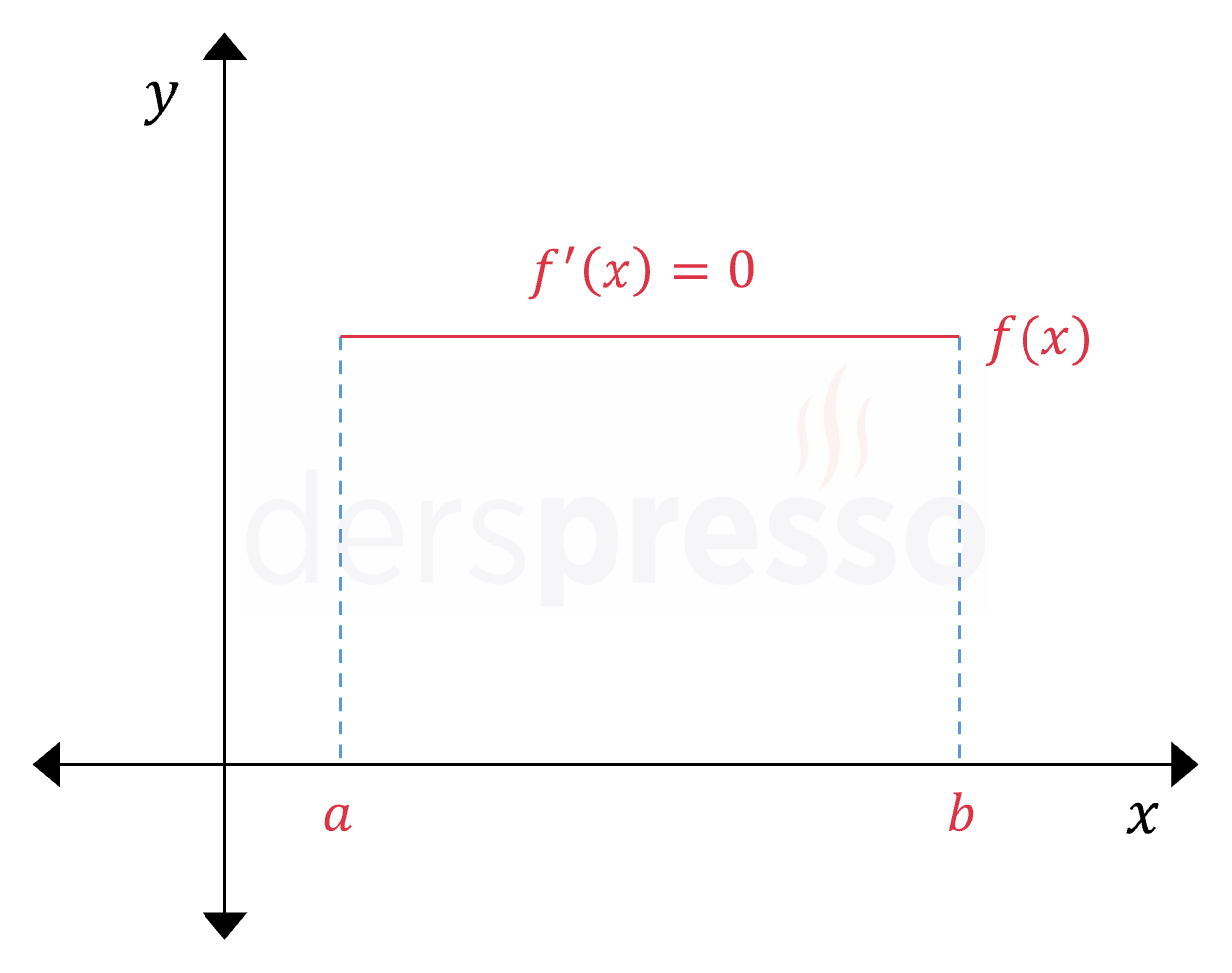
Artan Aralık
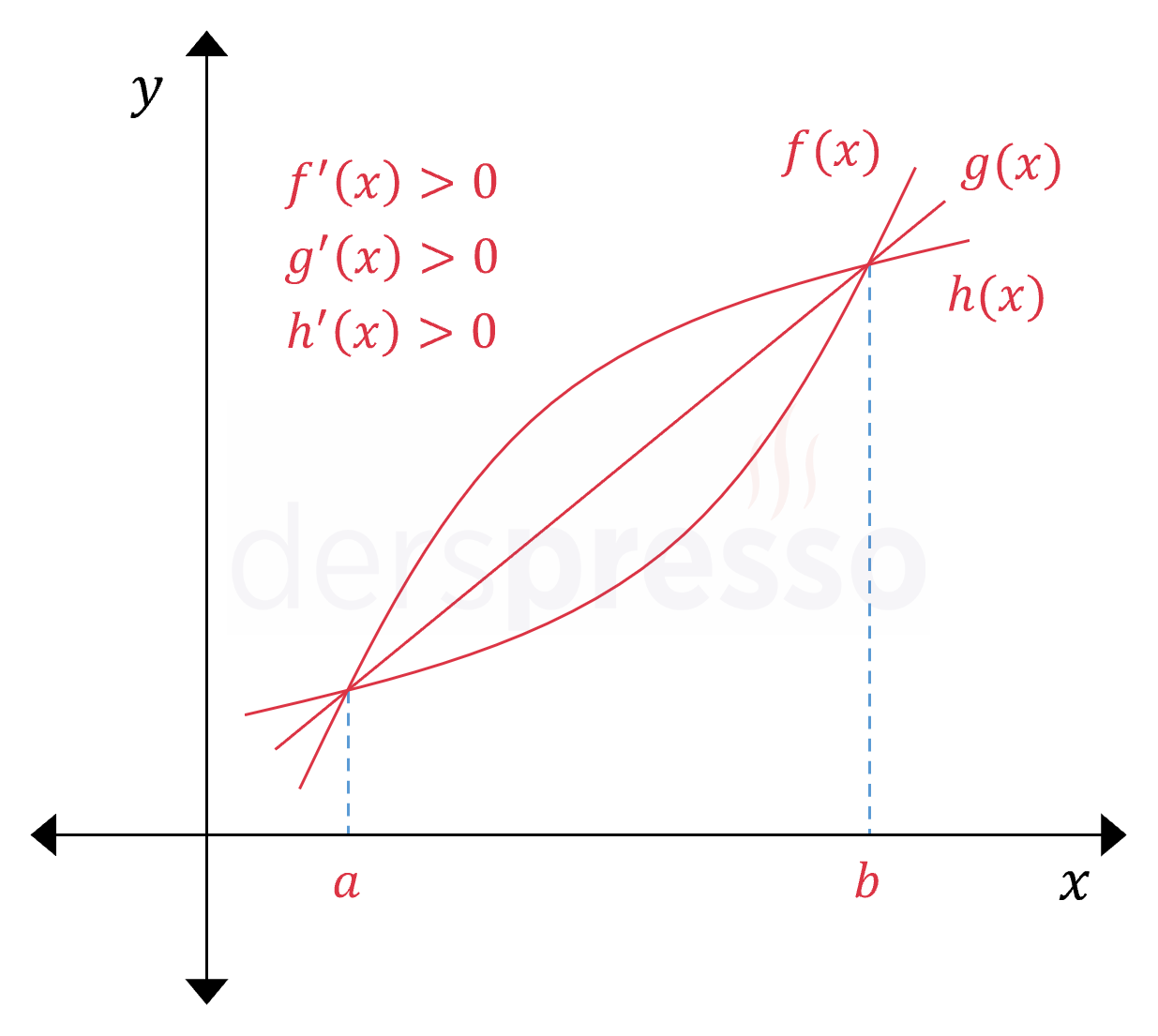
Bir fonksiyonun belirli bir aralıkta birinci türevi pozitif ise grafiği bu aralıkta artandır. Aşağıdaki şekildeki üç fonksiyonun da verilen aralıkta birinci türevleri pozitiftir, dolayısıyla üçü de verilen aralıkta artandır.
Azalan Aralık
Bir fonksiyonun belirli bir aralıkta birinci türevi negatif ise grafiği bu aralıkta azalandır. Aşağıdaki şekildeki üç fonksiyonun da verilen aralıkta birinci türevleri negatiftir, dolayısıyla üçü de verilen aralıkta azalandır.
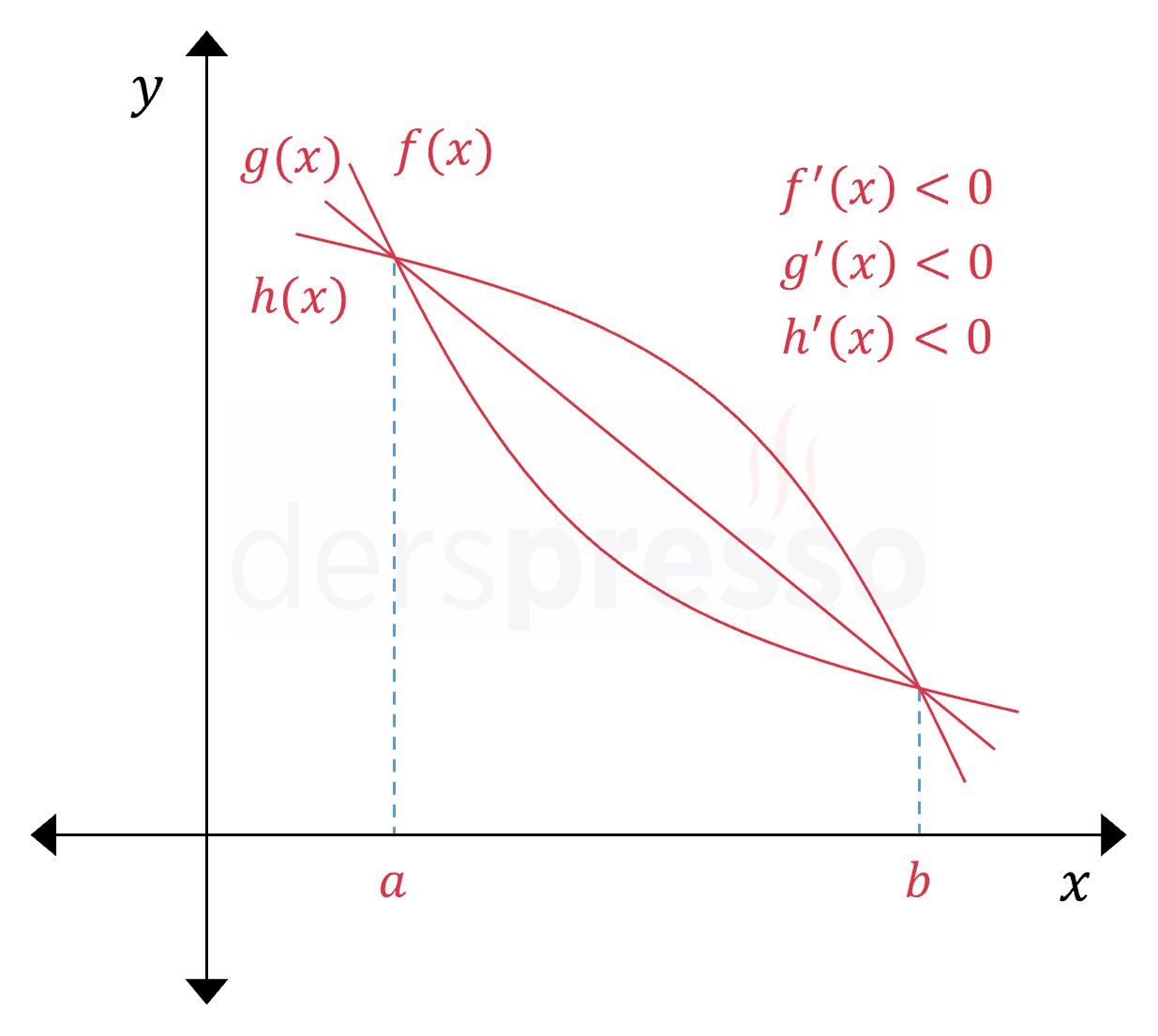
İkinci Türev ve Konkavlık
Konkavlık, bir fonksiyonun grafiğinin belirli bir aralıkta hangi yönde kıvrıldığını gösterir.
Bir fonksiyonun grafiğinin yönü (sabit, artan ya da azalan olması) birinci türevinin işareti ile ilgili iken, konkavlığı ikinci türevinin işareti ile ilgilidir.
Yukarı Konkav (Dışbükey) Aralık
Bir fonksiyonun belirli bir aralıkta eğimi sürekli artıyorsa fonksiyon bu aralıkta yukarı konkavdır (dışbükeydir) ve grafiği \( x \) artarken sola doğru kıvrılır. Yukarı konkav bir grafik (tamamen ya da kısmen) "\( \cup \)" şekli oluşturur.
Yukarı konkav bir eğri şekildeki \( f \) fonksiyonu gibi artan (pozitif eğim ve birinci türev) ya da \( g \) fonksiyonu gibi azalan (negatif eğim ve birinci türev) olabilir, ancak eğimi (birinci türevi) her zaman artandır, dolayısıyla ikinci türevi pozitiftir.
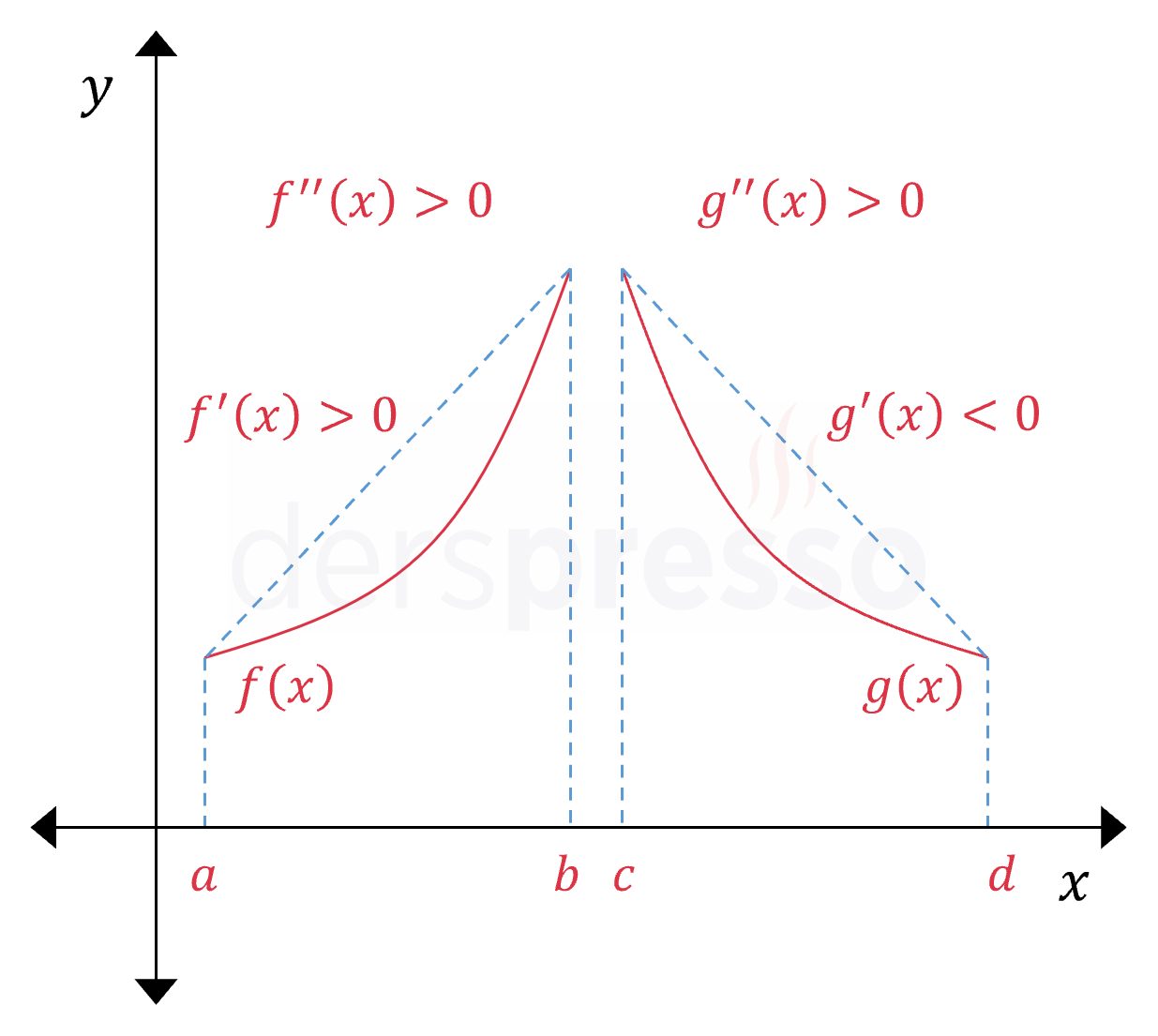
Belirli bir aralıkta yukarı konkav olan bir eğri, bu aralıktaki her noktada eğriye çizilen teğet doğruların üstünde kalır.
Aşağı Konkav (İçbükey) Aralık
Bir fonksiyonun belirli bir aralıkta eğimi sürekli azalıyorsa fonksiyon bu aralıkta aşağı konkavdır (içbükeydir) ve grafiği \( x \) artarken sağa doğru kıvrılır. Aşağı konkav bir grafik (tamamen ya da kısmen) "\( \cap \)" şekli oluşturur.
Aşağı konkav bir eğri şekildeki \( f \) fonksiyonu gibi artan (pozitif eğim ve birinci türev) ya da \( g \) fonksiyonu gibi azalan (negatif eğim ve birinci türev) olabilir, ancak eğimi (birinci türevi) her zaman azalandır, dolayısıyla ikinci türevi negatiftir.

Belirli bir aralıkta aşağı konkav olan bir eğri, bu aralıktaki her noktada eğriye çizilen teğet doğruların altında kalır.
\( f(x) = x^4 - 4x^3 + 6x + 1 \) fonksiyonunun yukarı ve aşağı konkav olduğu aralıkları bulalım.
Bir fonksiyonun grafiğinin yukarı konkav olduğu bir aralıkta ikinci türevi pozitiftir (yani birinci türevi artandır).
Bir fonksiyonun grafiğinin aşağı konkav olduğu bir aralıkta ikinci türevi negatiftir (yani birinci türevi azalandır).
Fonksiyonun birinci ve ikinci türevlerini bulalım.
\( f'(x) = 4x^3 - 12x^2 + 6 \)
\( f''(x) = 12x^2 - 24x \)
\( = 12x(x - 2) \)
İkinci türevin farklı aralıklardaki işaretini bulmak için bir işaret tablosu hazırlayalım.

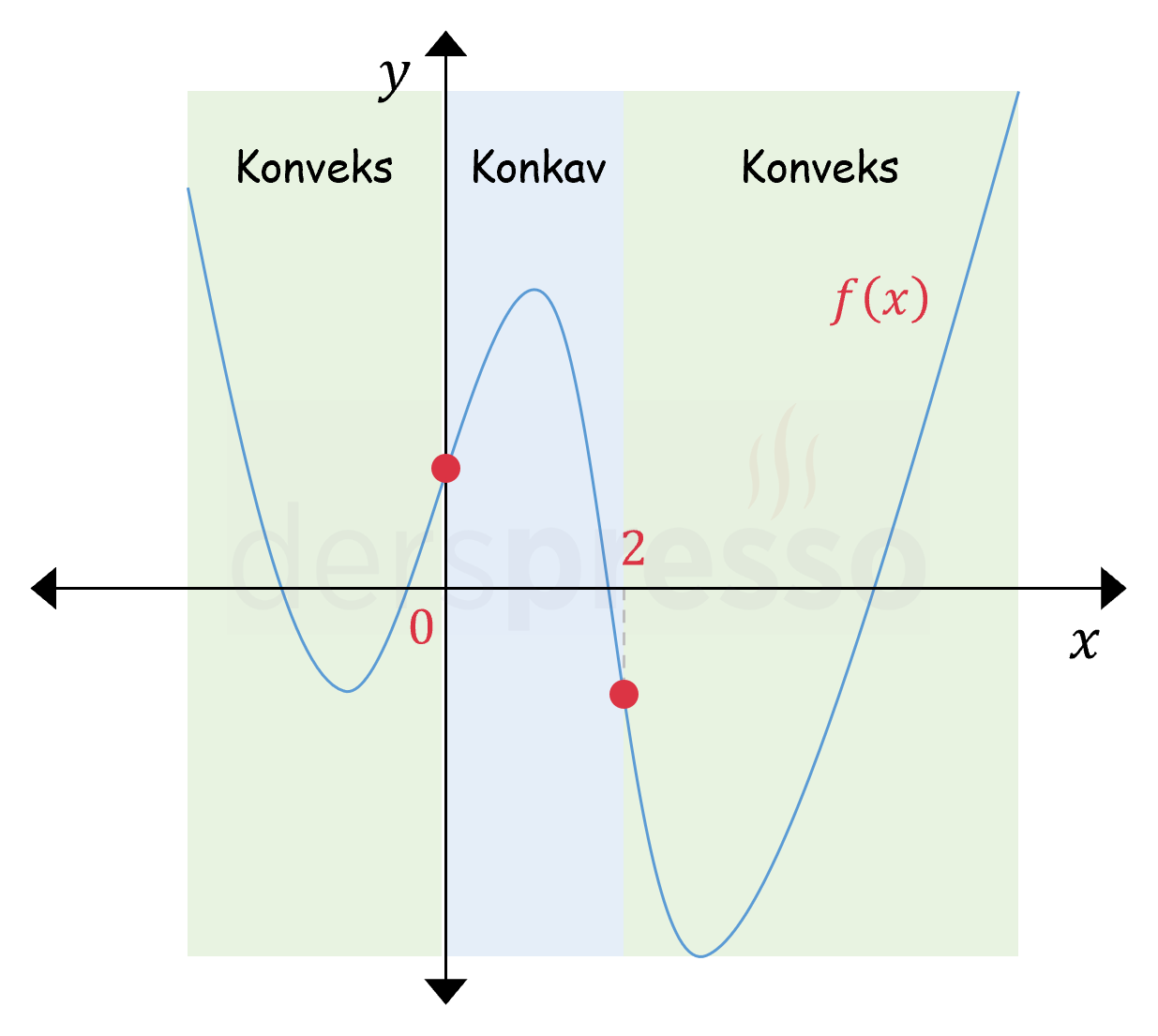
\( (-\infty, 0) \) ve \( (2, \infty) \) aralıklarında ikinci türev pozitiftir, dolayısıyla fonksiyon yukarı konkavdır.
\( (0, 2) \) aralığında ikinci türev negatiftir, dolayısıyla fonksiyon aşağı konkavdır.
Aşağıdaki şekilde fonksiyonun yukarı ve aşağı konkav olduğu aralıklar görülebilir.
Örnek Grafikler
Yukarıda verdiğimiz bilgiler doğrultusunda, bazı temel fonksiyonların grafikleri ve birinci/ikinci türevleri ile ilişkileri aşağıda gösterilmiştir.
| Grafik | Açıklama |
|---|---|

|
Sabit Aralık Ana fonksiyonun değeri sabittir. Ana fonksiyonun eğimi sabit ve sıfır olduğu için birinci türev de sabit ve sıfırdır (\( f'(x) = 0 \)). Birinci türevin eğimi sabit ve sıfır olduğu için ikinci türev de sabit ve sıfırdır (\( f''(x) = 0 \)). |
|
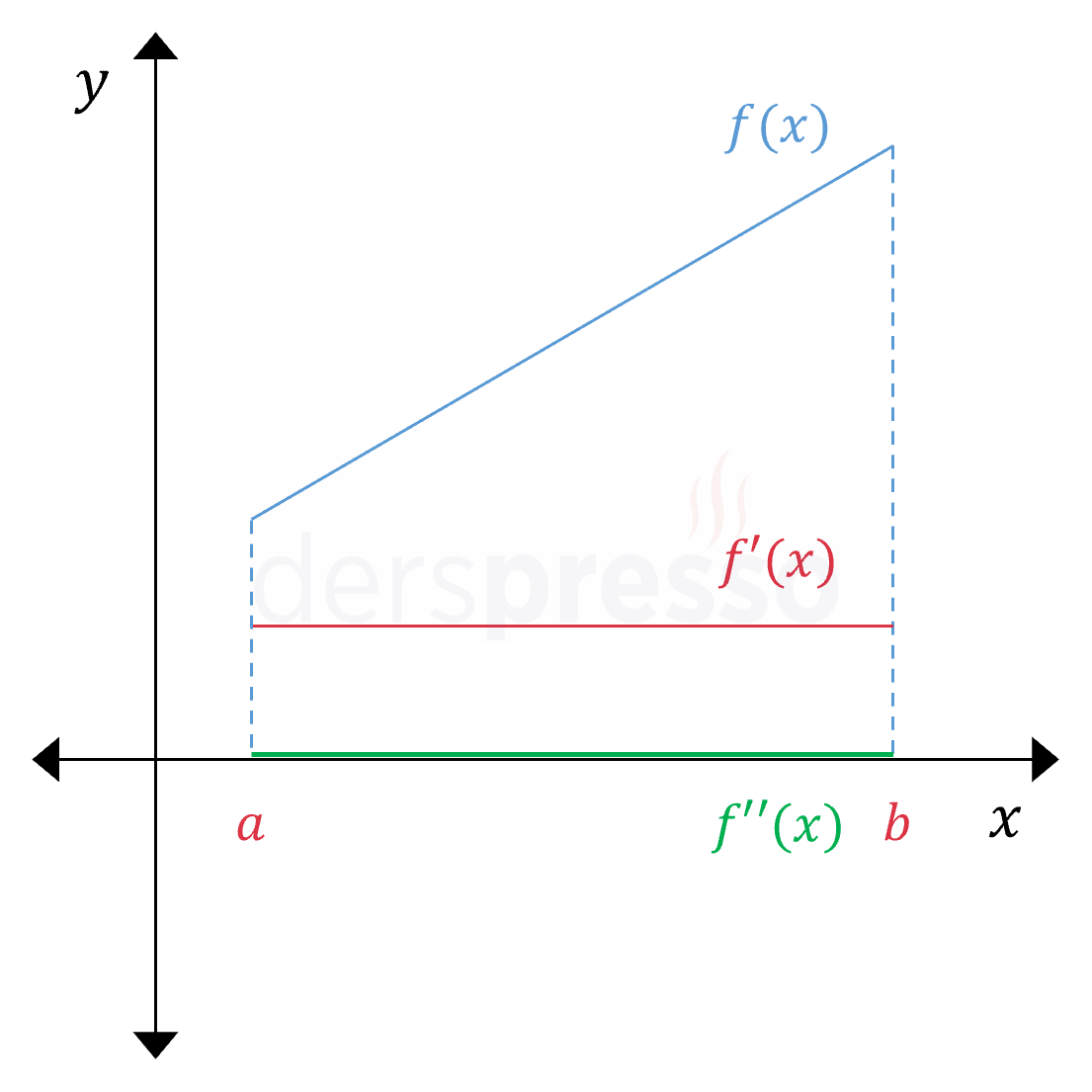
Doğrusal Artan Aralık Ana fonksiyonun değeri doğrusal bir şekilde artar. Ana fonksiyonun eğimi sabit ve pozitif olduğu için birinci türev de sabit ve pozitiftir (\( f'(x) \gt 0 \)). Birinci türevin eğimi sabit ve sıfır olduğu için ikinci türev de sabit ve sıfırdır (\( f''(x) = 0 \)). |
|
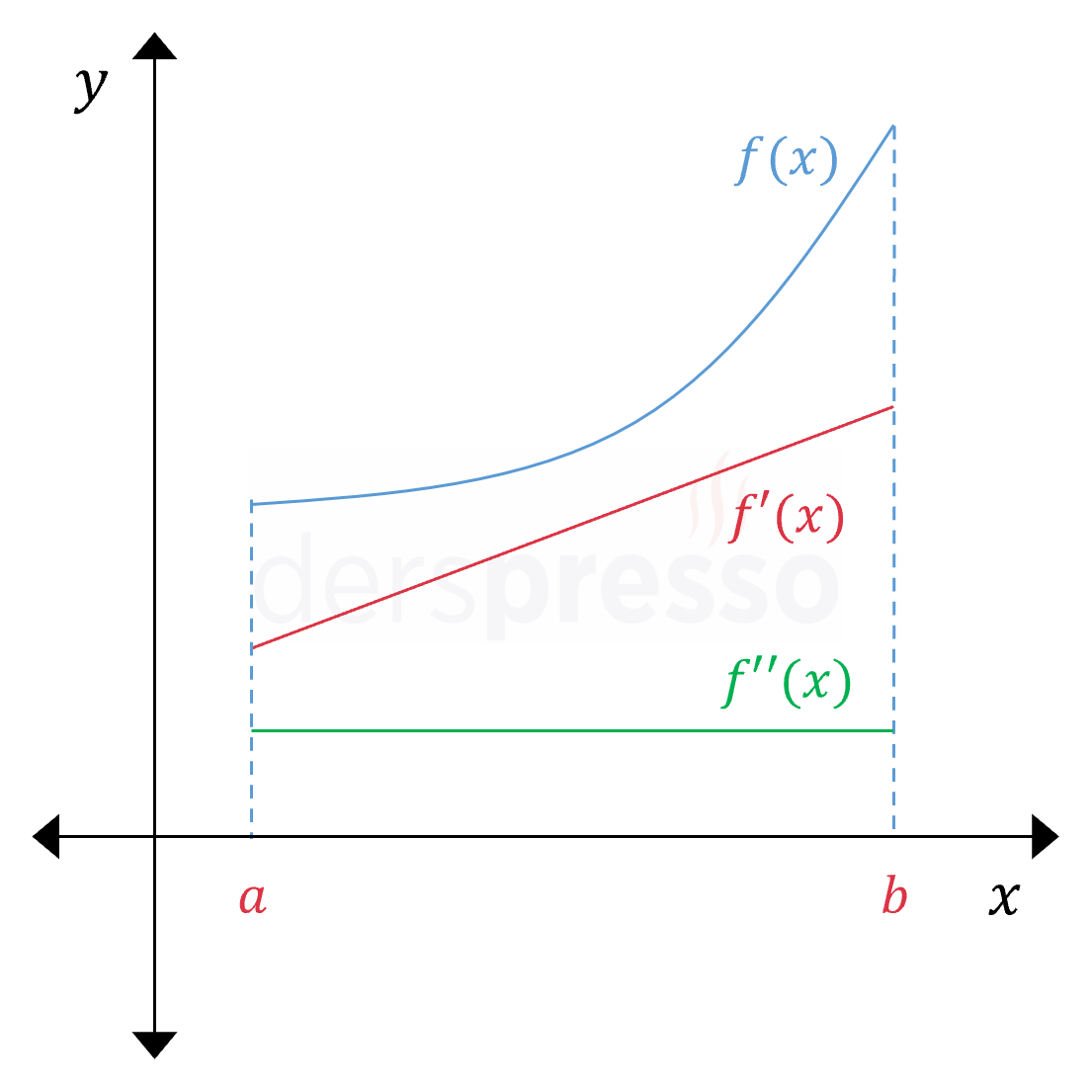
Yukarı Konkav Artan Aralık Ana fonksiyonun değeri artan bir hızla artar. Ana fonksiyonun eğimi pozitif ve artan olduğu için birinci türev de pozitif ve artandır (\( f'(x) \gt 0 \)). Birinci türev artan olduğu için ikinci türev pozitiftir (\( f''(x) \gt 0 \)). NOT: Ana fonksiyonun grafiğine göre, birinci türevin grafiği pozitif ve artan olmak koşuluyla doğrusal ya da eğrisel olabilir. Buna bağlı olarak ikinci türevin grafiği pozitif tarafta kalmak koşuluyla artan ya da azalan, doğrusal ya da eğrisel olabilir. |
|
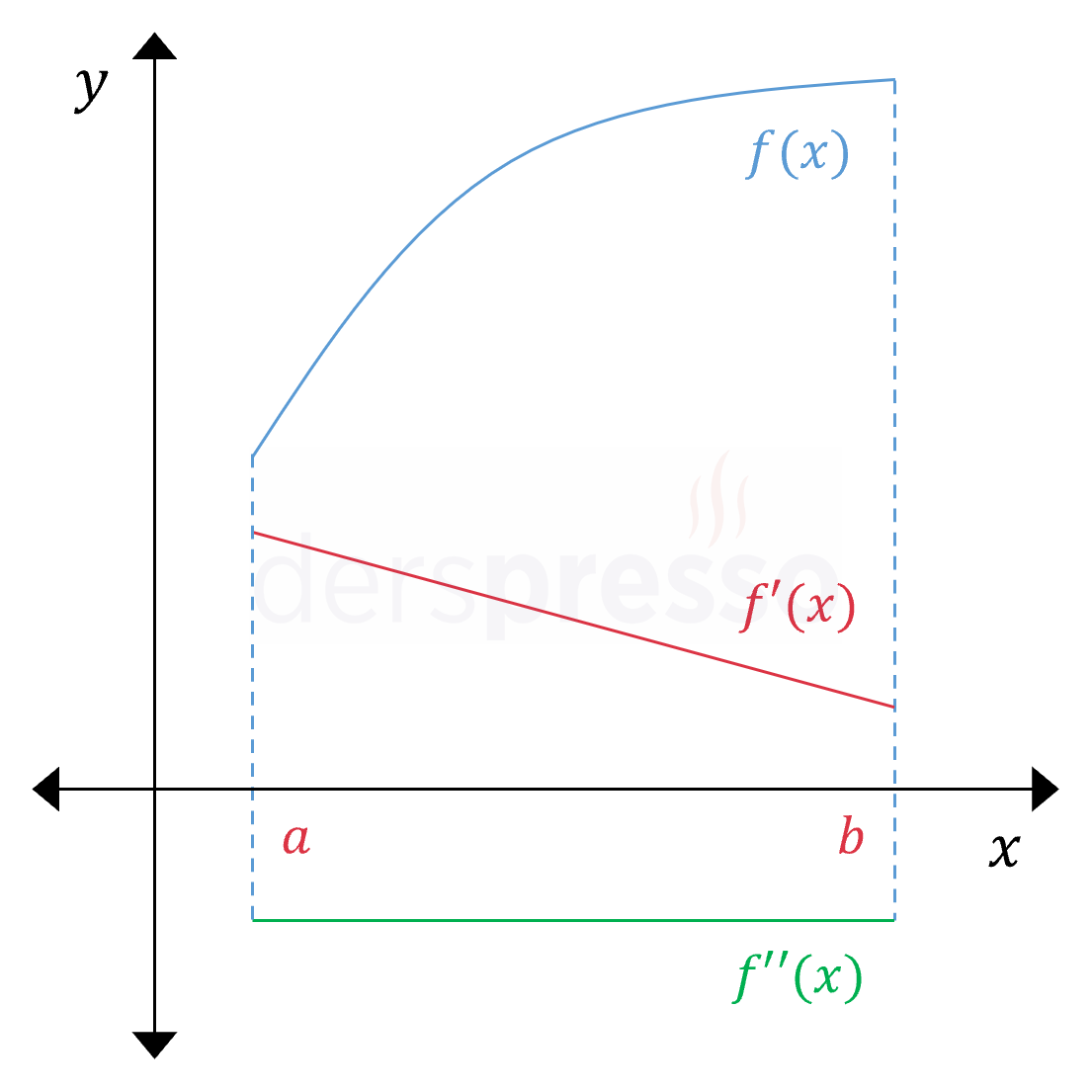
Aşağı Konkav Artan Aralık Ana fonksiyonun değeri azalan bir hızla artar. Ana fonksiyonun eğimi pozitif ve azalan olduğu için birinci türev de pozitif ve azalandır (\( f'(x) \gt 0 \)). Birinci türev azalan olduğu için ikinci türev negatiftir (\( f''(x) \lt 0 \)). Yukarıda paylaştığımız not bu grafik için de geçerlidir. |
|
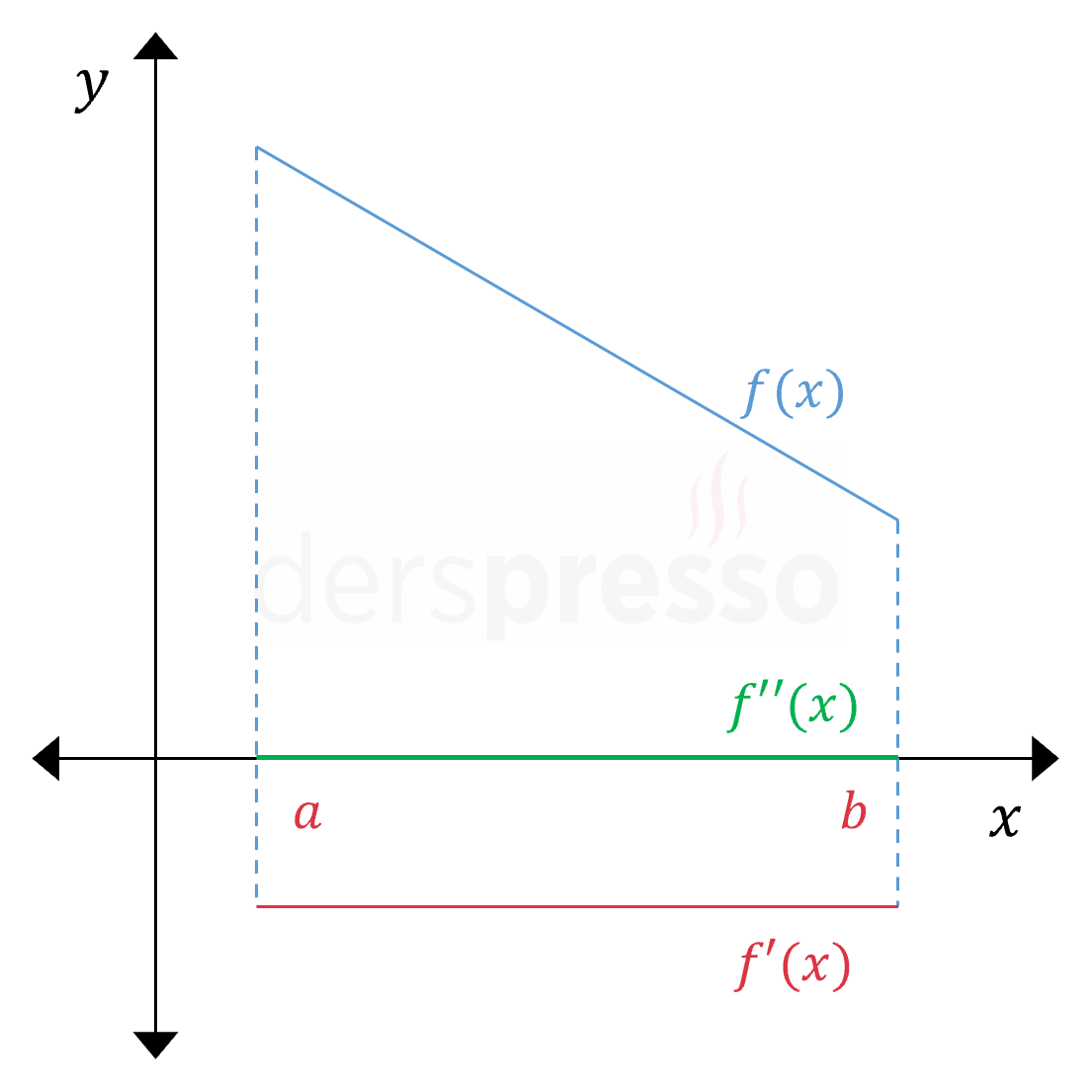
Doğrusal Azalan Aralık Ana fonksiyonun değeri doğrusal bir şekilde azalır. Ana fonksiyonun eğimi sabit ve negatif olduğu için birinci türev de sabit ve negatiftir (\( f'(x) \lt 0 \)). Birinci türevin eğimi sabit ve sıfır olduğu için ikinci türev de sabit ve sıfırdır (\( f''(x) = 0 \)). |
|
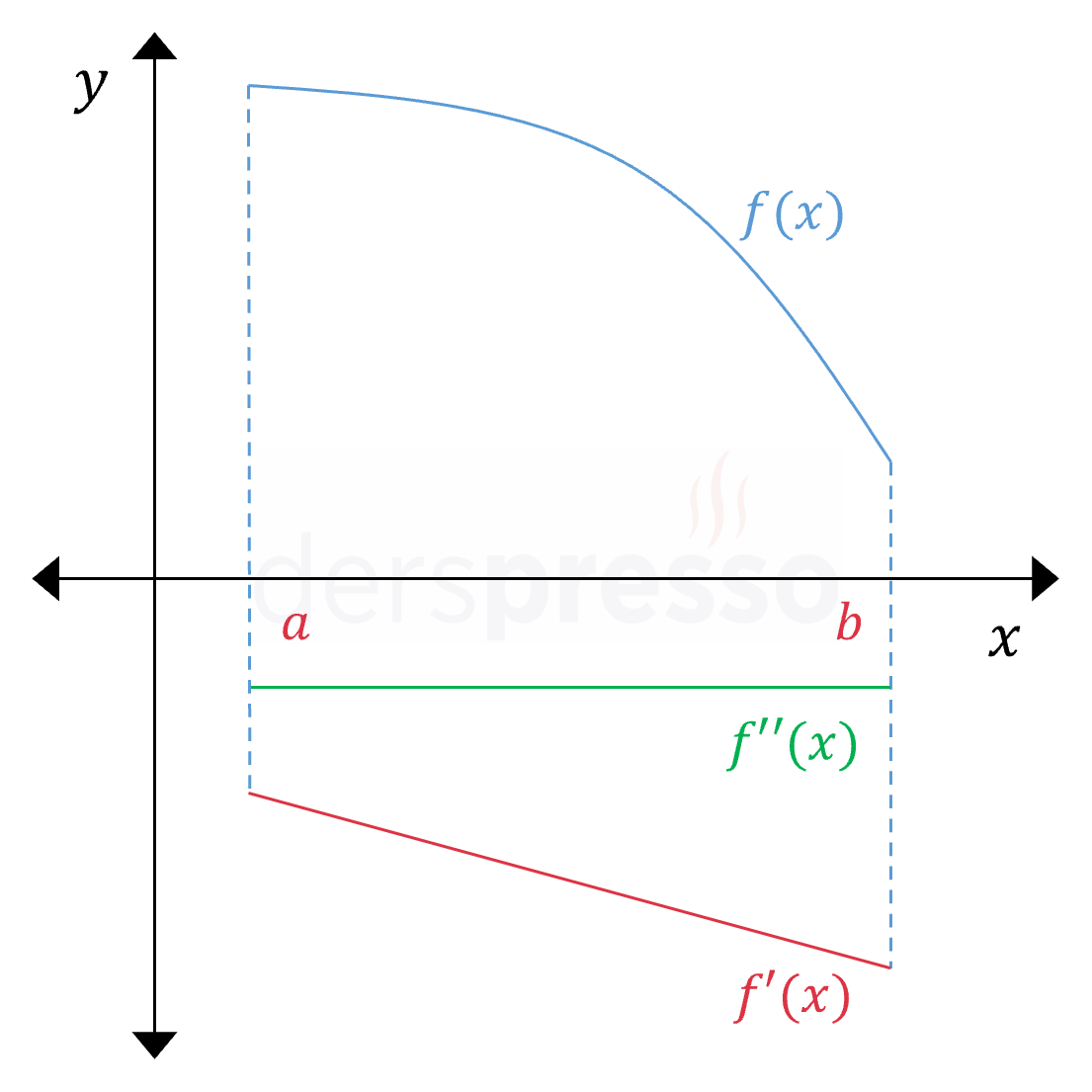
Aşağı Konkav Azalan Aralık Ana fonksiyonun değeri artan bir hızla azalır. Ana fonksiyonun eğimi negatif ve azalan olduğu için birinci türev de negatif ve azalandır (\( f'(x) \lt 0 \)). Birinci türev azalan olduğu için ikinci türev negatiftir (\( f''(x) \lt 0 \)). Yukarıda paylaştığımız not bu grafik için de geçerlidir. |
|
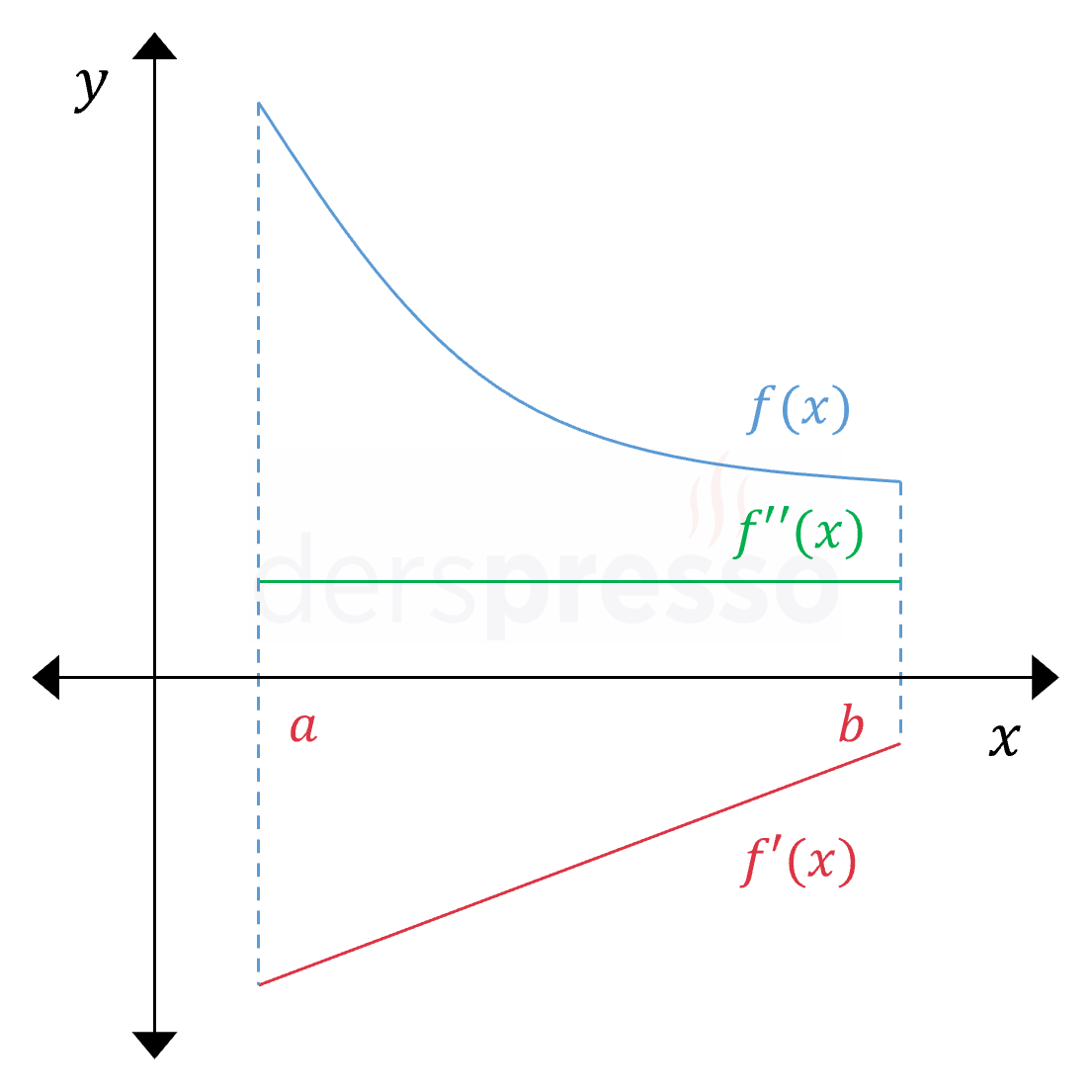
Yukarı Konkav Azalan Aralık Ana fonksiyonun değeri azalan bir hızla azalır. Ana fonksiyonun eğimi negatif ve artandır, dolayısıyla birinci türev de negatif ve artandır (\( f'(x) \lt 0 \)). Birinci türev artan olduğu için ikinci türev pozitiftir (\( f''(x) \gt 0 \)). Yukarıda paylaştığımız not bu grafik için de geçerlidir. |
|
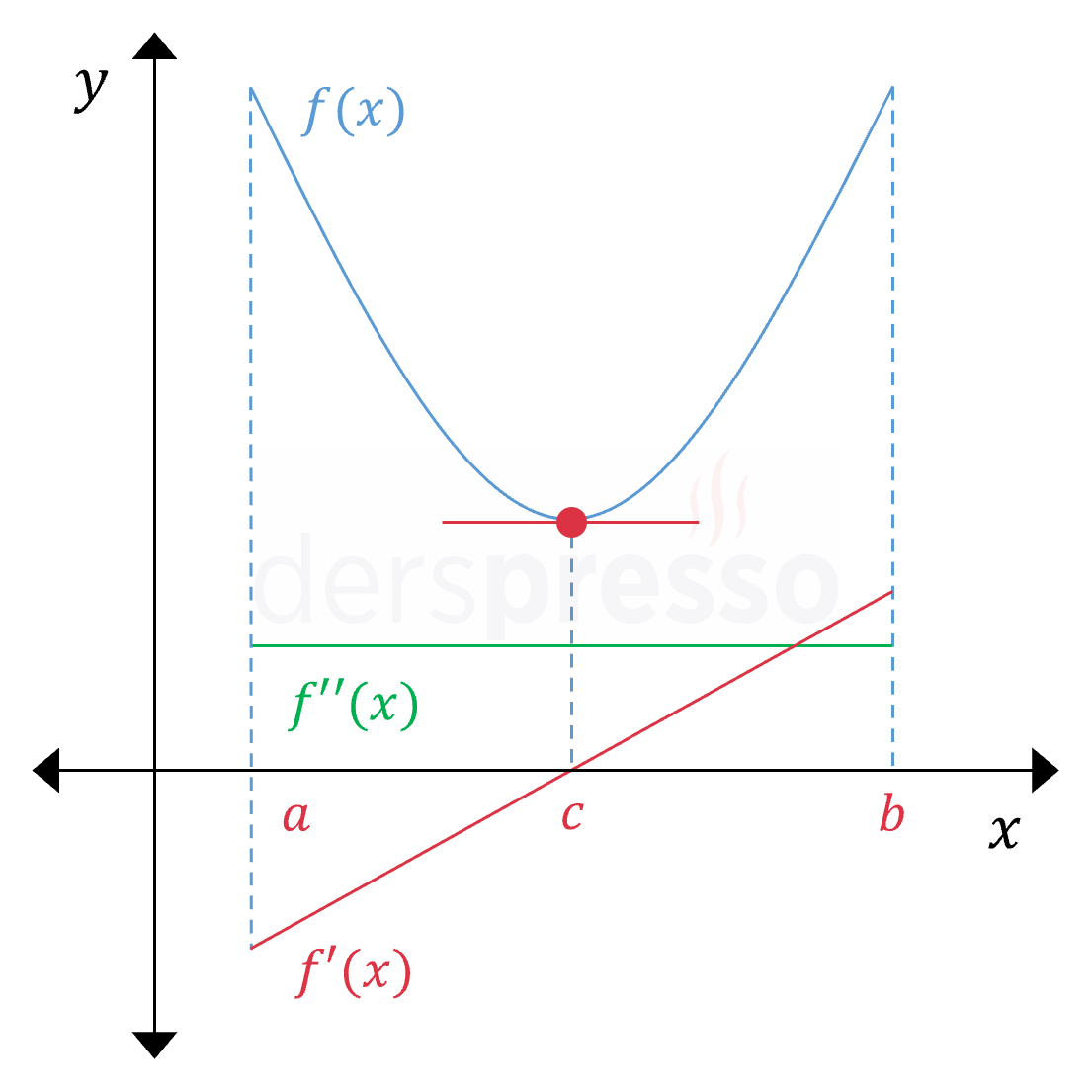
Önce Azalan Sonra Artan Aralık Ana fonksiyonun değeri \( (a, c) \) aralığında azalan bir hızla azalır, \( (c, b) \) aralığında ise artan bir hızla artar. Ana fonksiyonun eğimi \( (a, c) \) aralığında negatif, \( c \) noktasında sıfır, \( (c, b) \) aralığında pozitiftir ve tüm aralıkta artandır. Birinci türev tüm aralıkta artan olduğu için ikinci türev pozitiftir (\( f''(x) \gt 0 \)). Yukarıda paylaştığımız not bu grafik için de geçerlidir. |
|
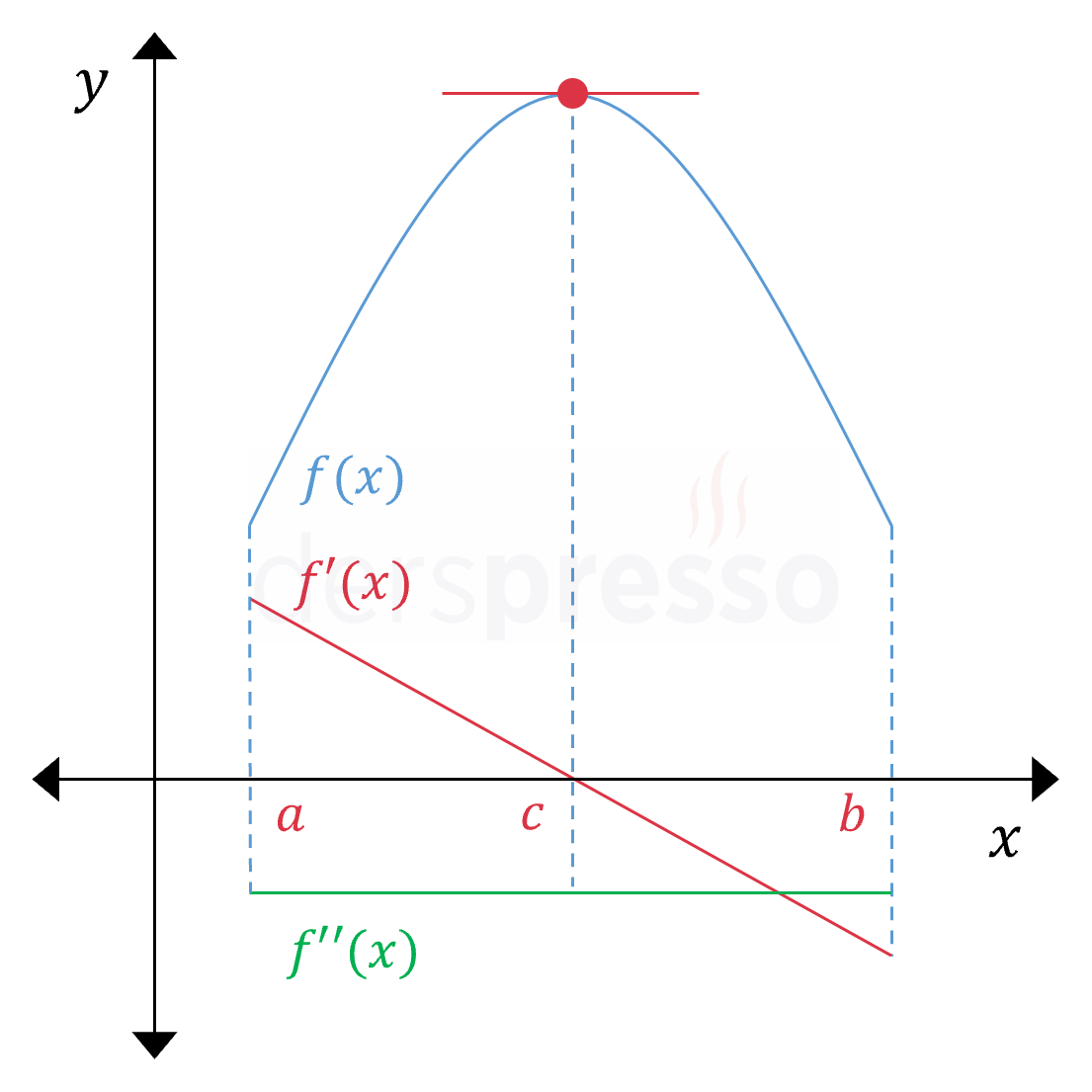
Önce Artan Sonra Azalan Aralık Ana fonksiyonun değeri \( (a, c) \) aralığında azalan bir hızla artar, \( (c, b) \) aralığında ise artan bir hızla azalır. Ana fonksiyonun eğimi \( (a, c) \) aralığında pozitif, \( c \) noktasında sıfır, \( (c, b) \) aralığında negatiftir ve tüm aralıkta azalandır. Birinci türev tüm aralıkta azalan olduğu için ikinci türev negatiftir (\( f''(x) \lt 0 \)). Yukarıda paylaştığımız not bu grafik için de geçerlidir. |