Mutlak Minimum ve Maksimum Noktaları
Bir fonksiyonun tanım kümesi içinde aldığı en küçük değere fonksiyonun mutlak minimum değeri, bu değeri aldığı nokta ya da noktalara mutlak minimum noktası denir.
Bir fonksiyonun tanım kümesi içinde aldığı en büyük değere fonksiyonun mutlak maksimum değeri, bu değeri aldığı nokta ya da noktalara mutlak maksimum noktası denir.
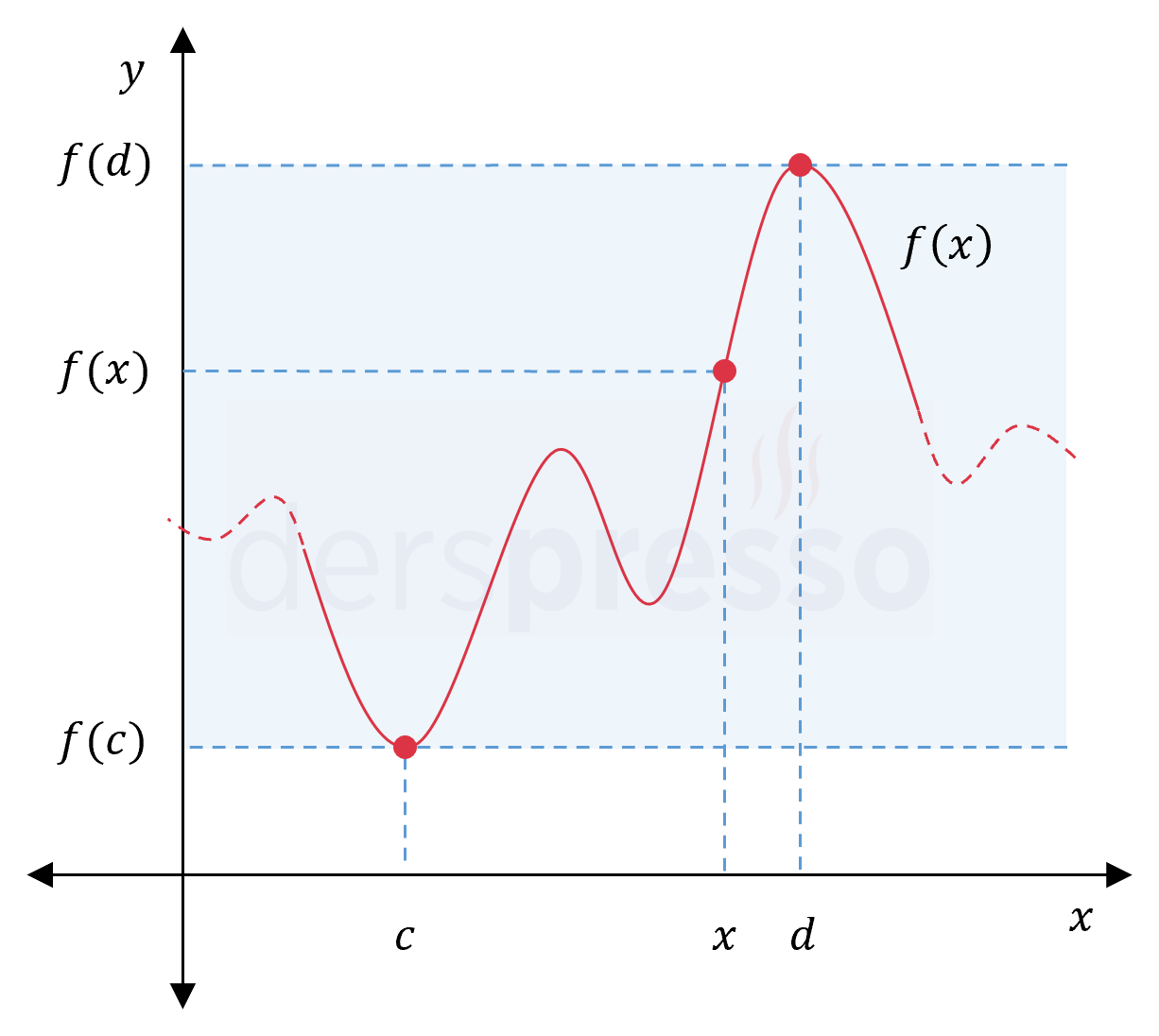
\( f: D \to \mathbb{R} \) olmak üzere,
Her \( x \in D \) için \( f(c) \le f(x) \) ise,
\( f(c) \) fonksiyonun mutlak minimum değeri, \( x = c \) fonksiyonun mutlak minimum noktasıdır.
Her \( x \in D \) için \( f(x) \le f(d) \) ise,
\( f(d) \) fonksiyonun mutlak maksimum değeri, \( x = d \) fonksiyonun mutlak maksimum noktasıdır.
Bir fonksiyonun mutlak minimum ve maksimum noktalarına genel bir terim olarak mutlak ekstremum noktaları da denir.
Bir fonksiyonun aşağıda birer örneği verilen iki sebeple mutlak minimum ya da maksimum noktası bulunmayabilir.
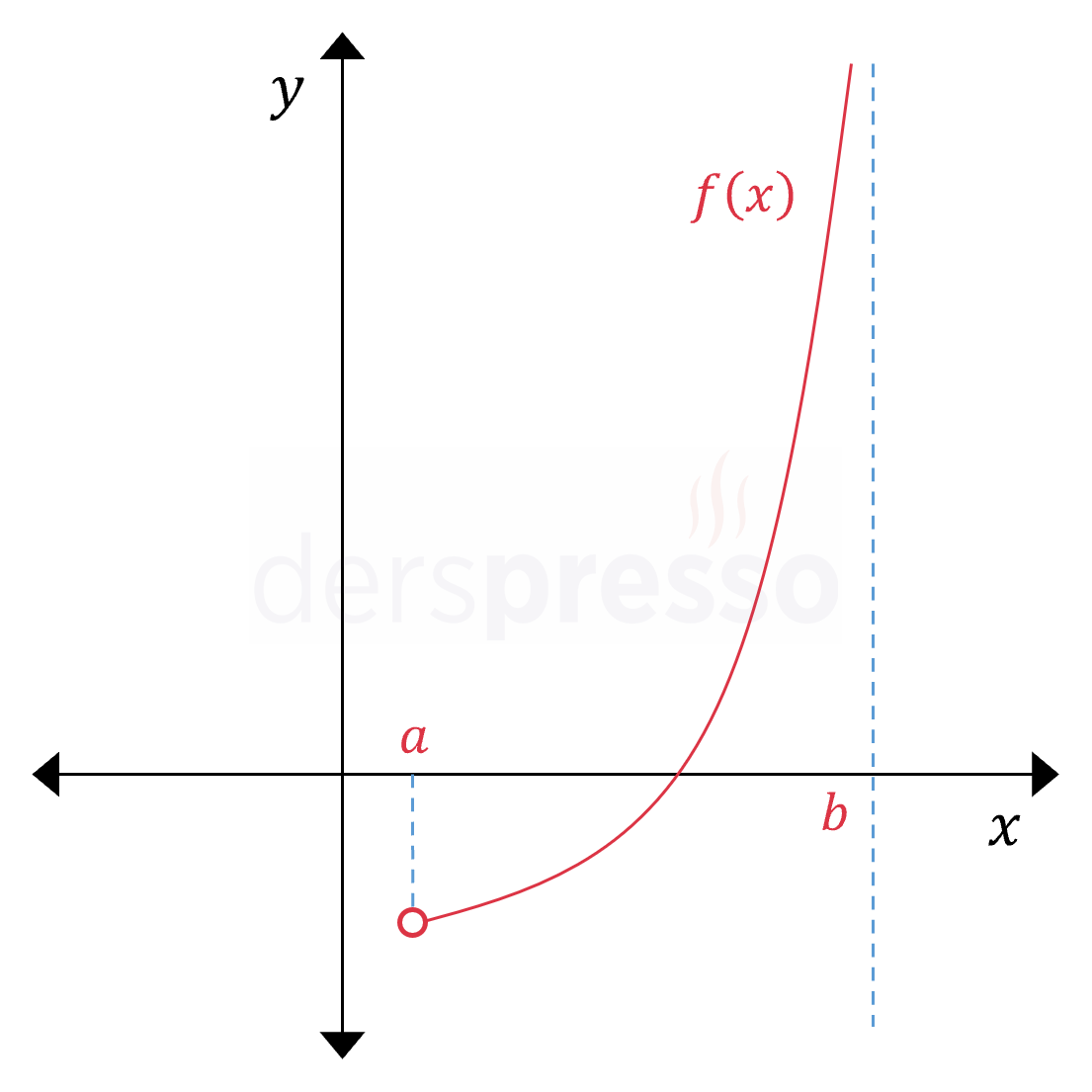
- Fonksiyon pozitif ya da negatif sonsuza gider: \( f \) fonksiyonu \( x = b \) noktasına soldan yaklaşırken değeri pozitif sonsuza gider ve hiçbir noktada fonksiyonun en büyük değeri denebilecek reel sayı bir değer almaz, dolayısıyla fonksiyonun mutlak maksimum noktası yoktur.
- Fonksiyon bir minimum ya da maksimum değere yaklaşır ama o değeri almaz: \( f \) fonksiyonu \( x = a \) noktasına sağdan yaklaşırken değeri \( c \) değerine yaklaşır ama bu değeri almaz ve hiçbir noktada fonksiyonun en küçük değeri denebilecek reel sayı bir değer almaz, dolayısıyla fonksiyonun mutlak minimum noktası yoktur.
Bir fonksiyonun yerel minimum (maksimum) noktalarının olması, mutlak minimum (maksimum) noktalarının da olmasını gerektirmez, Örneğin \( (a, \infty) \) aralığında tanımlı aşağıdaki fonksiyonun \( x = b \) ve \( x = c \) noktalarında sırasıyla yerel maksimum ve minimum noktaları olsa da, mutlak minimum/maksimum noktaları yoktur.
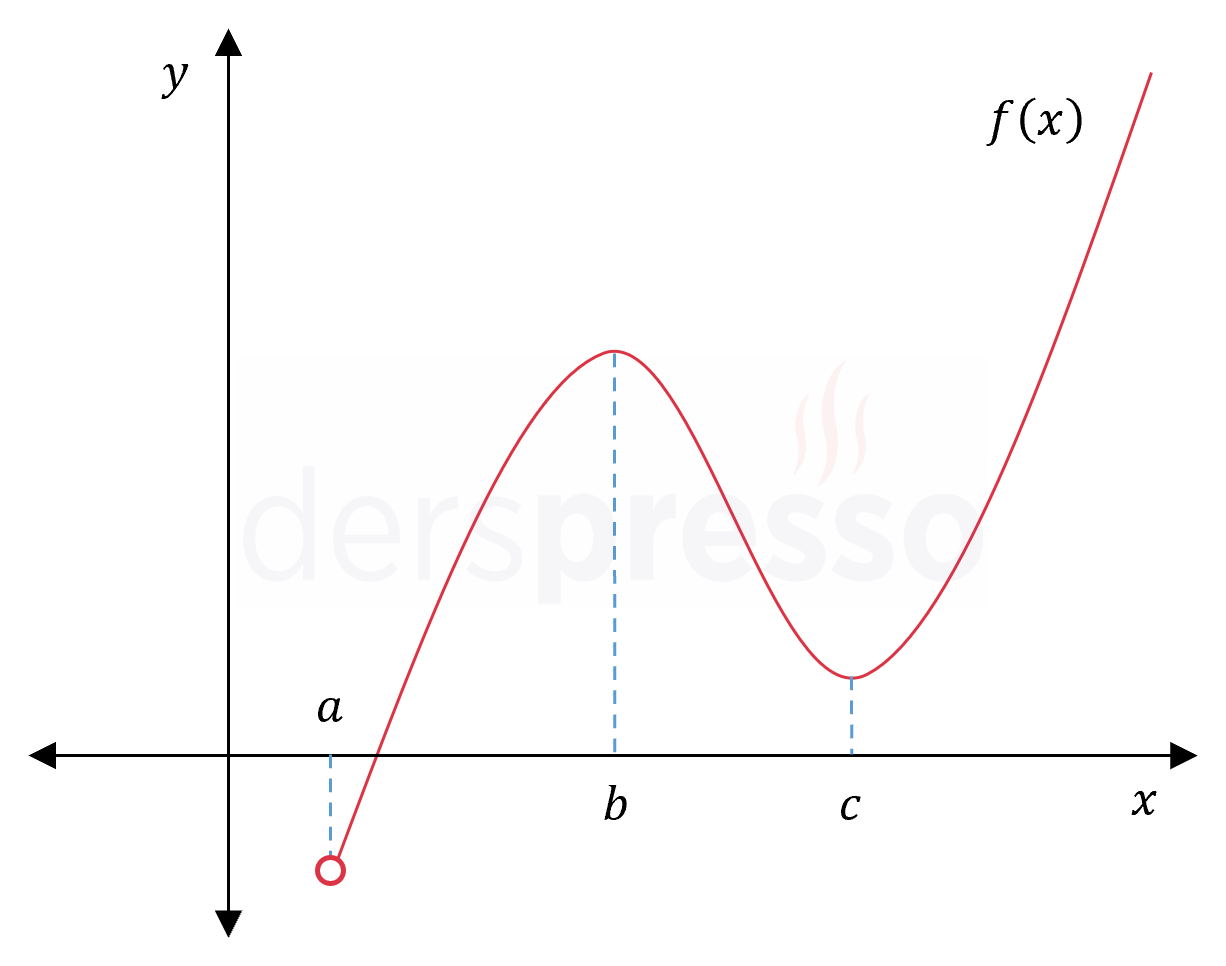
Bunun bir sonucu olarak, bir fonksiyonun yerel minimum (maksimum) noktaları içinde en küçük (büyük) değere sahip olan nokta her durumda fonksiyonun mutlak minimum (maksimum) noktası olarak belirlenemez.
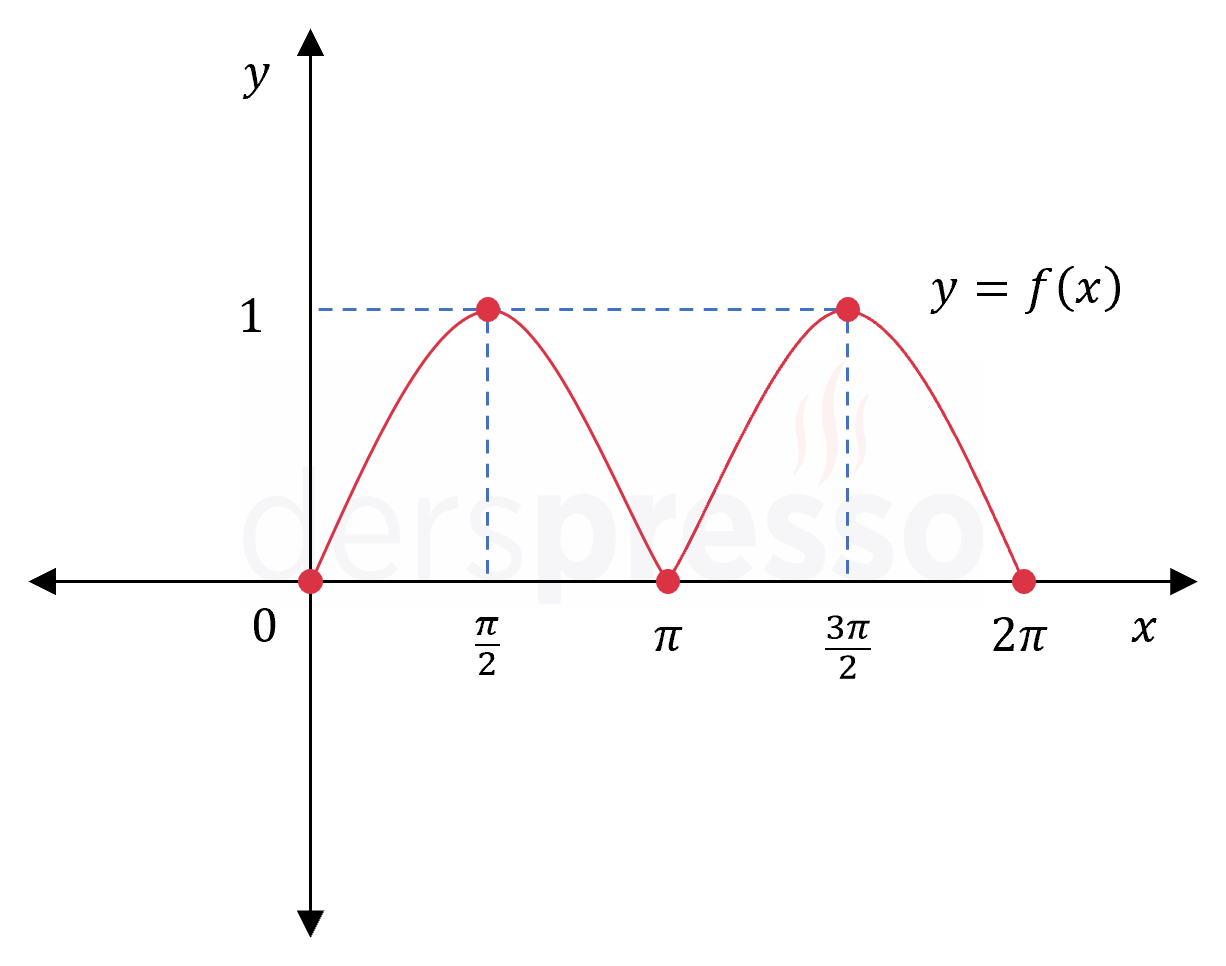
Aşağıdaki periyodik fonksiyon örneğinde görülebileceği üzere, bir fonksiyon mutlak minimum ve maksimum değerlerini birden fazla (hatta sonsuz) sayıda noktada alabilir.
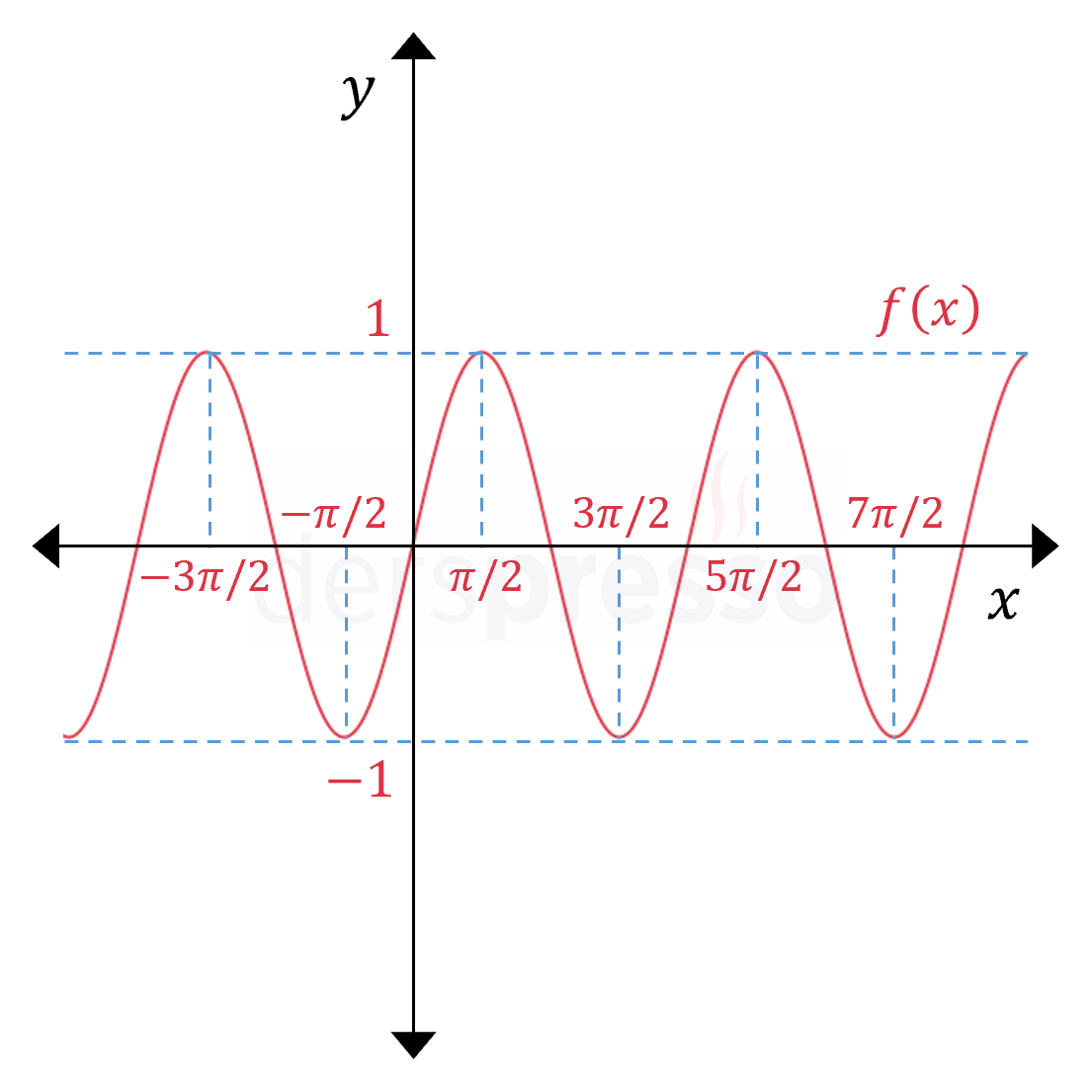
Mutlak minimum ve maksimum noktalarının bulunma yöntemini, (1) fonksiyonun kapalı aralıkta tanımlı ve sürekli olduğu durum ve (2) diğer durumlar için ayrı ayrı incelememiz gerekir.
Kapalı Aralıkta Tanımlı, Sürekli Fonksiyonlar
Uç Değer Teoremi
Uç değer teoremi, kapalı bir aralıkta tanımlı ve sürekli bir fonksiyonun mutlak minimum ve maksimum değerlerinin ve noktalarının varlığını garanti eder. Bir diğer ifadeyle; \( [a, b] \) kapalı aralığında tanımlı ve sürekli bir \( f \) fonksiyonu, bu aralıkta en az bir kez mutlak minimum ve en az bir kez mutlak maksimum değeri alır.
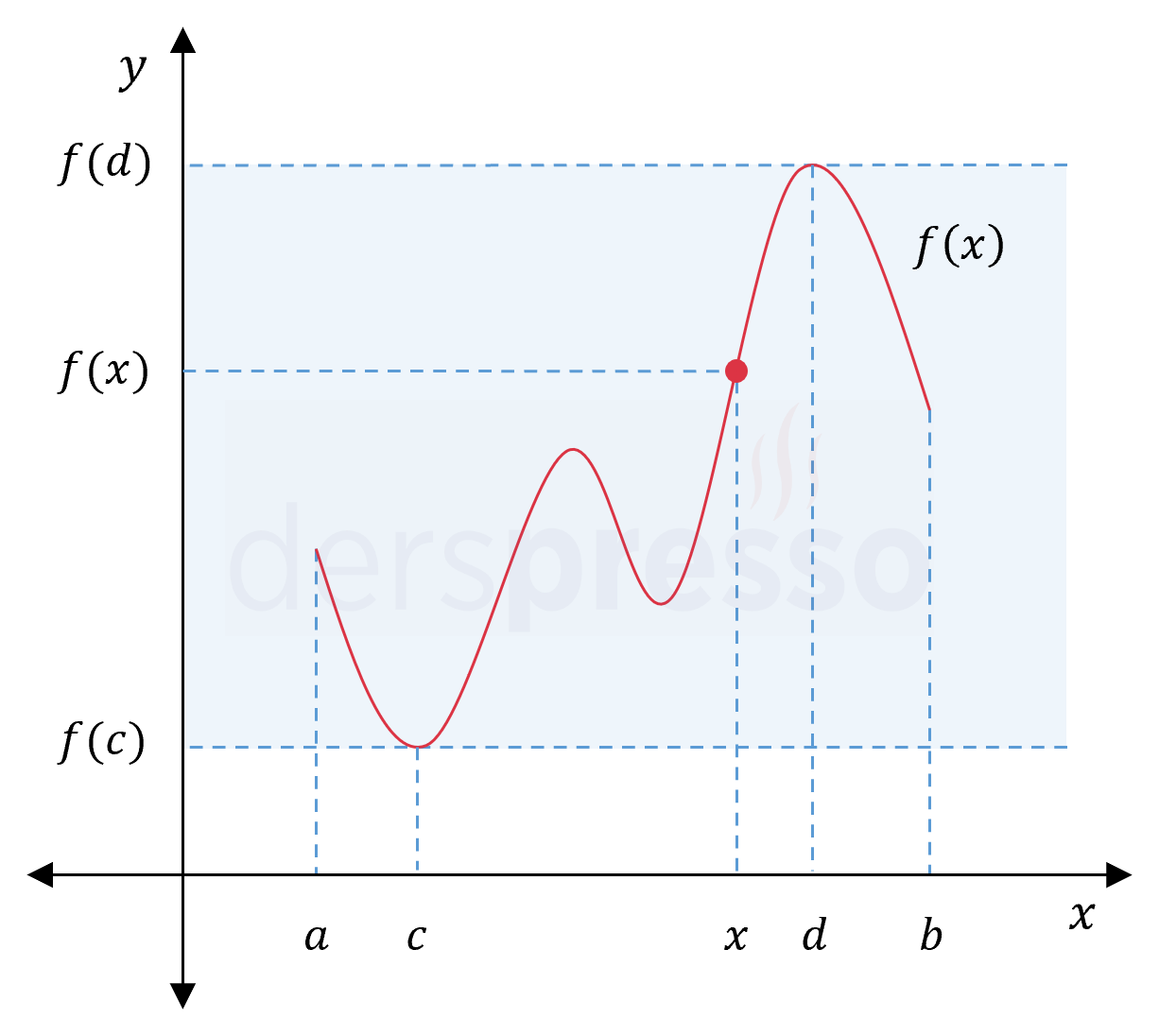
\( f \) fonksiyonu \( [a, b] \) kapalı aralığında tanımlı ve sürekli ise,
Her \( x \in [a, b] \) değeri için aşağıdaki koşulu sağlayan en az bir \( c \) ve en az bir \( d \) değeri vardır.
\( f(c) \le f(x) \le f(d) \)
Bu durumda \( x = c \) ve \( x = d \) noktaları sırasıyla fonksiyonun mutlak minimum ve maksimum noktaları, \( f(c) \) ve \( f(d) \) değerleri de mutlak minimum ve maksimum değerleri olur.
Kapalı bir aralıkta tanımlı ve sürekli bir fonksiyonun mutlak minimum ve maksimum noktaları aşağıdaki noktalardan birinde oluşur.
- Kritik noktalar
- Tanım aralığının kapalı uç noktaları
Buna göre bu koşulları sağlayan bir fonksiyonun mutlak minimum ve maksimum noktaları aşağıdaki adımlar takip edilerek bulunur.
- Fonksiyonun tanım aralığındaki kritik noktalar bulunur.
- Kritik ve kapalı uç noktalardaki fonksiyon değerleri bulunur.
- Bulunan değerlerden en küçüğü (en büyüğü) mutlak minimum (maksimum) değeri, fonksiyonun bu değeri aldığı nokta ya da noktalar da mutlak minimum (maksimum) noktaları olur.
Bu tip fonksiyonların mutlak ekstremum noktalarını bulmayı bir örnek üzerinde gösterelim.
\( x \in [-2, 6] \) olmak üzere,
\( f(x) = x^3 - 3x^2 - 9x + 5 \)
fonksiyonunun mutlak minimum ve maksimum değerlerini ve noktalarını bulalım.
\( f \) fonksiyonu kapalı bir aralıkta tanımlıdır ve bir polinom fonksiyonu olduğu için süreklidir.
Kapalı bir aralıkta tanımlı ve sürekli bir fonksiyon, mutlak minimum ve maksimum değerlerini kritik ya da kapalı uç noktalarından birinde alır.
Fonksiyonun kritik noktaları birinci türevin sıfır ya da tanımsız olduğu iç noktalardır.
\( f'(x) = 3x^2 - 6x - 9 \)
Fonksiyonun birinci türevinin sıfır olduğu iç noktaları bulalım.
\( 3(x + 1)(x - 3) = 0 \)
\( x \in \{ -1, 3 \} \)
Fonksiyonun birinci türevinin tanımsız olduğu iç nokta yoktur.
Kritik noktalar: \( x \in \{ -1, 3 \} \)
Fonksiyonun kritik noktalardaki değerini bulalım.
\( f(-1) = (-1)^3 - 3(-1)^2 - 9(-1) + 5 = 10 \)
\( f(3) = 3^3 - 3(3)^2 - 9(3) + 5 = -22 \)
Fonksiyonun kapalı uç noktalarındaki değerini bulalım.
\( f(-2) = (-2)^3 - 3(-2)^2 - 9(-2) + 5 = 3 \)
\( f(6) = 6^3 - 3(6)^2 - 9(6) + 5 = 59 \)
Bu değerleri karşılaştırdığımızda fonksiyonun mutlak minimum ve maksimum değerleri ve noktaları aşağıdaki gibi bulunur.
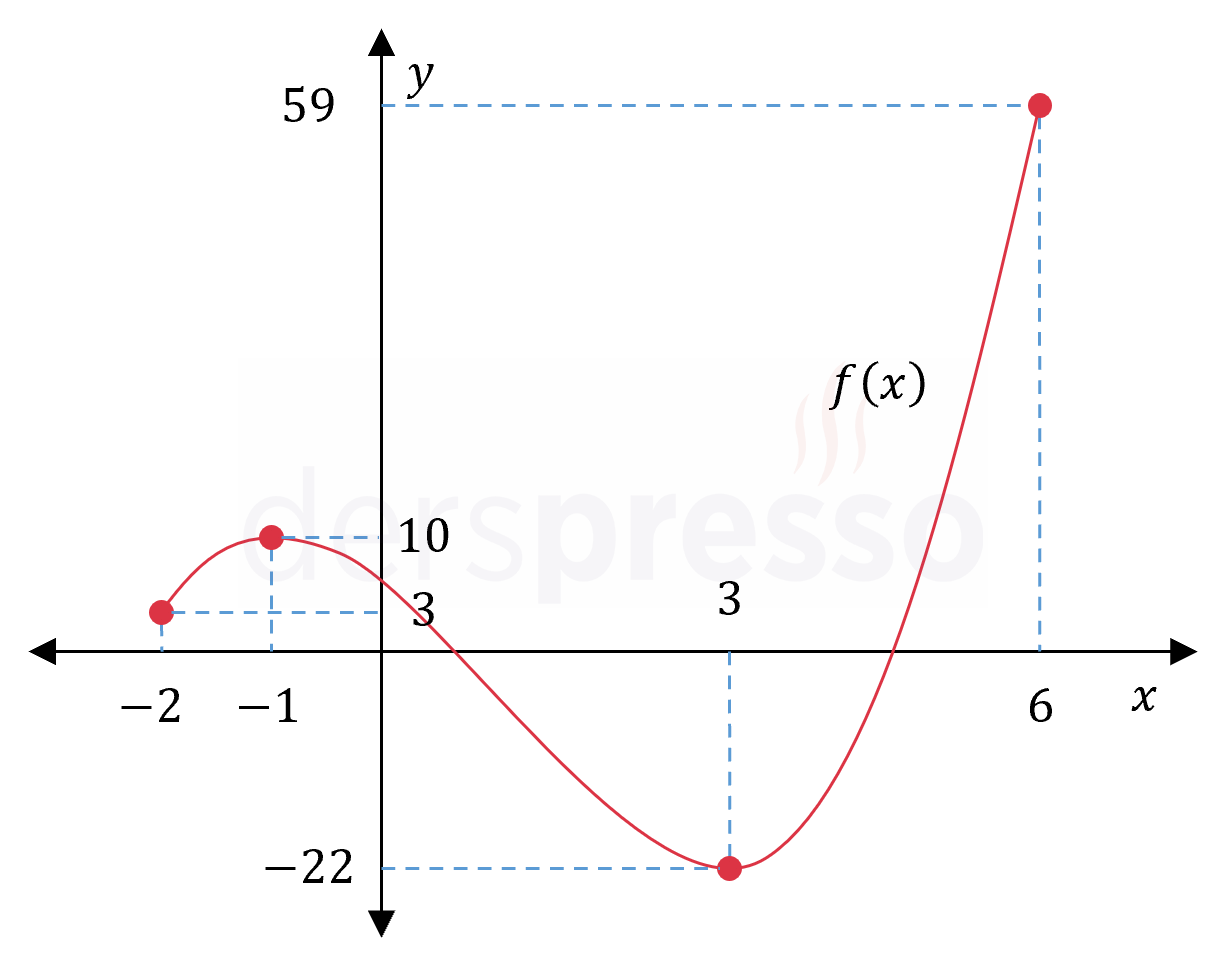
Mutlak minimum: Fonksiyonun \( -22 \) değerini aldığı \( x = 3 \) noktası
Mutlak maksimum: Fonksiyonun \( 59 \) değerini aldığı \( x = 6 \) noktası
Fonksiyonun grafiği ve karşılaştırma yaptığımız nokta ve değerler aşağıdaki şekilde gösterilmiştir.
Diğer Fonksiyonlar
Uç değer teoremi koşullarını (kapalı aralıkta tanımlı ve sürekli) sağlamayan aşağıdaki tipteki fonksiyonların mutlak minimum ve maksimum noktaları her zaman bulunmayabilir, dolayısıyla bu noktaların varlığı için ek kontroller yapılmalıdır.
Açık Uç Noktaları
Bir fonksiyon kapalı bir aralıkta tanımlı değilse tanım aralığının uç noktalarından en az biri açıktır. Bu tip fonksiyonlar uç noktaları pozitif ya da negatif sonsuz olan fonksiyonları da içerir.
\( (a, b), [a, b), (a, b] \)
\( (a, \infty), [a, \infty), (-\infty, b), (-\infty, b] \)
\( (-\infty, \infty) \)
Bir fonksiyon böyle bir uç noktada tanımlı olmadığı için bu nokta civarındaki davranışı limiti alınarak bulunabilir, dolayısıyla bu tip bir fonksiyonun mutlak ekstremum noktaları bulunurken açık uç noktalarında fonksiyon değeri yerine aşağıdaki limit değerlerine bakılır.
- Açık ve reel sayı uç noktalar için tek taraflı limit
- Sonsuz uç noktaları için sonsuzdaki limit
Bu limitler fonksiyonun pozitif ya da negatif sonsuza gidip gitmediğini, eğer limit değeri bir reel sayı ise yaklaştığı ama almadığı değerleri bulmamızı sağlar ve mutlak ekstremum noktalarının varlığı hakkında bilgi verir.
Bu değerler arasında karşılaştırma yapılırken, açık uç noktalarındaki bir limit;
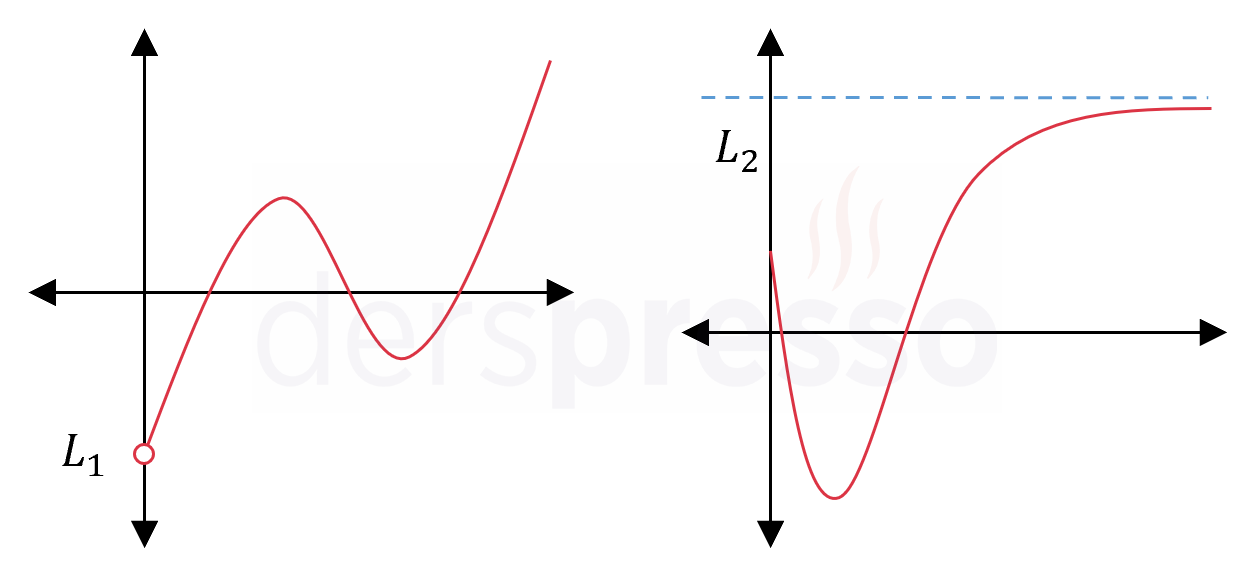
- Pozitif sonsuz ise mutlak maksimum noktası yoktur.
- Yukarıdaki soldaki grafikte \( x \to \infty \) iken limit pozitif sonsuz olduğu için fonksiyonun mutlak maksimum noktası yoktur.
- Negatif sonsuz ise mutlak minimum noktası yoktur.
- Bir reel sayı ise fonksiyon bu limit değerine yaklaşır ama değeri almaz, dolayısıyla bu limit değeri karşılaştırma yapılan diğer değerlerden büyükse mutlak maksimum noktası, küçükse mutlak minimum noktası yoktur.
- Soldaki grafikte \( x \to 0^+ \) iken limit değeri (\( L_1 \)) karşılaştırma yaptığımız diğer değerlerden küçük olduğu ve fonksiyon bu limit değerini almadığı için fonksiyonun mutlak minimum noktası yoktur.
- Sağdaki grafikte \( x \to \infty \) iken limit değeri (\( L_2 \)) karşılaştırma yaptığımız diğer değerlerden büyük olduğu ve fonksiyon bu limit değerini almadığı için fonksiyonun mutlak maksimum noktası yoktur.
Bu tip fonksiyonların mutlak ekstremum noktalarını bulmayı bir örnek üzerinde gösterelim.
\( x \in (0, 6) \) olmak üzere,
\( f(x) = \dfrac{2x^3 - 13x^2 - 9}{2x} \)
fonksiyonunun mutlak minimum ve maksimum değerlerini ve noktalarını bulalım.
\( f \) fonksiyonu açık bir aralıkta tanımlıdır ve bir rasyonel fonksiyon olduğu için paydayı sıfır yapan ve tanım aralığı dışındaki \( x = 0 \) noktası hariç süreklidir.
Fonksiyonun açık uç noktalarındaki limitini bulalım.
\( \lim\limits_{x \to 0^+} {\dfrac{2x^3 - 13x^2 - 9}{2x}} = \dfrac{2(0)^3 - 13(0)^2 - 9}{2(0^+)} \)
\( = -\infty \)
Buna göre fonksiyonun mutlak minimum noktası yoktur.
\( \lim\limits_{x \to 6^-} {\dfrac{2x^3 - 13x^2 - 9}{2x}} = \dfrac{2(6)^3 - 13(6)^2 - 9}{2(6)} \)
\( = -\dfrac{15}{4} \)
Fonksiyonun mutlak maksimum noktasının olup olmadığını bulmak için kritik noktalardaki değerini bulalım.
Fonksiyonun kritik noktaları birinci türevin sıfır ya da tanımsız olduğu iç noktalardır.
\( f'(x) = \dfrac{(6x^2 - 26x)(2x) - (2x^3 - 13x^2 - 9)(2)}{(2x)^2} \)
\( = \dfrac{4x^3 - 13x^2 + 9}{2x^2} \)
Fonksiyonun tanım kümesi içinde birinci türevinin sıfır olduğu iç noktaları bulalım.
\( \dfrac{(4x + 3)(x - 1)(x - 3)}{2x^2} = 0 \)
\( x \in \{ 1, 3 \} \)
Fonksiyonun tanım kümesi içinde birinci türevinin tanımsız olduğu iç nokta yoktur.
Kritik noktalar: \( x \in \{ 1, 3 \} \)
Fonksiyonun kritik noktalardaki değerini bulalım.
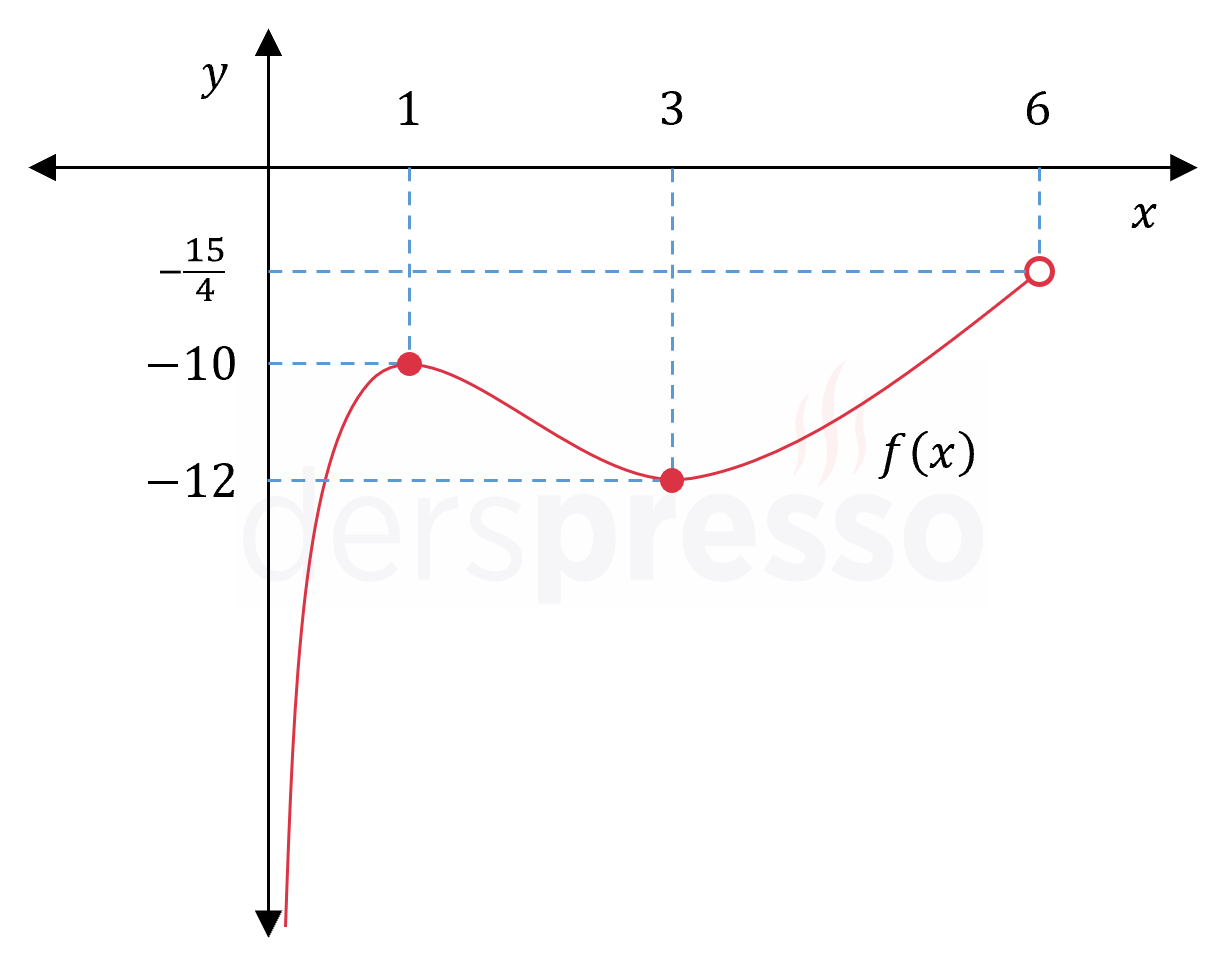
\( f(1) = \dfrac{2(1)^3 - 13(1)^2 - 9}{2(1)} = -10 \)
\( f(3) = \dfrac{2(3)^3 - 13(3)^2 - 9}{2(3)} = -12 \)
Bu değerleri karşılaştırdığımızda fonksiyonun mutlak minimum ve maksimum değerleri ve noktaları aşağıdaki gibi bulunur.
Mutlak minimum: \( x \to 0^+ \) iken limit negatif sonsuz olduğu için fonksiyonun mutlak minimum noktası yoktur.
Mutlak maksimum: \( x \to 6^- \) iken limit değeri (\( -\frac{15}{4} \)) karşılaştırma yaptığımız diğer değerlerden büyük olduğu ve fonksiyon bu limit değerini almadığı için fonksiyonun mutlak maksimum noktası yoktur.
Fonksiyonun grafiği ve karşılaştırma yaptığımız nokta ve değerler aşağıdaki şekilde gösterilmiştir.
Süreksiz İç Noktalar
Bir fonksiyon tanımlı olduğu ya da olmadığı bazı noktalarda süreksizlik içeriyorsa fonksiyonun mutlak ekstremum noktaları bulunurken bu noktalarda aşağıdaki limit değerlerine bakılır.
- Soldan tek taraflı limit
- Sağdan tek taraflı limit
Bu değerler arasında karşılaştırma yapılırken, süreksizlik noktalarındaki tek taraflı bir limit;

- Pozitif sonsuz ise mutlak maksimum noktası yoktur.
- Yukarıdaki soldaki grafikte \( x \to a^- \) iken limit pozitif sonsuz olduğu için fonksiyonun mutlak maksimum noktası yoktur.
- Negatif sonsuz ise mutlak minimum noktası yoktur.
- Soldaki grafikte \( x \to a^+ \) iken limit negatif sonsuz olduğu için fonksiyonun mutlak minimum noktası yoktur.
- Bir reel sayı ise ve fonksiyon bu limit değerini almıyorsa, bu limit değeri karşılaştırma yapılan diğer değerlerden büyükse mutlak maksimum noktası, küçükse mutlak minimum noktası yoktur.
- Soldaki grafikte \( x \to b^- \) iken limit değeri (\( L \)) karşılaştırma yaptığımız diğer değerlerden küçük olduğu ve fonksiyon bu limit değerini almadığı için fonksiyonun mutlak minimum noktası yoktur.
Eğer fonksiyon süreksizlik içerdiği bir noktada tanımlı ise bu noktadaki türevi tanımsız olduğu için fonksiyonun bir kritik noktası olarak karşılaştırmaya dahil edilir.
Bu tip fonksiyonların mutlak ekstremum noktalarını bulmayı bir örnek üzerinde gösterelim.
\( x \in [-10, 10] \) olmak üzere,
\( f(x) = \dfrac{x^2 - 16}{x - 5} \)
fonksiyonunun mutlak minimum ve maksimum değerlerini ve noktalarını bulalım.
\( f \) fonksiyonu kapalı bir aralıkta tanımlıdır ve \( x = 5 \) noktasında tanımsız olduğu için bu noktada süreksizlik içerir.
Fonksiyonun süreksiz olduğu \( x = 5 \) noktasındaki soldan ve sağdan limit değerlerini bulalım.
\( \lim\limits_{x \to 5^-} {\dfrac{x^2 - 16}{x - 5}} = \dfrac{5^2 - 16}{5^- - 5} \)
\( = \dfrac{9}{0^-} = -\infty \)
Buna göre fonksiyonun mutlak minimum noktası yoktur.
\( \lim\limits_{x \to 5^+} {\dfrac{x^2 - 16}{x - 5}} = \dfrac{5^2 - 16}{5^+ - 5} \)
\( = \dfrac{9}{0^+} = \infty \)
Buna göre fonksiyonun mutlak maksimum noktası yoktur.
Mutlak minimum: \( x \to 5^- \) iken limit negatif sonsuz olduğu için fonksiyonun mutlak minimum noktası yoktur.
Mutlak maksimum: \( x \to 5^+ \) iken limit pozitif sonsuz olduğu için fonksiyonun mutlak maksimum noktası yoktur.
Bu durumda fonksiyonun kritik ve kapalı uç noktalarındaki değerlerini bulmamıza gerek olmasa da, bu noktaları grafik üzerinde gösterebilmek adına bu değerleri de bulalım.
Fonksiyonun kritik noktaları birinci türevin sıfır ya da tanımsız olduğu iç noktalardır.
\( f'(x) = \dfrac{2x(x - 5) - (x^2 - 16)(1)}{(x - 5)^2} \)
\( = \dfrac{x^2 - 10x + 16}{(x - 5)^2} \)
Fonksiyonun tanım kümesi içinde birinci türevinin sıfır olduğu iç noktaları bulalım.
\( \dfrac{(x - 2)(x - 8)}{(x - 5)^2} = 0 \)
\( x \in \{ 2, 8 \} \)
Fonksiyonun tanım kümesi içinde birinci türevinin tanımsız olduğu iç nokta yoktur.
Kritik noktalar: \( x \in \{ 2, 8 \} \)
Fonksiyonun kritik noktalardaki değerini bulalım.
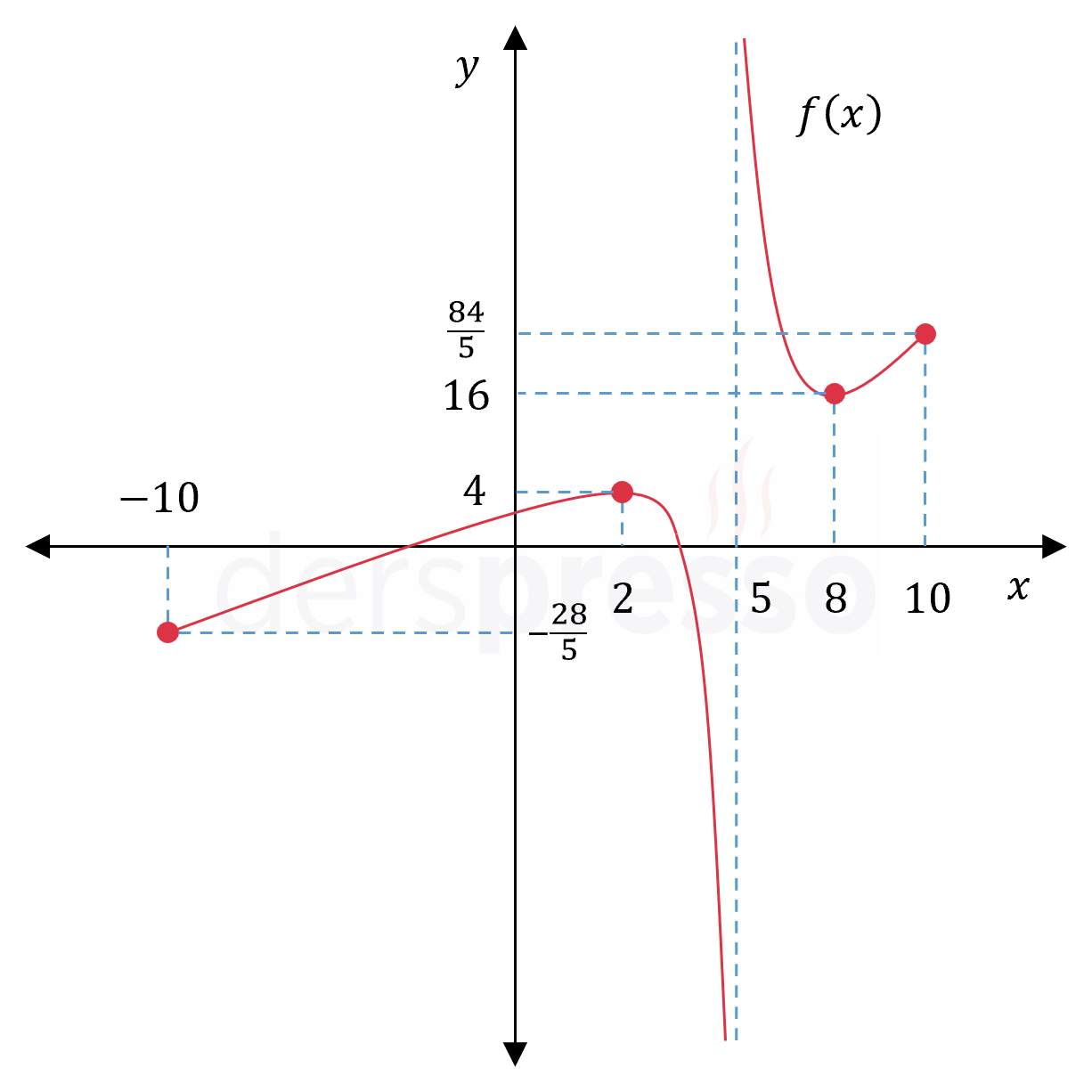
\( f(2) = \dfrac{2^2 - 16}{2 - 5} = 4 \)
\( f(8) = \dfrac{8^2 - 16}{8 - 5} = 16 \)
Fonksiyonun kapalı uç noktalarındaki değerini bulalım.
\( f(-10) = \dfrac{(-10)^2 - 16}{-10 - 5} = -\dfrac{28}{5} \)
\( f(10) = \dfrac{10^2 - 16}{10 - 5} = \dfrac{84}{5} \)
Fonksiyonun grafiği ve karşılaştırma yaptığımız nokta ve değerler aşağıdaki şekilde gösterilmiştir.
Parçalı Fonksiyonlar
Parçalı fonksiyonların mutlak minimum ve maksimum noktaları, uç noktalarının açık ya da kapalı olma ve geçiş noktalarındaki süreklilik durumuna göre yukarıda paylaştığımız yöntemlerle bulunabilir.
\( f(x) = \begin{cases} x^3 - 9x & 0 \le x \le 3 \\ x^2 - 8x + 10 & 3 \lt x \le 6 \end{cases} \)
fonksiyonunun mutlak minimum ve maksimum değerlerini ve noktalarını bulalım.
\( f \) parçalı fonksiyonunun \( x = 3 \) noktasında sürekli olup olmadığını bulalım.
\( x = 3 \) noktasındaki soldan limiti bulalım.
\( \lim\limits_{x \to 3^-} {f(x)} = \lim\limits_{x \to 3^-} (x^3 - 9x) \)
\( = 3^3 - 9(3) = 0 \)
\( x = 3 \) noktasındaki sağdan limiti bulalım.
\( \lim\limits_{x \to 3^+} {f(x)} = \lim\limits_{x \to 3^+} (x^2 - 8x + 10) \)
\( = 3^2 - 8(3) + 10 = -5 \)
Soldan ve sağdan limitler birbirine eşit olmadığı için fonksiyon \( x = 3 \) noktasında süreksizdir.
Fonksiyonun mutlak minimum ve maksimum noktalarının olup olmadığını bulmak için kritik ve kapalı uç noktalarındaki değerini bulalım.
\( f \) fonksiyonunun türevini bulalım.
Fonksiyon \( x = 3 \) noktasında süreksiz olduğu için türevi tanımsızdır.
\( f'(x) = \begin{cases} 3x^2 - 9 & 0 \le x \lt 3 \\ \text{Tanımsız} & x = 3 \\ 2x - 8 & 3 \lt x \le 6 \end{cases} \)
Fonksiyonun kritik noktaları birinci türevin sıfır ya da tanımsız olduğu iç noktalardır.
Fonksiyonun tanım kümesi içinde birinci türevinin sıfır olduğu iç noktaları bulalım.
\( 0 \le x \lt 3 \) için:
\( 3x^2 - 9 = 0 \)
\( x = \sqrt{3} \)
\( 3 \lt x \le 6 \) için:
\( 2x - 8 = 0 \)
\( x = 4 \)
Fonksiyonun \( x = 3 \) noktasında birinci türevi tanımsızdır.
Kritik noktalar: \( x \in \{ \sqrt{3}, 3, 4 \} \)
Fonksiyonun kritik noktalardaki değerini bulalım.
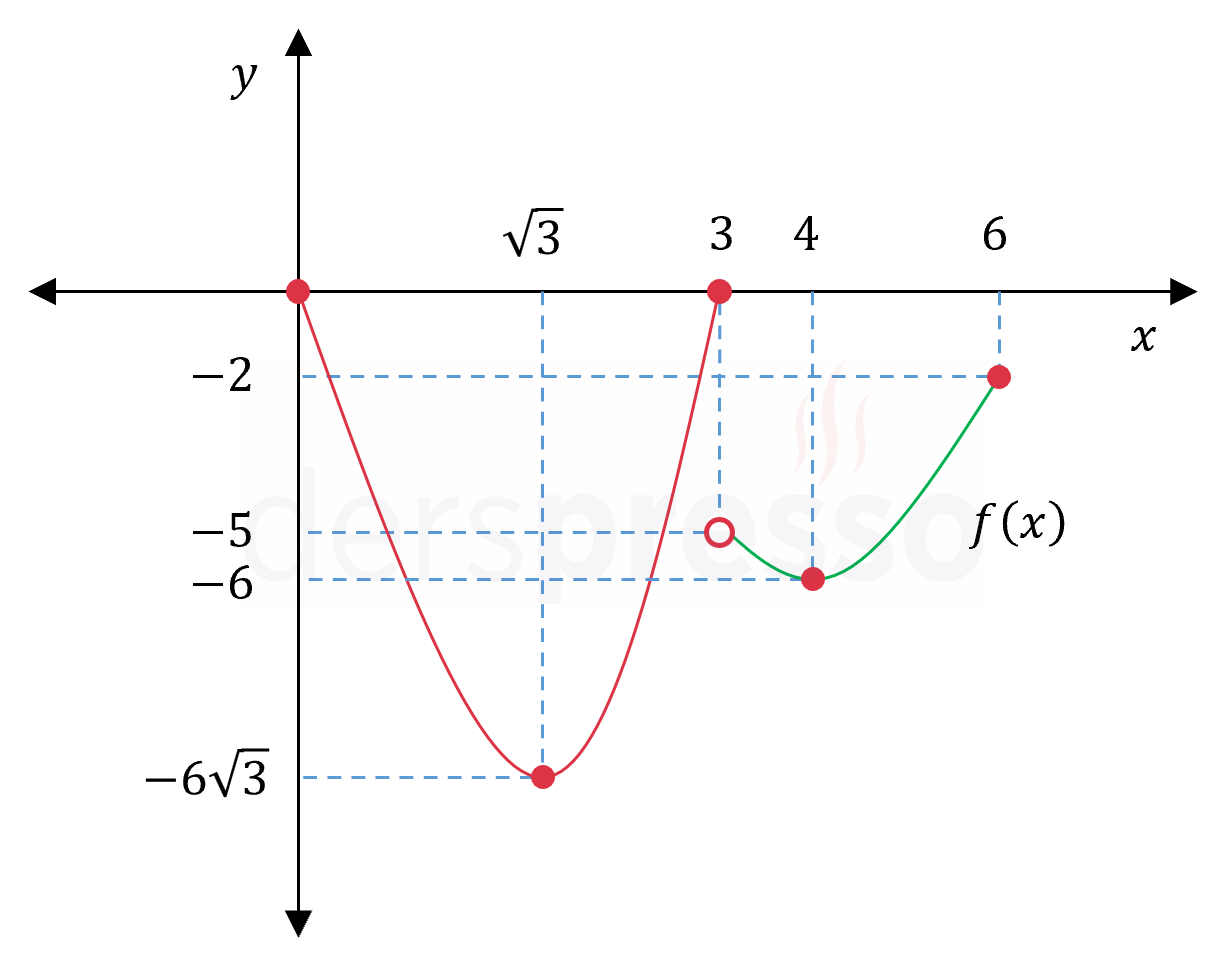
\( f(\sqrt{3}) = (\sqrt{3})^3 - 9\sqrt{3} = -6\sqrt{3} \)
\( f(3) = 3^3 - 9(3) = 0 \)
\( f(4) = 4^2 - 8(4) + 10 = -6 \)
Fonksiyonun kapalı uç noktalarındaki değerini bulalım.
\( f(0) = 0^3 - 9(0) = 0 \)
\( f(6) = 6^2 - 8(6) + 10 = -2 \)
Bu değerleri karşılaştırdığımızda fonksiyonun mutlak minimum ve maksimum değerleri ve noktaları aşağıdaki gibi bulunur.
Mutlak minimum: Fonksiyonun \( -6\sqrt{3} \) değerini aldığı \( x = \sqrt{3} \) noktası
Mutlak maksimum: Fonksiyonun \( 0 \) değerini aldığı \( x = 0 \) ve \( x = 3 \) noktaları
Fonksiyonun grafiği ve karşılaştırma yaptığımız nokta ve değerler aşağıdaki şekilde gösterilmiştir.
Mutlak Değer Fonksiyonları
Mutlak değer fonksiyonlarının mutlak minimum ve maksimum noktalarını bulmak için fonksiyon önce bir parçalı fonksiyon şeklinde yazılır, daha sonra yukarıda paylaştığımız yöntemler uygulanır.
Bir fonksiyonun mutlak ekstremum noktaları ile ilgili aşağıdaki önermelerden hangileri doğrudur?
I. Her fonksiyonun mutlak minimum (maksimum) noktası vardır.
II. Bir fonksiyonun birden fazla mutlak minimum (maksimum) noktası olabilir.
III. Sabit fonksiyonun her noktası mutlak minimum ve mutlak maksimum noktasıdır.
IV. Bir fonksiyonun mutlak minimum (maksimum) değerini bulmak için yerel minimum (maksimum) değerlerinin en küçüğü (en büyüğü) alınır.
Çözümü GösterI. öncül:
Fonksiyon değeri negatif (pozitif) sonsuza giden ya da aldığı diğer tüm değerlerden daha küçük (büyük) bir değere yaklaşan ama bu değeri almayan fonksiyonların mutlak minimum (maksimum) noktası yoktur.
I. öncül yanlıştır.
II. öncül:
Bir fonksiyonun (varsa) mutlak minimum (maksimum) değerini aldığı tüm noktalar mutlak minimum (maksimum) noktasıdır.
II. öncül doğrudur.
III. öncül:
Sabit fonksiyon her noktada fonksiyonun en küçük (en büyük) değerini aldığı için her nokta mutlak minimum (maksimum) noktasıdır.
III. öncül doğrudur.
IV. öncül:
Yukarıda bahsettiğimiz üzere, yerel ekstremum noktaları olan bir fonksiyonun mutlak ekstremum noktaları olmayabilir.
IV. öncül yanlıştır.
\( f: [-3, 4] \to \mathbb{R} \) olmak üzere,
\( f(x) = 3x^2 - 6x - 15 \)
fonksiyonunun mutlak minimum ve maksimum değerlerini ve noktalarını bulunuz.
Çözümü Göster\( f \) fonksiyonu kapalı bir aralıkta tanımlıdır ve bir polinom fonksiyonu olduğu için süreklidir.
Kapalı bir aralıkta tanımlı ve sürekli bir fonksiyon, mutlak minimum ve maksimum değerlerini kritik ya da kapalı uç noktalarından birinde alır.
Fonksiyonun kritik noktaları birinci türevin sıfır ya da tanımsız olduğu iç noktalardır.
\( f'(x) = 6x - 6 \)
Fonksiyonun birinci türevinin sıfır olduğu iç noktaları bulalım.
\( 6x - 6 = 0 \)
\( x = 1 \)
Fonksiyonun birinci türevinin tanımsız olduğu iç nokta yoktur.
Kritik nokta: \( x = 1 \)
Fonksiyonun kritik noktadaki değerini bulalım.
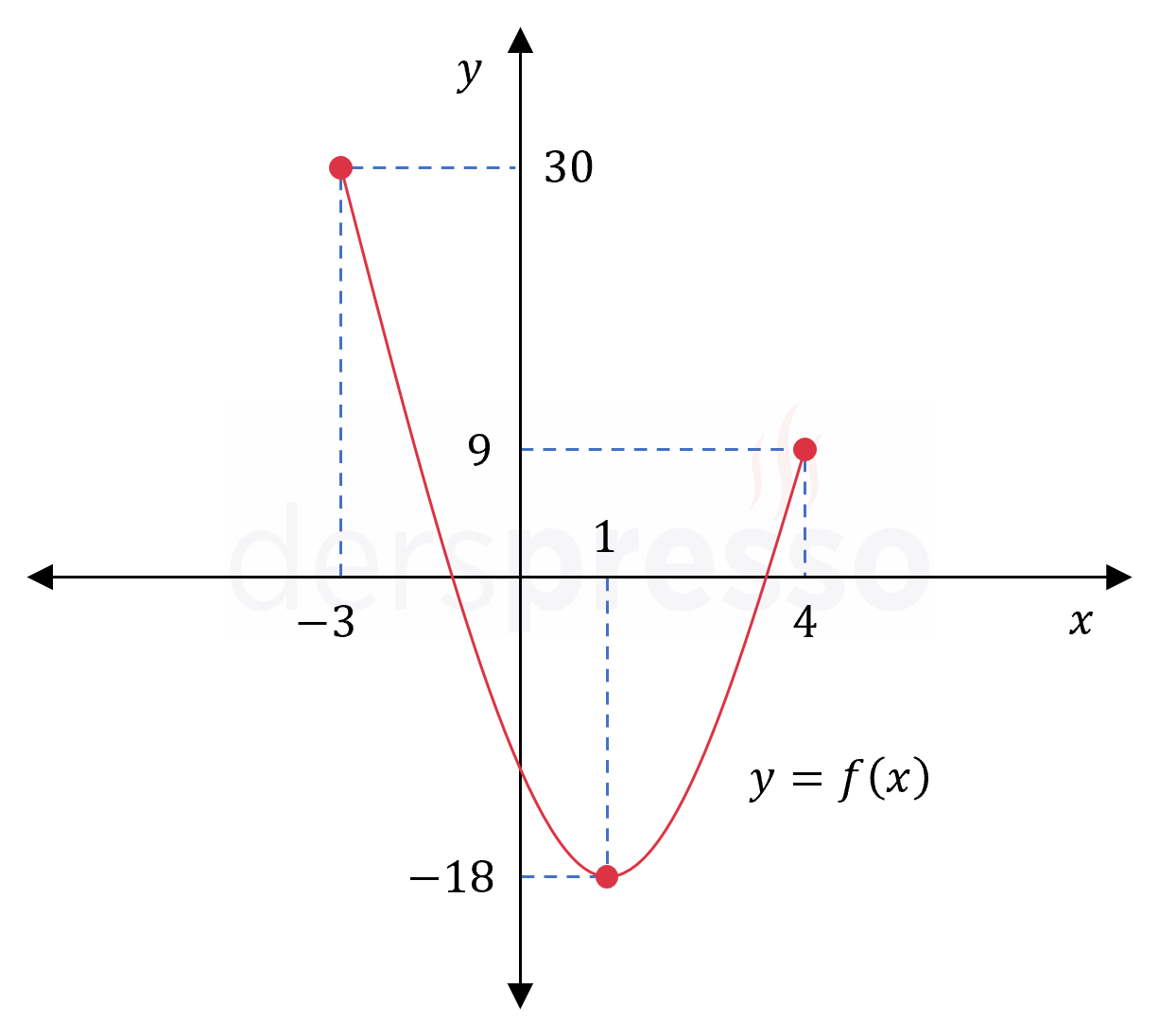
\( f(1) = 3(1)^2 - 6(1) - 15 = -18 \)
Fonksiyonun kapalı uç noktalarındaki değerini bulalım.
\( f(-3) = 3(-3)^2 - 6(-3) - 15 = 30 \)
\( f(4) = 3(4)^2 - 6(4) - 15 = 9 \)
Bu değerleri karşılaştırdığımızda fonksiyonun mutlak minimum ve maksimum değerleri ve noktaları aşağıdaki gibi bulunur.
Mutlak minimum: Fonksiyonun \( -18 \) değerini aldığı \( x = 1 \) noktası
Mutlak maksimum: Fonksiyonun \( 30 \) değerini aldığı \( x = -3 \) noktası
Fonksiyonun grafiği ve karşılaştırma yaptığımız nokta ve değerler aşağıdaki şekilde gösterilmiştir.
\( f: [0, \pi] \to \mathbb{R} \) olmak üzere,
\( f(x) = \cos{x} - \sin{x} \)
fonksiyonunun mutlak minimum ve maksimum değerlerini ve noktalarını bulunuz.
Çözümü Göster\( f \) fonksiyonu kapalı bir aralıkta tanımlıdır ve iki sürekli fonksiyonun farkından oluştuğu için süreklidir.
Kapalı bir aralıkta tanımlı ve sürekli bir fonksiyon, mutlak minimum ve maksimum değerlerini kritik ya da kapalı uç noktalarından birinde alır.
Fonksiyonun kritik noktaları birinci türevin sıfır ya da tanımsız olduğu iç noktalardır.
\( f'(x) = -\sin{x} - \cos{x} \)
Fonksiyonun birinci türevinin sıfır olduğu iç noktaları bulalım.
\( -\sin{x} - \cos{x} = 0 \)
\( -\sin{x} = \cos{x} \)
\( \tan{x} = -1 \)
Tanjant fonksiyonu \( -1 \) değerini verilen tanım aralığında aşağıdaki açı değerinde alır.
\( x = \dfrac{3\pi}{4} \)
Fonksiyonun birinci türevinin tanımsız olduğu iç nokta yoktur.
Kritik nokta: \( x = \frac{3\pi}{4} \)
Fonksiyonun kritik noktadaki değerini bulalım.
\( f(\dfrac{3\pi}{4}) = \cos{\dfrac{3\pi}{4}} - \sin{\dfrac{3\pi}{4}} \)
\( = -\dfrac{\sqrt{2}}{2} - \dfrac{\sqrt{2}}{2} = -\sqrt{2} \)
Fonksiyonun kapalı uç noktalarındaki değerini bulalım.
\( f(0) = \cos{0} - \sin{0} \)
\( = 1 - 0 = 1 \)
\( f(\pi) = \cos{\pi} - \sin{\pi} \)
\( = -1 - 0 = -1 \)
Bu değerleri karşılaştırdığımızda fonksiyonun mutlak minimum ve maksimum değerleri ve noktaları aşağıdaki gibi bulunur.
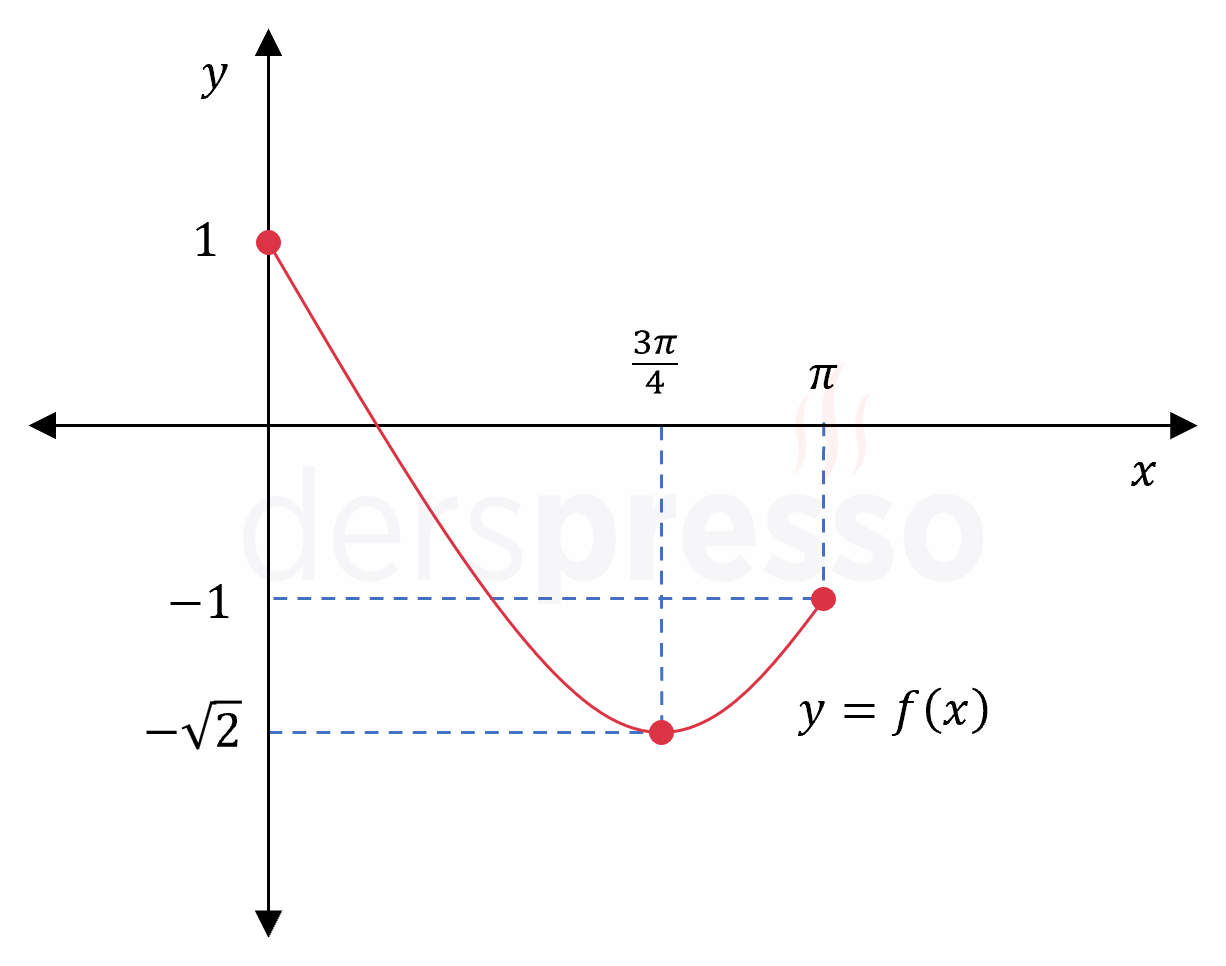
Mutlak minimum: Fonksiyonun \( -\sqrt{2} \) değerini aldığı \( x = \frac{3\pi}{4} \) noktası
Mutlak maksimum: Fonksiyonun \( 1 \) değerini aldığı \( x = 0 \) noktası
Fonksiyonun grafiği ve karşılaştırma yaptığımız nokta ve değerler aşağıdaki şekilde gösterilmiştir.
\( f: [-1, 3] \to \mathbb{R} \) olmak üzere,
\( f(x) = x^2e^{-x} \)
fonksiyonunun mutlak minimum ve maksimum değerlerini ve noktalarını bulunuz.
Çözümü Göster\( f \) fonksiyonu kapalı bir aralıkta tanımlıdır ve iki sürekli fonksiyonun çarpımından oluştuğu için süreklidir.
Kapalı bir aralıkta tanımlı ve sürekli bir fonksiyon, mutlak minimum ve maksimum değerlerini kritik ya da kapalı uç noktalarından birinde alır.
Fonksiyonun kritik noktaları birinci türevin sıfır ya da tanımsız olduğu iç noktalardır.
\( f'(x) = 2xe^{-x} - x^2e^{-x} \)
\( = e^{-x}x(2 - x) \)
Fonksiyonun birinci türevinin sıfır olduğu iç noktaları bulalım.
\( e^{-x}x(2 - x) = 0 \)
\( x \in \{ 0, 2 \} \)
Fonksiyonun birinci türevinin tanımsız olduğu iç nokta yoktur.
Kritik noktalar: \( x \in \{ 0, 2 \} \)
Fonksiyonun kritik noktalardaki değerini bulalım.
\( f(0) = 0^2e^{-0} = 0 \)
\( f(2) = 2^2e^{-2} = \dfrac{4}{e^2}\)
Fonksiyonun kapalı uç noktalarındaki değerini bulalım.
\( f(-1) = (-1)^2e^{-(-1)} = e \)
\( f(3) = 3^2e^{-3} = \dfrac{9}{e^3}\)
Bu değerleri karşılaştırdığımızda fonksiyonun mutlak minimum ve maksimum değerleri ve noktaları aşağıdaki gibi bulunur.
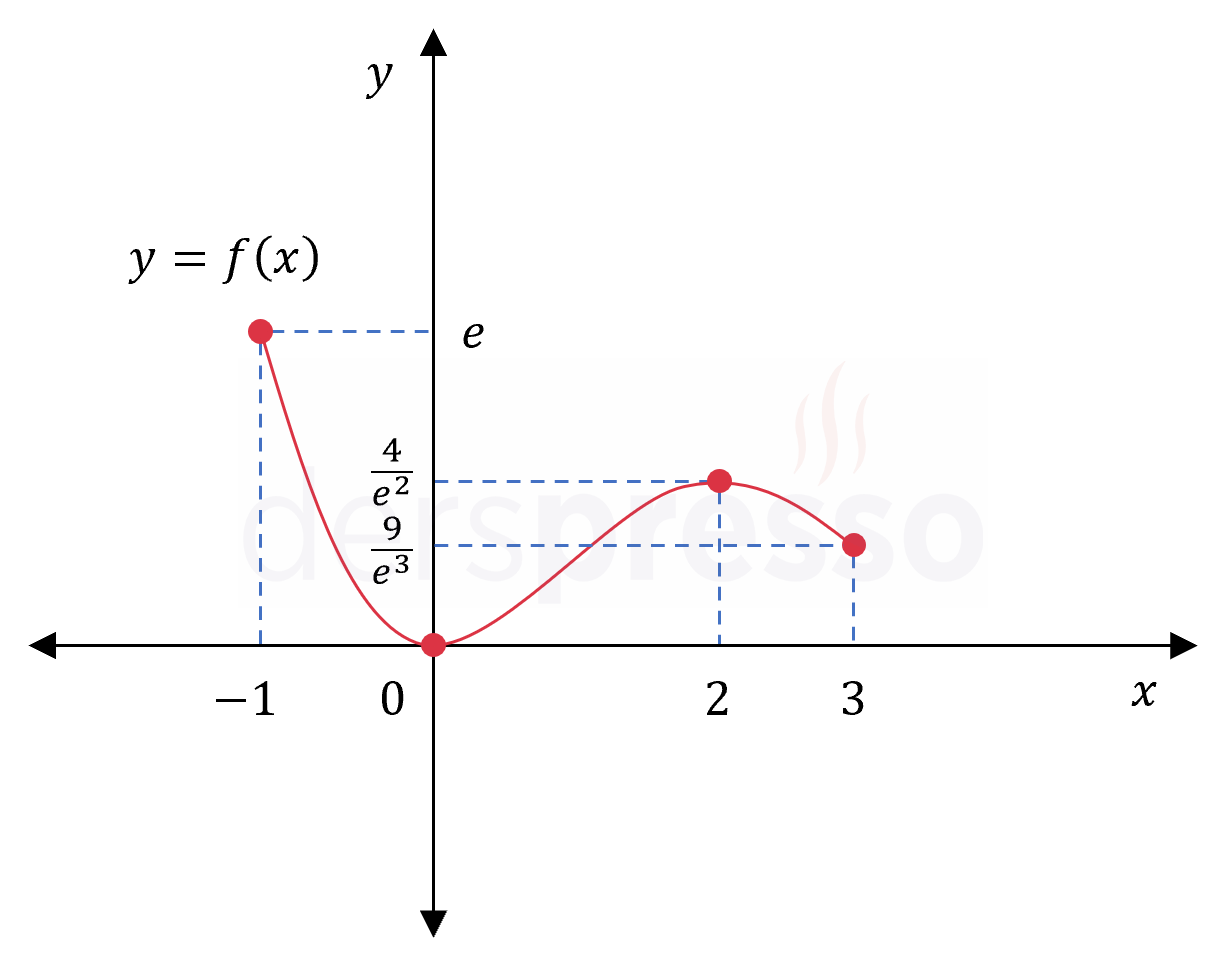
Mutlak minimum: Fonksiyonun \( 0 \) değerini aldığı \( x = 0 \) noktası
Mutlak maksimum: Fonksiyonun \( e \) değerini aldığı \( x = -1 \) noktası
Fonksiyonun grafiği ve karşılaştırma yaptığımız nokta ve değerler aşağıdaki şekilde gösterilmiştir.
\( f: [-4, 3] \to \mathbb{R} \) olmak üzere,
\( f(x) = \ln(4x^2 + 2) \)
fonksiyonunun mutlak minimum ve maksimum değerlerini ve noktalarını bulunuz.
Çözümü Göster\( f \) fonksiyonu kapalı bir aralıkta tanımlıdır ve bir logaritma fonksiyonu olduğu için tanım kümesi içinde süreklidir.
Kapalı bir aralıkta tanımlı ve sürekli bir fonksiyon, mutlak minimum ve maksimum değerlerini kritik ya da kapalı uç noktalarından birinde alır.
Fonksiyonun kritik noktaları birinci türevin sıfır ya da tanımsız olduğu iç noktalardır.
\( f'(x) = \dfrac{8x}{4x^2 + 2} \)
\( = \dfrac{4x}{2x^2 + 1} \)
Fonksiyonun birinci türevinin sıfır olduğu iç noktaları bulalım.
\( \dfrac{4x}{2x^2 + 1} = 0 \)
\( x = 0 \)
Fonksiyonun birinci türevinin tanımsız olduğu iç nokta yoktur.
Kritik nokta: \( x = 0 \)
Fonksiyonun kritik noktadaki değerini bulalım.
\( f(0) = \ln(4(0)^2 + 2) = \ln{2} \)
Fonksiyonun kapalı uç noktalarındaki değerini bulalım.
\( f(-4) = \ln(4(-4)^2 + 2) = \ln{66} \)
\( f(3) = \ln(4(3)^2 + 2) = \ln{38} \)
Bu değerleri karşılaştırdığımızda fonksiyonun mutlak minimum ve maksimum değerleri ve noktaları aşağıdaki gibi bulunur.
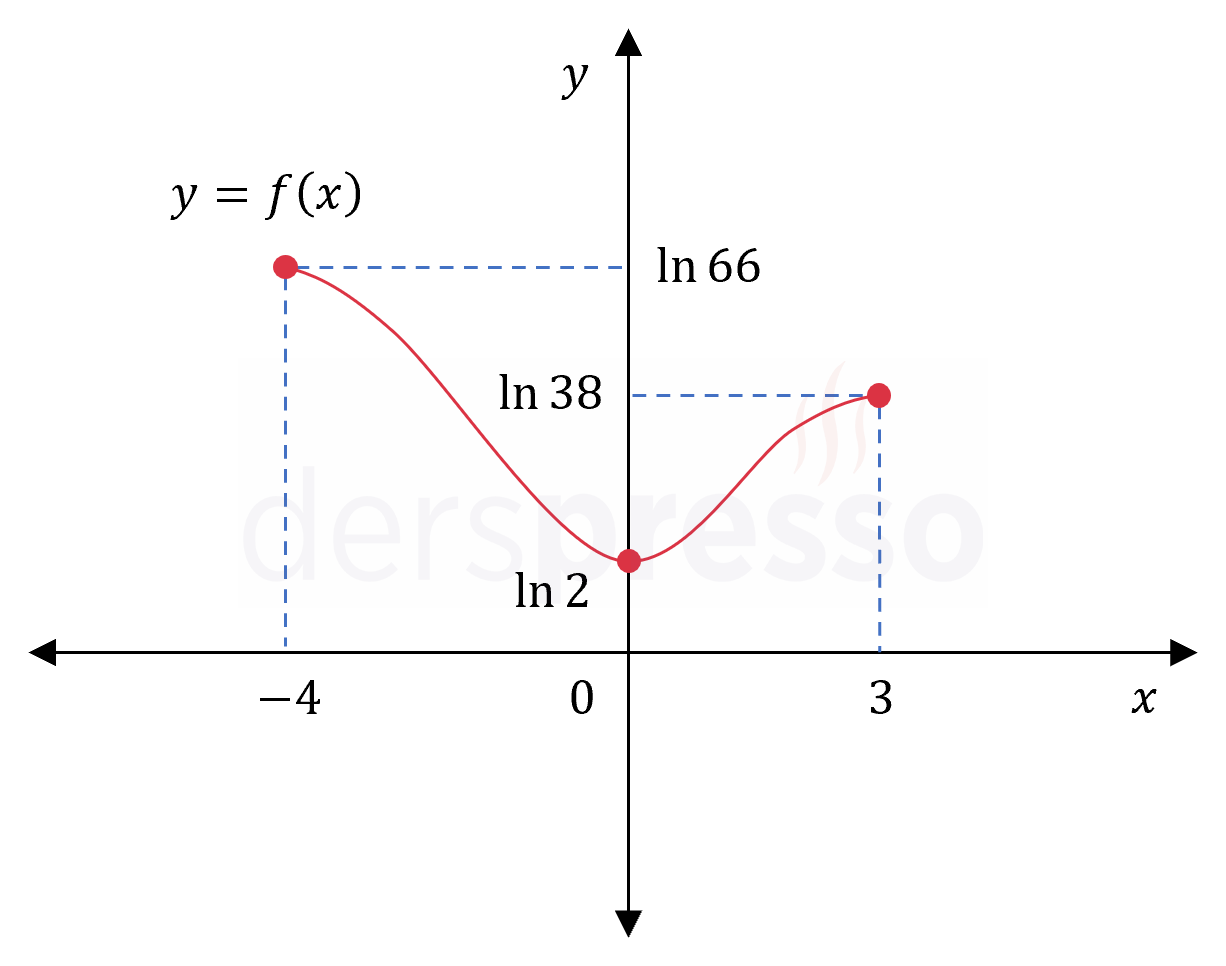
Mutlak minimum: Fonksiyonun \( \ln{2} \) değerini aldığı \( x = 0 \) noktası
Mutlak maksimum: Fonksiyonun \( \ln{66} \) değerini aldığı \( x = -4 \) noktası
Fonksiyonun grafiği ve karşılaştırma yaptığımız nokta ve değerler aşağıdaki şekilde gösterilmiştir.
\( f: (2, 6] \to \mathbb{R} \) olmak üzere,
\( f(x) = x^2 - 8x + 7 \)
fonksiyonunun mutlak minimum ve maksimum değerlerini ve noktalarını bulunuz.
Çözümü Göster\( f \) fonksiyonu yarı açık bir aralıkta tanımlıdır ve bir polinom fonksiyonu olduğu için süreklidir.
Fonksiyonun açık uç noktasındaki limitini bulalım.
\( \lim\limits_{x \to 2^+} (x^2 - 8x + 7) = 2^2 - 8(2) + 7 = -5 \)
Fonksiyonun mutlak minimum ve maksimum noktalarının olup olmadığını bulmak için kritik ve kapalı uç noktasındaki değerini bulalım.
Fonksiyonun kritik noktaları birinci türevin sıfır ya da tanımsız olduğu iç noktalardır.
\( f'(x) = 2x - 8 \)
Fonksiyonun tanım kümesi içinde birinci türevinin sıfır olduğu iç noktaları bulalım.
\( 2x - 8 = 0 \)
\( x = 4 \)
Fonksiyonun birinci türevinin tanımsız olduğu iç nokta yoktur.
Kritik nokta: \( x = 4 \)
Fonksiyonun kritik noktadaki değerini bulalım.
\( f(4) = 4^2 - 8(4) + 7 = -9 \)
Fonksiyonun kapalı uç noktasındaki değerini bulalım.
\( f(6) = 6^2 - 8(6) + 7 = -5 \)
Bu değerleri karşılaştırdığımızda fonksiyonun mutlak minimum ve maksimum değerleri ve noktaları aşağıdaki gibi bulunur.
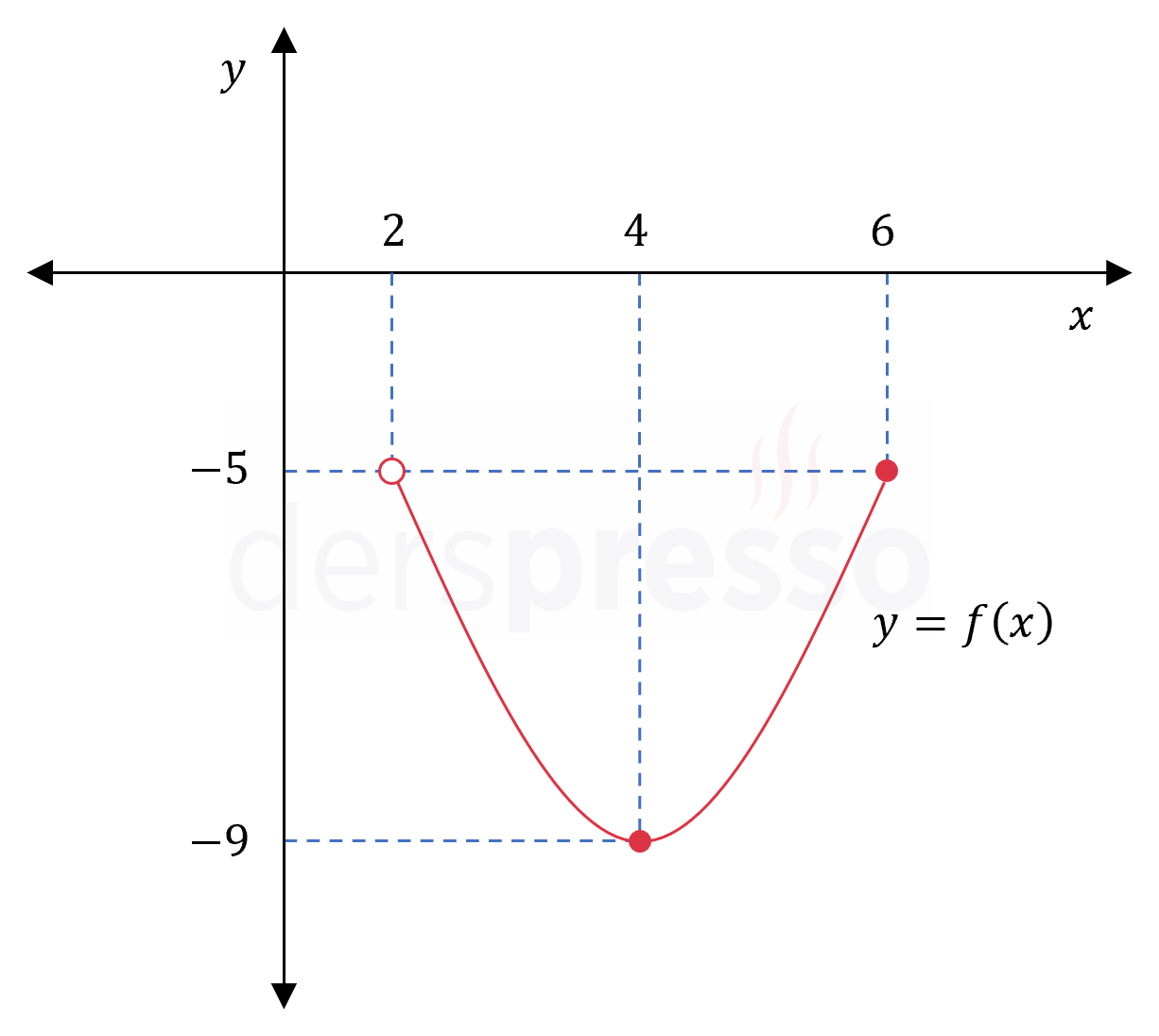
Mutlak minimum: Fonksiyonun \( -9 \) değerini aldığı \( x = 4 \) noktası
Mutlak maksimum: Fonksiyonun \( -5 \) değerini aldığı \( x = 6 \) noktası
Fonksiyonun grafiği ve karşılaştırma yaptığımız nokta ve değerler aşağıdaki şekilde gösterilmiştir.
\( f: [0, 2\pi] \to \mathbb{R} \) olmak üzere,
\( f(x) = 2\sin{x} + x - \sqrt{3} \) fonksiyonunun alabileceği en küçük değer kaçtır?
Çözümü Göster\( f \) fonksiyonu kapalı bir aralıkta tanımlıdır ve iki sürekli fonksiyonun toplamından oluştuğu için süreklidir.
Bir fonksiyonun alabileceği en küçük değer mutlak minimum değeridir.
Kapalı bir aralıkta tanımlı ve sürekli bir fonksiyon, mutlak minimum değerini kritik ya da kapalı uç noktalarından birinde alır.
Fonksiyonun kritik noktaları birinci türevin sıfır ya da tanımsız olduğu iç noktalardır.
\( f'(x) = 2\cos{x} + 1 \)
Fonksiyonun birinci türevinin sıfır olduğu iç noktaları bulalım.
\( 2\cos{x} + 1 = 0 \)
\( \cos{x} = -\dfrac{1}{2} \)
Kosinüs fonksiyonu \( -\frac{1}{2} \) değerini verilen tanım aralığında aşağıdaki açı değerlerinde alır.
\( x \in \{ \dfrac{2\pi}{3}, \dfrac{4\pi}{3} \} \)
Fonksiyonun birinci türevinin tanımsız olduğu iç nokta yoktur.
Kritik noktalar: \( x \in \{ \dfrac{2\pi}{3}, \dfrac{4\pi}{3} \} \)
Fonksiyonun kritik noktalardaki değerini bulalım.
\( f(\dfrac{2\pi}{3}) = 2\sin{\dfrac{2\pi}{3}} + \dfrac{2\pi}{3} - \sqrt{3} \)
\( = 2 \cdot \dfrac{\sqrt{3}}{2} + \dfrac{2\pi}{3} - \sqrt{3} \)
\( = \dfrac{2\pi}{3} \)
\( f(\dfrac{4\pi}{3}) = 2\sin{\dfrac{4\pi}{3}} + \dfrac{4\pi}{3} - \sqrt{3} \)
\( = 2(-\dfrac{\sqrt{3}}{2}) + \dfrac{4\pi}{3} - \sqrt{3} \)
\( = \dfrac{4\pi}{3} - 2\sqrt{3} \)
Fonksiyonun kapalı uç noktalarındaki değerini bulalım.
\( f(0) = 2\sin{0} + 0 - \sqrt{3} \)
\( = 2(0) + 0 - \sqrt{3} = -\sqrt{3} \)
\( f(2\pi) = 2\sin{2\pi} + 2\pi - \sqrt{3} \)
\( = 2(0) + 2\pi - \sqrt{3} = 2\pi - \sqrt{3} \)
Bu değerleri karşılaştırdığımızda fonksiyonun mutlak minimum değeri olarak \( -\sqrt{3} \) değeri bulunur.
Fonksiyonun grafiği ve karşılaştırma yaptığımız nokta ve değerler aşağıdaki şekilde gösterilmiştir.
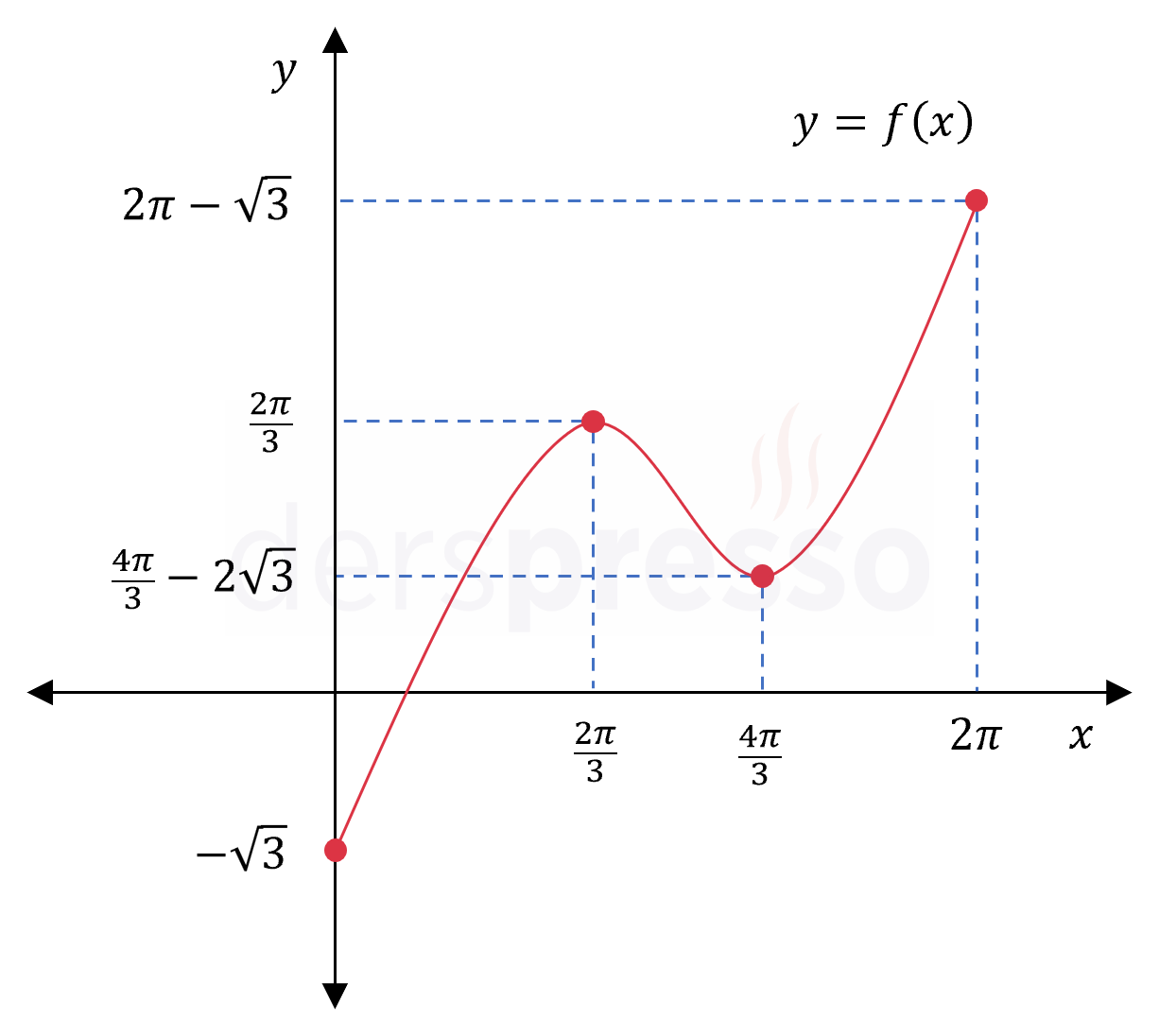
\( f: [0, \pi] \to \mathbb{R} \) olmak üzere,
\( f(x) = e^{x}\cos{x} \) fonksiyonunun alabileceği en küçük değer nedir?
Çözümü Göster\( f \) fonksiyonu kapalı bir aralıkta tanımlıdır ve iki sürekli fonksiyonun çarpımından oluştuğu için süreklidir.
Bir fonksiyonun alabileceği en küçük değer mutlak minimum değeridir.
Kapalı bir aralıkta tanımlı ve sürekli bir fonksiyon, mutlak minimum değerini kritik ya da kapalı uç noktalarından birinde alır.
Fonksiyonun kritik noktaları birinci türevin sıfır ya da tanımsız olduğu iç noktalardır.
\( f'(x) = e^{x}\cos{x} - e^{x}\sin{x} \)
\( = e^{x}(\cos{x} - \sin{x}) \)
Fonksiyonun birinci türevinin sıfır olduğu iç noktaları bulalım.
\( e^{x}(\cos{x} - \sin{x}) = 0 \)
\( e^{x} \) tüm reel sayılarda pozitiftir.
\( \cos{x} - \sin{x} = 0 \)
\( \cos{x} = \sin{x} \)
\( \tan{x} = 1 \)
Tanjant fonksiyonu \( 1 \) değerini verilen tanım aralığında aşağıdaki açı değerinde alır.
\( x = \dfrac{\pi}{4} \)
Fonksiyonun birinci türevinin tanımsız olduğu iç nokta yoktur.
Kritik nokta: \( x = \dfrac{\pi}{4} \)
Fonksiyonun kritik noktadaki değerini bulalım.
\( f(\dfrac{\pi}{4}) = e^{\frac{\pi}{4}}\cos{\dfrac{\pi}{4}} = \dfrac{\sqrt{2}e^{\frac{\pi}{4}}}{2} \)
Fonksiyonun kapalı uç noktalarındaki değerini bulalım.
\( f(0) = e^{0}\cos{0} \)
\( = 1 \cdot 1 = 1 \)
\( f(\pi) = e^{\pi}\cos{\pi} \)
\( = e^{\pi}(-1) = -e^{\pi} \)
Bu değerleri karşılaştırdığımızda fonksiyonun mutlak minimum değeri olarak \( -e^{\pi} \) değeri bulunur
Fonksiyonun grafiği ve karşılaştırma yaptığımız nokta ve değerler aşağıdaki şekilde gösterilmiştir.
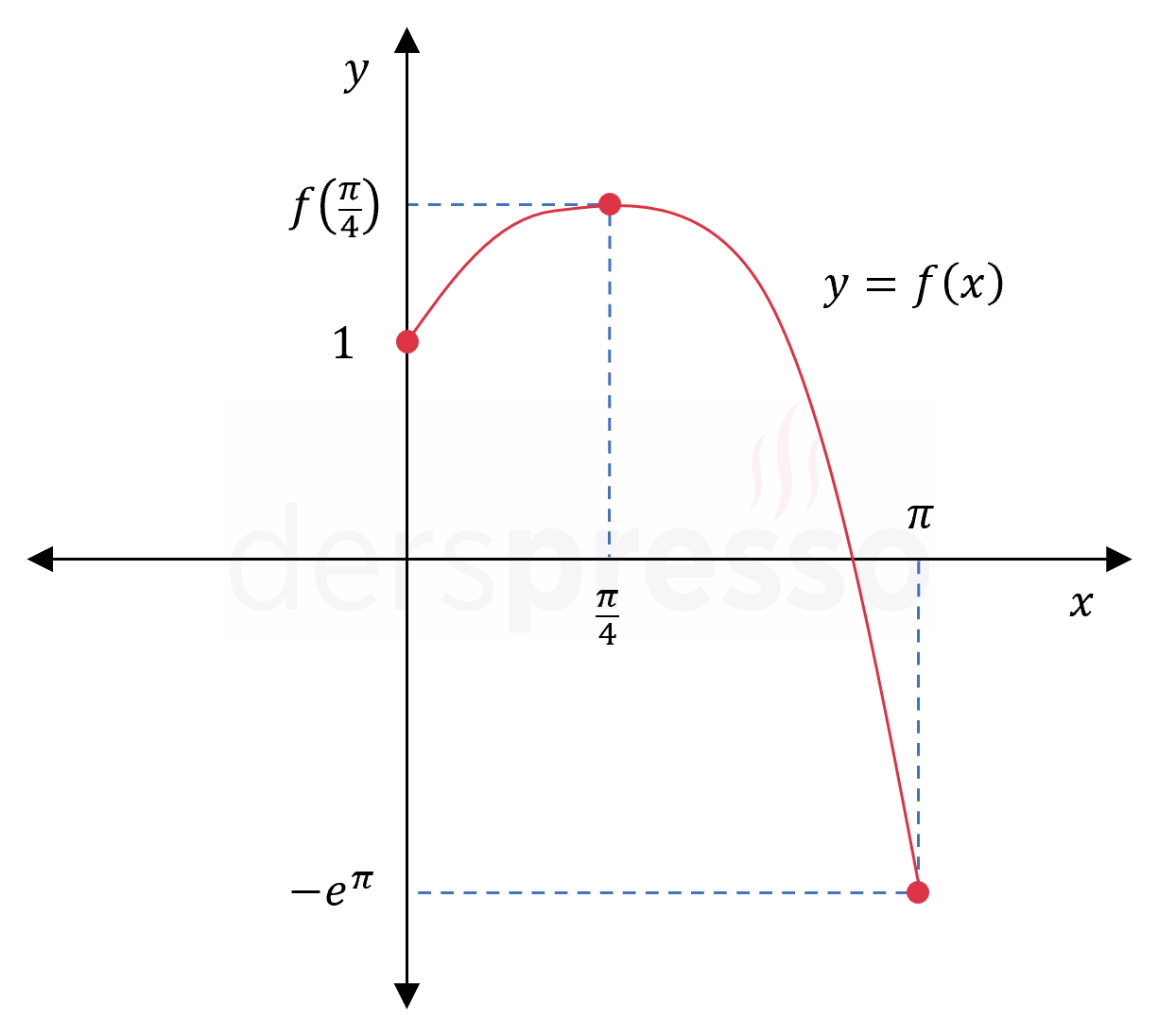
\( f(x) = x^4 + 2x^3 - 2x^2 - 3 \)
fonksiyonunun tanımlı olduğu en geniş aralıkta mutlak minimum ve maksimum değerlerini ve noktalarını bulunuz.
Çözümü Göster\( f \) fonksiyonu sonsuz aralıkta tanımlıdır ve bir polinom fonksiyonu olduğu için süreklidir.
Fonksiyonun sonsuzdaki limitlerini bulalım.
\( \lim\limits_{x \to \infty} (x^4 + 2x^3 - 2x^2 - 3) = \lim\limits_{x \to \infty} {x^4} = \infty \)
Buna göre fonksiyonun mutlak maksimum noktası yoktur.
\( \lim\limits_{x \to -\infty} (x^4 + 2x^3 - 2x^2 - 3) = \lim\limits_{x \to -\infty} {x^4} = \infty \)
Fonksiyonun mutlak minimum noktasının olup olmadığını bulmak için kritik noktalardaki değerini bulalım.
Fonksiyonun kritik noktaları birinci türevin sıfır ya da tanımsız olduğu iç noktalardır.
\( f'(x) = 4x^3 + 6x^2 - 4x \)
Fonksiyonun tanım kümesi içinde birinci türevinin sıfır olduğu iç noktaları bulalım.
\( 2x(2x - 1)(x + 2) = 0 \)
\( x \in \{ -2, 0, \frac{1}{2} \} \)
Fonksiyonun birinci türevinin tanımsız olduğu iç nokta yoktur.
Kritik noktalar: \( x \in \{ -2, 0, \frac{1}{2} \} \)
Fonksiyonun kritik noktalardaki değerini bulalım.
\( f(-2) = (-2)^4 + 2(-2)^3 - 2(-2)^2 - 3 = -11 \)
\( f(0) = 0^4 + 2(0)^3 - 2(0)^2 - 3 = -3 \)
\( f(\dfrac{1}{2}) = (\dfrac{1}{2})^4 + 2(\dfrac{1}{2})^3 - 2(\dfrac{1}{2})^2 - 3 = -\dfrac{51}{16} \)
Bu değerleri karşılaştırdığımızda fonksiyonun mutlak minimum ve maksimum değerleri ve noktaları aşağıdaki gibi bulunur.
Mutlak minimum: Fonksiyonun \( -11 \) değerini aldığı \( x = -2 \) noktası
Mutlak maksimum: \( x \to \infty \) ve \( x \to -\infty \) iken limit pozitif sonsuz olduğu için fonksiyonun mutlak maksimum noktası yoktur.
Fonksiyonun grafiği ve karşılaştırma yaptığımız nokta ve değerler aşağıdaki şekilde gösterilmiştir.
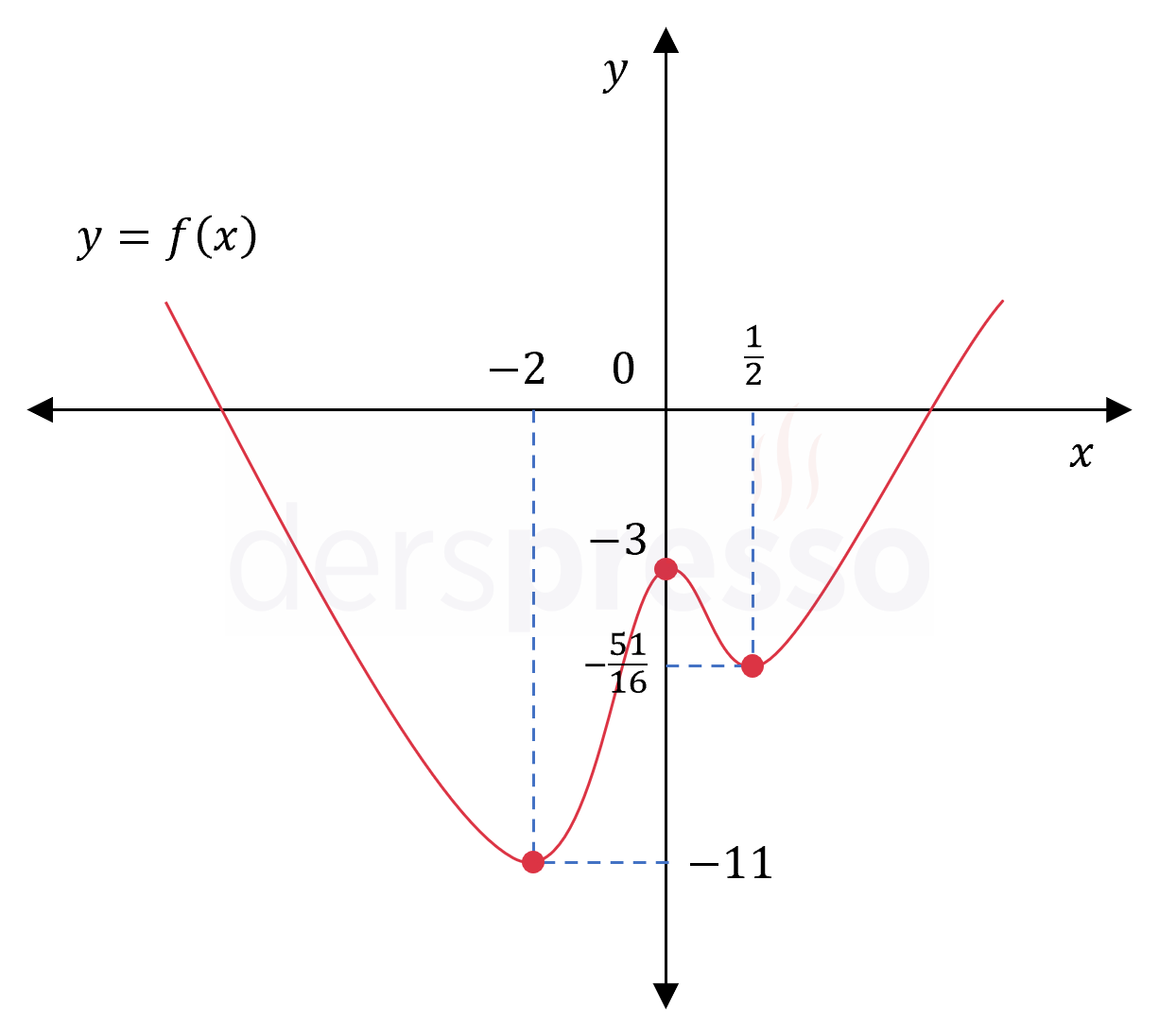
\( f: [-2, 2] \to \mathbb{R} \) olmak üzere,
\( f(x) = \dfrac{3x^3}{x + 4} \)
fonksiyonunun mutlak minimum ve maksimum değerlerini ve noktalarını bulunuz.
Çözümü Göster\( f \) fonksiyonu kapalı bir aralıkta tanımlıdır ve bir rasyonel fonksiyon olduğu için paydayı sıfır yapan ve tanım aralığı dışındaki \( x = -4 \) noktası hariç süreklidir.
Kapalı bir aralıkta tanımlı ve sürekli bir fonksiyon, mutlak minimum ve maksimum değerlerini kritik ya da kapalı uç noktalarından birinde alır.
Fonksiyonun kritik noktaları birinci türevin sıfır ya da tanımsız olduğu iç noktalardır.
\( f'(x) = \dfrac{9x^2(x + 4) - 3x^3(1)}{(x + 4)^2} \)
\( = \dfrac{6x^3 + 36x^2}{(x + 4)^2} \)
\( = \dfrac{6x^2(x + 6)}{(x + 4)^2} \)
Fonksiyonun tanım kümesi içinde birinci türevinin sıfır olduğu iç noktaları bulalım.
\( \dfrac{6x^2(x + 6)}{(x + 4)^2} = 0 \)
\( x = 0 \)
Fonksiyonun tanım kümesi içinde birinci türevinin tanımsız olduğu nokta yoktur.
Kritik nokta: \( x = 0 \)
Fonksiyonun kritik noktadaki değerini bulalım.
\( f(0) = \dfrac{3(0)^3}{0 + 4} = 0 \)
Fonksiyonun kapalı uç noktalarındaki değerini bulalım.
\( f(-2) = \dfrac{3(-2)^3}{(-2) + 4} = -12 \)
\( f(2) = \dfrac{3(2)^3}{2 + 4} = 4 \)
Bu değerleri karşılaştırdığımızda fonksiyonun mutlak minimum ve maksimum değerleri ve noktaları aşağıdaki gibi bulunur.
Mutlak minimum: Fonksiyonun \( -12 \) değerini aldığı \( x = -2 \) noktası
Mutlak maksimum: Fonksiyonun \( 4 \) değerini aldığı \( x = 2 \) noktası
Fonksiyonun grafiği ve karşılaştırma yaptığımız nokta ve değerler aşağıdaki şekilde gösterilmiştir.
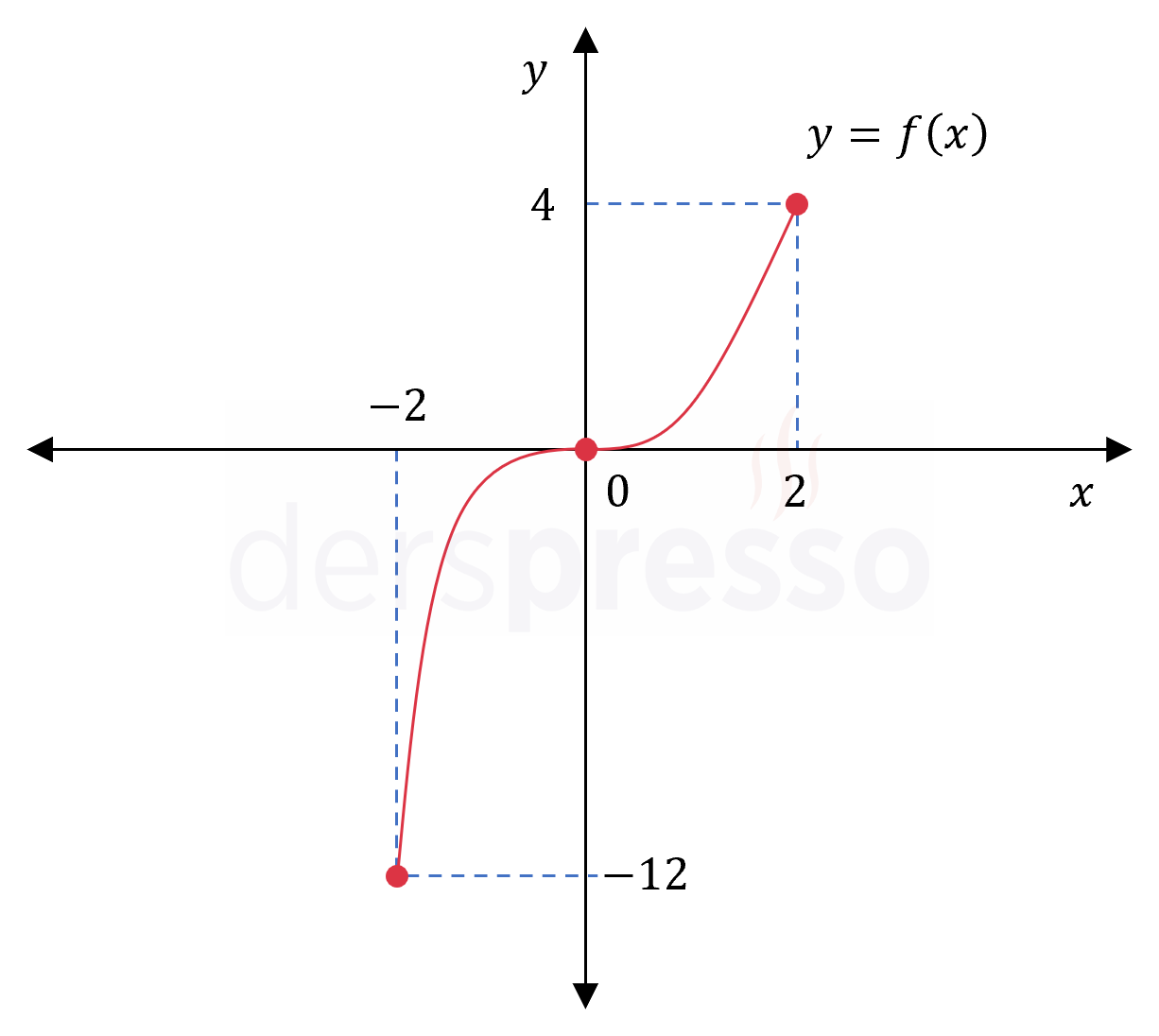
\( f: [-2, 2] \to \mathbb{R} \) olmak üzere,
\( f(x) = \dfrac{x + 3}{x^2 - 5} \)
fonksiyonunun mutlak minimum ve maksimum değerlerini ve noktalarını bulunuz.
Çözümü Göster\( f \) fonksiyonu kapalı bir aralıkta tanımlıdır ve bir rasyonel fonksiyon olduğu için paydayı sıfır yapan ve tanım aralığı dışındaki \( x = \pm\sqrt{5} \) noktaları hariç süreklidir.
Kapalı bir aralıkta tanımlı ve sürekli bir fonksiyon, mutlak minimum ve maksimum değerlerini kritik ya da kapalı uç noktalarından birinde alır.
Fonksiyonun kritik noktaları birinci türevin sıfır ya da tanımsız olduğu iç noktalardır.
\( f'(x) = \dfrac{1(x^2 - 5) - (x + 3)(2x)}{(x^2 - 5)^2} \)
\( = \dfrac{-x^2 - 6x - 5}{(x^2 - 5)^2} \)
\( = -\dfrac{(x + 5)(x + 1)}{(x^2 - 5)^2} \)
Fonksiyonun tanım kümesi içinde birinci türevinin sıfır olduğu iç noktaları bulalım.
\( -\dfrac{(x + 5)(x + 1)}{(x^2 - 5)^2} = 0 \)
\( x = -1 \)
Fonksiyonun tanım kümesi içinde birinci türevinin tanımsız olduğu nokta yoktur.
Kritik nokta: \( x = -1 \)
Fonksiyonun kritik noktadaki değerini bulalım.
\( f(-1) = \dfrac{-1 + 3}{(-1)^2 - 5} = -\dfrac{1}{2} \)
Fonksiyonun kapalı uç noktalarındaki değerini bulalım.
\( f(-2) = \dfrac{-2 + 3}{(-2)^2 - 5} = -1 \)
\( f(2) = \dfrac{2 + 3}{2^2 - 5} = -5 \)
Bu değerleri karşılaştırdığımızda fonksiyonun mutlak minimum ve maksimum değerleri ve noktaları aşağıdaki gibi bulunur.
Mutlak minimum: Fonksiyonun \( -5 \) değerini aldığı \( x = 2 \) noktası
Mutlak maksimum: Fonksiyonun \( -\frac{1}{2} \) değerini aldığı \( x = -1 \) noktası
Fonksiyonun grafiği ve karşılaştırma yaptığımız nokta ve değerler aşağıdaki şekilde gösterilmiştir.
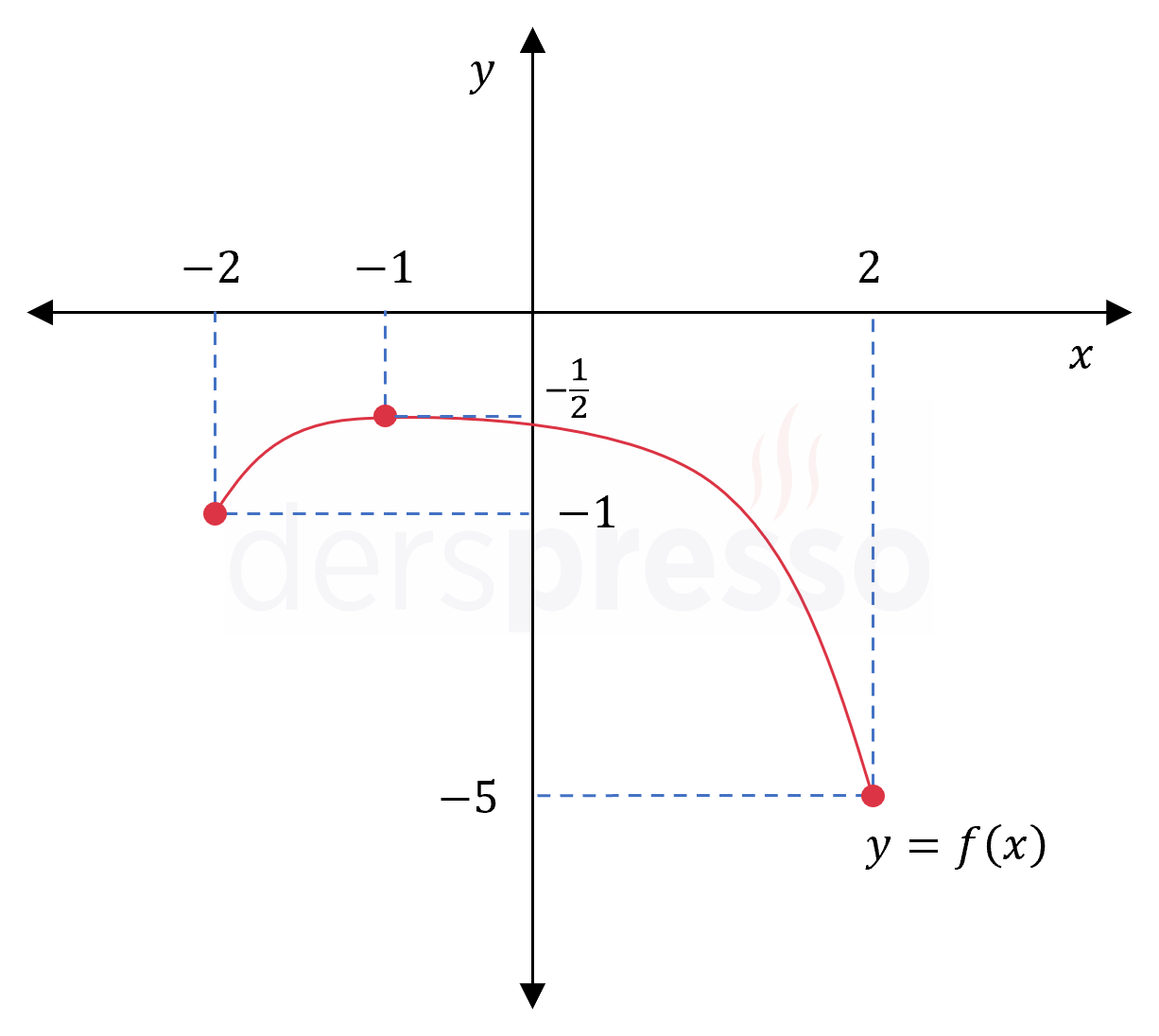
\( f: [1, 10] \to \mathbb{R} \) olmak üzere,
\( f(x) = \abs{x - 4} \)
fonksiyonunun mutlak minimum ve maksimum değerlerini ve noktalarını bulunuz.
Çözümü GösterMutlak değer fonksiyonunu parçalı fonksiyon şeklinde yazalım.
\( f(x) = \begin{cases} 4 - x & 1 \le x \lt 4 \\ x - 4 & 4 \le x \le 10 \end{cases} \)
\( f \) parçalı fonksiyonunun \( x = 4 \) geçiş noktasında sürekli olup olmadığını bulalım.
\( x = 4 \) noktasındaki soldan limiti bulalım.
\( \lim\limits_{x \to 4^-} {f(x)} = \lim\limits_{x \to 4^-} (4 - x) \)
\( = 4 - 4 = 0 \)
\( x = 4 \) noktasındaki sağdan limiti bulalım.
\( \lim\limits_{x \to 4^+} {f(x)} = \lim\limits_{x \to 4^+} (x - 4) \)
\( = 4 - 4 = 0 \)
\( x = 4 \) noktasındaki fonksiyon değerini bulalım.
\( f(4) = 4 - 4 = 0 \)
Buna göre bu noktada soldan ve sağdan limitler ve fonksiyon değeri birer reel sayı olarak tanımlı ve birbirine eşittir, dolayısıyla fonksiyon \( x = 4 \) noktasında süreklidir.
\( f(4^-) = f(4^+) = f(4) \)
Fonksiyonun mutlak minimum ve maksimum noktalarının olup olmadığını bulmak için kritik ve kapalı uç noktalarındaki değerini bulalım.
\( f \) fonksiyonunun türevini bulalım.
Sürekliliğini gösterdiğimiz bu noktadaki türevlenebilirliği kontrol edelim.
Fonksiyonun \( x = 4 \) noktasındaki soldan türevini bulalım.
\( f'(x) = -1 \)
\( f'(4^-) = -1 \)
Fonksiyonun \( x = 4 \) noktasındaki sağdan türevini bulalım.
\( f'(x) = 1 \)
\( f'(4^+) = 1 \)
Buna göre bu noktada soldan ve sağdan türevler birbirine eşit değildir, dolayısıyla fonksiyonun \( x = 4 \) noktasında türevi tanımsızdır.
\( f'(x) = \begin{cases} -1 & 1 \le x \lt 4 \\ \text{Tanımsız} & x = 4 \\ 1 & 4 \lt x \le 10 \end{cases} \)
Fonksiyonun kritik noktaları birinci türevin sıfır ya da tanımsız olduğu iç noktalardır.
Fonksiyonun tanım kümesi içinde birinci türevinin sıfır olduğu iç noktaları bulalım.
Her iki aralık için de türev sabittir ve sırasıyla \( -1 \) ve \( 1 \) değerlerini alır. Dolayısıyla türevi sıfır yapan bir \( x \) değeri yoktur.
Fonksiyonun \( x = 4 \) noktasında birinci türevi tanımsızdır.
Kritik nokta: \( x = 4 \)
Fonksiyonun kritik noktadaki değerini bulalım.
\( f(4) = 4 - 4 = 0 \)
Fonksiyonun kapalı uç noktalarındaki değerini bulalım.
\( f(1) = 4 - 1 = 3 \)
\( f(10) = 10 - 4 = 6 \)
Bu değerleri karşılaştırdığımızda fonksiyonun mutlak minimum ve maksimum değerleri ve noktaları aşağıdaki gibi bulunur.
Mutlak minimum: Fonksiyonun \( 0 \) değerini aldığı \( x = 4 \) noktası
Mutlak maksimum: Fonksiyonun \( 6 \) değerini aldığı \( x = 10 \) noktası
Fonksiyonun grafiği ve karşılaştırma yaptığımız nokta ve değerler aşağıdaki şekilde gösterilmiştir.
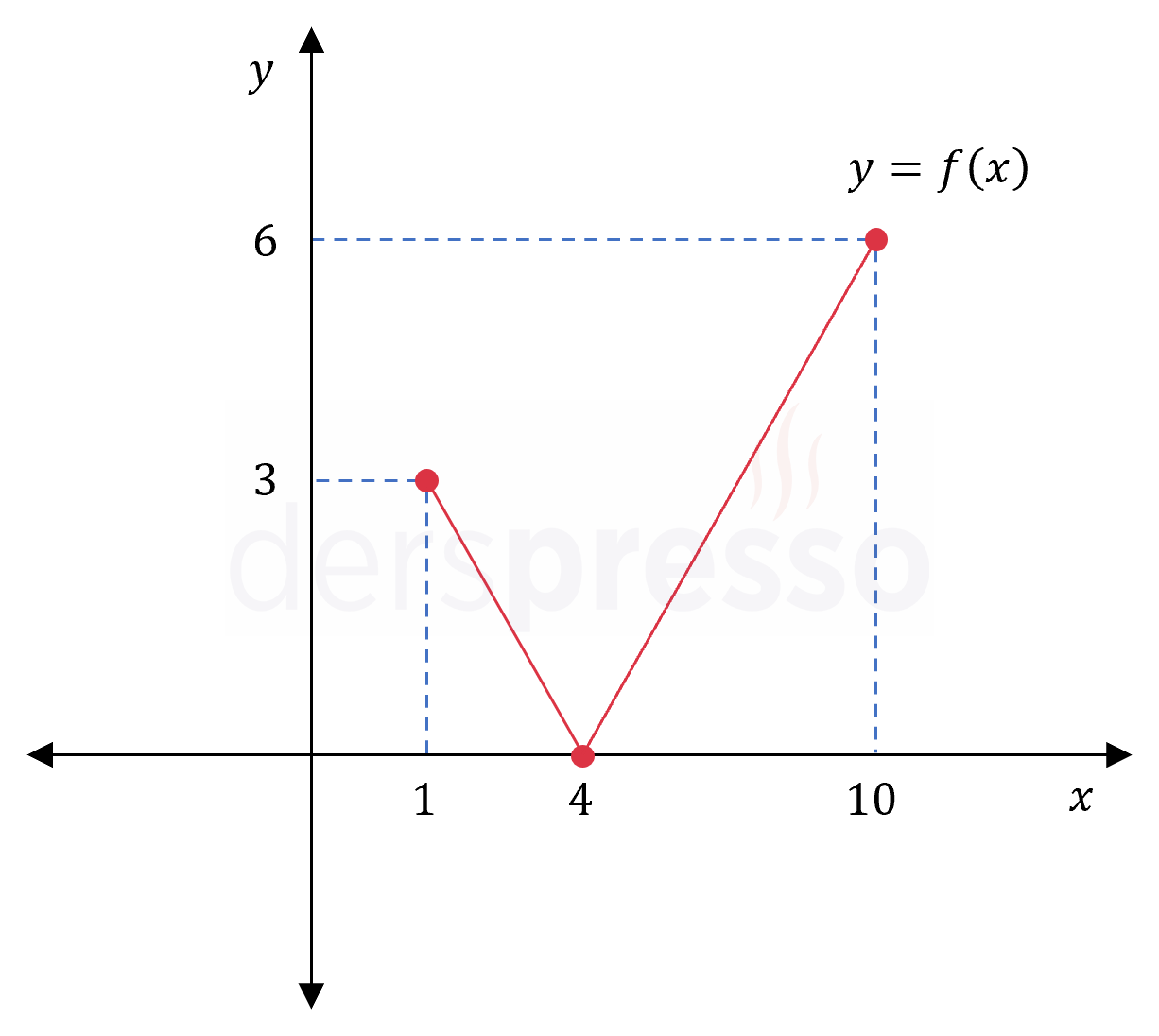
\( f(x) = \dfrac{x + 4}{x - 4} \)
fonksiyonunun tanımlı olduğu en geniş aralıkta mutlak minimum ve maksimum değerlerini ve noktalarını bulunuz.
Çözümü Göster\( f \) fonksiyonu sonsuz aralıkta tanımlıdır ve bir rasyonel fonksiyon olduğu için paydayı sıfır yapan \( x = 4 \) noktası hariç süreklidir.
Fonksiyonun sonsuzdaki limitlerini bulalım.
\( \lim\limits_{x \to \infty} {\dfrac{x + 4}{x - 4}} = 1 \)
\( \lim\limits_{x \to -\infty} {\dfrac{x + 4}{x - 4}} = 1 \)
Fonksiyonun süreksiz olduğu \( x = 4 \) noktasındaki soldan ve sağdan limitlerini bulalım.
\( \lim\limits_{x \to 4^+} {\dfrac{x + 4}{x - 4}} = \dfrac{4 + 4}{4^+ - 4} \)
\( = \dfrac{8}{0^+} = \infty \)
Buna göre fonksiyonun mutlak maksimum noktası yoktur.
\( \lim\limits_{x \to 4^-} {\dfrac{4 + 4}{4^- - 4}} \)
\( = \dfrac{8}{0^-} = -\infty \)
Buna göre fonksiyonun mutlak minimum noktası yoktur.
Mutlak minimum: \( x \to 4^- \) iken limit negatif sonsuz olduğu için fonksiyonun mutlak minimum noktası yoktur.
Mutlak maksimum: \( x \to 4^+ \) iken limit pozitif sonsuz olduğu için fonksiyonun mutlak maksimum noktası yoktur.
Fonksiyonun grafiği ve karşılaştırma yaptığımız nokta ve değerler aşağıdaki şekilde gösterilmiştir.
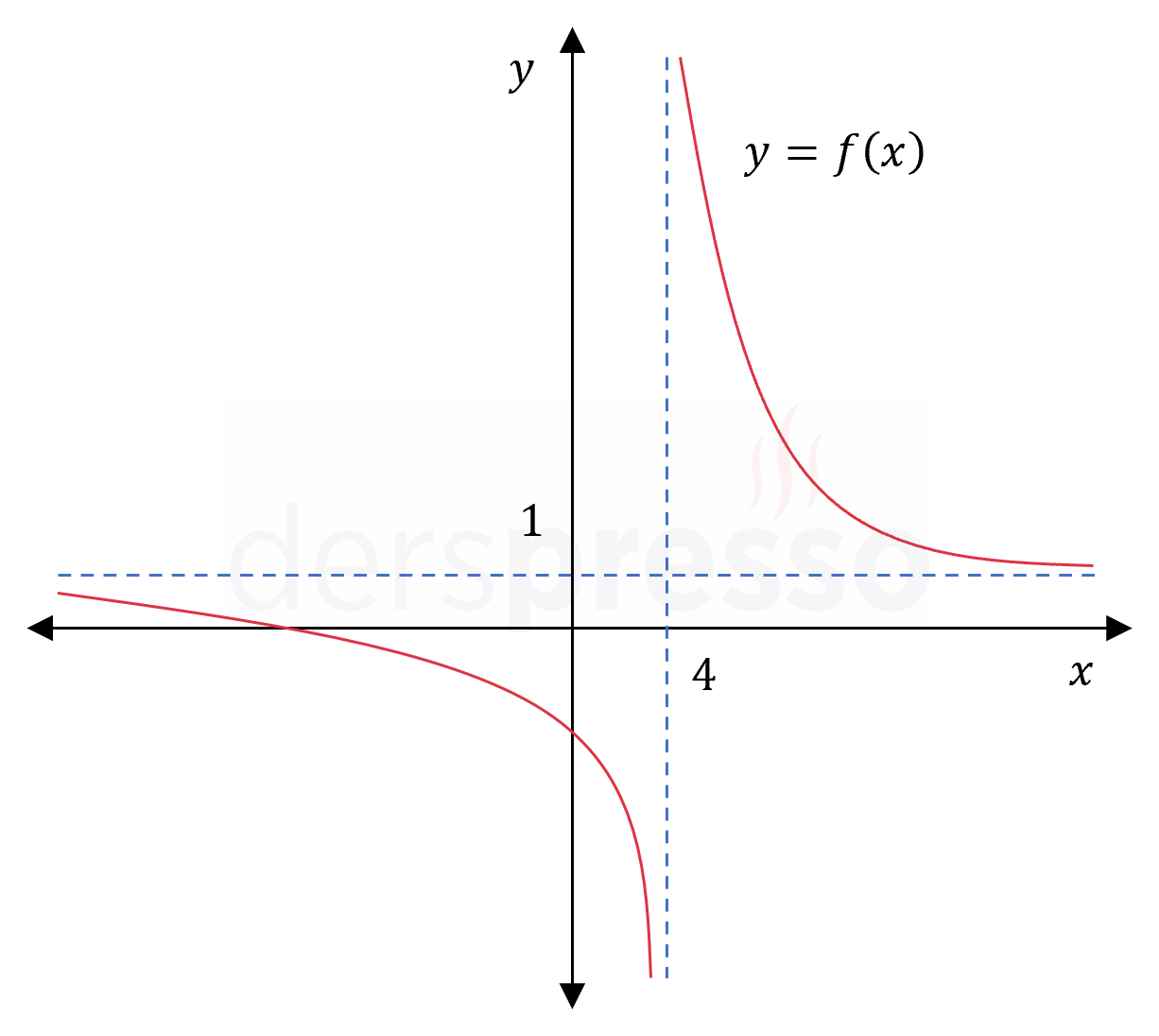
\( f(x) = \dfrac{x^2 + 1}{x^2 - 9} \)
fonksiyonunun tanımlı olduğu en geniş aralıkta mutlak minimum ve maksimum değerlerini ve noktalarını bulunuz.
Çözümü Göster\( f \) fonksiyonu sonsuz aralıkta tanımlıdır ve bir rasyonel fonksiyon olduğu için paydayı sıfır yapan \( x = \pm 3 \) noktaları hariç süreklidir.
Fonksiyonun sonsuzdaki limitlerini bulalım.
\( \lim\limits_{x \to \infty} {\dfrac{x^2 + 1}{x^2 - 9}} = 1 \)
\( \lim\limits_{x \to -\infty} {\dfrac{x^2 + 1}{x^2 - 9}} = 1 \)
Fonksiyonun süreksiz olduğu \( x = \pm 3 \) noktalarındaki soldan ve sağdan limitlerini bulalım.
\( \lim\limits_{x \to 3^+} {\dfrac{x^2 + 1}{x^2 - 9}} = \dfrac{3^2 + 1}{(3^+)^2 - 9} \)
\( = \dfrac{10}{0^+} = \infty \)
Buna göre fonksiyonun mutlak maksimum noktası yoktur.
\( \lim\limits_{x \to 3^-} {\dfrac{x^2 + 1}{x^2 - 9}} = \dfrac{3^2 + 1}{(3^-)^2 - 9} \)
\( = \dfrac{10}{0^-} = -\infty \)
Buna göre fonksiyonun mutlak minimum noktası yoktur.
\( \lim\limits_{x \to -3^+} {\dfrac{x^2 + 1}{x^2 - 9}} = \dfrac{(-3)^2 + 1}{(-3^+)^2 - 9} \)
\( = \dfrac{10}{0^-} = -\infty \)
\( \lim\limits_{x \to -3^-} {\dfrac{x^2 + 1}{x^2 - 9}} = \dfrac{(-3)^2 + 1}{(-3^-)^2 - 9} \)
\( = \dfrac{10}{0^+} = \infty \)
Mutlak minimum: \( x \to 3^- \) ve \( x \to -3^+ \) iken limit negatif sonsuz olduğu için fonksiyonun mutlak minimum noktası yoktur.
Mutlak maksimum: \( x \to 3^+ \) ve \( x \to -3^- \) iken limit pozitif sonsuz olduğu için fonksiyonun mutlak maksimum noktası yoktur.
Fonksiyonun grafiği ve karşılaştırma yaptığımız nokta ve değerler aşağıdaki şekilde gösterilmiştir.
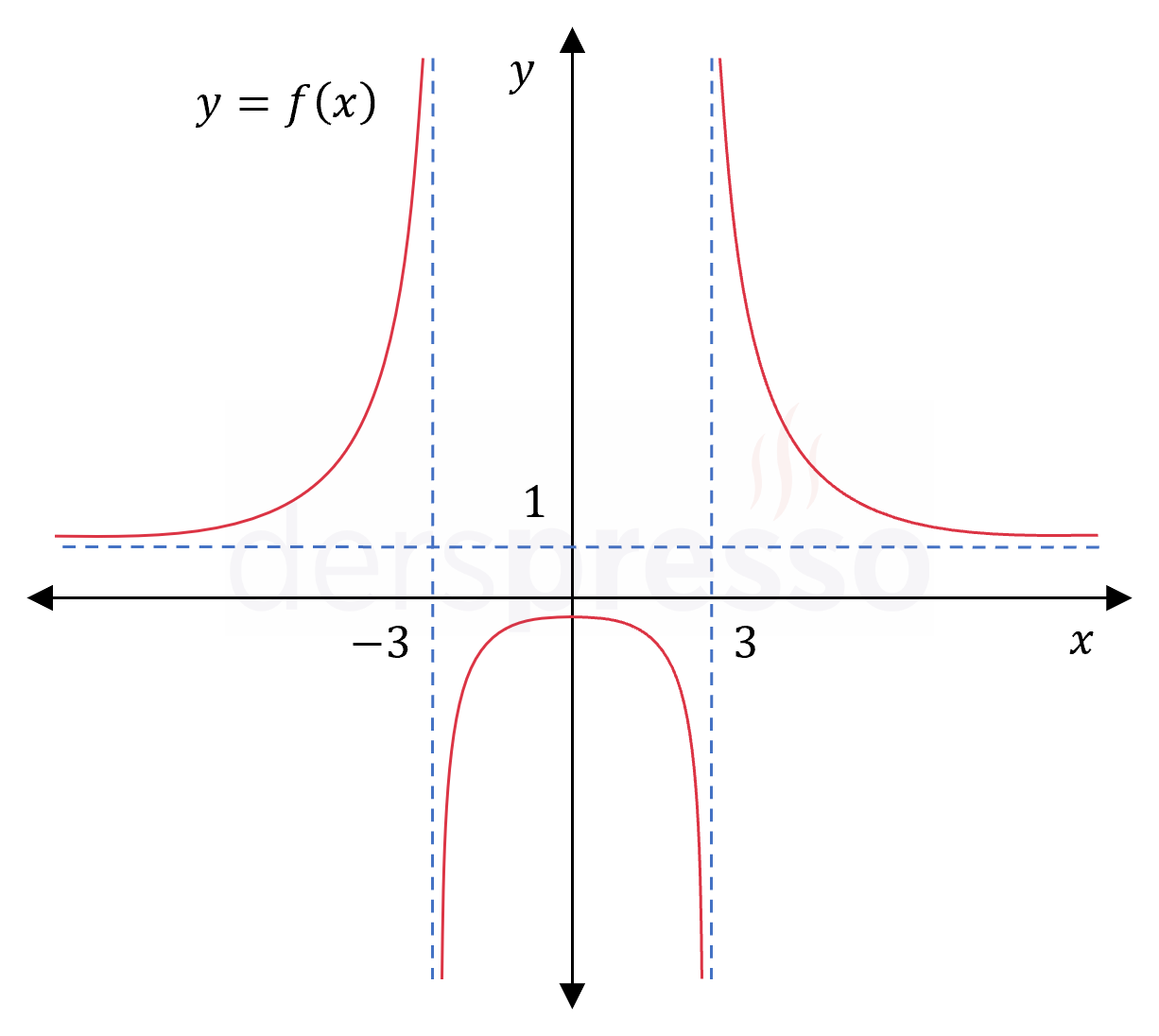
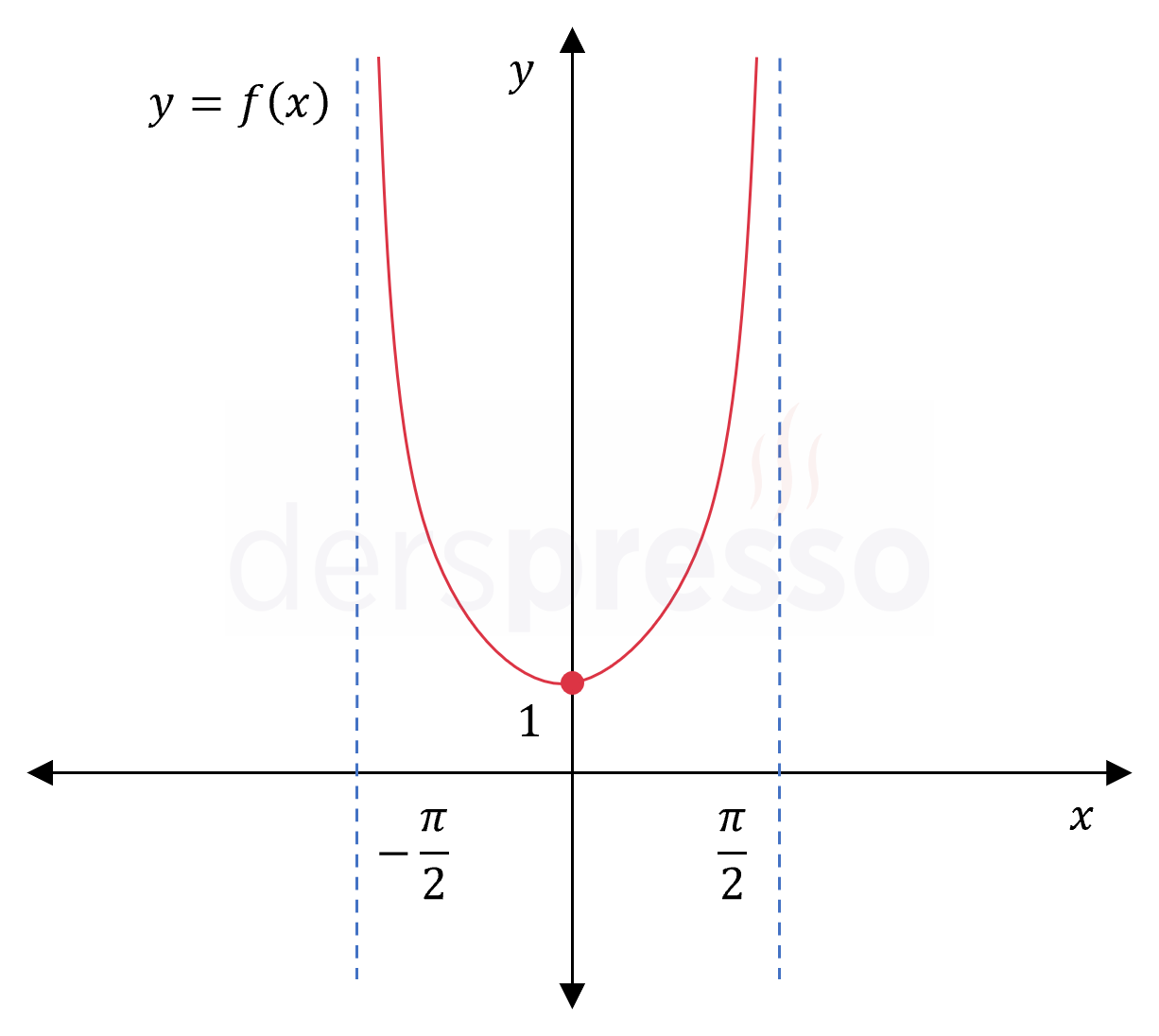
\( f: (-\frac{\pi}{2}, \frac{\pi}{2}) \to \mathbb{R} \) olmak üzere,
\( f(x) = \dfrac{1}{\cos{x}} \)
fonksiyonunun mutlak minimum ve maksimum değerlerini ve noktalarını bulunuz.
Çözümü Göster\( f \) fonksiyonu açık bir aralıkta tanımlıdır ve bir rasyonel fonksiyon olduğu için paydayı sıfır yapan ve tanım aralığı dışındaki \( x = \pm \frac{\pi}{2} \) noktaları hariç süreklidir.
Fonksiyonun açık uç noktalarındaki limitini bulalım.
\( \lim\limits_{x \to -\frac{\pi}{2}^+} {\dfrac{1}{\cos{x}}} = \dfrac{1}{\cos(-\frac{\pi}{2}^+)} \)
\( = \dfrac{1}{0^+} = \infty \)
Buna göre fonksiyonun mutlak maksimum noktası yoktur.
\( \lim\limits_{x \to \frac{\pi}{2}^-} {\dfrac{1}{\cos{x}}} = \dfrac{1}{\cos{\frac{\pi}{2}^-}} \)
\( = \dfrac{1}{0^+} = \infty \)
Fonksiyonun mutlak minimum noktasının olup olmadığını bulmak için kritik noktalardaki değerini bulalım.
Fonksiyonun kritik noktaları birinci türevin sıfır ya da tanımsız olduğu iç noktalardır.
\( f'(x) = \dfrac{\sin{x}}{\cos^2{x}} \)
Fonksiyonun tanım kümesi içinde birinci türevinin sıfır olduğu iç noktaları bulalım.
\( \dfrac{\sin{x}}{\cos^2{x}} = 0 \)
\( \sin{x} = 0 \)
Sinüs fonksiyonu \( 0 \) değerini verilen tanım aralığında aşağıdaki \( x \) değerinde alır.
\( x = 0 \)
Fonksiyonun tanım kümesi içinde birinci türevinin tanımsız olduğu iç nokta yoktur.
Kritik nokta: \( x = 0 \)
Fonksiyonun kritik noktadaki değerini bulalım.
\( f(0) = \dfrac{1}{\cos{0}} = \dfrac{1}{1} = 1 \)
Bu değerleri karşılaştırdığımızda fonksiyonun mutlak minimum ve maksimum değerleri ve noktaları aşağıdaki gibi bulunur.
Mutlak minimum: Fonksiyonun \( 1 \) değerini aldığı \( x = 0 \) noktası
Mutlak maksimum: \( x \to -\frac{\pi}{2}^+ \) ve \( x \to \frac{\pi}{2}^- \) iken limit sonsuz olduğu için fonksiyonun mutlak maksimum noktası yoktur.
Fonksiyonun grafiği ve karşılaştırma yaptığımız nokta ve değerler aşağıdaki şekilde gösterilmiştir.
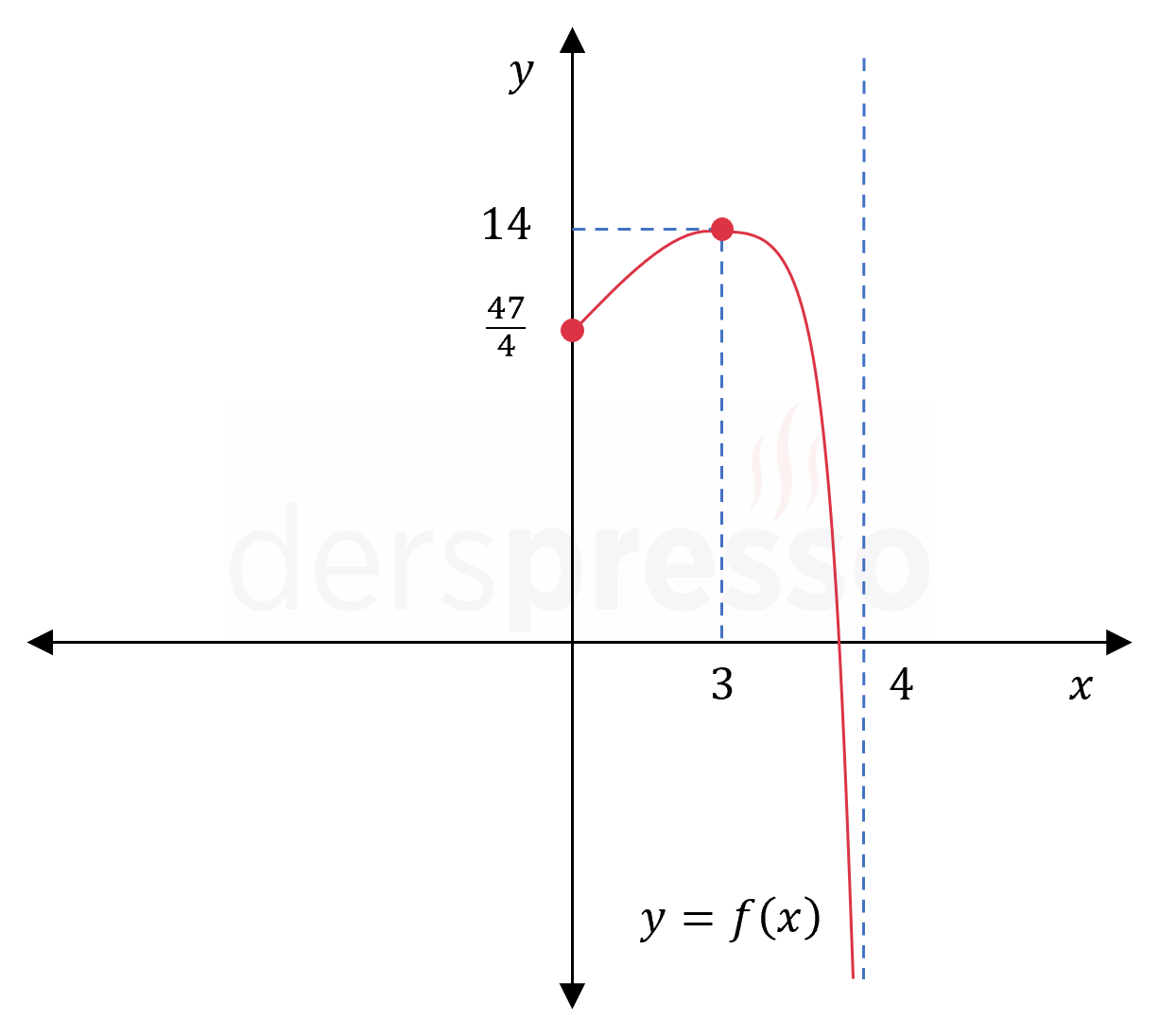
\( f: [0, 4) \to \mathbb{R} \) olmak üzere,
\( f(x) = \dfrac{x^2 + 8x - 47}{x - 4} \)
fonksiyonunun mutlak minimum ve maksimum değerlerini ve noktalarını bulunuz.
Çözümü Göster\( f \) fonksiyonu yarı açık bir aralıkta tanımlıdır ve bir rasyonel fonksiyon olduğu için paydayı sıfır yapan ve tanım aralığı dışındaki \( x = 4 \) noktası hariç süreklidir.
Fonksiyonun açık uç noktasındaki limitini bulalım.
\( \lim\limits_{x \to 4^-} {\dfrac{x^2 + 8x - 47}{x - 4}} = \dfrac{4^2 + 8(4) - 47}{4^- - 4} \)
\( = \dfrac{1}{0^-} = -\infty \)
Buna göre fonksiyonun mutlak minimum noktası yoktur.
Fonksiyonun mutlak maksimum noktasının olup olmadığını bulmak için kritik ve kapalı uç noktasındaki değerini bulalım.
Fonksiyonun kritik noktaları birinci türevin sıfır ya da tanımsız olduğu iç noktalardır.
\( f'(x) = \dfrac{(2x + 8)(x - 4) - (x^2 + 8x - 47)(1)}{(x - 4)^2} \)
\( = \dfrac{x^2 - 8x + 15}{(x - 4)^2} \)
Fonksiyonun tanım kümesi içinde birinci türevinin sıfır olduğu iç noktaları bulalım.
\( \dfrac{(x - 3)(x - 5)}{(x - 4)^2} = 0\)
\( x = 3 \)
Fonksiyonun tanım kümesi içinde birinci türevinin tanımsız olduğu nokta yoktur.
Kritik nokta: \( x = 3 \)
Fonksiyonun kritik noktadaki değerini bulalım.
\( f(3) = \dfrac{3^2 + 8(3) - 47}{3 - 4} = 14 \)
Fonksiyonun kapalı uç noktasındaki değerini bulalım.
\( f(0) = \dfrac{0^2 + 8(0) - 47}{0 - 4} = \dfrac{47}{4} \)
Bu değerleri karşılaştırdığımızda fonksiyonun mutlak minimum ve maksimum değerleri ve noktaları aşağıdaki gibi bulunur.
Mutlak minimum: \( x \to 4^- \) iken limit negatif sonsuz olduğu için fonksiyonun mutlak minimum noktası yoktur.
Mutlak maksimum: Fonksiyonun \( 14 \) değerini aldığı \( x = 3 \) noktası
Fonksiyonun grafiği ve karşılaştırma yaptığımız nokta ve değerler aşağıdaki şekilde gösterilmiştir.
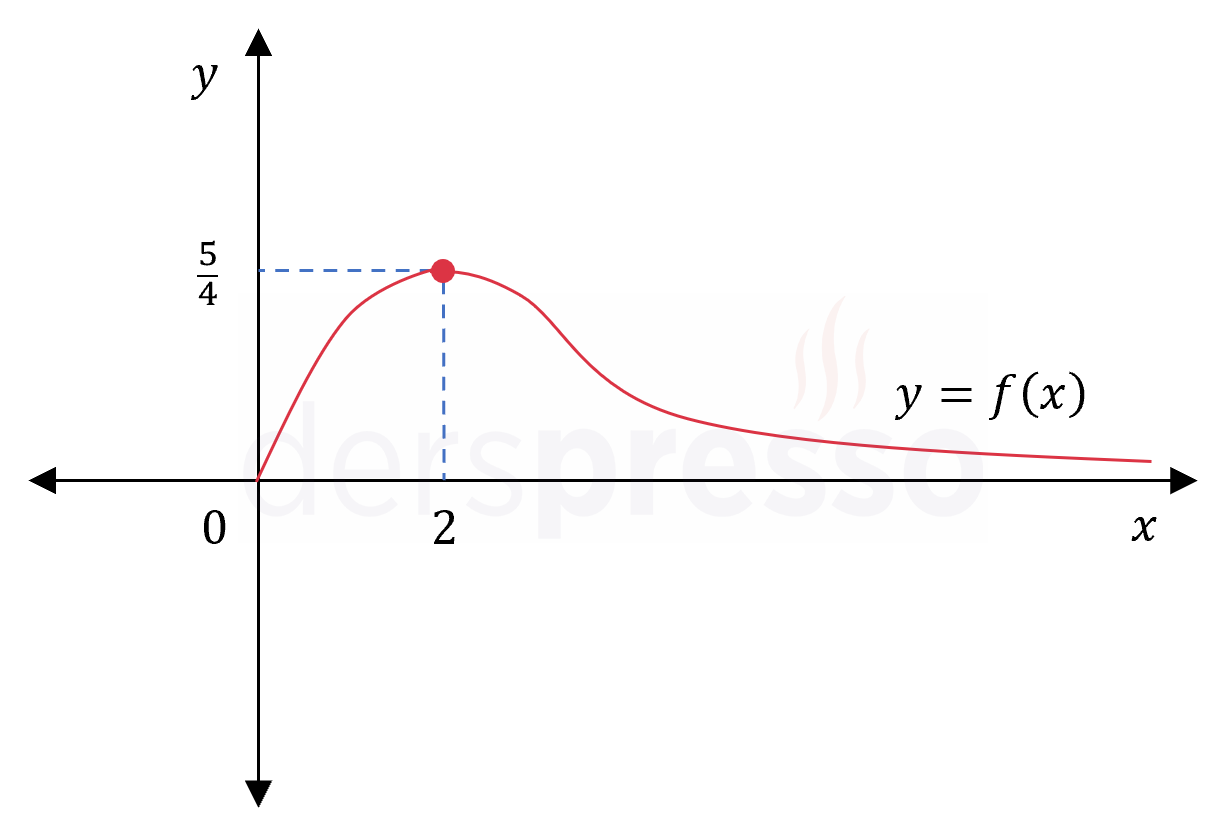
\( f: (0, \infty) \to \mathbb{R} \) olmak üzere,
\( f(x) = \dfrac{5x}{x^2 + 4} \)
fonksiyonunun mutlak minimum ve maksimum değerlerini ve noktalarını bulunuz.
Çözümü Göster\( f \) fonksiyonu sonsuz aralıkta tanımlıdır ve paydası tüm reel sayılarda pozitif olan bir rasyonel fonksiyon olduğu için süreklidir.
Fonksiyonun açık uç noktalarındaki limitini bulalım.
\( \lim\limits_{x \to 0^+} {\dfrac{5x}{x^2 + 4}} = \dfrac{5(0)}{0^2 + 4} = 0 \)
\( \lim\limits_{x \to \infty} {\dfrac{5x}{x^2 + 4}} = 0 \)
Fonksiyonun mutlak minimum ve maksimum noktasının olup olmadığını bulmak için kritik noktalardaki değerini bulalım.
Fonksiyonun kritik noktaları birinci türevin sıfır ya da tanımsız olduğu iç noktalardır.
\( f'(x) = \dfrac{5(x^2 + 4) - 5x(2x)}{(x^2 + 4)^2} \)
\( = \dfrac{-5(x^2 - 4)}{(x^2 + 4)^2} \)
Fonksiyonun tanım kümesi içinde birinci türevinin sıfır olduğu iç noktaları bulalım.
\( \dfrac{-5(x - 2)(x + 2)}{(x^2 + 4)^2} = 0 \)
\( x = 2 \)
Fonksiyonun birinci türevinin tanımsız olduğu iç nokta yoktur.
Kritik nokta: \( x = 2 \)
Fonksiyonun kritik noktadaki değerini bulalım.
\( f(2) = \dfrac{5(2)}{2^2 + 4} = \dfrac{5}{4} \)
Bu değerleri karşılaştırdığımızda fonksiyonun mutlak minimum ve maksimum değerleri ve noktaları aşağıdaki gibi bulunur.
Mutlak minimum: \( x \to 0^+ \) ve \( x \to \infty \) iken limit sıfır olduğu, ancak fonksiyon bu değeri almadığı için fonksiyonun mutlak minimum noktası yoktur.
Mutlak maksimum: Fonksiyonun \( \frac{5}{4} \) değerini aldığı \( x = 2 \) noktası
Fonksiyonun grafiği ve karşılaştırma yaptığımız nokta ve değerler aşağıdaki şekilde gösterilmiştir.
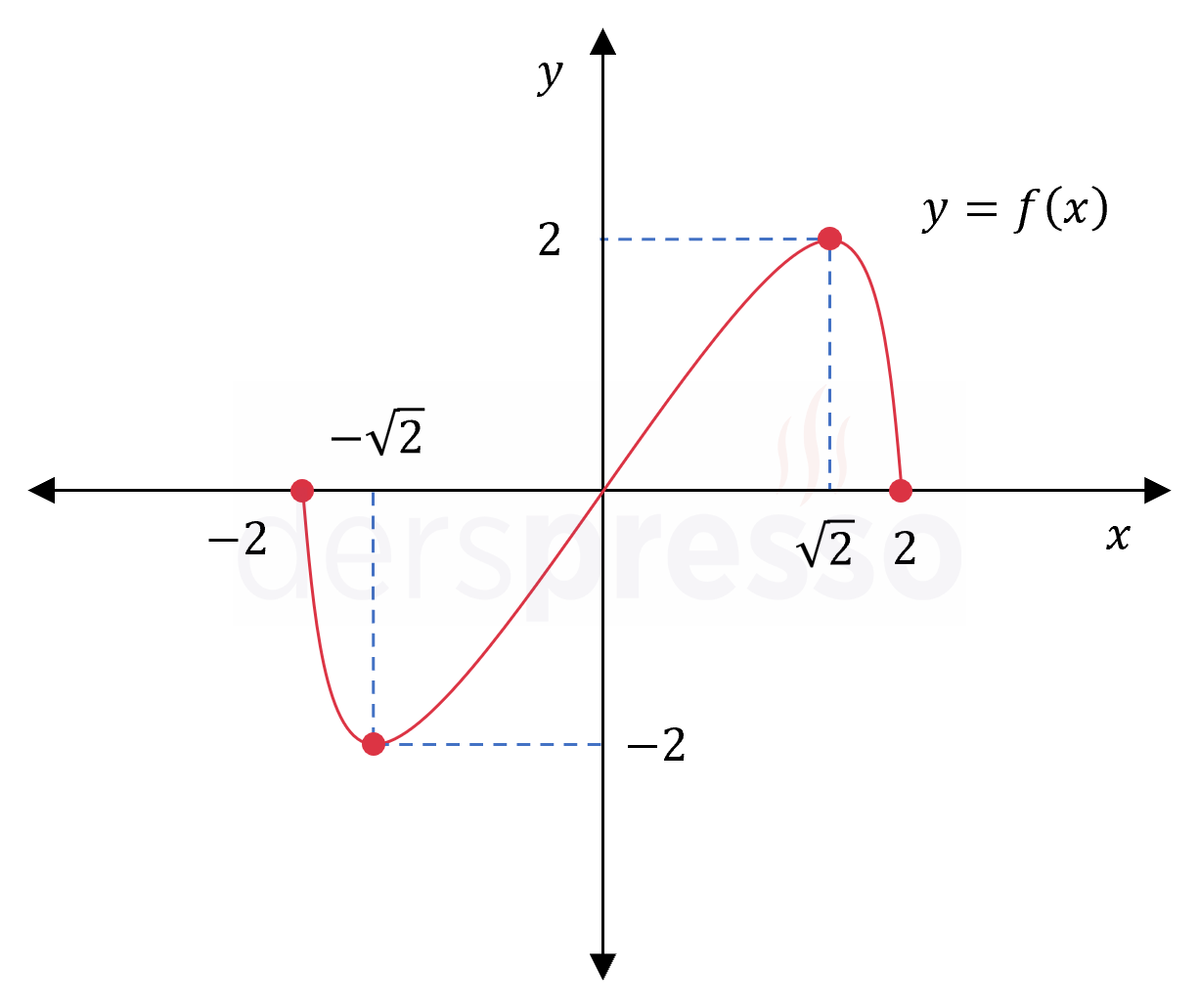
\( f: [-2, 2] \to \mathbb{R} \) olmak üzere,
\( f(x) = x\sqrt{4 - x^2} \)
fonksiyonunun mutlak minimum ve maksimum değerlerini ve noktalarını bulunuz.
Çözümü Göster\( f \) fonksiyonu kapalı bir aralıkta tanımlıdır ve iki sürekli fonksiyonun çarpımından oluştuğu için tanım kümesi içinde süreklidir.
Kapalı bir aralıkta tanımlı ve sürekli bir fonksiyon, mutlak minimum ve maksimum değerlerini kritik ya da kapalı uç noktalarından birinde alır.
Fonksiyonun kritik noktaları birinci türevin sıfır ya da tanımsız olduğu iç noktalardır.
\( f'(x) = \sqrt{4 - x^2} -\dfrac{x^2}{\sqrt{4 - x^2}} \)
\( = \dfrac{4 - 2x^2}{\sqrt{4 - x^2}} \)
Fonksiyonun birinci türevinin sıfır olduğu iç noktaları bulalım.
\( \dfrac{4 - 2x^2}{\sqrt{4 - x^2}} = 0 \)
\( 4 - 2x^2 = 0 \)
\( x = \pm \sqrt{2} \)
Fonksiyonun birinci türevinin tanımsız olduğu iç nokta yoktur.
Kritik noktalar: \( x = \pm \sqrt{2} \)
Fonksiyonun kritik noktalardaki değerini bulalım.
\( f(-\sqrt{2}) = -\sqrt{2}\sqrt{4 - (-\sqrt{2})^2} = -2 \)
\( f(\sqrt{2}) = \sqrt{2}\sqrt{4 - (\sqrt{2})^2} = 2 \)
Fonksiyonun kapalı uç noktalarındaki değerini bulalım.
\( f(-2) = -2\sqrt{4 - (-2)^2} = 0 \)
\( f(2) = 2\sqrt{4 - 2^2} = 0 \)
Bu değerleri karşılaştırdığımızda fonksiyonun mutlak minimum ve maksimum değerleri ve noktaları aşağıdaki gibi bulunur.
Mutlak minimum: Fonksiyonun \( -2 \) değerini aldığı \( x = -\sqrt{2} \) noktası
Mutlak maksimum: Fonksiyonun \( 2 \) değerini aldığı \( x = \sqrt{2} \) noktası
Fonksiyonun grafiği ve karşılaştırma yaptığımız nokta ve değerler aşağıdaki şekilde gösterilmiştir.
\( f(x) = \begin{cases} x^2 - 4x - 12 & x \lt 0 \\ x + 2 & x \ge 0 \end{cases} \)
fonksiyonunun tanımlı olduğu en geniş aralıkta mutlak minimum ve maksimum değerlerini ve noktalarını bulunuz.
Çözümü Göster\( f \) fonksiyonu sonsuz aralıkta tanımlıdır.
Fonksiyonun sonsuzdaki limitlerini bulalım.
\( \lim\limits_{x \to -\infty} {f(x)} = \lim\limits_{x \to -\infty} (x^2 - 4x - 12) \)
\( = \lim\limits_{x \to -\infty} {x^2} = \infty \)
Buna göre fonksiyonun mutlak maksimum değeri yoktur.
\( \lim\limits_{x \to \infty} {f(x)} = \lim\limits_{x \to \infty} (x + 2) = \infty \)
\( f \) parçalı fonksiyonunun \( x = 0 \) geçiş noktasında sürekli olup olmadığını bulalım.
\( x = 0 \) noktasındaki soldan limiti bulalım.
\( \lim\limits_{x \to 0^-} {f(x)} = \lim\limits_{x \to 0^-} (x^2 - 4x - 12) \)
\( = 0^2 - 4(0) - 12 = -12 \)
\( x = 0 \) noktasındaki sağdan limiti bulalım.
\( \lim\limits_{x \to 0^+} {f(x)} = \lim\limits_{x \to 0^+} (x + 2) \)
\( = 0 + 2 = 2 \)
Soldan ve sağdan limitler birbirine eşit olmadığı için fonksiyon \( x = 0 \) noktasında süreksizdir.
Fonksiyonun mutlak minimum noktasının olup olmadığını bulmak için kritik noktadaki değerini bulalım.
\( f \) fonksiyonunun türevini bulalım.
Fonksiyon \( x = 0 \) noktasında süreksiz olduğu için türevi tanımsızdır.
\( f'(x) = \begin{cases} 2x - 4 & x \lt 0 \\ \text{Tanımsız} & x = 0 \\ 1 & x \gt 0 \end{cases} \)
Fonksiyonun kritik noktaları birinci türevin sıfır ya da tanımsız olduğu iç noktalardır.
Fonksiyonun tanım kümesi içinde birinci türevinin sıfır olduğu iç noktaları bulalım.
\( x \lt 0 \) için:
\( 2x - 4 = 0 \)
Bu aralıkta bu denklemi sağlayan bir \( x \) değeri yoktur.
\( x \gt 0 \) için:
\( 1 = 0 \)
Bu denklemi sağlayan bir \( x \) değeri yoktur.
Fonksiyonun \( x = 0 \) noktasında birinci türevi tanımsızdır.
Kritik nokta: \( x = 0 \)
Fonksiyonun kritik noktadaki değerini bulalım.
\( f(0) = 0 + 2 = 2 \)
Bu değerleri karşılaştırdığımızda fonksiyonun mutlak minimum ve maksimum değerleri ve noktaları aşağıdaki gibi bulunur.
Mutlak minimum: \( x \to 0^- \) iken limit değeri (\( -12 \)) karşılaştırma yaptığımız diğer değerlerden küçük olduğu ve fonksiyon bu limit değerini almadığı için fonksiyonun mutlak minimum noktası yoktur.
Mutlak maksimum: \( x \to \infty \) ve \( x \to -\infty \) iken limit sonsuz olduğu için fonksiyonun mutlak maksimum noktası yoktur.
Fonksiyonun grafiği ve karşılaştırma yaptığımız nokta ve değerler aşağıdaki şekilde gösterilmiştir.

\( f: [0, 2\pi] \to \mathbb{R} \) olmak üzere,
\( f(x) = \abs{\sin{x}} \)
fonksiyonunun mutlak minimum ve maksimum değerlerini ve noktalarını bulunuz.
Çözümü GösterMutlak değer fonksiyonunu parçalı fonksiyon şeklinde yazalım.
Sinüs fonksiyonu birinci ve ikinci bölgede pozitif, üçüncü ve dördüncü bölgede negatif değer alır.
\( f(x) = \begin{cases} \sin{x} & 0 \le x \le \pi \\ -\sin{x} & \pi \lt x \le 2\pi \end{cases} \)
\( f \) parçalı fonksiyonunun \( x = \pi \) geçiş noktasında sürekli olup olmadığını bulalım.
\( x = \pi \) noktasındaki soldan limiti bulalım.
\( \lim\limits_{x \to \pi^-} {f(x)} = \lim\limits_{x \to \pi^-} {\sin{x}} \)
\( = \sin{\pi} = 0 \)
\( x = \pi \) noktasındaki sağdan limiti bulalım.
\( \lim\limits_{x \to \pi^+} {f(x)} = \lim\limits_{x \to \pi^+} (-\sin{x}) \)
\( = -\sin{\pi} = 0 \)
\( x = \pi \) noktasındaki fonksiyon değerini bulalım.
\( f(\pi) = \sin{\pi} = 0 \)
Buna göre bu noktada soldan ve sağdan limitler ve fonksiyon değeri birer reel sayı olarak tanımlı ve birbirine eşittir, dolayısıyla fonksiyon \( x = \pi \) noktasında süreklidir.
\( f(\pi^-) = f(\pi^+) = f(\pi) \)
Fonksiyonun mutlak minimum ve maksimum noktalarının olup olmadığını bulmak için kritik ve kapalı uç noktalarındaki değerini bulalım.
\( f \) fonksiyonunun türevini bulalım.
Sürekliliğini gösterdiğimiz \( x = \pi \) noktasındaki türevlenebilirliği kontrol edelim.
Fonksiyonun \( x = \pi \) noktasındaki soldan türevini bulalım.
\( f'(x) = \cos{x} \)
\( f'(\pi^-) = \cos{\pi} = -1 \)
Fonksiyonun \( x = \pi \) noktasındaki sağdan türevini bulalım.
\( f'(x) = -\cos{x} \)
\( f'(\pi^+) = -\cos{\pi} = 1 \)
Buna göre bu noktada soldan ve sağdan türevler birbirine eşit değildir, dolayısıyla fonksiyonun \( x = \pi \) noktasında türevi tanımsızdır.
\( f'(x) = \begin{cases} \cos{x} & 0 \le x \lt \pi \\ \text{Tanımsız} & x = \pi \\ -\cos{x} & \pi \lt x \le 2\pi \end{cases} \)
Fonksiyonun kritik noktaları birinci türevin sıfır ya da tanımsız olduğu iç noktalardır.
Fonksiyonun tanım kümesi içinde birinci türevinin sıfır olduğu iç noktaları bulalım.
\( 0 \le x \lt \pi \) için:
\( \cos{x} = 0 \)
Kosinüs fonksiyonu \( 0 \) değerini verilen tanım aralığı içinde aşağıdaki açı değerinde alır.
\( x = \dfrac{\pi}{2} \)
\( \pi \lt x \le 2\pi \) için:
\( -\cos{x} = 0 \)
Kosinüs fonksiyonu \( 0 \) değerini verilen tanım aralığı içinde aşağıdaki açı değerinde alır.
\( x = \dfrac{3\pi}{2} \)
Fonksiyonun \( x = \pi \) noktasında birinci türevi tanımsızdır.
Kritik noktalar: \( x \in \{ \frac{\pi}{2}, \pi, \frac{3\pi}{2} \} \)
Fonksiyonun kritik noktalardaki değerini bulalım.
\( f(\dfrac{\pi}{2}) = \sin{\dfrac{\pi}{2}} = 1 \)
\( f(\pi) = \sin{\pi} = 0 \)
\( f(\dfrac{3\pi}{2}) = -\sin{\dfrac{3\pi}{2}} = 1 \)
Fonksiyonun kapalı uç noktalarındaki değerini bulalım.
\( f(0) = \sin{0} = 0 \)
\( f(2\pi) = -\sin(2\pi) = 0 \)
Bu değerleri karşılaştırdığımızda fonksiyonun mutlak minimum ve maksimum değerleri ve noktaları aşağıdaki gibi bulunur.
Mutlak minimum: Fonksiyonun \( 0 \) değerini aldığı \( x = 0, x = \pi \) ve \( x = 2\pi \) noktaları
Mutlak maksimum: Fonksiyonun \( 1 \) değerini aldığı \( x = \frac{\pi}{2} \) ve \( x = \frac{3\pi}{2} \) noktaları
Fonksiyonun grafiği ve karşılaştırma yaptığımız nokta ve değerler aşağıdaki şekilde gösterilmiştir.
\( f: [0, 2] \to \mathbb{R} \) olmak üzere,
\( f(x) = \sqrt{\abs{4x - 2}} \)
fonksiyonunun mutlak minimum ve maksimum değerlerini ve noktalarını bulunuz.
Çözümü GösterMutlak değer fonksiyonunu parçalı fonksiyon şeklinde yazalım.
\( f(x) = \begin{cases} \sqrt{2 - 4x} & 0 \le x \lt \dfrac{1}{2} \\ \sqrt{4x - 2} & \dfrac{1}{2} \le x \le 2 \end{cases} \)
\( f \) parçalı fonksiyonunun \( x = \frac{1}{2} \) geçiş noktasında sürekli olup olmadığını bulalım.
\( x = \frac{1}{2} \) noktasındaki soldan limiti bulalım.
\( \lim\limits_{x \to \frac{1}{2}^-} {f(x)} = \lim\limits_{x \to \frac{1}{2}^-} {\sqrt{2 - 4x}} \)
\( = \sqrt{2 - 4(\frac{1}{2})} = 0 \)
\( x = \frac{1}{2} \) noktasındaki sağdan limiti bulalım.
\( \lim\limits_{x \to \frac{1}{2}^+} {f(x)} = \lim\limits_{x \to \frac{1}{2}^+} {\sqrt{4x - 2}} \)
\( = \sqrt{4(\frac{1}{2}) - 2} = 0 \)
\( x = \frac{1}{2} \) noktasındaki fonksiyon değerini bulalım.
\( f(\frac{1}{2}) = \sqrt{4(\frac{1}{2}) - 2} = 0 \)
Buna göre bu noktada soldan ve sağdan limitler ve fonksiyon değeri birer reel sayı olarak tanımlı ve birbirine eşittir, dolayısıyla fonksiyon \( x = \frac{1}{2} \) noktasında süreklidir.
\( f(\frac{1}{2}^-) = f(\frac{1}{2}^+) = f(\frac{1}{2}) \)
Fonksiyonun mutlak minimum ve maksimum noktalarının olup olmadığını bulmak için kritik ve kapalı uç noktalarındaki değerini bulalım.
\( f \) fonksiyonunun türevini bulalım.
Sürekliliğini gösterdiğimiz \( x = \frac{1}{2} \) noktasındaki türevlenebilirliği kontrol edelim.
Fonksiyonun \( x = \frac{1}{2} \) noktasındaki soldan türevini bulalım.
\( f'(x) = -\dfrac{2}{\sqrt{2 - 4x}} \)
\( f'(\frac{1}{2}^-) = -\dfrac{2}{\sqrt{2 - 4(\frac{1}{2}^-)}} \)
\( = -\dfrac{2}{\sqrt{0^+}} = -\infty \)
Fonksiyonun \( x = \frac{1}{2} \) noktasındaki sağdan türevini bulalım.
\( f'(x) = \dfrac{2}{\sqrt{4x - 2}} \)
\( f'(\frac{1}{2}^+) = \dfrac{2}{\sqrt{4(\frac{1}{2}^+) - 2}} \)
\( = \dfrac{2}{\sqrt{0^+}} = \infty \)
Buna göre bu noktada soldan ve sağdan türevler birer reel sayı olarak tanımlı değildir, dolayısıyla fonksiyonun \( x = \frac{1}{2} \) noktasında türevi tanımsızdır.
\( f'(x) = \begin{cases} -\dfrac{2}{\sqrt{2 - 4x}} & 0 \le x \lt \dfrac{1}{2} \\ \text{Tanımsız} & x = \dfrac{1}{2} \\ \dfrac{2}{\sqrt{4x - 2}} & \dfrac{1}{2} \lt x \le 2 \end{cases} \)
Fonksiyonun kritik noktaları birinci türevin sıfır ya da tanımsız olduğu iç noktalardır.
Fonksiyonun tanım kümesi içinde birinci türevinin sıfır olduğu iç noktaları bulalım.
\( 0 \le x \lt \frac{1}{2} \) için:
\( -\dfrac{2}{\sqrt{2 - 4x}} = 0 \)
Bu denklemi sağlayan bir \( x \) değeri yoktur.
\( \frac{1}{2} \lt x \le 2 \) için:
\( \dfrac{2}{\sqrt{2 - 4x}} = 0 \)
Bu denklemi sağlayan bir \( x \) değeri yoktur.
Fonksiyonun \( x = \frac{1}{2} \) noktasında birinci türevi tanımsızdır.
Kritik nokta: \( x = \frac{1}{2} \)
Fonksiyonun kritik noktadaki değerini bulalım.
\( f(\frac{1}{2}) = \sqrt{4(\frac{1}{2}) - 2} = 0 \)
Fonksiyonun kapalı uç noktalarındaki değerini bulalım.
\( f(0) = \sqrt{2 - 4(0)} = \sqrt{2} \)
\( f(2) = \sqrt{4(2) - 2} = \sqrt{6} \)
Bu değerleri karşılaştırdığımızda fonksiyonun mutlak minimum ve maksimum değerleri ve noktaları aşağıdaki gibi bulunur.
Mutlak minimum: Fonksiyonun \( 0 \) değerini aldığı \( x = \frac{1}{2} \) noktası
Mutlak maksimum: Fonksiyonun \( \sqrt{6} \) değerini aldığı \( x = 2 \) noktası
Fonksiyonun grafiği ve karşılaştırma yaptığımız nokta ve değerler aşağıdaki şekilde gösterilmiştir.

\( f: [a, b] \to \mathbb{R} \) olmak üzere,
\( f(x) = -x^3 - 2x - 12 \)
fonksiyonunun mutlak minimum ve maksimum noktalarını bulunuz.
Çözümü Göster\( f \) fonksiyonu kapalı bir aralıkta tanımlıdır ve bir polinom fonksiyonu olduğu için süreklidir.
Kapalı bir aralıkta tanımlı ve sürekli bir fonksiyon, mutlak minimum ve maksimum değerlerini kritik ya da kapalı uç noktalarından birinde alır.
Fonksiyonun kritik noktaları birinci türevin sıfır ya da tanımsız olduğu iç noktalardır.
\( f'(x) = -3x^2 - 2 \)
Fonksiyonun birinci türevinin sıfır olduğu iç noktaları bulalım.
\( -3x^2 - 2 = 0 \)
\( x^2 = -\dfrac{2}{3} \)
Fonksiyonun birinci türevinin sıfır olduğu nokta yoktur.
Fonksiyonun birinci türevinin tanımsız olduğu iç nokta yoktur.
Kritik noktalar: \( x \in \emptyset \)
Uç değer teoremine göre, kapalı bir aralıkta tanımlı ve sürekli bir fonksiyon bu aralıkta en az bir kez mutlak minimum ve en az bir kez mutlak maksimum değeri alır.
Buna göre fonksiyon, mutlak ekstremum değerlerini sınır noktalarında alır.
Türev fonksiyonu tüm tanım aralığında negatiftir.
\( f'(x) = -3x^2 - 2 \lt 0 \)
Dolayısıyla \( f \) fonksiyonu daima azalandır.
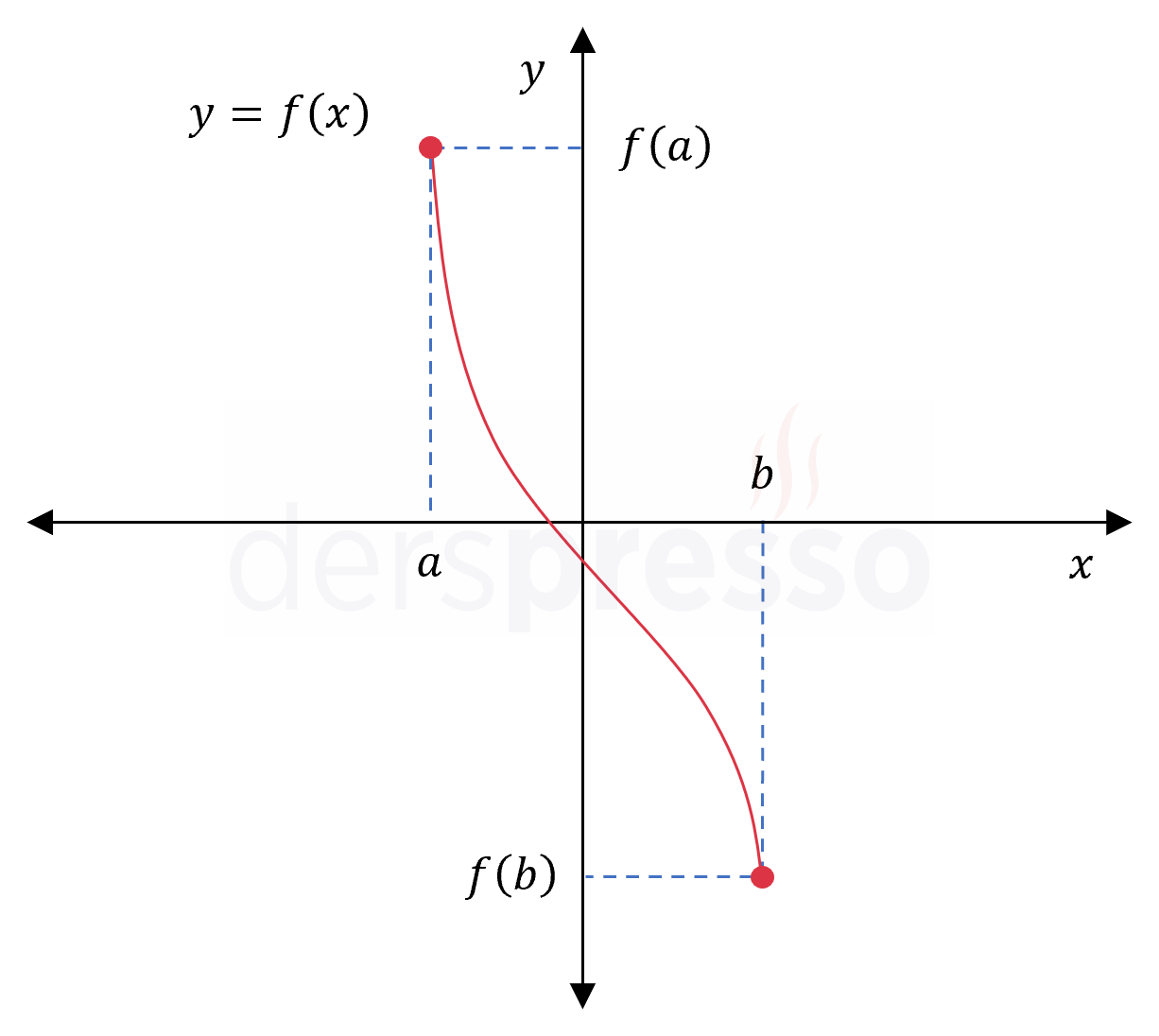
Bu nedenle fonksiyon en büyük değerini tanım aralığının sol uç noktasında, en küçük değerini de sağ uç noktasında alır.
Buna göre fonksiyonun mutlak minimum ve maksimum noktaları aşağıdaki gibi bulunur.
Mutlak minimum: \( x = b \) noktası
Mutlak maksimum: \( x = a \) noktası
Fonksiyonun grafiği ve karşılaştırma yaptığımız nokta ve değerler aşağıdaki şekilde gösterilmiştir.
\( f: [-4, 10] \to \mathbb{R} \) olmak üzere,
\( f(x) = \abs{x + 3} + \abs{x - 7} \)
fonksiyonunun mutlak minimum ve maksimum değerlerini ve noktalarını bulunuz.
Çözümü GösterMutlak değer fonksiyonunu parçalı fonksiyon şeklinde yazalım.
\( f(x) = \begin{cases} -x - 3 - x + 7 & -4 \le x \lt -3 \\ x + 3 - x + 7 & -3 \le x \lt 7 \\ x + 3 + x - 7 & 7 \le x \le 10 \end{cases} \)
İfadeyi düzenleyelim.
\( f(x) = \begin{cases} 4 - 2x & -4 \le x \lt -3 \\ 10 & -3 \le x \lt 7 \\ 2x - 4 & 7 \le x \le 10 \end{cases} \)
\( f \) parçalı fonksiyonunun \( x = -3 \) geçiş noktasında sürekli olup olmadığını bulalım.
\( x = -3 \) noktasındaki soldan limiti bulalım.
\( \lim\limits_{x \to -3^-} {f(x)} = \lim\limits_{x \to -3^-} (4 - 2x) \)
\( = 4 - 2(-3) = 10 \)
\( x = -3 \) noktasındaki sağdan limiti bulalım.
\( \lim\limits_{x \to -3^+} {f(x)} = \lim\limits_{x \to -3^+} {10} = 10 \)
\( x = -3 \) noktasındaki fonksiyon değerini bulalım.
\( f(-3) = 10 \)
Buna göre bu noktada soldan ve sağdan limitler ve fonksiyon değeri birer reel sayı olarak tanımlı ve birbirine eşittir, dolayısıyla fonksiyon \( x = -3 \) noktasında süreklidir.
\( f(-3^-) = f(-3^+) = f(-3) \)
\( f \) parçalı fonksiyonunun \( x = 7 \) geçiş noktasında sürekli olup olmadığını bulalım.
\( x = 7 \) noktasındaki soldan limiti bulalım.
\( \lim\limits_{x \to 7^-} {f(x)} = \lim\limits_{x \to 7^-} {10} = 10 \)
\( x = 7 \) noktasındaki sağdan limiti bulalım.
\( \lim\limits_{x \to 7^+} {f(x)} = \lim\limits_{x \to 7^+} (2x - 4) \)
\( = 2(7) - 4 = 10 \)
\( x = 7 \) noktasındaki fonksiyon değerini bulalım.
\( f(7) = 2(7) - 4 = 10 \)
Buna göre bu noktada soldan ve sağdan limitler ve fonksiyon değeri birer reel sayı olarak tanımlı ve birbirine eşittir, dolayısıyla fonksiyon \( x = 7 \) noktasında süreklidir.
\( f(7^-) = f(7^+) = f(7) \)
Fonksiyonun mutlak minimum ve maksimum noktalarının olup olmadığını bulmak için kritik ve kapalı uç noktalarındaki değerini bulalım.
\( f \) fonksiyonunun türevini bulalım.
Sürekliliğini gösterdiğimiz bu noktalardaki türevlenebilirliği kontrol edelim.
Fonksiyonun \( x = -3 \) noktasındaki soldan türevini bulalım.
\( f'(x) = -2 \)
\( f'(-3^-) = -2 \)
Fonksiyonun \( x = -3 \) noktasındaki sağdan türevini bulalım.
\( f'(x) = 0 \)
\( f'(-3^+) = 0 \)
Buna göre bu noktada soldan ve sağdan türevler birbirine eşit değildir, dolayısıyla fonksiyonun \( x = -3 \) noktasında türevi tanımsızdır.
Fonksiyonun \( x = 7 \) noktasındaki soldan türevini bulalım.
\( f'(x) = 0 \)
\( f'(7^-) = 0 \)
Fonksiyonun \( x = 7 \) noktasındaki sağdan türevini bulalım.
\( f'(x) = 2 \)
\( f'(7^+) = 2 \)
Buna göre bu noktada soldan ve sağdan türevler birbirine eşit değildir, dolayısıyla fonksiyonun \( x = 7 \) noktasında türevi tanımsızdır.
\( f'(x) = \begin{cases} -2 & -4 \le x \lt -3 \\ \text{Tanımsız} & x = -3 \\ 0 & -3 \lt x \lt 7 \\ \text{Tanımsız} & x = 7 \\ 2 & 7 \lt x \le 10 \end{cases} \)
Fonksiyonun kritik noktaları birinci türevin sıfır ya da tanımsız olduğu iç noktalardır.
Fonksiyonun tanım kümesi içinde birinci türevinin sıfır olduğu iç noktaları bulalım.
\( -4 \le x \lt -3 \) için:
\( -2 = 0 \)
Bu denklemi sağlayan bir \( x \) değeri yoktur.
\( -3 \lt x \lt 7 \) için:
\( 0 = 0 \)
Bu aralıktaki tüm \( x \) değerleri denklemi sağlar.
\( x \in (-3, 7) \)
\( 7 \lt x \le 10 \) için:
\( 2 = 0 \)
Bu denklemi sağlayan bir \( x \) değeri yoktur.
Fonksiyonun \( x = -3 \) ve \( x = 7 \) noktalarında birinci türevi tanımsızdır.
Kritik noktalar: \( x \in [-3, 7] \)
Fonksiyonun kritik noktalardaki değerini bulalım.
\( x \in [-3, 7) \) aralığında fonksiyon sabit 10 değerini alır.
\( f(7) = 2(7) - 4 = 10 \)
Fonksiyonun kapalı uç noktalarındaki değerini bulalım.
\( f(-4) = 4 - 2(-4) = 12 \)
\( f(10) = 2(10) - 4 = 16 \)
Bu değerleri karşılaştırdığımızda fonksiyonun mutlak minimum ve maksimum değerleri ve noktaları aşağıdaki gibi bulunur.
Mutlak minimum: Fonksiyonun \( 10 \) değerini aldığı \( x \in [-3, 7] \) aralığındaki noktalar
Mutlak maksimum: Fonksiyonun \( 16 \) değerini aldığı \( x = 10 \) noktası
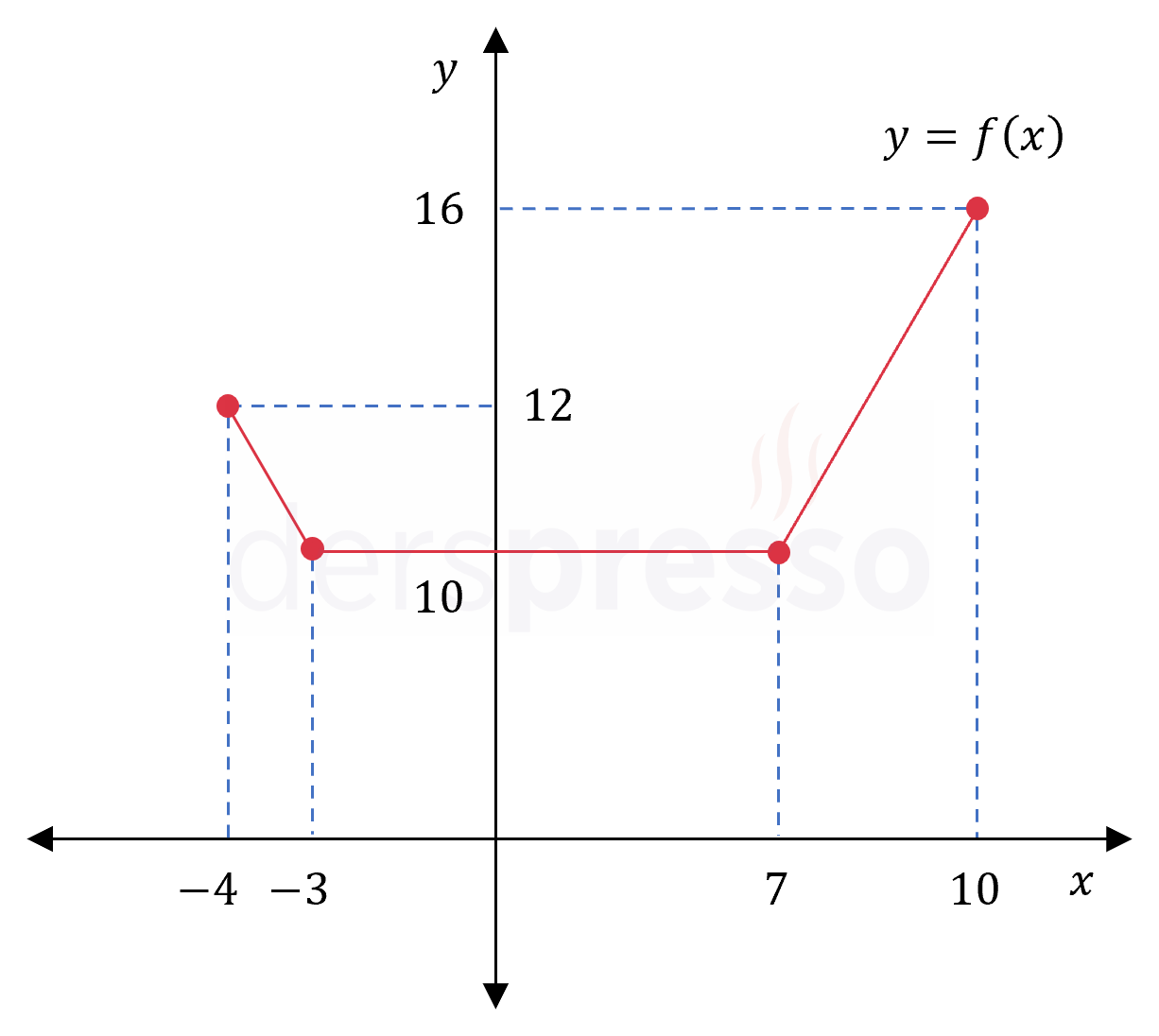
Fonksiyonun grafiği ve karşılaştırma yaptığımız nokta ve değerler aşağıdaki şekilde gösterilmiştir.
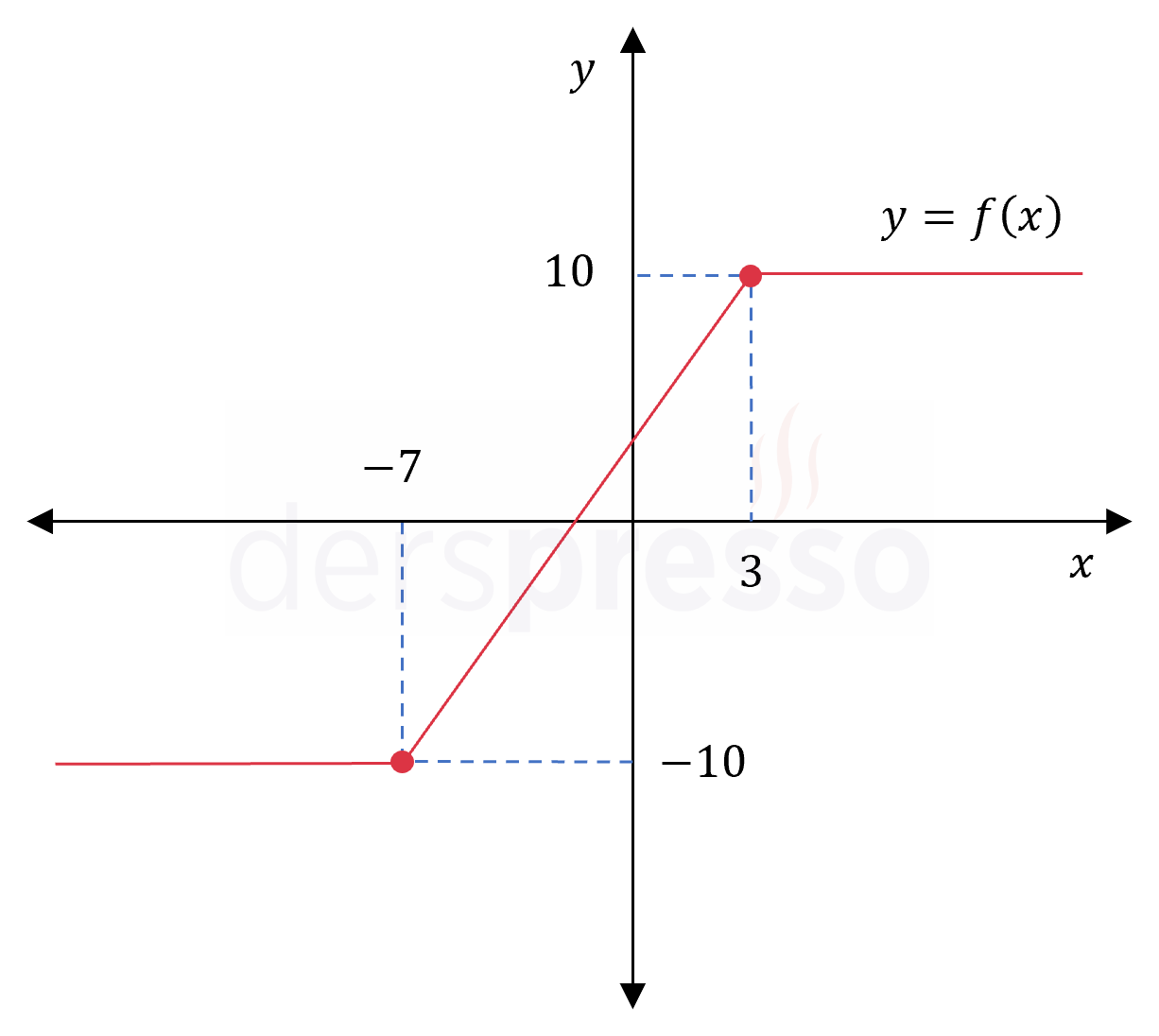
\( f(x) = \abs{x + 7} - \abs{x - 3} \)
fonksiyonunun tanımlı olduğu en geniş aralıkta mutlak minimum ve maksimum değerlerini ve noktalarını bulunuz.
Çözümü GösterMutlak değer fonksiyonunu parçalı fonksiyon şeklinde yazalım.
\( f(x) = \begin{cases} -x - 7 - (-x + 3) & x \lt -7 \\ x + 7 - (-x + 3) & -7 \le x \lt 3 \\ x + 7 - (x - 3) & 3 \le x \end{cases} \)
İfadeyi düzenleyelim.
\( f(x) = \begin{cases} -10 & x \lt -7 \\ 2x + 4 & -7 \le x \lt 3 \\ 10 & 3 \le x \end{cases} \)
\( f \) fonksiyonu sonsuz aralıkta tanımlıdır.
Fonksiyonun sonsuzdaki limitlerini bulalım.
\( \lim\limits_{x \to \infty} {f(x)} = \lim\limits_{x \to \infty} {10} = 10 \)
\( \lim\limits_{x \to -\infty} {f(x)} = \lim\limits_{x \to \infty} (-10) = -10 \)
\( f \) parçalı fonksiyonunun \( x = -7 \) geçiş noktasında sürekli olup olmadığını bulalım.
\( x = -7 \) noktasındaki soldan limiti bulalım.
\( \lim\limits_{x \to -7^-} {f(x)} = \lim\limits_{x \to -7^-} {-10} = -10 \)
\( x = -7 \) noktasındaki sağdan limiti bulalım.
\( \lim\limits_{x \to -7^+} {f(x)} = \lim\limits_{x \to -7^+} (2x + 4) \)
\( = 2(-7) + 4 = -10 \)
\( x = -7 \) noktasındaki fonksiyon değerini bulalım.
\( f(-7) = 2(-7) + 4 = -10 \)
Buna göre bu noktada soldan ve sağdan limitler ve fonksiyon değeri birer reel sayı olarak tanımlı ve birbirine eşittir, dolayısıyla fonksiyon \( x = -7 \) noktasında süreklidir.
\( f(-7^-) = f(-7^+) = f(-7) \)
\( f \) parçalı fonksiyonunun \( x = 3 \) geçiş noktasında sürekli olup olmadığını bulalım.
\( x = 3 \) noktasındaki soldan limiti bulalım.
\( \lim\limits_{x \to 3^-} {f(x)} = \lim\limits_{x \to 3^-} (2x + 4) \)
\( = 2(3) + 4 = 10 \)
\( x = 3 \) noktasındaki sağdan limiti bulalım.
\( \lim\limits_{x \to 3^+} {f(x)} = \lim\limits_{x \to 3^+} {10} = 10 \)
\( x = 3 \) noktasındaki fonksiyon değerini bulalım.
\( f(3) = 10 \)
Buna göre bu noktada soldan ve sağdan limitler ve fonksiyon değeri birer reel sayı olarak tanımlı ve birbirine eşittir, dolayısıyla fonksiyon \( x = 3 \) noktasında süreklidir.
\( f(3^-) = f(3^+) = f(3) \)
Fonksiyonun mutlak minimum ve maksimum noktalarının olup olmadığını bulmak için kritik noktalardaki değerini bulalım.
\( f \) fonksiyonunun türevini bulalım.
Sürekliliğini gösterdiğimiz bu noktalardaki türevlenebilirliği kontrol edelim.
Fonksiyonun \( x = -7 \) noktasındaki soldan türevini bulalım.
\( f'(x) = 0 \)
\( f'(-7^-) = 0 \)
Fonksiyonun \( x = -7 \) noktasındaki sağdan türevini bulalım.
\( f'(x) = 2 \)
\( f'(-7^+) = 2 \)
Buna göre bu noktada soldan ve sağdan türevler birbirine eşit değildir, dolayısıyla fonksiyonun \( x = -7 \) noktasında türevi tanımsızdır.
Fonksiyonun \( x = 3 \) noktasındaki soldan türevini bulalım.
\( f'(x) = 2 \)
\( f'(3^-) = 2 \)
Fonksiyonun \( x = 3 \) noktasındaki sağdan türevini bulalım.
\( f'(x) = 0 \)
\( f'(3^+) = 0 \)
Buna göre bu noktada soldan ve sağdan türevler birbirine eşit değildir, dolayısıyla fonksiyonun \( x = 3 \) noktasında türevi tanımsızdır.
\( f'(x) = \begin{cases} 0 & x \lt -7 \\ \text{Tanımsız} & x = -7 \\ 2 & -7 \lt x \lt 3 \\ \text{Tanımsız} & x = 3 \\ 0 & 3 \lt x \end{cases} \)
Fonksiyonun kritik noktaları birinci türevin sıfır ya da tanımsız olduğu iç noktalardır.
Fonksiyonun tanım kümesi içinde birinci türevinin sıfır olduğu iç noktaları bulalım.
\( x \lt -7 \) için:
\( 0 = 0 \)
Bu aralıktaki tüm \( x \) değerleri denklemi sağlar.
\( x \in (-\infty, -7) \)
\( -7 \lt x \lt 3 \\ \) için:
\( 2 = 0 \)
Bu denklemi sağlayan bir \( x \) değeri yoktur.
\( 3 \lt x \) için:
\( 0 = 0 \)
Bu aralıktaki tüm \( x \) değerleri denklemi sağlar.
\( x \in (3, \infty) \)
Fonksiyonun \( x = -7 \) ve \( x = 3 \) noktalarında birinci türevi tanımsızdır.
Kritik noktalar: \( x \in (-\infty, -7] \cup [3, \infty) \)
Fonksiyonun kritik noktalardaki değerini bulalım.
\( x \in (-\infty, -7) \) aralığında fonksiyon sabit \( -10 \) değerini alır.
\( x \in [3, \infty) \) aralığında fonksiyon sabit \( 10 \) değerini alır.
\( f(-7) = 2(-7) + 4 = -10 \)
\( f(3) = 2(3) + 4 = 10 \)
Bu değerleri karşılaştırdığımızda fonksiyonun mutlak minimum ve maksimum değerleri ve noktaları aşağıdaki gibi bulunur.
Mutlak minimum: Fonksiyonun \( -10 \) değerini aldığı \( x \in (-\infty, -7] \) aralığındaki noktalar
Mutlak maksimum: Fonksiyonun \( 10 \) değerini aldığı \( x \in [3, \infty) \) aralığındaki noktalar
Fonksiyonun grafiği ve karşılaştırma yaptığımız nokta ve değerler aşağıdaki şekilde gösterilmiştir.