Diferansiyel Kavramı
Konu tekrarı için: Lineerleştirme
\( f \) fonksiyonunun \( x \) noktasındaki diferansiyeli \( dy \) ya da \( df \) ile ifade edilir ve aşağıdaki formülle bulunur.
\( dy = f'(x)\ dx \)
Bu formüldeki \( dx \) ifadesi \( x \) değişkeninin diferansiyelidir ve \( x \) değerindeki sonsuz küçüklükteki değişimi ifade eder (\( x \to x + dx \)). Matematikte sonsuz küçüklük, sıfıra tüm reel sayılardan daha yakın olan ama sıfır olmayan bir büyüklük olarak tanımlanabilir.
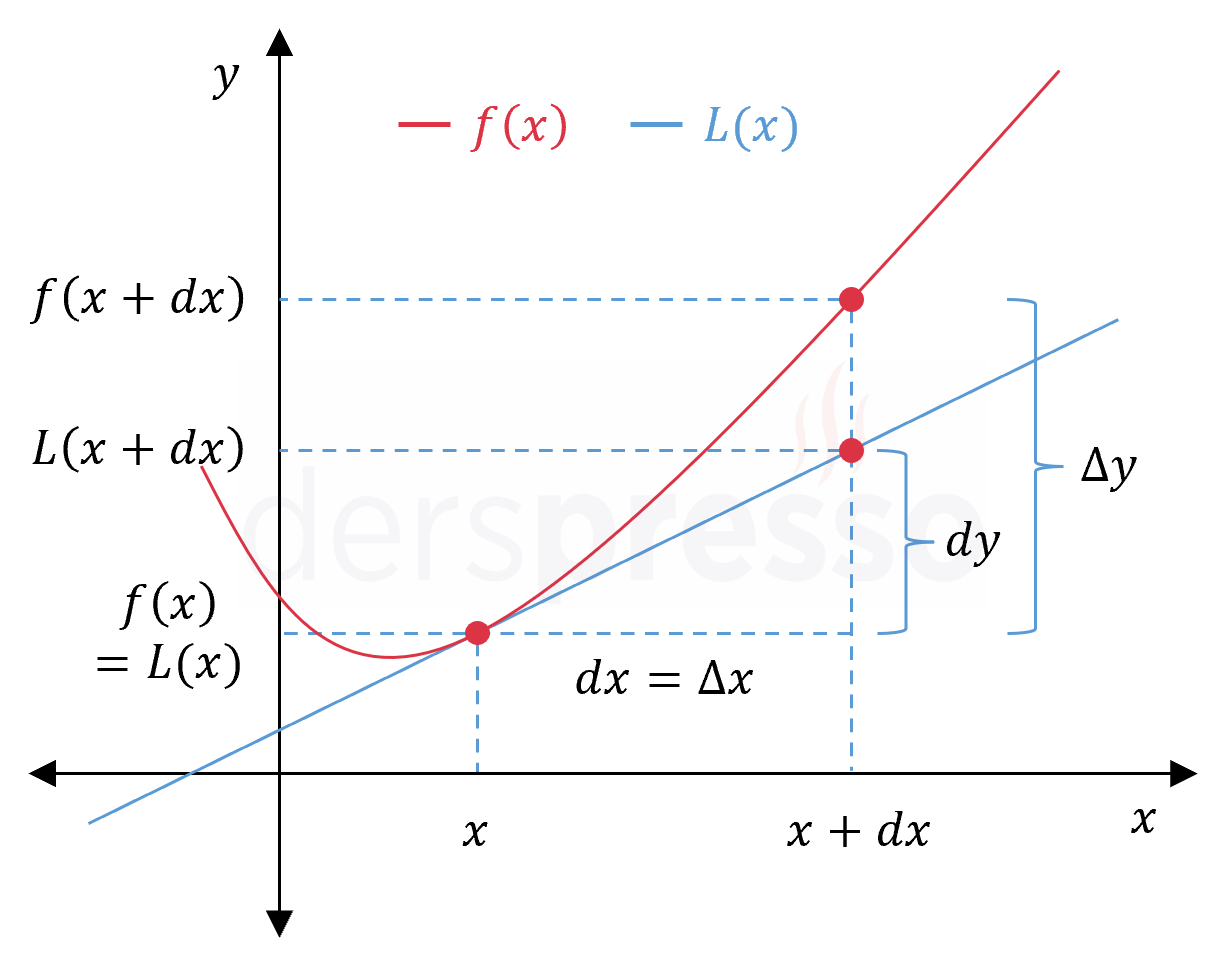
Fonksiyona \( x \) noktasında teğet olan doğru ve önceki bölümde gördüğümüz lineerleştirme yöntemi kullanılarak, bu değişim sonucunda \( x + dx \) noktasındaki yaklaşık fonksiyon değeri aşağıdaki formülle bulunur.
\( L(x + dx) = f(x) + f'(x)\ dx \)
Bu formülü düzenlediğimizde \( dy \) diferansiyelinin lineerleştirme yöntemi ile bulunan yaklaşık değişim miktarına eşit olduğu görülür.
\( L(x + dx) - f(x) = f'(x)\ dx = dy \)
Buna göre \( dy \) diferansiyeli, \( y = f(x) \) fonksiyonunda \( x \) değişkeni sonsuz küçüklükte \( dx \) kadar değişim gösterdiğinde \( y \) değişkenindeki yaklaşık değişim olarak tanımlanabilir.
Aynı aralıkta fonksiyon değerinin gösterdiği gerçek değişime \( \Delta y \) diyelim.
\( \Delta y = f(x + dx) - f(x) \)
\( dy \) diferansiyeli fonksiyon değerinde oluşan \( \Delta y \) miktarındaki gerçek değişimin yaklaşık değeridir ve \( dx \) sıfıra yaklaştıkça gerçek değişim değerine yaklaşır.
\( dy \approx \Delta y \)
Diferansiyelin Özellikleri
Türev işlem kuralları benzer şekilde diferansiyel işlemine uygulanabilir.
\( d(u + v) = du + dv \)
\( d(cu) = cdu \)
\( d(uv) = vdu + udv \)
\( d\left( \dfrac{u}{v} \right) = \dfrac{vdu - udv}{v^2} \)
Fonksiyonların türev kuralları kullanılarak diferansiyelleri bulunabilir.
\( d(c) = 0 \)
\( d(x^n) = nx^{n-1}\ dx \)
\( d(\sin{x}) = \cos{x}\ dx \)
\( d(\cos{x}) = -\sin{x}\ dx \)
\( d(e^x) = e^x\ dx \)
\( d(\ln{x}) = \dfrac{\ dx}{x} \)