Süreklilik Tanımı
Sürekliliğin pratik tanımlarından birine göre, bir fonksiyonun tanımlı olduğu bir noktadaki değeri anlık bir değişim (sıçrama) içermiyorsa fonksiyon bu noktada süreklidir, aksi durumda süreksizdir. Bu tanıma göre sürekliliği bir fonksiyonun grafiğini tanımlı olduğu bir noktadan geçerken kalemi kaldırmadan çizebilmemiz şeklinde düşünebiliriz.
Sürekliliğin daha çok kabul gören tanımlarından biri olan limit tanımından aşağıda, standart tanımı diyebileceğimiz epsilon-delta tanımından ise önümüzdeki bölümde bahsedeceğiz.
Bir fonksiyonun sürekliliğini bir nokta, bir aralık ve fonksiyonun tümü için inceleyebiliriz.
Sürekliliğin Limit Tanımı
Bir Noktada Süreklilik
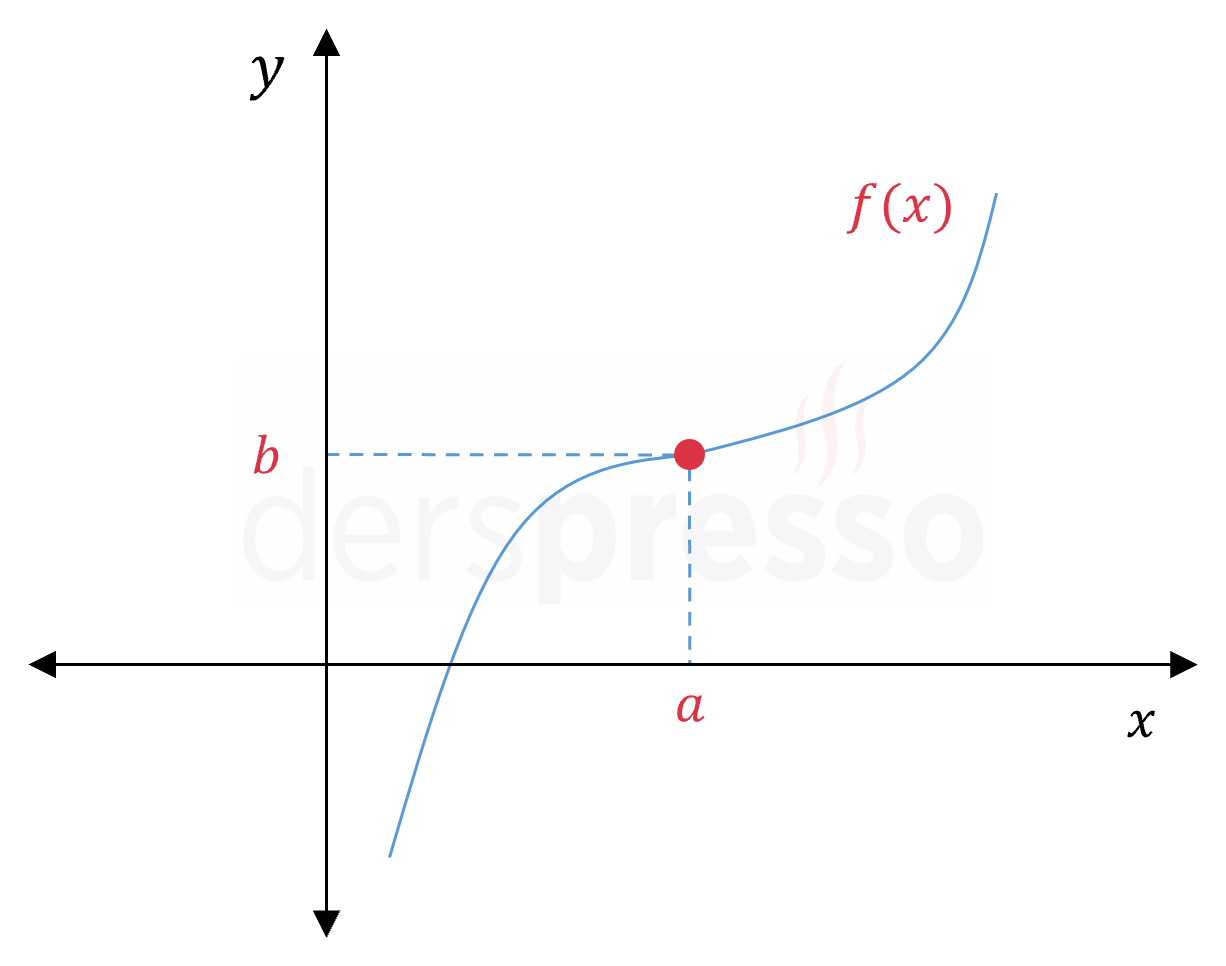
Bir \( f \) fonksiyonunun uç nokta olmayan bir \( x = a \) noktasında sürekli olması için aşağıdaki üç koşul sağlanmalıdır.
- Fonksiyonun bu noktada limiti tanımlı olmalıdır (\( \lim_{x \to a} f(x) \)).
- Fonksiyon bu noktada tanımlı olmalıdır (\( f(a) \)).
- Fonksiyonun bu noktadaki limit değeri fonksiyon değerine eşit olmalıdır (\( \lim_{x \to a} f(x) = f(a)) \).
Bu üç koşuldan herhangi birinin sağlanmaması durumunda \( f \) fonksiyonu bu noktada süreksiz olur.
\( A \) reel sayılarda tanımlı ve \( a \) noktasını içeren açık bir aralık olmak üzere,
\( f: A \to \mathbb{R} \) olmak üzere,
\( \lim_{x \to a} f(x) \) ve \( f(a) \) tanımlı ve
\( \lim_{x \to a} f(x) = f(a) \) ise,
\( f \) fonksiyonu \( x = a \) noktasında süreklidir.
Aksi takdirde, \( f \) fonksiyonu \( x = a \) noktasında süreksizdir.
Bu tanıma göre, bir fonksiyon bir noktada sürekli ise o noktada tanımlıdır ve limiti vardır. Bunun karşıtı doğru olmayabilir, yani bir fonksiyonun bir noktada tanımlı olması ya da limitinin var olması tek başına o noktada sürekli olması için yeterli değildir.
Soldan ve Sağdan Süreklilik
Bir noktanın soldan ve sağdan limitini tanımlayabildiğimiz gibi soldan ve sağdan sürekliliğini de tanımlayabiliriz.
Bir fonksiyonun uç nokta olan ya da olmayan bir \( x = a \) noktası için soldan limiti bu noktadaki fonksiyon değerine eşitse fonksiyon bu noktada soldan süreklidir.
\( f: A \to \mathbb{R} \) olmak üzere,
\( \lim_{x \to a^-} f(x) \) ve \( f(a) \) tanımlı ve
\( \lim_{x \to a^-} f(x) = f(a) \) ise,
\( f \) fonksiyonu \( x = a \) noktasında soldan süreklidir.
Aksi takdirde, \( f \) fonksiyonu \( x = a \) noktasında soldan sürekli değildir.
Bir fonksiyonun uç nokta olan ya da olmayan bir \( x = a \) noktası için sağdan limiti bu noktadaki fonksiyon değerine eşitse fonksiyon bu noktada sağdan süreklidir.
\( f: A \to \mathbb{R} \) olmak üzere,
\( \lim_{x \to a^+} f(x) \) ve \( f(a) \) tanımlı ve
\( \lim_{x \to a^+} f(x) = f(a) \) ise,
\( f \) fonksiyonu \( x = a \) noktasında sağdan süreklidir.
Aksi takdirde, \( f \) fonksiyonu \( x = a \) noktasında sağdan sürekli değildir.
Aşağıda \( x = a \) noktasında soldan sürekli olan ama sağdan sürekli olmayan bir fonksiyonun grafiği verilmiştir.
\( \lim_{x \to a^-} f(x) = f(a) = b \)
\( \lim_{x \to a^+} f(x) \ne f(a) \)
Uç Noktalarda Süreklilik
Belirli bir \( [a, b] \) aralığında tanımlı bir fonksiyonun uç noktalarındaki süreklilik için fonksiyonun sadece tanımlı olduğu yönlerdeki sürekliliğe, yani \( x = a \) noktasında sağdan, \( x = b \) noktasında ise soldan sürekliliğe bakmamız yeterlidir.
\( f: [a, b] \to \mathbb{R} \) olmak üzere,
\( \lim_{x \to a^+} f(x) = f(a) \) ise,
\( f \) fonksiyonu \( x = a \) noktasında süreklidir.
\( \lim_{x \to b^-} f(x) = f(b) \) ise,
\( f \) fonksiyonu \( x = b \) noktasında süreklidir.
Buna göre \( [a, b] \) aralığında tanımlı aşağıdaki \( f \) fonksiyonu \( x = a \) noktasında sürekli iken \( x = b \) noktasında süreksizdir. Dikkat edilirse, uç noktalardaki süreklilik tek yönlü sürekliliğe bağlı olduğu için \( x = a \) için sadece "sağdan sürekli" değil, bir yön belirtmeden "sürekli" ifadesini de kullanabiliriz.
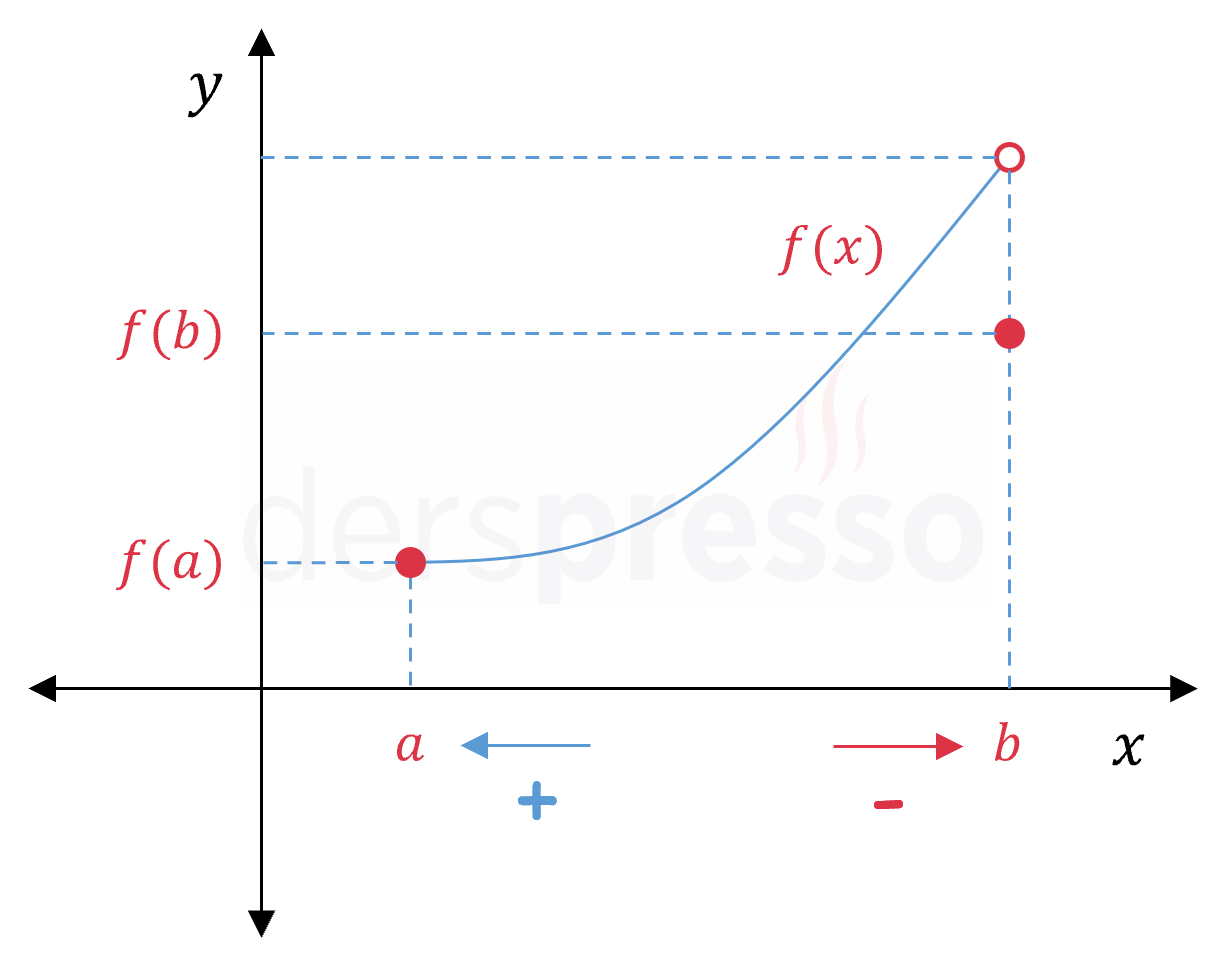
\( f: [a, b] \to \mathbb{R} \) olmak üzere,
\( \lim_{x \to a^+} f(x) = f(a) \)
\( \lim_{x \to b^-} f(x) \ne f(b) \)
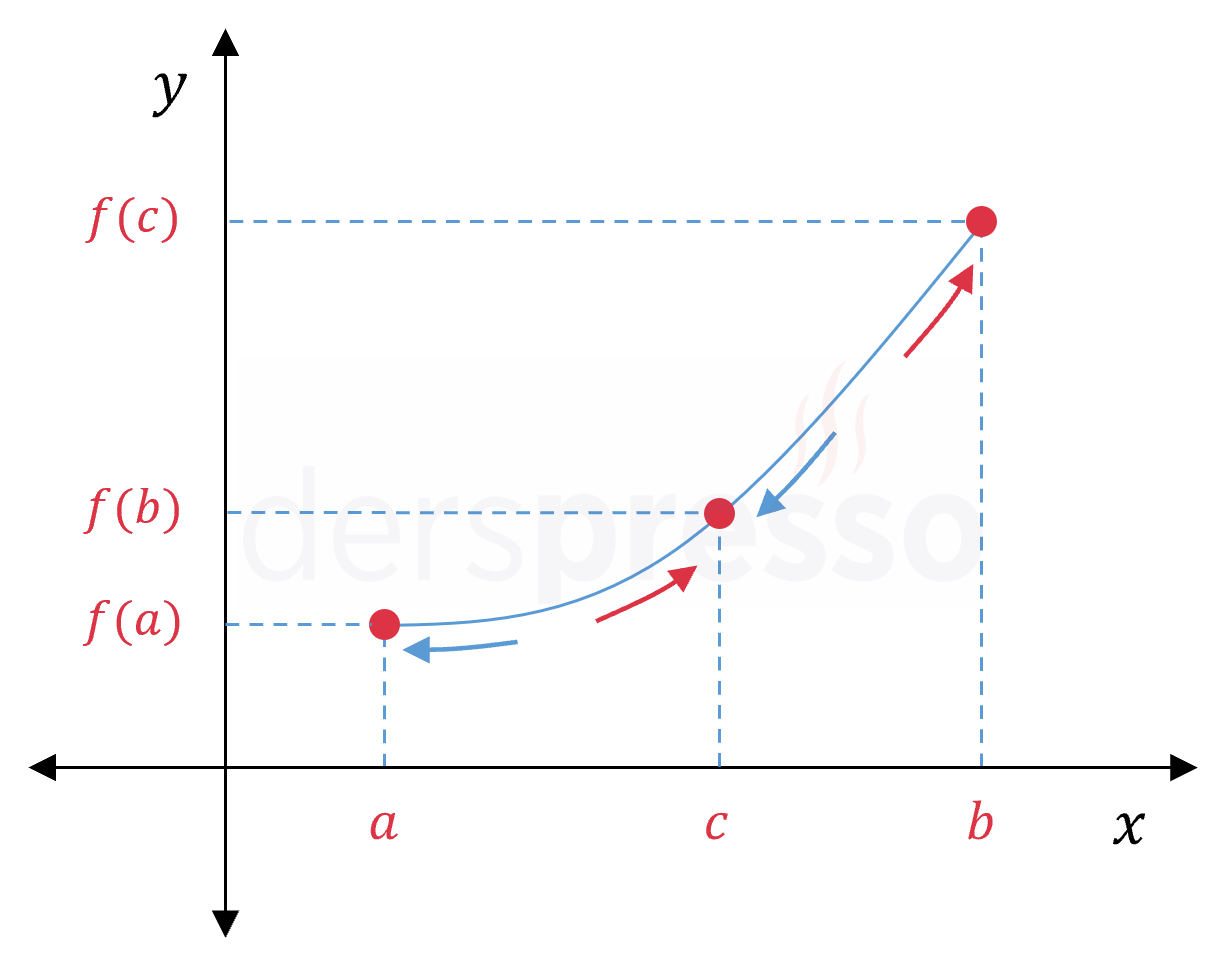
İç ve uç noktalardaki sürekliliği özetlememiz gerekirse, bir fonksiyonun iç bir noktasında sürekli olması için (\( x = c \) noktası) o noktada hem soldan hem de sağdan sürekli olmalıdır. Fonksiyonun bir uç noktasında (\( x = a \) ve \( x = b \) noktaları) sürekli olması için ise tanımlı olduğu yönde (soldan ya da sağdan) sürekli olması yeterlidir.
Bir Aralıkta Süreklilik
Yukarıda bahsettiğimiz iç ve uç noktalardaki süreklilik tanımlarını bir aralıktaki sürekliliğe aşağıdaki şekilde uyarlayabiliriz.
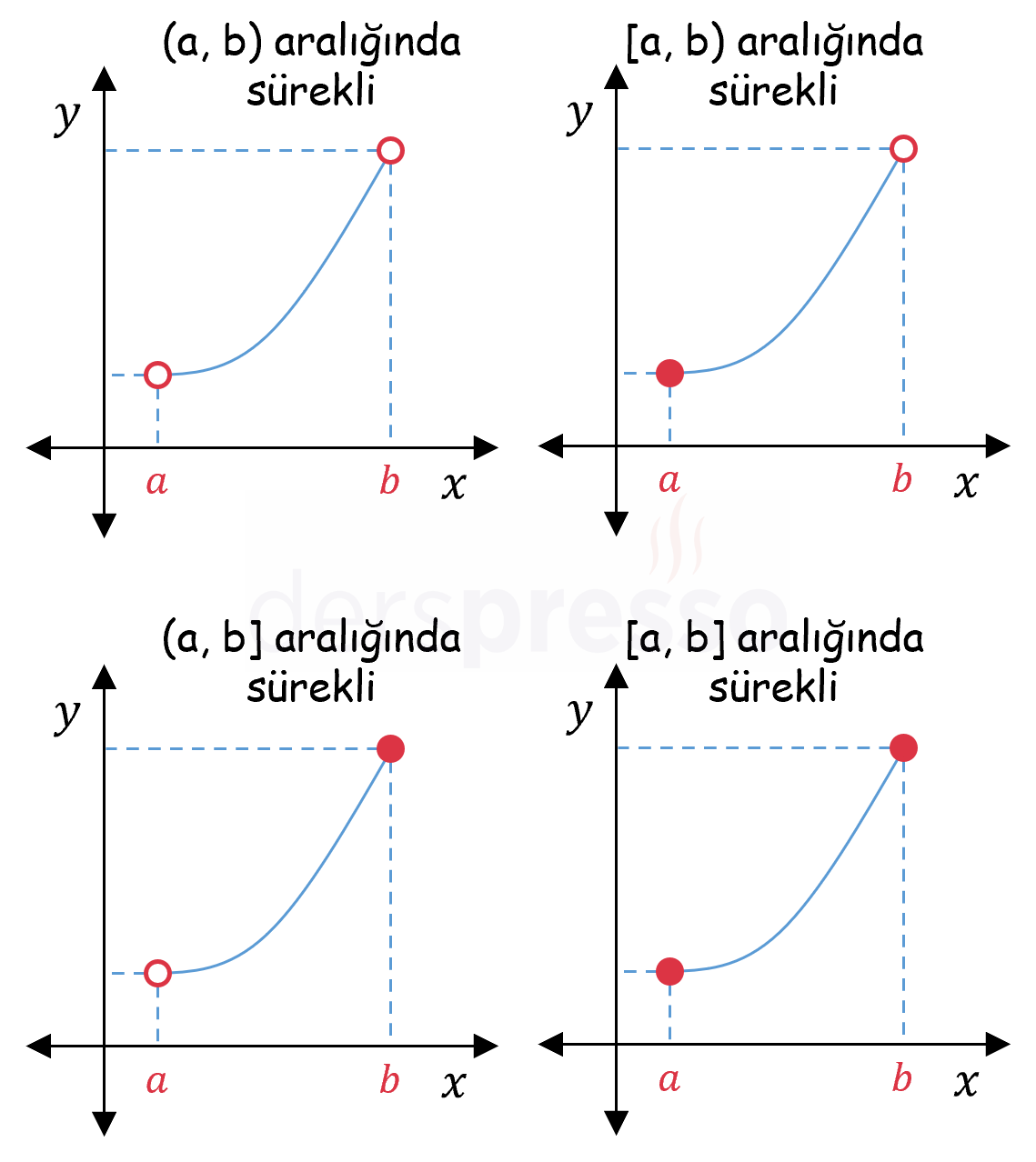
\( f \) fonksiyonu \( (a, b) \) aralığındaki tüm noktalarda sürekli ise \( (a, b) \) açık aralığında süreklidir.
\( f \) fonksiyonu \( (a, b) \) aralığındaki tüm noktalarda sürekli ise ve ayrıca \( a \) noktasında sağdan sürekli ise \( [a, b) \) yarı açık aralığında süreklidir.
\( f \) fonksiyonu \( (a, b) \) aralığındaki tüm noktalarda sürekli ise ve ayrıca \( b \) noktasında soldan sürekli ise \( (a, b] \) yarı açık aralığında süreklidir.
\( f \) fonksiyonu \( (a, b) \) aralığındaki tüm noktalarda sürekli ise ve ayrıca \( a \) noktasında sağdan, \( b \) noktasında soldan sürekli ise \( [a, b] \) kapalı aralığında süreklidir.
Bir Fonksiyonun Sürekliliği
Bir fonksiyon tanım kümesindeki tüm noktalarda süreklilik koşullarını sağlıyorsa sürekli bir fonksiyondur. Buna göre bir fonksiyonun sürekli bir fonksiyon olup olmadığına karar vermek için sadece tanımlı olduğu noktalardaki sürekliliğini incelememiz yeterlidir.
Buna göre reel sayıların bir alt kümesinde tanımlı olan aşağıdaki fonksiyonlar yukarıdaki koşulları sağladıkları için sürekli fonksiyonlardır.
- Tanım kümesi \( [0, +\infty) \) olan karekök fonksiyonu
- Tanım kümesi \( (0, +\infty) \) olan logaritma fonksiyonu
Benzer şekilde tanımsız noktaları olan aşağıdaki fonksiyonlar da yukarıdaki koşulları sağladıkları için sürekli fonksiyonlardır.
- Tanım kümesi \( \{\frac{\pi}{2} + k\pi\} \) hariç tüm reel sayılar olan tanjant fonksiyonu
- Tanım kümesi \( \{k\pi\} \) hariç tüm reel sayılar olan kotanjant fonksiyonu
Tanımsız Noktalarda Süreklilik
Bir fonksiyonun tanımlı olduğu bir noktadaki sürekliliğini yukarıda yaptığımız tanımlar doğrultusunda inceleyebilir ve fonksiyonun o noktada sürekli ya da süreksiz olduğuna karar verebiliriz.
Bir fonksiyonun tanımsız olduğu bir noktadaki sürekliliği ile ilgili ise iki görüş vardır.
- Birinci görüşe göre fonksiyonun tanımsız olduğu bir noktada süreksiz olduğundan da bahsedilemez, bu nokta süreklilik açısından incelenemez.
- İkinci görüşe göre fonksiyon bir noktada sürekli değilse (o noktada tanımsız da olsa) süreksizdir. Biz de bu konu anlatımında bu görüşü benimseyeceğiz.
Aşağıda verilen örnek fonksiyon tanım kümesindeki tüm noktalarda sürekli olduğu için sürekli bir fonksiyondur. Bahsettiğimiz birinci görüşe göre fonksiyonun tanımsız olduğu \( x = 5 \) noktasında sürekliliği incelenmez ve bu noktada süreksiz olduğundan da bahsedilemez. İkinci görüşe göre ise fonksiyonun bu noktada süreksiz olduğunu (ya da süreksizlik içerdiğini) söyleyebiliriz. Bir fonksiyonun sürekliliği tanım kümesindeki noktaların sürekliliğe bağlı olduğu için, \( x = 5 \) noktasında fonksiyonun süreksiz olduğunu söylememiz fonksiyonu süreksiz yapmaz.
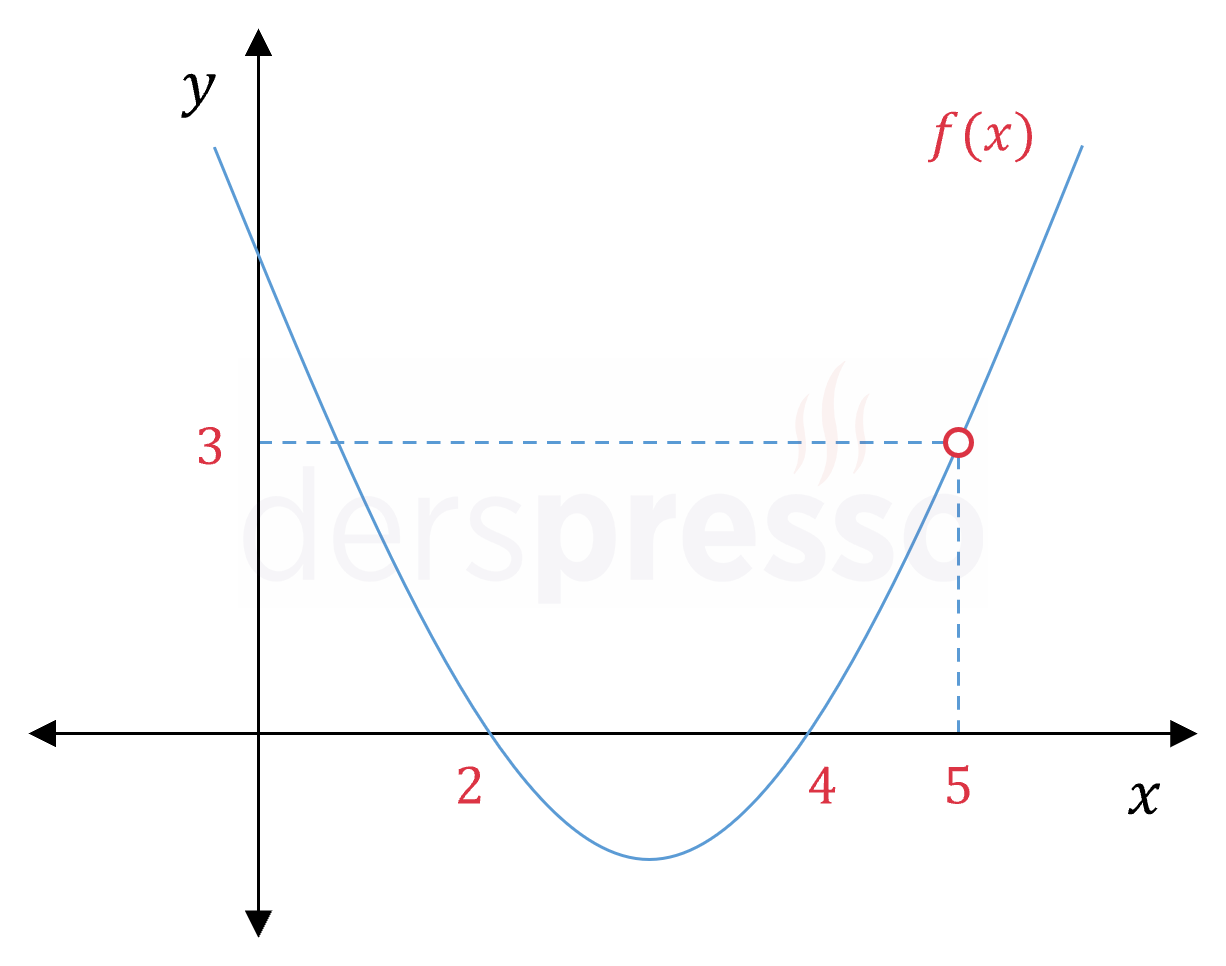
\( f: \mathbb{R} - \{5\} \to \mathbb{R} \)
\( f(x) = \dfrac{(x - 2)(x - 4)(x - 5)}{x - 5} \)
Gerçek Hayattan Örnekler
Sürekli fonksiyonlara gerçek hayattan aşağıdaki örnekleri verebiliriz. Bu fonksiyonların değeri anlık sıçramalar göstermez, örneğin bir odanın sıcaklığı 20 dereceden 22 dereceye bir anda çıkmaz, aradaki tüm reel sayı değerlerini alarak sürekli bir grafik şeklinde değişim gösterir.
- Bir ağacın boyunun zamana göre grafiği
- Bir aracın konumunun zamana göre grafiği
- Bir aracın hızının zamana göre grafiği
- Bir gün içindeki hava sıcaklığının zamana göre grafiği
Sürekli olmayan fonksiyonlara aşağıdaki örnekleri verebiliriz.
- Bir banka hesabındaki bakiyenin zamana göre grafiği: Gelen ve giden transferlerle bakiyede anlık sıçramalar oluşur.
- Bir ürünün fiyatının zamana göre grafiği: Fiyat belirli aralıklarda sabit kalır, belirli noktalarda anlık değişimler gösterir.
Bir fonksiyonun tanım kümesinin uç noktası olmayan bir noktasındaki durumu ile ilgili aşağıdaki ifadelerden hangileri her zaman doğrudur?
I. Sürekli ise tanımlıdır.
II. Sürekli ise limiti vardır.
III. Limiti varsa süreklidir.
IV. Limiti varsa tanımlıdır.
Çözümü Göster