Yerel Minimum ve Maksimum Noktaları
Yerel Ekstremum Noktası Tanımı
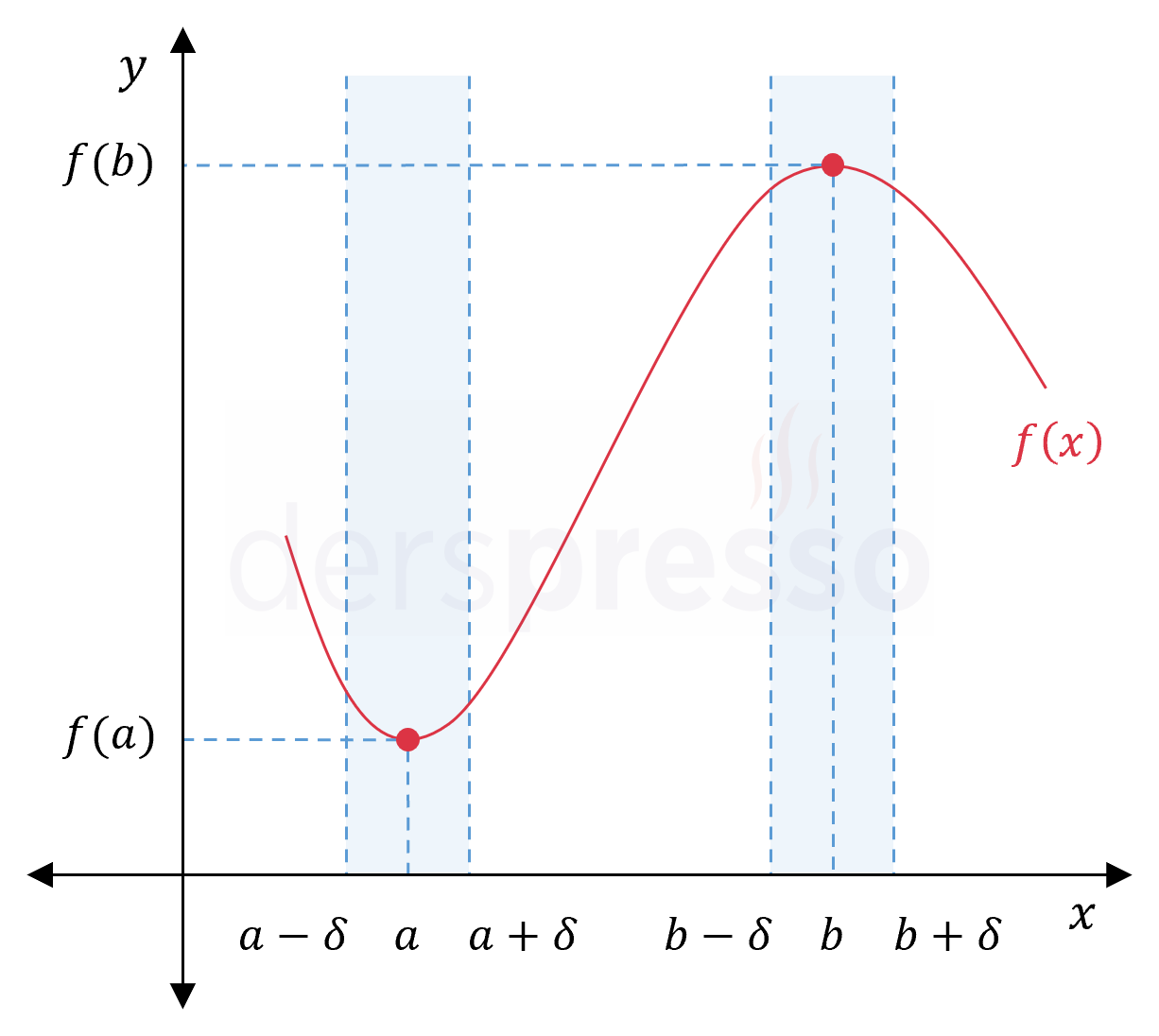
Bir noktadaki fonksiyon değeri, bu noktanın hemen solunda ve sağında bulunan tanım kümesi içindeki noktaların fonksiyon değerinden küçük ya da onlara eşitse bu noktaya yerel minimum noktası denir.
Bir noktadaki fonksiyon değeri, bu noktanın hemen solunda ve sağında bulunan tanım kümesi içindeki noktaların fonksiyon değerinden büyük ya da onlara eşitse bu noktaya yerel maksimum noktası denir.
Yerel minimum ve maksimum noktalarının matematiksel tanımı aşağıdaki gibidir.
\( f: A \to \mathbb{R} \) ve \( \delta \in \mathbb{R} \) olmak üzere,
Bir \( a \in A \) noktası çevresinde \( (a - \delta, a + \delta) \cap A \) şeklinde tanımlı bir açık aralıktaki her \( x \) değeri için;
\( f(a) \le f(x) \) koşulunu sağlayan bir \( \delta \gt 0 \) varsa \( x = a \) fonksiyonun bir yerel minimum noktasıdır.
\( f(a) \ge f(x) \) koşulunu sağlayan bir \( \delta \gt 0 \) varsa \( x = a \) fonksiyonun bir yerel maksimum noktasıdır.
Bir fonksiyonun yerel minimum ve maksimum noktalarına genel bir terim olarak yerel ekstremum noktaları da denir.
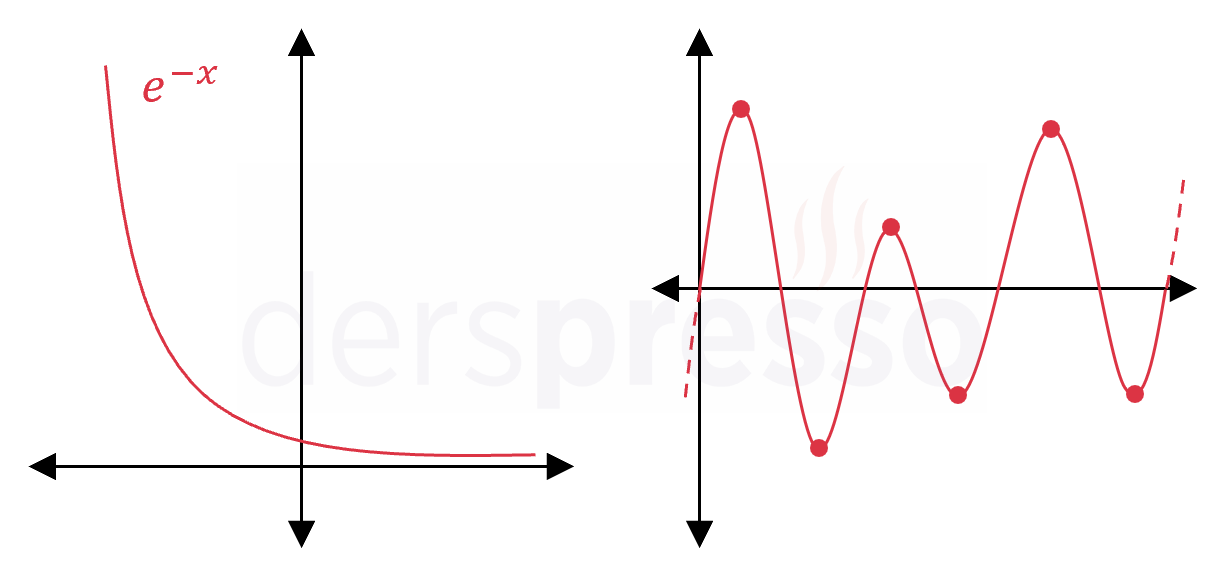
Bir fonksiyonun herhangi bir sayıda (sıfır ve sonsuz dahil) yerel ekstremum noktası olabilir. Örneğin aşağıda soldaki fonksiyonun hiçbir yerel ekstremum noktası yokken sağdaki periyodik fonksiyonun sonsuz sayıda yerel ekstremum noktası vardır.
Türevlenebilir Noktalar
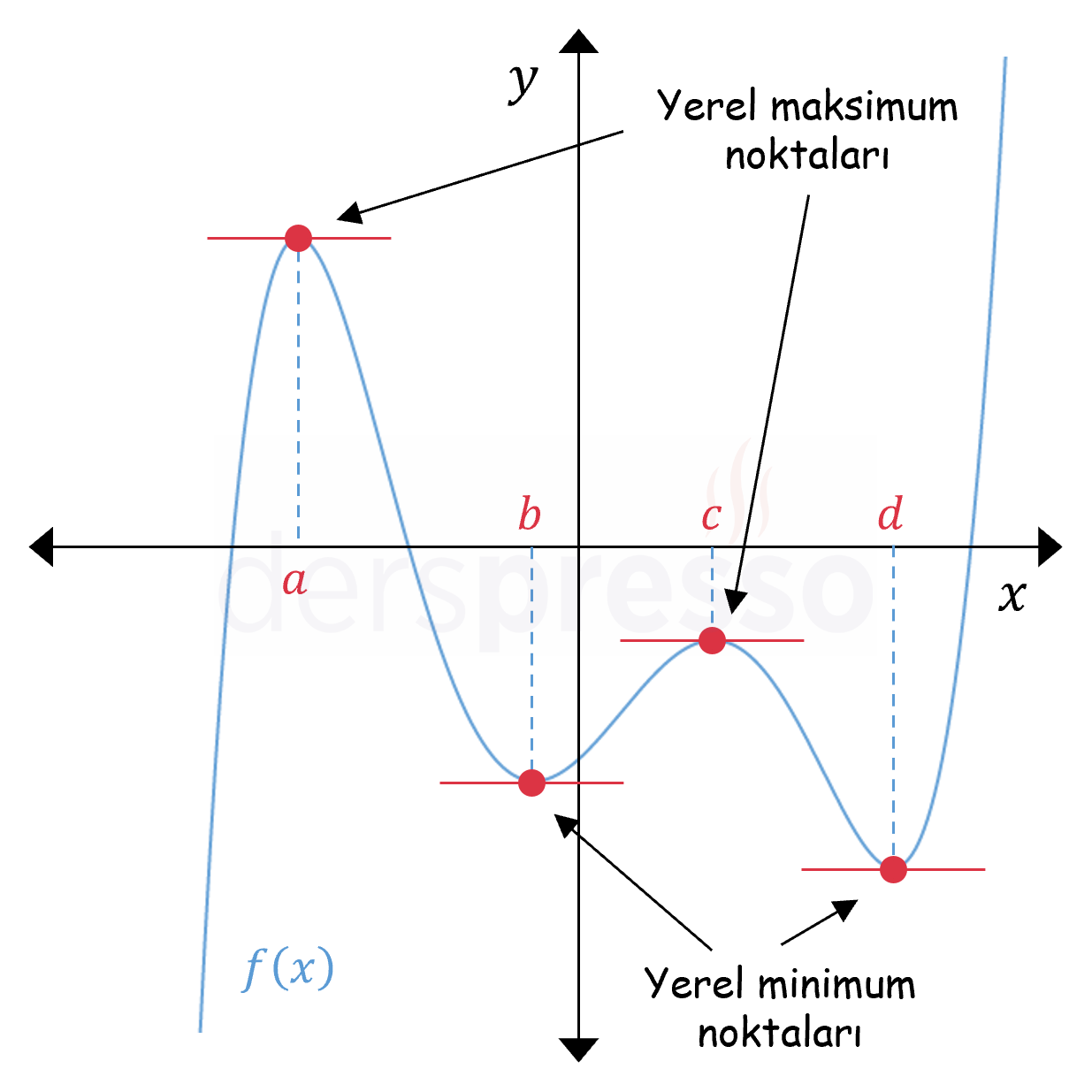
Bir fonksiyonun birinci türevinin sıfır olduğu ve işaret değiştirdiği noktalar yukarıdaki tanımı sağlar, buna göre aşağıdaki grafikteki \( A \) ve \( C \) noktaları yerel maksimum, \( B \) ve \( D \) noktaları da yerel minimum noktalarıdır. Birinci türevin sıfır olduğu, ancak işaret değiştirmediği \( E \) noktası ise bir yerel ekstremum noktası değildir.
Fermat teoremine göre, bir fonksiyonun iç noktaları içinde türevlenebilir olan yerel ekstremum noktaları birer durağan noktadır, yani bu noktalardaki birinci türevi sıfırdır.
\( f \) fonksiyonunun \( x = a \) noktasında bir iç yerel ekstremum noktası varsa ve fonksiyon bu noktada türevlenebilir ise,
\( f'(a) = 0 \) olur.
Yukarıdaki \( E \) noktası örneğinde gördüğümüz üzere, Fermat teoreminin karşıtı her zaman doğru değildir, yani bir fonksiyonun birinci türevinin sıfır olduğu her nokta yerel ekstremum noktası değildir.
Türevlenebilir Olmayan Noktalar
Ekstremum noktaların türevlenebilir olma zorunluluğu yoktur. Aşağıdaki grafikteki türevlenebilir olmayan \( A \) ve \( B \) noktaları, yukarıda tanımı sağladıkları için sırasıyla birer yerel maksimum ve minimum noktasıdır.
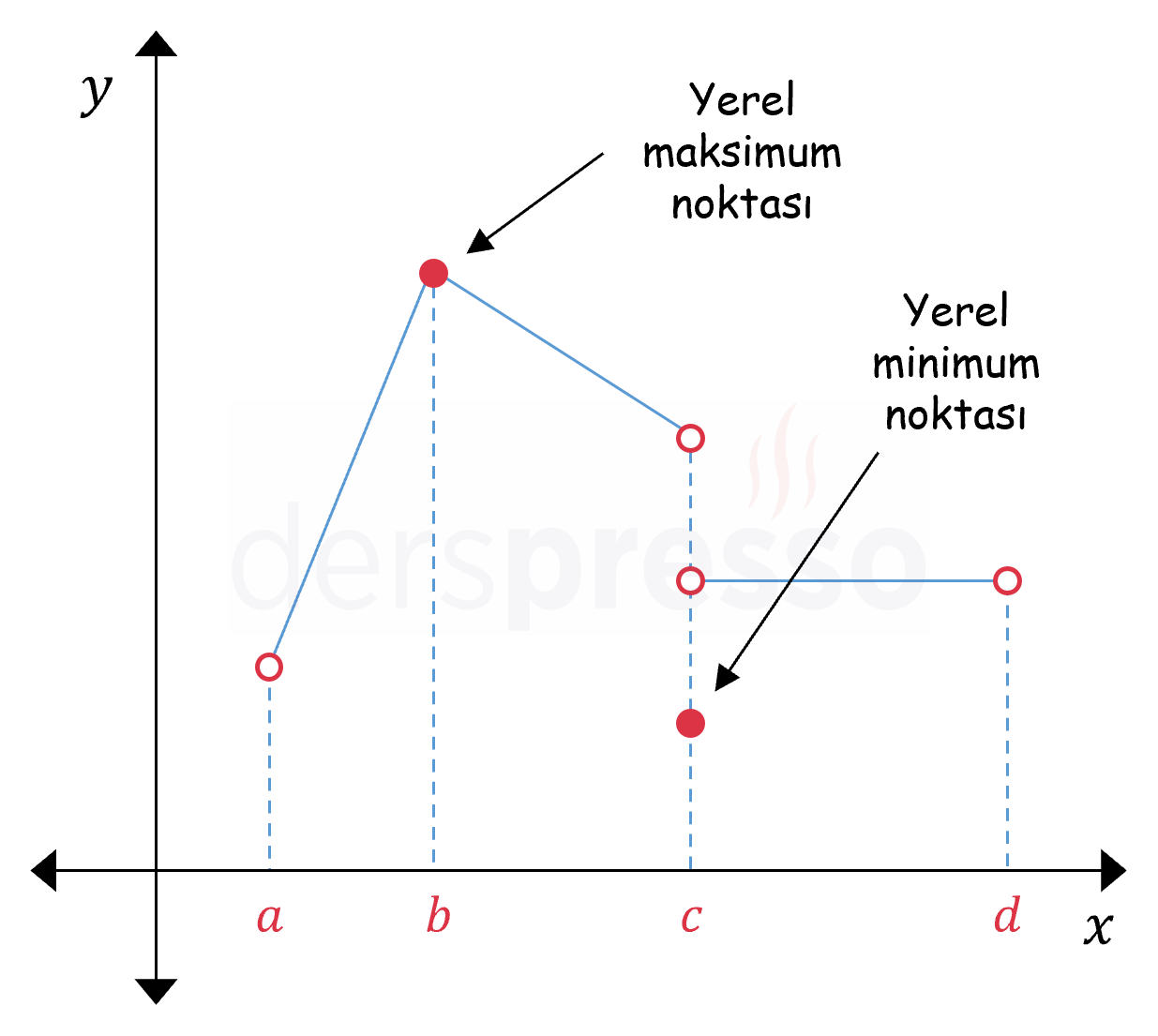
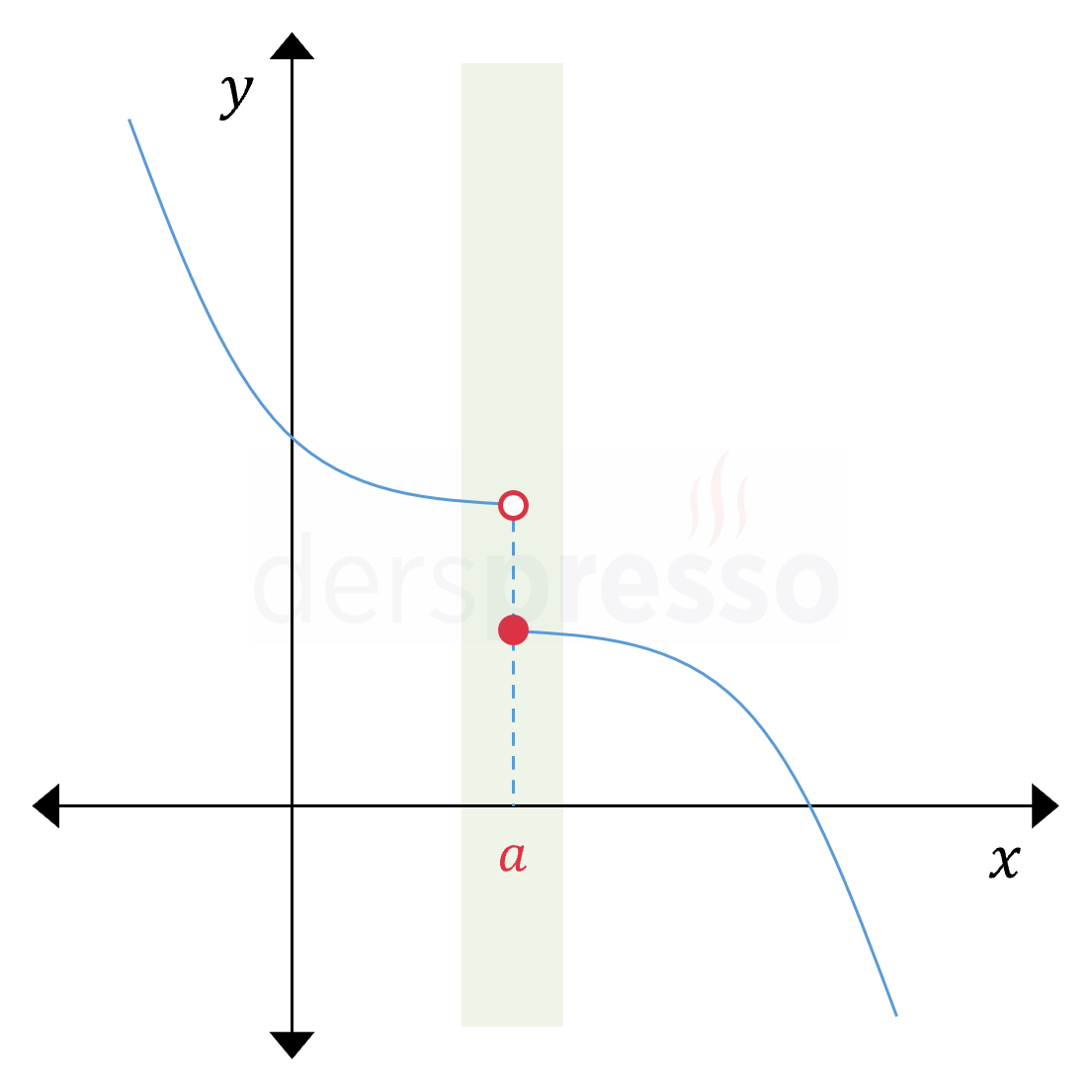
Aşağıdaki grafikte \( f \) fonksiyonunun üç noktasının yerel minimum olma durumları incelenmiştir. Buna göre fonksiyon \( x = a \) noktasının hemen solundaki ve sağındaki noktalar içinde en küçük değerini \( A \) noktasında almaz, bu yüzden bu nokta bir yerel minimum noktası değildir. Fonksiyon \( x = b \) ve \( x = c \) noktalarının hemen solundaki ve sağındaki noktalar içinde en küçük değerini \( B \) ve \( C \) noktalarında alır, bu yüzden bu iki nokta birer yerel minimum noktasıdır.
Sabit Aralıklar
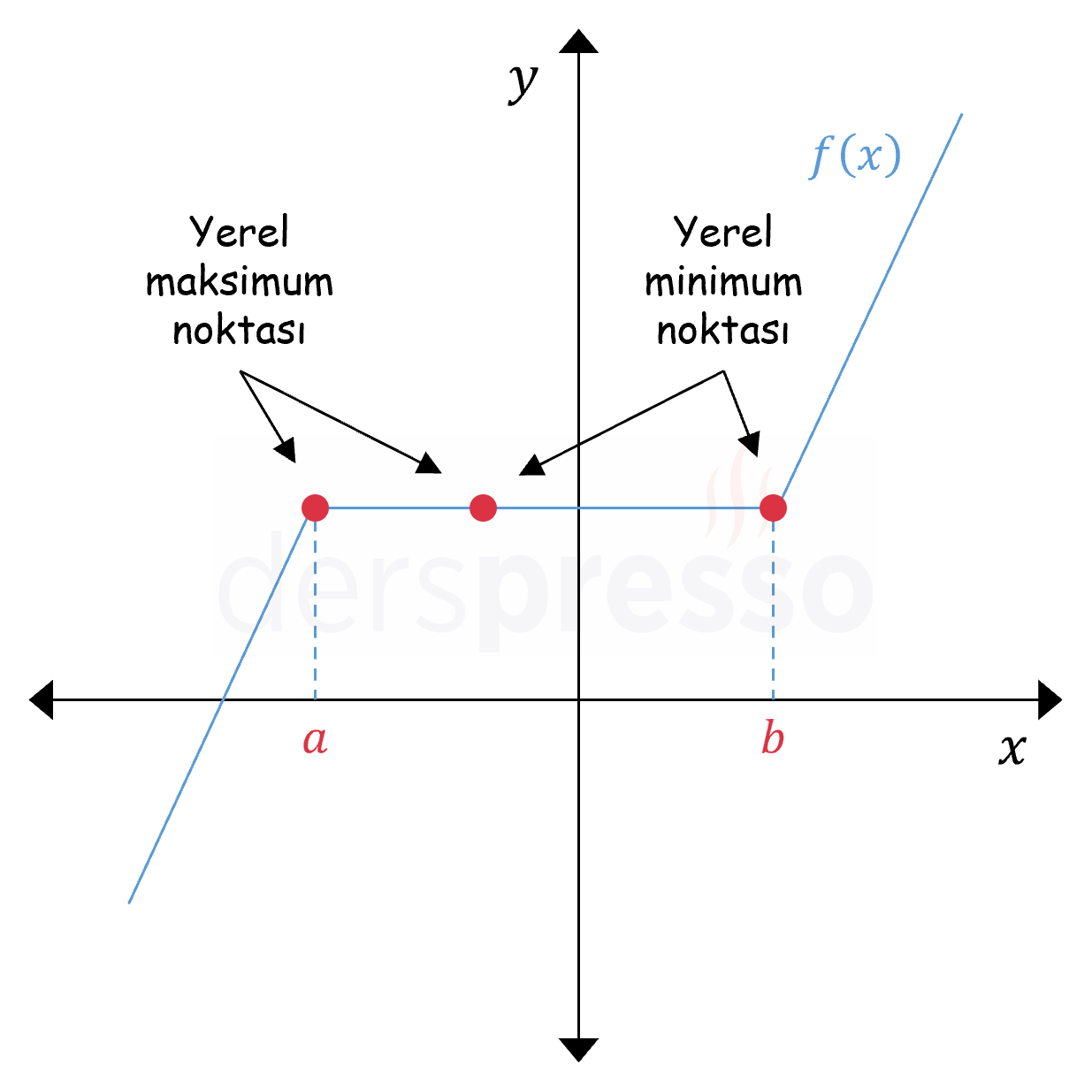
Bir fonksiyonun sabit olduğu bir açık aralıktaki tüm noktalar yukarıdaki tanımı sağladığı için hem yerel minimum hem de yerel maksimum noktalarıdır. Buna göre aşağıdaki grafikte \( A \) bir yerel maksimum noktası, \( C \) bir yerel minimum noktasıdır, \( (a, c) \) açık aralığındaki tüm noktalar da hem yerel minimum hem de yerel maksimum noktalarıdır.
Uç Noktaları
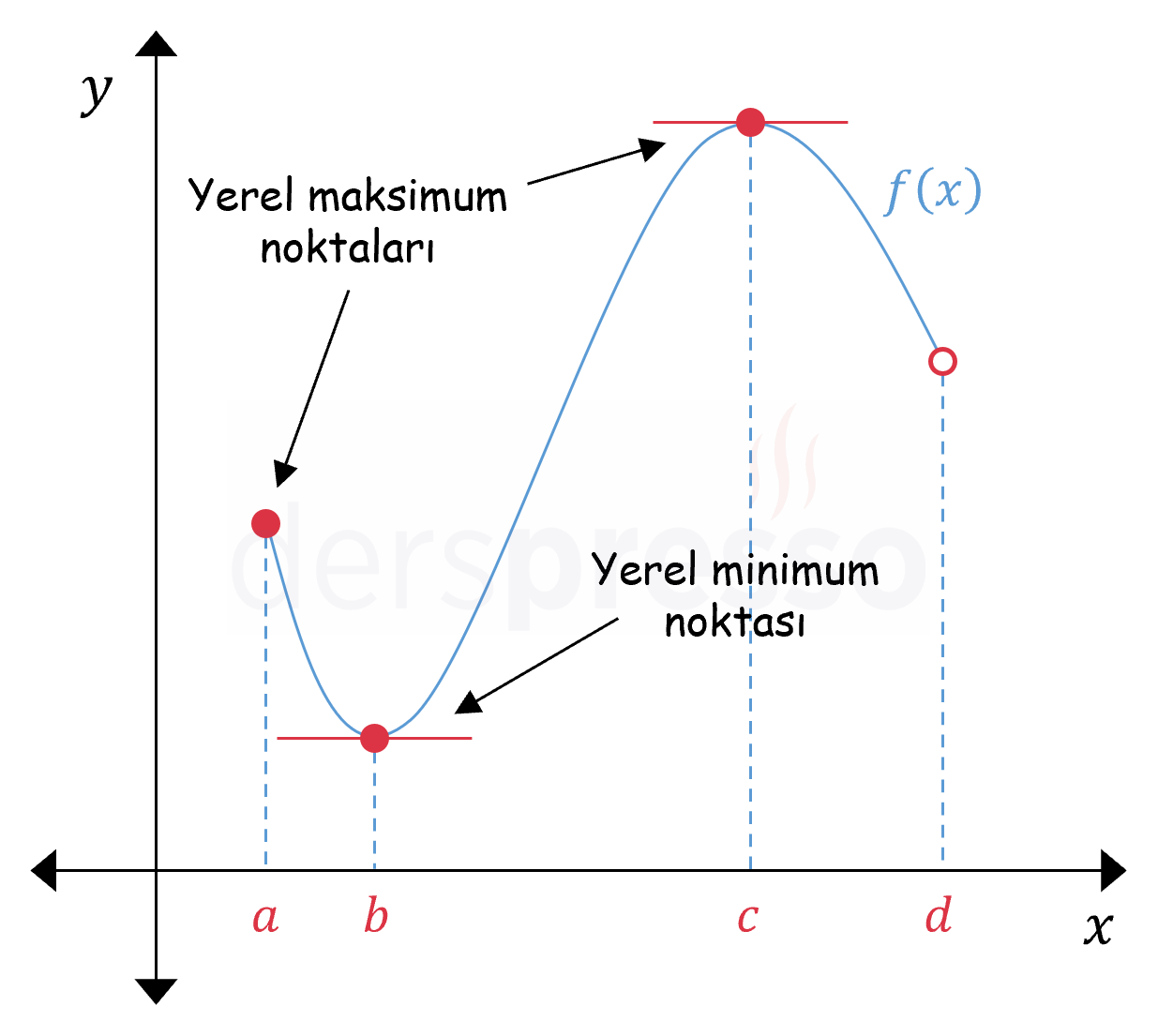
Yukarıdaki tanıma göre; bir fonksiyonun tanım aralığının uç noktaları da yerel extremum noktası olabilir. Buna göre aşağıdaki \( f \) fonksiyonunda \( A \) bir yerel minimum noktası, \( B \) bir yerel maksimum noktasıdır.
NOT: Farklı kaynaklarda yerel ekstremum noktalarının fonksiyonun iç noktaları ile sınırlı olacak şekilde tanımlandığı görülebilir. Biz burada tanımı uç noktalarını da kapsayacak şekilde yapıyoruz.
Yerel Ekstremum Noktalarının Bulunması
Yerel ekstremum noktaları türevlenebilir noktalarda oluşabildiği gibi, türevlenebilir olmayan noktalarda da oluşabilir.
Türevlenebilir Yerel Ekstremum Noktaları
Fermat teoremine göre, bir fonksiyonun türevlenebilir yerel ekstremum noktalarında birinci türevi sıfırdır, dolayısıyla bu noktaları bulmak için öncelikle birinci türevin sıfır olduğu noktaları bulmamız gerekir. Bununla birlikte, birinci türevin sıfır olduğu noktalar iki tipte olabilir ve bunlardan sadece birincisi yerel ekstremum noktalarıdır.
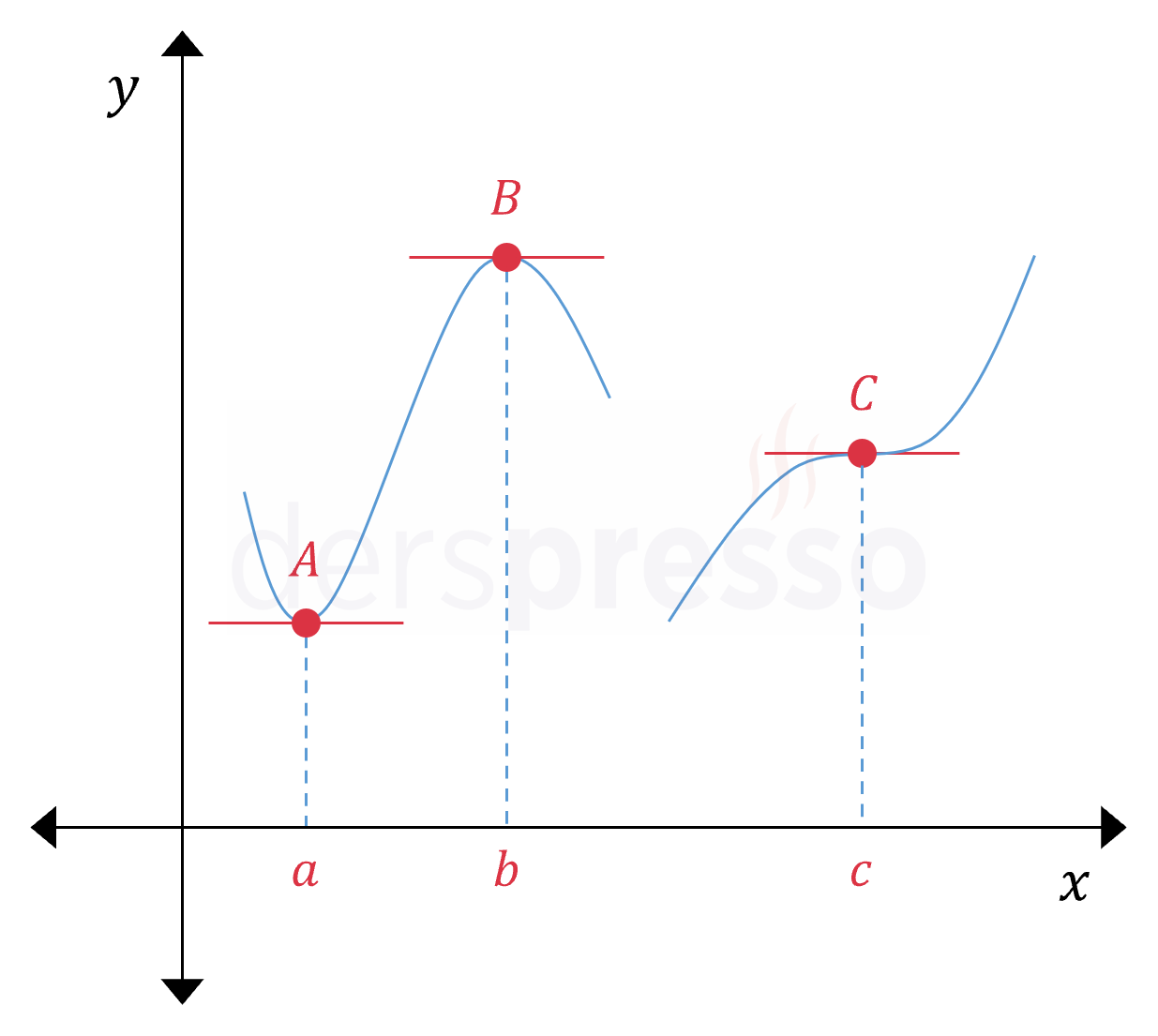
- Türevlenebilir ekstremum noktaları: Bu noktalarda fonksiyonun grafiğinde bir yerel minimum ya da maksimum oluşur. Şekildeki \( A \) ve \( B \) noktaları bu tipte noktalardır.
- Yatay büküm noktası: Bu noktalarda fonksiyonun grafiğinde bir yerel minimum ya da maksimum oluşmaz. Şekildeki \( C \) noktası bu tipte bir noktadır.
Birinci türevin sıfır olduğu bu iki tipteki noktalar arasından hangilerinin yerel ekstremum noktaları olduğunu bulabilmek için kullanılabilecek iki yöntem birinci ve ikinci türev testleridir.
Birinci Türev Testi
Aşağıdaki şekilde birinci türevin sıfır olduğu iki tipte nokta verilmiştir.
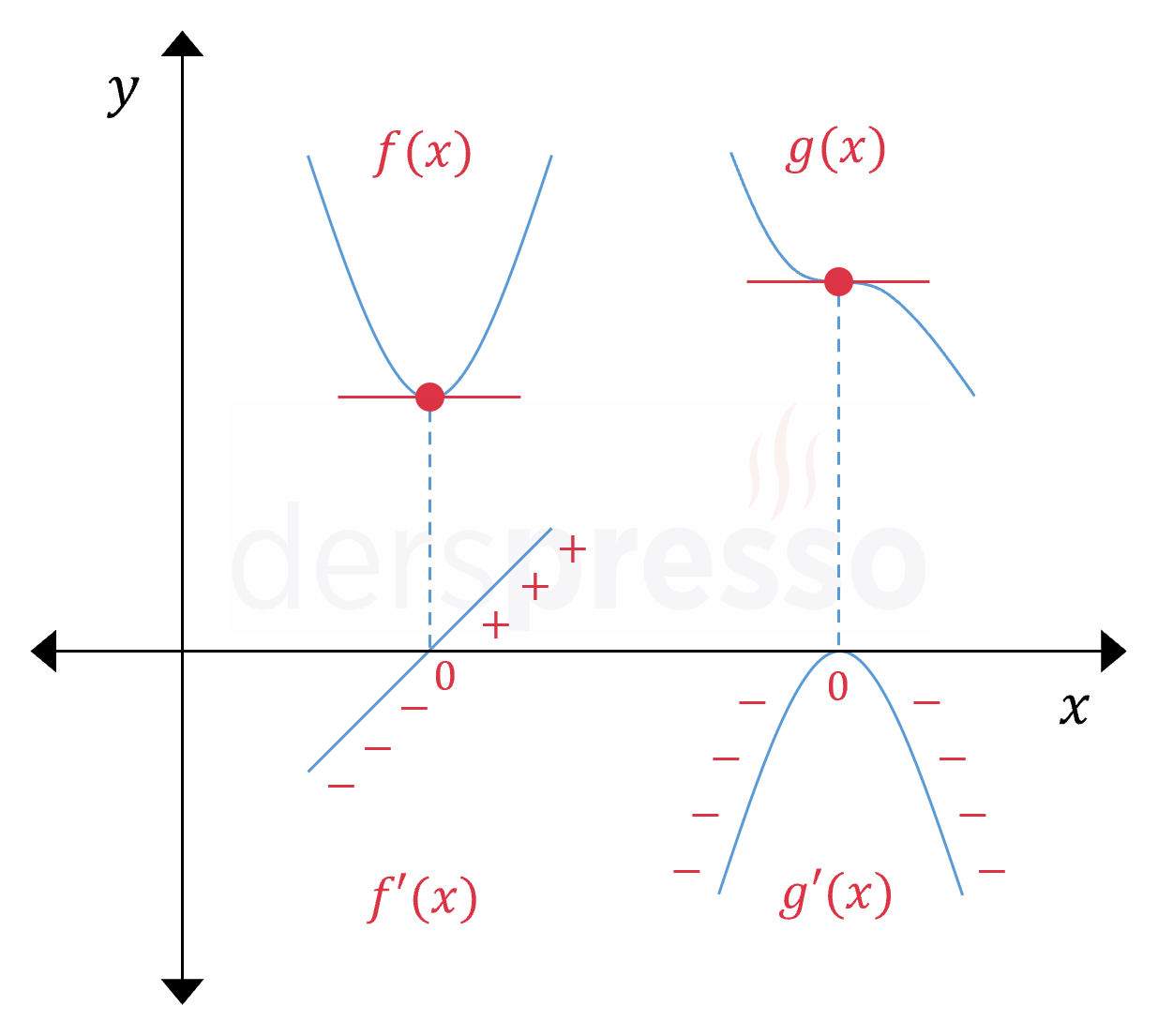
- Soldaki grafikte eğim sırasıyla negatif, sıfır ve pozitif olmakta ve \( A \) noktasında bir yerel minimum noktası oluşmaktadır.
- Sağdaki grafikte ise eğim sırasıyla negatif, sıfır ve negatif olmakta ve \( B \) noktasında bir yerel minimum noktası değil, yatay büküm noktası oluşmaktadır.
Her iki fonksiyonun birinci türev grafikleri karşılaştırıldığında, bir yerel minimumun oluştuğu \( A \) noktasını \( B \) noktasından ayıran özelliğin, \( A \) noktasında birinci türevin negatiften pozitife işaret değiştirmesi olduğu görülebilir.
Benzer şekilde, aşağıdaki şekilde bir yerel maksimumun oluştuğu \( A \) noktasını \( B \) noktasından ayıran özelliğin, yine \( A \) noktasında birinci türevin pozitiften negatife işaret değiştirmesi olduğu görülebilir.
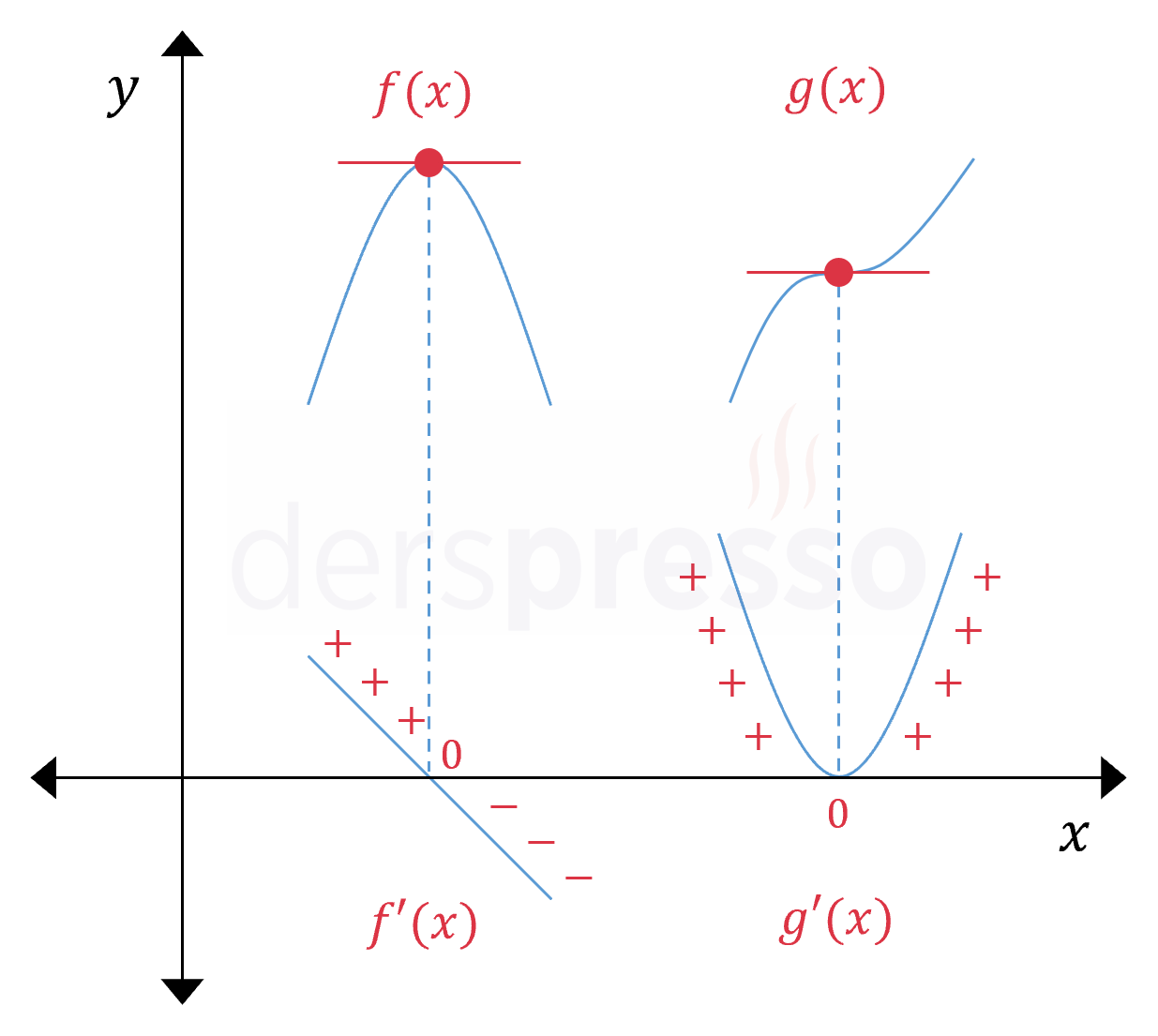
Birinci türev testinde, birinci türevin sıfır olduğu noktalardan hangilerinin yerel minimum noktası, hangilerinin yerel maksimum noktası olduğunu, hangilerinin ikisi de olmadığını anlamak için birinci türevin ilgili noktadaki işaret değişimine bakılır.
\( x = a \) noktası \( f \) fonksiyonunun sürekli olduğu bir kritik noktası olmak üzere,
\( f'(x) \) fonksiyonunun bu noktada işareti;
- negatiften pozitife dönüyorsa nokta bir yerel minimum noktasıdır,
- pozitiften negatife dönüyorsa nokta bir yerel maksimum noktasıdır,
- değişmiyorsa nokta bir yerel ekstremum noktası değildir.
Fonksiyonun birinci türevinin \( x = a \) noktasında çift katlı (2, 4, 6, vb.) bir kökü varsa birinci türev bu noktada işaret değiştirmeyeceği için bu noktada bir yerel minimum ya da maksimum nokta oluşmaz.
\( f(x) = \frac{1}{4}x^4 + \frac{1}{3}x^3 - 3x^2 + 10 \) fonksiyonunun yerel minimum ve maksimum noktalarını birinci türev testi ile bulalım.
Verilen fonksiyon bir polinom fonksiyonudur ve tüm reel sayılarda türevlenebilirdir.
Fonksiyonun birinci türevini bulalım.
\( f'(x) = x^3 + x^2 - 6x \)
\( = x(x + 3)(x - 2) \)
Fonksiyonun türevlenebilir ekstremum noktalarında birinci türevi sıfır olur.
\( f'(x) = x(x + 3)(x - 2) = 0 \)
Bu eşitliği sağlayan noktalar fonksiyonun durağan noktalarıdır.
\( x \in \{ -3, 0, 2 \} \)
Bir işaret tablosu oluşturalım ve bu durağan noktaların oluşturduğu farklı aralıklarda birinci türevin işaretini bulalım.
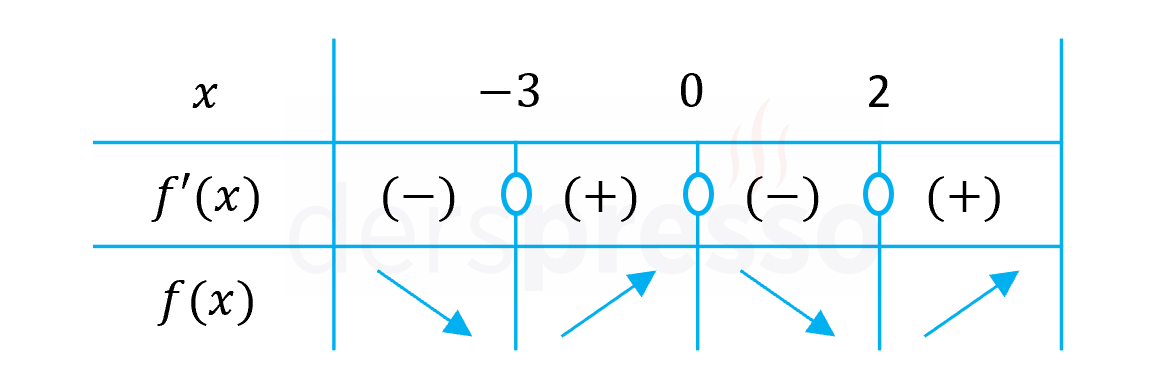
\( x = -3 \) ve \( x = 2 \) noktalarında birinci türevin işareti negatiften pozitife döndüğü için bu iki noktada yerel minimum noktaları oluşur.
\( x = 0 \) noktasında birinci türevin işareti pozitiften negatife döndüğü için bu noktada bir yerel maksimum noktası oluşur.
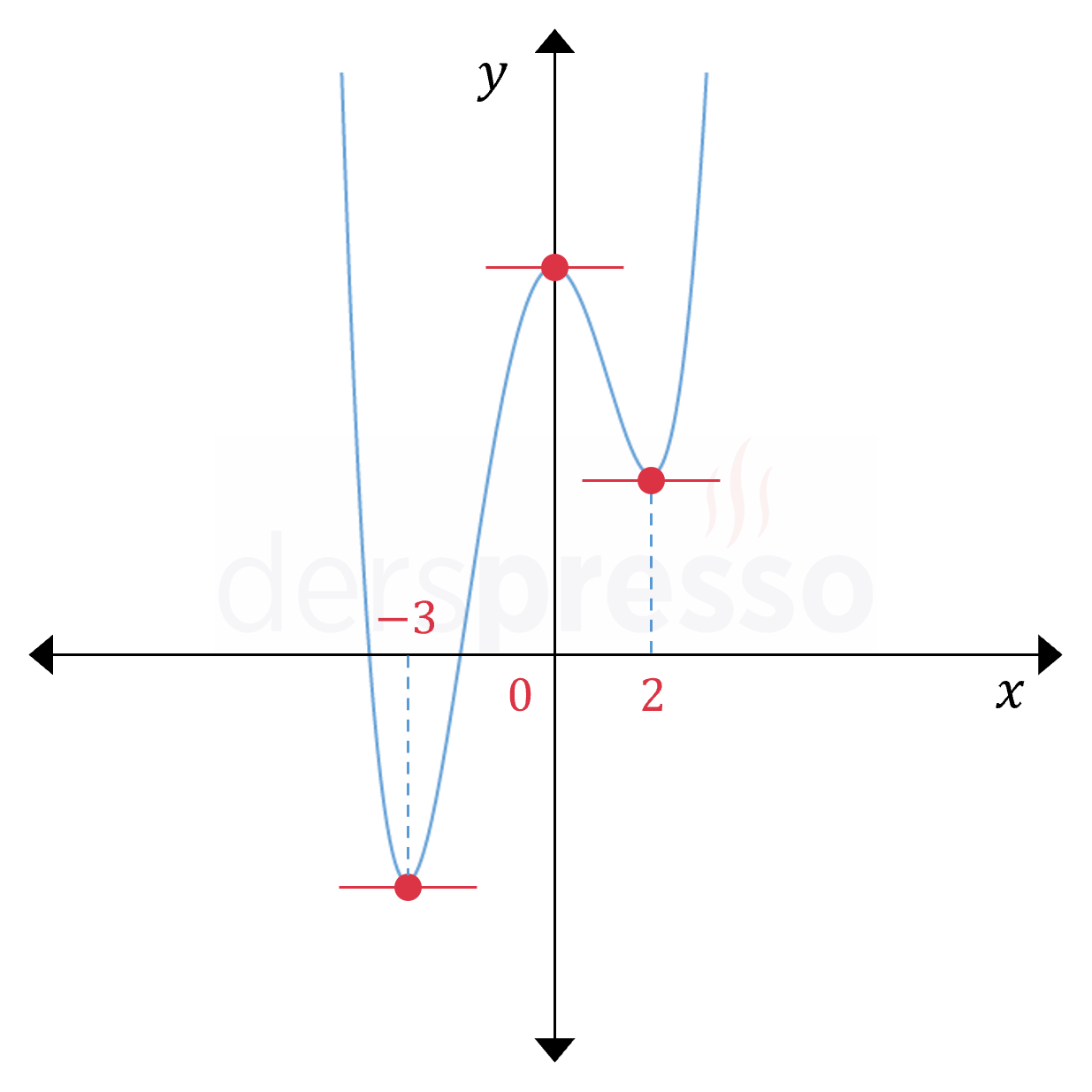
Bulduğumuz sonuç \( f \) fonksiyonun aşağıdaki grafiği ile teyit edilebilir.
Yukarıda yaptığımız tanıma göre, birinci türev testi sadece fonksiyonun türevlenebilir olduğu durağan noktalarda değil, birinci türevin tanımsız olduğu kritik noktalarda da kullanılabilir. Burada önemli olan koşul, fonksiyonun \( x = a \) noktasında sürekli ve bu nokta civarında türevlenebilir olmasıdır. Örneğin, \( f(x) = \abs{x} \) fonksiyonunun sürekli olduğu ancak türevlenebilir olmadığı \( x = 0 \) noktasındaki yerel minimum noktası birinci türev testi ile bulunabilir.
İkinci Türev Testi
Birinci türevin sıfır olduğu noktalardan hangilerinin yerel minimum ya da maksimum noktası olduğu fonksiyonun ikinci türevi ile de anlaşılabilir.
Yukarıda yerel minimum noktası için kullandığımız grafiklerin ikinci türev fonksiyonları eklenmiş hali aşağıdadır. Her iki fonksiyonun ikinci türevinin grafiğini incelediğimizde, bir yerel minimumun oluştuğu \( A \) noktasını \( B \) noktasından ayıran özelliğin, \( A \) noktasında ikinci türevin pozitif olduğunu görebiliriz.
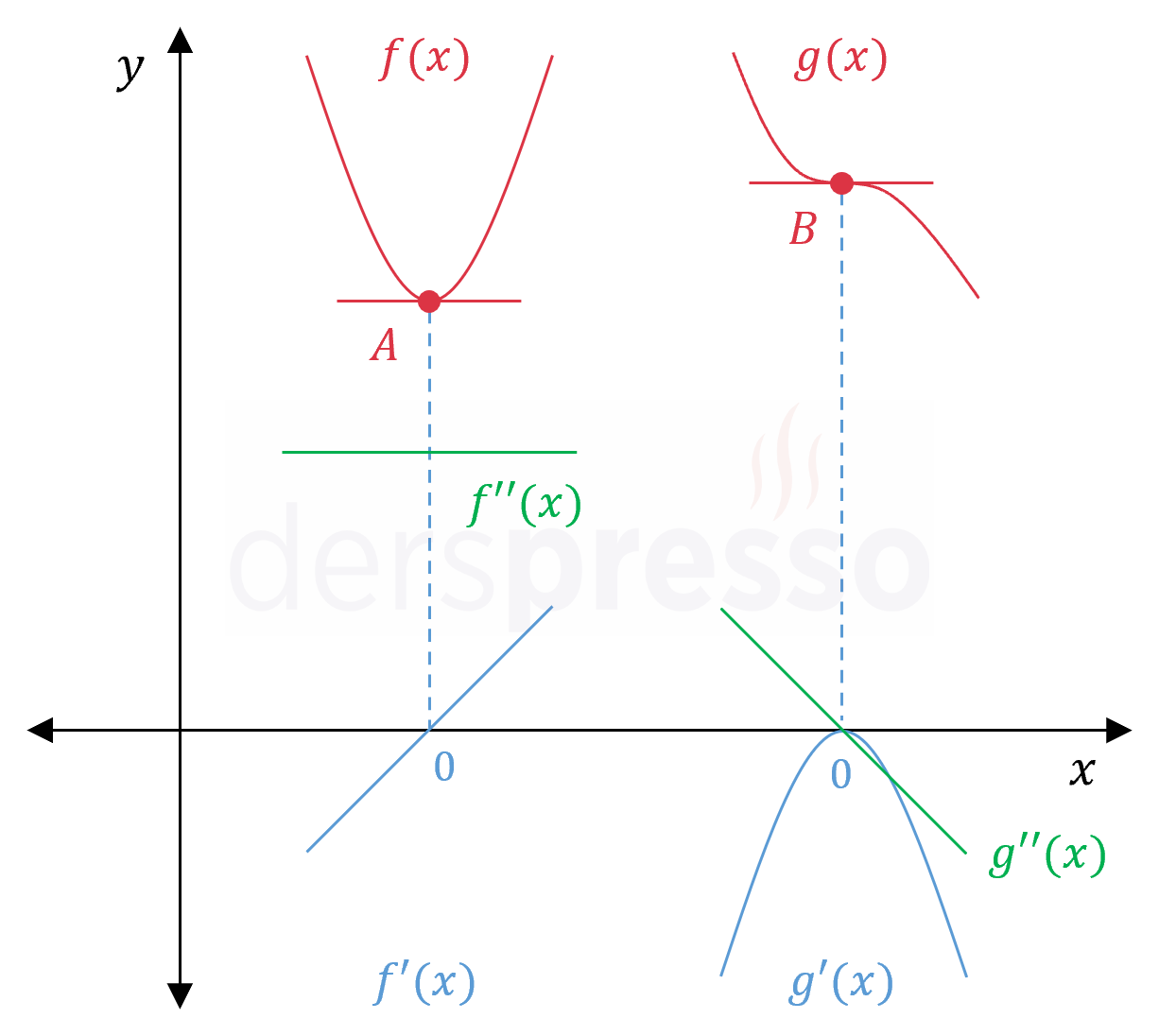
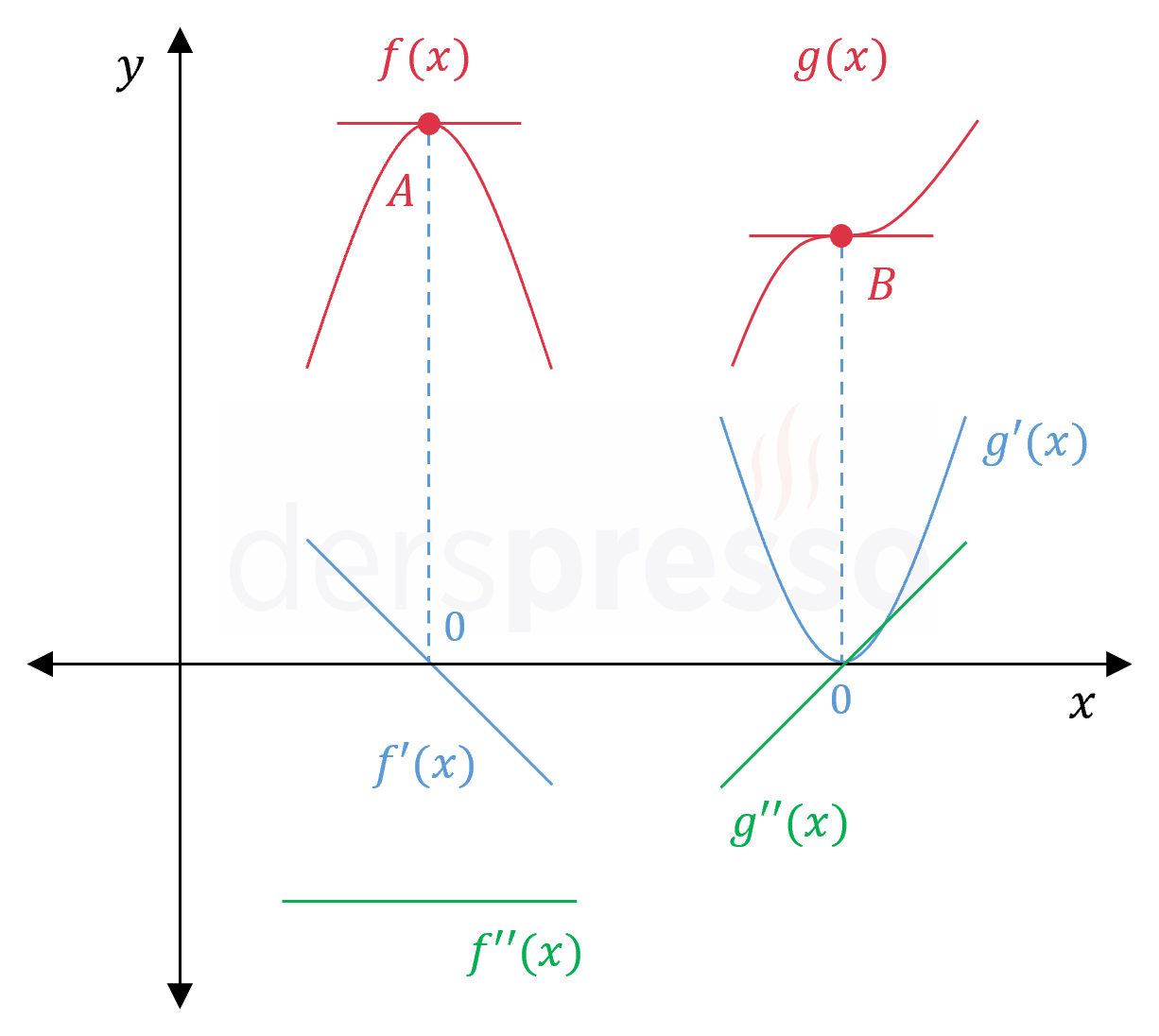
İkinci türev testinde, birinci türevin sıfır olduğu noktalardan hangilerinin yerel minimum noktası, hangilerinin yerel maksimum noktası olduğunu, hangilerinin ikisi de olmadığını anlamak için ikinci türevin ilgili noktadaki işaretine bakılır.
\( x = a \) noktası \( f \) fonksiyonunun bir durağan noktası olmak üzere,
- \( f''(a) \gt 0 \) ise bu nokta bir yerel minimum noktasıdır.
- \( f''(a) \lt 0 \) ise bu nokta bir yerel maksimum noktasıdır.
- \( f''(a) = 0 \) ise ya da \( f''(a) \) tanımlı değilse bu nokta bir yerel minimum ya da yerel maksimum noktası olabilir ya da ikisi de olmayabilir.
Fonksiyonun ikinci türevinin bir noktada pozitif (ya da negatif) olması bu noktada birinci türevin artan (ya da azalan) olması anlamına gelir. Birinci türevin bu noktada sıfır olduğunu bildiğimiz için, bu durumda birinci türev negatiften pozitife (ya da pozitiften negatife) işaret değiştiriyor olmalıdır, bu da bu noktada bir yerel minimum (ya da yerel maksimum) noktası bulunduğunu gösterir.
\( f(x) = \frac{1}{4}x^4 + \frac{1}{3}x^3 - 3x^2 + 10 \) fonksiyonunun yerel minimum ve maksimum noktalarını fonksiyonun ikinci türevini kullanarak bulalım.
Verilen fonksiyon bir polinom fonksiyonudur ve tüm reel sayılarda türevlenebilirdir.
Fonksiyonun birinci türevini alalım.
\( f'(x) = x^3 + x^2 - 6x \)
\( = x(x + 3)(x - 2) \)
Fonksiyonun durağan noktalarında birinci türevi sıfıra eşit olur.
\( f'(x) = x(x + 3)(x - 2) = 0 \)
Buna göre aşağıdaki noktalar fonksiyonun durağan noktalarıdır.
\( x \in \{-3, 0, 2\} \)
Bu noktaların yerel minimum ya da yerel maksimum nokta olup olmadığını bulmak için ikinci türev testini uygulayalım.
\( f''(x) = 3x^2 + 2x - 6 \)
\( f''(-3) = 3(-3)^2 + 2(-3) - 6 = 15 \)
\( f''(-3) \gt 0 \) olduğu için \( x = -3 \) bir yerel minimum noktasıdır.
\( f''(0) = 3(0)^2 + 2(0) - 6 = -6 \)
\( f''(0) \lt 0 \) olduğu için \( x = 0 \) bir yerel maksimum noktasıdır.
\( f''(2) = 3(2)^2 + 2(2) - 6 = 10 \)
\( f''(2) \gt 0 \) olduğu için \( x = 2 \) bir yerel minimum noktasıdır.
Bu şekilde yukarıda birinci türev testini kullandığımız örnekle aynı sonucu elde etmiş olduk.
Birinci ve ikinci türev testleri arasında tercih yaparken dikkate alınabilecek iki nokta aşağıdaki gibidir.
- Birinci türev testi bir noktanın yerel minimum ya da maksimum nokta olup olmadığı konusunda kesin sonuç verir. İkinci türev testi ise yukarıda belirttiğimiz koşullar sağlandığında çalışır.
- Fonksiyonun ikinci türevini almanın kolay olmadığı durumlarda birinci türev testi tercih edilebilir. Benzer şekilde, ikinci türevi almanın kolay olduğu durumlarda ikinci türev testi kullanılabilir.
Aşağıdaki fonksiyonların en geniş tanım kümelerindeki yerel minimum ve maksimum noktalarını fonksiyonların ikinci türevlerini kullanarak bulunuz.
(a) \( f(x) = \dfrac{1}{3}x^3 - \dfrac{1}{2}x^2 - 2x \)
(b) \( g(x) = x^3 + 15x^2 + 72x \)
(c) \( h(x) = 2x + \dfrac{8}{x}, \quad x \ne 0 \)
Çözümü GösterBir fonksiyonun türevlenebilir olduğu bir aralıkta yerel minimum ve maksimum noktaları birinci türevin işaret değiştirdiği noktalarda oluşur. Bu noktaları ikinci türevi kullanarak bulmak için birinci türevin sıfır, ikinci türevin sıfırdan farklı olduğu noktaları bulmamız gerekir.
Buna göre birinci türevin sıfır olduğu bir noktada ikinci türev pozitif ise bu nokta bir yerel minimum noktası, negatif ise bir yerel maksimum noktasıdır.
(a) seçeneği:
\( f(x) = \dfrac{1}{3}x^3 - \dfrac{1}{2}x^2 - 2x \)
Verilen fonksiyon bir polinom fonksiyonudur ve tüm reel sayılarda tanımlı ve türevlenebilirdir.
Fonksiyonun birinci türevini alalım.
\( f'(x) = x^2 - x - 2 \)
Fonksiyonun birinci türevinin sıfıra eşit olduğu noktaları bulalım.
\( f'(x) = x^2 - x - 2 = 0 \)
\( (x + 1)(x - 2) = 0 \)
\( x \in \{-1, 2\} \)
Bu \( x \) değerlerini fonksiyonda yerine yazarak bu noktalardaki ordinat değerlerini bulalım.
\( f(-1) = \dfrac{1}{3}(-1)^3 - \dfrac{1}{2}(-1)^2 - 2(-1) = \dfrac{7}{6} \)
\( f(2) = \dfrac{1}{3}2^3 - \dfrac{1}{2}2^2 - 2(2) = -\dfrac{10}{3} \)
Bu noktaların yerel minimum ya da yerel maksimum nokta olup olmadığını bulmak için bu noktalarda ikinci türevin işaretini inceleyelim.
Fonksiyonun ikinci türevini alalım.
\( f''(x) = 2x - 1 \)
\( f''(-1) = 2(-1) - 1 = -3 \)
\( f''(-1) \lt 0 \) olduğu için \( (-1, \frac{7}{6}) \) bir yerel maksimum noktasıdır.
\( f''(2) = 2(2) - 1 = 3 \)
\( f''(2) \gt 0 \) olduğu için \( (2, -\frac{10}{3}) \) bir yerel minimum noktasıdır.
(b) seçeneği:
\( g(x) = x^3 + 15x^2 + 72x \)
Verilen fonksiyon bir polinom fonksiyonudur ve tüm reel sayılarda tanımlı ve türevlenebilirdir.
Fonksiyonun birinci türevini alalım.
\( g'(x) = 3x^2 + 30x + 72 \)
Fonksiyonun birinci türevinin sıfıra eşit olduğu noktaları bulalım.
\( g'(x) = 3x^2 + 30x + 72 = 0 \)
\( 3(x + 6)(x + 4) = 0 \)
\( x \in \{-6, -4\} \)
Bu \( x \) değerlerini fonksiyonda yerine yazarak bu noktalardaki ordinat değerlerini bulalım.
\( g(-6) = (-6)^3 + 15(-6)^2 + 72(-6) = -108 \)
\( g(-4) = (-4)^3 + 15(-4)^2 + 72(-4) = -112 \)
Bu noktaların yerel minimum ya da yerel maksimum nokta olup olmadığını bulmak için bu noktalarda ikinci türevin işaretini inceleyelim.
Fonksiyonun ikinci türevini alalım.
\( g''(x) = 6x + 30 \)
\( g''(-6) = 6(-6) + 30 = -6 \)
\( g''(-6) \lt 0 \) olduğu için \( (-6, -108) \) bir yerel maksimum noktasıdır.
\( g''(-4) = 6(-4) + 30 = 6 \)
\( g''(-4) \gt 0 \) olduğu için \( (-4, -112) \) bir yerel minimum noktasıdır.
(c) seçeneği:
\( h(x) = 2x + \dfrac{8}{x} \)
Verilen fonksiyon \( x = 0 \) noktası hariç tüm reel sayılarda tanımlı ve türevlenebilirdir.
Fonksiyonun birinci türevini alalım.
\( h'(x) = 2 - \dfrac{8}{x^2} \)
Fonksiyonun birinci türevinin sıfıra eşit olduğu noktaları bulalım.
\( h'(x) = 2 - \dfrac{8}{x^2} = 0 \)
\( x^2 = 4 \)
\( x \in \{-2, 2\} \)
Bu \( x \) değerlerini fonksiyonda yerine yazarak bu noktalardaki ordinat değerlerini bulalım.
\( h(-2) = 2(-2) + \dfrac{8}{-2} = -8 \)
\( h(2) = 2(2) + \dfrac{8}{2} = 8 \)
Bu noktaların yerel minimum ya da yerel maksimum nokta olup olmadığını bulmak için bu noktalarda ikinci türevin işaretini inceleyelim.
Fonksiyonun ikinci türevini alalım.
\( h''(x) = \dfrac{16}{x^3} \)
\( h''(-2) = \dfrac{16}{(-2)^3} = -2 \)
\( h''(-2) \lt 0 \) olduğu için \( (-2, -8) \) bir yerel maksimum noktasıdır.
\( h''(2) = \dfrac{16}{2^3} = 2 \)
\( h''(2) \gt 0 \) olduğu için \( (2, 8) \) bir yerel minimum noktasıdır.
Aşağıdaki fonksiyonların en geniş tanım kümelerindeki yerel minimum ve maksimum noktalarını fonksiyonların ikinci türevlerini kullanarak bulunuz.
(a) \( f(x) = 20\sqrt{x} - \dfrac{5}{3}\sqrt{x^3} \)
(b) \( g(x) = \dfrac{5}{2}x^2 - 3\sqrt[3]{x^5} \)
(c) \( h(x) = \dfrac{1}{x} - \dfrac{2}{3\sqrt{x}} \)
Çözümü GösterBir fonksiyonun türevlenebilir olduğu bir aralıkta yerel minimum ve maksimum noktaları birinci türevin işaret değiştirdiği noktalarda oluşur. Bu noktaları ikinci türevi kullanarak bulmak için birinci türevin sıfır, ikinci türevin sıfırdan farklı olduğu noktaları bulmamız gerekir.
Buna göre birinci türevin sıfır olduğu bir noktada ikinci türev pozitif ise bu nokta bir yerel minimum noktası, negatif ise bir yerel maksimum noktasıdır.
(a) seçeneği:
\( f(x) = 20\sqrt{x} - \dfrac{5}{3}\sqrt{x^3} \)
Verilen fonksiyon karekök ifadesinden dolayı pozitif reel sayılarda tanımlı ve türevlenebilirdir.
\( f(x) = 20x^{\frac{1}{2}} - \dfrac{5}{3}x^{\frac{3}{2}} \)
Fonksiyonun birinci türevini alalım.
\( f'(x) = 10x^{-\frac{1}{2}} - \dfrac{5}{2}x^{\frac{1}{2}} \)
Fonksiyonun birinci türevinin sıfıra eşit olduğu noktaları bulalım.
\( f'(x) = 10x^{-\frac{1}{2}} - \dfrac{5}{2}x^{\frac{1}{2}} = 0 \)
\( 10x^{-\frac{1}{2}} = \dfrac{5}{2}x^{\frac{1}{2}} \)
\( \dfrac{4}{x^{\frac{1}{2}}} = x^{\frac{1}{2}} \)
\( x = 4 \)
Bu \( x \) değerini fonksiyonda yerine yazarak bu noktalardaki ordinat değerlerini bulalım.
\( f(4) = 20\sqrt{4} - \dfrac{5}{3}\sqrt{4^3} = \dfrac{80}{3} \)
Bu noktanın yerel minimum ya da yerel maksimum nokta olup olmadığını bulmak için bu noktada ikinci türevin işaretini inceleyelim.
Fonksiyonun ikinci türevini alalım.
\( f''(x) = -5x^{-\frac{3}{2}} - \dfrac{5}{4}x^{-\frac{1}{2}} \)
\( f''(4) = -5(4)^{-\frac{3}{2}} - \dfrac{5}{4}4^{-\frac{1}{2}} = -\dfrac{5}{2} \)
\( f''(4) \lt 0 \) olduğu için \( (4, \frac{80}{3}) \) bir yerel maksimum noktasıdır.
(b) seçeneği:
\( g(x) = \dfrac{5}{2}x^2 - 3\sqrt[3]{x^5} \)
Verilen fonksiyon tüm reel sayılarda tanımlı ve türevlenebilirdir.
\( g(x) = \dfrac{5}{2}x^2 - 3x^{\frac{5}{3}} \)
Fonksiyonun birinci türevini alalım.
\( g'(x) = 5x - 5x^{\frac{2}{3}} \)
Fonksiyonun birinci türevinin sıfıra eşit olduğu noktaları bulalım.
\( g'(x) = 5x - 5x^{\frac{2}{3}} = 0 \)
\( 5x = 5x^{\frac{2}{3}} \)
\( x^{\frac{1}{3}} = 1 \)
\( x = 1 \)
Bu \( x \) değerini fonksiyonda yerine yazarak bu noktalardaki ordinat değerlerini bulalım.
\( g(1) = \dfrac{5}{2}1^2 - 3\sqrt[3]{1^5} = -\dfrac{1}{2} \)
Bu noktanın yerel minimum ya da yerel maksimum nokta olup olmadığını bulmak için bu noktada ikinci türevin işaretini inceleyelim.
Fonksiyonun ikinci türevini alalım.
\( g''(x) = 5 - \dfrac{10}{3}x^{-\frac{1}{3}} \)
\( g''(1) = 5 - \dfrac{10}{3}1^{-\frac{1}{3}} = \dfrac{5}{3} \)
\( g''(1) \gt 0 \) olduğu için \( (1, -\frac{1}{2}) \) bir yerel minimum noktasıdır.
(c) seçeneği:
\( h(x) = \dfrac{1}{x} - \dfrac{2}{3\sqrt{x}} \)
Verilen fonksiyon karekök ifadesinden dolayı pozitif reel sayılarda tanımlı ve türevlenebilirdir.
\( h(x) = x^{-1} - \dfrac{2}{3}x^{-\frac{1}{2}} \)
Fonksiyonun birinci türevini alalım.
\( h'(x) = -x^{-2} + \dfrac{1}{3}x^{-\frac{3}{2}} \)
Fonksiyonun birinci türevinin sıfıra eşit olduğu noktaları bulalım.
\( h'(x) = -x^{-2} + \dfrac{1}{3}x^{-\frac{3}{2}} = 0 \)
\( x^{-2} = \dfrac{1}{3}x^{-\frac{3}{2}} \)
\( \dfrac{1}{x^2} = \dfrac{1}{3x^{\frac{3}{2}}} \)
\( x^2 = 3x^{\frac{3}{2}} \)
\( x^{\frac{1}{2}} = 3 \)
\( x = 9 \)
Bu \( x \) değerini fonksiyonda yerine yazarak bu noktalardaki ordinat değerlerini bulalım.
\( h(9) = \dfrac{1}{9} - \dfrac{2}{3\sqrt{9}} = -\dfrac{1}{9} \)
Bu noktanın yerel minimum ya da yerel maksimum nokta olup olmadığını bulmak için bu noktada ikinci türevin işaretini inceleyelim.
Fonksiyonun ikinci türevini alalım.
\( h''(x) = 2x^{-3} - \dfrac{1}{2}x^{-\frac{5}{2}} \)
\( h''(9) = 2(9)^{-3} - \dfrac{1}{2}9^{-\frac{5}{2}} = \dfrac{1}{2 \cdot 3^6} \)
\( h''(9) \gt 0 \) olduğu için \( (9, -\frac{1}{9}) \) bir yerel minimum noktasıdır.
\( f: \mathbb{R} \to \mathbb{R} \)
\( f(x) = 3\sqrt[3]{x^5} - 15\sqrt[3]{x^4} - 25x + 10 \)
Yukarıdaki fonksiyonun yerel minimum ve yerel maksimum noktalarını bulunuz.
Çözümü GösterBir fonksiyonun türevlenebilir olduğu bir aralıkta yerel minimum ve maksimum noktaları birinci türevin işaret değiştirdiği noktalarda oluşur. Bu noktaları ikinci türevi kullanarak bulmak için birinci türevin sıfır, ikinci türevin sıfırdan farklı olduğu noktaları bulmamız gerekir.
Buna göre birinci türevin sıfır olduğu bir noktada ikinci türev pozitif ise bu nokta bir yerel minimum noktası, negatif ise bir yerel maksimum noktasıdır.
\( f(x) = 3x^{\frac{5}{3}} - 15x^{\frac{4}{3}} - 25x + 10 \)
\( f'(x) = 5x^{\frac{2}{3}} - 20x^{\frac{1}{3}} - 25 \)
Birinci türevin sıfır olduğu noktaları bulalım.
\( 5x^{\frac{2}{3}} - 20x^{\frac{1}{3}} - 25 = 0 \)
\( x^{\frac{2}{3}} - 4x^{\frac{1}{3}} - 5 = 0 \)
\( (x^{\frac{1}{3}})^2 - 4x^{\frac{1}{3}} - 5 = 0 \)
\( (x^{\frac{1}{3}} + 1)(x^{\frac{1}{3}} - 5) = 0 \)
\( x^{\frac{1}{3}} = -1 \Longrightarrow x = -1 \)
\( x^{\frac{1}{3}} = 5 \Longrightarrow x = 125 \)
\( x \in \{-1, 125\} \)
Bu noktaların yerel minimum ya da yerel maksimum nokta olup olmadığını bulmak için bu noktalarda ikinci türevin işaretini inceleyelim.
Fonksiyonun ikinci türevini alalım.
\( f''(x) = \dfrac{10}{3}x^{-\frac{1}{3}} - \dfrac{20}{3}x^{-\frac{2}{3}} \)
\( f''(-1) = \dfrac{10}{3}(-1)^{-\frac{1}{3}} - \dfrac{20}{3}(-1)^{-\frac{2}{3}} = -10 \)
\( f''(-1) \lt 0 \) olduğu için \( x = -1 \) apsisli noktada bir yerel maksimum noktasıdır.
\( f''(125) = \dfrac{10}{3}(125)^{-\frac{1}{3}} - \dfrac{20}{3}(125)^{-\frac{2}{3}} = \dfrac{2}{5} \)
\( f''(125) \gt 0 \) olduğu için \( x = 125 \) apsisli noktada bir yerel minimum noktasıdır.
\( f(x) = x^2 + ax - b \)
fonksiyonunun \( A(-1, 4) \) noktasında yerel maksimumu olduğuna göre, \( a + b \) kaçtır?
Çözümü Göster\( A(-1, 4) \) noktası fonksiyon grafiği üzerinde bir nokta olduğu için fonksiyon denklemini sağlar.
\( f(-1) = 4 \)
\( (-1)^2 + a(-1) - b = 4 \)
\( -a - b = 3 \)
Verilen fonksiyon bir polinom fonksiyonudur ve tüm reel sayılarda türevlenebilirdir.
Bir fonksiyonun türevlenebilir ekstremum noktalarında birinci türevi sıfıra eşit olur.
\( f'(x) = 2x + a \)
\( f'(-1) = 0 \)
\( 2(-1) + a = 0 \)
\( a = 2 \)
\( -a - b = 3 \Longrightarrow b = -5 \)
\( a + b = 2 + (-5) = -3 \) bulunur.
\( f(x) = x^3 + (a + 1)x^2 + (b - 1)x + 4 \)
fonksiyonunun \( x = 1 \) apsisli noktada yerel minimumu, \( x = -1 \) apsisli noktada yerel maksimumu olduğuna göre, \( a - b \) kaçtır?
Çözümü GösterVerilen fonksiyon bir polinom fonksiyonudur ve tüm reel sayılarda türevlenebilirdir.
Bir fonksiyonun türevlenebilir ekstremum noktalarında birinci türevi sıfıra eşit olur.
\( f'(x) = 3x^2 + 2(a + 1)x + b - 1 \)
\( x = 1 \) apsisli noktada birinci türev sıfır olur.
\( f'(1) = 0 \)
\( 3 + 2(a + 1) + b - 1 = 0 \)
\( 2a + b = -4 \)
\( x = -1 \) apsisli noktada birinci türev sıfır olur.
\( f'(-1) = 0 \)
\( 3 - 2(a + 1) + b - 1 = 0 \)
\( -2a + b = 0 \)
\( a \) ve \( b \) bilinmeyenlerinden oluşan iki denklemi ortak çözelim.
\( a = -1, \quad b = -2 \)
\( a - b = -1 - (-2) = 1 \) bulunur.
\( f(x) = e^{2x} + 2e^{-x} \) fonksiyonunun yerel ekstremum noktalarını bulunuz.
Çözümü GösterVerilen fonksiyon üstel fonksiyonların toplamından oluşur ve tüm reel sayılarda türevlenebilirdir.
Bir fonksiyonun iç noktaları içinde türevlenebilir olan yerel ekstremum noktaları birer durağan noktadır, yani bu noktalardaki birinci türevi sıfırdır.
Fonksiyonun birinci türevini alalım.
\( f'(x) = 2e^{2x} - 2e^{-x} \)
Fonksiyonun birinci türevinin sıfıra eşit olduğu noktaları bulalım.
\( f'(x) = 2e^{2x} - 2e^{-x} = 0 \)
\( 2e^{2x} - \dfrac{2}{e^{x}} = 0 \)
\( \dfrac{2e^{3x} - 2}{e^{x}} = 0 \)
Üstel fonksiyonlar tüm reel sayılarda pozitiftir, dolayısıyla paydadaki ifade her zaman pozitiftir.
\( e^{x} \gt 0 \)
Paydaki ifadeyi inceleyelim.
\( 2e^{3x} - 2 = 0 \)
\( e^{3x} = 1 \)
\( 3x = 0 \)
\( x = 0 \)
Birinci türevin sıfır olduğu bir noktada ikinci türev pozitif ise bu nokta bir yerel minimum noktası, negatif ise bir yerel maksimum noktasıdır.
Bu noktanın yerel minimum ya da maksimum nokta olup olmadığını bulmak için bu noktada ikinci türevin işaretini inceleyelim.
Fonksiyonun ikinci türevini alalım.
\( f''(x) = 4e^{2x} + 2e^{-x} \)
\( f''(0) = 4e^{2(0)} + 2e^{-0} = 6 \gt 0 \)
\( f''(0) \gt 0 \) olduğu için \( x = 0 \) apsisli nokta fonksiyonun bir yerel minimum noktasıdır.
\( x \in (0, \infty) \) olmak üzere,
\( f(x) = \sqrt{x}\ln{x} \) fonksiyonunu yerel ekstremum noktalarını bulunuz.
Çözümü GösterVerilen fonksiyon logaritma ve köklü fonksiyonların çarpımından oluşur ve tüm tanım kümesi içinde türevlenebilirdir.
Bir fonksiyonun iç noktaları içinde türevlenebilir olan yerel ekstremum noktaları birer durağan noktadır, yani bu noktalardaki birinci türevi sıfırdır.
Fonksiyonun birinci türevini alalım.
\( f'(x) = \dfrac{1}{2\sqrt{x}}\ln{x} + \dfrac{1}{x}\sqrt{x} \)
\( = \dfrac{\ln{x} + 2}{2\sqrt{x}} \)
Fonksiyonun birinci türevinin sıfıra eşit olduğu noktaları bulalım.
\( f'(x) = \dfrac{\ln{x} + 2}{2\sqrt{x}} = 0 \)
Paydadaki ifade fonksiyonun tanım kümesi içinde her zaman pozitiftir.
\( 2\sqrt{x} \gt 0 \)
Paydaki ifadeyi inceleyelim.
\( \ln{x} + 2 = 0 \)
\( \ln{x} = -2 \)
\( x = e^{-2} \)
Birinci türevin sıfır olduğu bir noktada ikinci türev pozitif ise bu nokta bir yerel minimum noktası, negatif ise bir yerel maksimum noktasıdır.
Bu noktanın yerel minimum ya da maksimum nokta olup olmadığını bulmak için bu noktada ikinci türevin işaretini inceleyelim.
Fonksiyonun ikinci türevini alalım.
\( f''(x) = \dfrac{(\ln{x} + 2)'(2\sqrt{x}) - (\ln{x} + 2)(2\sqrt{x})'}{(2\sqrt{x})^2} \)
\( = -\dfrac{\ln{x}}{4x\sqrt{x}} \)
\( f''(e^{-2}) = -\dfrac{\ln{e^{-2}}}{4\sqrt{(e^{-2})^3}} \)
\( = \dfrac{1}{2e^{-3}} \)
\( = \dfrac{e^3}{2} \gt 0 \)
\( f''(e^{-2}) \gt 0 \) olduğu için \( x = e^{-2} \) apsisli nokta fonksiyonun bir yerel minimum noktasıdır.
\( f(x) = \cos(2x) \) fonksiyonunun yerel minimum ve maksimum noktalarını bulunuz.
Çözümü GösterKosinüs fonksiyonu tüm reel sayılarda tanımlı ve türevlenebilirdir.
Bir fonksiyonun iç noktaları içinde türevlenebilir olan yerel ekstremum noktaları birer durağan noktadır, yani bu noktalardaki birinci türevi sıfırdır.
Fonksiyonun birinci türevini alalım.
\( f'(x) = -2\sin(2x) \)
Birinci türevi sıfıra eşitleyelim.
\( f'(x) = -2\sin(2x) = 0 \)
\( \sin(2x) = 0 \)
Sinüs fonksiyonu sıfır değerini aşağıdaki açı değerlerinde alır.
\( k \in \mathbb{R} \) olmak üzere,
\( 2x = \pi k \)
\( x = \dfrac{\pi}{2}k \)
Birinci türevin sıfır olduğu bir noktada ikinci türev pozitif ise bu nokta bir yerel minimum noktası, negatif ise bir yerel maksimum noktasıdır.
Bu noktaların yerel minimum ya da maksimum noktalar olup olmadığını bulmak için bu noktalarda ikinci türevin işaretini inceleyelim.
Fonksiyonun ikinci türevini alalım.
\( f''(x) = -4\cos(2x) \)
Kosinüs fonksiyonu \( \pi \)'nin çift katlarında 1, tek katlarında -1 değerini alır.
\( n \in \mathbb{Z} \) olmak üzere,
\( k = 2n + 1 \) için (tek sayı \( k \) değerleri):
\( f''(\frac{\pi}{2}k) = f''(\frac{\pi}{2}(2n + 1)) \)
\( = -4\cos(2(\frac{\pi}{2}(2n + 1))) \)
\( = -4\cos((2n + 1)\pi) \)
\( = -4(-1) = 4 \gt 0 \)
\( f''(\frac{\pi}{2}k) \gt 0 \) olduğu için \( k \)'nın tek sayı değerleri için \( x = \frac{\pi}{2}k \) apsisli noktalar fonksiyonun yerel minimum noktalarıdır.
\( x \in \{ \ldots, -\frac{\pi}{2}, \frac{\pi}{2}, \frac{3\pi}{2}, \ldots \} \)
\( k = 2n \) için (çift sayı \( k \) değerleri):
\( f''(\frac{\pi}{2}k) = f''(\frac{\pi}{2}(2n)) \)
\( = -4\cos(2(\frac{\pi}{2}(2n))) \)
\( = -4\cos(2n\pi) \)
\( = -4(1) = -4 \lt 0 \)
\( f''(\frac{\pi}{2}k) \lt 0 \) olduğu için \( k \)'nın çift sayı değerleri için \( x = \frac{\pi}{2}k \) apsisli noktalar fonksiyonun yerel maksimum noktalarıdır.
\( x \in \{ \ldots, -\pi, 0, \pi, \ldots \} \)
Buna göre fonksiyonun sonsuz sayıda yerel minimum ve maksimum noktası vardır.
\( f(x) = 2(x - 3)^3 \) fonksiyonunun yerel extremum noktalarını bulunuz.
Çözümü GösterVerilen fonksiyon bir kuvvet fonksiyonudur ve tüm reel sayılarda tanımlı ve türevlenebilirdir.
Bir fonksiyonun iç noktaları içinde türevlenebilir olan yerel ekstremum noktaları birer durağan noktadır, yani bu noktalardaki birinci türevi sıfırdır.
Fonksiyonun birinci türevini alalım.
\( f'(x) = 6(x - 3)^2 \)
Birinci türevi sıfıra eşitleyelim.
\( f'(x) = 6(x - 3)^2 = 0 \)
\( x = 3 \) çift katlı köktür ve birinci türev bu noktada işaret değiştirmez, dolayısıyla bu noktada bir yerel minimum ya da maksimum nokta bulunmaz.
Fonksiyonun yerel ekstremum noktası yoktur.
\( x \in [-a, a] \) olmak üzere,
\( f(x) = \sqrt{a^2 - x^2} \) fonksiyonunun yerel minimum ve maksimum noktalarını bulunuz.
Çözümü GösterFonksiyon verilen tanım kümesi içinde türevlenebilirdir.
Bir fonksiyonun iç noktaları içinde türevlenebilir olan yerel ekstremum noktaları birer durağan noktadır, yani bu noktalardaki birinci türevi sıfırdır.
Fonksiyonun birinci türevini alalım.
\( f'(x) = -\dfrac{x}{\sqrt{a^2 - x^2}} \)
Birinci türevi sıfıra eşitleyelim.
\( f'(x) = -\dfrac{x}{\sqrt{a^2 - x^2}} = 0 \)
\( x = 0 \)
Birinci türevin sıfır olduğu bir noktada ikinci türev pozitif ise bu nokta bir yerel minimum noktası, negatif ise bir yerel maksimum noktasıdır.
Bu noktanın yerel minimum ya da maksimum nokta olup olmadığını bulmak için bu noktada ikinci türevin işaretini inceleyelim.
Fonksiyonun ikinci türevini alalım.
\( f''(x) = -\dfrac{(x)'(\sqrt{a^2 - x^2}) - x(\sqrt{a^2 - x^2})'}{(\sqrt{a^2 - x^2})^2} \)
\( = -\dfrac{a^2}{(a^2 - x^2)^{\frac{3}{2}}} \)
\( f''(0) = -\dfrac{a^2}{(a^2 - 0^2)^{\frac{3}{2}}} \)
\( = -\dfrac{1}{a} \)
Fonksiyonun tanım kümesi \( [-a, a] \) olarak verildiğine göre \( a \) pozitif bir sayıdır.
\( f''(0) = -\dfrac{1}{a} \lt 0 \)
\( f''(0) \lt 0 \) olduğu için \( x = 0 \) apsisli nokta fonksiyonun bir yerel maksimum noktasıdır.
\( f(x) = \dfrac{x^2 + 5}{x + 2} \) fonksiyonunun en geniş tanım kümesi içindeki yerel minimum ve maksimum noktalarını bulunuz.
Çözümü GösterVerilen fonksiyon \( x = -2 \) noktası hariç tüm reel sayılarda tanımlı ve türevlenebilirdir.
Bir fonksiyonun iç noktaları içinde türevlenebilir olan yerel ekstremum noktaları birer durağan noktadır, yani bu noktalardaki birinci türevi sıfırdır.
Fonksiyonun birinci türevini alalım.
\( f'(x) = \dfrac{(x^2 + 5)'(x + 2) - (x^2 + 5)(x + 2)'}{(x + 2)^2} \)
\( = \dfrac{x^2 + 4x - 5}{(x + 2)^2} \)
Fonksiyonun birinci türevinin sıfıra eşit olduğu noktaları bulalım.
\( f'(x) = \dfrac{x^2 + 4x - 5}{(x + 2)^2} = 0 \)
\( x^2 + 4x - 5 = 0 \)
\( (x + 5)(x - 1) = 0 \)
\( x \in \{ -5, 1 \} \)
Bu noktaların yerel minimum ya da maksimum nokta olup olmadığını bulmak için bu noktalarda ikinci türevin işaretini inceleyelim.
Fonksiyonun ikinci türevini alalım.
\( f''(x) = \dfrac{(x^2 + 4x - 5)'(x + 2)^2 - (x^2 + 4x - 5)((x + 2)^2)'}{((x + 2)^2)^2} \)
\( = \dfrac{18}{(x + 2)^3} \)
\( f''(-5) = \dfrac{18}{(-5 + 2)^3} = -\dfrac{2}{3} \)
\( f''(-5) \lt 0 \) olduğu için \( x = -5 \) apsisli nokta fonksiyonun bir yerel maksimum noktasıdır.
\( f''(1) = \dfrac{18}{(1 + 2)^3} = \dfrac{2}{3} \)
\( f''(1) \gt 0 \) olduğu için \( x = 1 \) apsisli nokta fonksiyonun bir yerel minimum noktasıdır.
\( f: \mathbb{R} \to \mathbb{R} \) olmak üzere,
\( f(x) = \dfrac{2x^3}{3} - 14x \)
fonksiyonunun yerel ekstremum noktaları \( A \) ve \( B \) olduğuna göre, \( [AB] \) doğru parçasının eğimi kaçtır?
Çözümü GösterVerilen fonksiyon bir polinom fonksiyonudur ve tüm reel sayılarda türevlenebilirdir.
Bir fonksiyonun türevlenebilir ekstremum noktalarında birinci türevi sıfıra eşit olur.
\( f'(x) = 2x^2 - 14 \)
\( 2x^2 - 14 = 0 \)
\( x^2 = 7 \)
Buna göre ekstremum noktaların apsis değerleri aşağıdaki gibi olur.
\( x \in \{-\sqrt{7}, \sqrt{7}\} \)
Bu noktaların ordinat değerlerini bulalım.
\( f(\sqrt{7}) = \dfrac{14\sqrt{7}}{3} - 14\sqrt{7} = -\dfrac{28\sqrt{7}}{3} \)
\( f(-\sqrt{7}) = -\dfrac{14\sqrt{7}}{3} + 14\sqrt{7} = \dfrac{28\sqrt{7}}{3} \)
Yerel ekstremum noktalarının koordinatları aşağıdaki gibi olur.
\( A(\sqrt{7}, -\dfrac{28\sqrt{7}}{3}) \)
\( B(-\sqrt{7}, \dfrac{28\sqrt{7}}{3}) \)
Bu iki noktadan geçen doğrunun eğimini bulalım.
\( m = \dfrac{y_2 - y_1}{x_2 - x_1} \)
\( = \dfrac{\frac{28\sqrt{7}}{3} - (-\frac{28\sqrt{7})}{3}}{-\sqrt{7} - \sqrt{7}} \)
\( = -\dfrac{28}{3} \) bulunur.
\( f(x) = x^4 + 4x^3 - 8x^2 + 10 \) fonksiyonunun yerel minimum noktalarının apsis değerlerinin çarpımı kaçtır?
Çözümü GösterVerilen fonksiyon bir polinom fonksiyonudur ve tüm reel sayılarda türevlenebilirdir.
Fonksiyonun birinci türevini alalım.
\( f'(x) = 4x^3 + 12x^2 - 16x \)
\( = 4x(x^2 + 3x - 4) \)
\( = 4x(x + 4)(x - 1) \)
Bir fonksiyonun türevlenebilir ekstremum noktalarında birinci türevi sıfıra eşit olur.
\( f'(x) = 0 \)
\( 4x(x + 4)(x - 1) = 0 \)
Buna göre fonksiyonun aşağıdaki noktalarda birer yerel ekstremum noktası vardır.
\( x \in \{-4, 0, 1\} \)
Bu noktaların hangilerinin yerel minimum, hangilerinin yerel maksimum nokta olduğunu bulmak için ikinci türev testini uygulayalım.
\( f''(x) = 12x^2 + 24x - 16 \)
\( f''(-4) = 12(-4)^2 + 24(-4) - 16 = 80 \)
\( f''(-4) \gt 0 \) olduğu için \( x = -4 \) bir yerel minimum noktasıdır.
\( f''(0) = 12(0)^2 + 24(0) - 16 = -16 \)
\( f''(0) \lt 0 \) olduğu için \( x = 0 \) bir yerel maksimum noktasıdır.
\( f''(1) = 12(1)^2 + 24(1) - 16 = 20 \)
\( f''(1) \gt 0 \) olduğu için \( x = 1 \) bir yerel minimum noktasıdır.
Buna göre yerel minimum noktalarının apsis değerlerinin çarpımı \( -4 \cdot 1 = -4 \) olarak bulunur.
\( f(x) = x^3 + 2x^2 - kx + 5 \) fonksiyonunun \( (1, 3) \) aralığında sadece bir yerel ekstremum noktası olduğuna göre, \( k \)'nın alabileceği kaç tam sayı değeri vardır?
Çözümü GösterYerel ekstremum noktaları, türevlenebilir bir fonksiyonun birinci türevinin sıfır olduğu noktalarda oluşur.
\( f'(x) = 3x^2 + 4x - k \)
Bir \( f \) fonksiyonunun belirli bir \( (a, b) \) aralığında sadece bir yerel ekstremum noktası varsa birinci türevin bu aralıkta sadece bir kökü vardır ve birinci türev bu noktada işaret değiştirir.
Bu koşul, birinci türevin aralığın başlangıç ve bitiş noktalarında zıt işaretli olması anlamına gelir.
\( f'(a)f'(b) \lt 0 \)
Soruda verilen aralığı kullanarak bu eşitsizliği oluşturalım.
\( f'(1)f'(3) \lt 0 \)
\( f'(1) = 3(1)^2 + 4(1) - k = 7 - k \)
\( f'(3) = 3(3)^2 + 4(3) - k = 39 - k \)
\( (7 - k)(39 - k) \lt 0 \)
\( (k - 7)(k - 39) \lt 0 \)
\( 7 \lt k \lt 39 \)
Bu aralıkta \( k \)'nın alabileceği \( 38 - 8 + 1 = 31 \) farklı tam sayı değeri vardır.
\( f(x) = (k + 2)x^3 + (2k + 5)x^2 - (4k + 4)x + k^3 \)
fonksiyonunun \( x = -2 \) noktasında yerel maksimumu olduğuna göre, \( k \)'nin en küçük tam sayı değeri kaçtır?
Çözümü GösterVerilen fonksiyon bir polinom fonksiyonudur ve tüm reel sayılarda türevlenebilirdir.
\( f \) fonksiyonunun \( x = -2 \) noktasında yerel maksimumu olduğuna göre bu noktada birinci türevi sıfıra eşittir.
\( f'(x) = 3(k + 2)x^2 + 2(2k + 5)x - 4k - 4 \)
\( f'(-2) = 3(k + 2)(-2)^2 + 2(2k + 5)(-2) - 4k - 4 = 0 \)
\( 12k + 24 - 8k - 20 - 4k - 4 = 0 \)
\( 24 - 20 - 4 = 0 = 0 \)
Bu eşitliğin \( k \) değerinden bağımsız olarak sağlandığını görüyoruz, bu da fonksiyonun her \( k \) değeri için bu noktada bir yerel ekstremumu (yerel minimumu ya da maksimumu) olduğunu gösterir.
\( x = -2 \) noktası bir yerel maksimum noktası ise bu noktada ayrıca ikinci türev de negatif olmalıdır.
\( f''(x) \lt 0 \)
\( f''(x) = 6(k + 2)x + 2(2k + 5) \)
\( f''(-2) = 6(k + 2)(-2) + 2(2k + 5) \lt 0 \)
\( -12k - 24 + 4k + 10 \lt 0 \)
\( 8k \gt -14 \)
\( k \gt -\dfrac{7}{4} \)
Buna göre \( k \)'nin alabileceği en küçük tam sayı değeri -1 olur.
NOT: Bu sonucu yorumlamamız gerekirse, \( x = -2 \) noktası her \( k \) değeri için bir yerel ekstremum noktasıdır. \( k \gt -\frac{7}{4} \) için nokta bir yerel maksimum nokta iken \( k \lt -\frac{7}{4} \) için yerel minimum nokta olmaktadır, \( k = -\frac{7}{4} \) için ise bir yatay büküm noktasıdır.
\( f(x) = \dfrac{x^3}{3} + 2x^2 + cx + d \)
fonksiyonunun sadece iki yerel ektremum noktası olduğuna göre, \( c \) ve \( d \) hangi değerleri alabilir?
Çözümü GösterVerilen fonksiyon bir polinom fonksiyonudur ve tüm reel sayılarda tanımlı ve türevlenebilirdir.
Bir fonksiyonun iç noktaları içinde türevlenebilir olan yerel ekstremum noktaları birer durağan noktadır, yani bu noktalardaki birinci türevi sıfırdır.
Fonksiyonun birinci türevini alalım.
\( f'(x) = x^2 + 4x + c \)
Birinci türevi sıfıra eşitleyelim.
\( f'(x) = x^2 + 4x + c = 0 \)
Fonksiyonunun iki farklı yerel ektremum noktası olduğuna göre, birinci türevin 2 farklı kökü olmalıdır.
İkinci dereceden bir denklemin iki farklı reel sayı kökü olması için deltası sıfırdan büyük olmalıdır.
\( \Delta = b^2 - 4ac \gt 0 \)
\( = 16 - 4c \gt 0 \)
\( c \lt 4 \)
Denklemin köklerini bulalım.
\( x_{1, 2} = \dfrac{-b \pm \sqrt{\Delta}}{2a} \)
\( = \dfrac{-4 \pm \sqrt{16 - 4c}}{2} \)
\( = -2 \pm \sqrt{4 - c} \)
Denklemin köklerinin yerel ekstremum nokta olabilmesi için birinci türev bu noktalarda işaret değiştirmelidir.
Birinci türevin sıfır olduğu bir noktada ikinci türev pozitif ise bu nokta bir yerel minimum noktası, negatif ise bir yerel maksimum noktasıdır.
Bu noktaların yerel minimum ya da maksimum noktalar olup olmadığını bulmak için bu noktalarda ikinci türevin işaretini inceleyelim.
Fonksiyonun ikinci türevini alalım.
\( f''(x) = 2x + 4 \)
Bulduğumuz değerleri ikinci türev fonksiyonunda yerine yazalım.
\( f''(-2 - \sqrt{4 - c}) = 2(-2 - \sqrt{4 - c}) + 4 \)
\( = -2\sqrt{4 - c} \lt 0 \)
\( f''(-2 - \sqrt{4 - c}) \lt 0 \) olduğu için \( x = -2 - \sqrt{4 - c} \) apsisli nokta bir yerel maksimum noktasıdır.
\( f''(-2 + \sqrt{4 - c}) = 2(-2 + \sqrt{4 - c}) + 4 \)
\( = 2\sqrt{4 - c} \gt 0 \)
\( f''(-2 + \sqrt{4 - c}) \gt 0 \) olduğu için \( x = -2 + \sqrt{4 - c} \) apsisli nokta bir yerel minimum noktasıdır.
Bu şekilde \( f \) fonksiyonunun sadece iki yerel ekstremum noktası vardır.
\( d \) sabit terimi birinci türevde yer almadığı için yerel ekstremum noktalarının varlığı ve sayısı \( d \)'ye bağlı değildir.
\( c \in (-\infty, 4) \) ve \( d \in \mathbb{R} \) bulunur.
\( f(x) = (2x - 3)^{\frac{2}{3}} \) fonksiyonunun yerel minimum ve maksimum noktalarını bulunuz.
Çözümü GösterVerilen fonksiyon bir kuvvet fonksiyonudur ve tüm reel sayılarda tanımlı ve süreklidir.
Bir fonksiyonun iç noktaları içinde türevlenebilir olan yerel ekstremum noktaları birer durağan noktadır, yani bu noktalardaki birinci türevi sıfırdır.
Fonksiyonun birinci türevini alalım.
\( f'(x) = \dfrac{4}{3\sqrt[3]{2x - 3}} \)
Birinci türevin sıfıra eşit olduğu bir nokta yoktur.
Türevlenebilir olmayan ekstremum noktaları inceleyelim.
Paydayı sıfır yapan \( x = \frac{3}{2} \) noktasında birinci türev tanımsızdır.
Bu noktanın bir ekstremum nokta olup olmadığını bulmak için birinci türev testini uygulayalım.
\( x = 1 \lt \frac{3}{2} \) değerinde birinci türevin işaretini inceleyelim.
\( f'(1) = \dfrac{4}{3\sqrt[3]{2(1) - 3}} \)
\( = -\dfrac{4}{3} \lt 0 \)
\( x = 2 \gt \frac{3}{2} \) değerinde birinci türevin işaretini inceleyelim.
\( f'(2) = \dfrac{4}{3\sqrt[3]{2(2) - 3}} \)
\( = \dfrac{4}{3} \gt 0 \)
Buna göre birinci türev bu noktada negatiften pozitife işaret değiştirmiştir.
Dolayısıyla, \( x = \frac{3}{2} \) apsisli nokta fonksiyonun bir yerel minimum noktasıdır.