Parçalı Fonksiyonların Limiti
Konu tekrarı için: Parçalı Fonksiyonlar
Tanım kümesinin farklı aralıklarında farklı tanımlara sahip olan fonksiyonlara parçalı fonksiyon denir. Bir parçalı fonksiyonun farklı tanıma sahip olduğu alt aralıklara fonksiyonun dalları ya da parçaları, fonksiyon tanımının değiştiği noktalara fonksiyonun sınır noktaları denir.
Bir parçalı fonksiyonun bir sınır noktasında limitinin tanımlı olması için, limit tanımı gereği bu noktanın her iki tarafında tanımlı olan parçaların bu noktadaki soldan ve sağdan limit değerleri tanımlı ve birbirine eşit olmalıdır. Tek taraflı limitlerden en az biri tanımlı değilse ya da bu limit değerleri birbirine eşit değilse parçalı fonksiyonun bu noktada limiti tanımlı değildir.
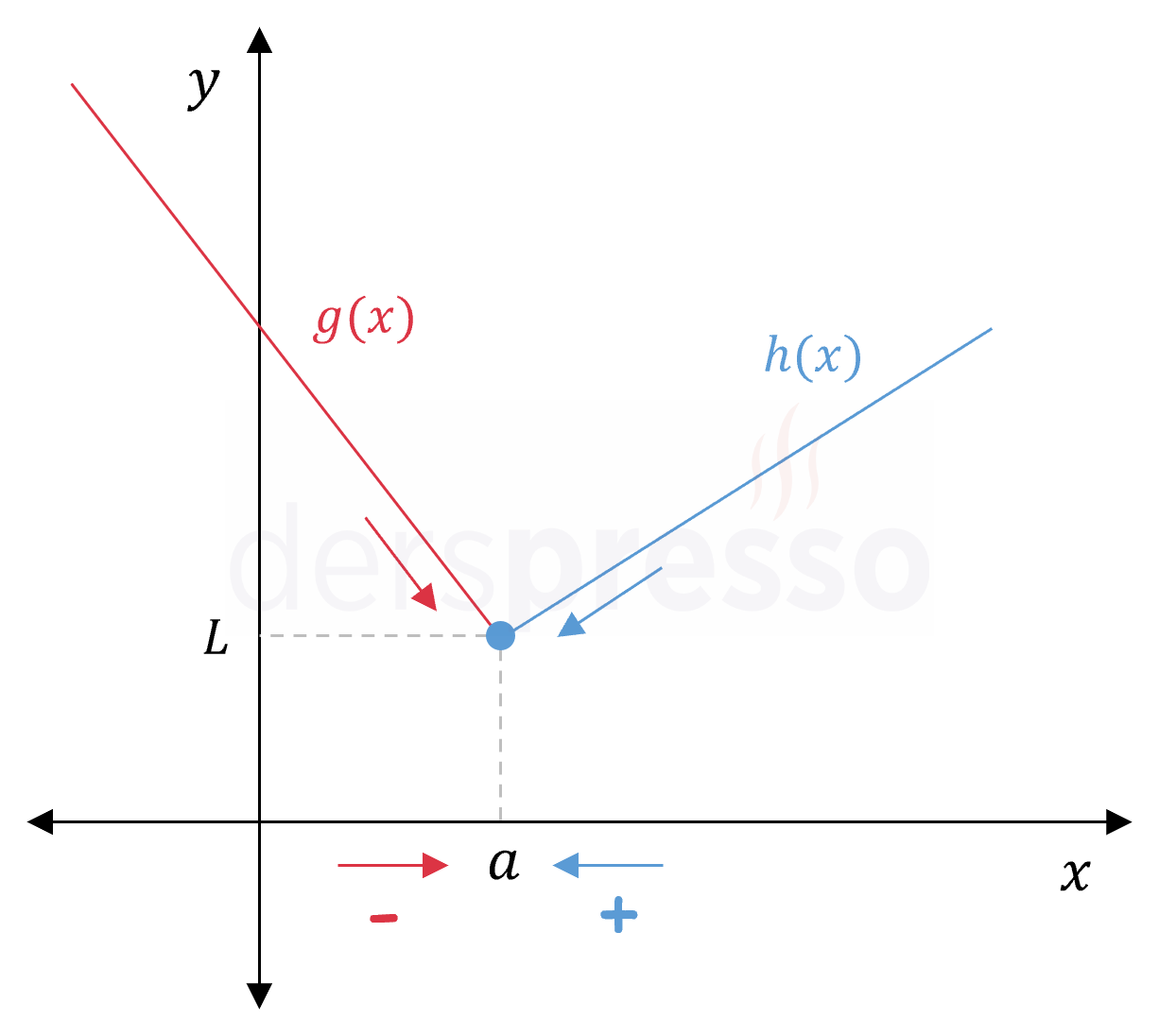
\( a, L \in \mathbb{R} \) olmak üzere,
\( f(x) = \begin{cases} g(x) & x \lt a \\ h(x) & x \ge a \end{cases} \)
parçalı fonksiyonunun \( x = a \) kritik noktasındaki soldan ve sağdan limitleri aşağıdaki gibi tanımlı ve \( L \)'ye eşit ise,
\( \lim\limits_{x \to a^-} g(x) = \lim\limits_{x \to a^+} h(x) = L \)
fonksiyonunun bu noktadaki iki taraflı limiti de tanımlı ve \( L \)'ye eşittir.
\( \lim\limits_{x \to a} f(x) = L \)
Aksi takdirde fonksiyonun bu noktadaki limiti tanımsızdır.
Parçalı fonksiyonların sınır noktalarındaki limitini iki örnek üzerinde gösterelim.
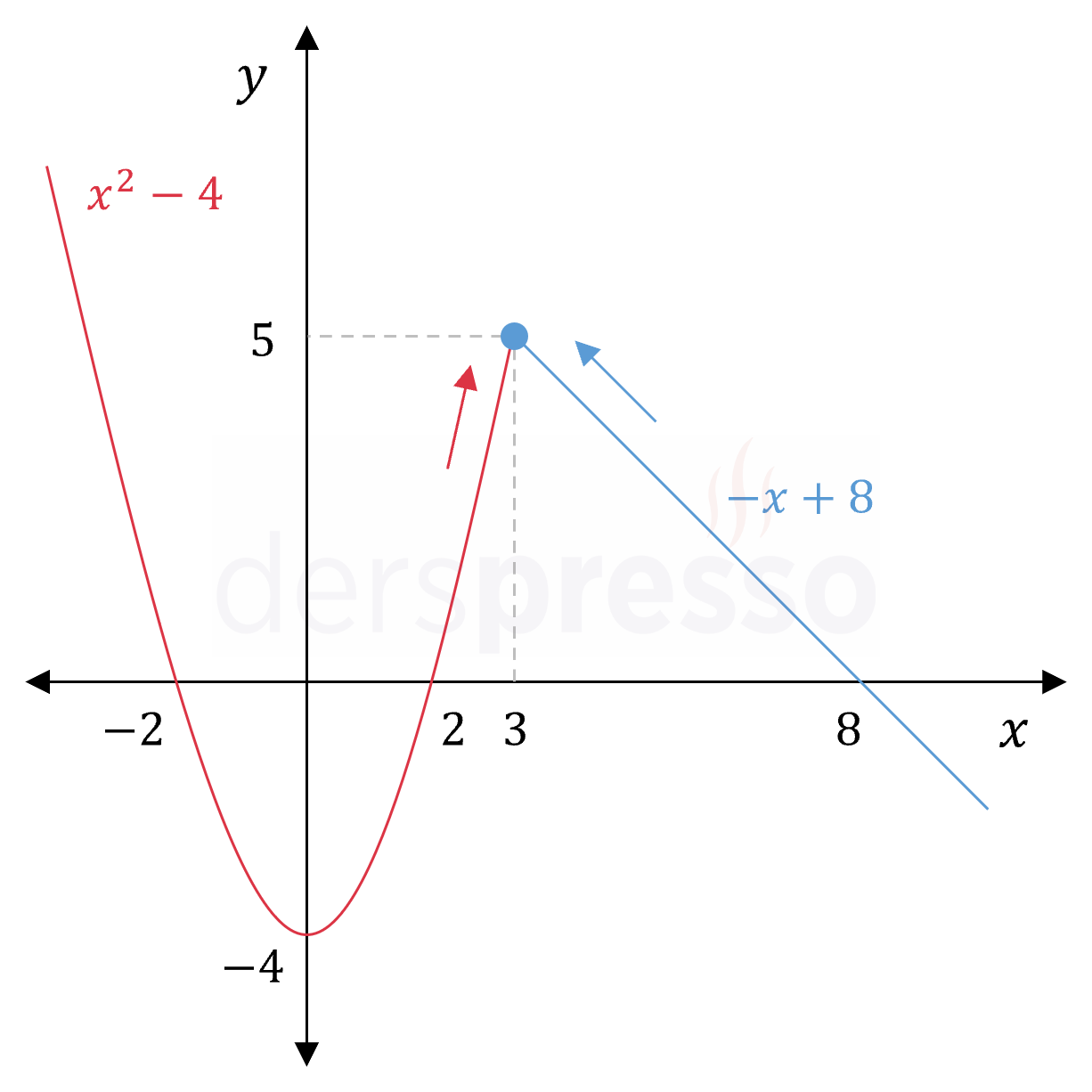
\( f(x) = \begin{cases} x^2 - 4 & x \lt 3 \\ -x + 8 & x \ge 3 \end{cases} \)
fonksiyonunun \( x = 3 \) noktasındaki limitini bulalım.
\( x = 3 \) parçalı fonksiyonun bir sınır noktasıdır.
Fonksiyonun \( x = 3 \) noktasında limitinin tanımlı olması için, bu noktanın her iki tarafında tanımlı olan parçaların bu noktadaki soldan ve sağdan limit değerleri tanımlı ve birbirine eşit olmalıdır.
Bu noktadaki soldan limit için \( x \)'in 3'ten küçük olduğu (birinci) aralıktaki fonksiyon tanımına bakılır. Fonksiyon bu aralıkta ikinci dereceden bir polinom olduğu için süreklidir ve doğrudan yerine koyma yöntemi ile limitini bulabiliriz.
\( \lim\limits_{x \to 3^-} f(x) = \lim\limits_{x \to 3^-} (x^2 - 4) \) \( = 3^2 - 4 = 5 \)
Bu noktadaki sağdan limit için \( x \)'in 3'ten büyük olduğu (ikinci) aralıktaki fonksiyon tanımına bakılır. Fonksiyon bu aralıkta doğrusal olduğu için süreklidir ve doğrudan yerine koyma yöntemi ile limitini bulabiliriz.
\( \lim\limits_{x \to 3^+} f(x) = \lim\limits_{x \to 3^+} (-x + 8) \) \( = -3 + 8 = 5 \)
Soldan ve sağdan limitler tanımlı ve birbirine eşit olduğu için bu noktada limit tanımlıdır ve soldan/sağdan limit değerine eşittir.
\( \lim\limits_{x \to 3} f(x) = 5 \)
Parçalı fonksiyonun grafiğini incelediğimizde bu noktada soldan ve sağdan limitlerin tanımlı ve birbirine eşit olduğunu görebiliriz.
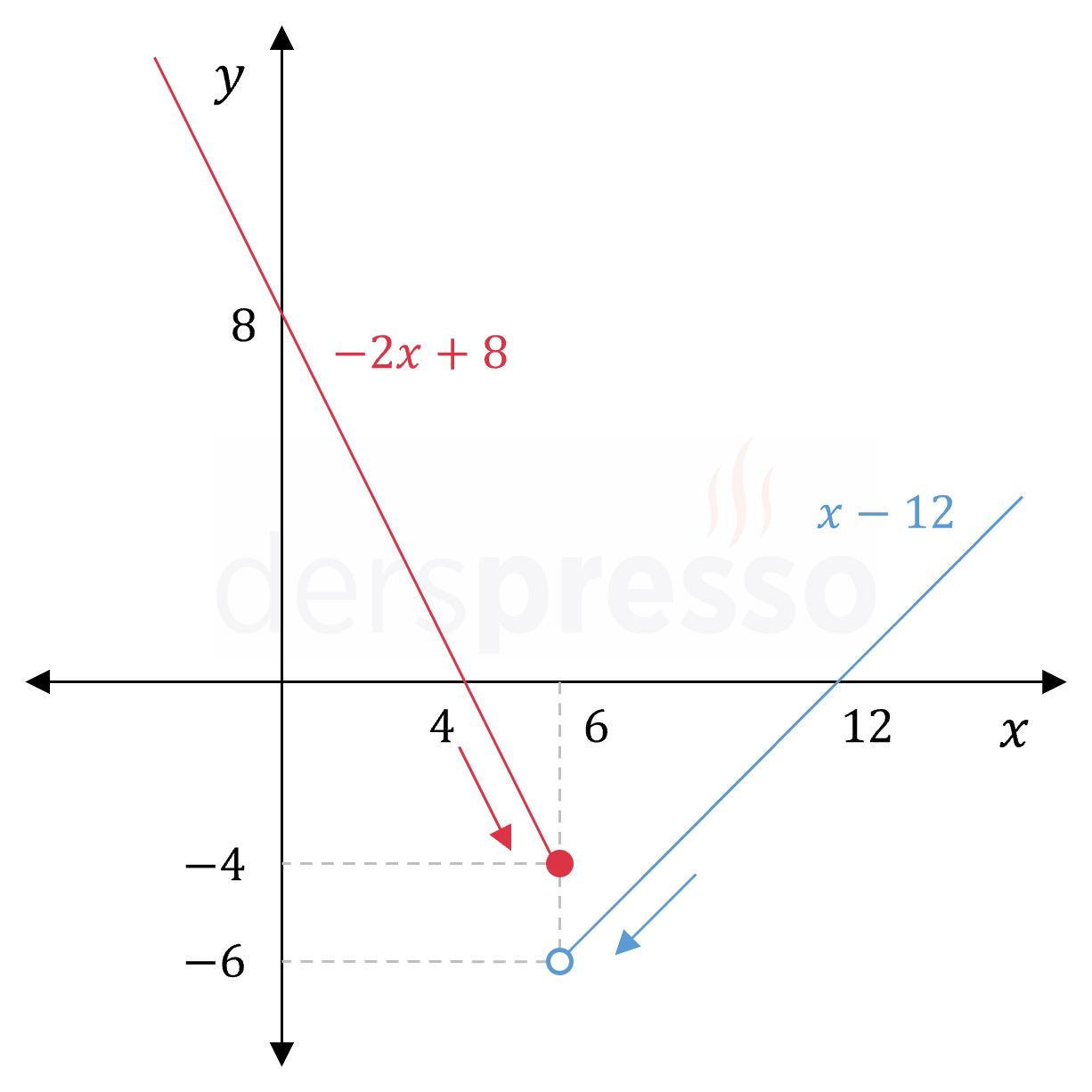
\( f(x) = \begin{cases} -2x + 8 & x \le 6 \\ x - 12 & x \gt 6 \end{cases} \)
fonksiyonunun \( x = 6 \) noktasındaki limitini bulalım.
\( x = 6 \) parçalı fonksiyonun bir sınır noktasıdır.
Fonksiyonun \( x = 6 \) noktasında limitinin tanımlı olması için, bu noktanın her iki tarafında tanımlı olan parçaların bu noktadaki soldan ve sağdan limit değerleri tanımlı ve birbirine eşit olmalıdır.
Bu noktadaki soldan limit için \( x \)'in 6'dan küçük olduğu (birinci) aralıktaki fonksiyon tanımına bakılır. Fonksiyon bu aralıkta doğrusal olduğu için süreklidir ve doğrudan yerine koyma yöntemi ile limitini bulabiliriz.
\( \lim\limits_{x \to 6^-} f(x) = \lim\limits_{x \to 6^-} (-2x + 8) \) \( = -2(6) + 8 = -4 \)
Bu noktadaki sağdan limit için \( x \)'in 6'dan büyük olduğu (ikinci) aralıktaki fonksiyon tanımına bakılır. Fonksiyon bu aralıkta doğrusal olduğu için süreklidir ve doğrudan yerine koyma yöntemi ile limitini bulabiliriz.
\( \lim\limits_{x \to 6^+} f(x) = \lim\limits_{x \to 6^+} (x - 12) \) \( = 6 - 12 = -6 \)
Soldan ve sağdan limitler tanımlı olsa da birbirine eşit olmadığı için bu noktada limit tanımsızdır.
\( \lim\limits_{x \to 6} f(x) \Longrightarrow \) Tanımsız
Parçalı fonksiyonun grafiğini incelediğimizde bu noktada soldan ve sağdan limitlerin tanımlı olduğunu, ancak birbirine eşit olmadığını görebiliriz.
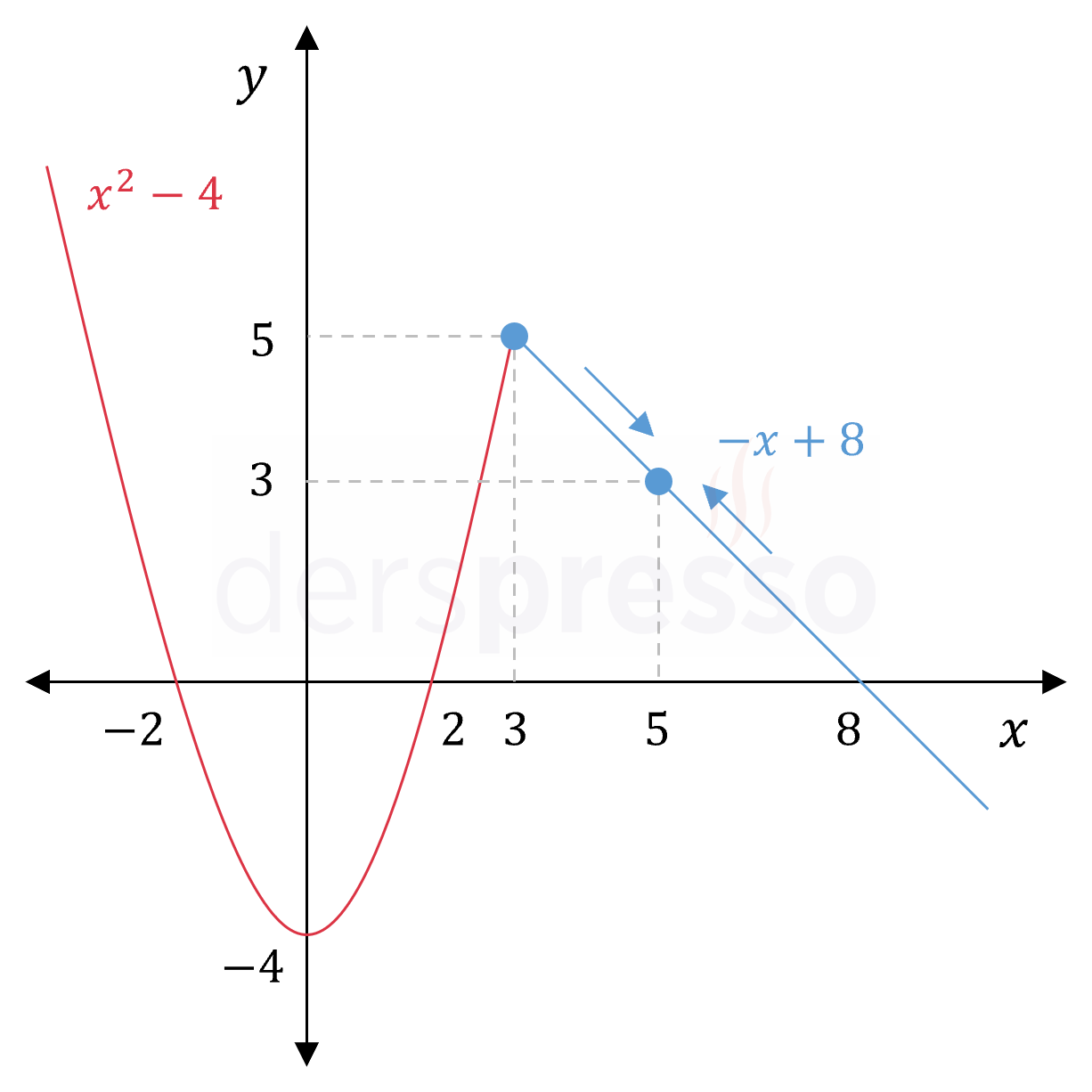
Bir parçalı fonksiyonun sınır noktası olmayan bir noktasındaki limiti, noktanın tanımlı olduğu parçanın bu noktadaki limitine eşittir.
\( f(x) = \begin{cases} x^2 - 4 & x \lt 3 \\ -x + 8 & x \ge 3 \end{cases} \)
fonksiyonunun \( x = 5 \) noktasındaki limitini bulalım.
\( x = 5 \) parçalı fonksiyonun bir sınır noktası değildir. Bu nokta için parçalı fonksiyonun \( f(x) = -x + 8 \) tanımı geçerlidir, dolayısıyla bu tanımın \( x = 5 \) noktasındaki limitini bulalım.
\( \lim\limits_{x \to 5} f(x) = \lim\limits_{x \to 5} (-x + 8) \)
Fonksiyon bu aralıkta doğrusal olduğu için süreklidir ve doğrudan yerine koyma yöntemi ile limitini bulabiliriz.
\( \lim\limits_{x \to 5} (-x + 8) = -5 + 8 = 3 \)
Parçalı fonksiyonun grafiğini incelediğimizde bu noktada soldan ve sağdan limitlerin tanımlı ve birbirine eşit olduğunu görebiliriz.
Bir sınır noktasındaki tek taraflı limit değerini bulmak için noktanın incelenen tarafında tanımlı olan parçanın tek taraflı limitini hesaplamamız yeterlidir.
\( f(x) = \begin{cases} x^2 - x & x \lt 2 \\ 2x + 2 & 2 \le x \end{cases} \) olduğuna göre,
\( \lim\limits_{x \to 2^-} f(x) + \lim\limits_{x \to 2^+} f(x) \) toplamını bulalım.
\( x = 2 \) parçalı fonksiyonun sınır noktasıdır.
Bu noktadaki soldan limit için \( x \)'in 2'den küçük olduğu (birinci) aralıktaki fonksiyon tanımına bakılır.
\( \lim\limits_{x \to 2^-} f(x) = \lim\limits_{x \to 2^-} (x^2 - x) = 2^2 - 2 = 2 \)
Bu noktadaki sağdan limit için \( x \)'in 2'den büyük olduğu (ikinci) aralıktaki fonksiyon tanımına bakılır.
\( \lim\limits_{x \to 2^+} f(x) = \lim\limits_{x \to 2^+} (2x + 2) = 2 \cdot 2 + 2 = 6 \)
Buna göre soldan ve sağdan limitlerin toplamı aşağıdaki gibi bulunur.
\( \lim\limits_{x \to 2^-} f(x) + \lim\limits_{x \to 2^+} f(x) \) \( = 2 + 6 = 8 \)
Soruda iki taraflı limit değeri istenmediği için soldan ve sağdan limitlerin eşitliğine bakmamıza gerek yoktur. Bu noktada iki taraflı limit tanımlı olmasa da tek taraflı limitler tanımlıdır.
\( f(x) = \begin{cases} x^2 + 1 & x \lt 3 \\ 5 & x = 3 \\ -(x - 3)^2 + 10 & 3 \lt x \end{cases} \)
parçalı fonksiyonunun sınır noktalarındaki limit değerlerini bulun.
Çözümü GösterTanımı verilen parçalı fonksiyonun grafiği aşağıdaki gibidir.
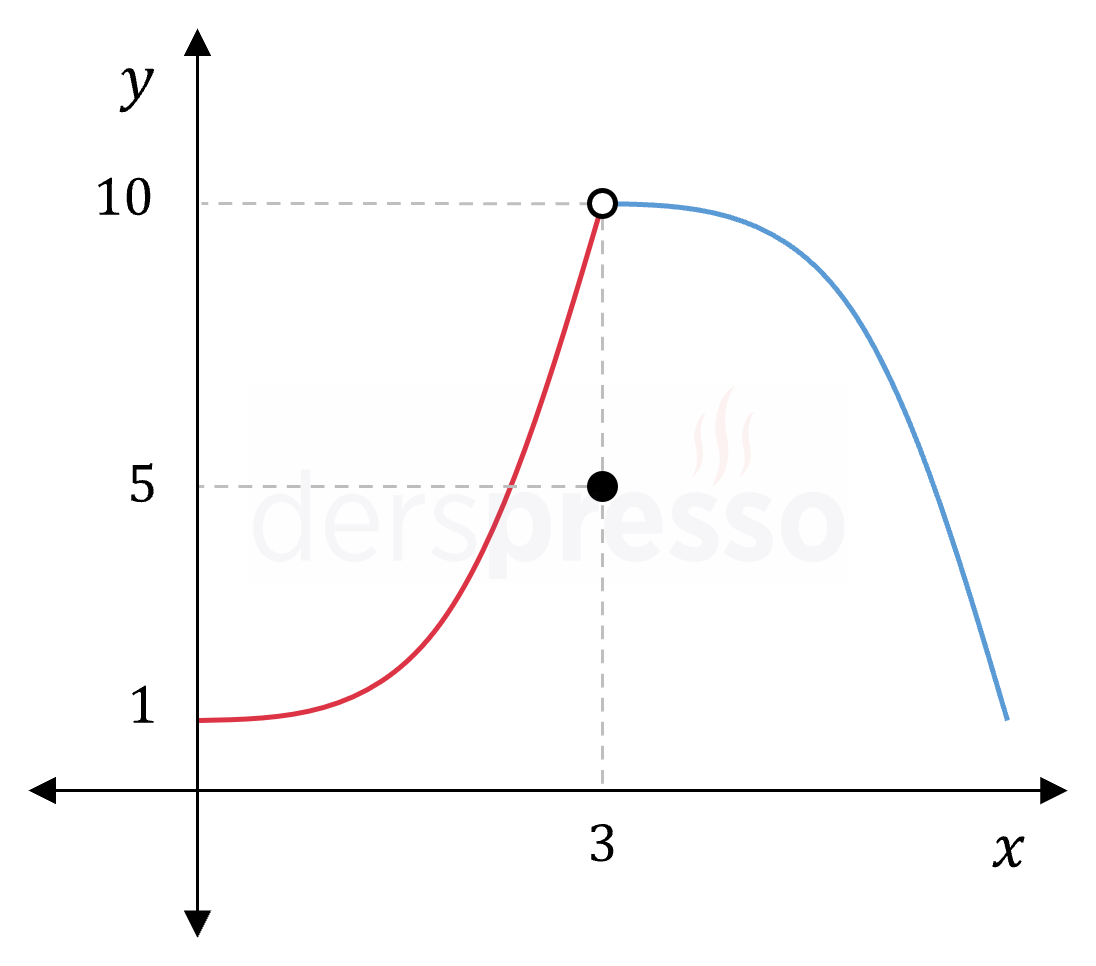
Fonksiyonunun sınır noktası fonksiyonun tanımının değiştiği \( x = 3 \) noktasıdır.
Fonksiyonun bir sınır noktasında limitinin tanımlı olması için, bu noktanın her iki tarafında tanımlı olan fonksiyonların bu noktadaki soldan ve sağdan limit değerleri tanımlı ve birbirine eşit olmalıdır.
\( x = 3 \) noktasındaki soldan limit:
\( \lim\limits_{x \to 3^-} f(x) = \lim\limits_{x \to 3^-} (x^2 + 1) = 10 \)
\( x = 3 \) noktasındaki sağdan limit:
\( \lim\limits_{x \to 3^+} f(x) = \lim\limits_{x \to 3^+} [-(x - 3)^2 + 10] = 10 \)
Soldan ve sağdan limitler tanımlı ve birbirine eşit oldukları için, fonksiyonun \( x = 3 \) noktasında limiti tanımlıdır ve değeri \( 10 \)'dur.
Dikkat edilirse, fonksiyonun \( x = 3 \) noktası için de \( f(x) = 5 \) olmak üzere bir tanımı vardır. Bir noktadaki limit değeri fonksiyonun o noktadaki değil o nokta civarındaki değeri ile ilgili olduğu için, parçalı fonksiyonun bu noktadaki tanımını dikkate almamıza gerek yoktur.
\( f(x) = \begin{cases} 3 & x \lt -3 \\ -x & -3 \le x \lt 2 \\ x & 2 \le x \end{cases} \)
parçalı fonksiyonunun sınır noktalarındaki limit değerlerini bulun.
Çözümü GösterTanımı verilen parçalı fonksiyonun grafiği aşağıdaki gibidir.
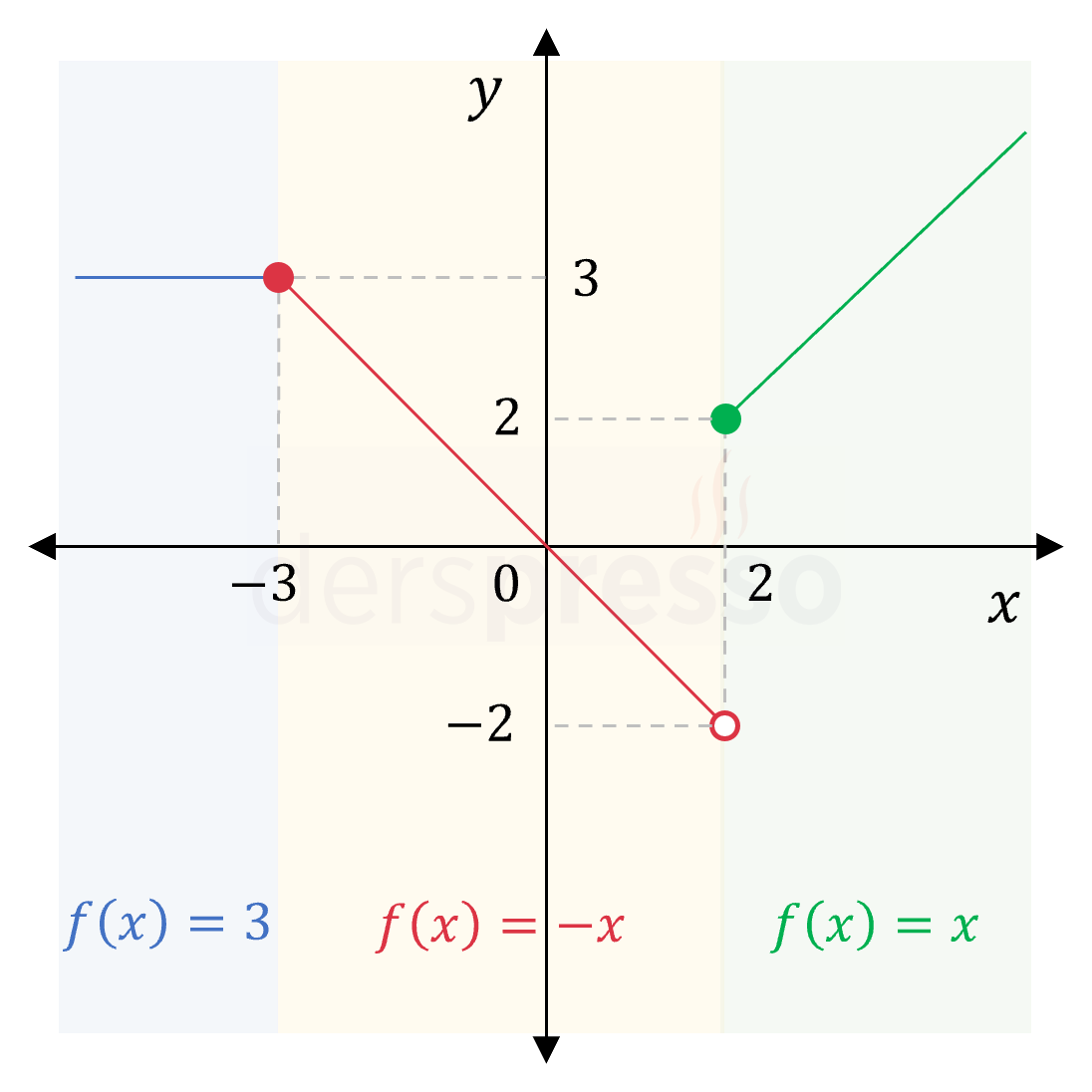
Fonksiyonunun sınır noktaları fonksiyonun tanımının değiştiği \( x = -3 \) ve \( x = 2 \) noktalarıdır.
Fonksiyonun bir sınır noktasında limitinin tanımlı olması için, bu noktanın her iki tarafında tanımlı olan fonksiyonların bu noktadaki soldan ve sağdan limit değerleri tanımlı ve birbirine eşit olmalıdır.
\( x = -3 \) noktasındaki soldan limit:
\( \lim\limits_{x \to -3^-} f(x) = \lim\limits_{x \to -3^-} 3 = 3 \)
\( x = -3 \) noktasındaki sağdan limit:
\( \lim\limits_{x \to -3^+} f(x) = \lim\limits_{x \to -3^+} (-x) = 3 \)
Soldan ve sağdan limitler tanımlı ve birbirine eşit oldukları için, fonksiyonun \( x = -3 \) noktasında limiti tanımlıdır ve değeri \( 3 \)'tür.
\( \lim\limits_{x \to -3} f(x) = 3 \)
Fonksiyonun \( x = 2 \) noktasındaki limitini benzer şekilde bulalım.
\( x = 2 \) noktasındaki soldan limit:
\( \lim\limits_{x \to 2^-} f(x) = \lim\limits_{x \to 2^-} (-x) = -2 \)
\( x = 2 \) noktasındaki sağdan limit:
\( \lim\limits_{x \to 2^+} f(x) = \lim\limits_{x \to 2^+} x = 2 \)
Soldan ve sağdan limitler tanımlı ancak birbirinden farklı oldukları için, fonksiyonun \( x = 2 \) noktasında limiti tanımsızdır.
\( \lim\limits_{x \to 2} f(x) \): Tanımsız
\( f(x) = \begin{cases} x^2 + 1 & x \lt -2 \\ 0 & x = -2 \\ ax - 3 & -2 \lt x \end{cases} \)
parçalı fonksiyonunun \( x = -2 \) noktasında limiti tanımlı olduğuna göre, \( a \) değeri kaçtır?
Çözümü GösterFonksiyonun bir sınır noktası olan \( x = -2 \) noktasında limiti tanımlı olduğuna göre, bu noktada soldan ve sağdan limitler tanımlı ve birbirine eşit olmalıdır.
\( x = -2 \) noktasındaki soldan limit:
\( \lim\limits_{x \to -2^-} (x^2 + 1) = (-2)^2 + 1 = 5 \)
\( x = -2 \) noktasındaki sağdan limit:
\( \lim\limits_{x \to -2^+} (ax - 3) = a(-2) - 3 = -2a - 3 \)
Soldan ve sağdan limit değerlerini birbirine eşitleyelim.
\( -2a - 3 = 5 \)
\( a = -4 \) bulunur.
\( f: \mathbb{R} \to \mathbb{R} \) olmak üzere,
\( f(x) = \begin{cases} x^2 + 2x + 3, & x \lt 1 \\ 8x + 7, & x = 1 \\ 2x + 4, & x \gt 1 \end{cases} \)
parçalı fonksiyonu için aşağıdaki ifadelerden hangileri doğrudur?
I. \( \lim\limits_{x \to 1} f(x) = 6 \)
II. \( \lim\limits_{x \to -2} f(x) = 3 \)
III. \( \lim\limits_{x \to 3^-} f(x) = 18 \)
Çözümü GösterI. öncül:
\( x = 1 \) noktası parçalı fonksiyonun sınır noktası olduğu için bu noktadaki limit için soldan ve sağdan limitlere bakılır.
Bu noktaya soldan yaklaşırken fonksiyonun 1. tanımı geçerlidir.
\( \lim\limits_{x \to 1^-} f(x) = 1^2 + 2(1) + 3 \) \( = 6 \)
Bu noktaya sağdan yaklaşırken fonksiyonun 3. tanımı geçerlidir.
\( \lim\limits_{x \to 1^+} f(x) = 2(1) + 4 \) \( = 6 \)
Soldan ve sağdan limit değerleri tanımlı ve birbirine eşit olduğu için bu noktada iki taraflı limit de tanımlıdır ve bu iki limit değerine eşittir.
I. öncül doğrudur.
II. öncül:
\( x = -2 \) noktası parçalı fonksiyonun bir sınır noktası olmadığı için ilgili aralıkta geçerli olan fonksiyon tanımı için limite bakılır.
\( -2 \lt 1 \) olduğu için bu noktada fonksiyonun 1. tanımı geçerlidir.
\( \lim\limits_{x \to -2} f(x) = (-2)^2 + 2 \cdot (-2) + 3 \) \( = 3 \)
II. öncül doğrudur.
III. öncül:
\( x = 3 \) noktası parçalı fonksiyonun bir sınır noktası olmadığı için ilgili aralıkta geçerli olan fonksiyon tanımı için limite bakılır.
\( 1 \lt 3 \) olduğu için bu noktada fonksiyonun 3. tanımı geçerlidir.
\( \lim\limits_{x \to 3^-} f(x) = 2 \cdot 3 + 4 = 10 \)
III. öncül yanlıştır.
Buna göre I. ve II. öncüller doğrudur.
\( f: \mathbb{R} \to \mathbb{R} \) olmak üzere,
\( f(x) = \begin{cases} \dfrac{2ax + bx}{1 + x}, & x \le 1 \\ \dfrac{ax + 1}{x}, & x \gt 1 \end{cases} \)
fonksiyonunun \( x = 1 \) noktasında limitinin olması için \( a \) ve \( b \) sayıları ne olmalıdır?
Çözümü Göster\( x = 1 \) noktası parçalı fonksiyonun sınır noktasıdır.
Fonksiyonun bir sınır noktasında limitinin tanımlı olması için, bu noktanın her iki tarafında tanımlı olan fonksiyonların bu noktadaki soldan ve sağdan limit değerleri tanımlı ve birbirine eşit olmalıdır.
\( x = 1 \) noktasındaki soldan limit:
Bu noktaya soldan yaklaşırken fonksiyonun 1. tanımı geçerlidir.
\( \lim\limits_{x \to 1^-} f(x) = \lim\limits_{x \to 1^-} \dfrac{2a \cdot 1 + b \cdot 1}{1 + 1} \)
\( = \dfrac{2a + b}{2} \)
\( x = 1 \) noktasındaki sağdan limit:
Bu noktaya sağdan yaklaşırken fonksiyonun 2. tanımı geçerlidir.
\( \lim\limits_{x \to 1^+} f(x) = \lim\limits_{x \to 1^+} \dfrac{a \cdot 1 + 1}{1} \)
\( = a + 1 \)
Soldan ve sağdan limit değerlerini eşitleyelim.
\( \dfrac{2a + b}{2} = a + 1 \)
\( 2a + b = 2a + 2 \)
\( b = 2 \)
\( a \) değişkenleri sadeleştiği için \( a \) her reel sayı değerini alabilir, bir diğer ifadeyle \( b = 2 \) olduğu sürece \( a \) hangi değeri alırsa alsın fonksiyonun \( x = 1 \) noktasında limiti tanımlı olur.
\( f: \mathbb{R} \to \mathbb{R} \) olmak üzere,
\( f(x) = \begin{cases} x + 2, & x \lt 0 \\ x^2 + 8, & 0 \le x \lt 4 \\ \dfrac{5x + 2}{3}, & x \ge 4 \end{cases} \)
Yukarıdaki parçalı fonksiyon tanımına göre aşağıdaki ifadenin değeri kaçtır?
\( \lim\limits_{x \to 0^-} f(x) + \lim\limits_{x \to 4^-} f(x) \) \( + \lim\limits_{x \to 5} f(x) \)
Çözümü Göster\( x = 0 \) ve \( x = 4 \) noktaları parçalı fonksiyonun sınır noktalarıdır.
\( x = 0 \) noktasındaki soldan limit:
Bu noktaya soldan yaklaşırken fonksiyonun 1. tanımı geçerlidir.
\( \lim\limits_{x \to 0^-} f(x) = 0 + 2 = 2 \)
\( x = 4 \) noktasındaki soldan limit:
Bu noktaya soldan yaklaşırken fonksiyonun 2. tanımı geçerlidir.
\( \lim\limits_{x \to 4^-} f(x) = 4^2 + 8 = 24 \)
\( x = 5 \) noktasındaki limit:
Bu nokta bir sınır noktası değildir ve bu noktanın bulunduğu aralıkta fonksiyonun 3. tanımı geçerlidir.
\( \lim\limits_{x \to 5} f(x) = \lim\limits_{x \to 5} \dfrac{5 \cdot 5 + 2}{3} = 9 \)
Bulduğumuz limit değerlerini toplayalım.
\( = 2 + 24 + 9 = 35 \) bulunur.
\( f: \mathbb{R} \to \mathbb{R} \) olmak üzere,
\( f(x) = \begin{cases} x^3 + 2, & x \lt 1 \\ -2, & x = 1 \\ x(1 - n), & x \gt 1 \end{cases} \)
parçalı fonksiyonunun \( x = 1 \) noktasında limiti tanımlı olduğuna göre, \( f(n) \) değeri kaçtır?
Çözümü Göster\( x = 1 \) noktası parçalı fonksiyonun sınır noktasıdır.
Fonksiyonun sınır noktasında limiti tanımlı olduğuna göre, bu noktada soldan ve sağdan limitler tanımlı ve birbirine eşit olmalıdır.
\( x = 1 \) noktasındaki soldan limit:
Bu noktaya soldan yaklaşırken fonksiyonun 1. tanımı geçerlidir.
Polinom fonksiyonunun bir noktadaki limit değeri o noktadaki fonksiyon değerine eşittir.
\( \lim\limits_{x \to 1^-} (x^3 + 2) = 1^3 + 2 = 3 \)
\( x = 1 \) noktasındaki sağdan limit:
Bu noktaya sağdan yaklaşırken fonksiyonun 3. tanımı geçerlidir.
\( \lim\limits_{x \to 1^+} (x(1 - n)) = 1(1 - n) = 1 - n \)
Soldan ve sağdan limit değerlerini birbirine eştleyelim.
\( 3 = 1 - n \)
\( n = -2 \)
\( f(n) = f(-2) \) değerini bulalım.
Bu noktada fonksiyonun 1. tanımı geçerlidir.
\( = (-2)^3 + 2 = -6 \) bulunur.
\( f: (-2, 4] \to \mathbb{R} \) fonksiyonunun tanımı aşağıdaki gibidir.
\( f(x) = \begin{cases} 2, & -2 \lt x \le 0 \\ -3, & 0 \lt x \le 2 \\ 4, & 2 \lt x \le 4 \end{cases} \)
\( a, b \in \mathbb{Z} \) olmak üzere,
\( \lim\limits_{x \to a^+} f(x) \gt \lim\limits_{x \to b^-} f(x) \)
eşitsizliğini sağlayan kaç \( (a, b) \) sıralı ikilisi yazılabilir?
Çözümü GösterVerilen parçalı fonksiyonun grafiği aşağıdaki gibidir.
Fonksiyon bu aralıkta -3, 2, 4 olmak üzere üç farklı değer alır, dolayısıyla herhangi bir noktadaki limit değeri de bu üç değerden biri olabilir.
Verilen eşitsizlik için üç farklı durum vardır, bu durumları tek tek kontrol edelim.
Durum 1: \( \lim\limits_{x \to a^+} f(x) = 4 \)
Fonksiyonun sağdan limitinin 4 olduğu \( a \in \{2, 3\} \) olmak üzere iki nokta vardır.
Bu durumda fonksiyonun soldan limitinin 4'ten küçük olduğu \( b \in \{-1, 0, 1, 2\} \) olmak üzere dört nokta vardır.
Bu durum için \( 2 \times 4 = 8 \) farklı \( (a, b) \) sıralı ikilisi yazılabilir.
Durum 2: \( \lim\limits_{x \to a^+} f(x) = 2 \)
Fonksiyonun sağdan limitinin 2 olduğu \( a \in \{-2, -1\} \) olmak üzere iki nokta vardır.
Bu durumda fonksiyonun soldan limitinin 2'den küçük olduğu \( b \in \{1, 2\} \) olmak üzere iki nokta vardır.
Bu durum için \( 2 \times 2 = 4 \) farklı \( (a, b) \) sıralı ikilisi yazılabilir.
Durum 3: \( \lim\limits_{x \to a^+} f(x) = -3 \)
Fonksiyonun sağdan limitinin -3 olduğu \( a \in \{0, 1\} \) olmak üzere iki nokta vardır.
Fonksiyonun soldan limitinin -3'ten küçük olduğu nokta yoktur, dolayısıyla bu durum için bir \( (a, b) \) sıralı ikilisi yazılamaz.
Buna göre soruda verilen koşulu sağlayan \( 8 + 4 = 12 \) farklı \( (a, b) \) sıralı ikilisi yazılabilir.