Mutlak Değerli İfadelerin Limiti
Mutlak değerli fonksiyonları her bir mutlak değerli ifadenin içini sıfır yapan \( x \) değerleri birer geçiş noktası olacak şekilde parçalı fonksiyon şeklinde yazabiliriz.
\( f(x) = \abs{2x - 4} - x \)
Mutlak değerli ifadenin kritik noktasını bulalım.
\( 2x - 4 = 0 \Longrightarrow x = 2 \)
\( x \lt 2 \) için mutlak değer içindeki ifade dışarı negatif işaretli çıkar.
\( f(x) = -(2x - 4) - x = 4 - 3x \)
\( x \ge 2 \) için mutlak değer içindeki ifade dışarı pozitif işaretli çıkar.
\( f(x) = (2x - 4) - x = x - 4 \)
Buna göre fonksiyonun parçalı fonksiyon tanımı aşağıdaki gibi olur.
\( f(x) = \begin{cases} 4 - 3x & x \lt 2 \\ x - 4 & 2 \le x \end{cases} \)
Bir mutlak değerli fonksiyonun kritik bir noktasındaki limit değerini bulmak için, fonksiyon önce yukarıda örneğini verdiğimiz şekilde parçalı fonksiyon olarak tanımlanır, daha sonra önceki parçalı fonksiyonların limiti sayfasında bahsettiğimiz yöntemle limiti bulunur.
Bir mutlak değerli fonksiyonun kritik olmayan bir noktasındaki limit değerini bulmak için, mutlak değer içindeki ifade bu noktadaki değerinin işareti dikkate alınarak pozitif ya da negatif işaretli olarak mutlak değerden çıkarılır ve normal limit kuralları ile limiti hesaplanır.
\( f(x) = \abs{2x - 6} + 2x \)
fonksiyonunun \( x = 3 \) noktasındaki soldan, sağdan ve iki taraflı limit değerlerini bulalım.
Önce mutlak değerli ifadenin kritik noktasını bulalım.
\( 2x - 6 = 0 \)
\( x = 3 \)
Fonksiyonu geçiş noktası \( x = 3 \) olacak şekilde parçalı fonksiyon şeklinde yazalım.
\( x \lt 3 \) aralığı için:
\( f(x) = -(2x - 6) + 2x = 6 \)
\( x \ge 3 \) aralığı için:
\( f(x) = (2x - 6) + 2x = 4x - 6 \)
\( f(x) = \begin{cases} 6 & x \lt 3 \\ 4x - 6 & x \ge 3 \end{cases} \)
Fonksiyonun \( x = 3 \) noktasındaki soldan ve sağdan limitlerini hesaplayalım.
Soldan limit için \( x \lt 3 \) aralığındaki tanımı kullanmalıyız.
\( L_1 = \lim\limits_{x \to 3^-} 6 = 6 \)
Sağdan limit için \( x \ge 3 \) aralığındaki tanımı kullanmalıyız.
\( L_2 = \lim\limits_{x \to 3^+} (4x - 6) = 4 \cdot 3 - 6 = 6 \)
\( L_1 = L_2 = 6 \) olduğu için, fonksiyonun \( x = 3 \) noktasında limiti tanımlıdır ve değeri \( 6 \)'dır.
\( f(x) = \dfrac{\abs{x}}{x} \)
fonksiyonunun \( x = 0 \) noktasındaki soldan, sağdan ve iki taraflı limit değerlerini bulalım.
Önce mutlak değerli ifadenin kritik noktasını bulalım.
\( x = 0 \)
Fonksiyonu geçiş noktası \( x = 0 \) olacak şekilde parçalı fonksiyon şeklinde yazalım.
\( x \lt 0 \) aralığı için:
\( f(x) = \dfrac{-x}{x} = -1 \)
\( x \ge 0 \) aralığı için:
\( f(x) = \dfrac{x}{x} = 1 \)
\( f(x) = \begin{cases} -1 & x \lt 0 \\ 1 & x \ge 0 \end{cases} \)
Fonksiyonun \( x = 0 \) noktasındaki soldan ve sağdan limitlerini hesaplayalım.
Soldan limit için \( x \lt 0 \) aralığındaki tanımı kullanmalıyız.
\( L_1 = \lim\limits_{x \to 0^-} {f(x)} = -1 \)
Sağdan limit için \( x \ge 0 \) aralığındaki tanımı kullanmalıyız.
\( L_2 = \lim\limits_{x \to 0^+} {f(x)} = 1 \)
\( L_1 \ne L_2 \) olduğu için, fonksiyonun \( x = 0 \) noktasında limiti tanımlı değildir.
\( f(x) = \dfrac{x^2 - 4}{\abs{x - 2}} \)
fonksiyonunun \( x = 2 \) noktasındaki soldan, sağdan ve iki taraflı limit değerlerini bulunuz.
Çözümü GösterÖnce mutlak değer ifadesinin kritik noktasını bulalım.
\( x - 2 = 0 \Longrightarrow x = 2 \)
Fonksiyonu kritik noktası \( x = 2 \) olacak şekilde parçalı fonksiyon şeklinde yazalım.
\( x \lt 2 \) aralığı için:
\( f(x) = \dfrac{(x - 2)(x + 2)}{-(x - 2)} = -x - 2 \)
\( x \ge 2 \) aralığı için:
\( f(x) = \dfrac{(x - 2)(x + 2)}{x - 2} = x + 2 \)
\( f(x) = \begin{cases} -x - 2 & x \lt 2 \\ x + 2 & x \ge 2 \end{cases} \)
Fonksiyonun \( x = 2 \) noktasındaki soldan ve sağdan limitlerini hesaplayalım.
Soldan limit için \( x \lt 2 \) aralığındaki tanımı kullanmalıyız.
\( L_1 = \lim\limits_{x \to 2^-} (-x - 2) = -2 - 2 = -4 \)
Sağdan limit için \( x \ge 2 \) aralığındaki tanımı kullanmalıyız.
\( L_2 = \lim\limits_{x \to 2^+} (x + 2) = 2 + 2 = 4 \)
\( L_1 \ne L_2 \) olduğu için, fonksiyonun \( x = 2 \) noktasında iki taraflı limiti tanımlı değildir.
\( \lim\limits_{x \to 2^+} \dfrac{\abs{x - 2}}{x - 2} + \lim\limits_{x \to -2^-} \dfrac{x^2 - 4}{\abs{x + 2}} \) toplamı kaçtır?
Çözümü Gösterİlk önce ilk limit ifadesinin değerini bulalım.
\( x = 2 \) noktası \( \abs{x - 2} \) ifadesinin kritik noktasıdır.
\( x \to 2^+ \) iken \( x - 2 \to 0^+ \) olur, dolayısıyla ifade mutlak değerden olduğu gibi çıkar.
\( \lim\limits_{x \to 2^+} \dfrac{\abs{x - 2}}{x - 2} = \lim\limits_{x \to 2^+} \dfrac{x - 2}{x - 2} \)
\( = \lim\limits_{x \to 2^+} 1 = 1 \)
Şimdi ikinci limit ifadesinin değerini bulalım.
\( x = -2 \) noktası \( \abs{x + 2} \) ifadesinin kritik noktasıdır.
\( x \to -2^- \) iken \( x + 2 \to 0^- \) olur, dolayısıyla ifade mutlak değerden negatif işaretli çıkar.
\( \lim\limits_{x \to -2^-} \dfrac{x^2 - 4}{\abs{x + 2}} = \lim\limits_{x \to -2^-} \dfrac{x^2 - 4}{-(x + 2)} \)
\( = \lim\limits_{x \to -2^-} \dfrac{(x + 2)(x - 2)}{-(x + 2)} \)
\( = \lim\limits_{x \to -2^-} [-(x - 2)] = -(-2 - 2) = 4 \)
İki limit ifadesinin toplamı \( 1 + 4 = 5 \) olarak bulunur.
\( \lim\limits_{x \to -2} \dfrac{\abs{2x + 4}}{x^2 - 4} \) iki taraflı limitinin tanımlı olup olmadığını inceleyiniz.
Çözümü GösterLimiti alınan ifadeyi düzenleyelim.
\( \lim\limits_{x \to -2} \dfrac{2\abs{x + 2}}{(x - 2)(x + 2)} \)
\( x = -2 \) noktası \( \abs{x + 2} \) ifadesinin kritik noktasıdır. Bu noktadaki limiti bulmak için soldan ve sağdan limit değerlerini hesaplayalım.
\( x = -2 \) için soldan limiti bulalım.
\( \lim\limits_{x \to -2^-} \dfrac{2\abs{x + 2}}{(x - 2)(x + 2)} \)
\( x \to -2^- \) iken \( x + 2 \to 0^- \) olur, dolayısıyla ifade mutlak değerden negatif işaretli çıkar.
\( = \lim\limits_{x \to -2^-} \dfrac{-2(x + 2)}{(x - 2)(x + 2)} \)
\( = \lim\limits_{x \to -2^-} \dfrac{-2}{x - 2} \)
\( = \dfrac{-2}{-2 - 2} = \dfrac{1}{2} \)
\( x = -2 \) için sağdan limiti bulalım.
\( \lim\limits_{x \to -2^+} \dfrac{2\abs{x + 2}}{(x - 2)(x + 2)} \)
\( x \to -2^+ \) iken \( x + 2 \to 0^+ \) olur, dolayısıyla ifade mutlak değerden olduğu gibi çıkar.
\( = \lim\limits_{x \to -2^+} \dfrac{2(x + 2)}{(x - 2)(x + 2)} \)
\( = \lim\limits_{x \to -2^+} \dfrac{2}{x - 2} \)
\( = \dfrac{2}{-2 - 2} = -\dfrac{1}{2} \)
Bu noktada soldan ve sağdan limitler tanımlı, ancak birbirinden farklı oldukları için fonksiyonun iki taraflı limiti tanımlı değildir.
\( \lim\limits_{x \to 3^+} \dfrac{\abs{3 - x}}{x - 3} + \lim\limits_{x \to 7^-} \dfrac{x - 7}{\abs{x - 7}} \) limitinin değeri kaçtır?
Çözümü GösterBirinci limit ifadesinin değerini bulalım.
\( x \to 3^+ \) iken \( 3 - x \to 0^- \) olur, dolayısıyla ifade mutlak değerden negatif işaretli çıkar.
\( \lim\limits_{x \to 3^+} \dfrac{\abs{3 - x}}{x - 3} = \lim\limits_{x \to 3^+} \dfrac{-(3 - x)}{x - 3} = 1 \)
İkinci limit ifadesinin değerini bulalım.
\( x \to 7^- \) iken \( x - 7 \to 0^- \) olur, dolayısıyla ifade mutlak değerden negatif işaretli çıkar.
\( \lim\limits_{x \to 7^-} \dfrac{x - 7}{\abs{x - 7}}= \lim\limits_{x \to 7^-} \dfrac{x - 7}{-(x - 7)} = -1 \)
Limit ifadelerinin toplamı \( 1 + (- 1) = 0 \) olarak bulunur.
\( \lim\limits_{x \to 4} \dfrac{\abs{x^2 - x - 12}}{x - 4} \) iki taraflı limitinin tanımlı olup olmadığını inceleyiniz.
Çözümü GösterPaydaki ifadeyi çarpanlarına ayıralım.
\( \lim\limits_{x \to 4} \dfrac{\abs{(x + 3)(x - 4)}}{x - 4} \)
İki ifadenin çarpımının mutlak değeri mutlak değerlerinin çarpımına eşittir.
\( = \lim\limits_{x \to 4} \dfrac{\abs{x + 3}\abs{x - 4}}{x - 4} \)
\( x = 4 \) ikinci mutlak değer ifadesinin kritik noktasıdır. Bu noktadaki limiti bulmak için soldan ve sağdan limit değerlerini hesaplayalım.
\( x = 4 \) için soldan limiti bulalım.
\( \lim\limits_{x \to 4^-} \dfrac{\abs{x + 3}\abs{x - 4}}{x - 4} \)
\( x \to 4^- \) iken \( x + 3 \to 7^- \) ve \( x - 4 \to 0^- \) olur, dolayısıyla birinci ifade mutlak değerden olduğu gibi, ikinci ifade negatif işaretli çıkar.
\( = \lim\limits_{x \to 4^-} \dfrac{(x + 3)(-(x - 4))}{x - 4} \)
\( = \lim\limits_{x \to 4^-} (-(x + 3)) \)
\( = -(4 + 3) = -7 \)
\( x = 4 \) için sağdan limiti bulalım.
\( \lim\limits_{x \to 4^+} \dfrac{\abs{x + 3}\abs{x - 4}}{x - 4} \)
\( x \to 4^+ \) iken \( x + 3 \to 7^+ \) ve \( x - 4 \to 0^+ \) olur, dolayısıyla iki ifade de mutlak değerden olduğu gibi çıkar.
\( = \lim\limits_{x \to 4^+} \dfrac{(x + 3)(x - 4)}{x - 4} \)
\( = \lim\limits_{x \to 4^+} (x + 3) \)
\( = 4 + 3 = 7 \)
Sağdan ve soldan limitler tanımlı, ancak birbirinden farklı oldukları için fonksiyonun bu noktada iki taraflı limiti tanımlı değildir.
\( \lim\limits_{x \to -4} \dfrac{x^2 - 2\abs{x} - 3}{2 - \abs{-x}} \) limitinin değeri kaçtır?
Çözümü GösterVerilen fonksiyonun kritik noktası \( x = 0 \) noktasıdır.
Bir mutlak değerli fonksiyonun kritik olmayan bir noktasındaki limit değerini bulmak için, mutlak değer içindeki ifade bu noktadaki değerinin işareti dikkate alınarak pozitif ya da negatif işaretli olarak mutlak değerden çıkarılır ve normal limit kuralları ile limiti hesaplanır.
\( -4 \lt 0 \) olduğu için paydaki \( \abs{x} \) ifadesi negatif olur ve mutlak değerden negatif işaretli çıkar, paydadaki \( \abs{-x} \) ifadesi ise pozitif olur ve mutlak değerden olduğu gibi çıkar.
\( \lim\limits_{x \to -4} \dfrac{x^2 - 2(-x) - 3}{2 - (-x)} \)
\( = \lim\limits_{x \to -4} \dfrac{x^2 + 2x - 3}{2 + x} \)
Pay ve payda birer polinom fonksiyonu olduğu için limiti alınan ifade bir rasyonel fonksiyondur. Limiti alınan \( x \) değeri paydayı sıfır yapmamak koşuluyla, rasyonel fonksiyonun bir noktadaki limit değeri o noktadaki fonksiyon değerine eşittir.
\( = \dfrac{(-4)^2 + 2(-4) - 3}{2 + (-4)} \)
\( = -\dfrac{5}{2} \) bulunur.
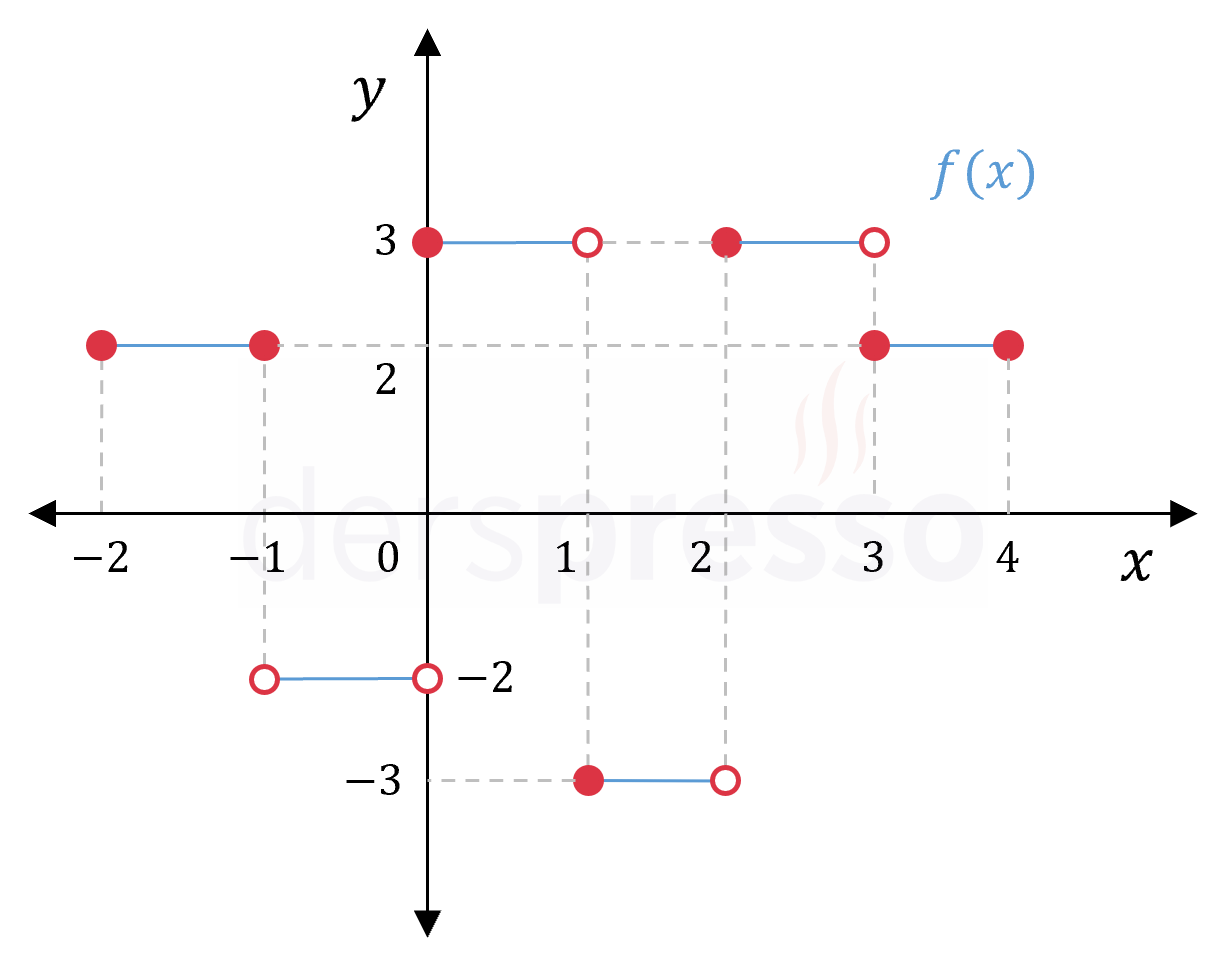
\( f: [-2, 4] \to \mathbb{R} \) olduğuna göre,
\( \lim\limits_{x \to a} \abs{f(x)} \) iki taraflı limitinin tanımlı olduğu kaç \( a \) tam sayısı vardır?
Çözümü GösterBir fonksiyonun çıktısının mutlak değeri alındığında \( x \) ekseninin altında kalan noktaların \( x \) eksenine göre yansımaları alınır.
Buna göre \( \abs{f(x)} \) fonksiyonunun grafiği aşağıdaki gibi olur.
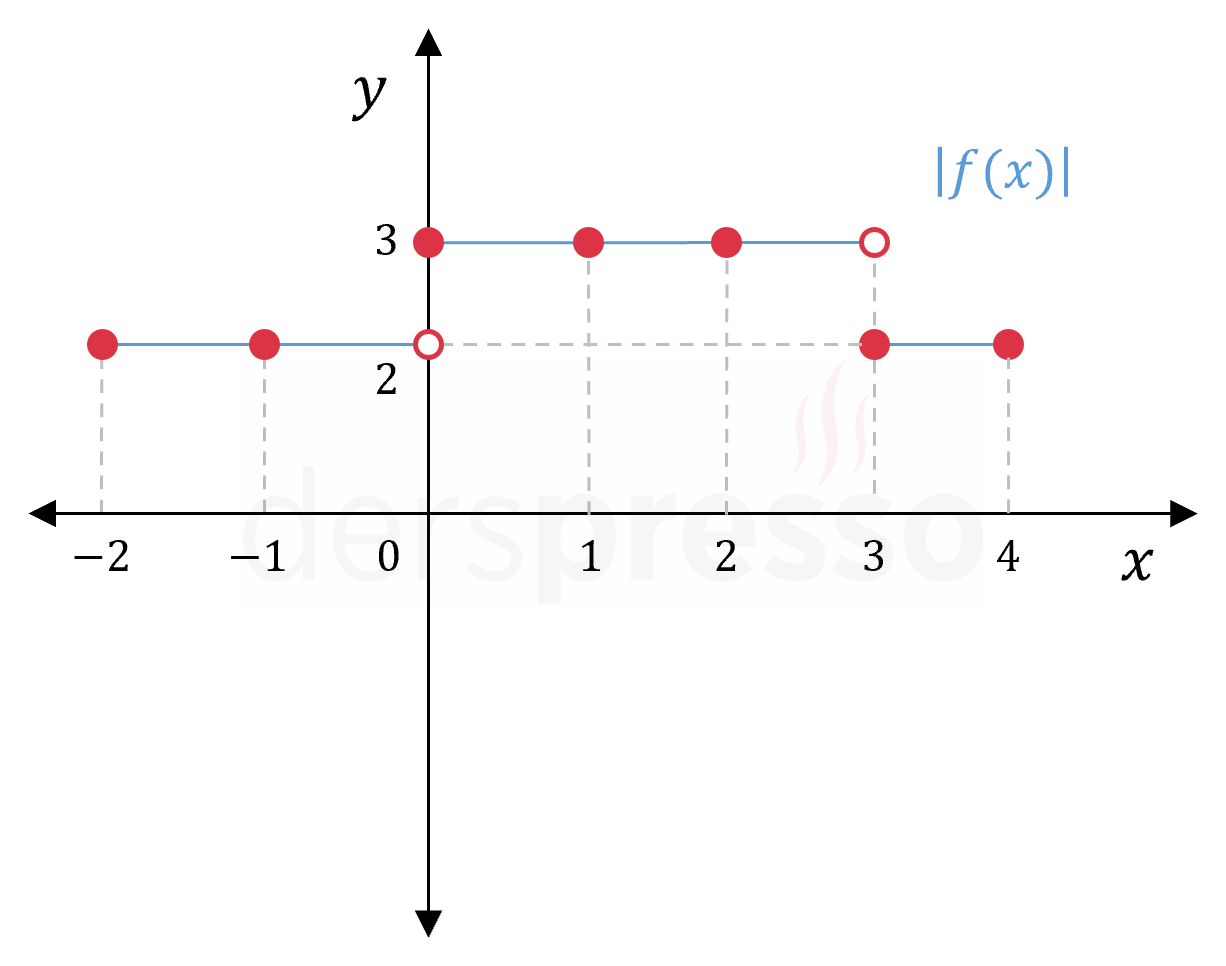
Bu grafiğe göre fonksiyonun aşağıdaki apsisli noktalarda iki taraflı limiti tanımlıdır.
\( a \in \{-1, 1, 2\} \)
Buna göre sorudaki iki taraflı limitin tanımlı olduğu üç \( a \) tam sayısı vardır.
\( f(x) = \dfrac{\abs{x^2 - 16}}{x^2 - 6x + 8} \)
fonksiyonunun \( x = -4 \) ve \( x = 4 \) noktalarındaki soldan, sağdan ve iki taraflı limit değerlerini bulunuz.
Çözümü GösterÖnce mutlak değer ifadesinin kritik noktalarını bulalım.
\( x^2 - 16 = 0 \)
\( x = -4 \) ve \( x = 4 \)
Fonksiyonu kritik noktaları \( x = -4 \) ve \( x = 4 \) olacak şekilde parçalı fonksiyon şeklinde yazalım.
\( x^2 - 16 \) ifadesi kritik noktaların arasındaki aralıkta negatif, dışındaki aralıkta pozitiftir.
\( x \le -4 \) aralığı için:
\( f(x) = \dfrac{x^2 - 16}{(x - 4)(x - 2)} = \dfrac{x + 4}{x - 2} \)
\( -4 \lt x \lt 4 \) aralığı için:
\( f(x) = \dfrac{-(x^2 - 16)}{(x - 4)(x - 2)} = \dfrac{-x - 4}{x - 2} \)
\( x \ge 4 \) aralığı için:
\( f(x) = \dfrac{x^2 - 16}{(x - 4)(x - 2)} = \dfrac{x + 4}{x - 2} \)
Buna göre fonksiyonun parçalı fonksiyon tanımı aşağıdaki gibi olur.
\( f(x) = \begin{cases} \dfrac{x + 4}{x - 2} & x \le -4 \\ \dfrac{-x - 4}{x - 2} & -4 \lt x \lt 4 \\ \dfrac{x + 4}{x - 2} & x \ge 4 \end{cases} \)
Fonksiyonun \( x = -4 \) noktasındaki soldan ve sağdan limitlerini hesaplayalım.
Soldan limit için fonksiyonun birinci tanımı kullanılır.
\( L_1 = \lim\limits_{x \to -4^-} \dfrac{x + 4}{x - 2} = \dfrac{-4 + 4}{-4 - 2} = 0 \)
Sağdan limit için fonksiyonun ikinci tanımı kullanılır.
\( L_2 = \lim\limits_{x \to -4^+} \dfrac{-x - 4}{x - 2} = \dfrac{-(-4) - 4}{-4 - 2} = 0 \)
\( L_1 = L_2 = 0 \) olduğu için, fonksiyonun \( x = -4 \) noktasında limiti tanımlıdır ve değeri \( 0 \)'dır.
Fonksiyonun \( x = 4 \) noktasındaki soldan ve sağdan limitlerini hesaplayalım.
Soldan limit için fonksiyonun ikinci tanımı kullanılır.
\( L_3 = \lim\limits_{x \to 4^-} \dfrac{-x - 4}{x - 2} = \dfrac{-4 - 4}{4 - 2} = -4 \)
Sağdan limit için fonksiyonun üçüncü tanımı kullanılır.
\( L_4 = \lim\limits_{x \to 4^+} \dfrac{x + 4}{x - 2} = \dfrac{4 + 4}{4 - 2} = 4 \)
\( L_3 \ne L_4 \) olduğu için, fonksiyonun \( x = 4 \) noktasında limiti tanımlı değildir.
\( f(x) = \dfrac{\sqrt{x^2 + 8x + 16}}{x - 3} \)
fonksiyonunun \( x = -4 \) noktasındaki soldan, sağdan ve iki taraflı limit değerlerini bulunuz.
Çözümü GösterVerilen fonksiyonu düzenleyelim.
\( f(x) = \dfrac{\sqrt{(x + 4)^2}}{x - 3} \)
\( n \) çift sayı olmak üzere, \( \sqrt[n]{x^n} \) şeklindeki köklü ifadenin sonucu \( \abs{x} \) olur.
\( f(x) = \dfrac{\abs{x + 4}}{x - 3} \)
\( x = -4 \) noktası mutlak değer ifadesinin kritik noktasıdır. Fonksiyonu önce parçalı fonksiyon şeklinde yazalım.
\( x \lt -4 \) aralığı için:
\( x \lt -4 \) iken \( x + 4 \) ifadesi negatif olur, dolayısıyla mutlak değerden negatif işaretli çıkar.
\( f(x) = \dfrac{-(x + 4)}{x - 3} \)
\( x \ge -4 \) aralığı için:
\( x \ge -4 \) iken \( x + 4 \) ifadesi pozitif olur, dolayısıyla mutlak değerden olduğu gibi çıkar.
\( f(x) = \dfrac{x + 4}{x - 3} \)
Parçalı fonksiyon tanımı aşağıdaki gibi olur.
\( f(x) = \begin{cases} \dfrac{-(x + 4)}{x - 3}, & x \lt -4 \\ \dfrac{x + 4}{x - 3}, & x \ge -4 \end{cases} \)
Soldan limit için fonksiyonun birinci tanımı kullanılır.
\( \lim\limits_{x \to -4^-} \dfrac{-(x + 4)}{x - 3} \)
\( = \dfrac{-(-4 + 4)}{-4 - 3} = 0 \)
Sağdan limit için fonksiyonun ikinci tanımı kullanılır.
\( \lim\limits_{x \to -4^+} \dfrac{x + 4}{x - 3} \)
\( = \dfrac{-4 + 4}{-4 - 3} = 0 \)
Soldan ve sağdan limitler tanımlı ve birbirine eşit olduğu için fonksiyonun \( x = -4 \) noktasında iki taraflı limiti tanımlıdır ve değeri 0'dır.
\( \lim\limits_{x \to -4} f(x) = 0 \)
\( f(x) = \dfrac{2x - 2}{\abs{x^3 - x^2}} \) olduğuna göre,
\( \lim\limits_{x \to 1} f(x) \) limitinin değeri kaçtır?
Çözümü GösterVerilen fonksiyonu düzenleyelim.
\( f(x) = \dfrac{2(x - 1)}{\abs{x^2(x - 1)}} \)
İki ifadenin çarpımının mutlak değeri mutlak değerlerinin çarpımına eşittir.
\( = \dfrac{2(x - 1)}{\abs{x^2}\abs{x - 1}} \)
\( x^2 \) ifadesi negatif olamayacağı için mutlak değerden olduğu gibi çıkar.
\( = \dfrac{2(x - 1)}{x^2\abs{x - 1}} \)
\( x = 1 \) noktası mutlak değer ifadesinin kritik noktasıdır. Fonksiyonu önce parçalı fonksiyon şeklinde yazalım.
\( x \lt 1 \) aralığı için:
\( x \lt 1 \) iken \( x - 1 \) ifadesi negatif olur, dolayısıyla mutlak değerden negatif işaretli çıkar.
\( f(x) = \dfrac{2(x - 1)}{x^2[-(x - 1)]} \)
\( = -\dfrac{2}{x^2} \)
\( x \ge 1 \) aralığı için:
\( x \ge 1 \) iken \( x - 1 \) ifadesi pozitif olur, dolayısıyla mutlak değerden olduğu gibi çıkar.
\( f(x) = \dfrac{2(x - 1)}{x^2(x - 1)} \)
\( = \dfrac{2}{x^2} \)
Parçalı fonksiyon tanımı aşağıdaki gibi olur.
\( f(x) = \begin{cases} \dfrac{-2}{x^2}, & x \lt 1 \\ \dfrac{2}{x^2}, & x \ge 1 \end{cases} \)
Soldan limit için fonksiyonun birinci tanımı kullanılır.
\( \lim\limits_{x \to 1^-} \dfrac{-2}{x^2} = \dfrac{-2}{1^2} = -2 \)
Sağdan limit için fonksiyonun ikinci tanımı kullanılır.
\( \lim\limits_{x \to 1^+} \dfrac{2}{x^2} = \dfrac{2}{1^2} = 2 \)
Soldan ve sağdan limitler tanımlı, ancak birbirinden farklı olduğu için fonksiyonun \( x = 1 \) noktasında limiti tanımlı değildir.
Aşağıdaki fonksiyonlardan hangilerinin \( x = 9 \) noktasıda limiti tanımlıdır?
\( f(x) = \dfrac{x - 9}{\abs{x - 9}} \)
\( g(x) = \sqrt{x^2 - 18x + 81} \)
\( h(x) = \dfrac{\sqrt[3]{x - 9}}{x + 9} \)
Çözümü Göster\( f \) fonksiyonu:
\( f \) fonksiyonunun soldan ve sağdan limitlerini bulalım.
\( x = 9 \) noktası mutlak değer ifadesinin kritik noktasıdır.
Bu noktadaki soldan limiti bulalım.
\( \lim\limits_{x \to 9^-} \dfrac{x - 9}{\abs{x - 9}} \)
\( x \to 9^- \) iken \( x - 9 \to 0^- \) olur, dolayısıyla ifade mutlak değerden negatif işaretli çıkar.
\( = \lim\limits_{x \to 9^-} \dfrac{x - 9}{-(x - 9)} = -1 \)
Bu noktadaki sağdan limiti bulalım.
\( \lim\limits_{x \to 9^+} \dfrac{x - 9}{\abs{x - 9}} \)
\( x \to 9^+ \) iken \( x - 9 \to 0^+ \) olur, dolayısıyla ifade mutlak değerden olduğu gibi çıkar.
\( = \lim\limits_{x \to 9^+} \dfrac{x - 9}{x - 9} = 1 \)
Soldan ve sağdan limitler tanımlı olsa da değerleri birbirinden farklı olduğu için \( f \) fonksiyonunun \( x = 9 \) noktasında limiti yoktur.
\( g \) fonksiyonu:
\( g(x) = \sqrt{x^2 - 18x + 81} \)
\( = \sqrt{(x - 9)^2} = \abs{x - 9} \)
Mutlak değer fonksiyonu tüm reel sayılarda sürekli olduğu için limiti de tanımlıdır ve bu noktadaki fonksiyon değerine eşittir.
\( \lim\limits_{x \to 9} \abs{x - 9} = \abs{9 - 9} = 0 \)
\( h \) fonksiyonu:
\( \lim\limits_{x \to 9} \dfrac{\sqrt[3]{x - 9}}{x + 9} \)
\( n \) bir pozitif tam sayı olmak üzere, \( \sqrt[2n + 1]{x} \) fonksiyonu tüm reel sayılarda süreklidir ve limiti tanımlıdır. Paydadaki ifade de bir polinom fonksiyonudur ve tüm reel sayılarda süreklidir ve limiti tanımlıdır, ayrıca limit değeri sıfırdan farklıdır.
Buna göre limit bölme kuralı ile limiti paya ve paydaya dağıtabiliriz ve doğrudan yerine koyma yöntemi ile limit değerlerini bulabiliriz.
\( = \dfrac{\lim\limits_{x \to 9} \sqrt[3]{x - 9}}{\lim\limits_{x \to 9} (x + 9)} \)
\( = \dfrac{\sqrt[3]{9 - 9}}{9 + 9} = 0 \)
\( h \) fonksiyonunun \( x = 9 \) noktasında limiti tanımlıdır ve değeri 0'dır.
Buna göre \( g \) ve \( h \) fonksiyonlarının \( x = 9 \) noktasında limiti tanımlıdır.