Trigonometrik Fonksiyonların Limiti
Tüm trigonometrik fonksiyonlar tanım kümeleri içinde sürekli oldukları için, limiti alınan nokta ilgili fonksiyonun tanım kümesinde olmak koşuluyla, trigonometrik fonksiyonların tek ve iki taraflı limitleri fonksiyonun o noktadaki değerine eşittir.
\( \lim\limits_{x \to a} \sin{x} = \sin{a} \)
\( \lim\limits_{x \to a} \cos{x} = \cos{a} \)
\( \lim\limits_{x \to a} \tan{x} = \tan{a} \)
\( \lim\limits_{x \to a} \cot{x} = \cot{a} \)
\( \lim\limits_{x \to a} \sec{x} = \sec{a} \)
\( \lim\limits_{x \to a} \csc{x} = \csc{a} \)
\( \lim\limits_{x \to \frac{\pi}{4}} \sin{x} = \sin{\dfrac{\pi}{4}} = \dfrac{\sqrt{2}}{2} \)
\( \lim\limits_{x \to \pi^+} \cos{x} = \cos{\pi} = -1 \)
Benzer şekilde, tüm ters trigonometrik fonksiyonlar tanım kümeleri içinde sürekli oldukları için, limiti alınan nokta ilgili fonksiyonun tanım kümesinde olmak koşuluyla, ters trigonometrik fonksiyonların tek ve iki taraflı limitleri fonksiyonun o noktadaki değerine eşittir.
\( \lim\limits_{x \to a} \arcsin{x} = \arcsin{a} \)
\( \lim\limits_{x \to a} \arccos{x} = \arccos{a} \)
\( \lim\limits_{x \to a} \arctan{x} = \arctan{a} \)
\( \lim\limits_{x \to a} \arccot{x} = \arccot{a} \)
\( \lim\limits_{x \to a} \arcsec{x} = \arcsec{a} \)
\( \lim\limits_{x \to a} \arccsc{x} = \arccsc{a} \)
\( \lim\limits_{x \to 1} \arctan{x} = \arctan{1} = \dfrac{\pi}{4} \)
Özel Trigonometrik Limitler
Aşağıda ispatlarıyla birlikte verdiğimiz üç trigonometrik limit, daha karmaşık ifadelerin limitini hesaplarken sıklıkla kullanılmaktadır.
\( \lim\limits_{x \to 0} \dfrac{\sin{x}}{x} = 1 \)
İSPATI GÖSTER
Önce aşağıdaki gibi bir birim çember çizelim.
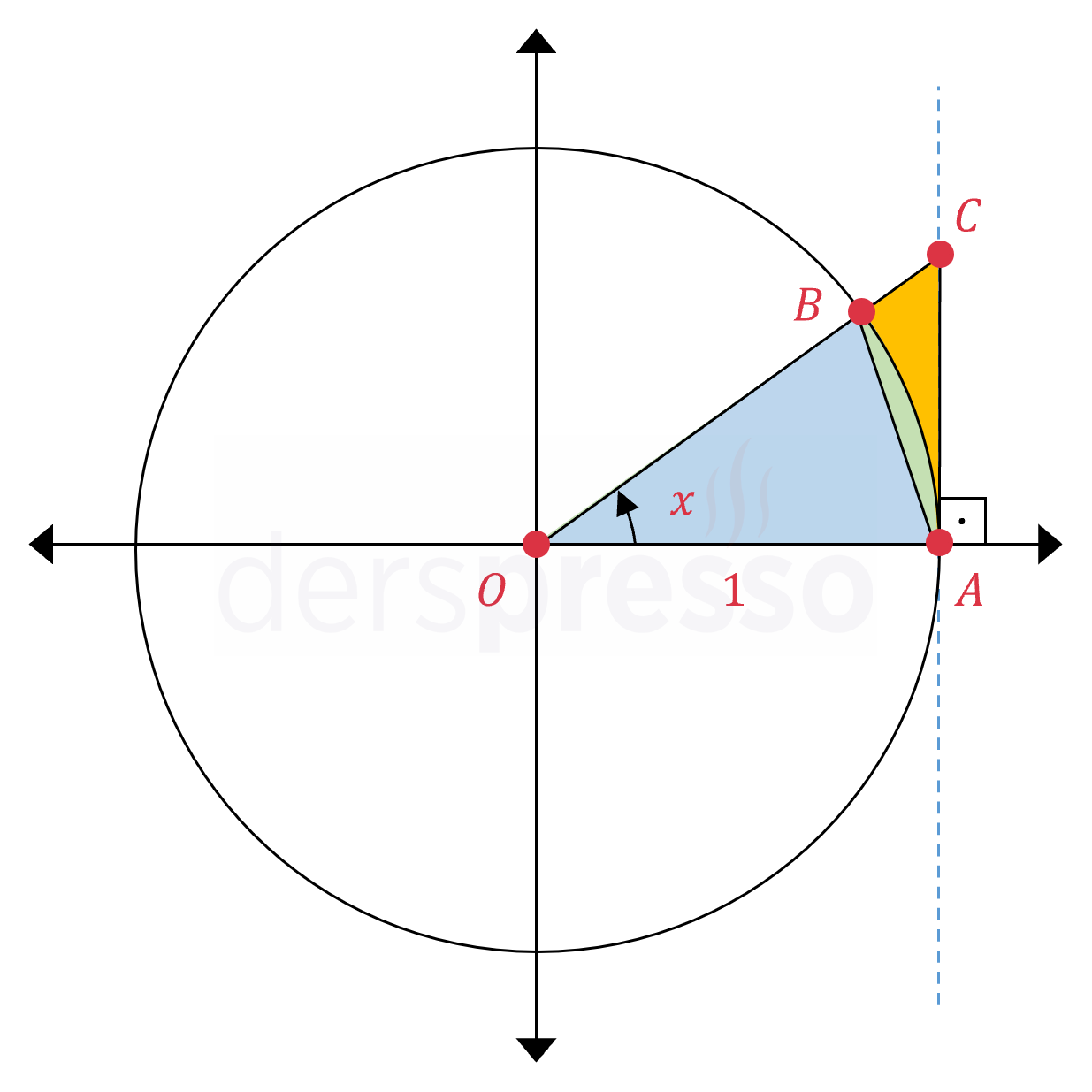
\( x \) açısının kollarının birim çemberi ve tanjant eksenini kestiği noktalar ve orijin, \( AOB \) üçgenini, \( AOB \) daire dilimini ve \( AOC \) üçgenini oluşturur.
Bu şekillerin alanlarını aşağıdaki gibi sıralayabiliriz.
\( AOB \) üçgeni alanı \( \le \) \( AOB \) daire dilimi alanı \( \le \) \( AOC \) üçgeni alanı
Bu alanların her birinin formülünü aşağıdaki gibi yazabiliriz.
\( AOB \) üçgeninin tabanı 1, yüksekliği \( B \) noktasının ordinatı olan \( \sin{x} \)'tir.
\( AOB = \dfrac{1 \cdot \sin{x}}{2} = \dfrac{\sin{x}}{2} \)
\( AOB \) daire diliminin alanını \( x \) açısının tam çember açısı olan \( 2\pi \) radyana oranını tüm daire alanı ile çarparak bulabiliriz. Birim çember için \( r = 1 \) olur.
Daire dilimi \( = \pi r^2 \cdot \dfrac{x}{2\pi} = \dfrac{x}{2} \)
\( AOC \) üçgeninin tabanı 1, yüksekliği \( \tan{x} \)'tir.
\( AOC = \dfrac{1 \cdot \tan{x}}{2} = \dfrac{\tan{x}}{2} \)
Bu üç alan değerini yukarıdaki sıralamada yerlerine koyalım.
\( \dfrac{\sin{x}}{2} \le \dfrac{x}{2} \le \dfrac{\tan{x}}{2} \)
\( \sin{x} \le x \le \tan{x} \)
Üç ifadeyi de \( \sin{x} \)'e bölelim.
\( 1 \le \dfrac{x}{\sin{x}} \le \dfrac{\tan{x}}{\sin{x}} \)
Tanjant sinüsün kosinüse bölümüne eşit olduğu için üçüncü ifade aşağıdaki şekilde sadeleşir.
\( 1 \le \dfrac{x}{\sin{x}} \le \dfrac{1}{\cos{x}} \)
Eşitsizlik işlem özelliklerine göre her bir ifadenin çarpmaya göre tersini alırsak eşitsizlikler yön değiştirir.
\( \cos{x} \le \dfrac{\sin{x}}{x} \le 1 \)
Birinci ve üçüncü ifadelerin \( x \) sıfıra giderken limitini alalım.
Birinci ifadedeki kosinüs fonksiyonu tüm reel sayılarda sürekli olduğu için direkt yerine koyma yöntemiyle limitini bulabiliriz.
\( \lim\limits_{x \to 0} \cos{x} = \cos{0} = 1 \)
Üçüncü ifadedeki 1 sabit bir değerdir ve limiti kendisine eşittir.
\( \lim\limits_{x \to 0} 1 = 1 \)
Buna göre bu iki ifadenin \( x = 0 \) noktasındaki limitleri eşittir.
\( \lim\limits_{x \to 0} \cos{x} = \lim\limits_{x \to 0} 1 = 1 \)
Sıkıştırma teoremine göre, bir \( f \) fonksiyonunun değerinin belirli bir aralıkta diğer iki fonksiyonun değerinin arasında kaldığını ve ayrıca bu diğer iki fonksiyonun bu aralıktaki bir \( a \) noktasındaki limitlerinin eşit olduğunu gösterebiliyorsak, \( f \) fonksiyonunun da bu \( a \) noktasındaki limiti bu değere eşit olur.
Yukarıda \( \frac{\sin{x}}{x} \) fonksiyonunun değerinin her zaman \( \cos{x} \) ve sabit \( 1 \) fonksiyonlarının arasında kaldığını gösterdik. Ayrıca bu iki fonksiyonun \( x = 0 \) noktasıdaki limitlerinin de 1'e eşit olduğunu gösterdik.
Buna göre verilen ifadenin limitini de 1 olarak bulmuş olduk.
\( \lim\limits_{x \to 0} \dfrac{\sin{x}}{x} = 1 \)
\( \lim\limits_{x \to 0} \dfrac{1 - \cos{x}}{x} = 0 \)
İSPATI GÖSTER
Önce ifadenin payını ve paydasını \( (1 + \cos{x}) \) ile çarpalım.
\( \lim\limits_{x \to 0} \dfrac{1 - \cos{x}}{x} \)
\( = \lim\limits_{x \to 0} \dfrac{(1 - \cos{x})(1 + \cos{x})}{x(1 + \cos{x})} \)
\( = \lim\limits_{x \to 0} \dfrac{1 - \cos^2{x}}{x(1 + \cos{x})} \)
\( \sin^2{x} + \cos^2{x} = 1 \) özdeşliğini kullanarak payı \( \sin{x} \) cinsinden yazalım.
\( = \lim\limits_{x \to 0} \dfrac{\sin^2{x}}{x(1 + \cos{x})} \)
Limit ifadesinin içini iki çarpana ayıralım.
\( = \lim\limits_{x \to 0} \left[ \dfrac{\sin{x}}{x} \cdot \dfrac{\sin{x}}{1 + \cos{x}} \right] \)
Biraz sonra her iki limitin de tanımlı olduğunu göstereceğimiz için, limit çarpma kuralını kullanarak bu çarpımı iki farklı limitin çarpımı şeklinde yazabiliriz.
\( = \lim\limits_{x \to 0} \dfrac{\sin{x}}{x} \cdot \lim\limits_{x \to 0} \dfrac{\sin{x}}{1 + \cos{x}} \)
Birinci limit ifadesinin 1'e eşit olduğunu ispatıyla birlikte göstermiştik.
\( \lim\limits_{x \to 0} \dfrac{\sin{x}}{x} = 1 \)
Buna göre limit ifadesi aşağıdaki şekilde sadeleşir.
\( = 1 \cdot \lim\limits_{x \to 0} \dfrac{\sin{x}}{1 + \cos{x}} \)
İkinci limit ifadesinde herhangi bir belirsizlik olmadığı ve rasyonel ifadeyi oluşturan fonksiyonların sürekli olduklarını bildiğimiz için direkt yerine koyma yöntemi ile limitini hesaplayabiliriz.
\( = \dfrac{\sin{0}}{1 + \cos{0}} \)
\( = \dfrac{0}{1 + 1} = 0 \)
İlk satırda verilen ifadenin limit değerinin 0 olduğunu bu şekilde göstermiş olduk.
\( \lim\limits_{x \to 0} \dfrac{\tan{x}}{x} = 1 \)
İSPATI GÖSTER
Tanjant fonksiyonunu sinüs ve kosinüs cinsinden yazalım.
\( \lim\limits_{x \to 0} \dfrac{\tan{x}}{x} \)
\( = \lim\limits_{x \to 0} \dfrac{\sin{x}}{\cos{x} \cdot x} \)
Limit ifadesinin içini iki çarpana ayıralım.
\( = \lim\limits_{x \to 0} \left[ \dfrac{\sin{x}}{x} \cdot \dfrac{1}{\cos{x}} \right] \)
Biraz sonra her iki limitin de tanımlı olduğunu göstereceğimiz için, limit çarpma kuralını kullanarak bu çarpımı iki farklı limitin çarpımı şeklinde yazabiliriz.
\( = \lim\limits_{x \to 0} \dfrac{\sin{x}}{x} \cdot \lim\limits_{x \to 0} \dfrac{1}{\cos{x}} \)
Birinci limit ifadesinin 1'e eşit olduğunu ispatıyla birlikte göstermiştik.
\( \lim\limits_{x \to 0} \dfrac{\sin{x}}{x} = 1 \)
Buna göre limit ifadesi aşağıdaki şekilde sadeleşir.
\( = 1 \cdot \lim\limits_{x \to 0} \dfrac{1}{\cos{x}} \)
İkinci limit ifadesinde herhangi bir belirsizlik olmadığı ve kosinüs fonksiyonunun sürekli olduğunu bildiğimiz için direkt yerine koyma yöntemi ile limitini hesaplayabiliriz.
\( = \dfrac{1}{\cos{0}} = 1 \)
İlk satırda verilen ifadenin limit değerinin 1 olduğunu bu şekilde göstermiş olduk.
Yukarıdaki sinüs limit kuralı aşağıdaki tipteki ifadelere de uygulanabilir.
\( a, b \in \mathbb{R} \) olmak üzere,
\( \lim\limits_{x \to 0} \dfrac{\sin(ax)}{bx} = \dfrac{a}{b} \)
İSPATI GÖSTER
Sinüs fonksiyonunun içindeki \( ax \) ifadesine değişken değiştirme uygulayalım.
\( \lim\limits_{x \to 0} \dfrac{\sin(ax)}{bx} \)
\( t = ax \Longrightarrow x = \frac{t}{a} \)
\( x \) sıfıra giderken \( t = ax \) değişkeni de sıfıra gider.
\( = \lim\limits_{t \to 0} \dfrac{\sin{t}}{b \cdot \frac{t}{a}} \)
\( = \lim\limits_{t \to 0} \dfrac{a\sin{t}}{bt} \)
Limit ifadesinin içini iki çarpana ayıralım.
\( = \lim\limits_{t \to 0} \left[ \dfrac{a}{b} \cdot \dfrac{\sin{t}}{t} \right] \)
Limit ifadesinin içindeki ilk çarpan sabit bir sayı olduğu için limitin dışına çıkarabiliriz.
\( = \dfrac{a}{b}\lim\limits_{t \to 0} \dfrac{\sin{t}}{t} \)
Kalan limit ifadesinin 1'e eşit olduğunu ispatıyla birlikte göstermiştik.
\( \lim\limits_{x \to 0} \dfrac{\sin{x}}{x} = 1 \)
Buna göre limit ifadesi aşağıdaki şekilde sadeleşir.
\( = \dfrac{a}{b} \cdot 1 = \dfrac{a}{b} \)
İlk satırda verilen ifadenin limit değerinin \( \frac{a}{b} \) olduğunu bu şekilde göstermiş olduk.
Yukarıdaki tanjant limit kuralı aşağıdaki tipteki ifadelere de uygulanabilir.
\( a, b \in \mathbb{R} \) olmak üzere,
\( \lim\limits_{x \to 0} \dfrac{\tan(ax)}{bx} = \dfrac{a}{b} \)
İSPATI GÖSTER
Tanjant fonksiyonunun içindeki \( ax \) ifadesine değişken değiştirme uygulayalım.
\( \lim\limits_{x \to 0} \dfrac{\tan(ax)}{bx} \)
\( t = ax \Longrightarrow x = \frac{t}{a} \)
\( x \) sıfıra giderken \( t = ax \) değişkeni de sıfıra gider.
\( = \lim\limits_{t \to 0} \dfrac{\tan{t}}{b \cdot \frac{t}{a}} \)
\( = \lim\limits_{t \to 0} \dfrac{a\tan{t}}{bt} \)
\( = \lim\limits_{t \to 0} \dfrac{a \cdot \frac{\sin{t}}{\cos{t}}}{bt} \)
\( = \lim\limits_{t \to 0} \dfrac{a\sin{t}}{bt\cos{t}} \)
\( = \lim\limits_{t \to 0} \left[ \dfrac{a}{b\cos{t}} \cdot \dfrac{\sin{t}}{t} \right] \)
Aşağıda göreceğimiz üzere, iki çarpanın da \( t = 0 \) noktasında limitleri tanımlı olduğu için limit çarpma kuralını uygulayabiliriz.
\( = \lim\limits_{t \to 0} \dfrac{a}{b\cos{t}} \cdot \lim\limits_{t \to 0} \dfrac{\sin{t}}{t} \)
Kosinüs fonksiyonu tüm reel sayılarda sürekli olduğu için birinci çarpanın limitini doğrudan yerine koyma yöntemi ile bulabiliriz.
İkinci çarpanın limitini ispatıyla 1 olarak göstermiştik.
\( = \lim\limits_{t \to 0} \dfrac{a}{b\cos{0}} \cdot 1 \)
\( = \dfrac{a}{b} \) bulunur.
Aşağıdaki limitleri hesaplayınız.
(a) \( \lim\limits_{x \to 0} {\dfrac{\tan(7x)}{2x}} \)
(b) \( \lim\limits_{x \to 0} {\dfrac{6\sin(\frac{5}{2}x)}{5x}} \)
(c) \( \lim\limits_{x \to 0} \left( \dfrac{\sin(8x)}{2x} - \dfrac{\tan(3x)}{6x} \right) \)
Çözümü Göster(a) seçeneği:
\( \lim\limits_{x \to 0} {\dfrac{\tan(7x)}{2x}} \)
Aşağıdaki limit kuralını kullanalım.
\( a, b \in \mathbb{R} \) olmak üzere,
\( \lim\limits_{x \to 0} \dfrac{\tan(ax)}{bx} = \dfrac{a}{b} \)
\( \lim\limits_{x \to 0} {\dfrac{\tan(7x)}{2x}} = \dfrac{7}{2} \)
(b) seçeneği:
\( \lim\limits_{x \to 0} {\dfrac{6\sin(\frac{5}{2}x)}{5x}} \)
\( = 6\lim\limits_{x \to 0} {\dfrac{\sin(\frac{5}{2}x)}{5x}} \)
Aşağıdaki limit kuralını kullanalım.
\( a, b \in \mathbb{R} \) olmak üzere,
\( \lim\limits_{x \to 0} \dfrac{\sin(ax)}{bx} = \dfrac{a}{b} \)
\( = 6\lim\limits_{x \to 0} {\dfrac{\sin(\frac{5}{2}x)}{5x}} \)
\( = 6 \cdot \dfrac{\frac{5}{2}}{5} = 3 \)
(c) seçeneği:
\( \lim\limits_{x \to 0} \left( \dfrac{\sin(8x)}{2x} - \dfrac{\tan(3x)}{6x} \right) \)
Aşağıda göstereceğimiz üzere, limiti alınan ifadenin terimlerinin limiti ayrı ayrı tanımlı olduğu için, limit işlem kurallarını kullanarak limiti terimlere dağıtabiliriz.
\( = \lim\limits_{x \to 0} {\dfrac{\sin(8x)}{2x}} - \lim\limits_{x \to 0} {\dfrac{\tan(3x)}{6x}} \)
Aşağıdaki limit kurallarını kullanalım.
\( a, b \in \mathbb{R} \) olmak üzere,
\( \lim\limits_{x \to 0} \dfrac{\sin(ax)}{bx} = \dfrac{a}{b} \)
\( \lim\limits_{x \to 0} {\dfrac{\sin(8x)}{2x}} = \dfrac{8}{2} = 4 \)
\( \lim\limits_{x \to 0} \dfrac{\tan(ax)}{bx} = \dfrac{a}{b} \)
\( \lim\limits_{x \to 0} {\dfrac{\tan(3x)}{6x}} = \dfrac{3}{6} = \dfrac{1}{2} \)
Bulduğumuz değerleri limit ifadesinde yerine koyalım.
\( = 4 - \dfrac{1}{2} = \dfrac{7}{2} \)
Aşağıdaki limitleri hesaplayınız.
(a) \( \lim\limits_{x \to \frac{\pi}{4}} (\cos^2{x} + \sin(2x)) \)
(b) \( \lim\limits_{x \to \frac{\pi}{2}} {\dfrac{\cos^2(2x)}{\sin(3x)}} \)
(c) \( \lim\limits_{x \to 0} {\dfrac{\sin(5x) + 2}{4\cos{\frac{x}{2}} - 3\sin^2{x}}} \)
Çözümü GösterSinüs ve kosinüs fonksiyonları tüm reel sayılarda süreklidir. Sürekli fonksiyonlar arasındaki toplama, çıkarma, çarpma ve (payda sıfırdan farklı olmak koşuluyla) bölme işlemleri sonucunda oluşan fonksiyonlar da süreklidir.
(a) seçeneği:
\( \lim\limits_{x \to \frac{\pi}{4}} (\cos^2{x} + \sin(2x)) \)
Limiti alınan fonksiyon tüm reel sayılarda süreklidir, dolayısıyla doğrudan yerine koyma yöntemi ile limit değerini bulabiliriz.
\( = \cos^2{\dfrac{\pi}{4}} + \sin(2 \cdot \dfrac{\pi}{4}) \)
\( = (\dfrac{\sqrt{2}}{2})^2 + 1 = \dfrac{3}{2} \)
(b) seçeneği:
\( \lim\limits_{x \to \frac{\pi}{2}} {\dfrac{\cos^2(2x)}{\sin(3x)}} \)
Limiti alınan fonksiyon paydayı sıfır yapan \( x \) değerleri hariç tüm reel sayılarda süreklidir, dolayısıyla doğrudan yerine koyma yöntemi ile limit değerini bulabiliriz.
\( = \dfrac{\cos^2(2 \cdot \frac{\pi}{2})}{\sin(3 \cdot \frac{\pi}{2})} \)
\( = \dfrac{(-1)^2}{-1} = -1 \)
(c) seçeneği:
\( \lim\limits_{x \to 0} {\dfrac{\sin(5x) + 2}{4\cos{\frac{x}{2}} - 3\sin^2{x}}} \)
Limiti alınan fonksiyon paydayı sıfır yapan \( x \) değerleri hariç tüm reel sayılarda süreklidir, dolayısıyla doğrudan yerine koyma yöntemi ile limit değerini bulabiliriz.
\( = \dfrac{\sin(5(0)) + 2}{4\cos{\frac{0}{2}} - 3\sin^2{0}} \)
\( = \dfrac{0 + 2}{4(1) - 3(0)^2} = \dfrac{1}{2} \)
\( \lim\limits_{x \to \frac{\pi}{7}} \dfrac{\sin^2{x} - \cos^2{x}}{\sqrt{3}\cos(2x)} \) limitinin değeri kaçtır?
Çözümü GösterLimit ifadesini düzenleyelim.
\( \lim\limits_{x \to \frac{\pi}{7}} \dfrac{-(\cos^2{x} - \sin^2{x})}{\sqrt{3}\cos(2x)} \)
Kosinüs iki kat açı formülünü kullanalım.
\( \cos(2x) = \cos^2{x} - \sin^2{x} \)
\( = \lim\limits_{x \to \frac{\pi}{7}} \dfrac{-\cos(2x)}{\sqrt{3}\cos(2x)} \)
\( = \lim\limits_{x \to \frac{\pi}{7}} \dfrac{-1}{\sqrt{3}} \)
Sabit fonksiyonun limit değeri fonksiyon değerine eşittir.
\( = -\dfrac{1}{\sqrt{3}} \) bulunur.
\( \lim\limits_{x \to \frac{\pi}{16}} \dfrac{\sin(4x) + \sin(8x) + \sin(16x)}{\cos(4x) + \cos(8x) + \cos(16x)} \) limitinin değeri kaçtır?
Çözümü GösterÖnce pay ve paydadaki ifadelerin ayrı ayrı limitini bulalım.
Sinüs ve kosinüs fonksiyonları tüm reel sayılarda süreklidir. Sürekli fonksiyonlar arasındaki toplama, çıkarma, çarpma ve (payda sıfırdan farklı olmak koşuluyla) bölme işlemleri sonucunda oluşan fonksiyonlar da süreklidir.
Buna göre pay ve paydadaki ifadeler tüm reel sayılarda süreklidir ve doğrudan yerine koyma yöntemi ile limit değerlerini bulabiliriz.
\( \lim\limits_{x \to \frac{\pi}{16}} (\sin(4x) + \sin(8x) + \sin(16x)) \)
\( = \sin(4 \cdot \frac{\pi}{16}) + \sin(8 \cdot \frac{\pi}{16}) + \sin(16 \cdot \frac{\pi}{16}) \)
\( = \sin{\frac{\pi}{4}} + \sin{\frac{\pi}{2}} + \sin{\pi} \)
\( = \dfrac{\sqrt{2}}{2} + 1 + 0 = \dfrac{\sqrt{2} + 2}{2} \)
\( \lim\limits_{x \to \frac{\pi}{16}} (\cos(4x) + \cos(8x) + \cos(16x)) \)
\( = \cos(4 \cdot \frac{\pi}{16}) + \cos(8 \cdot \frac{\pi}{16}) + \cos(16 \cdot \frac{\pi}{16}) \)
\( = \cos{\frac{\pi}{4}} + \cos{\frac{\pi}{2}} + \cos{\pi} \)
\( = \dfrac{\sqrt{2}}{2} + 0 + (-1) = \dfrac{\sqrt{2} - 2}{2} \)
Pay ve paydadaki ifadelerin limiti tanımlı ve paydadaki ifadenin limiti sıfırdan farklı olduğu için limit bölme kuralını kullanabiliriz.
\( \lim\limits_{x \to \frac{\pi}{16}} \dfrac{\sin(4x) + \sin(8x) + \sin(16x)}{\cos(4x) + \cos(8x) + \cos(16x)} \)
\( = \dfrac{\lim\limits_{x \to \frac{\pi}{16}} (\sin(4x) + \sin(8x) + \sin(16x))}{\lim\limits_{x \to \frac{\pi}{16}} (\cos(4x) + \cos(8x) + \cos(16x))} \)
\( = \dfrac{\frac{\sqrt{2} + 2}{2}}{\frac{\sqrt{2} - 2}{2}} = \dfrac{\sqrt{2} + 2}{\sqrt{2} - 2} \)
Paydadaki ifadeyi eşleniği ile çarpıp rasyonel hale getirelim.
\( = \dfrac{(\sqrt{2} + 2)(\sqrt{2} + 2)}{(\sqrt{2} - 2)(\sqrt{2} + 2)} \)
\( = \dfrac{2 + 4\sqrt{2} + 4 }{2 - 4} \)
\( = -3 - 2\sqrt{2} \) bulunur.
\( \lim\limits_{x \to \frac{\pi}{2}} \dfrac{6x - \pi}{\cos^2{x} - \sin^3{x} + 2} \) limitinin değeri kaçtır?
Çözümü GösterÖnce pay ve paydadaki ifadelerin ayrı ayrı limitini bulalım.
Sinüs ve kosinüs fonksiyonları tüm reel sayılarda süreklidir. Sürekli fonksiyonlar arasındaki toplama, çıkarma, çarpma ve (payda sıfırdan farklı olmak koşuluyla) bölme işlemleri sonucunda oluşan fonksiyonlar da süreklidir.
Buna göre pay ve paydadaki ifadeler tüm reel sayılarda süreklidir ve doğrudan yerine koyma yöntemi ile limit değerlerini bulabiliriz.
\( \lim\limits_{x \to \frac{\pi}{2}} (6x - \pi) = 6 \cdot \dfrac{\pi}{2} - \pi = 2\pi \)
\( \lim\limits_{x \to \frac{\pi}{2}} (\cos^2{x} - \sin^3{x} + 2) = \cos^2{\frac{\pi}{2}} - \sin^3{\frac{\pi}{2}} + 2 \)
\( = 0^2 - 1^3 + 2 = 1 \)
Pay ve paydadaki ifadelerin limiti tanımlı ve paydadaki ifadenin limiti sıfırdan farklı olduğu için limit bölme kuralını kullanabiliriz.
\( \lim\limits_{x \to \frac{\pi}{2}} \dfrac{6x - \pi}{\cos^2{x} - \sin^3{x} + 2} = \dfrac{\lim\limits_{x \to \frac{\pi}{2}} (6x - \pi)}{\lim\limits_{x \to \frac{\pi}{2}} (\cos^2{x} - \sin^3{x} + 2)} \)
\( = \dfrac{2\pi}{1} = 2\pi \) bulunur.
\( \lim\limits_{x \to \frac{\pi}{4}} \dfrac{\sec{x}\cot^2{x}}{2\cos^2(2x) - 1} \) limitinin değeri kaçtır?
Çözümü GösterÖnce pay ve paydadaki ifadelerin ayrı ayrı limitini bulalım.
Kosinüs fonksiyonu tüm reel sayılarda, kotanjant fonksiyonu \( \{ k\pi, k \in \mathbb{Z} \} \) hariç, sekant fonksiyonu \( \{ \frac{\pi}{2} + k\pi, k \in \mathbb{Z} \} \) hariç tüm noktalarda süreklidir. Sürekli fonksiyonlar arasındaki toplama, çıkarma, çarpma ve (payda sıfırdan farklı olmak koşuluyla) bölme işlemleri sonucunda oluşan fonksiyonlar da süreklidir.
Buna göre pay ve paydadaki ifadeler tüm reel sayılarda süreklidir ve doğrudan yerine koyma yöntemi ile limit değerlerini bulabiliriz.
\( \lim\limits_{x \to \frac{\pi}{4}} (\sec{x}\cot^2{x}) = \sec{\frac{\pi}{4}}\cot^2{\frac{\pi}{4}} \)
\( = \sqrt{2} \cdot 1^2 = \sqrt{2} \)
\( \lim\limits_{x \to \frac{\pi}{4}} (2\cos^2(2x) - 1) = 2\cos^2(2 \cdot \frac{\pi}{4}) - 1 \)
\( = 0 - 1 = -1 \)
Pay ve paydadaki ifadelerin limiti tanımlı ve paydadaki ifadenin limiti sıfırdan farklı olduğu için limit bölme kuralını kullanabiliriz.
\( \lim\limits_{x \to \frac{\pi}{4}} \dfrac{\sec{x}\cot^2{x}}{2\cos^2(2x) - 1} = \dfrac{\lim\limits_{x \to \frac{\pi}{4}} (\sec{x}\cot^2{x})}{\lim\limits_{x \to \frac{\pi}{4}} (2\cos^2(2x) - 1)} \)
\( = \dfrac{\sqrt{2}}{-1} = -\sqrt{2} \) bulunur.
\( \lim\limits_{x \to \frac{\pi}{3}} \dfrac{\cos{x} + \sqrt{3}\cot{x}}{\sin{x}\tan{x}} \) limitinin değeri kaçtır?
Çözümü GösterÖnce pay ve paydadaki ifadelerin ayrı ayrı limitini bulalım.
Sinüs ve kosinüs fonksiyonları tüm reel sayılarda, tanjant fonksiyonu \( \{ \frac{\pi}{2} + k\pi, k \in \mathbb{Z} \} \) hariç, kotanjant fonksiyonu \( \{ k\pi, k \in \mathbb{Z} \} \) hariç tüm noktalarda süreklidir. Sürekli fonksiyonlar arasındaki toplama, çıkarma, çarpma ve (payda sıfırdan farklı olmak koşuluyla) bölme işlemleri sonucunda oluşan fonksiyonlar da süreklidir.
Buna göre pay ve paydadaki ifadeler tüm reel sayılarda süreklidir ve doğrudan yerine koyma yöntemi ile limit değerlerini bulabiliriz.
\( \lim\limits_{x \to \frac{\pi}{3}} (\cos{x} + \sqrt{3}\cot{x}) = \cos{\dfrac{\pi}{3}} + \sqrt{3}\cot{\dfrac{\pi}{3}} \)
\( = \dfrac{1}{2} + \sqrt{3} \cdot \dfrac{\sqrt{3}}{3} = \dfrac{3}{2} \)
\( \lim\limits_{x \to \frac{\pi}{3}} (\sin{x}\tan{x}) = \sin{\dfrac{\pi}{3}}\tan{\dfrac{\pi}{3}} \)
\( = \dfrac{\sqrt{3}}{2} \cdot \sqrt{3} = \dfrac{3}{2} \)
Pay ve paydadaki ifadelerin limiti tanımlı ve paydadaki ifadenin limiti sıfırdan farklı olduğu için limit bölme kuralını kullanabiliriz.
\( \lim\limits_{x \to \frac{\pi}{3}} \dfrac{\cos{x} + \sqrt{3}\cot{x}}{\sin{x}\tan{x}} = \dfrac{\lim\limits_{x \to \frac{\pi}{3}} (\cos{x} + \sqrt{3}\cot{x})}{\lim\limits_{x \to \frac{\pi}{3}} (\sin{x}\tan{x})} \)
\( = \dfrac{\frac{3}{2}}{\frac{3}{2}} = 1 \) bulunur.
\( \lim\limits_{x \to \frac{\pi}{6}} \left( \dfrac{\cos(2x)}{\sin{x}} + \tan(2x)\cot{x} \right) \) limitinin değeri kaçtır?
Çözümü GösterSinüs ve kosinüs fonksiyonları tüm reel sayılarda, tanjant fonksiyonu \( \{ \frac{\pi}{2} + k\pi, k \in \mathbb{Z} \} \) hariç, kotanjant fonksiyonu \( \{ k\pi, k \in \mathbb{Z} \} \) hariç tüm noktalarda süreklidir. Sürekli fonksiyonlar arasındaki toplama, çıkarma, çarpma ve (payda sıfırdan farklı olmak koşuluyla) bölme işlemleri sonucunda oluşan fonksiyonlar da süreklidir.
Buna göre pay ve paydadaki ifadeler tüm reel sayılarda süreklidir ve doğrudan yerine koyma yöntemi ile limit değerlerini bulabiliriz.
\( \lim\limits_{x \to \frac{\pi}{6}} \left( \dfrac{\cos(2x)}{\sin{x}} + \tan(2x)\cot{x} \right) = \dfrac{\cos(2 \cdot \frac{\pi}{6})}{\sin{\frac{\pi}{6}}} + \tan(2 \cdot \frac{\pi}{6})\cot{\frac{\pi}{6}} \)
\( = \dfrac{\frac{1}{2}}{\frac{1}{2}} + \sqrt{3} \cdot \sqrt{3} \)
\( = 1 + 3 = 4 \) bulunur.