Sıkıştırma teoremi ya da bir diğer adıyla sandviç teoremi, şu ana kadar öğrendiğimiz limit kural ve yöntemlerinin yeterli olmadığı bazı durumlarda bir fonksiyonun limitini bulmamızı sağlar.
Sıkıştırma teoremine göre, bir \( f \) fonksiyonunun \( x = a \) noktasını içeren bir aralıkta, bu noktadaki limit değerlerini birbirine eşit ve \( L \) olarak hesaplayabildiğimiz \( g \) ve \( h \) fonksiyonları arasında kaldığını gösterebiliyorsak, \( f \) fonksiyonunun bu noktadaki limiti de \( L \) olmak zorundadır.
Limit fonksiyonun \( x = a \) noktasındaki değeri ile ilgilenmediği için, sıkıştırma teoreminin bir koşulu olarak belirttiğimiz \( g(x) \le f(x) \le h(x) \) eşitsizliği \( x = a \) noktasında geçerli olmak zorunda değildir, önemli olan \( f(x) \) değerinin bu aralıkta \( x = a \) dışındaki noktalarda iki fonksiyonun arasında kalmasıdır.
Sıkıştırma teoremini grafiksel olarak aşağıdaki gibi gösterebiliriz. Bu grafikte \( g \) ve \( h \) fonksiyonları sırasıyla \( f \) fonksiyonunun üst ve alt sınırlarını oluşturmaktadır, dolayısıyla bu iki fonksiyonun bir noktadaki limitinin tanımlı ve eşit olduğunu biliyorsak, \( f \) fonksiyonunun da bu noktadaki limitinin bu değere eşit olması gerekmektedir.
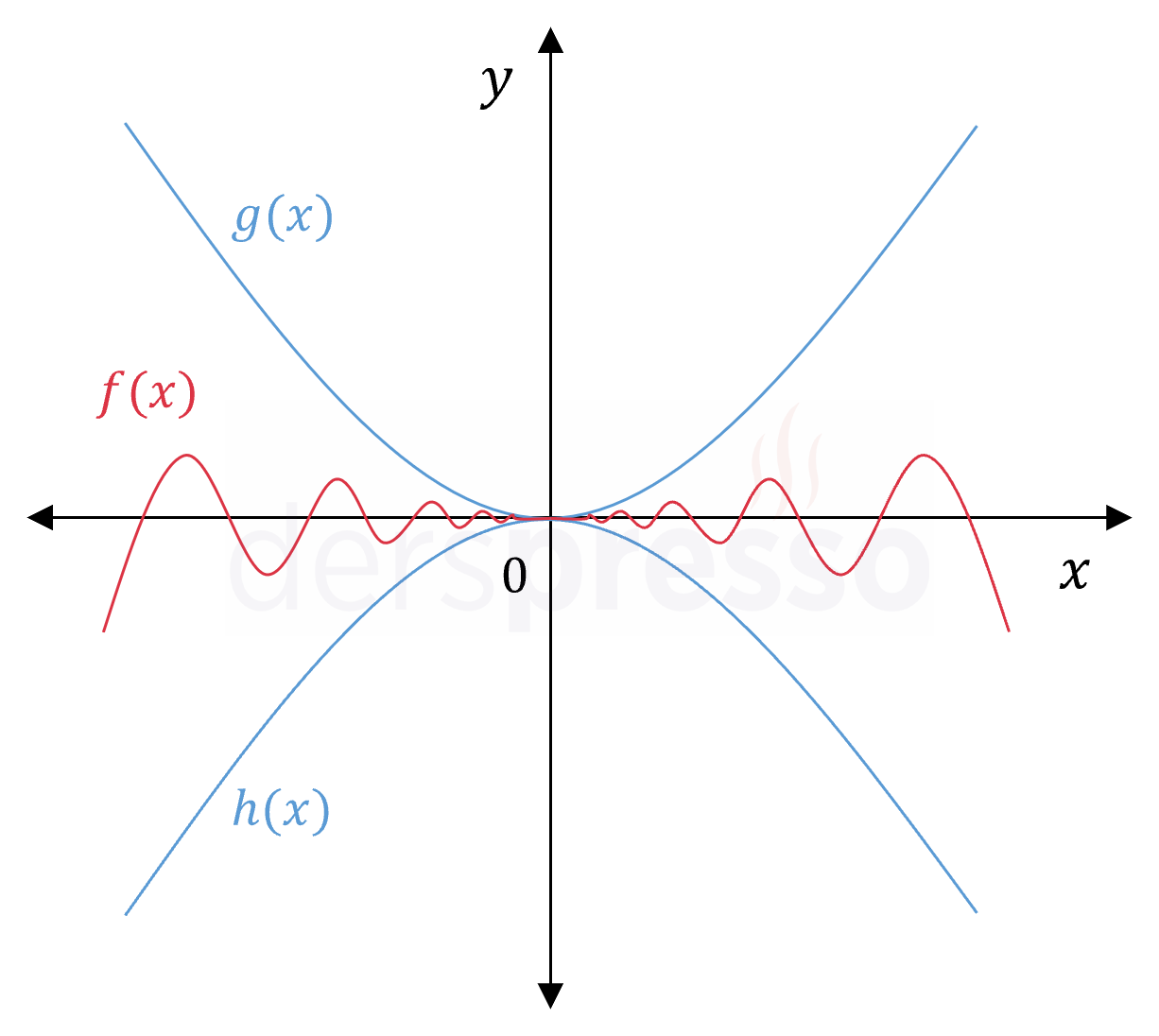
Sıkıştırma teoremi ile limit hesaplamaya bir örnek verelim.
ÖRNEK:
Aşağıdaki ifadenin limit değerini bulalım.
\( \lim_{x \to +\infty} \dfrac{\sin{x}}{x} \)
Önce sinüs fonksiyonunun değer aralığını yazalım.
\( \quad -1 \le \sin{x} \le 1 \)
Eşitsizliğin üç ifadesini de \( x \)'e bölelim. Hesapladığımız limitte \( x \) pozitif sonsuza gittiği için \( x \)'i pozitif bir değer olarak alabiliriz, dolayısıyla eşitsizlik işaretlerinin yönünü değiştirmemize gerek yoktur.
\( \quad \dfrac{-1}{x} \le \dfrac{\sin{x}}{x} \le \dfrac{1}{x} \)
Limitini bulmak istediğimiz ifadenin iki ayrı fonksiyonun arasında kaldığını görüyoruz. Bu iki fonksiyonun \( x \) pozitif sonsuza giderken limit değerlerine baktığımızda, \( \dfrac{-1}{x} \) ifadesinin negatif taraftan, \( \dfrac{1}{x} \) ifadesinin pozitif taraftan sıfıra yaklaştığını görebiliriz.
\( \quad \lim_{x \to +\infty} \dfrac{-1}{x} = \lim_{x \to +\infty} \dfrac{1}{x} = 0 \)
Dolayısıyla bizden istenen fonksiyonun limitinin de bu iki fonksiyonun limit değerlerinin arasında kalacağını, dolayısıyla sıfıra eşit olacağını söyleyebiliriz.
\( \quad \lim_{x \to +\infty} \dfrac{\sin{x}}{x} = 0 \)
SORU 1:
\( f \) fonksiyonunun grafiğinin tüm reel sayılarda \( g(x) = 2x \) grafiğinin üstünde ve \( h(x) = x^2 + 1 \) grafiğinin altında kaldığı biliniyor.
Buna göre \( \lim\limits_{x \to 1} f(x) \) limitinin sonucunu bulunuz.
Çözümü Göster
Dikkat edilirse soruda \( f \) fonksiyonunun tanımı verilmemiş, sadece grafiğinin tüm reel sayılarda \( g(x) \) ve \( h(x) \) grafikleri arasında kaldığı bilgisi verilmiştir.
\( g(x) \le f(x) \le h(x) \)
Eşitsizliğin taraflarının \( x \) 1'e giderken limitini alalım.
\( \lim\limits_{x \to 1} g(x) \le \lim\limits_{x \to 1} f(x) \le \lim\limits_{x \to 1} h(x) \)
\( g(x) \) ve \( h(x) \) fonksiyonlarının \( x = 1 \) noktasındaki limit değerlerini bulalım.
Her iki fonksiyonun da sürekli olduğunu bildiğimiz için doğrudan yerine koyma yöntemi ile limit değerlerini bulabiliriz.
\( \lim\limits_{x \to 1} g(x) = g(1) = 2(1) = 2 \)
\( \lim\limits_{x \to 1} h(x) = h(1) = 1^2 + 1 = 2 \)
\( 2 \le \lim\limits_{x \to 1} f(x) \le 2 \)
\( g(x) \) ve \( h(x) \) fonksiyonlarının bu noktadaki limit değerlerinin eşit olduğunu görüyoruz, bu yüzden sıkıştırma teoremine göre tüm reel sayılarda bu iki fonksiyonun arasında kalan \( f \) fonksiyonunun bu noktadaki limiti 2 olmak zorundadır.
\( \lim\limits_{x \to 1} f(x) = 2 \)
SORU 2:
\( \lim\limits_{x \to +\infty} \dfrac{\sin(5x)}{e^\frac{x}{4}} \) limitinin sonucunu bulunuz.
Çözümü Göster
Sinüs fonksiyonunun değer aralığını yazalım.
\( -1 \le \sin(5x) \le 1 \)
Eşitsizliğin taraflarını \( e^\frac{x}{4} \)'e bölelim.
\( e^\frac{x}{4} \) tüm reel sayılarda pozitif olduğu için eşitsizliğin yönü değişmez.
\( -\dfrac{1}{e^\frac{x}{4}} \le \dfrac{\sin(5x)}{e^\frac{x}{4}} \le \dfrac{1}{e^\frac{x}{4}} \)
Eşitsizliğin taraflarının \( x \) pozitif sonsuza giderken limitini alalım.
\( \lim\limits_{x \to +\infty} -\dfrac{1}{e^\frac{x}{4}} \le \lim\limits_{x \to +\infty} \dfrac{\sin(5x)}{e^\frac{x}{4}} \le \lim\limits_{x \to +\infty} \dfrac{1}{e^\frac{x}{4}} \)
Limitini bulmak istediğimiz ifadenin iki ayrı fonksiyonun arasında kaldığını görüyoruz. Bu iki fonksiyonun \( x \) pozitif sonsuza giderken limit değerlerine baktığımızda, her iki fonksiyonun sıfıra yaklaştığını görebiliriz.
\( \lim\limits_{x \to +\infty} -\dfrac{1}{e^\frac{x}{4}} = \lim\limits_{x \to +\infty} \dfrac{1}{e^\frac{x}{4}} = 0 \)
\( 0 \le \lim\limits_{x \to +\infty} \dfrac{\sin(5x)}{e^\frac{x}{4}} \le 0 \)
Sıkıştırma teoremine göre, verilen fonksiyonun limitinin de bu iki fonksiyonun limit değerlerinin arasında kalacağını, dolayısıyla sıfıra eşit olacağını söyleyebiliriz.
\( \lim\limits_{x \to +\infty} \dfrac{\sin(5x)}{e^\frac{x}{4}} = 0 \) bulunur.
SORU 3:
\( \lim\limits_{x \to +\infty} \dfrac{5 + e^{-x}\sin{x}}{e^{-x} + 10} \) limitinin sonucunu bulunuz.
Çözümü Göster
\( \lim\limits_{x \to +\infty} \dfrac{5 + e^{-x}\sin{x}}{e^{-x} + 10} \)
Aşağıda göstereceğimiz üzere, payın ve paydanın limiti ayrı ayrı birer reel sayı olarak tanımlı olduğu için ifadeyi iki limitin bölümü şeklinde yazabiliriz.
\( = \dfrac{\lim\limits_{x \to +\infty} (5 + e^{-x}\sin{x})}{\lim\limits_{x \to +\infty} (e^{-x} + 10)} \)
Paydaki limit ifadesinin değerini sıkıştırma teoremi ile bulalım.
Sinüs fonksiyonunun değer aralığını yazalım.
\( -1 \le \sin{x} \le 1 \)
Eşitsizliğin taraflarını \( e^{-x} \) ile çarpalım.
\( -e^{-x} \le e^{-x}\sin{x} \le e^{-x} \)
Eşitsizliğin taraflarına 5 ekleyelim.
\( 5 - e^{-x} \le 5 + e^{-x}\sin{x} \le 5 + e^{-x} \)
Eşitsizliğin taraflarının \( x \) pozitif sonsuza giderken limitini alalım.
\( \lim\limits_{x \to +\infty} (5 - e^{-x}) \le \lim\limits_{x \to +\infty} (5 + e^{-x}\sin{x}) \le \lim\limits_{x \to +\infty} (5 + e^{-x}) \)
Limitini bulmak istediğimiz ifadenin iki ayrı fonksiyonun arasında kaldığını görüyoruz. Bu iki fonksiyonun \( x \) pozitif sonsuza giderken limit değerlerine baktığımızda, her iki fonksiyonun 5 değerine yaklaştığını görebiliriz.
\( \lim\limits_{x \to +\infty} (5 - e^{-x}) = 5 \)
\( \lim\limits_{x \to +\infty} (5 + e^{-x}) = 5 \)
\( 5 \le \lim\limits_{x \to +\infty} (5 + e^{-x}\sin{x}) \le 5 \)
Sıkıştırma teoremine göre, paydaki ifadenin limitinin de bu iki fonksiyonun limit değerlerinin arasında kalacağını, dolayısıyla 5'e eşit olacağını söyleyebiliriz.
\( \lim\limits_{x \to +\infty} (5 + e^{-x}\sin{x}) = 5 \)
Paydadaki limit ifadesinin değerini bulalım.
\( x \to +\infty \) iken \( e^{-x} \to 0 \) olur.
\( \lim\limits_{x \to +\infty} (e^{-x} + 10) = 10 \)
Tüm ifadenin değerini bulalım.
\( \dfrac{\lim\limits_{x \to +\infty} (5 + e^{-x}\sin{x})}{\lim\limits_{x \to +\infty} (e^{-x} + 10)} \)
\( = \dfrac{5}{10} = \dfrac{1}{2} \) bulunur.
SORU 4:
\( \lim\limits_{x \to 0} (x^6\cos{\frac{4}{x^2}}) \) limitinin sonucunu bulunuz.
Çözümü Göster
Kosinüs fonksiyonunun değer aralığını yazalım.
\( -1 \le \cos{\frac{4}{x^2}} \le 1 \)
Eşitsizliğin taraflarını \( x^6 \) ile çarpalım.
\( x^6 \) pozitif bir sayı olduğu için eşitsizliğin yönü değişmez.
\( -x^6 \le x^6\cos{\frac{4}{x^2}} \le x^6 \)
Eşitsizliğin taraflarının \( x \) sıfıra giderken limitini alalım.
\( \lim\limits_{x \to 0} (-x^6) \le \lim\limits_{x \to 0} (x^6\cos{\frac{4}{x^2}}) \le \lim\limits_{x \to 0} x^6 \)
Limitini bulmak istediğimiz ifadenin iki ayrı fonksiyonun arasında kaldığını görüyoruz. Bu iki fonksiyonun \( x \) sıfıra giderken limit değerlerine baktığımızda, her iki fonksiyonun sıfıra yaklaştığını görebiliriz.
\( \lim\limits_{x \to 0} (-x^6) = \lim\limits_{x \to 0} {x^6} = 0 \)
\( 0 \le \lim\limits_{x \to 0} (x^6\cos{\frac{4}{x^2}}) \le 0 \)
Sıkıştırma teoremine göre, verilen ifadenin limitinin de bu iki fonksiyonun limit değerlerinin arasında kalacağını, dolayısıyla sıfıra eşit olacağını söyleyebiliriz.
\( \lim\limits_{x \to 0} (x^6\cos{\frac{4}{x^2}}) = 0 \)
SORU 5:
\( \lim\limits_{x \to 0} \dfrac{3x^4\sin(\frac{1}{x^3})}{\sin(2x)} \) limitinin sonucunu bulunuz.
Çözümü Göster
Limit ifadesini düzenleyelim.
\( \lim\limits_{x \to 0} (\dfrac{3x}{\sin(2x)} \cdot x^3\sin(\frac{1}{x^3})) \)
Aşağıda göstereceğimiz üzere, iki çarpanın limiti ayrı ayrı birer reel sayı olarak tanımlı olduğu için ifadeyi iki limitin çarpımı şeklinde yazabiliriz.
\( = \underbrace{\lim\limits_{x \to 0} \dfrac{3x}{\sin(2x)}}_{L_1} \cdot \underbrace{\lim\limits_{x \to 0} (x^3\sin(\frac{1}{x^3}))}_{L_2} \)
Birinci çarpan için ispatıyla birlikte verdiğimiz trigonometrik limit kurallarını kullanalım.
\( \lim\limits_{x \to 0} \dfrac{\sin(ax)}{bx} = \dfrac{a}{b} \)
\( L_1 = \lim\limits_{x \to 0} \dfrac{3x}{\sin(2x)} = \dfrac{3}{2} \)
İkinci çarpan için sıkıştırma teoremini kullanalım.
Sinüs fonksiyonunun değer aralığını yazalım.
\( -1 \le \sin(\frac{1}{x^3}) \le 1 \)
Eşitsizliğin taraflarını \( x^3 \) ile çarpalım.
\( -x^3 \le x^3\sin(\frac{1}{x^3}) \le x^3 \)
Eşitsizliğin taraflarının \( x \) sıfıra giderken limitini alalım.
\( \lim\limits_{x \to 0} (-x^3) \le \lim\limits_{x \to 0} (x^3\sin(\frac{1}{x^3})) \le \lim\limits_{x \to 0} x^3 \)
Limitini bulmak istediğimiz ifadenin iki ayrı fonksiyonun arasında kaldığını görüyoruz. Bu iki fonksiyonun \( x \) sıfıra giderken limit değerlerine baktığımızda, her iki fonksiyonun sıfıra yaklaştığını görebiliriz.
\( \lim\limits_{x \to 0} (-x^3) = \lim\limits_{x \to 0} x^3 = 0 \)
\( 0 \le \lim\limits_{x \to 0} x^3\sin(\frac{1}{x^3}) \le 0 \)
Sıkıştırma teoremine göre, verilen ifadenin limitinin de bu iki fonksiyonun limit değerlerinin arasında kalacağını, dolayısıyla sıfıra eşit olacağını söyleyebiliriz.
\( L_2 = \lim\limits_{x \to 0} (x^3\sin(\frac{1}{x^3})) = 0 \)
\( L_1 \cdot L_2 = \dfrac{3}{2} \cdot 0 = 0 \) bulunur.
SORU 6:
\( \abs{f(x) - 3} \le x^3 \) eşitsizliği veriliyor.
\( \lim\limits_{x \to 0} f(x) \) limitinin sonucunu bulunuz.
Çözümü Göster
Verilen eşitsizliği mutlak değerden kurtaralım.
\( -x^3 \le f(x) - 3 \le x^3 \)
\( \underbrace{-x^3 + 3}_{g(x)} \le f(x) \le \underbrace{x^3 + 3}_{h(x)} \)
\( g(x) \le f(x) \le h(x) \)
Eşitsizliğin taraflarının \( x \) sıfıra giderken limitini alalım.
\( \lim\limits_{x \to 0} g(x) \le \lim\limits_{x \to 0} f(x) \le \lim\limits_{x \to 0} h(x) \)
Limitini bulmak istediğimiz ifadenin iki ayrı fonksiyonun arasında kaldığını görüyoruz. Bu iki fonksiyonun \( x \) sıfıra giderken limit değerlerine baktığımızda, her iki fonksiyonun 3 değerine yaklaştığını görebiliriz.
\( \lim\limits_{x \to 0} g(x) = \lim\limits_{x \to 0} (-x^3 + 3) \)
\( = -0^3 + 3 = 3 \)
\( \lim\limits_{x \to 0} h(x) = \lim\limits_{x \to 0} (x^3 + 3) \)
\( = 0^3 + 3 = 3 \)
\( 3 \le \lim\limits_{x \to 0} f(x) \le 3 \)
Sıkıştırma teoremine göre, verilen fonksiyonun limitinin de bu iki fonksiyonun limit değerlerinin arasında kalacağını, dolayısıyla 3'e eşit olacağını söyleyebiliriz.
\( \lim\limits_{x \to 0} f(x) = 3 \) bulunur.
SORU 7:
\( 5 \le f(x) \le x^3 - 5x - 7 \) olduğuna göre,
\( \lim\limits_{x \to 3} f(x) \) limitinin sonucunu bulunuz.
Çözümü Göster
\( 5 \le f(x) \le x^3 - 5x - 7 \)
Eşitsizliğin taraflarının \( x \) 3'e giderken limitini alalım.
\( \lim\limits_{x \to 3} 5 \le \lim\limits_{x \to 3} f(x) \le \lim\limits_{x \to 3} (x^3 - 5x - 7) \)
Limitini bulmak istediğimiz ifadenin iki ayrı fonksiyonun arasında kaldığını görüyoruz. Bu iki fonksiyonun \( x \) 3'e giderken limit değerlerine baktığımızda, her iki fonksiyonun 5 değerine yaklaştığını görebiliriz.
\( \lim\limits_{x \to 3} 5 = 5 \)
\( \lim\limits_{x \to 3} (x^3 - 5x - 7) = 3^3 - 5(3) - 7 = 5 \)
\( 5 \le \lim\limits_{x \to 3} f(x) \le 5 \)
Sıkıştırma teoremine göre, verilen ifadenin limitinin de bu iki fonksiyonun limit değerlerinin arasında kalacağını, dolayısıyla 5'e eşit olacağını söyleyebiliriz.
\( \lim\limits_{x \to 3} f(x) = 5 \)
