Limit Kuralları
Bu bölümde çoğu fonksiyonun limitini bulmakta kullanabileğimiz limit kurallarından bahsedeceğiz. Bu kuralların tümünün ispatları limitin epsilon-delta tanımına dayanmaktadır.
Temel Limit Kuralları
Fonksiyonların limitini bulurken kullanılan en temel iki kural birim ve sabit fonksiyonların limitidir.
Birim Fonksiyonun Limiti
Birim fonksiyonun her noktadaki limiti fonksiyonun o noktadaki değerine eşittir.
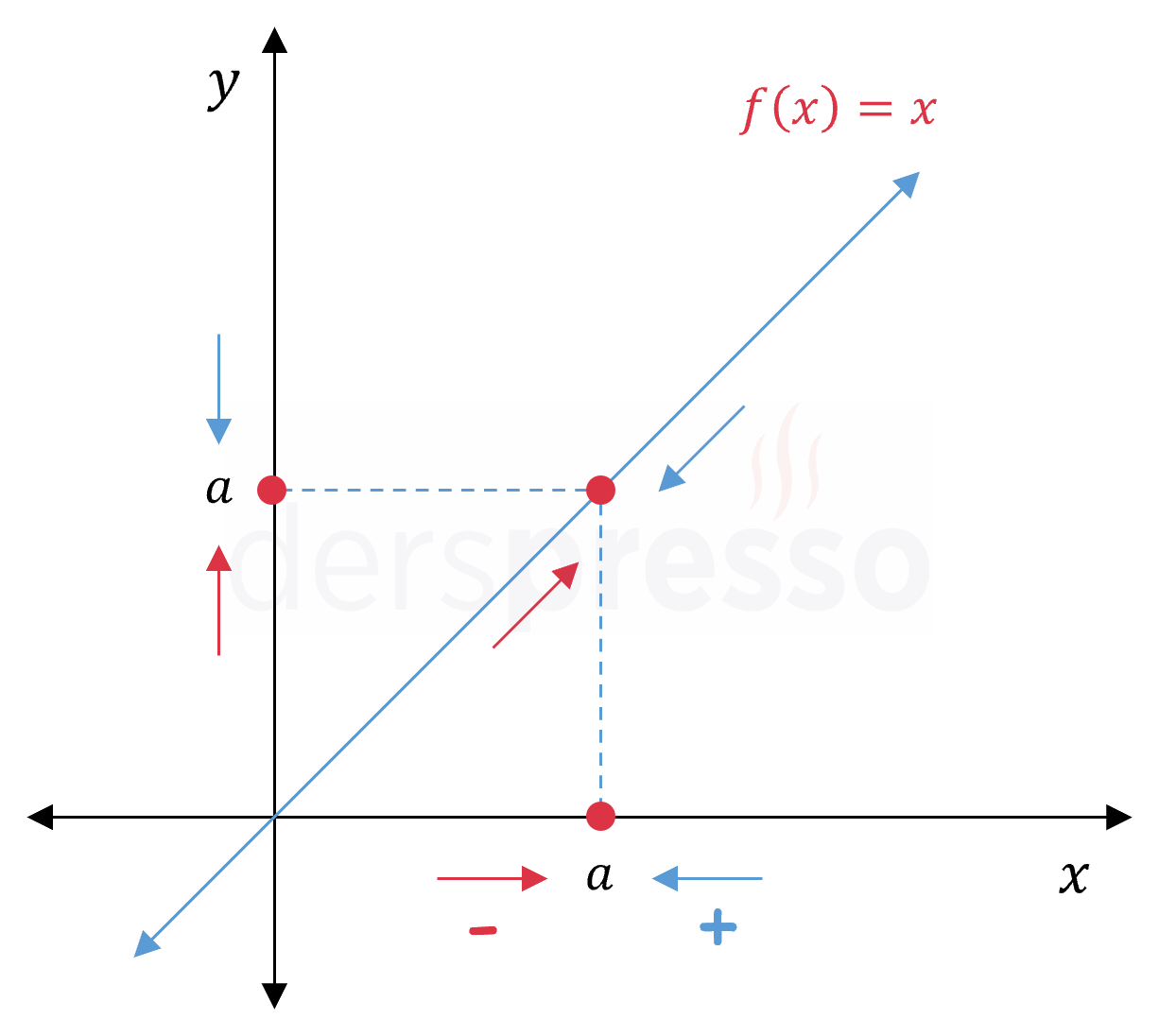
\( \lim\limits_{x \to a} {x} = a \)
\( \lim\limits_{x \to 3} {x} = 3 \)
İSPATI GÖSTER
Adım 1: Tanım
\( \lim\limits_{x \to a} {f(x)} = L \)
Yukarıdaki limit, her \( \varepsilon \gt 0 \) değeri için aşağıdaki koşullu önermeyi sağlayan bir \( \delta \gt 0 \) değeri bulunabiliyorsa mevcuttur ve \( L \) değerine eşittir.
\( 0 \lt \abs{x - a} \lt \delta \Longrightarrow \abs{f(x) - L} \lt \varepsilon \)
Bu tanımı kullanarak aşağıdaki limitin doğruluğunu gösterelim.
\( \lim\limits_{x \to a} {x} = a \)
Bu limit ifadesindeki bilgileri önermede yerine koyalım.
\( 0 \lt \abs{x - a} \lt \delta \Longrightarrow \abs{x - a} \lt \varepsilon \)
Adım 2: İspat
Herhangi bir \( \varepsilon \gt 0 \) verilmiş olsun.
\( \delta = \varepsilon \) olarak seçelim.
\( 0 \lt \abs{x - a} \lt \delta \) olarak kabul edelim.
\( \abs{x - a} \lt \delta = \varepsilon \)
Verilen limitin doğruluğunu epsilon-delta tanımını kullanarak göstermiş olduk.
\( \lim\limits_{x \to a} {x} = a \)
Sabit Fonksiyonun Limiti
Sabit fonksiyonun her noktadaki limiti fonksiyonun sabit değerine eşittir.
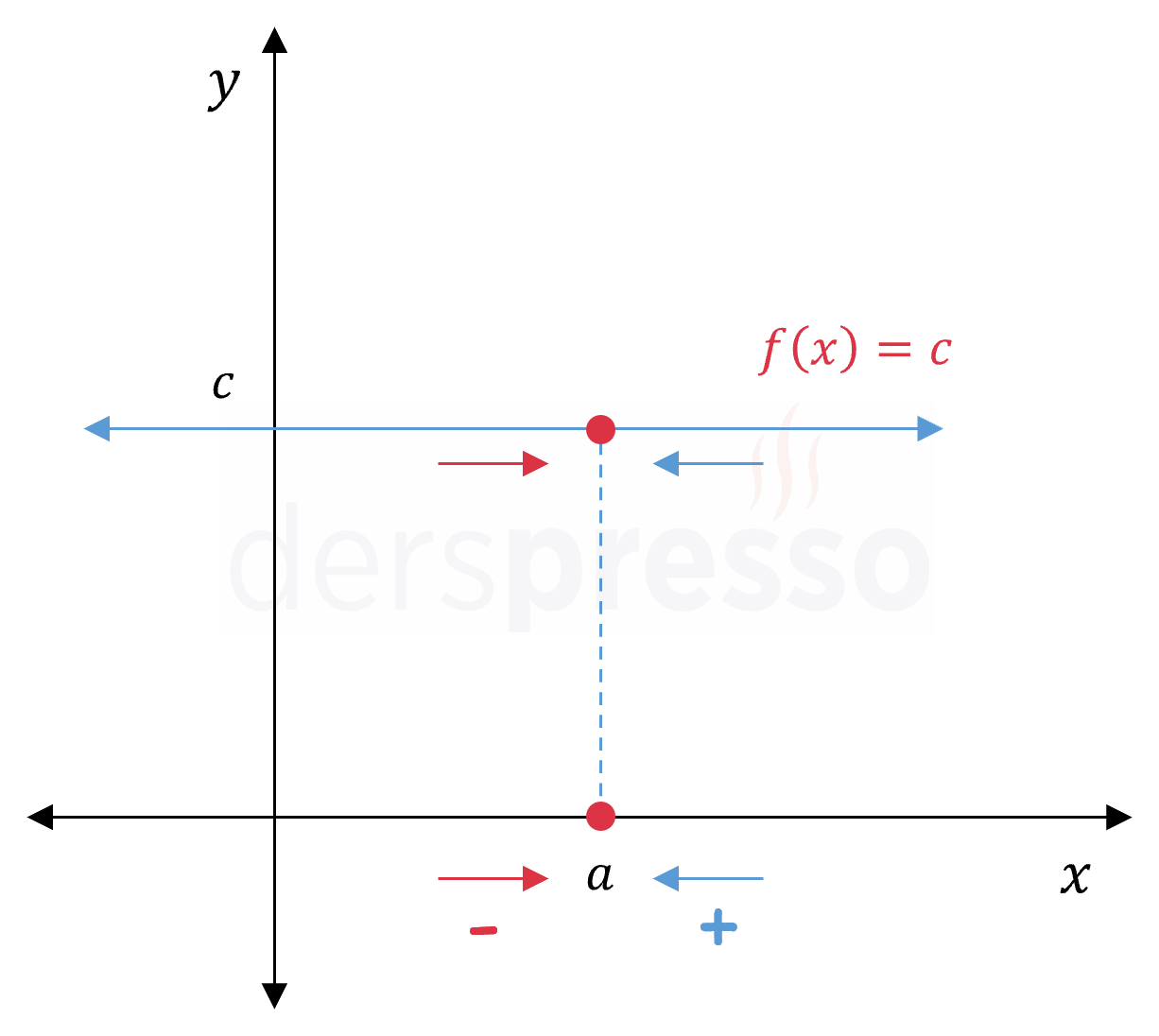
\( c \in \mathbb{R} \) olmak üzere,
\( \lim\limits_{x \to a} {c} = c \)
\( \lim\limits_{x \to 3} {5} = 5 \)
İSPATI GÖSTER
Adım 1: Tanım
\( \lim\limits_{x \to a} {f(x)} = L \)
Yukarıdaki limit, her \( \varepsilon \gt 0 \) değeri için aşağıdaki koşullu önermeyi sağlayan bir \( \delta \gt 0 \) değeri bulunabiliyorsa mevcuttur ve \( L \) değerine eşittir.
\( 0 \lt \abs{x - a} \lt \delta \Longrightarrow \abs{f(x) - L} \lt \varepsilon \)
Bu tanımı kullanarak aşağıdaki limitin doğruluğunu gösterelim.
\( c \in \mathbb{R} \) olmak üzere,
\( \lim\limits_{x \to a} {c} = c \)
Bu limit ifadesindeki bilgileri önermede yerine koyalım.
\( 0 \lt \abs{x - a} \lt \delta \Longrightarrow \abs{c - c} \lt \varepsilon \)
\( 0 \lt \abs{x - a} \lt \delta \Longrightarrow 0 \lt \varepsilon \)
Adım 2: İspat
Herhangi bir \( \varepsilon \gt 0 \) verilmiş olsun.
\( \varepsilon \gt 0 \) olduğu için önermenin sağ tarafı her zaman sağlanır.
Verilen limitin doğruluğunu epsilon-delta tanımını kullanarak göstermiş olduk.
\( \lim\limits_{x \to a} {c} = c \)
Limit İşlem Kuralları
\( f \) ve \( g \), bir \( a \) noktasında limitleri birer reel sayı olarak tanımlı iki fonksiyon olsun.
\( L, M \in \mathbb{R} \) olmak üzere,
\( \lim\limits_{x \to a} {f(x)} = L \)
\( \lim\limits_{x \to a} {g(x)} = M \)
Bu iki fonksiyon arasındaki işlemlerin sonucu olan fonksiyonların limit hesaplamalarında aşağıdaki kurallar geçerlidir. Fonksiyonlardan herhangi birinin limitinin tanımsız olduğu durumlarda bu kurallar geçerli olmayacaktır.
Sabit Sayı İle Çarpma
Bir fonksiyonun sabit bir sayı ile çarpımının limiti fonksiyonun limitinin sabit sayı ile çarpımına eşittir.
\( c \in \mathbb{R} \) olmak üzere,
\( \lim\limits_{x \to a} [cf(x)] = c\lim\limits_{x \to a} {f(x)} = cL \)
\( \lim\limits_{x \to 5} (3x) = 3\lim\limits_{x \to 5} {x} = 3 \cdot 5 = 15 \)
\( \lim\limits_{x \to -2} (-5x) = -5\lim\limits_{x \to -2} {x} = -5 \cdot (-2) = 10 \)
İSPATI GÖSTER
\( c = 0 \) olduğu durumda limit ifadesi aşağıdaki formda olur.
\( \lim\limits_{x \to a} [0f(x)] = 0L = 0 \)
Bu durumda ifade sabit fonksiyona dönüştüğü için, yukarıda paylaştığımız sabit fonksiyonun limitinin ispatı kullanılabilir.
Aşağıda \( c \ne 0 \) olduğu durum için ispatı vereceğiz.
Adım 1: Tanım
\( \lim\limits_{x \to a} {f(x)} = L \)
Yukarıdaki limit, her \( \varepsilon \gt 0 \) değeri için aşağıdaki koşullu önermeyi sağlayan bir \( \delta \gt 0 \) değeri bulunabiliyorsa mevcuttur ve \( L \) değerine eşittir.
\( 0 \lt \abs{x - a} \lt \delta \Longrightarrow \abs{f(x) - L} \lt \varepsilon \)
Bu tanımı kullanarak aşağıdaki limitin doğruluğunu gösterelim.
\( c \in \mathbb{R} \) olmak üzere,
\( \lim\limits_{x \to a} [cf(x)] = cL \)
Bu limit ifadesindeki bilgileri önermede yerine koyalım.
\( 0 \lt \abs{x - a} \lt \delta \Longrightarrow \abs{cf(x) - cL} \lt \varepsilon \)
Adım 2: İspat
\( \lim\limits_{x \to a} {f(x)} = L \)
Yukarıdaki limitin tanımlı olduğu bilindiğine göre, her \( \varepsilon \gt 0 \) değeri için aşağıdaki önermeyi sağlayan bir \( \delta \gt 0 \) değeri bulunur.
\( 0 \lt \abs{x - a} \lt \delta \Longrightarrow \abs{f(x) - L} \lt \varepsilon \)
Bu önerme her \( \varepsilon \gt 0 \) değeri için geçerli olduğu için, aşağıdaki şekilde tanımlayacağımız pozitif \( \varepsilon' \) değeri için de geçerli olur.
\( \varepsilon' = \dfrac{\varepsilon}{\abs{c}} \)
Buna göre, her \( \varepsilon' = \frac{\varepsilon}{\abs{c}} \gt 0 \) değeri için aşağıdaki önermeyi sağlayan bir \( \delta' \gt 0 \) değeri bulunur.
\( 0 \lt \abs{x - a} \lt \delta' \Longrightarrow \abs{f(x) - L} \lt \varepsilon' = \dfrac{\varepsilon}{\abs{c}} \)
Eşitsizliğin taraflarını \( \abs{c} \) ile çarpalım.
\( \abs{c}\abs{f(x) - L} \lt \varepsilon \)
\( \abs{c(f(x) - L)} \lt \varepsilon \)
\( \abs{cf(x) - cL} \lt \varepsilon \)
Verilen limitin doğruluğunu epsilon-delta tanımını kullanarak göstermiş olduk.
\( \lim\limits_{x \to a} [cf(x)] = cL \)
Toplama ve Çıkarma
İki fonksiyonun toplamının/farkının limiti fonksiyonların limitlerinin toplamına/farkına eşittir.
\( \lim\limits_{x \to a} [f(x) + g(x)] = \lim\limits_{x \to a} {f(x)} + \lim\limits_{x \to a} {g(x)} = L + M \)
\( \lim\limits_{x \to a} [f(x) - g(x)] = \lim\limits_{x \to a} {f(x)} - \lim\limits_{x \to a} {g(x)} = L - M \)
\( \lim\limits_{x \to 2} (2x + 5) = 2\lim\limits_{x \to 2} {x} + \lim\limits_{x \to 2} {5} = 2 \cdot 2 + 5 = 9 \)
İSPATI GÖSTER
Adım 1: Tanım
\( \lim\limits_{x \to a} {f(x)} = L \)
Yukarıdaki limit, her \( \varepsilon \gt 0 \) değeri için aşağıdaki koşullu önermeyi sağlayan bir \( \delta \gt 0 \) değeri bulunabiliyorsa mevcuttur ve \( L \) değerine eşittir.
\( 0 \lt \abs{x - a} \lt \delta \Longrightarrow \abs{f(x) - L} \lt \varepsilon \)
Bu tanımı kullanarak aşağıdaki limitin doğruluğunu gösterelim.
\( \lim\limits_{x \to a} {f(x)} = L \) ve
\( \lim\limits_{x \to a} {g(x)} = M \) olmak üzere,
\( \lim\limits_{x \to a} [f(x) + g(x)] = L + M \)
Bu limit ifadesindeki bilgileri önermede yerine koyalım.
\( 0 \lt \abs{x - a} \lt \delta \Longrightarrow \abs{(f(x) + g(x)) - (L + M)} \lt \varepsilon \)
Adım 2: İspat
\( \lim\limits_{x \to a} {f(x)} = L \)
Yukarıdaki limitin tanımlı olduğu bilindiğine göre, her \( \varepsilon_1 = \frac{\varepsilon}{2} \gt 0 \) değeri için aşağıdaki önermeyi sağlayan bir \( \delta_1 \gt 0 \) değeri bulunur.
\( 0 \lt \abs{x - a} \lt \delta_1 \Longrightarrow \abs{f(x) - L} \lt \dfrac{\varepsilon}{2} \)
\( \lim\limits_{x \to a} {g(x)} = M \)
Yukarıdaki limitin tanımlı olduğu bilindiğine göre, her \( \varepsilon_2 = \frac{\varepsilon}{2} \gt 0 \) değeri için aşağıdaki önermeyi sağlayan bir \( \delta_2 \gt 0 \) değeri bulunur.
\( 0 \lt \abs{x - a} \lt \delta_2 \Longrightarrow \abs{g(x) - M} \lt \dfrac{\varepsilon}{2} \)
Bu önermeler her \( \varepsilon \gt 0 \) değeri için geçerli olduğu için, yukarıda tanımladığımız şekilde \( \frac{\varepsilon}{2} \gt 0 \) değerleri için de geçerli olur.
Aşağıdaki gibi bir \( \delta \) değeri tanımlayalım. Bu değeri \( \delta_1 \) ve \( \delta_2 \) değerlerinin küçüğü olarak tanımlamamızın sebebi, her iki fonksiyon için yazdığımız koşullu önermeleri birlikte sağlayacak bir değer olmasıdır.
\( \delta = \min(\delta_1, \delta_2) \gt 0 \)
\( 0 \lt \abs{x - a} \lt \delta = \min(\delta_1, \delta_2) \)
Aşağıdaki iki eşitsizliği taraf tarafa toplayalım.
\( \abs{f(x) - L} \lt \dfrac{\varepsilon}{2} \)
\( \abs{g(x) - M} \lt \dfrac{\varepsilon}{2} \)
\( \abs{f(x) - L} + \abs{g(x) - M} \lt \dfrac{\varepsilon}{2} + \dfrac{\varepsilon}{2} \)
Üçgen eşitsizliğine göre, iki sayının toplamının mutlak değeri sayıların mutlak değerlerinin toplamından büyük olamaz.
\( \abs{(f(x) - L) + (g(x) - M)} \le \abs{f(x) - L} + \abs{g(x) - M} \lt \varepsilon \)
Mutlak değer içini düzenleyelim.
\( \abs{(f(x) + g(x)) - (L + M)} \lt \varepsilon \)
Elde ettiğimiz koşullu önermeyi birlikte yazalım.
\( 0 \lt \abs{x - a} \lt \delta \Longrightarrow \abs{(f(x) + g(x)) - (L + M)} \lt \varepsilon \)
Verilen limitin doğruluğunu epsilon-delta tanımını kullanarak göstermiş olduk.
\( \lim\limits_{x \to a} [f(x) + g(x)] = L + M \)
Çarpma
İki fonksiyonun birbiriyle çarpımının limiti fonksiyonların limitlerinin çarpımına eşittir.
\( \lim\limits_{x \to a} [f(x) \cdot g(x)] = \lim\limits_{x \to a} {f(x)} \cdot \lim\limits_{x \to a} {g(x)} = L \cdot M \)
\( \lim\limits_{x \to 4} (x \cdot x) = \lim\limits_{x \to 4} {x} \cdot \lim\limits_{x \to 4} {x} = 4 \cdot 4 = 16 \)
Bölme
İki fonksiyonun birbirine bölümünün limiti fonksiyonların limitlerinin birbirine bölümüne eşittir.
\( M \ne 0 \) olmak üzere,
\( \lim\limits_{x \to a} \dfrac{f(x)}{g(x)} = \dfrac{\lim\limits_{x \to a} {f(x)}}{\lim\limits_{x \to a} {g(x)}} = \dfrac{L}{M} \)
\( \lim\limits_{x \to -2} \dfrac{6}{x} = \dfrac{\lim\limits_{x \to -2} 6}{\lim\limits_{x \to -2} {x}} = \dfrac{6}{-2} = -3 \)
Tanımda belirtildiği üzere, bölen fonksiyonunun limitinin sıfır olduğu durumda bu kural kullanılamaz.
Üslü İfadeler
Bir fonksiyonun bir sabit sayı kuvvetinin limiti fonksiyonun limitinin kuvvetine eşittir.
\( n \in \mathbb{Z} \) olmak üzere,
\( \lim\limits_{x \to a} [f(x)]^n = [\lim\limits_{x \to a} {f(x)}]^n = L^n \)
\( \lim\limits_{x \to a} {x^n} = [\lim\limits_{x \to a} {x}]^n = a^n \)
\( \lim\limits_{x \to 3} {x^4} = (\lim\limits_{x \to 3} {x})^4 = 3^4 = 81 \)
Köklü İfadeler
Bir fonksiyonun \( n \). dereceden kökünün limiti fonksiyonun limitinin \( n \). dereceden köküne eşittir.
\( n \in \mathbb{Z^+}, \quad n \ge 2 \),
\( n \) tek sayı ya da
\( n \) çift sayı ve \( L \ge 0 \) olmak üzere,
\( \lim\limits_{x \to a} {\sqrt[n]{x}} = \sqrt[n]{\lim\limits_{x \to a} {x}} = \sqrt[n]{a} \)
\( \lim\limits_{x \to 64} {\sqrt[3]{x}} = \sqrt[3]{\lim\limits_{x \to 64} {x}} = \sqrt[3]{64} = 4 \)
Yukarıda verilen limit kuralları çok terimli fonksiyonlara tekrarlı bir şekilde uygulanarak aşağıdaki sorulardakine benzer pek çok fonksiyonun limiti hesaplanabilir.
\( \lim\limits_{x \to 2} (2x^3 - 3x^2 + 5x - 8) \) limit değerini bulunuz.
Çözümü GösterParantez içindeki ifadeye adım adım limit kurallarını uygulayarak limit değerini hesaplayalım.
\( \lim\limits_{x \to 2} (2x^3 - 3x^2 + 5x - 8) = L \)
İlk adımda toplama ve çıkarma kurallarını uygulayalım ve limiti her terime dağıtalım.
\( L = \lim\limits_{x \to 2} {2x^3} - \lim\limits_{x \to 2} {3x^2} + \lim\limits_{x \to 2} {5x} - \lim\limits_{x \to 2} {8} \)
Sonra sabit sayı ile çarpma kuralını uygulayarak limit içindeki katsayıları limit dışına alalım.
\( L = 2\lim\limits_{x \to 2} {x^3} - 3\lim\limits_{x \to 2} {x^2} + 5\lim\limits_{x \to 2} {x} - \lim\limits_{x \to 2} {8} \)
Son olarak üs alma kuralını uygulayalım ve üslü ifadelerin üssünü limit dışına alalım.
\( L = 2(\lim\limits_{x \to 2} {x})^3 - 3(\lim\limits_{x \to 2} {x})^2 + 5(\lim\limits_{x \to 2} {x}) - \lim\limits_{x \to 2} {8} \)
Limit ifadeleri içinde sadece temel limit kuralları olarak adlandırdığımız birim ve sabit fonksiyonların kaldığını görebiliriz. Bu limit ifadeleri için limit değerlerini aşağıdaki gibi hesaplayabiliriz.
\( \lim\limits_{x \to 2} {x} = 2 \)
\( \lim\limits_{x \to 2} {8} = 8 \)
\( L = 2(2)^3 - 3(2)^2 + 5(2) - 8 = 6 \)
\( \lim\limits_{x \to 1} {\dfrac{4x^2 + 2x + 3}{2x^2 + 1}} \) limit değerini bulunuz.
Çözümü GösterAynı limit kurallarını bu sefer bölme kuralını da ekleyerek fonksiyona uygulayalım.
\( \lim\limits_{x \to 1} {\dfrac{4x^2 + 2x + 3}{2x^2 + 1}} = L \)
İlk adımda bölme, toplama ve çıkarma kurallarını uygulayalım ve limiti pay ve paydadaki terimlere dağıtalım.
\( L = \dfrac{\lim\limits_{x \to 1} {4x^2} + \lim\limits_{x \to 1} {2x} + \lim\limits_{x \to 1} {3}}{\lim\limits_{x \to 1} {2x^2} + \lim\limits_{x \to 1} {1}} \)
Sonra sabit sayı ile çarpma kuralını uygulayarak limit içindeki katsayıları limit dışına alalım.
\( L = \dfrac{4\lim\limits_{x \to 1} {x^2} + 2\lim\limits_{x \to 1} {x} + \lim\limits_{x \to 1} {3}}{2\lim\limits_{x \to 1} {x^2} + \lim\limits_{x \to 1} {1}} \)
Son olarak üs alma kuralını uygulayalım ve üslü ifadelerin üssünü limit dışına alalım.
\( L = \dfrac{4(\lim\limits_{x \to 1} {x})^2 + 2\lim\limits_{x \to 1} {x} + \lim\limits_{x \to 1} {3}}{2(\lim\limits_{x \to 1} {x})^2 + \lim\limits_{x \to 1} {1}} \)
Limit ifadeleri içinde sadece temel limit kuralları olarak adlandırdığımız birim ve sabit fonksiyonların kaldığını görebiliriz. Bu limit ifadeleri için limit değerlerini aşağıdaki gibi hesaplayabiliriz.
\( \lim\limits_{x \to 1} {x} = 1 \)
\( \lim\limits_{x \to 1} {3} = 3 \)
\( \lim\limits_{x \to 1} {1} = 1 \)
\( L = \dfrac{4(1)^2 + 2(1) + 3}{2(1)^2 + 1} = 3 \)
Fonksiyonların Limiti
Polinom Fonksiyonu
Her polinom fonksiyonunun limiti limit kuralları kullanılarak birim ve sabit fonksiyonların limitine indirgenebileceği için, polinom fonksiyonunun bir noktadaki limit değeri o noktadaki fonksiyon değerine eşit olur.
\( p(x) \) bir polinom fonksiyonu olmak üzere,
\( \lim\limits_{x \to a} {p(x)} = p(a) \)
\( p(x) = x^4 - 5x^2 + 2x - 3 \)
\( \lim\limits_{x \to 3} {p(x)} = p(3) \)
\( = 3^4 - 5(3)^2 + 2(3) - 3 = 39 \)
İSPATI GÖSTER
\( p(x) = a_nx^n + a_{n-1}x^{n-1} + \ldots + a_2x^2 + a_1x + a_0 \) olmak üzere,
\( \lim_{x \to a} p(x) \)
\( = \lim_{x \to a} (a_nx^n + a_{n-1}x^{n-1} + \ldots + a_2x^2 + a_1x + a_0) \)
\( = \lim_{x \to a} a_nx^n + \lim_{x \to a} a_{n-1}x^{n-1} + \ldots + \lim_{x \to a} a_2x^2 + \lim_{x \to a} a_1x + \lim_{x \to a} a_0 \)
\( = a_n\lim_{x \to a} x^n + a_{n-1}\lim_{x \to a} x^{n-1} + \ldots + a_2\lim_{x \to a} x^2 + a_1\lim_{x \to a} x + \lim_{x \to a} a_0 \)
\( = a_n(\lim_{x \to a} x)^n + a_{n-1}(\lim_{x \to a} x)^{n-1} + \ldots + a_2(\lim_{x \to a} x)^2 + a_1(\lim_{x \to a} x) + \lim_{x \to a} a_0 \)
\( = a_na^n + a_{n-1}a^{n-1} + \ldots + a_2a^2 + a_1a + a_0 \)
\( = p(a) \)
Rasyonel Fonksiyon
İki polinom fonksiyonunun birbirine bölümünden oluşan rasyonel fonksiyonlara bölme limit kuralı uygulandığında, fonksiyonun limitinin pay ve paydadaki polinom fonksiyonlarının bu noktadaki fonksiyon değerlerinin bölümüne eşit olduğu görülür.
\( p(x) \) ve \( q(x) \) polinom fonksiyonları,
\( q(a) \ne 0 \) olmak üzere,
\( \lim\limits_{x \to a} {\dfrac{p(x)}{q(x)}} = \dfrac{p(a)}{q(a)} \)
\( \lim\limits_{x \to -2} {\dfrac{x^2 - 8}{x + 3}} = \dfrac{(-2)^2 - 8}{(-2) + 3} = -4 \)
İSPATI GÖSTER
\( p(x) \) ve \( q(x) \) birer polinom fonksiyonu ve \( q(a) \ne 0 \) olmak üzere,
\( \lim_{x \to a} \dfrac{p(x)}{q(x)} \)
Paydanın limiti alınan noktadaki değerinin sıfırdan farklı olduğunu bildiğimiz için bölme limit kuralını uygulayabiliriz.
\( = \dfrac{\lim_{x \to a} p(x)}{\lim_{x \to a} q(x)} \)
Pay ve paydadaki polinom fonksiyonlarının belirli bir noktadaki limiti o noktadaki fonksiyon değerine eşittir.
\( = \dfrac{p(a)}{q(a)} \)
Aşağıdaki limitleri hesaplayınız.
(a) \( \lim\limits_{x \to 3} (x^3 - 6x^2 - 7x + 2) \)
(b) \( \lim\limits_{x \to 2} (5x^4 + 3x^2 - 2x + 6) \)
(c) \( \lim\limits_{x \to -1} (4x^5 + 5x^4 + 8x + 1) \)
Çözümü GösterTüm seçeneklerde limiti alınan ifadeler polinom fonksiyonudur. Polinom fonksiyonlarının bir noktadaki limit değeri o noktadaki fonksiyon değerine eşittir.
(a) seçeneği:
\( \lim\limits_{x \to 3} (x^3 - 6x^2 - 7x + 2) \)
\( = 3^3 - 6(3)^2 - 7(3) + 2 \)
\( = 27 - 54 - 21 + 2 = -46 \)
(b) seçeneği:
\( \lim\limits_{x \to 2} (5x^4 + 3x^2 - 2x + 6) \)
\( = 5(2)^4 + 3(2)^2 - 2(2) + 6 \)
\( = 80 + 12 - 4 + 6 = 94 \)
(c) seçeneği:
\( \lim\limits_{x \to -1} (4x^5 + 5x^4 + 8x + 1) \)
\( = 4(-1)^5 + 5(-1)^4 + 8(-1) + 1 \)
\( = -4 + 5 - 8 + 1 = -6 \)
Aşağıdaki limitleri hesaplayınız.
(a) \( \lim\limits_{x \to 5} {\dfrac{9x + 3}{x^2 - 9}} \)
(b) \( \lim\limits_{x \to 2} {\dfrac{4x^2 + 2}{x - 3}} \)
(c) \( \lim\limits_{x \to -3} {\dfrac{5x^3 - 2x + 6}{x^2 - 4x + 6}} \)
Çözümü GösterTüm seçeneklerde pay ve payda polinom fonksiyonu olduğu için limiti alınan ifadeler rasyonel fonksiyondur. Limiti alınan \( x \) değeri paydayı sıfır yapmamak koşuluyla, rasyonel fonksiyonların bir noktadaki limit değeri o noktadaki fonksiyon değerine eşittir.
(a) seçeneği:
\( \lim\limits_{x \to 5} {\dfrac{9x + 3}{x^2 - 9}} = \dfrac{9(5) + 3}{5^2 - 9} \)
\( = \dfrac{48}{16} = 3 \)
(b) seçeneği:
\( \lim\limits_{x \to 2} {\dfrac{4x^2 + 2}{x - 3}} = \dfrac{4(2)^2 + 2}{2 - 3} \)
\( = \dfrac{18}{-1} = -18 \)
(c) seçeneği:
\( \lim\limits_{x \to -3} {\dfrac{5x^3 - 2x + 6}{x^2 - 4x + 6}} = \dfrac{5(-3)^3 - 2(-3) + 6}{(-3)^2 - 4(-3) + 6} \)
\( = \dfrac{-123}{27} = -\dfrac{41}{9} \)
\( \lim\limits_{x \to 4} (x^2 + 3x - 2a) = 44 \)
olduğuna göre, \( a \) kaçtır?
Çözümü GösterLimiti alınan ifade bir polinom fonksiyonudur. Polinom fonksiyonunun bir noktadaki limit değeri o noktadaki fonksiyon değerine eşittir.
\( \lim\limits_{x \to 4} (x^2 + 3x - 2a) = 44 \)
\( 4^2 + 3(4) - 2a = 44 \)
\( 16 + 12 - 2a = 44 \)
\( a = -8 \) bulunur.
\( \lim\limits_{x \to 4} (2x^2 - x + a) = \lim\limits_{x \to 3} (x^4 - 4x + b) \)
olduğuna göre, \( b - a\) kaçtır?
Çözümü GösterLimiti alınan iki ifade de birer polinom fonksiyonudur. Polinom fonksiyonunun bir noktadaki limit değeri o noktadaki fonksiyon değerine eşittir.
\( \lim\limits_{x \to 4} (2x^2 - x + a) = \lim\limits_{x \to 3} (x^4 - 4x + b) \)
\( 2(4)^2 - 4 + a = 3^4 - 4 \cdot 3 + b \)
\( 32 - 4 + a = 81 - 12 + b \)
\( 28 + a = 69 + b \)
\( b - a = -41 \) bulunur.
\( f(x) = x^2 + 2x - 5 \) ve
\( g(x) \) bir polinom fonksiyonu olmak üzere,
\( \lim\limits_{x \to 2^+} [f(x) \cdot g(x - 2)] = 21 \)
olduğuna göre, \( \lim\limits_{x \to 0^+} g(x) \) kaçtır?
Çözümü Göster\( f \) ve \( g \) birer polinom fonksiyonudur ve polinom fonksiyonlarının limiti tüm reel sayılarda tanımlıdır.
İki fonksiyonun da limiti tanımlı olduğu için limit çarpma kuralını kullanabiliriz.
\( \lim\limits_{x \to 2^+} [f(x) \cdot g(x - 2)] = 21 \)
\( \lim\limits_{x \to 2^+} f(x) \cdot \lim\limits_{x \to 2^+} g(x - 2) = 21 \)
Polinom fonksiyonlarının bir noktadaki limit değeri o noktadaki fonksiyon değerine eşittir.
\( f(2) \cdot \lim\limits_{x \to 2^+} g(x - 2) = 21 \)
\( (2^2 + 2(2) - 5) \cdot \lim\limits_{x \to 2^+} g(x - 2) = 21 \)
\( \lim\limits_{x \to 2^+} g(x - 2) = 7 \)
\( x \to 2^+ \) iken \( x - 2 \to 0^+ \) olur.
Buna göre verilen ifade \( g \) fonksiyonunun \( x = 0 \) noktasındaki sağdan limitidir.
\( \lim\limits_{x \to 2^+} g(x - 2) = g(0^+) = 7 \)
Soruda sorulan limit ifadesi de aynı limite eşittir.
\( \lim\limits_{x \to 0^+} g(x) = g(0^+) \)
Buna göre \( \lim\limits_{x \to 0^+} g(x) = 7 \) bulunur.
\( a \in \mathbb{R} \) ve \( f, g \) birer polinom fonksiyonu olmak üzere,
\( \lim\limits_{x \to 2} f(x + 1) = a + 2 \)
\( \lim\limits_{x \to 1} g(x + 2) = a^2 - 2a + 4 \)
\( \lim\limits_{x \to 3} [f(x)g(x)] = 133 \)
olduğuna göre, \( a \) kaçtır?
Çözümü GösterPolinom fonksiyonunun bir noktadaki limit değeri o noktadaki fonksiyon değerine eşittir.
\( \lim\limits_{x \to 2} f(x + 1) = a + 2 \)
\( f(2 + 1) = f(3) = a + 2 \)
\( \lim\limits_{x \to 1} g(x + 2) = a^2 - 2a + 4 \)
\( g(1 + 2) = g(3) = a^2 - 2a + 4 \)
\( \lim\limits_{x \to 3} [f(x)g(x)] = 133 \)
Polinom fonksiyonlarının limiti tüm reel sayılarda tanımlı olduğu için limit çarpma kuralını kullanabiliriz.
\( \lim\limits_{x \to 3} f(x) \cdot \lim\limits_{x \to 3} g(x) = 133 \)
\( f(3)g(3) = 133 \)
\( f(3) \) ve \( g(3) \) değerlerini eşitlikte yerine koyalım.
\( (a + 2)(a^2 - 2a + 4) = 133 \)
Bu ifade küp toplamı özdeşliğinin açılımıdır.
\( x^3 + y^3 = (x + y)(x^2 - xy + y^2) \)
\( a^3 + 2^3 = 133 \)
\( a^3 = 125 \)
\( a = 5 \) bulunur.
\( f \) bir polinom fonksiyonu olmak üzere,
\( \lim\limits_{x \to 3} [(x^2 + 3)f(x + 1)] = 60 \) ise,
\( \lim\limits_{x \to 4} \dfrac{x + f(x)}{3x + 5} \) limitinin değeri kaçtır?
Çözümü GösterVerilen eşitlikteki \( x^2 + 3 \) ve \( f(x + 1) \) ifadeleri birer polinom fonksiyonudur. Polinom fonksiyonlarının limiti tüm reel sayılarda tanımlı olduğu için limit çarpma kuralını kullanabiliriz.
\( \lim\limits_{x \to 3} [(x^2 + 3)f(x + 1)] = 60 \)
\( \lim\limits_{x \to 3} (x^2 + 3) \cdot \lim\limits_{x \to 3} f(x + 1) = 60 \)
Polinom fonksiyonunun bir noktadaki limit değeri o noktadaki fonksiyon değerine eşittir.
\( (3^2 + 3)f(3 + 1) = 60 \)
\( f(4) = 5 \)
Pay ve payda birer polinom fonksiyonu olduğu için limit değeri sorulan ifade bir rasyonel fonksiyondur. Limiti alınan \( x \) değeri paydayı sıfır yapmamak koşuluyla, rasyonel fonksiyonun bir noktadaki limit değeri o noktadaki fonksiyon değerine eşittir.
\( \lim\limits_{x \to 4} \dfrac{x + f(x)}{3x + 5} = \dfrac{4 + f(4)}{3(4) + 5} \)
\( = \dfrac{4 + 5}{17} = \dfrac{9}{17} \) bulunur.
\( L \in \mathbb{R} \) olmak üzere,
Reel sayılar kümesinde tanımlı \( f \) ve \( g \) fonksiyonları için aşağıdaki eşitlik sağlanıyor.
\( \lim\limits_{x \to 4} f(x) = \lim\limits_{x \to 4} g(x) = L \)
Buna göre aşağıdakilerden hangileri her zaman doğrudur?
I. \( f(4) = g(4) \)
II. \( \lim\limits_{x \to 4} (f(x) + g(x)) = 2L \)
III. \( \lim\limits_{x \to 4} (2f(x) - g(x)) = L \)
IV. \( \lim\limits_{ x \to 4} \dfrac{f(x)}{g(x)} = 1 \)
Çözümü GösterI. öncül:
Limit bir fonksiyonun belirli bir nokta civarında nasıl davrandığı ile ilgilenir, fonksiyonun o noktadaki değeri ya da o noktada tanımlı olup olmaması ile ilgilenmez. Dolayısıyla iki fonksiyonun bir noktadaki limitlerinin eşit olması fonksiyon değerlerinin de eşit olmasını gerektirmez.
I. öncül her zaman doğru değildir.
II. öncül:
İki fonksiyonun da limiti tanımlı olduğu için, limit toplama kuralı gereği toplamlarının limiti limitlerinin toplamına eşittir.
\( \lim\limits_{x \to 4} (f(x) + g(x)) = \lim\limits_{x \to 4} {f(x)} + \lim\limits_{x \to 4} {g(x)} \)
\( = L + L = 2L \)
II. öncül her zaman doğrudur.
III. öncül:
İki fonksiyonun da limiti tanımlı olduğu için, limit çıkarma ve sabit sayı ile çarpma kurallarını uyguladığımızda verilen değeri buluruz.
\( \lim\limits_{x \to 4} (2f(x) - g(x)) = \lim\limits_{x \to 4} (2f(x)) - \lim\limits_{x \to 4} {g(x)} \)
\( = 2\lim\limits_{x \to 4} {f(x)} - \lim\limits_{x \to 4} {g(x)} \)
\( = 2L - L = L \)
III. öncül her zaman doğrudur.
IV. öncül:
Limit bölme kuralı paydadaki ifadenin limiti sıfır (\( L = 0 \)) olduğu durumda geçerli değildir.
IV. öncül her zaman doğru değildir.
Buna göre sadece II. ve III. öncüller her zaman doğrudur.
\( \lim\limits_{x \to a} \dfrac{x^2 - 4}{x + 2} = 9 \) olduğuna göre, \( a \) kaçtır?
Çözümü GösterPay ve payda birer polinom fonksiyonu olduğu için limiti alınan ifade bir rasyonel fonksiyondur. Limiti alınan değer paydayı sıfır yapmamak koşuluyla, rasyonel fonksiyonun bir noktadaki limit değeri o noktadaki fonksiyon değerine eşittir.
\( \lim\limits_{x \to a} \dfrac{x^2 - 4}{x + 2} = 9 \)
\( \dfrac{a^2 - 4}{a + 2} = 9 \)
\( \dfrac{a^2 - 4}{a + 2} - 9 = 0 \)
\( \dfrac{a^2 - 4 - 9(a + 2)}{a + 2} = 0 \)
\( \dfrac{a^2 - 9a - 22}{a + 2} = 0 \)
\( \dfrac{(a - 11)(a + 2)}{a + 2} = 0 \)
Bu denklemin çözüm kümesi payı sıfır yapan ama paydayı sıfır yapmayan değerlerden oluşur.
Buna göre \( a = 11 \) bulunur.
\( f(x) = 4x - 3 \) olduğuna göre,
\( \lim\limits_{x \to 4} \dfrac{f(x - 1) + 2f(x + 3)}{f(x^3) - 40} \) limitinin değeri kaçtır?
Çözümü Göster\( f \) bir polinom fonksiyonu olduğu için \( f(x - 1) \), \( f(x + 3) \) ve \( f(x^3) \) bileşke fonksiyonları da birer polinom fonksiyonudur.
Pay ve payda birer polinom fonksiyonu olduğu için limit değeri sorulan ifade bir rasyonel fonksiyondur. Limiti alınan \( x \) değeri paydayı sıfır yapmamak koşuluyla, rasyonel fonksiyonun bir noktadaki limit değeri o noktadaki fonksiyon değerine eşittir.
\( \lim\limits_{x \to 4} \dfrac{f(x - 1) + 2f(x + 3)}{f(x^3) - 40} \)
\( = \dfrac{f(4 - 1) + 2f(4 + 3)}{f(4^3) - 40} \)
\( = \dfrac{f(3) + 2f(7)}{f(64) - 40} \)
\( f \) fonksiyon tanımını kullanarak fonksiyon değerlerini bulalım.
\( = \dfrac{(4(3) - 3) + 2(4(7) - 3)}{(4(64) - 3) - 40} \)
\( = \dfrac{59}{213} \) bulunur.
Reel sayılar kümesinde tanımlı \( f \) fonksiyonu için,
\( \lim\limits_{x \to 2^-} f(x) = 4 \)
\( \lim\limits_{x \to 2^+} f(x) = 7 \)
olduğuna göre, aşağıdaki ifadenin değeri kaçtır?
\( \lim\limits_{x \to 1^+} [(3x + 7)f(3x - 1)] + \lim\limits_{x \to 2^+} [(x^2 + 4x)f(4 - x)] \)
Çözümü Göster\( \lim\limits_{x \to 2^-} f(x) = f(2^-) = 4 \)
\( \lim\limits_{x \to 2^+} f(x) = f(2^+) = 7 \)
Sorudaki iki limit ifadesinin birinci çarpanları birer polinom fonksiyonudur. Polinom fonksiyonlarının limiti tüm reel sayılarda tanımlıdır.
İki limit ifadesinin ikinci çarpanlarının limitinin tanımlı olup olmadığını kontrol edelim.
\( x \to 1^+ \) iken \( 3x - 1 \to 2^+ \) olur.
Buna göre verilen ifade \( f \) fonksiyonunun \( x = 2 \) noktasındaki sağdan limitidir.
\( \lim\limits_{x \to 1^+} f(3x - 1) = f(2^+) = 7 \)
\( x \to 2^+ \) iken \( 4 - x \to 2^- \) olur.
Buna göre verilen ifade \( f \) fonksiyonunun \( x = 2 \) noktasındaki soldan limitidir.
\( \lim\limits_{x \to 2^+} f(4 - x) = f(2^-) = 4 \)
İki limit ifadesinin ikinci çarpanlarının limiti alınan noktada limitlerinin tanımlı olduğunu göstermiş olduk.
Buna göre iki limit ifadesinin ikişer çarpanının da limiti tanımlı olduğu için limit çarpma kuralını kullanabiliriz.
\( \lim\limits_{x \to 1^+} [(3x + 7)f(3x - 1)] + \lim\limits_{x \to 2^+} [(x^2 + 4x)f(4 - x)] \)
\( = \lim\limits_{x \to 1^+} (3x + 7) \cdot \lim\limits_{x \to 1^+} f(3x - 1) + \lim\limits_{x \to 2^+} (x^2 + 4x) \cdot \lim\limits_{x \to 2^+} f(4 - x) \)
Polinom fonksiyonunun bir noktadaki limit değeri o noktadaki fonksiyon değerine eşittir.
\( = (3(1) + 7)f(2^+) + (2^2 + 4(2))f(2^-) \)
\( = 10 \cdot 7 + 12 \cdot 4 = 118 \) bulunur.