Asimptot
Bir fonksiyonda \( x \) ve \( y \) değerleri ayrı ayrı ya da birlikte pozitif ya da negatif sonsuza giderken, fonksiyonun grafiği bir doğru ya da eğriye aralarındaki uzaklık sıfıra yaklaşacak şekilde yaklaşıyorsa bu doğruya/eğriye fonksiyonun bir asimptotu denir.
Aşağıdaki grafikte mavi kesikli çizgi ile gösterilen üç doğru fonksiyonun asimptotlarıdır.
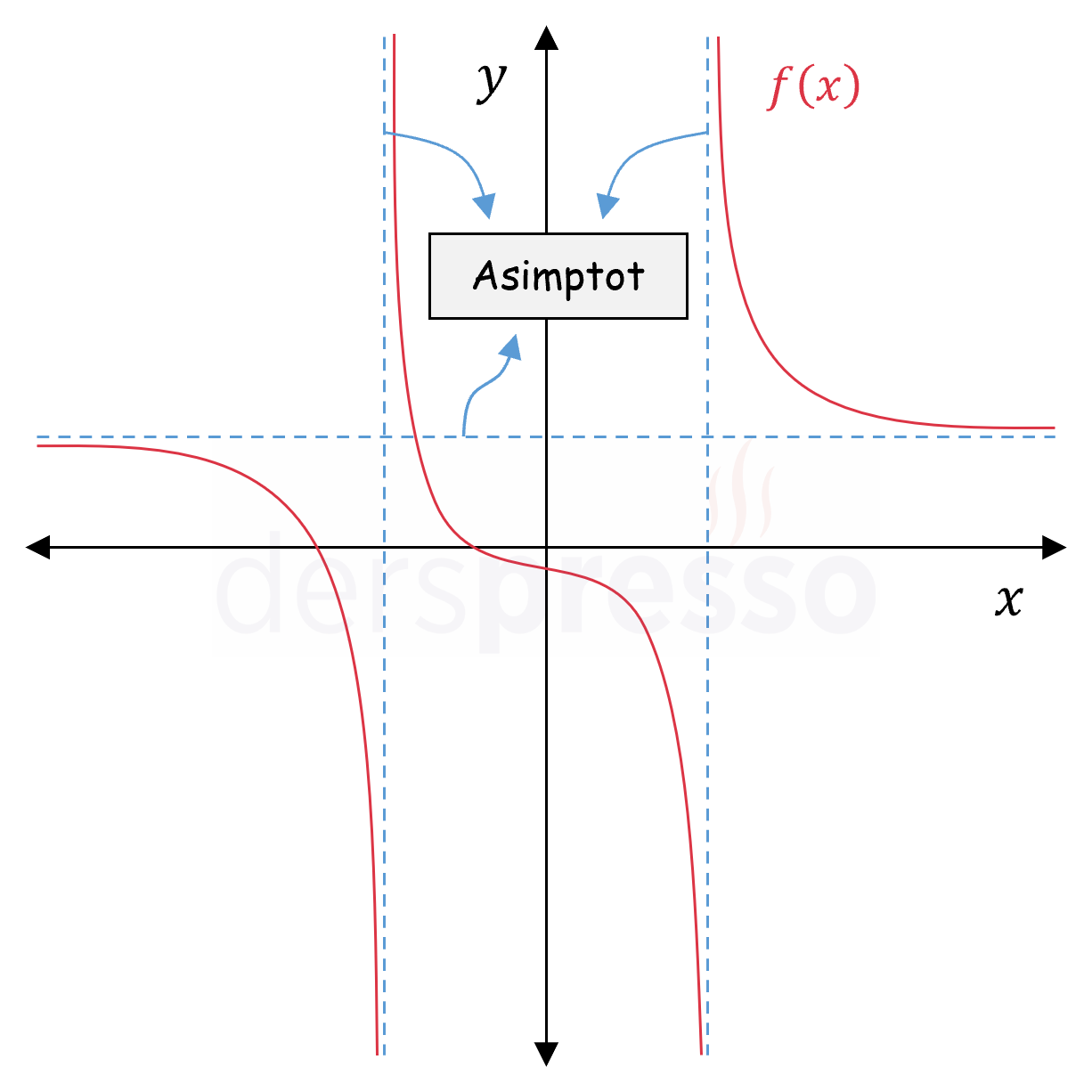
Asimptotlar fonksiyon grafiğinin bir parçası olmayıp fonksiyonun belirli bir nokta civarındaki ya da sonsuzdaki davranışının daha kolay anlaşılmasını sağlamak için çizilir.
Asimptotlar dört tipte olabilir. Bunlardan birincisini önümüzdeki sonsuz limit bölümünde, diğer üçünü bir sonraki sonsuzda limit bölümünde inceleyeceğiz.
- Dikey asimptot
- Yatay asimptot
- Eğik asimptot
- Eğri asimptot