Fonksiyonlara Giriş
Konu tekrarı için: Sıralı İkililer | Kartezyen Çarpımı | Bağıntı
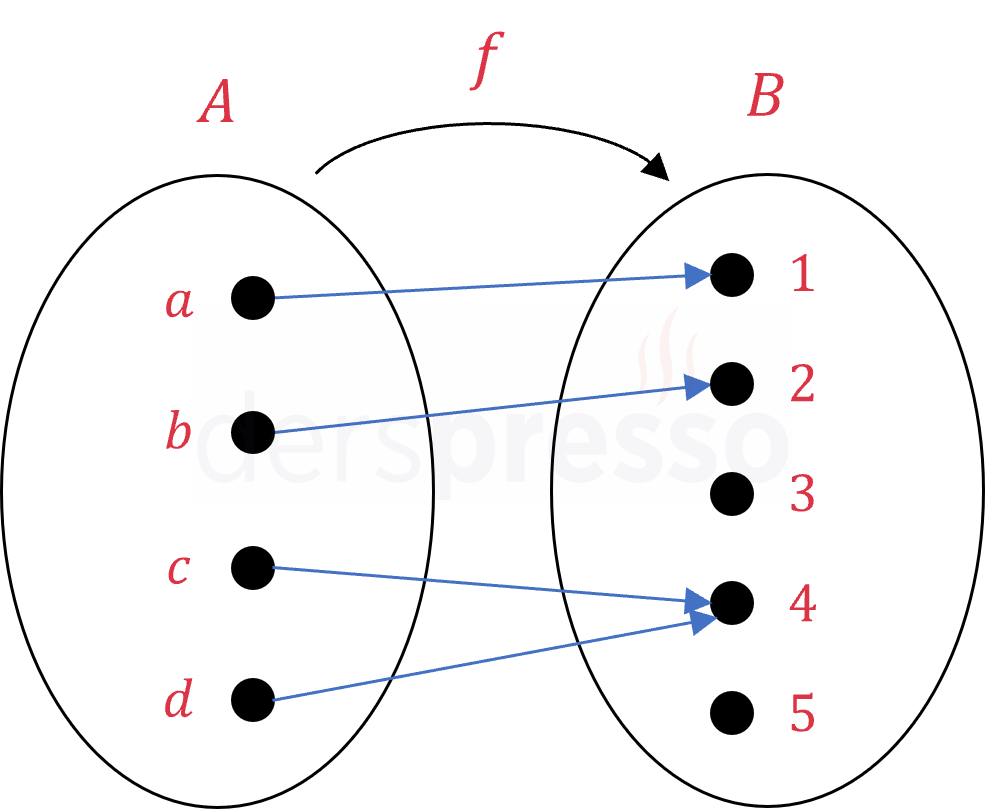
\( A \) ve \( B \) boş kümeden farklı iki küme olmak üzere, \( A \) kümesinin her elemanını \( B \) kümesinin sadece bir elemanı ile eşleyen bağıntıya \( A \)'dan \( B \)'ye tanımlı fonksiyon denir.
Fonksiyonlar genellikle \( f \), \( g \), \( h \) gibi küçük harflerle gösterilirler. Sıklıkla kullanılan \( \sin \), \( \cos \), \( \tan \), \( \log \), \( \ln \) gibi ifadeler de ilgili trigonometrik ve logaritmik fonksiyonlar için kullanılan benzer kısaltmalardır.
\( A \) kümesinin elemanlarını \( B \) kümesinin elemanları ile eşleyen \( f \) fonksiyonu aşağıdaki şekilde tanımlanır.
\( f: A \to B \)
Bu tanımdaki aşağıda detayları verilen üç bileşen bir fonksiyonun ayrılmaz birer parçasıdır ve herhangi biri olmadan bir fonksiyon tanımlanamaz.
- \( A \) kümesine tanım kümesi denir. Bir fonksiyon tanım kümesinin her elemanını \( B \) kümesinin bir elemanı ile eşler.
- \( B \) kümesine değer kümesi denir. Bu küme \( A \) kümesinin elemanlarının eşlenebileceği değerleri içeren kümedir.
- \( f \) iki küme arasındaki eşleme kuralını içeren fonksiyonun adıdır.

Bir fonksiyonun tanım ve değer kümeleri farklı tipte kümeler olabilir:
- Sayı kümeleri: \( \mathbb{N}, \mathbb{Z}, \mathbb{Z^+}, \mathbb{R} \) vb.
- Sayı kümelerinin herhangi bir alt kümesi: \( (0, 10) \), \( [-2\pi, +2\pi] \), \( \{1, 2, 3\} \) vb.
- Herhangi bir sonlu küme: Bir sınıftaki öğrenciler, alfabedeki harfler, ülkeler vb.
Tanım ve değer kümeleri aynı olan (\( \mathbb{R} \to \mathbb{R}, A \to A \)) fonksiyonlar için "reel sayılarda tanımlı fonksiyon", "\( A \) kümesi üzerinde tanımlı fonksiyon" gibi ifadeler de kullanılabilir.
Bir \( f \) fonksiyonunda tanım kümesindeki bir \( a \) elemanının değer kümesinde eşlendiği \( b \) elemanına \( a \)'nın \( f \) fonksiyonuna göre görüntüsü denir ve \( f(a) = b \) şeklinde gösterilir.

Bir fonksiyonun tanım ve değer kümelerini ve iki kümenin elemanları arasındaki eşlemeleri yukarıdaki örnekteki gibi Venn şeması ve oklar yardımıyla tanımlayabiliriz.
Bu tanımlamayı yapabileceğimiz ikinci bir yöntem kümeler konusunda gördüğümüz liste yöntemidir. Örneğin aşağıdaki fonksiyon bir okulda 10. sınıftaki öğrencilerin şubelerle eşlemelerini listelemektedir.
\( A = \{ \text{Ali}, \text{Ela}, \ldots, \text{Cem} \} \)
\( B = \{ \text{10-A}, \text{10-B}, \text{10-C}, \text{10-D} \} \) olmak üzere,
\( g: A \to B \)
\( g = \{ (\text{Ali}, \text{10-B}), (\text{Ela}, \text{10-D}), \ldots, (\text{Cem}, \text{10-B}) \} \)
\( g(\text{Ela}) = \text{10-D} \)
Bu örnekte görebileceğimiz gibi, tanım ve değer kümelerinin elemanları arasındaki eşlemeleri "\( (\text{Ela}, \text{10-D}) \)" şeklinde birer sıralı ikili olarak ifade edebiliriz. Bu açıdan baktığımızda bir fonksiyonu elemanları birer sıralı ikili olan bir küme olarak da düşünebiliriz.
En sık şekilde kullanacağımız bir diğer yöntemde ise eşleme kuralını bir matematiksel ifade şeklinde tanımlayabiliriz. Örneğin aşağıdaki fonksiyon derece cinsinden bir sıcaklığı Fahrenheit karşılığı ile eşlemektedir.
\( h: \mathbb{R} \to \mathbb{R} \)
\( h(x) = 1.8x + 32 \)
\( h = \{ \ldots, (0, 32), \ldots, (10, 50), \ldots \} \)
\( h(10) = 50 \)
Tanım kümesinin elemanlarını ifade etmek için en sık kullanılan değişken \( x \) olsa da, farklı değişkenler de kullanılabilir.
\( f(t) = 3t^2 - 4 \)
\( f(2) = 3(2)^2 - 4 = 8 \)
\( g(\theta) = 90 + \frac{\theta}{2} \)
\( g(60) = 90 + \frac{60}{2} = 120 \)
Bir fonksiyonun matematiksel tanımının bileşenleri aşağıdaki şekilde gösterilmiştir.
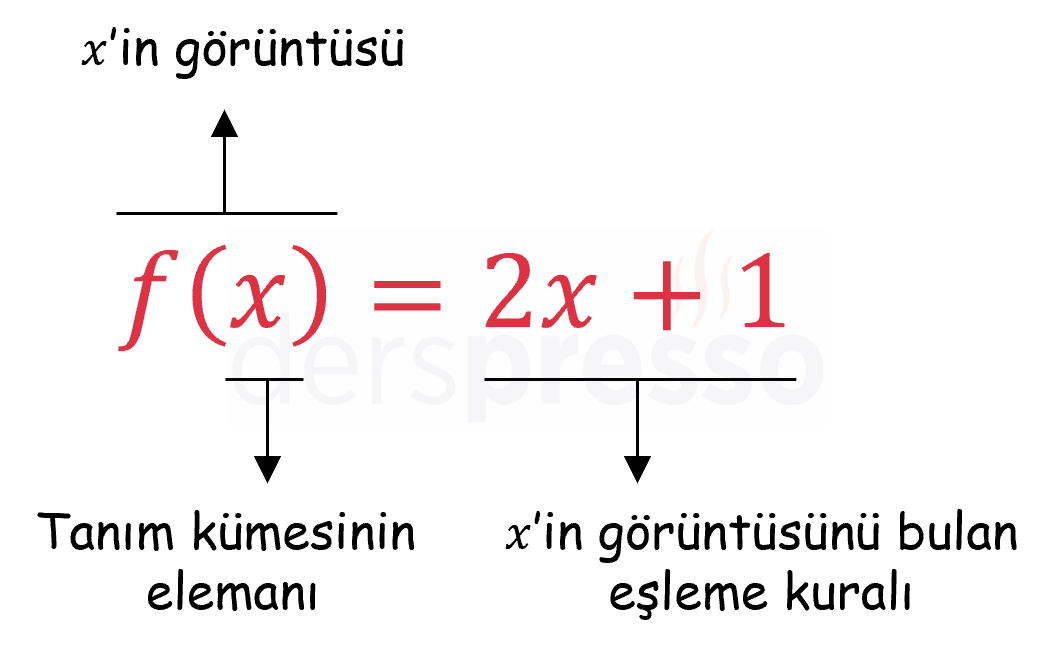
\( f \) ve \( f(x) \) arasındaki ayrımı vurgulamamız gerekirse \( f \) fonksiyonun adı, \( f(x) \) ise fonksiyonun belirli bir \( x \) değeri için ürettiği fonksiyon değeridir.
Fonksiyon - Makine Benzetmesi
Sık kullanılan ve faydalı bir benzetmeye göre, bir \( f \) fonksiyonunu tanım kümesindeki elemanları (\( x \)) girdi olarak alan ve her elemanı değer kümesinin tek bir elemanı (\( f(x) \)) ile eşleyerek bir çıktıya dönüştüren bir makine şeklinde düşünebiliriz.
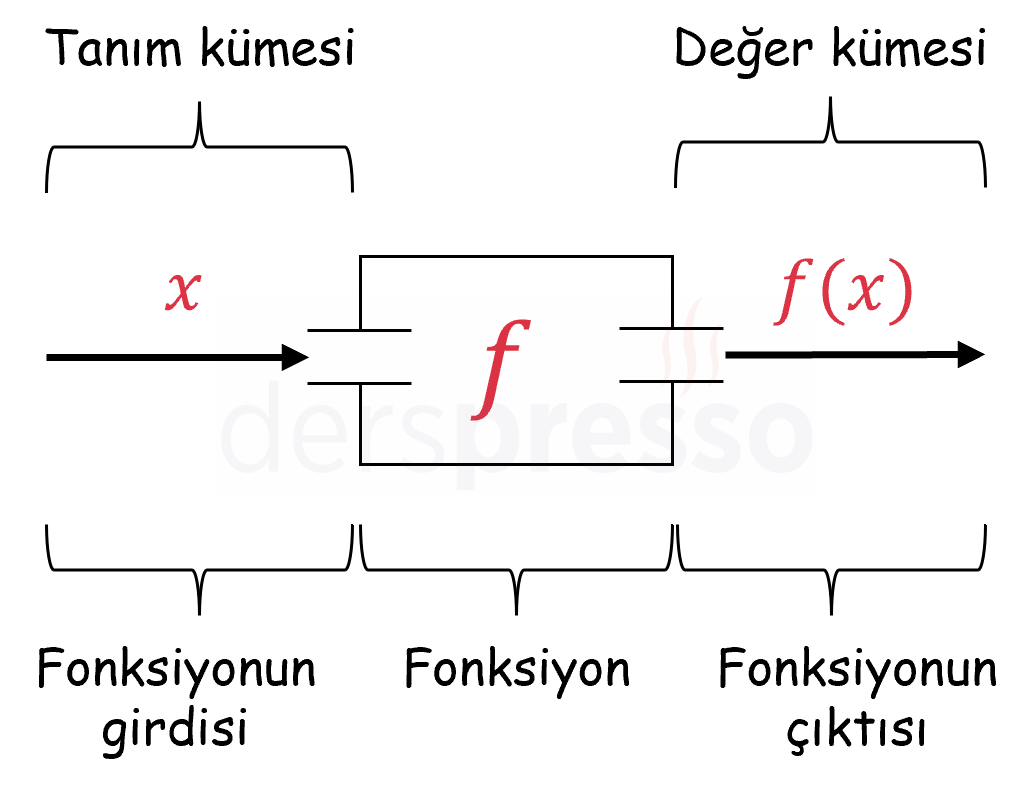
Bağımsız ve Bağımlı Değişkenler
Bir fonksiyonun girdisini temsil eden \( x \) değişkenine aynı zamanda bağımsız değişken, çıktısını temsil eden \( y \) değişkenine de bağımlı değişken denir.
Bir fonksiyonda davranışını incelediğimiz değişken bağımlı değişkendir. Bağımlı değişkenin davranışını anlayabilmemiz ve yorumlayabilmemiz için bağımsız değişkene farklı değerler vererek bağımlı değişken üzerindeki etkisini gözlemleriz.
\( f(x) = x^2 - 2x + 4 \) olduğuna göre, \( f(0) + f(1) + f(2) \) kaçtır?
Çözümü Göster\( f(\dfrac{x - 1}{x + 1}) = x^2 - 4x - 7 \) olduğuna göre, \( f(3) \) kaçtır?
Çözümü Göster4 yanlışın bir doğruyu götürdüğü 25 soruluk bir sınavda tüm soruları cevaplayan ve doğru cevap sayısı \( n \) olan bir öğrencinin net sayısını veren fonksiyon nedir?
Çözümü Göster\( f: \mathbb{N} \to \mathbb{N} \)
\( f \) fonksiyonu tanım kümesindeki her elemanı o sayıya en yakın tam kare sayının karekökü ile eşlemektedir.
Buna göre \( f(11) + f(34) \) kaçtır?
Çözümü Göster\( f(x) = \dfrac{x - 3}{2} \)
\( g(x) = 2x + 1 \)
\( f(2a + 1) + g(a - 1) = 10 \) olduğuna göre, \( a \) kaçtır?
Çözümü Göster\( f: \{ 1, 2, 3, 4 \} \to B \) fonksiyonunun değer tablosu aşağıdaki gibidir.
| \( x \) | \( 1 \) | \( 2 \) | \( 3 \) | \( 4 \) |
|---|---|---|---|---|
| \( f(x) \) | \( 3 \) | \( a \) | \( 2 \) | \( a - 4 \) |
\( f(1) \cdot f(3) = f(2) \cdot f(4) + 10 \) olduğuna göre, \( a \) kaçtır?
Çözümü GösterBir fonksiyon makinesine giren her \( x \) değeri \( 2x + 4 \) olarak çıkmaktadır.
Bu fonksiyon makinesinde \( K = \{ -\frac{1}{2}, 2, 3, \frac{7}{2} \} \) kümesinin elemanları girdi olarak kullanıldığında elde edilen çıktıların toplamı kaç olur?
Çözümü Göster\( f(9^x + 52) = \dfrac{3}{9^x} + 4 \) olduğuna göre, \( f(55) \) kaçtır?
Çözümü Göster\( f^2(x) = -x^2 + 4f(x) \) olduğuna göre, \( f(2) \) ifadesinin değeri kaçtır?
Çözümü Göster\( f(x) = \abs{\abs{x - 2} - 3} \) fonksiyonunda \( f(x) \le 6 \) şartını sağlayan \( x \) tam sayılarının toplamı kaçtır?
Çözümü Göster\( f(x) \) terimleri derecelerine göre sıralandığında katsayıları ardışık tam sayılar olan 2. dereceden bir polinom fonksiyonudur.
\( f(2) - f(1) = 35 \) olduğuna göre, \( f(-1) \) kaçtır?
Çözümü Göster\( f(x - 3) = 3f(x - 1) - 2f(x) \)
\( f(0) = 1, f(2) = 7, f(-3) = -8 \)
olduğuna göre, \( f(1) \) kaçtır?
Çözümü Göster\( x \ne 1 \) olmak üzere,
\( 4f(x) + 5f(1 + \frac{60}{x - 1}) = 20x - 100 \)
olduğuna göre, \( f(4) \) kaçtır?
Çözümü Göster1. Bir tam sayı seç.
2. Bu sayıya 4 ekle.
3. Bulduğun sonucun karesini al.
4. Bulduğun sonucu -2 ile çarp.
5. Bulduğun sonuçtan 1 çıkar.
Yukarıda verilen adımlar uygulandığında elde edilen fonksiyon için aşağıda verilen ifadelerden hangileri her zaman doğrudur?
I. Sonuç tek sayıdır.
II. Sonuç negatiftir.
III. Sonuç asal sayıdır.
Çözümü Göster