Örten ve İçine Fonksiyon
Bir fonksiyonun tanım kümesindeki elemanların değer kümesindeki elemanlarla eşlenmesi sonucunda değer kümesinde hiçbir eleman açıkta kalmıyorsa bu fonksiyona örten fonksiyon ya da sürjektif fonksiyon denir. Bir diğer ifadeyle, bir örten fonksiyonda değer kümesindeki her eleman tanım kümesindeki en az bir elemanın görüntüsüdür.
Aşağıdaki fonksiyon değer kümesinde hiçbir eleman açıkta kalmadığı için örtendir.
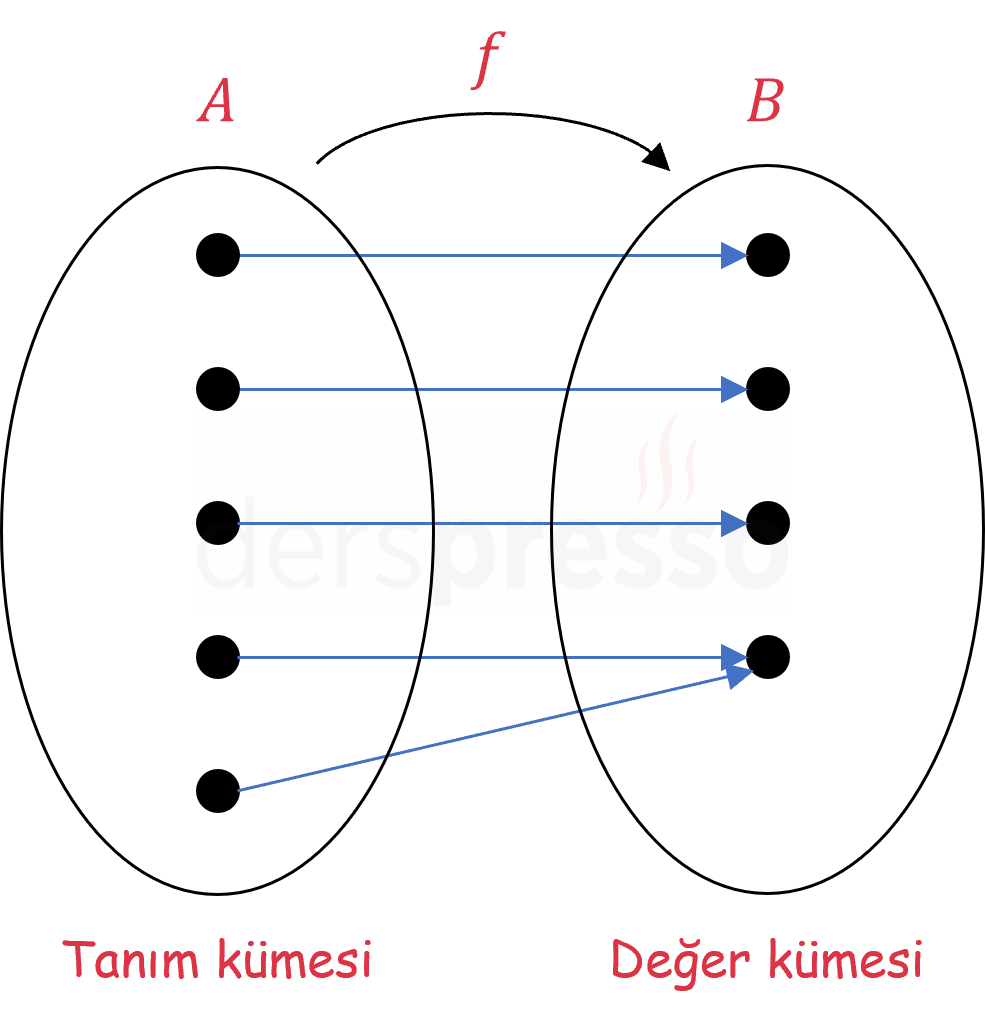
Bir fonksiyon örten değilse, yani değer kümesinde açıkta eleman kalıyorsa bu fonksiyona içine fonksiyon denir. Buna göre, bir fonksiyon ya örtendir ya da içinedir.
Aşağıdaki fonksiyon değer kümesindeki son eleman açıkta kaldığı için içine fonksiyondur.
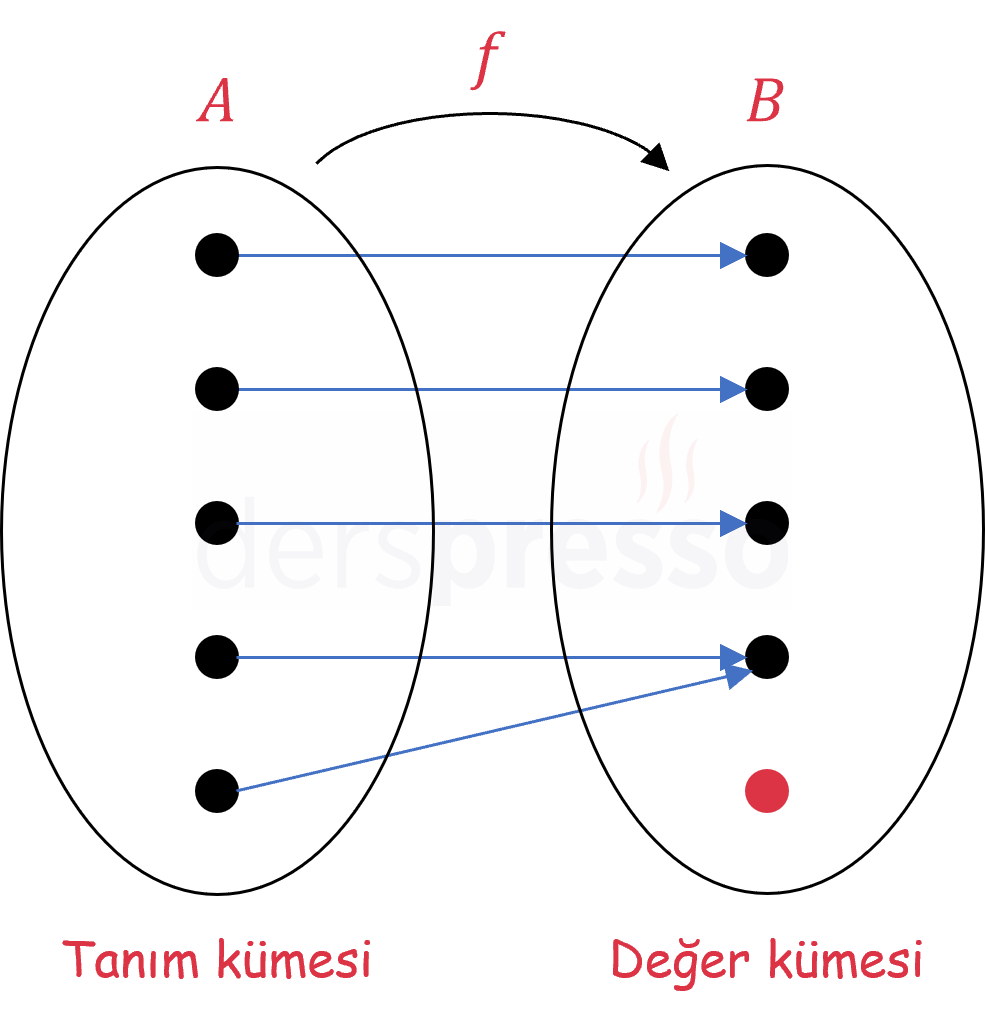
\( f: A \to B \) fonksiyonunda, her \( b \in B \) için,
\( f(a) = b \) olacak şekilde en az bir \( a \in A \) varsa,
\( f \) örten fonksiyondur.
Aksi takdirde \( f \) içine fonksiyondur.
\( A = \{ a, b, c, d \} \)
\( B = \{ 1, 2, 3 \} \)
\( f, g: A \to B \)
\( f \) değer kümesinde açıkta eleman kalmadığı için örtendir.
\( f = \{ (a, 1), (b, 2), (c, 3), (d, 3) \} \)
\( g \) değer kümesindeki "2" elemanı açıkta kaldığı için içinedir.
\( g = \{ (a, 1), (b, 3), (c, 3), (d, 1) \} \)
Örten fonksiyonlarda değer kümesindeki her eleman tanım kümesindeki en az bir elemanın görüntüsü olduğu için görüntü kümesi değer kümesine eşittir. İçine fonksiyonlarda değer kümesinde açıkta eleman(lar) kaldığı için görüntü kümesi değer kümesinin bir öz alt kümesidir.
\( f: A \to B \) fonksiyonunda,
\( f \) örten ise: \( \quad f(A) = B \)
\( f \) içine ise: \( \quad f(A) \subset B \)
İçine bir fonksiyon değer kümesi görüntü kümesine eşit olacak şekilde daraltılarak örten bir fonksiyona dönüştürülebilir. Benzer şekilde, örten bir fonksiyon değer kümesi genişletilerek içine bir fonksiyona dönüştürülebilir.
\( f(x) = x^2 \) olmak üzere,
\( f \) fonksiyonu aşağıdaki şekilde tanımlandığında içinedir.
\( f: \mathbb{R} \to \mathbb{R} \)
\( f \) fonksiyonu aşağıdaki şekilde tanımlandığında örtendir.
\( f: \mathbb{R} \to \mathbb{R^+} \cup \{0\} \)
Bir fonksiyonun örten olabilmesi için gerekli koşullardan biri, tanım kümesinin eleman sayısının değer kümesinin eleman sayısına eşit ya da ondan büyük olmasıdır. Aksi takdirde tanım kümesinde değer kümesindeki tüm elemanları "örtecek" kadar eleman bulunmaz.
\( f: A \to B \) fonksiyonunun örten olabilmesi için gerekli koşul:
\( s(A) \ge s(B) \)
Örten ve İçine Fonksiyon Sayısı
Örten fonksiyon sayısı aşağıdaki formülle hesaplanır.
\( f: A \to B \)
\( s(A) = n, \quad s(B) = k \) olmak üzere,
Örten fonksiyon sayısı \( = \begin{cases} 0 & n \lt k \\ k! & n = k \\ \sum_{i = 0}^{k} {(-1)^i \binom{k}{i} (k - i)^n} & n \gt k \end{cases} \)
5 elemanlı \( A \) kümesinden 5 elemanlı \( B \) kümesine tanımlanabilecek örten fonksiyon sayısı:
Örten fonksiyon sayısı \( = 5! \)
Yukarıdaki formülde üçüncü durumdaki formülün mantığını ve nasıl türetildiğini "Sayma" konusu altındaki dahil etme - hariç bırakma prensibi ve örten fonksiyon sayısı sayfalarında inceleyeceğiz.
İki küme arasında tanımlanabilecek içine fonksiyon sayısı, bu iki küme arasında tanımlanabilecek toplam fonksiyon sayısı ile örten fonksiyon sayısının farkına eşittir.
Örten ve İçine Fonksiyonların Grafik Yorumu
Grafiği verilen bir fonksiyonun örten olup olmadığını anlamak için değer kümesindeki tüm \( y \) değerleri için \( x \) eksenine paralel doğrular çizilir. Yatay doğru testi adı verilen bu yöntemde eğer doğruların tümü grafiği en az bir noktada kesiyorsa fonksiyon örtendir, doğruların bir kısmı grafiği kesmiyorsa fonksiyon içinedir.
Aşağıda farklı fonksiyonların örten ya da içine olma durumları yatay doğru testi ile yorumlanmıştır. Bu fonksiyonlarda değer kümeleri tüm reel sayılar olarak alınmıştır. Yukarıda bahsettiğimiz gibi fonksiyonların değer kümesi genişletilerek/daraltılarak örten bir fonksiyon içine bir fonksiyona, içine bir fonksiyon da örten bir fonksiyona dönüştürülebilir.
| Fonksiyon | Grafik |
|---|---|
|
Sabit fonksiyon \( f: \mathbb{R} \to \mathbb{R} \) \( f(x) = c \) Sabit fonksiyonlar görüntü kümeleri tek elemanlı olduğu için örten değil, içinedir. |

|
|
Doğrusal fonksiyon \( a \ne 0 \) olmak üzere, \( f: \mathbb{R} \to \mathbb{R} \) \( f(x) = ax + b \) Doğrusal fonksiyonlar her reel sayı değerini alabildikleri için örtendir. |

|
|
Mutlak değer fonksiyonu \( f: \mathbb{R} \to \mathbb{R} \) \( f(x) = \abs{x} \) Mutlak değer fonksiyonu negatif değer alamadığı için örten değil, içinedir. |

|
|
2. dereceden polinom fonksiyonu (parabol) \( a \ne 0 \) olmak üzere, \( f: \mathbb{R} \to \mathbb{R} \) \( f(x) = ax^2 + bx + c \) 2. dereceden polinom fonksiyonu \( a \gt 0 \) için tepe noktasının ordinat değerinden küçük, \( a \lt 0 \) için büyük değer alamaz, dolayısıyla örten değil, içinedir. Derecesi çift sayı olan tüm polinom fonksiyonları için aynı durum geçerlidir. |

|
|
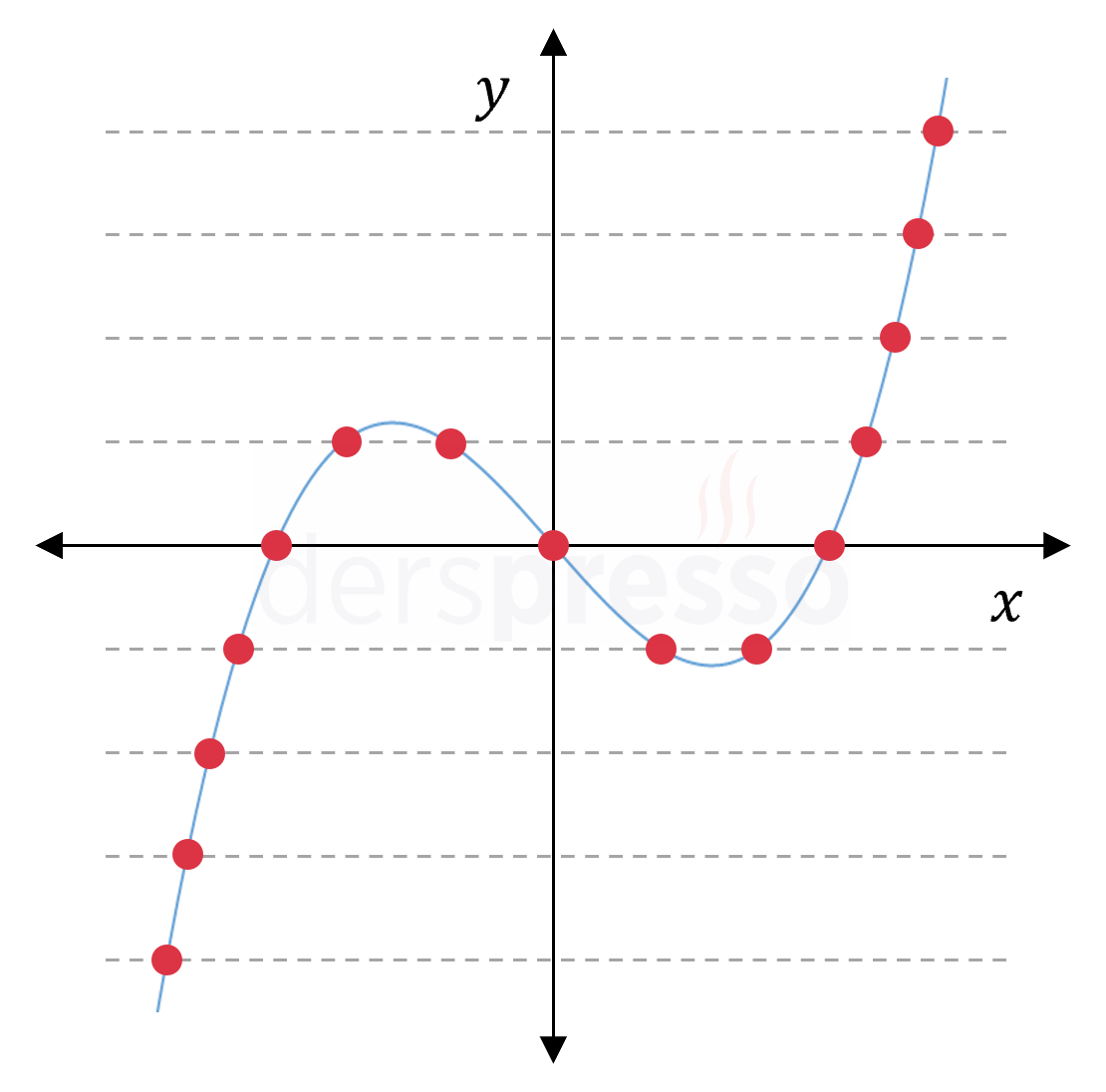
3. dereceden polinom fonksiyonu \( a \ne 0 \) olmak üzere, \( f: \mathbb{R} \to \mathbb{R} \) \( f(x) = ax^3 + bx^2 + cx + d \) 3. dereceden polinom fonksiyonu \( a \gt 0 \) için negatif sonsuzdan gelip pozitif sonsuza, \( a \lt 0 \) için pozitif sonsuzdan gelip negatif sonsuza gider, dolayısıyla tüm reel sayı değerlerini alır ve bu yüzden örtendir. Derecesi tek sayı olan tüm polinom fonksiyonları için aynı durum geçerlidir. |
|
|
Üstel fonksiyon \( a \gt 0, a \ne 1 \) olmak üzere, \( f: \mathbb{R} \to \mathbb{R} \) \( f(x) = a^x \) Üstel fonksiyon sıfır ve negatif değer alamadığı için örten değil, içinedir. |

|
|
Logaritma fonksiyonu \( a \gt 0, a \ne 1 \) olmak üzere, \( f: \mathbb{R^+} \to \mathbb{R} \) \( f(x) = \log_a{x} \) Logaritma fonksiyonu tüm reel sayı değerlerini alabildiği için örtendir. |

|
Yukarıda paylaştığımız örten fonksiyon tanımı ile yatay doğru testi arasındaki paralelliğin anlaşılması önem taşımaktadır. Örten bir fonksiyonda değer kümesinde açıkta eleman kalmadığını belirtmiştik. Yatay doğru testi de fonksiyonun değer kümesindeki tüm elemanların (grafiğin \( y \) değerleri) tanım kümesindeki en az bir elemanın görüntüsü olup olmadığını test etmektedir.
Bir fonksiyonun örten ya da içine bir fonksiyon olduğunu fonksiyon grafiğinden bir şekilde daha anlayabiliriz. Grafik üzerindeki tüm noktaların \( y \) ekseni üzerindeki izdüşümleri işaretlendiğinde tüm değer kümesi kapsanmış oluyorsa bu fonksiyon örtendir. Eğer \( y \) ekseni üzerinde değer kümesinde olup işaretlenmemiş değerler ya da aralıklar kalıyorsa bu fonksiyon örten değil, içinedir.
Yukarıdaki tabloda yatay doğru testi uyguladığımız iki fonksiyona aşağıda bu testi uygulayarak aynı sonuca ulaşabiliriz.
| Fonksiyon | Grafik |
|---|---|
|
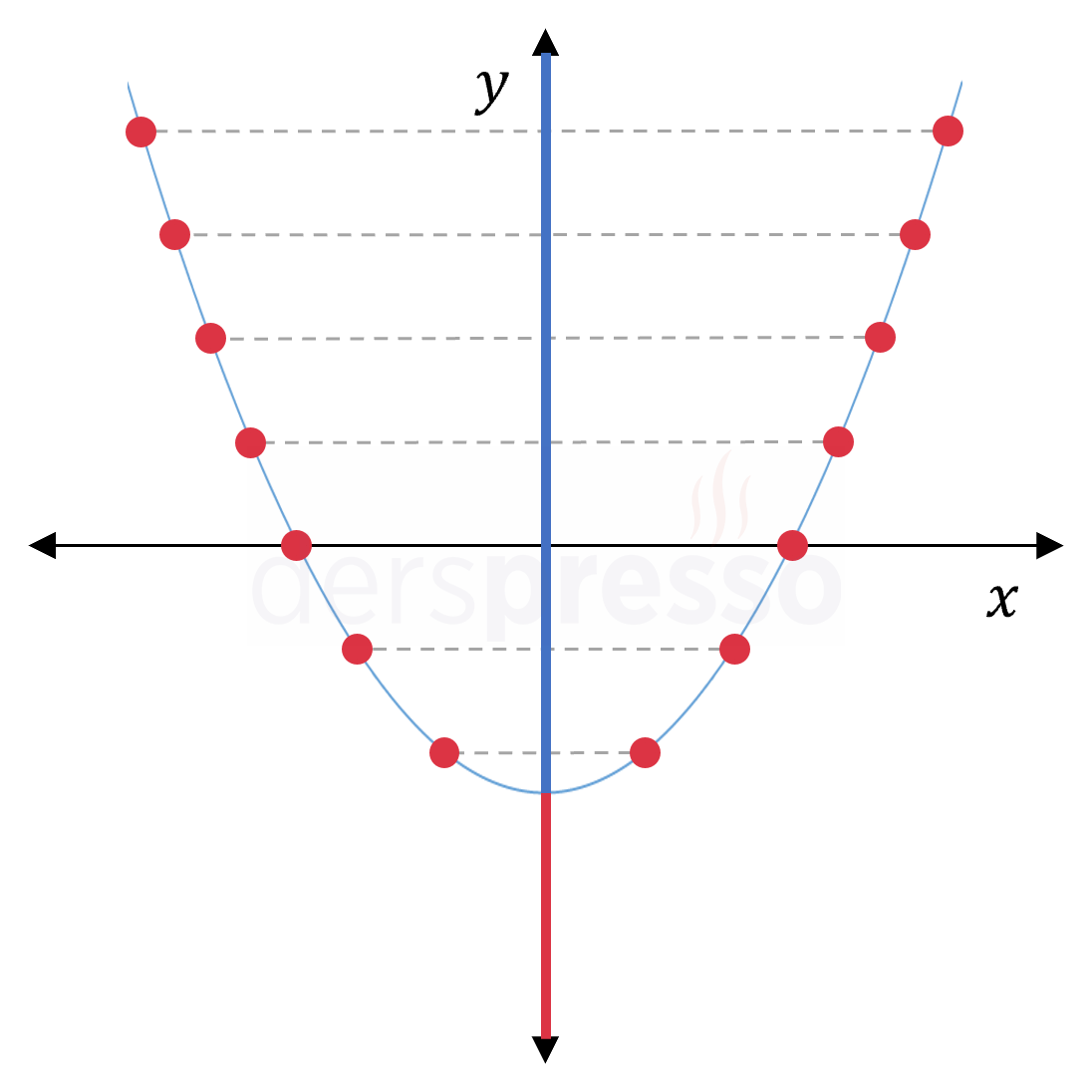
2. dereceden polinom fonksiyonu (parabol) \( f: \mathbb{R} \to \mathbb{R} \) \( a \ne 0 \) \( f(x) = ax^2 + bx + c \) Grafik üzerindeki tüm noktaların \( y \) ekseni üzerindeki izdüşümlerini mavi renkle işaretlediğimizde tepe noktasının alt kısmında kırmızı ile işaretlenmiş kısmın açıkta kaldığını görebiliriz. Bu yüzden bu fonksiyon örten değil, içinedir. |
|
|
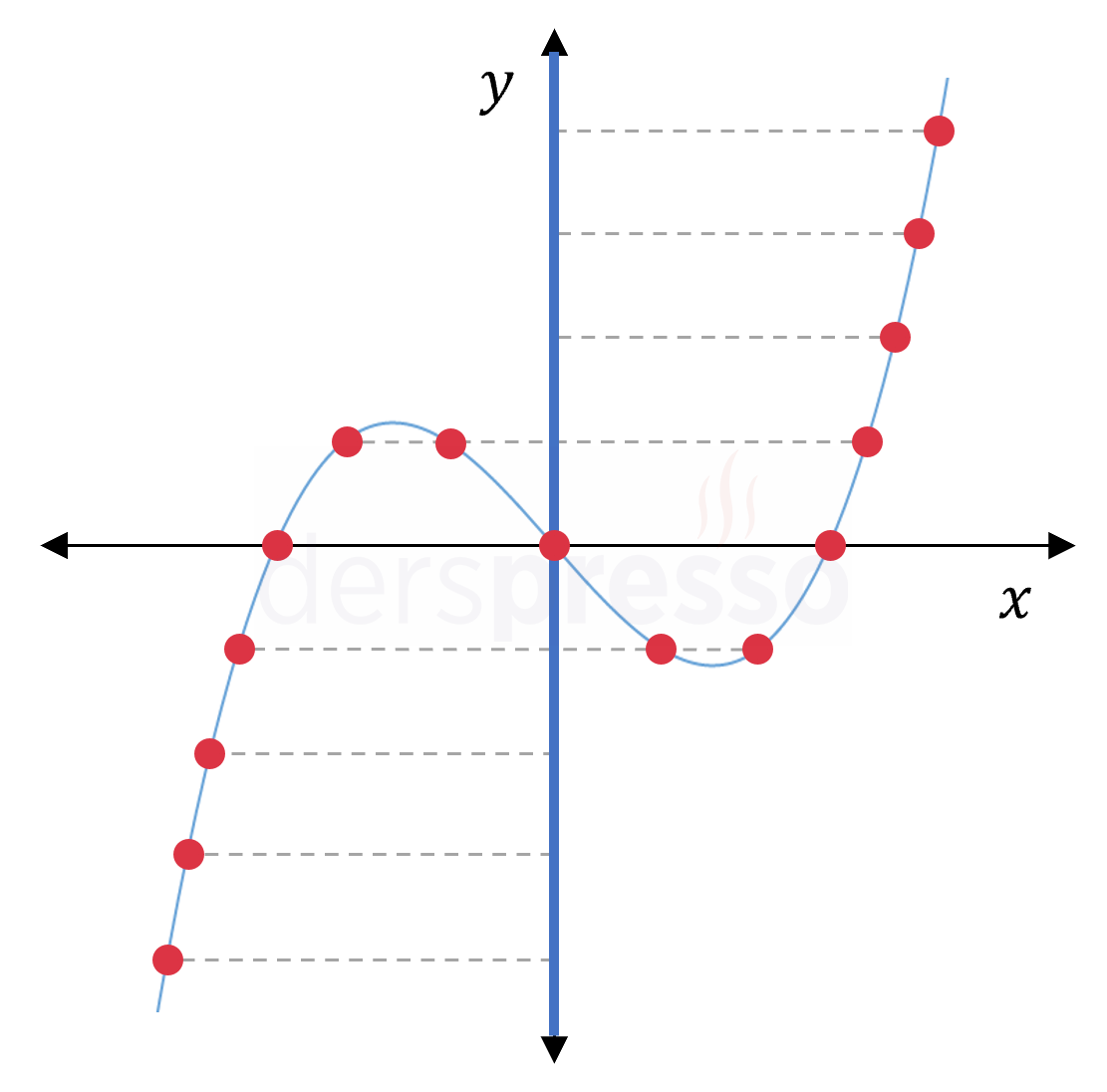
3. dereceden polinom fonksiyonu \( f: \mathbb{R} \to \mathbb{R} \) \( a \ne 0 \) \( f(x) = ax^3 + bx^2 + cx + d \) Grafik üzerindeki tüm noktaların \( y \) ekseni üzerindeki izdüşümlerini mavi renkle işaretlediğimizde grafiğin \( y \) ekseninin tümünü kapsadığını görebiliriz. Bu yüzden bu fonksiyon örtendir. |
|
\( A = \{ 1, 2, 3 \} \)
\( f : A \to A \) olmak üzere,
\( f = \{ (3, 1), (2, b), (a, 2) \} \)
fonksiyonu örten olduğuna göre, \( a + b \) kaçtır?
Çözümü GösterFonksiyon tanımı gereği tanım kümesinde açıkta eleman kalmamalıdır.
Bu koşulu sağlamak için \( a \) görüntüsü olmayan tek eleman olan 1'e eşit olmalıdır.
\( a = 1 \)
Fonksiyon örten olduğu için değer kümesindeki her eleman tanım kümesindeki bir elemanın görüntüsü olmalıdır.
Bu koşulu sağlamak için \( b \) açıkta kalan tek eleman olan 3'e eşit olmalıdır.
\( b = 3 \)
\( a + b = 1 + 3 = 4 \) bulunur.
\( A = \{ -3, -2, -1, 0, 1, 2, 3 \} \)
\( f : A \to B \) olmak üzere,
\( f(x) = x^2 + 2x + 2 \)
fonksiyonu içine olduğuna göre, \( B \) kümesinin eleman sayısı en az kaçtır?
Çözümü GösterTanım kümesindeki her bir elemanın görüntüsünü bulalım.
\( f(-3) = (-3)^2 + 2(-3) + 2 = 5 \)
\( f(-2) = (-2)^2 + 2(-2) + 2 = 2 \)
\( f(-1) = (-1)^2 + 2(-1) + 2 = 1 \)
\( f(0) = 0^2 + 2(0) + 2 = 2 \)
\( f(1) = 1^2 + 2(1) + 2 = 5 \)
\( f(2) = 2^2 + 2(2) + 2 = 10 \)
\( f(3) = 3^2 + 2(3) + 2 = 17 \)
Buna göre fonksiyonun görüntü kümesi 5 elemanlı olur.
\( f(A) = \{ 1, 2, 5, 10, 17 \} \)
Fonksiyonun içine olması için değer kümesinde açıkta en az bir eleman olmalıdır, dolayısıyla değer kümesi en az \( s(B) = 5 + 1 = 6 \) elemanlı olmalıdır.
\( A = \{ 2, 4, 6, 8 \} \)
\( B = \{ a, b, c, d \} \) olduğuna göre,
\( A \)'dan \( B \)'ye kaç farklı içine fonksiyon yazılabilir?
Çözümü GösterBir fonksiyon ya içine ya da örtendir, bu yüzden yazılabilecek içine fonksiyonların sayısı tüm fonksiyonların sayısının örten fonksiyonlardan farkına eşittir.
İçine fonksiyon sayısı = Tüm fonksiyonların sayısı - Örten fonksiyon sayısı
\( s(A) = m = 4 \)
\( s(B) = n = 4 \)
\( A \)'dan \( B \)'ye yazılabilecek fonksiyonların sayısı: \( n^m = 4^4 = 256 \)
\( s(A) = s(B) = 4 \) olduğu için yazılabilecek örten fonksiyonların sayısı: \( n! = 4! = 24 \)
Buna göre \( A \)'dan \( B \)'ye yazılabilecek içine fonksiyonların sayısı \( 256 - 24 = 232 \) olur.
\( s(A) = x^2 - 4 \) ve \( s(B) = 5x + 2 \) olmak üzere,
\( f: A \to B \) şeklinde tanımlı olan fonksiyon örtendir.
Buna göre \( B \) kümesi en az kaç elemanlıdır?
Çözümü GösterBir fonksiyonun örten olabilmesi için tanım kümesinin eleman sayısı değer kümesinin eleman sayısına eşit ya da ondan büyük olmalıdır.
\( s(A) \ge s(B) \)
\( x^2 - 4 \ge 5x + 2 \)
\( x^2 - 5x - 6 \ge 0 \)
\( (x + 1)(x - 6) \ge 0 \)
Eşitsizliğin sağlanması için \( x \le -1 \) ya da \( x \ge 6 \) olmalıdır.
\( x \le -1 \) aralığı için \( s(A) \) ve \( s(B) \) negatif değerler alır, bir kümenin eleman sayısı negatif olamayacağı için bu geçerli bir aralık değildir.
\( x \ge 6 \) aralığındaki en küçük değer olan 6'yı \( s(B) \) ifadesinde yerine koyarak \( B \) kümesinin eleman sayısının en küçük değerini bulalım.
\( s(B) = 5(6) + 2 = 32 \) bulunur.
\( f: \mathbb{R} \to B \)
\( f(x) = \begin{cases} -x + 8 & x \lt 3 \\ x + 1 & x \ge 3 \end{cases} \)
\( f \) fonksiyonu örten olduğuna göre, \( B \) kümesini bulunuz.
Çözümü GösterVerilen parçalı fonksiyonun grafiğini çizelim.
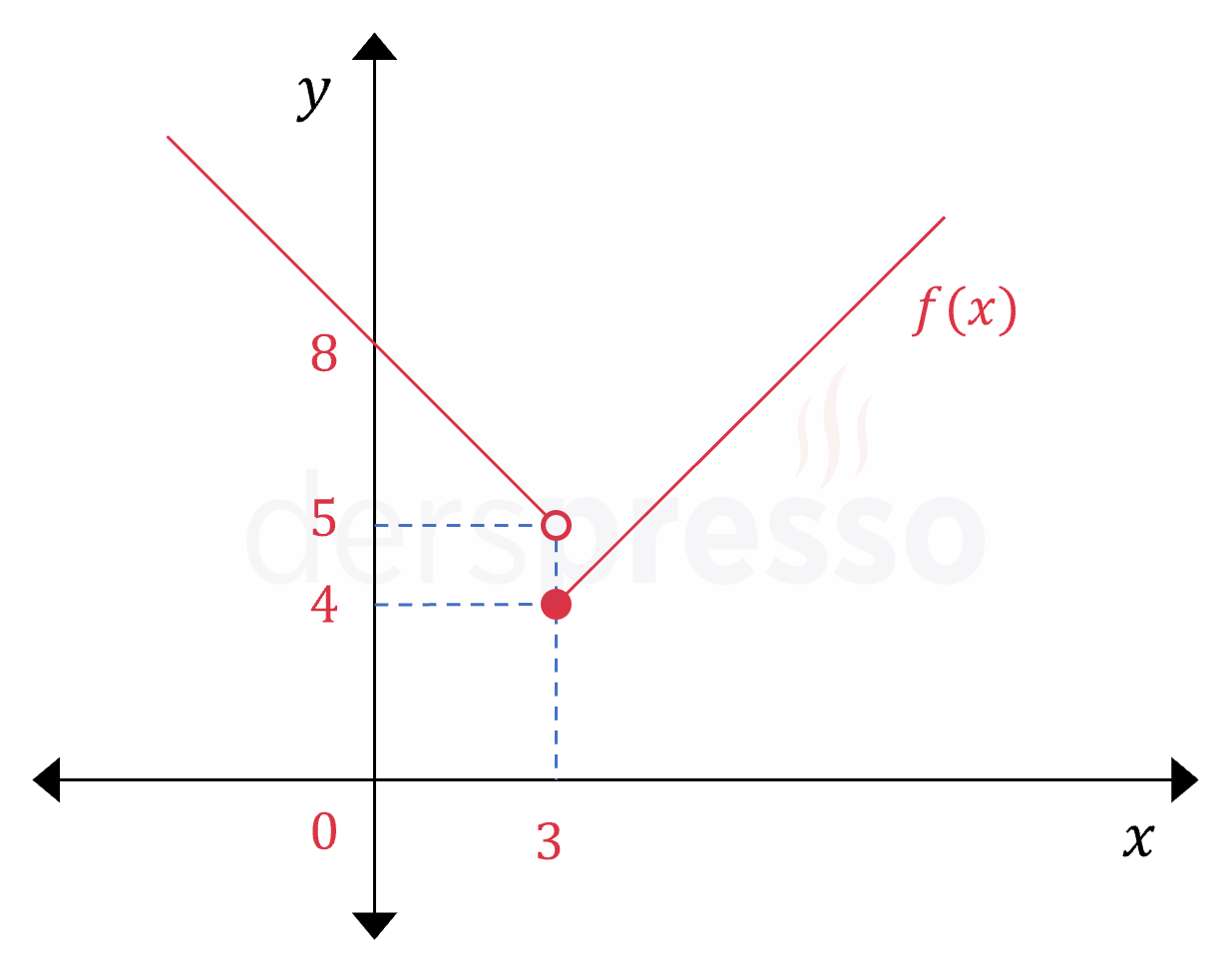
Grafikten görebileceğimiz üzere, fonksiyonun görüntü kümesi \( [4, \infty) \) olur.
\( f \) fonksiyonu örten olduğu için değer kümesi görüntü kümesine eşittir.
\( B = [4, \infty) \)
Aşağıdaki fonksiyonlardan hangileri içinedir?
(a) \( f: \mathbb{R} \to \mathbb{R}, \quad f(x) = x^2 \)
(b) \( g: \mathbb{N} \to \mathbb{N}, \quad g(x) = x + 2 \)
(c) \( h: \mathbb{R} \to \mathbb{R}, \quad h(x) = x\abs{x} \)
(d) \( k: \mathbb{Z} \to \mathbb{Z}, \quad k(x) = 5x - 7 \)
Çözümü Göster(a) seçeneği:
\( f: \mathbb{R} \to \mathbb{R}, \quad f(x) = x^2 \)
\( f \) fonksiyonunun tanım kümesindeki reel sayıların görüntüsü sadece sıfır ya da pozitif reel sayı olabileceği için değer kümesindeki negatif reel sayılar açıkta kalır.
\( f \) fonksiyonu içinedir.
(b) seçeneği:
\( g: \mathbb{N} \to \mathbb{N}, \quad g(x) = x + 2 \)
\( g \) fonksiyonunun tanım kümesindeki sayılar değer kümesinde kendilerinden iki fazla olan sayılarla eşlendiği için değer kümesindeki 0 ve 1 sayıları açıkta kalır.
\( g \) fonksiyonu içinedir.
(c) seçeneği:
\( h: \mathbb{R} \to \mathbb{R}, \quad h(x) = x\abs{x} \)
\( h \) fonksiyonu sıfır ve pozitif \( x \) değerleri için \( x^2 \) fonksiyonuna, negatif \( x \) değerleri için \( -x^2 \) fonksiyonuna eşittir ve tüm reel sayı değerlerini alır.
\( h \) fonksiyonu örtendir.
(d) seçeneği:
\( k: \mathbb{Z} \to \mathbb{Z}, \quad k(x) = 5x - 7 \)
\( k \) fonksiyonunda değer kümesinde açıkta e kalır (örneğin tanım kümesindeki hiçbir sayı değer kümesindeki 10 sayısı ile eşlenmez).
\( k \) fonksiyonu içinedir.
Buna göre \( f \), \( g \) ve \( k \) fonksiyonları içinedir.
\( B = \{-2, 0, 2, 4\} \)
\( f: A \to B \) olmak üzere,
\( f(x) = 2x - 4 \) fonksiyonu içine olduğuna göre, \( A \) kümesinin elemanları toplamı en fazla kaç olabilir?
Çözümü GösterFonksiyon içine olduğu için \( B \) kümesinin en az bir elemanı açıkta kalmalıdır.
Verilen fonksiyon tanımını kullanarak görüntüsü \( B \) kümesinin her bir elemanı olabilecek girdi değerlerini bulalım.
\( f(x) = -2 \) için:
\( 2x - 4 = -2 \Longrightarrow x = 1 \)
\( f(x) = 0 \) için:
\( 2x - 4 = 0 \Longrightarrow x = 2 \)
\( f(x) = 2 \) için:
\( 2x - 4 = 2 \Longrightarrow x = 3 \)
\( f(x) = 4 \) için:
\( 2x - 4 = 4 \Longrightarrow x = 4 \)
\( A \) kümesinin bu dört elemanı da içermesi durumunda fonksiyon örten olacaktır. Fonksiyon içine olduğu için en az bir eleman tanım kümesinin dışında kalmalıdır.
\( A \) kümesinin elemanları toplamının en büyük değeri \( x = 1 \) değeri hariç tutulduğunda elde edilir.
\( A = \{2, 3, 4\} \)
Buna göre \( A \) kümesinin elemanları toplamı en fazla \( 2 + 3 + 4 = 9 \) olur.
\( A = \{1, 2, 3\} \)
\( B = \{3, 4, 5\} \)
\( f: A \to B \) olmak üzere,
\( f \) fonksiyonu içine olduğuna göre, \( f(1) + f(2) + f(3) \) toplamı kaç farklı değer alabilir?
Çözümü GösterFonksiyon içine olduğuna göre, değer kümesinde en az bir eleman açıkta kalır, dolayısıyla görüntü kümesi 1 ya da 2 elemanlı olur.
Durum 1:
Görüntü kümesi 1 elemanlıdır.
\( f(1) + f(2) + f(3) = \)
\( 3 + 3 + 3 = 9 \)
\( 4 + 4 + 4 = 12 \)
\( 5 + 5 + 5 = 15 \)
Durum 2:
Görüntü kümesi 2 elemanlıdır.
\( f(1) + f(2) + f(3) = \)
\( 3 + 3 + 4 = 10 \)
\( 3 + 4 + 4 = 11 \)
\( 3 + 3 + 5 = 11 \)
\( 3 + 5 + 5 = 13 \)
\( 4 + 4 + 5 = 13 \)
\( 4 + 5 + 5 = 14 \)
Tüm olası durumları saydığımızda istenen toplamın 9 ve 15 arasında, yani \( 15 - 9 + 1 = 7 \) farklı değer alabildiğini görürüz.