Sabit Fonksiyon
Tanım kümesindeki tüm elemanların görüntüsü aynı sabit değer olan fonksiyonlara sabit fonksiyon denir. Sabit fonksiyonların değeri bir değişkene bağlı olarak değişmez.
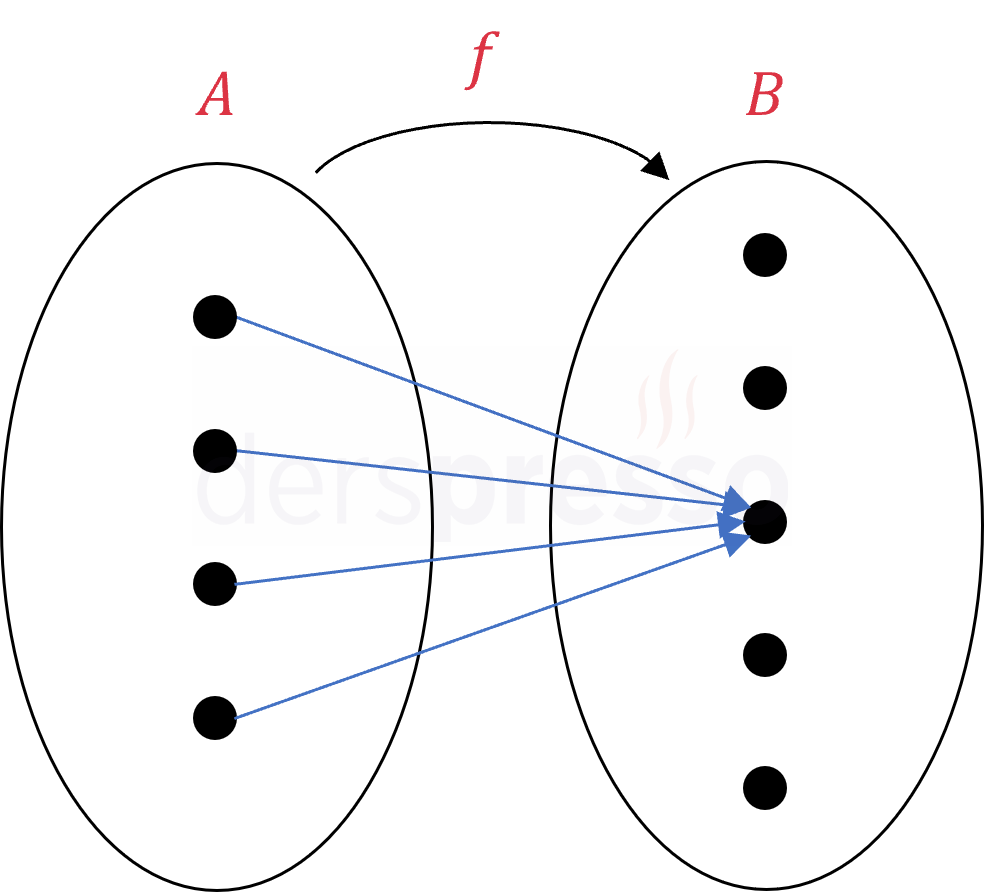
\( f: A \to B, \quad c \in B \) olmak üzere,
Her \( x \in A \) elemanı için \( f(x) = c \) ise,
\( f \) bir sabit fonksiyondur.
\( A = \{ a, b, c \} \)
\( B = \{ 0, 1, 2, 3 \} \)
\( f: A \to B \) olmak üzere,
\( f = \{ (a, 2), (b, 2), (c, 2) \} \) bir sabit fonksiyondur.
\( g: \mathbb{R} \to \mathbb{R} \) olmak üzere,
\( g(x) = 3 \) ise,
\( g(-2) = g(0) = g(4) = 3 \)
Sabit değeri sıfır olan sabit fonksiyonlara sıfır fonksiyonu da denir.
\( f(x) = 0 \) ise,
\( f \) sıfır fonksiyonudur.
Sabit fonksiyonun ve sıfır fonksiyonunun en geniş tanım kümeleri tüm reel sayılar, görüntü kümeleri de fonksiyonun sabit değeridir.
| Fonksiyon | Tanım Kümesi | Görüntü Kümesi |
|---|---|---|
| Sabit fonksiyon | \( \mathbb{R} \) | \( \{ c \} \) |
| Sıfır fonksiyonu | \( \mathbb{R} \) | \( \{ 0 \} \) |
Tüm sabit fonksiyonların grafiği yatay (eğimi sıfır olan) bir doğrudur.

Sabit fonksiyonlar bir değişken içermezler. Değişken içeren bir fonksiyonun sabit fonksiyon olduğu biliniyorsa değişkenli terimlerin katsayıları sıfır olmalıdır.
\( f(x) = ax^3 + bx^2 + cx + d \) bir sabit fonksiyon ise,
\( a = b = c = 0 \) koşulu sağlanmalıdır.
\( f(x) = (m + 3)x^2 + (2 - n)x - mn \) bir sabit fonksiyon ise,
\( m + 3 = 0 \Longrightarrow m = -3 \)
\( 2 - n = 0 \Longrightarrow n = 2 \)
\( f(x) = -mn = -(-6) = 6 \)
Değişken içeren aşağıdaki gibi bir rasyonel ifadenin sabit fonksiyon olduğu biliniyorsa değişken içeren terimler sadeleşecek ve sabit terim kalacak şekilde aşağıdaki oran sağlanmalıdır.
\( f(x) = \dfrac{ax + b}{cx + d} \) bir sabit fonksiyon ise,
\( \dfrac{a}{c} = \dfrac{b}{d} \) koşulu sağlanmalıdır.
\( f(x) = \dfrac{ax - 9}{2x + 3} \) bir sabit fonksiyon ise,
\( \dfrac{a}{2} = \dfrac{-9}{3} \Longrightarrow a = -6 \)
\( f(x) = \dfrac{-3(2x + 3)}{2x + 3} = -3 \)
Sabit Fonksiyon Sayısı
Sabit fonksiyonlarda tanım kümesinin tüm elemanları değer kümesinde aynı elemanla eşleneceği için, iki küme arasında tanımlanabilecek farklı sabit fonksiyon sayısı değer kümesinin eleman sayısına eşittir.
\( f: A \to B \)
Tanımlanabilecek sabit fonksiyon sayısı = \( s(B) \)
\( A = \{ a, b, c \} \)
\( B = \{ 1, 2, 3, 4 \} \)
\( f_1 = \{ (a, 1), (b, 1), (c, 1) \} \)
\( f_2 = \{ (a, 2), (b, 2), (c, 2) \} \)
\( f_3 = \{ (a, 3), (b, 3), (c, 3) \} \)
\( f_4 = \{ (a, 4), (b, 4), (c, 4) \} \)
Tüm sabit fonksiyonlar \( y \) eksenine göre simetrik oldukları için birer çift fonksiyondur. Özel bir durum olarak sıfır fonksiyonu (\( f(x) = 0 \)) aynı zamanda \( x \) eksenine göre de simetriktir ve hem çift hem tek fonksiyondur.
\( A = \{ a, b, c, d \} \)
\( B = \{ 0, 1, 2, 3, 4 \} \) olmak üzere,
\( A \)'dan \( B \)'ye görüntüsü çift sayı olan kaç sabit fonksiyon tanımlanabilir?
Çözümü Göster\( A \)'dan \( B \)'ye değer kümesindeki eleman sayısı kadar sabit fonksiyon tanımlanabilir. Bu fonksiyonlardan üçünde fonksiyonun görüntüsü bir çift sayıdır.
\( f(x) = 0 \)
\( f(x) = 2 \)
\( f(x) = 4 \)
\( f(x) = (a + b - 3)x^2 + 6a + 2(3b + 2) \)
bir sabit fonksiyon olduğuna göre, \( f(2a - b) \) kaçtır?
Çözümü Göster\( f \) sabit fonksiyon olduğu için \( x^2 \)'li terimin katsayısı sıfır olmalıdır.
\( a + b - 3 = 0 \Longrightarrow a + b = 3 \)
\( f(x) = 6a + 2(3b + 2) \)
\( = 6a + 6b + 4 \)
\( = 6(a + b) + 4 = 22 \)
Sabit fonksiyonun tüm \( x \) değerleri için değeri aynıdır.
\( f(2a - b) = 22 \) bulunur.
\( f(x) = \dfrac{ax^2 - bx + 9}{3x - b^2} \) bir sabit fonksiyon olduğuna göre, \( f(0) \) kaçtır?
Çözümü Göster\( f \) fonksiyonunun bir sabit fonksiyon olması için pay ve paydadaki ifadelerin sadeleşmesi sonucunda sabit bir terim kalmalıdır.
Paydaki ifadenin derecesi 2, paydadaki ifadenin derecesi 1 olduğunda \( x \)'li terimler tamamen sadeleşmeyeceği için paydaki \( x^2 \)'li terimin katsayısı sıfır olmalıdır.
\( a = 0 \)
\( f(x) = \dfrac{-bx + 9}{3x - b^2} \)
\( \dfrac{ax + b}{cx + d} \) formundaki bir fonksiyonun sabit fonksiyon olması için pay ve paydadaki aynı dereceli terimlerin katsayılarının oranı birbirine eşit olmalıdır.
\( \dfrac{-b}{3} = \dfrac{9}{-b^2} \)
\( b^3 = 27 \)
\( b = 3 \)
Buna göre fonksiyon tanımı aşağıdaki gibi olur.
\( f(x) = \dfrac{-3x + 9}{3x - 9} = -1 \)
\( f(0) = -1 \) olur.
\( f \) bir sabit fonksiyondur.
\( f(x - 11) = 5f(20 - x) - 12 \) olduğuna göre, \( f(113) \) kaçtır?
Çözümü Göster\( f \) sabit fonksiyon olduğundan tüm \( x \) değerleri için fonksiyonun görüntüsü aynıdır.
\( f(x) = a \) diyelim.
\( f(x - 11) = f(20 - x) = a \)
Sorudaki eşitliği \( a \) cinsinden yazalım.
\( a = 5a - 12 \)
\( a = 3 \)
\( f(113) = a = 3 \) bulunur.
\( f(x) = (n^2 - 4n - 2)x - 3 \)
bir sabit fonksiyon olduğuna göre, \( n \)'nin alabileceği değerlerin toplamı kaçtır?
Çözümü Göster\( f \) sabit fonksiyon olduğu için \( x \)'li terimin katsayısı sıfır olmalıdır.
\( n^2 - 4n - 2 = 0 \)
İkinci dereceden denklemin katsayılarını yazalım.
\( a = 1, \quad b = -4, \quad c = -2 \)
İkinci dereceden denklemin deltasını bulalım.
\( \Delta = b^2 - 4ac \)
\( = (-4)^2 - 4(1)(-2) = 24 \gt 0 \)
Denklemin deltası sıfırdan büyük olduğu için birbirinden farklı iki reel kökü vardır.
\( n \)'nin alabileceği değerler toplamı için denklemin kökler toplamını bulalım.
Kökler toplamı \( = -\dfrac{b}{a} = -\dfrac{-4}{1} = 4 \)
\( x = \dfrac{5f(x) - 2x + 1}{4f(x) - m} \) eşitliği veriliyor.
\( f \) bir sabit fonksiyon olduğuna göre, \( m \) kaçtır?
Çözümü GösterVerilen eşitlikte \( f(x) \)'i yalnız bırakalım.
\( x(4f(x) - m) = 5f(x) - 2x + 1 \)
\( 4xf(x) - mx = 5f(x) - 2x + 1 \)
\( 4xf(x) - 5f(x) = mx - 2x + 1 \)
\( f(x) = \dfrac{(m - 2)x + 1}{4x - 5} \)
\( \dfrac{ax + b}{cx + d} \) formundaki bir fonksiyonun sabit fonksiyon olması için pay ve paydadaki aynı dereceli terimlerin katsayılarının oranı birbirine eşit olmalıdır.
\( \dfrac{m - 2}{4} = \dfrac{1}{-5} \)
\( m - 2 = -\dfrac{4}{5} \)
\( m = \dfrac{6}{5} \) bulunur.
\( f \) bir sabit fonksiyondur.
\( f(1) \cdot f(2) \cdot f(3) \cdot \ldots \cdot f(100) = 2^{200} \) olduğuna göre,
\( f(17) + f(49) + f(98) \) ifadesinin en küçük değeri kaçtır?
Çözümü Göster\( a \in \mathbb{R} \) olmak üzere,
\( f(x) = a \) diyelim.
Soruda verilen eşitliği \( a \) cinsinden yazalım.
\( \underbrace{a \cdot a \cdot \ldots \cdot a}_\text{100 adet} = 2^{200} \)
\( a^{100} = 2^{200} = 4^{100} \)
\( a \) sayısının üssü çift sayı olduğundan \( a \) pozitif ya da negatif olabilir.
\( a = 4 \) ya da \( a = -4 \)
\( f \) sabit fonksiyon olduğundan tüm \( x \) değerleri için fonksiyonun görüntüsü aynıdır.
\( f(17) = f(49) = f(98) = a \)
\( f(17) + f(49) + f(98) = 3a \)
\( a = 4 \) için \( 3a = 12 \)
\( a = -4 \) için \( 3a = -12 \)
Buna göre \( f(17) + f(49) + f(98) \) ifadesinin en küçük değeri \( -12 \) olarak bulunur.
\( A = \{1, 3, 5, 7\} \)
\( B = \{1, 2, 4, 6\} \)
\( f: A \to B \) olmak üzere,
\( f = \{(1, b - 2a), (3, c), (b, d - 2), (7, a - 1)\} \) fonksiyonu sabit fonksiyon olduğuna göre, \( a + b + c + d \) kaçtır?
Çözümü GösterBir fonksiyonun tanım kümesindeki her elemanın bir görüntüsü olmalıdır, dolayısıyla \( b = 5 \) olmalıdır.
\( f = \{(1, 5 - 2a), (3, c), (5, d - 2), (7, a - 1)\} \)
\( f \) sabit fonksiyon olduğu için her elemanın görüntüsü aynı olmalıdır.
\( 5 - 2a = a - 1 \)
\( a = 2 \)
Buna göre fonksiyonun sabit değeri \( b - 2a = a - 1 = 1 \) olur.
\( f: \{(1, 1), (3, c), (5, d - 2), (7, 1)\} \)
\( c = 1 \)
\( d - 2 = 1 \Longrightarrow d = 3 \)
\( a + b + c + d = 2 + 5 + 1 + 3 = 11 \) bulunur.