Fonksiyonlarla İşlemler
Eşit Fonksiyonlar
Tanım kümeleri aynı olan ve tanım kümesindeki her eleman için fonksiyonların görüntüleri birbirine eşit olan fonksiyonlara eşit fonksiyon denir. Eşit fonksiyonlar \( f = g \) şeklinde gösterilirler.
\( f: A \to B, \quad g: A \to C \) olmak üzere,
her \( x \in A \) için \( f(x) = g(x) \) ise,
\( f \) ve \( g \) eşit fonksiyonlardır.
\( f = \{ (a, 1), (b, 2), (c, 3) \} \)
\( g = \{ (a, 1), (b, 2), (c, 3) \} \)
\( h = \{ (a, 1), (b, 2), (c, 4) \} \)
\( f = g, \quad f \ne h \)
\( f(x) = (m + 3)x^2 - 3x + np \)
\( g(x) = mnx + 5 \)
\( f(x) = g(x) \) olduğuna göre, \( m + n + p \) kaçtır?
Çözümü Gösterİki polinom fonksiyonunun eşit olabilmesi için (aynı girdi değerleri için aynı çıktı değerlerini üretebilmesi için) aynı dereceli terimlerin katsayıları birbirine eşit olmalıdır.
\( g \) fonksiyonunda \( x^2 \)'li bir terim olmadığı için \( f \) fonksiyonunda \( x^2 \)'li terimin katsayısı 0 olmalıdır.
\( m + 3 = 0 \Longrightarrow m = -3 \)
İki fonksiyonda \( x \)'li terimlerin katsayıları eşit olmalıdır.
\( -3 = mn \Longrightarrow n = 1 \)
İki fonksiyonda sabit terimler birbirlerine eşit olmalıdır.
\( np = 5 \Longrightarrow p = 5 \)
\( m + n + p = (-3) + 1 + 5 = 3 \) bulunur.
Fonksiyonlarla İşlemler
Tanım kümelerinin kesişimi boş küme olmayan fonksiyonlar arasında toplama/çarpma gibi temel işlemler yapılabilir ve bu işlemlerin sonucunda yeni birer fonksiyon elde edilir.
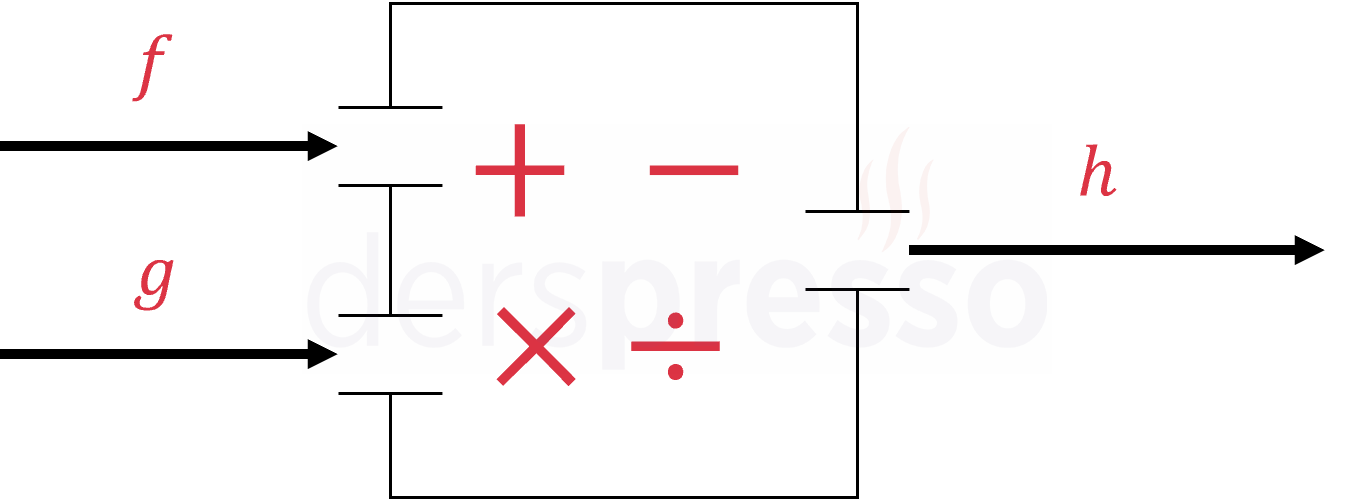
İki ya da daha fazla fonksiyon arasında yapılan işlemin sonucunun tanım kümesi, işlemin terimi olan fonksiyonların tanım kümelerinin kesişim kümesine eşittir.
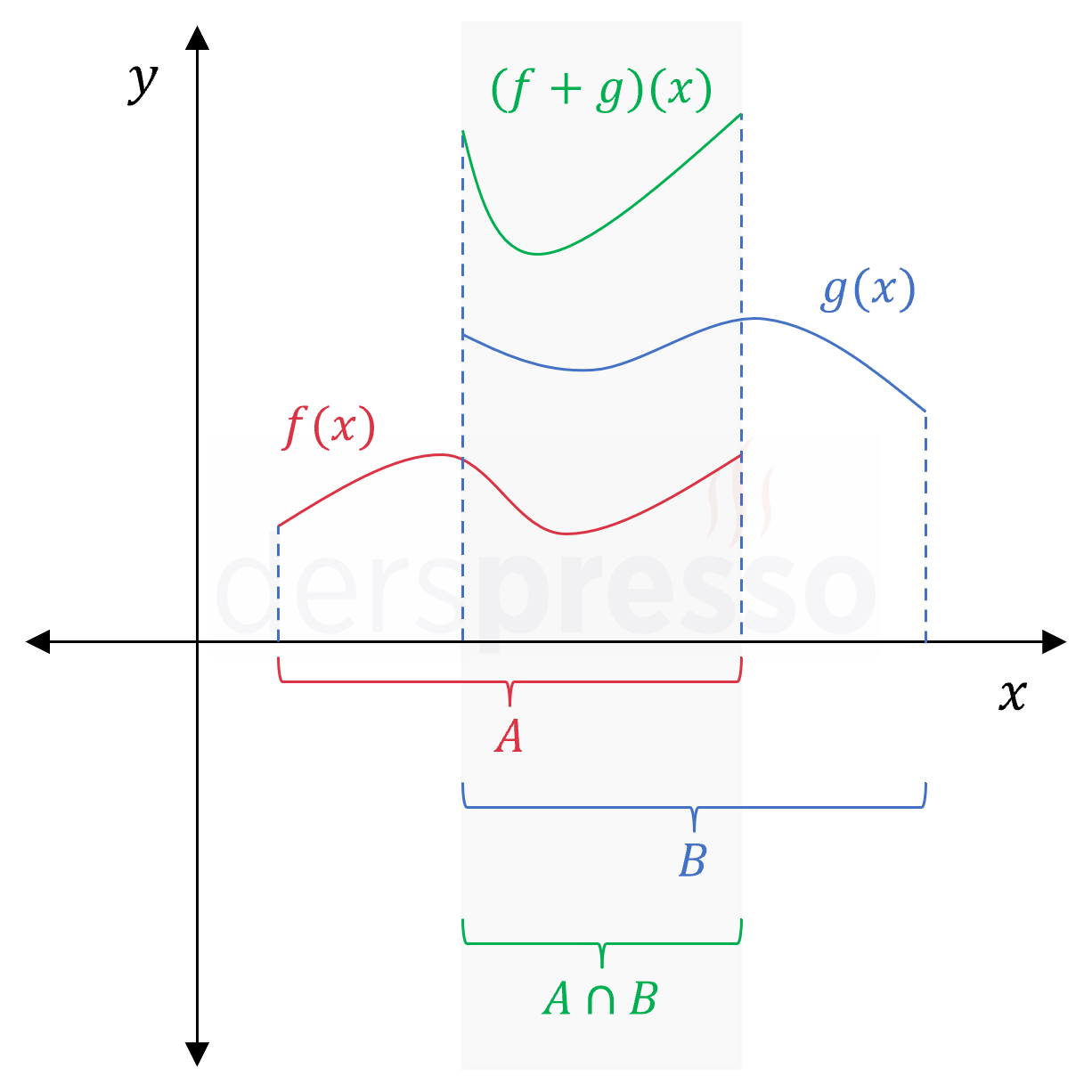
Bir işlemin terimi olan fonksiyonların değer kümeleri aynı olmalıdır ve bu değer kümesi sonuç fonksiyonunun da değer kümesi olur.
Fonksiyonlar arasındaki işlemleri aşağıdaki iki örnek fonksiyon üzerinden inceleyelim.
\( A \cap B \ne \emptyset \) olmak üzere,
\( f: A \to \mathbb{R} \)
\( f(x) = x^2 - 1 \)
\( f = \{ \ldots, (3, 8), (4, 15), \ldots \} \)
\( g: B \to \mathbb{R} \)
\( g(x) = x + 1 \)
\( g = \{ \ldots, (3, 4), (4, 5), \ldots \} \)
Toplama İşlemi
İki fonksiyon arasındaki toplama işleminde fonksiyonların tanım kümelerindeki ortak elemanların görüntüleri toplanır.
\( f + g: A \cap B \to \mathbb{R} \)
\( (f + g)(x) = f(x) + g(x) \)
\( (f + g)(x) = (x^2 - 1) + (x + 1) = x^2 + x \)
\( f + g = \{ \ldots, (3, 12), (4, 20), \ldots \} \)
Çıkarma İşlemi
İki fonksiyon arasındaki çıkarma işleminde fonksiyonların tanım kümelerindeki ortak elemanların görüntülerinin farkı alınır.
\( f - g: A \cap B \to \mathbb{R} \)
\( (f - g)(x) = f(x) - g(x) \)
\( (f - g)(x) = (x^2 - 1) - (x + 1) = x^2 - x - 2 \)
\( f - g = \{ \ldots, (3, 4), (4, 10), \ldots \} \)
Çarpma İşlemi
Bir fonksiyonun sabit bir sayı ile çarpma işleminde fonksiyonun tanım kümesindeki elemanların görüntüleri bu sayı ile çarpılır.
\( c \in \mathbb{R} \) olmak üzere,
\( (c \cdot f)(x) = c \cdot f(x) \)
\( (2 \cdot f)(x) = 2 \cdot (x^2 - 1) = 2x^2 - 2 \)
\( 2f = \{ \ldots, (3, 16), (4, 30), \ldots \} \)
İki fonksiyon arasındaki çarpma işleminde fonksiyonların tanım kümelerindeki ortak elemanların görüntüleri birbiriyle çarpılır.
\( f \cdot g: A \cap B \to \mathbb{R} \)
\( (f \cdot g)(x) = f(x) \cdot g(x) \)
\( (f \cdot g)(x) = (x^2 - 1) \cdot (x + 1) = x^3 + x^2 - x - 1 \)
\( f \cdot g = \{ \ldots, (3, 32), (4, 75), \ldots \} \)
Bölme İşlemi
İki fonksiyon arasındaki bölme işleminde fonksiyonların tanım kümelerindeki ortak elemanların görüntüleri birbirine bölünür.
\( g(x) \ne 0 \) olmak üzere,
\( f \div g: A \cap B \to \mathbb{R} \)
\( (f \div g)(x) = \dfrac{f(x)}{g(x)} \)
\( (f \div g)(x) = \dfrac{x^2 - 1}{x + 1} \)
\( f \div g = \{ \ldots, (3, 2), (4, 3), \ldots \} \)
Üs Alma İşlemi
Bir fonksiyonun üssünü alma işleminde fonksiyonun tanım kümesindeki elemanların görüntülerinin üssü alınır.
\( n \in \mathbb{Z^+} \) olmak üzere,
\( (f^n)(x) = f^n(x) \)
\( (f^2)(x) = f^2(x) = (x^2 - 1)^2 = x^4 - 2x^2 + 1 \)
\( f^2 = \{ \ldots, (3, 64), (4, 225), \ldots \} \)
\( f = \{(-1, 2), (0, 3), (1, -2)\} \)
\( g = \{(-1, 5), (0, 4), (1, -1)\} \) olduğuna göre,
\( \dfrac{(f \cdot g)(1)}{(f + g)(0)} \) ifadesinin değeri kaçtır?
Çözümü Gösterİki fonksiyon arasındaki toplama/çarpma işleminde fonksiyonların tanım kümelerindeki ortak elemanların görüntüleri birbiriyle toplanır/çarpılır.
\( \dfrac{(f \cdot g)(1)}{(f + g)(0)} = \dfrac{f(1) \cdot g(1)}{f(0) + g(0)} \)
\( = \dfrac{-2 \cdot (-1)}{3 + 4} = \dfrac{2}{7} \) bulunur.
\( f = \{(1, 7), (2, 6), (3, 4)\} \)
\( g = \{(0, 2), (1, 4), (2, -3), (4, 10)\} \)
olduğuna göre, \( f - g \) fonksiyonunun görüntü kümesi nedir?
Çözümü Göster\( f - g \) fonksiyonunun tanım kümesi iki kümenin tanım kümelerinin kesişim kümesinden oluşur.
\( f \) fonksiyonunun tanım kümesi \( \{1, 2, 3\} \) ve \( g \) fonksiyonunun tanım kümesi \( \{0, 1, 2, 4\} \) olduğu için, \( f - g \) fonksiyonunun tanım kümesi \( \{1, 2\} \) olur.
\( 1 \) elemanının \( f - g \) fonksiyonuna göre görüntüsünü bulalım.
\( f(1) = 7 \)
\( g(1) = 4 \)
\( (f - g)(1) = 7 - 4 = 3 \)
\( 2 \) elemanının \( f - g \) fonksiyonuna göre görüntüsünü bulalım.
\( f(2) = 6 \)
\( g(2) = -3 \)
\( (f - g)(2) = 6 - (-3) = 9 \)
\( f - g \) fonksiyonu aşağıdaki gibi olur.
\( f - g = \{(1, 3), (2, 9)\} \)
Buna göre \( f - g \) fonksiyonunun görüntü kümesi \( \{3, 9\} \) olur.
\( f(x) = k^x \) olduğuna göre, \( f(kx) \) ifadesinin sonucu \( f(x) \) cinsinden nedir?
Çözümü Göster\( f(kx) \) ifadesi için \( x \) yerine \( kx \) yazalım.
\( f(kx) = k^{kx} \)
\( = (k^x)^k \)
\( = [f(x)]^k \) bulunur.
\( (f + g)(x) = x^2 + 3 \)
\( (f - g)(2x) = x + 2 \)
olduğuna göre, \( f(2) \cdot g(2) \) kaçtır?
Çözümü GösterBirinci eşitlikte \( x = 2 \) yazalım.
\( (f + g)(2) = f(2) + g(2) = 2^2 + 3 = 7 \)
İkinci eşitlikte \( x = 1 \) yazalım.
\( (f - g)(2) = f(2) - g(2) = 1 + 2 = 3 \)
Elde ettiğimiz iki denklemi taraf tarafa toplayalım ve \( f(2) \) ve \( g(2) \) değerleri için çözelim.
\( 2f(2) = 10 \)
\( f(2) = 5 \)
\( g(2) = 2 \)
\( f(2) \cdot g(2) = 5 \cdot 2 = 10 \) olarak bulunur.
\( f \) doğrusal ve birebir bir fonksiyon olmak üzere,
\( (f + f)(x) = (f \circ f)(x) \) olduğuna göre, \( f(5) \) kaçtır?
Çözümü GösterDoğrusal \( f \) fonksiyonunu aşağıdaki şekilde tanımlayalım.
\( f(x) = ax + b \)
\( (f + f)(x) = (f \circ f)(x) \)
\( (ax + b) + (ax + b) = a(ax + b) + b \)
\( 2ax + 2b = a^2x + ab + b \)
İki polinomun eşitliğinde aynı dereceli terimlerin katsayıları birbirine eşit olur.
\( 2a = a^2 \Longrightarrow a \in \{0, 2\} \)
Fonksiyonun birebir olduğu verildiği için \( a = 0 \) olamaz, aksi durumda fonksiyon sabit fonksiyon olur ve birebir olmaz.
\( a = 2 \)
\( 2b = 2b + b \Longrightarrow b = 0 \)
Buna göre fonksiyon tanımı aşağıdaki gibi olur.
\( f(x) = 2x \)
\( f(5) = 10 \) olarak bulunur.
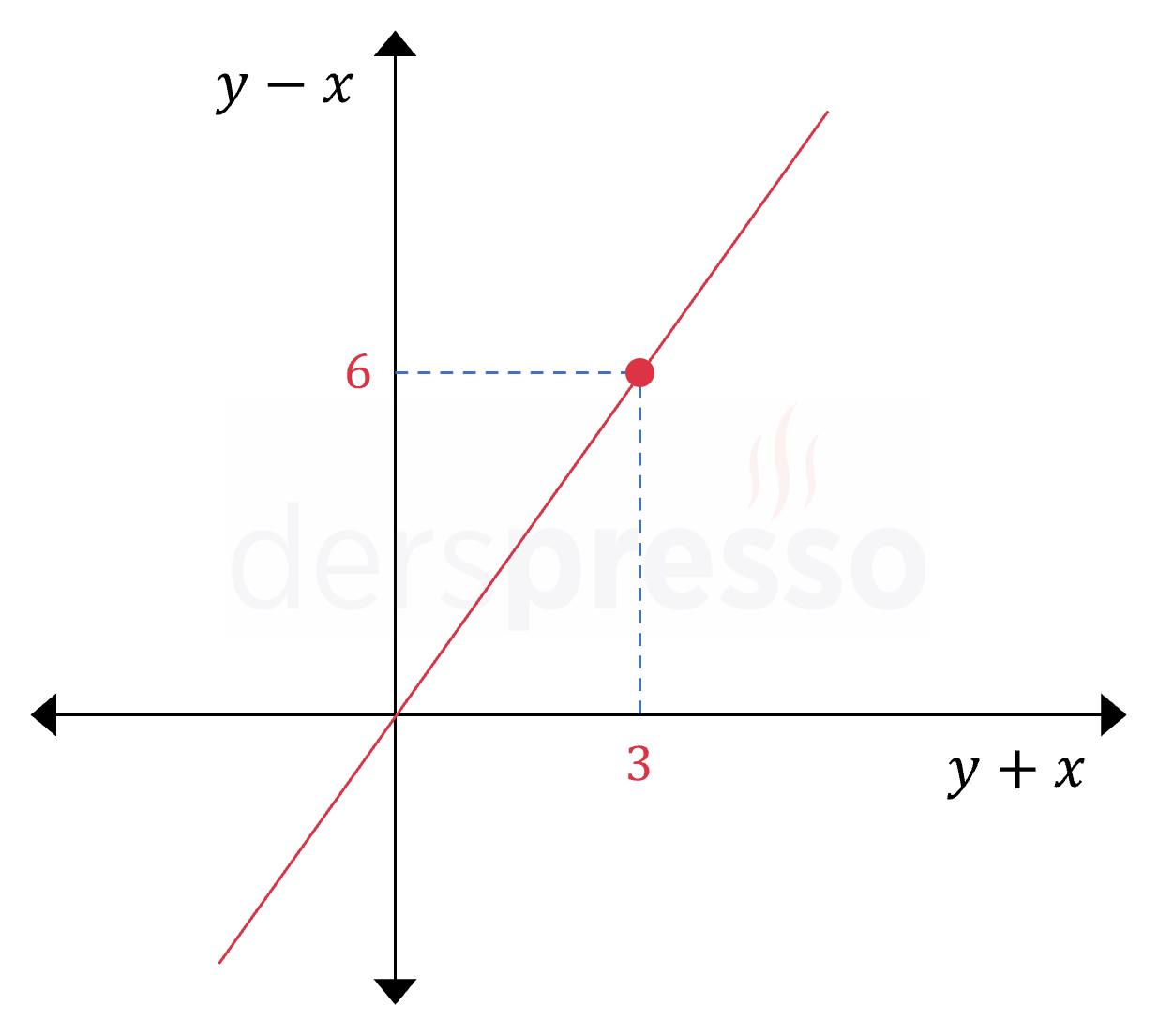
Yukarıdaki şekilde \( (y - x) \) değişkeninin \( (y + x) \) değişkenine göre grafiği verilmiştir.
Buna göre \( y \) değişkeninin \( x \) değişkenine göre grafiğini çiziniz.
Çözümü GösterVerilen şekilde grafiğin eğiminin 2 olduğunu görüyoruz.
\( \dfrac{y - x}{y + x} = \dfrac{6}{3} = 2 \)
\( y - x = 2y + 2x \)
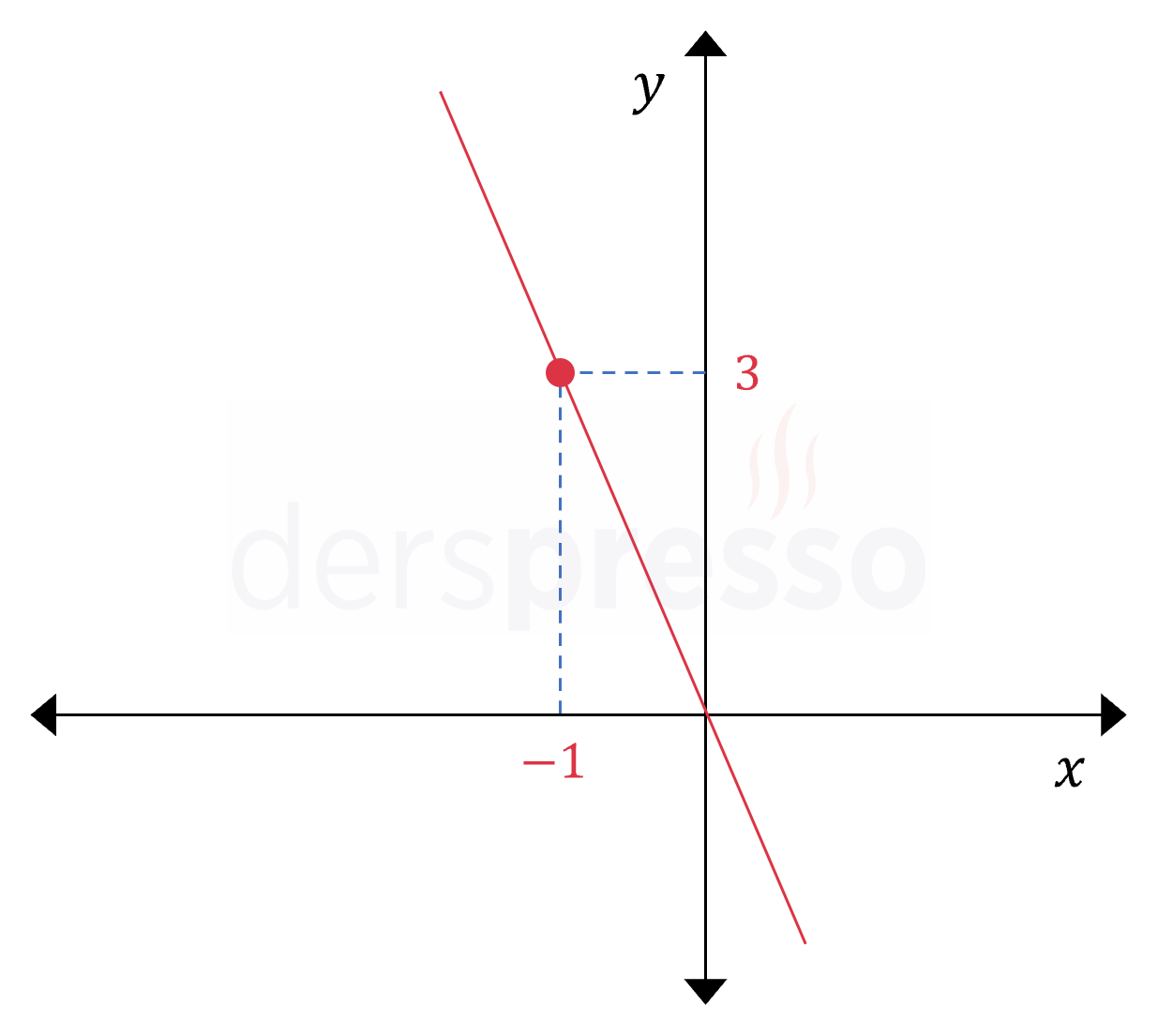
\( y = -3x \)
Buna göre \( y \) değişkeninin \( x \) değişkenine göre grafiği \( y = -3x \) doğrusudur.
\( f(x) = 2f(x - 1) - x \) ve \( f(0) = 1 \) olduğuna göre, \( f(3) \) kaçtır?
Çözümü Göster\( f(1) \) değerini bulmak için fonksiyonda \( x = 1 \) yazalım.
\( f(1) = 2f(0) - 1 = 2(1) - 1 = 1 \)
\( f(2) \) değerini bulmak için fonksiyonda \( x = 2 \) yazalım.
\( f(2) = 2f(1) - 2 = 2(1) - 2 = 0 \)
\( f(3) \) değerini bulmak için fonksiyonda \( x = 3 \) yazalım.
\( f(3) = 2f(2) - 3 = 2(0) - 3 = -3 \) bulunur.
\( f(x + 1) = f(x) + 5 \) ve \( f(1) = 3 \) olduğuna göre, \( f(32) \) kaçtır?
Çözümü Göster\( f(2) \) değerini bulmak için fonksiyonda \( x = 1 \) yazalım.
\( f(2) = f(1) + 5 = 3 + 5 = 8 \)
\( f(3) \) değerini bulmak için fonksiyonda \( x = 2 \) yazalım.
\( f(3) = f(2) + 5 = 8 + 5 = 13 \)
\( f(4) \) değerini bulmak için fonksiyonda \( x = 3 \) yazalım.
\( f(4) = f(3) + 5 = 13 + 5 = 18 \)
Görüldüğü üzere, \( x \) bir arttıkça \( f(x) \) beş artmaktadır.
Bu örüntüyü kullanarak fonksiyonu aşağıdaki şekilde tanımlayabiliriz.
\( f(x) = 5(x - 1) + 3 = 5x - 2 \)
\( f(32) \) değerini bulmak için \( x = 32 \) yazalım.
\( f(32) = 5(32) - 2 = 158 \) bulunur.
\( x \in \mathbb{Z^+} \) olmak üzere,
\( f(x + 1) = f(x) + f(x - 1) \)
\( f(7) = 102, \quad f(11) = 849 \)
Buna göre \( f(6) \) kaçtır?
Çözümü GösterEşitlikte sırasıyla \( x = 7 \), \( x = 8 \), \( x = 9 \), \( x = 10 \) yazalım.
\( f(8) = f(7) + f(6) \)
\( f(9) = f(8) + f(7) \)
\( f(10) = f(9) + f(8) \)
\( f(11) = f(10) + f(9) \)
Bilinmeyen her terimin yerine bir üst satırdaki karşılığını yazalım.
\( f(9) = f(8) + f(7) \)
\( = f(7) + f(6) + f(7) \)
\( = 2f(7) + f(6) \)
\( f(10) = f(9) + f(8) \)
\( = 2f(7) + f(6) + f(7) + f(6) \)
\( = 3f(7) + 2f(6) \)
\( f(11) = f(10) + f(9) \)
\( = 3f(7) + 2f(6) + 2f(7) + f(6) \)
\( = 5f(7) + 3f(6) \)
Soruda verilen değerleri bu eşitlikte yerine koyalım.
\( f(11) = 5f(7) + 3f(6) \)
\( 849 = 5(102) + 3f(6) \)
\( f(6) = 113 \) bulunur.
Bir \( f \) fonksiyonunun tanımı \( x \ge 1 \) için aşağıdaki şekilde veriliyor.
- \( x \) 2'ye bölünüp 5'e bölünmüyorsa: \( f(x) = f(x - 1) + 2 \)
- \( x \) 5'e bölünüp 2'ye bölünmüyorsa: \( f(x) = f(x - 1) - 3 \)
- \( x \) hem 2'ye hem 5'e bölünüyorsa: \( f(x) = f(x - 1) + 4 \)
- \( x \) ne 2'ye ne 5'e bölünmüyorsa: \( f(x) = f(x - 1) + 1 \)
\( f(0) = 0 \) olduğuna göre, \( f(4000) \) kaçtır?
Çözümü GösterVerilen fonksiyonu incelediğimizde her tam sayının görüntüsü ile bir eksiğinin görüntüsü arasında bir eşitlik kurulduğunu görüyoruz.
1 - 4000 arasındaki tam sayıları inceleyerek sadece 2'ye bölünen, sadece 5'e bölünen, iki sayıya da bölünen ve iki sayıya da bölünmeyen kaç tam sayı olduğunu bulalım.
2'ye bölünen sayılar:
\( x \in \{2, 4, \ldots, 3998, 4000\} \)
2'ye bölünen 2000 tam sayı bulunur.
5'e bölünen sayılar:
\( x \in \{5, 10, \ldots, 3995, 4000\} \)
5'e bölünen 800 tam sayı bulunur.
Hem 2'ye hem 5'e (10'a) bölünen sayılar:
\( x \in \{10, 20, \ldots, 3990, 4000\} \)
10'a bölünen 400 tam sayı bulunur.
2'ye bölünen ama 5'e bölünmeyen \( 2000 - 400 = 1600 \) tam sayı bulunur.
5'e bölünen ama 2'ye bölünmeyen \( 800 - 400 = 400 \) tam sayı bulunur.
Ne 2'ye ne de 5'e bölünen \( 4000 - 1600 - 400 - 400 = 1600 \) tam sayı bulunur.
Buna göre fonksiyon \( f(1) \) ve \( f(4000) \) arasında 1600 kez 2 artacak, 400 kez 3 azalacak, 400 kez 4 artacak, 1600 kez de 1 artacaktır.
Buna göre \( f(4000) \) değerini bulalım.
\( f(4000) = 0 + 1600 \cdot 2 + 400 \cdot (-3) + 400 \cdot 4 + 1600 \cdot 1 \)
\( = 3200 - 1200 + 1600 + 1600 \)
\( = 5200 \) olarak bulunur.
\( f(n) \) yinelemeli bir fonksiyon olmak üzere,
\( f(n) = \begin{cases} f(n - 1) + 1 & n \text{ tek sayı ise} \\ f(n - 3) + 4 & n \text{ çift sayı ise} \end{cases} \)
\( f(2) = 2 \) olduğuna göre, \( f(2023) \) kaça eşittir?
Çözümü GösterBir örüntü bulabilmek için \( n \)'ye birkaç değer verelim.
\( n = 2023 \Longrightarrow f(2023) = f(2022) + 1 \)
\( n = 2022 \Longrightarrow f(2022) = f(2019) + 4 \)
\( f(2022) \) değerini birinci eşitlikte yerine koyalım.
\( f(2023) = f(2022) + 1 = f(2019) + 4 + 1 \)
\( = f(2019) + 5 \)
Uyguladığımız iki adım sonunda \( n \) yine tek sayı olduğu için bu döngü her iki adımda bir tekrarlanacaktır.
Buna göre bu iki adımı tek adım olarak aşağıdaki şekilde ifade edebiliriz.
\( n \) tek sayı olmak üzere,
\( f(n) = f(n - 4) + 5 \)
\( 4 \cdot 505 + 3 = 2023 \)
Buna göre \( f(2023) \) değeri \( f(3) \) değerine 505 kez 5 eklenmesi ile oluşur.
\( f(2023) = f(3) + 505 \cdot 5 \)
\( = f(3) + 2525 \)
Orijinal fonksiyon tanımını kullanarak \( f(3) \) değerini \( f(2) \) cinsinden yazalım.
\( f(3) = f(2) + 1 \)
\( f(2023) = f(3) + 2525 \)
\( = f(2) + 1 + 2525 \)
\( = 2 + 1 + 2525 \)
\( = 2528 \) bulunur.
Özel Fonksiyonel İlişkiler
İki sayının toplamının görüntüsü, sayıların ayrı ayrı görüntülerinin toplamına eşit ise bu fonksiyon bir doğrusal fonksiyondur.
\( f(x) \ne 0 \) olmak üzere,
\( f(x + y) = f(x) + f(y) \) ise,
\( f(x) = ax \quad (a \in \mathbb{R}) \)
\( f(x) = 2x \)
\( f(3 + 5) = f(3) + f(5) \)
\( 2 \cdot 8 = 2 \cdot 3 + 2 \cdot 5 \)
İki sayının toplamının görüntüsü, sayıların ayrı ayrı görüntülerinin çarpımına eşit ise bu fonksiyon bir üstel fonksiyondur.
\( f(x) \ne 0 \) olmak üzere,
\( f(x + y) = f(x) \cdot f(y) \) ise,
\( f(x) = a^{kx} \quad (a, k \in \mathbb{R}) \)
\( f(x) = 2^x \)
\( f(3 + 5) = f(3) \cdot f(5) \)
\( 2^8 = 2^3 \cdot 2^5 \)
İki sayının çarpımının görüntüsü, sayıların ayrı ayrı görüntülerinin toplamına eşit ise bu fonksiyon bir logaritma fonksiyonudur.
\( f(x) \ne 0, \quad x, y \gt 0 \) olmak üzere,
\( f(x \cdot y) = f(x) + f(y) \) ise,
\( f(x) = k \cdot \ln{x} \quad (k \in \mathbb{R}) \)
\( f(x) = \ln{x} \)
\( f(3 \cdot 5) = f(3) + f(5) \)
\( \ln{15} = \ln{3} + \ln{5} \)
İki sayının çarpımın görüntüsü, sayıların ayrı ayrı görüntülerinin çarpımına eşit ise bu fonksiyon bir kuvvet fonksiyonudur.
\( f(x) \ne 0 \) olmak üzere,
\( f(x \cdot y) = f(x) \cdot f(y) \) ise,
\( f(x) = x^n \quad (n \in \mathbb{R}) \)
\( f(x) = x^3 \)
\( f(3 \cdot 5) = f(3) \cdot f(5) \)
\( (3 \cdot 5)^3 = 3^3 \cdot 5^3 \)
\( f(x \cdot y) = f(x) + f(y) \) ve \( f(3) = 6 \) olduğuna göre, \( f(27) \) kaçtır?
Çözümü Göster\( f(27) = f(3 \cdot 9) = f(3) + f(9) \)
\( = f(3) + f(3 \cdot 3) = f(3) + f(3) + f(3) \)
\( = 6 + 6 + 6 = 18 \) bulunur.
\( f(a + b) = f(a) \cdot f(b) \)
Aşağıdaki fonksiyonlardan hangileri her \( a \) ve \( b \) reel sayısı için yukarıdaki eşitliği sağlar?
I. \( f(x) = 3x \)
II. \( g(x) = x^3 \)
III. \( h(x) = 3^x \)
IV. \( k(x) = \log_3{x} \)
Çözümü GösterI. öncül:
\( f(x) = 3x \)
\( f(a + b) = 3(a + b) \)
\( f(a) = 3a \)
\( f(b) = 3b \)
\( 3(a + b) \ne 3a \cdot 3b \)
Bu öncül verilen koşulu sağlamaz.
II. öncül:
\( g(x) = x^3 \)
\( g(a + b) = (a + b)^3 \)
\( g(a) = a^3 \)
\( g(b) = b^3 \)
\( (a + b)^3 \ne a^3 \cdot b^3 \)
Bu öncül verilen koşulu sağlamaz.
III. öncül:
\( h(x) = 3^x \)
\( h(a + b) = 3^{a + b} \)
\( h(a) = 3^a \)
\( h(b) = 3^b \)
\( 3^{a + b} = 3^a \cdot 3^b \)
Bu öncül verilen koşulu sağlar.
IV. öncül:
\( k(x) = \log_3{x} \)
\( k(a + b) = \log_3(a + b) \)
\( k(a) = \log_3{a} \)
\( k(b) = \log_3{b} \)
\( \log_3(a + b) \ne \log_3{a} \cdot \log_3{b} \)
Bu öncül verilen koşulu sağlamaz.
Sadece III. öncüldeki fonksiyon verilen koşulu sağlar.