Birim Fonksiyon
Tanım kümesindeki tüm elemanların görüntüsü yine kendisi olan fonksiyona birim fonksiyon denir. Birim fonksiyonlar \( I \) ile gösterilir. Birim fonksiyona etkisiz fonksiyon ya da özdeş fonksiyon da denir.
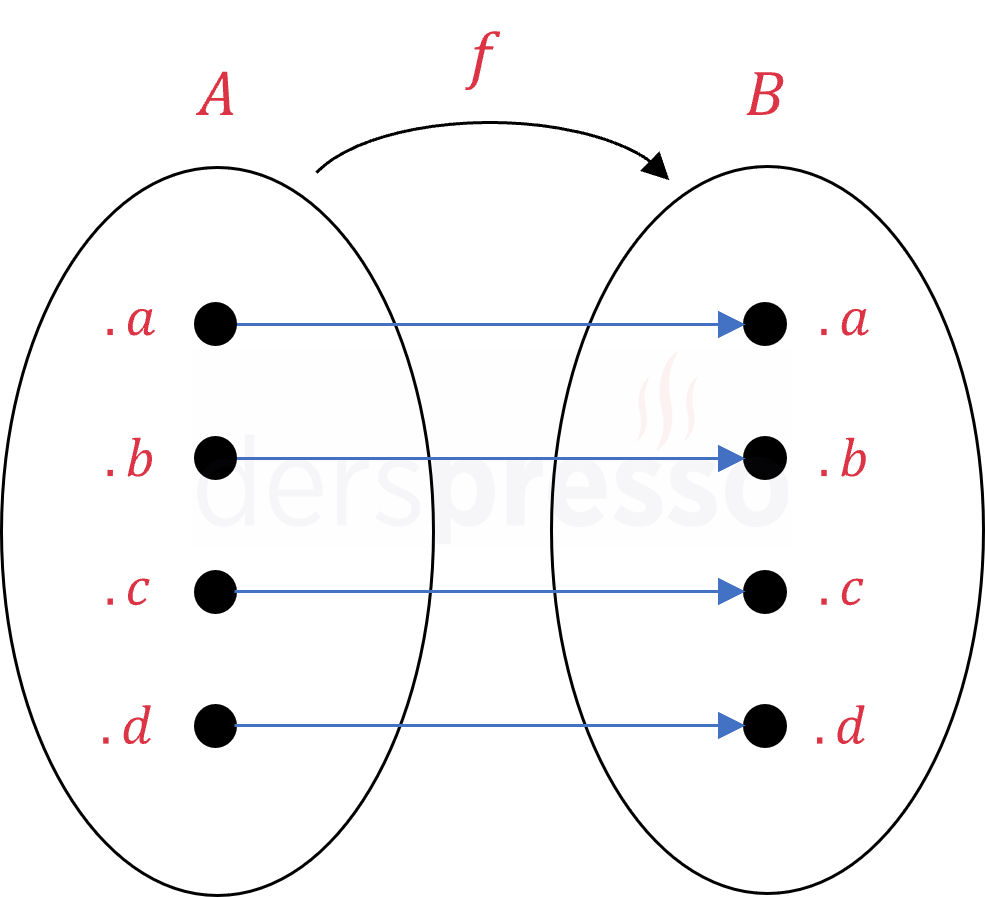
\( f: A \to A \) olmak üzere,
Her \( x \in A \) elemanı için \( f(x) = x \) ise,
\( f \) birim fonksiyondur.
Birim fonksiyon birebir ve örtendir.
\( f(2x + 1) = ax^2 + bx + a - 2b - c \) birim fonksiyon olduğuna göre, \( c \) kaçtır?
Çözümü GösterBirim fonksiyonun tanım kümesindeki tüm elemanların görüntüsü yine kendisidir.
Buna göre aşağıdaki eşitlik sağlanmalıdır.
\( f(2x + 1) = 2x + 1 \)
\( ax^2 + bx + a - 2b - c = 2x + 1 \)
İki polinomun eşitliğinde derecesi aynı olan terimlerin katsayıları birbirine eşittir.
\( a = 0 \)
\( b = 2 \)
\( a - 2b - c = 1 \)
\( 0 - 2(2) - c = 1 \)
\( c = -5 \) bulunur.
\( f(x - 1) = \dfrac{ax^2 + bx + c}{x - 2} \) birim fonksiyon olduğuna göre, \( f(a + b - c) \) kaçtır?
Çözümü GösterBirim fonksiyonun tanım kümesindeki tüm elemanların görüntüsü yine kendisidir.
Buna göre aşağıdaki eşitlik sağlanmalıdır.
\( f(x - 1) = x - 1 \)
\( \dfrac{ax^2 + bx + c}{x - 2} = x - 1 \)
\( ax^2 + bx + c = (x - 1)(x - 2) \)
\( ax^2 + bx + c = x^2 - 3x + 2 \)
İki polinomun eşitliğinde derecesi aynı olan terimlerin katsayıları birbirine eşittir.
\( a = 1, \quad b = -3, \quad c = 2 \)
\( f(a + b - c) = f(1 + (-3) - 2) = f(-4) \)
Birim fonksiyonda girdi ve çıktı değerleri birbirine eşittir.
\( = -4 \) bulunur.
\( f \) birim fonksiyon ve \( g \) sabit fonksiyon olmak üzere,
\( f(3k - 1) + g(n + 1) = f(k + 3) + g(2n) \) olduğuna göre, \( k \) kaçtır?
Çözümü Göster\( g \) sabit fonksiyon olduğu için \( g(n + 1) = g(2n) \) olur, dolayısıyla eşitliğin iki tarafındaki bu iki ifade birbirini götürür.
\( f(3k - 1) = f(k + 3) \)
\( f \) birim fonksiyon olduğu için \( f(x) = x \) olur.
\( f(3k - 1) = 3k - 1 \)
\( f(k + 3) = k + 3 \)
Bu değerleri eşitlikte yerine koyalım.
\( 3k - 1 = k + 3 \)
\( k = 2 \) bulunur.
\( f \) birim fonksiyondur.
\( f(k) + f(2k) + f(3k) + \ldots + f(24k) = 900 \) olduğuna göre, \( f(k^3) \) kaçtır?
Çözümü GösterBirim fonksiyon aşağıdaki şekilde tanımlıdır.
\( f(x) = x \)
\( f(k) = k, f(2k) = 2k, \ldots, f(24k) = 24k \)
\( k + 2k + 3k + \ldots + 24k = 900 \)
Ardaşık sayıların toplam formülünü kullanalım.
\( \dfrac{k + 24k}{2} \cdot 24 = 900 \)
\( 25k = 75 \)
\( k = 3 \)
\( f(k^3) = f(3^3) = f(27) = 27 \) bulunur.
Aşağıdaki fonksiyonların birim fonksiyon olduğu en geniş tanım kümelerini bulunuz.
(a) \( f(x) = e^{\ln{x}} \)
(b) \( g(x) = \ln{e^x} \)
(c) \( h(x) = \sin(\arcsin{x}) \)
Çözümü Göster(a) seçeneği:
\( f \) fonksiyonu birim fonksiyon şeklinde ifade edilebilir.
\( f(x) = e^{\ln{x}} = x \)
\( \ln{x} \) fonksiyonunun tanım kümesi \( x \in (0, \infty) \) olduğu için \( f \) fonksiyonunun tanım kümesi de bu aralık olur.
\( f: \mathbb{R^+} \to \mathbb{R^+} \)
(b) seçeneği:
\( g \) fonksiyonu birim fonksiyon şeklinde ifade edilebilir.
\( g(x) = \ln{e^x} = x\ln{e} = x \)
\( e^x \) ifadesinin tanım kümesi tüm reel sayılar ve görüntü kümesi pozitif reel sayılar olduğu için \( \ln{e^x} \) ifadesi tüm reel sayılarda tanımlıdır.
\( g: \mathbb{R} \to \mathbb{R} \)
(c) seçeneği:
\( h \) fonksiyonu birim fonksiyon şeklinde ifade edilebilir.
\( h(x) = \sin(\arcsin{x}) = x \)
\( \arcsin{x} \) fonksiyonunun tanım kümesi \( x \in [-1, 1] \) olduğu için \( h \) fonksiyonunun tanım kümesi de bu aralık olur.
\( h: [-1, 1] \to [-1, 1] \)