Ters Fonksiyon
Bir \( f \) fonksiyonunun \( (a, b) \) şeklindeki tüm eşlemelerini \( (b, a) \) şeklinde tersine çeviren fonksiyona \( f \) fonksiyonunun ters fonksiyonu denir ve \( f^{-1} \) ile gösterilir.
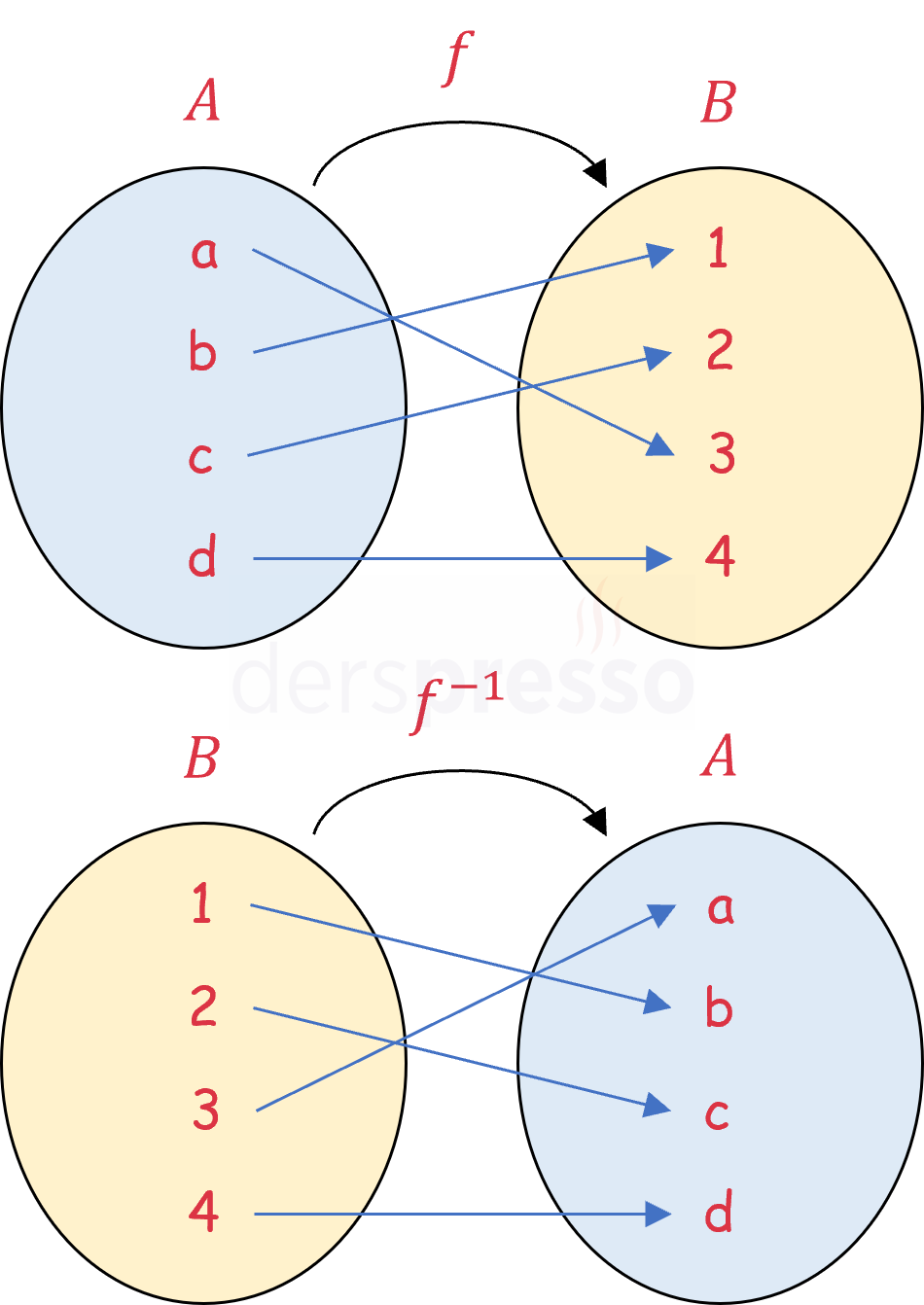
\( f: A \to B \) olmak üzere,
\( f \) fonksiyonunun tersi olan \( f^{-1} \) fonksiyonu (eğer tanımlı ise) aşağıdaki koşulları sağlar.
\( f^{-1}: B \to A \)
\( (a, b) \in f \iff (b, a) \in f^{-1} \)
\( f \): Kimyasal elementleri sembolleri ile eşleyen fonksiyon
\( f = \) {(Hidrojen, H), (Karbon, C), (Oksijen, O), (Demir, Fe), ...}
\( f^{-1} = \) {(H, Hidrojen), (C, Karbon), (O, Oksijen), (Fe, Demir), ...}
\( g \): Ülkeleri plaka kodları ile eşleyen fonksiyon
\( g = \) {(Almanya, D), (İtalya, I), (Meksika, MEX), (Türkiye, TR), ...}
\( g^{-1} = \) {(D, Almanya), (I, İtalya), (MEX, Meksika), (TR, Türkiye), ...}
Yukarıdaki birinci örneği kullanırsak, demirin \( f \) fonksiyonuna göre görüntüsü Fe'dir, Fe'nin \( f \) fonksiyonuna göre ters görüntüsü de demirdir.
\( f(\text{Demir}) = \text{Fe} \)
\( f^{-1}(\text{FE}) = \text{Demir} \)
Bir \( a \) değerinin \( f \) fonksiyonuna göre görüntüsünün yine \( f \) fonksiyonuna göre ters görüntüsü kendisine eşittir. Benzer şekilde, bir \( b \) değerinin \( f^{-1} \) fonksiyonuna göre görüntüsünün yine \( f^{-1} \) fonksiyonuna göre ters görüntüsü kendisine eşittir.
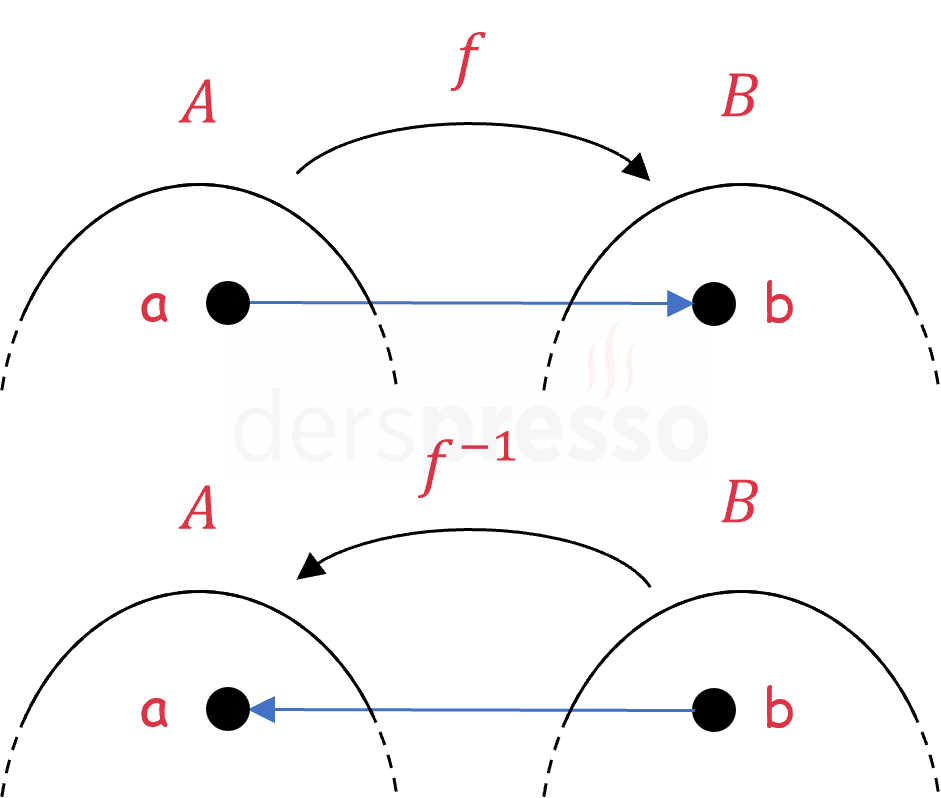
\( a \in A, \quad b \in B \) olmak üzere,
\( f^{-1}(f(\textcolor{red}{a})) = f^{-1}(b) = \textcolor{red}{a} \)
\( f(f^{-1}(\textcolor{blue}{b})) = f(a) = \textcolor{blue}{b} \)
Ters fonksiyonun gösteriminde kullanılan \( -1 \) üslü ifadelerde kullanılan üs ile karıştırılmamalıdır, yani bir fonksiyonun tersi o fonksiyonun -1. kuvveti yani çarpmaya göre tersi demek değildir.

Daha önce yaptığımız fonksiyon - makine benzetmesini ters fonksiyona aşağıdaki şekilde uyarlayabiliriz.
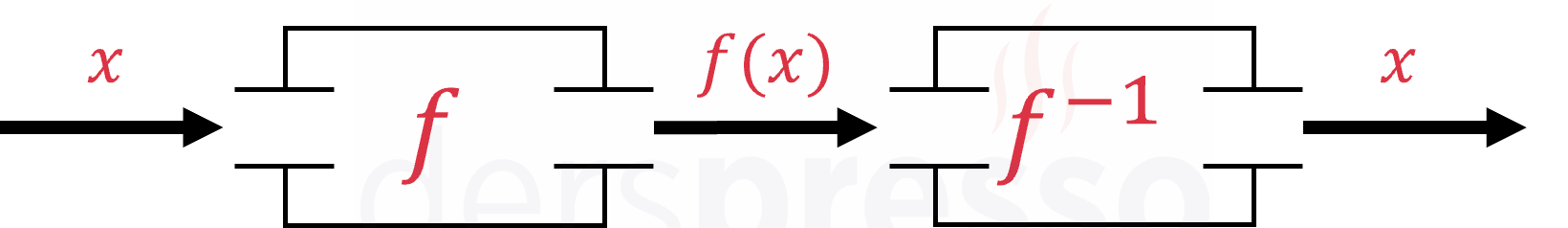
Ters Fonksiyonun Tanımlı Olma Koşulları
\( A \)'dan \( B \)'ye tanımlı bir bağıntının fonksiyon olabilmesi için gerekli iki koşulu aşağıdaki şekilde tanımlamıştık.
- \( A \) kümesinde \( B \) kümesinin bir elemanıyla eşlenmemiş açıkta eleman kalmamalıdır.
- \( A \) kümesinin her elemanı \( B \) kümesinde sadece bir elemanla eşlenmelidir (iyi tanımlılık).
\( f \) fonksiyonunun tersi olan \( f^{-1} \) de bir fonksiyon olduğu için bu iki koşulu sağlamalıdır. Aşağıda göstereceğimiz üzere, \( f^{-1} \) fonksiyonunun bu iki koşulu sağlaması için \( f \) fonksiyonu birebir ve örten olmalıdır.
Birebir ve örten olmayan bir \( f \) fonksiyonunun ters fonksiyonu tanımlı değildir.
Örten Olma Koşulu
\( f^{-1} \) fonksiyonunun birinci fonksiyon olma koşulunu sağlaması için, \( B \) kümesinde \( A \) kümesinin bir elemanıyla eşlenmemiş açıkta eleman kalmamalıdır, yani \( f \) örten olmalıdır.
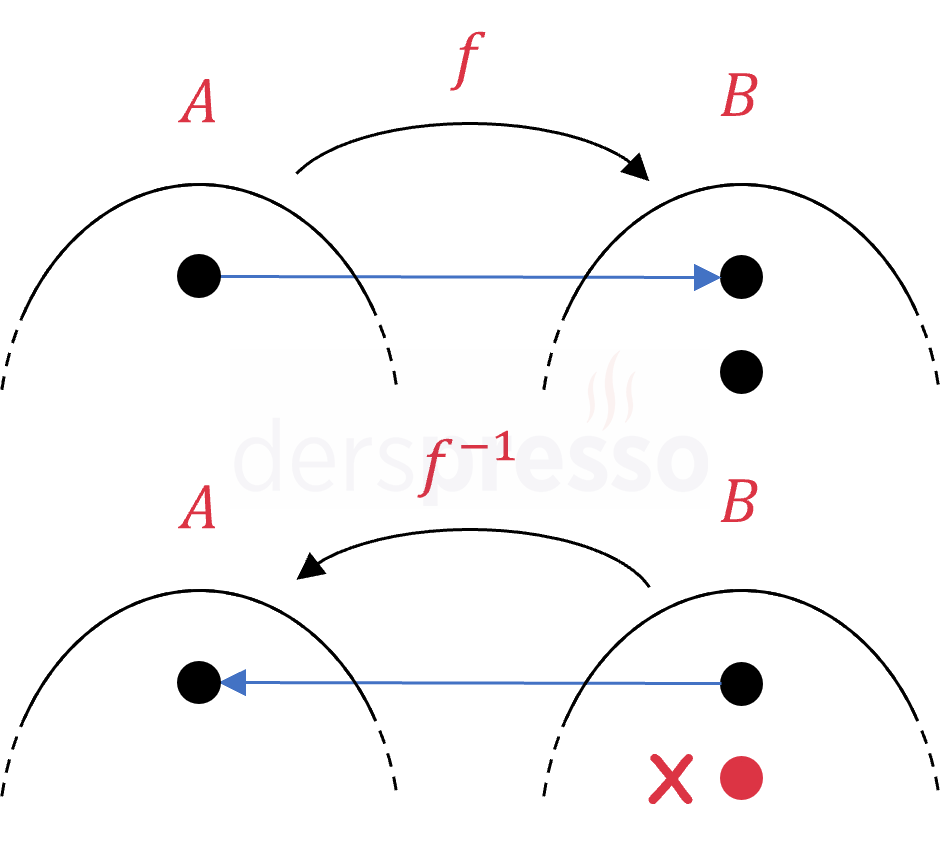
Yukarıdaki örnekteki gibi \( f \) fonksiyonunun örten olmadığı durumda \( B \) kümesinde açıkta eleman kalır ve bu elemanlar \( f^{-1} \) fonksiyonunda \( A \) kümesinin bir elemanıyla eşlenemez ve \( f^{-1} \) fonksiyonu için birinci fonksiyon olma koşulu sağlanmamış olur.
Birebir Olma Koşulu
\( f^{-1} \) fonksiyonunun ikinci fonksiyon olma koşulunu sağlaması için, \( B \) kümesinin her elemanı \( A \) kümesinde sadece bir elemanla eşlenmelidir, yani \( f \) birebir olmalıdır.
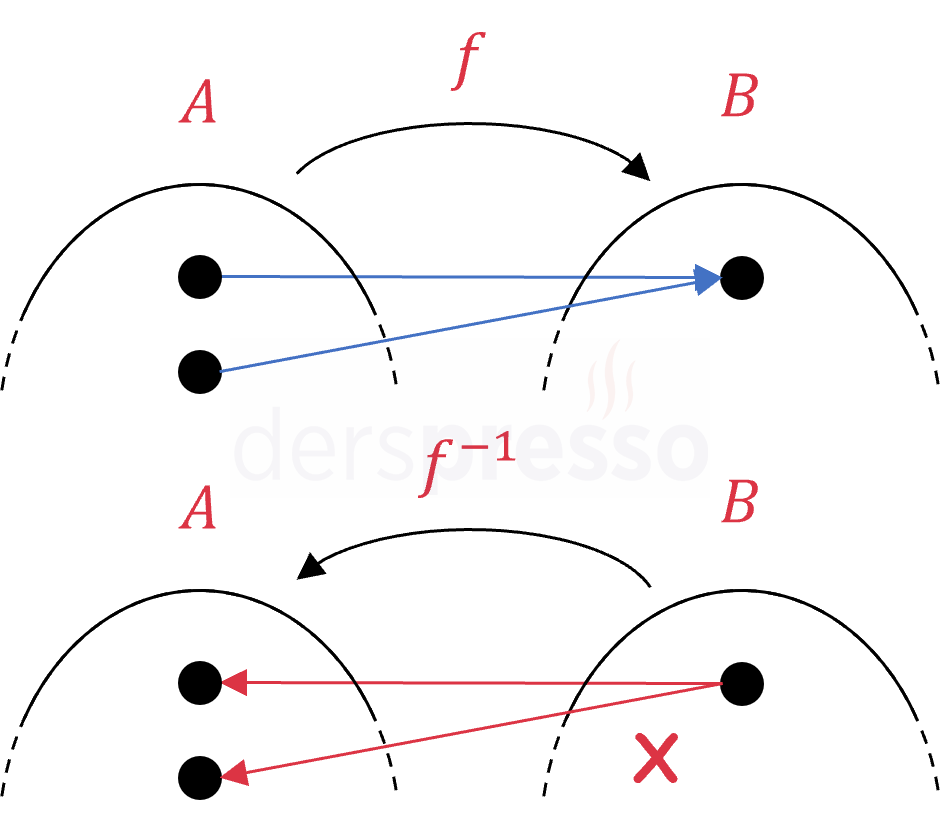
Yukarıdaki örnekteki gibi \( f \) fonksiyonunun birebir olmadığı durumda \( A \) kümesinin iki elemanı \( B \) kümesinde aynı elemanla eşlenir. Bu durum \( f^{-1} \) fonksiyonunda bu elemanın \( A \) kümesinde iki görüntüsü olması anlamına gelir ve \( f^{-1} \) fonksiyonu için ikinci fonksiyon olma koşulu sağlanmamış olur.
Sabit fonksiyonlar birebir olmadıkları için ters fonksiyonları yoktur.
Ters Fonksiyonun Tanım ve Görüntü Kümesi
\( f^{-1} \) ters fonksiyonu tanımlı ise \( f \) fonksiyonunun \( (a, b) \) şeklindeki tüm eşlemelerini \( (b, a) \) şeklinde tersine çevirir. Bunun bir sonucu olarak bir fonksiyonun tanım ve görüntü kümeleri ters fonksiyonda yer değiştirir, yani \( f \) fonksiyonunun görüntü kümesi \( f^{-1} \) fonksiyonunun tanım kümesi, \( f \) fonksiyonunun tanım kümesi \( f^{-1} \) fonksiyonunun görüntü kümesi olur.
\( f: A \to B \) ve \( f \) birebir ve örten olmak üzere,
\( f^{-1}: B \to A \)
\( f: \mathbb{R} \to \mathbb{R^+} \) ise,
\( f^{-1}: \mathbb{R^+} \to \mathbb{R} \)
Bir fonksiyon birebir ve içine ise değer kümesi görüntü kümesine eşit olacak şekilde daraltılarak fonksiyon örten yapılabilir ve ters fonksiyonu tanımlı hale getirilebilir.
\( f: \mathbb{R} - \{2\} \to \mathbb{R} \)
\( f(x) = \dfrac{x^2 - 4}{x - 2} \)
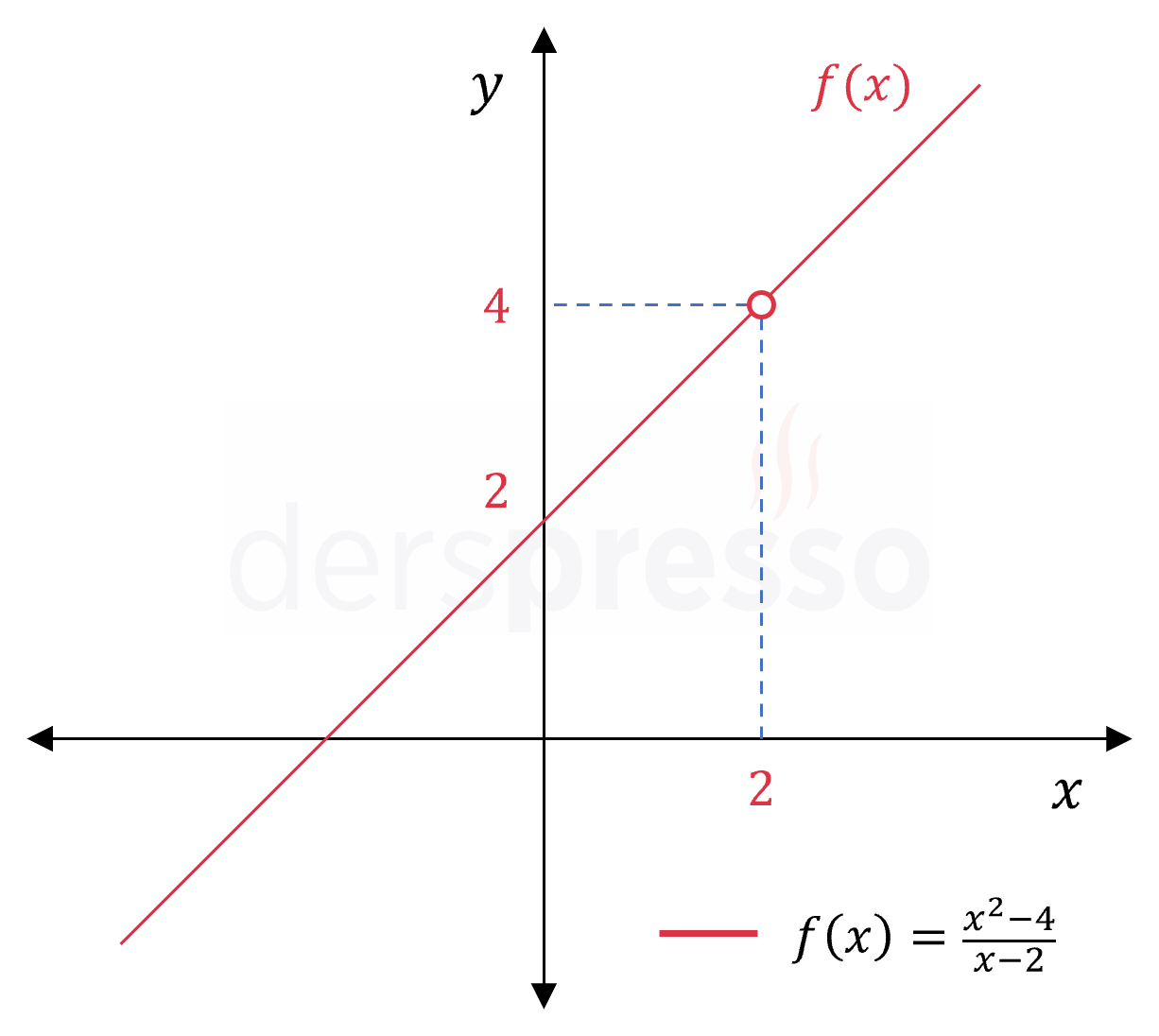
Yukarıdaki fonksiyon \( x = 2 \) noktasında tanımsız olduğu ve \( f(x) = 4 \) değerini alamadığı için içinedir, dolayısıyla ters fonksiyonu tanımlı değildir. Fonksiyonun değer kümesi görüntü kümesine eşit olacak şekilde daraltılırsa fonksiyon örten olur ve ters fonksiyonu tanımlı hale gelir.
\( f: \mathbb{R} - \{2\} \to \mathbb{R} - \{4\} \)
\( f^{-1}: \mathbb{R} - \{4\} \to \mathbb{R} - \{2\} \)
\( f^{-1}(x) = x - 2 \)
Birebir olmayan bazı fonksiyonların tanım kümesi fonksiyon her \( y \) değerini sadece bir kez alacak şekilde daraltılarak fonksiyon birebir yapılabilir ve ters fonksiyonu tanımlı hale getirilebilir.
\( f: \mathbb{R} \to \mathbb{R^+} \cup \{0\} \)
\( f(x) = x^2 \)
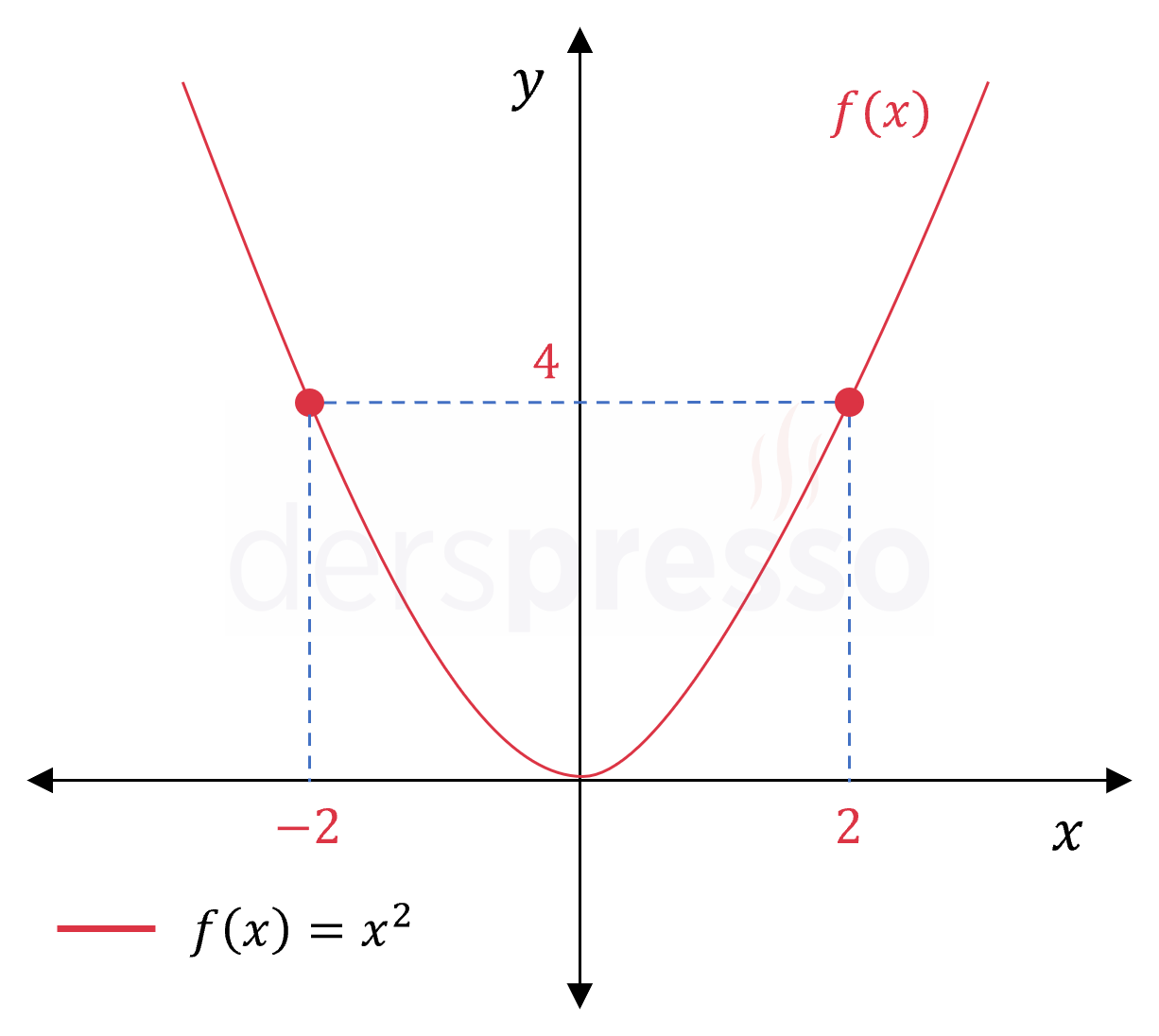
Yukarıdaki parabol fonksiyonu aynı \( y \) değerini birden fazla noktada aldığı için birebir değildir, dolayısıyla ters fonksiyonu tanımlı değildir. Fonksiyonun tanım kümesi aşağıdaki şekilde daraltılırsa fonksiyon birebir olur ve ters fonksiyonu tanımlı hale gelir.
\( f: [0, \infty) \to [0, \infty) \)
\( f^{-1}: [0, \infty) \to [0, \infty) \)
\( f^{-1}(x) = \sqrt{x} \)
Bir Fonksiyonun Ters Fonksiyonunu Bulma
Bir fonksiyonun ters fonksiyonu aşağıdaki adımlar takip edilerek bulunabilir.
- \( y = f(x) \) fonksiyonu yazılır.
- \( x = f(y) \) olacak şekilde \( x \) değişkeni yalnız bırakılır.
- \( x \) ve \( y \) değişkenleri aralarında yer değiştirilir.
- Elde edilen fonksiyon \( y = f^{-1}(x) \) fonksiyonudur.
\( f(x) = 5x - 2 \) fonksiyonunun ters fonksiyonunu bulalım.
\( y = f(x) \) fonksiyonunu yazalım.
\( y = 5x - 2 \)
\( x \) değişkenini yalnız bırakalım.
\( 5x = y + 2 \)
\( x = \dfrac{y + 2}{5} \)
\( x \) ve \( y \) değişkenlerini aralarında yer değiştirelim.
\( y = \dfrac{x + 2}{5} \)
Elde ettiğimiz fonksiyon \( y = f^{-1}(x) \) fonksiyonudur.
\( f^{-1}(x) = \dfrac{x + 2}{5} \)
Bir değerin \( f \) fonksiyonuna göre görüntüsünün ters görüntüsünün aynı değeri verip vermediğini kontrol edelim.
\( f(\textcolor{red}{5}) = 5(5) - 2 = \textcolor{blue}{23} \)
\( f^{-1}(\textcolor{blue}{23}) = \dfrac{23 + 2}{5} = \textcolor{red}{5} \)
\( g(x) = x^2 - 6x \) fonksiyonunun ters fonksiyonunu bulalım.
\( y = g(x) \) fonksiyonunu yazalım.
\( y = x^2 - 6x \)
\( x \) değişkenini yalnız bırakalım.
\( y + 9 = x^2 - 6x + 9 = (x - 3)^2 \)
\( x = \sqrt{y + 9} + 3 \)
\( x \) ve \( y \) değişkenlerini aralarında yer değiştirelim.
\( y = \sqrt{x + 9} + 3 \)
Elde ettiğimiz fonksiyon \( y = g^{-1}(x) \) fonksiyonudur.
\( g^{-1}(x) = \sqrt{x + 9} + 3 \)
Bir değerin \( g \) fonksiyonuna göre görüntüsünün ters görüntüsünün aynı değeri verip vermediğini kontrol edelim.
\( g(\textcolor{red}{8}) = 8^2 - 6(8) = \textcolor{blue}{16} \)
\( g^{-1}(\textcolor{blue}{16}) = \sqrt{16 + 9} + 3 = \textcolor{red}{8} \)
\( ax + b \) formundaki bir fonksiyonun ters fonksiyonunu kısa yoldan bulmak için \( b \)'nin işareti tersine döner, \( a \) paydaya iner.
\( f(x) = \textcolor{red}{a}x \textcolor{blue}{+ b} \) ise,
\( f^{-1}(x) = \dfrac{x \textcolor{blue}{- b}}{\textcolor{red}{a}} \)
\( f(x) = 2x - 3 \) ise,
\( f^{-1}(x) = \dfrac{x + 3}{2} \)
\( g(x) = 5x \) ise,
\( g^{-1}(x) = \dfrac{x}{5} \)
İSPATI GÖSTER
\( f(x) = ax + b \)
\( y = f(x) \) fonksiyonunu yazalım.
\( y = ax + b \)
\( x \) değişkenini yalnız bırakalım.
\( ax = y - b \)
\( x = \dfrac{y - b}{a} \)
\( x \) ve \( y \) değişkenlerini aralarında yer değiştirelim.
\( y = \dfrac{x - b}{a} \)
Elde ettiğimiz fonksiyon \( y = f^{-1}(x) \) fonksiyonudur.
\( f^{-1}(x) = \dfrac{x - b}{a} \)
\( \frac{ax + b}{cx + d} \) formundaki bir fonksiyonun ters fonksiyonunu kısa yoldan bulmak için \( a \) ve \( d \) katsayıları aralarında yer ve işaret değiştirir.
\( f(x) = \dfrac{\textcolor{red}{a}x + b}{cx \textcolor{blue}{+ d}} \) ise,
\( f^{-1}(x) = \dfrac{\textcolor{blue}{-d}x + b}{cx \textcolor{red}{-a}} \)
\( f(x) = \dfrac{-2x + 4}{3x + 5} \) ise,
\( f^{-1}(x) = \dfrac{-5x + 4}{3x + 2} \)
\( g(x) = \dfrac{3x - 1}{2x} \) ise,
\( g^{-1}(x) = \dfrac{-1}{2x - 3} \)
İSPATI GÖSTER
\( f(x) = \dfrac{ax + b}{cx + d} \)
\( y = f(x) \) fonksiyonunu yazalım.
\( y = \dfrac{ax + b}{cx + d} \)
\( x \) değişkenini yalnız bırakalım.
\( y(cx + d) = ax + b \)
\( cyx + dy = ax + b \)
\( cyx - ax = -dy + b \)
\( x(cy - a) = -dy + b \)
\( x = \dfrac{-dy + b}{cy - a} \)
\( x \) ve \( y \) değişkenlerinin yerlerini değiştirelim.
\( y = \dfrac{-dx + b}{cx - a} \)
Elde ettiğimiz fonksiyon \( y = f^{-1}(x) \) fonksiyonudur.
\( f^{-1}(x) = \dfrac{-dx + b}{cx - a} \)
Ters Fonksiyonun Grafiği
Noktanın simetriği konusunda analitik düzlemdeki bir \( (a, b) \) noktasının \( y = x \) noktasına göre simetriğinin \( (b, a) \) noktası olduğunu görmüştük.
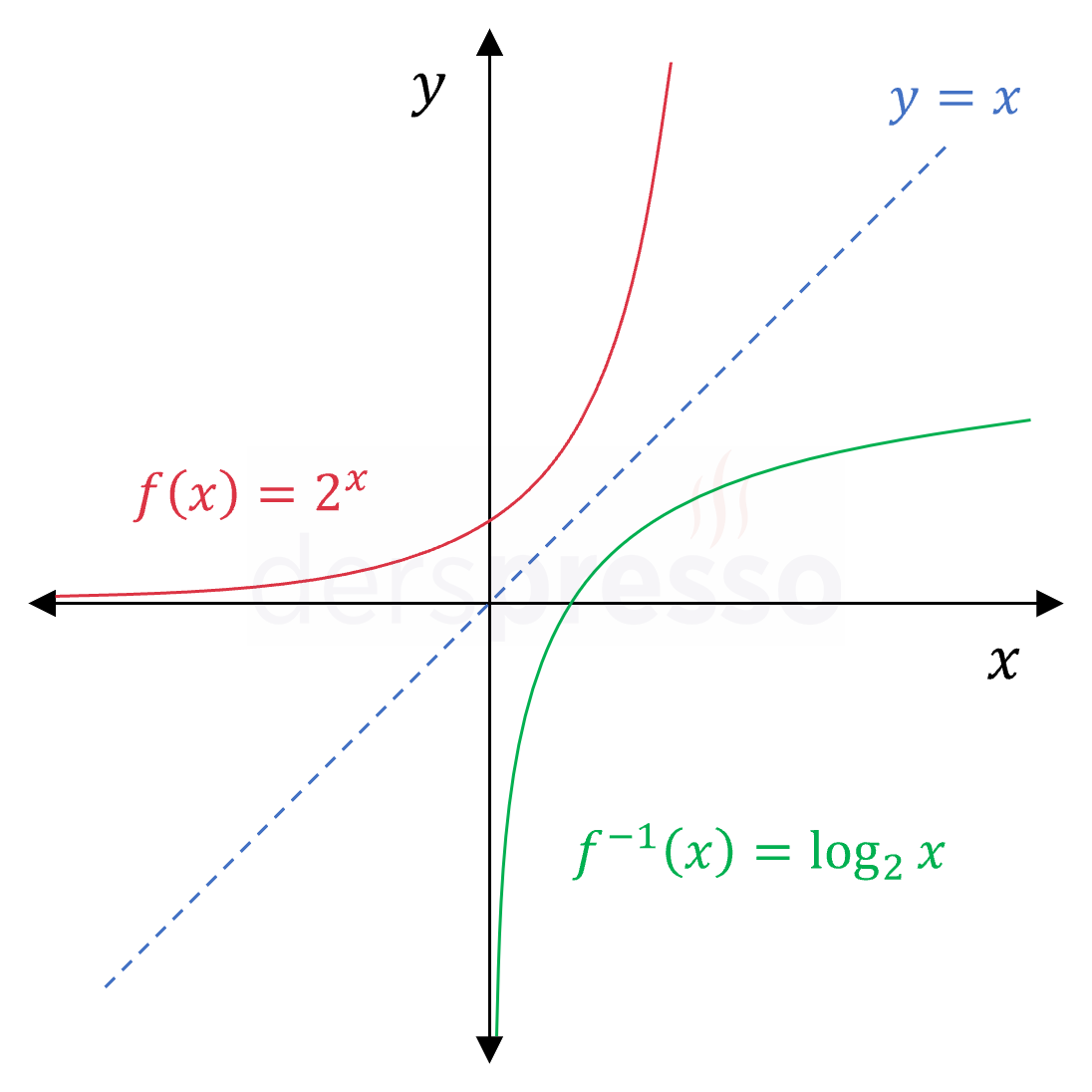
Bir fonksiyondaki her \( (a, b) \) ikilisi için ters fonksiyonda bir \( (b, a) \) ikilisi bulunduğu için, bir fonksiyonun ve tersinin grafikleri her zaman \( y = x \) doğrusuna göre simetriktir.

\( f(a) = b \)
\( f^{-1}(b) = a \)
Bir fonksiyonun örten veya birebir olup olmadığını anlamak için kullandığımız yatay doğru testine göre, bir fonksiyonun grafiğini birden fazla noktada kesen yatay bir doğru yoksa fonksiyon birebirdir.
Sürekli bir fonksiyon ve ters fonksiyonu birebir oldukları için grafiklerinin iniş ve çıkışları olmaz, yani ya kesin artan ya da kesin azalan fonksiyonlardır.
Aşağıda iki örnekte fonksiyonlar ve tersleri arasındaki \( y = x \) doğrusuna göre simetri gösterilmiştir.
| Fonksiyon ve Tersi | Grafik |
|---|---|
|
2. dereceden polinom fonksiyonu: \( f: [0, \infty) \to [0, \infty) \) \( f(x) = x^2 \) Karekök fonksiyonu: \( f^{-1}: [0, \infty) \to [0, \infty) \) \( f^{-1} = \sqrt{x} \) |
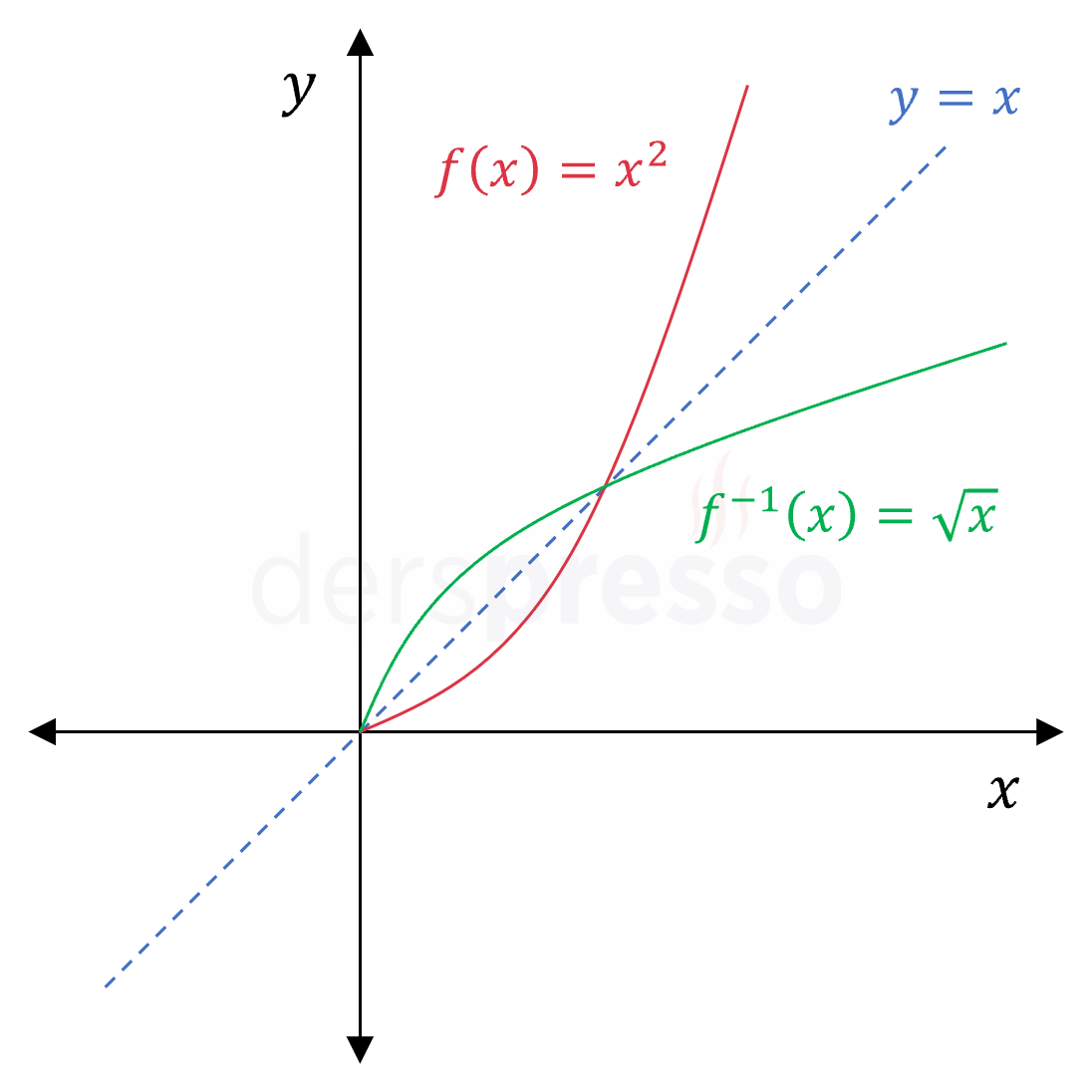
|
|
Üstel fonksiyon: \( f: \mathbb{R} \to (0, \infty) \) \( f(x) = 2^x \) Logaritma fonksiyonu: \( f^{-1}: (0, \infty) \to \mathbb{R} \) \( f^{-1} = \log_2{x} \) |
|
Temel Fonksiyonların Tersi
En sık kullanılan fonksiyonların ters fonksiyonları her iki fonksiyon için en geniş tanım ve görüntüleri ile birlikte aşağıda listelenmiştir.
| Fonksiyon | Ters Fonksiyon |
|---|---|
|
\( f: \mathbb{R} \to \mathbb{R} \) \( f(x) = ax + b \) |
\( f^{-1}: \mathbb{R} \to \mathbb{R} \) \( f^{-1}(x) = \dfrac{x - b}{a} \) |
|
\( f: [0, \infty) \to [0, \infty) \) \( f(x) = x^2 \) |
\( f^{-1}: [0, \infty) \to [0, \infty) \) \( f^{-1}(x) = \sqrt{x} \) |
|
\( f: \mathbb{R} \to \mathbb{R} \) \( f(x) = x^3 \) |
\( f^{-1}: \mathbb{R} \to \mathbb{R} \) \( f^{-1}(x) = \sqrt[3]{x} \) |
|
\( f: [-\frac{\pi}{2}, \frac{\pi}{2}] \to [-1, 1] \) \( f(x) = \sin{x} \) |
\( f^{-1}: [-1, 1] \to [-\frac{\pi}{2}, \frac{\pi}{2}] \) \( f^{-1}(x) = \arcsin{x} \) |
|
\( f: [0, \pi] \to [-1, 1] \) \( f(x) = \cos{x} \) |
\( f^{-1}: [-1, 1] \to [0, \pi] \) \( f^{-1}(x) = \arccos{x} \) |
|
\( f: (-\frac{\pi}{2}, \frac{\pi}{2}) \to \mathbb{R} \) \( f(x) = \tan{x} \) |
\( f^{-1}: \mathbb{R} \to (-\frac{\pi}{2}, \frac{\pi}{2}) \) \( f^{-1}(x) = \arctan{x} \) |
|
\( f: (0, \pi) \to \mathbb{R} \) \( f(x) = \cot{x} \) |
\( f^{-1}: \mathbb{R} \to (0, \pi) \) \( f^{-1}(x) = \arccot{x} \) |
|
\( f: \mathbb{R} \to \mathbb{R^+} \) \( f(x) = a^x \) |
\( f^{-1}: \mathbb{R^+} \to \mathbb{R} \) \( f^{-1}(x) = \log_a{x} \) |
Parçalı Fonksiyonların Tersi
Bir parçalı fonksiyonun ters fonksiyonu aşağıdaki adımlar takip edilerek bulunabilir.
- Parçalı fonksiyonun her aralığındaki tanımın ayrı ayrı ters fonksiyonu bulunur.
- Her aralık için bulunan ters fonksiyon o aralığın tanım kümesinde \( x \) yerine konur ve eşitsizlik \( x \) için çözülür. Elde edilen yeni \( x \) aralığı ters fonksiyonun o tanımının tanım aralığı olur.
\( f(x) = \begin{cases} 3x - 6 & x \le 2 \\ x - 2 & x \gt 2 \end{cases} \)
\( f^{-1}(x) \) fonksiyonunu bulalım.
Parçalı fonksiyonun her iki aralığındaki tanımların ayrı ayrı tersini bulalım.
Bir parçalı fonksiyonun ters fonksiyonunda aralıkların sınır değerleri de değişir.
1. aralık:
\( f(x) = 3x - 6 \)
\( f^{-1}(x) = \dfrac{x + 6}{3} \)
Ters fonksiyonda bu tanımın sınır değerini bulmak için \( x \) yerine ters fonksiyon tanımını yazalım ve \( x \)'i yalnız bırakalım.
\( \dfrac{x + 6}{3} \le 2 \)
\( x + 6 \le 6 \)
\( x \le 0 \)
2. aralık:
\( f(x) = x - 2 \)
\( f^{-1}(x) = x + 2 \)
Ters fonksiyonda bu tanımın sınır değerini bulmak için \( x \) yerine ters fonksiyon tanımını yazalım ve \( x \)'i yalnız bırakalım.
\( x + 2 \gt 2 \)
\( x \gt 0 \)
\( f^{-1} \) tanımı aşağıdaki şekilde olur.
\( f(x) = \begin{cases} \dfrac{x + 6}{3} & x \le 0 \\ x + 2 & x \gt 0 \end{cases} \)
Ters Fonksiyon İşlem Kuralları
Bir fonksiyonun ters fonksiyonu tanımlı ise tersinin tersi kendisine eşittir.
\( (f^{-1})^{-1} = f \)
Bir fonksiyonun tersi ile bileşkesi birim fonksiyona eşittir.
\( f \circ f^{-1} = f^{-1} \circ f = I \)
\( g \circ f \circ f^{-1} \circ h = g \circ I \circ h = g \circ h \)
\( f(x) = 2x + 1 \)
\( f^{-1}(x) = \dfrac{x - 1}{2} \)
\( (f \circ f^{-1})(x) = f(f^{-1}(x)) \)
\( = 2f^{-1}(x) + 1 = 2\dfrac{x - 1}{2} + 1 \)
\( = (x - 1) + 1 = x = I \)
\( (f^{-1} \circ f)(x) = f^{-1}(f(x)) \)
\( = \dfrac{f(x) - 1}{2} = \dfrac{(2x + 1) - 1}{2} \)
\( = \dfrac{2x}{2} = x = I \)
İSPATI GÖSTER
\( f: A \to B \) birebir ve örten bir fonksiyon ve
\( f^{-1}: B \to A \) \( f \)'nin ters fonksiyonu olmak üzere,
\( f(x) = y \Longleftrightarrow f^{-1}(y) = x \)
\( (f \circ f^{-1})(y) = I \) olduğunu gösterelim.
\( (f \circ f^{-1})(y) = f(f^{-1}(y)) \)
\( = f(x) = y \)
\( (f \circ f^{-1})(y) = y \) bulduğumuz için, yani \( f \circ f^{-1} \) bileşke fonksiyonunun girdi ve çıktı değerleri eşit ve \( y \) olduğu için bu fonksiyon birim fonksiyona eşittir.
\( (f \circ f^{-1})(y) = I \)
\( (f^{-1} \circ f)(x) = I \) olduğunu gösterelim.
\( (f^{-1} \circ f)(x) = f^{-1}(f(x)) \)
\( = f^{-1}(y) = x \)
\( (f^{-1} \circ f)(x) = x \) bulduğumuz için, yani \( f^{-1} \circ f \) bileşke fonksiyonunun girdi ve çıktı değerleri eşit ve \( x \) olduğu için bu fonksiyon birim fonksiyona eşittir.
\( (f^{-1} \circ f)(x) = I \)
İki ya da daha fazla fonksiyonun bileşkesinin ters fonksiyonu, fonksiyonların ters fonksiyonlarının ters sırada bileşkesine eşittir.
\( (g \circ f)^{-1} = f^{-1} \circ g^{-1} \)
\( (h \circ g \circ f)^{-1} = f^{-1} \circ g^{-1} \circ h^{-1} \)
İSPATI GÖSTER
\( f: A \to B \) ve
\( g: B \to C \) birebir ve örten fonksiyonlar olmak üzere,
\( g \circ f \) ifadesinin tersi \(f^{-1} \circ g^{-1} \) ise bu iki ifadenin bileşkesi birim fonksiyonu vermelidir.
\( (g \circ f) \circ (f^{-1} \circ g^{-1}) \)
Bileşke işleminin birleşme özelliği olduğu için parantezlerin yerini değiştirerek işlem sırasını değiştirebiliriz.
\( = g \circ ((f \circ f^{-1}) \circ g^{-1}) \)
Bir fonksiyonun tersi ile bileşkesi birim fonksiyona eşittir.
\( = g \circ (I \circ g^{-1}) \)
Birim fonksiyon bileşke işleminin etkisiz elemanıdır.
\( = g \circ g^{-1} = I \)
Sonuç birim fonksiyon olduğu için bileşkesini aldığımız iki ifadenin birbirinin tersi olduğu sonucuna varabiliriz.
\( (g \circ f)^{-1} = f^{-1} \circ g^{-1} \)
Aynı sonucu ikinci ifadenin yerlerini değiştirdiğimizde de elde ederiz.
\( (f^{-1} \circ g^{-1}) \circ (g \circ f) \)
Bileşke işleminin birleşme özelliği olduğu için parantezlerin yerini değiştirerek işlem sırasını değiştirebiliriz.
\( = f^{-1} \circ ((g^{-1} \circ g) \circ f) \)
Bir fonksiyonun tersi ile bileşkesi birim fonksiyona eşittir.
\( = f^{-1} \circ (I \circ f) \)
Birim fonksiyon bileşke işleminin etkisiz elemanıdır.
\( = f^{-1} \circ f = I \)
\( A = \{a, b, c, d, e\} \) kümesinde tanımlı \( f = \{(a, c), (b, d), (c, e), (d, a), (e, b)\} \) fonksiyonu veriliyor.
Buna göre, \( f^{-1} \) fonksiyonunu bulunuz.
Çözümü Göster\( f \) fonksiyonu tanım kümesindeki tüm elemanların görüntüsü farklı olduğu için birebir, değer kümesinde hiçbir eleman açıkta kalmadığı için örtendir. Dolayısıyla fonksiyonun ters fonksiyonu tanımlıdır ve elemanı olan ikililerin bileşenlerinin aralarında yer değiştirmesi ile elde edilir.
\( f(a) = c \Longrightarrow f^{-1}(c) = a \)
Buna göre ters fonksiyon aşağıdaki gibi olur.
\( f^{-1} = \{(c, a), (d, b), (e, c), (a, d), (b, e)\} \)
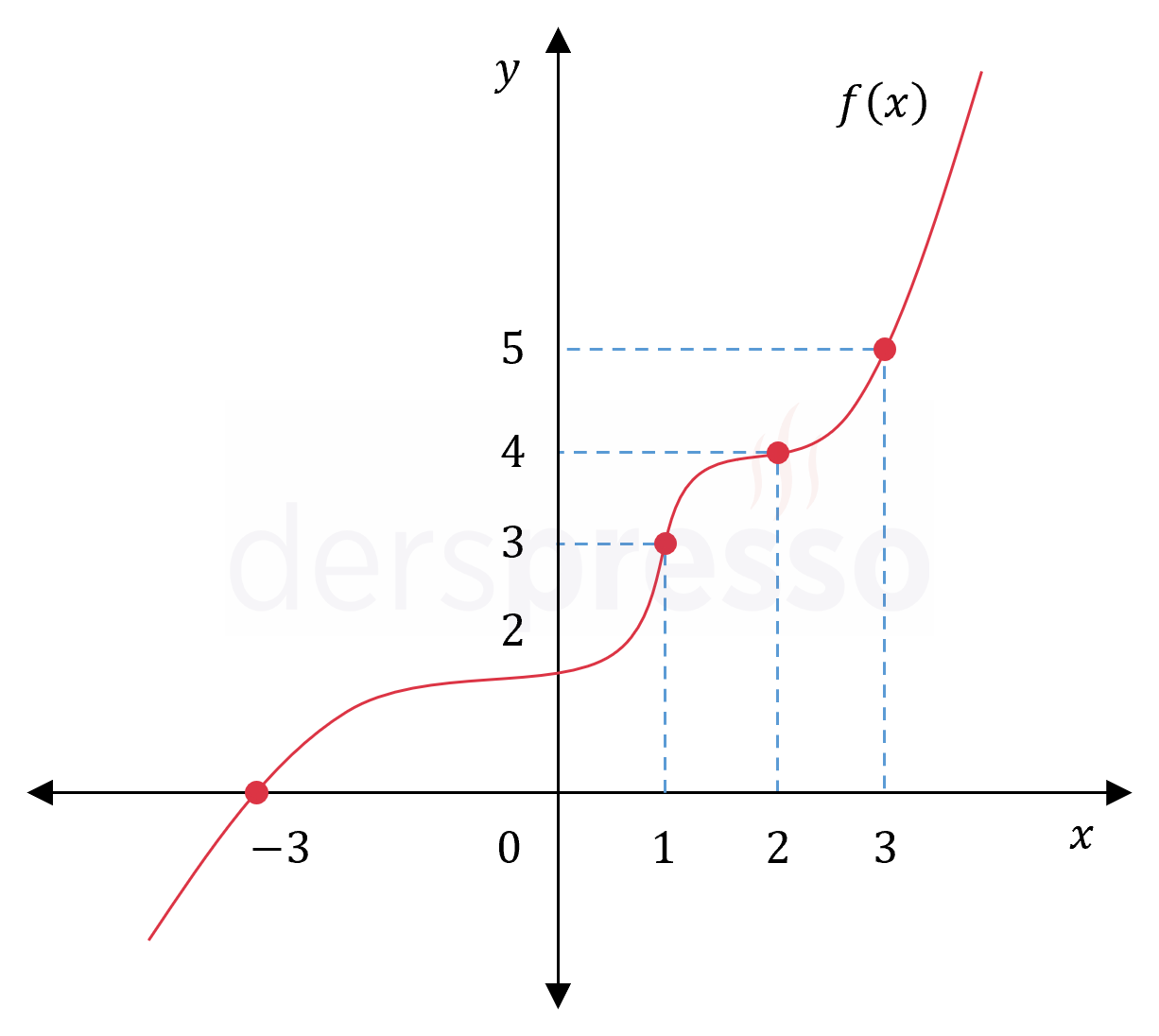
Yukarıda \( f \) fonksiyonunun grafiği verilmiştir.
Buna göre \( f(3) + f^{-1}(3) + f^{-1}(2) + f(0) + f^{-1}(0) \) toplamı kaçtır?
Çözümü Göster\( f \) fonksiyonunun grafiğini inceleyerek sorudaki ifadelerin değerlerini bulalım.
\( f(3) \), fonksiyonun \( x = 3 \) noktasındaki görüntüsünü ifade eder.
\( f(3) = 5 \)
\( f^{-1}(3) \), \( f \) fonksiyonuna göre görüntüsü 3 olan \( x \) değerini ifade eder.
\( f^{-1}(3) = 1 \)
\( f^{-1}(2) \), \( f \) fonksiyonuna göre görüntüsü 2 olan \( x \) değerini ifade eder.
\( f^{-1}(2) = 0 \)
\( f(0) \), fonksiyonun \( x = 0 \) noktasındaki görüntüsünü ifade eder.
\( f(0) = 2 \)
\( f^{-1}(0) \), \( f \) fonksiyonuna göre görüntüsü 0 olan \( x \) değerini ifade eder.
\( f^{-1}(0) = -3 \)
İstenen toplam \( 5 + 1 + 0 + 2 + (-3) = 5 \) olarak bulunur.
\( f: \mathbb{R} \to \mathbb{R} \) olmak üzere,
\( f(x + 2) = 3x - 2 + a \)
\( f^{-1}(4) = 3 \) olduğuna göre, \( a \) kaçtır?
Çözümü Göster\( f^{-1}(4) = 3 \) ise \( f(3) = 4 \) olur.
\( f(x + 2) \) ifadesinde \( x = 1 \) yazalım.
\( f(1 + 2) = 3(1) - 2 + a \)
\( f(3) = 1 + a = 4 \)
\( a = 3 \) olarak bulunur.
\( f(x) = 8x^3 - 36x^2 + 54x - 20 \)
\( f^{-1}(a^3 + 7) = 5 \)
olduğuna göre, \( a \) değeri kaçtır?
Çözümü Göster\( f^{-1}(a^3 + 7) = 5 \) ise,
\( f(5) = a^3 + 7 \)
\( f(5) \) değerini bulmak için fonksiyonda \( x = 5 \) yazalım.
\( f(5) = 8(5)^3 - 36(5)^2 + 54(5) - 20 \)
\( 1000 - 900 + 270 - 20 = a^3 + 7 \)
\( a^3 = 343 \)
\( a = 7 \) bulunur.
\( f: \mathbb{R} - \{ -\frac{1}{3} \} \to \mathbb{R} - \{ \frac{4}{3} \} \)
\( f(x) = \dfrac{4x - 2}{3x + 1} \) olduğuna göre, \( f^{-1}(-1) \) kaçtır?
Çözümü Göster\( f(x) = \dfrac{ax + b}{cx + d} \) formundaki bir fonksiyonun kısa yoldan tersini elde etmek için paydaki \( a \) ile paydadaki \( d \) işaret ve yer değiştirir.
\( f^{-1}(x) = \dfrac{-x - 2}{3x - 4} \)
\( f^{-1}(-1) \) değerini bulmak için \( x = -1 \) yazalım.
\( f^{-1}(-1) = \dfrac{-(-1) - 2}{3(-1) - 4} \)
\( = \dfrac{1}{7} \) bulunur.
\( f(x) = \dfrac{(a + 2)x - 4}{x - 3} \) fonksiyonunun tersi kendisine eşit olduğuna göre, \( a \) kaçtır?
Çözümü Göster\( f(x) = \dfrac{ax + b}{cx + d} \) formundaki bir fonksiyonun kısa yoldan tersini elde etmek için paydaki \( a \) ile paydadaki \( d \) işaret ve yer değiştirir.
\( f^{-1}(x) = \dfrac{3x - 4}{x - (a + 2)} \)
Buna göre fonksiyonun tersine eşit olabilmesi için \( a + 2 = 3 \) olmalıdır.
\( a = 1 \) bulunur.
\( f(x) = 3^{x - 1} - 11 \) olduğuna göre, \( f^{-1}(70) \) kaçtır?
Çözümü Göster\( f^{-1}(70) = a \) diyelim.
\( f(a) = 70 \)
\( f \) fonksiyonunun görüntüsünü 70 yapan \( a \) değerini bulalım.
\( f(a) = 3^{a - 1} - 11 = 70 \)
\( 3^{a - 1} = 81 = 3^4 \)
\( a = 5 \)
\( f^{-1}(70) = a = 5 \) bulunur.
\( f: A \to B \) olmak üzere,
\( f(x) = \dfrac{x^2 - k}{x + 3} \) fonksiyonu veriliyor.
\( (2, 3) \in f^{-1} \) ise \( k \) kaçtır?
Çözümü Göster\( f^{-1} \) fonksiyonunda 2'nin görüntüsü 3 ise \( f \) fonksiyonunda 3'ün görüntüsü 2 olur.
\( (3, 2) \in f \)
\( f(3) = 2 \)
Bu değerleri fonksiyonda yerine koyalım.
\( f(3) = \dfrac{3^2 - k}{3 + 3} = 2 \)
\( 9 - k = 12 \)
\( k = -3 \) bulunur.
\( f: \mathbb{R} \to \mathbb{R} \) olmak üzere,
\( f(x) = x^4 + 2x^2 + mx + 5 \)
\( f^{-1}(x) \) fonksiyonunun grafiği \( (-2, 1) \) noktasından geçtiğine göre, \( m \) kaçtır?
Çözümü Göster\( f^{-1}(x) \) fonksiyonunun grafiği \( (-2, 1) \) noktasından geçtiğine göre, \( f^{-1}(-2) = 1 \) olur.
\( f^{-1}(-2) = 1 \) ise \( f(1) = -2 \) olur.
\( f \) fonksiyonunda \( x = 1 \) yazalım.
\( f(1) = 1^4 + 2(1)^2 + m(1) + 5 = -2 \)
\( 1 + 2 + m + 5 = -2 \)
\( m = -10 \) bulunur.
\( f(2x - 1) = 3x + 5 \) ve \( f^{-1}(2a - 5) = 11 \)
olduğuna göre, \( a \) kaçtır?
Çözümü Göster\( f^{-1}(2a - 5) = 11 \) ise,
\( f(11) = 2a - 5 \)
Birinci eşitlikte fonksiyonun içindeki ifadeyi 11 yapan \( x \) değerini bulalım.
\( 2x - 1 = 11 \Longrightarrow x = 6 \)
\( f(11) \) değerini bulmak için \( x = 6 \) yazalım.
\( f(2(6) - 1) = 3(6) + 5 \)
\( f(11) = 23 = 2a - 5 \)
\( a = 14 \) bulunur.
\( f(x) = 2x + 1 \) ve \( g(x) = x^3 + 2 \)
olduğuna göre, \( (f^{-1} \circ g)(1) \) kaçtır?
Çözümü Göster\( (f^{-1} \circ g)(1) = f^{-1}(g(1)) = a \) diyelim.
\( g(1) = 1^3 + 2 = 3 \)
\( f^{-1}(g(1)) = f^{-1}(3) = a \)
Bu eşitliği aşağıdaki şekilde yazabiliriz.
\( f(a) = 3 \)
\( 2a + 1 = 3 \)
\( a = 1 \) bulunur.
\( f(x) = \dfrac{3x - 2}{3} \)
\( (f \circ g)(x) = x + 2 \)
olduğuna göre, \( g^{-1}(2) \) kaçtır?
Çözümü Göster\( (f \circ g)(x) = f(g(x)) = x + 2 \)
\( f(x) \) fonksiyonunda \( x \) yerine \( g(x) \) yazalım.
\( f(g(x)) = \dfrac{3g(x) - 2}{3} \)
\( f(g(x)) \) için elimizdeki iki ifadeyi birbirine eşitleyelim.
\( x + 2 = \dfrac{3g(x) - 2}{3} \)
\( 3x + 6 = 3g(x) - 2 \)
\( g(x) = \dfrac{3x + 8}{3} \)
\( g(x) \) fonksiyonunun tersini alalım.
\( g^{-1}(x) = \dfrac{3x - 8}{3} \)
\( g^{-1}(2) \) değerini bulmak için \( x = 2 \) yazalım.
\( g^{-1}(2) = \dfrac{3(2) - 8}{3} = -\dfrac{2}{3} \) bulunur.
\( f(x) = \dfrac{3f(x) + 6}{2x - 1} \)
\( f^{-1}(3) = m - 3 \)
olduğuna göre, \( m \) kaçtır?
Çözümü GösterBirinci eşitlikte \( f(x) \)'i yalnız bırakalım.
\( 2xf(x) - f(x) = 3f(x) + 6 \)
\( 2xf(x) - 4f(x) = 6 \)
\( f(x)(2x - 4) = 6 \)
\( f(x) = \dfrac{6}{2x - 4} \)
\( f(x) = \frac{ax + b}{cx + d} \) formundaki bir fonksiyonun kısa yoldan tersini elde etmek için paydaki \( a \) ile paydadaki \( d \) işaret ve yer değiştirir.
\( f^{-1}(x) = \dfrac{4x + 6}{2x} \)
\( f^{-1}(3) \) değerini bulmak için \( x = 3 \) yazalım.
\( f^{-1}(3) = \dfrac{4(3) + 6}{2(3)} = m - 3 \)
\( m - 3 = 3 \)
\( m = 6 \) bulunur.
\( \dfrac{f(x) + 3}{f(x)} = 2x + 3 \) olduğuna göre, \( f^{-1}(x) \) fonksiyonunu bulunuz.
Çözümü GösterBir fonksiyonun tersini bulmak için \( x \) yalnız bırakılır. Verilen ifadede \( x \) bu forma çok yakındır.
\( 2x + 3 = \dfrac{f(x) + 3}{f(x)} \)
\( 2x = \dfrac{f(x) + 3}{f(x)} - 3 \)
\( 2x = \dfrac{3 - 2f(x)}{f(x)} \)
\( x = \dfrac{3 - 2f(x)}{2f(x)} \)
Eşitliğin sağ tarafında \( f(x) \) yerine \( x \) yazdığımızda \( f^{-1} \) fonksiyonunu elde ederiz.
\( f^{-1}(x) = \dfrac{3 - 2x}{2x} \)
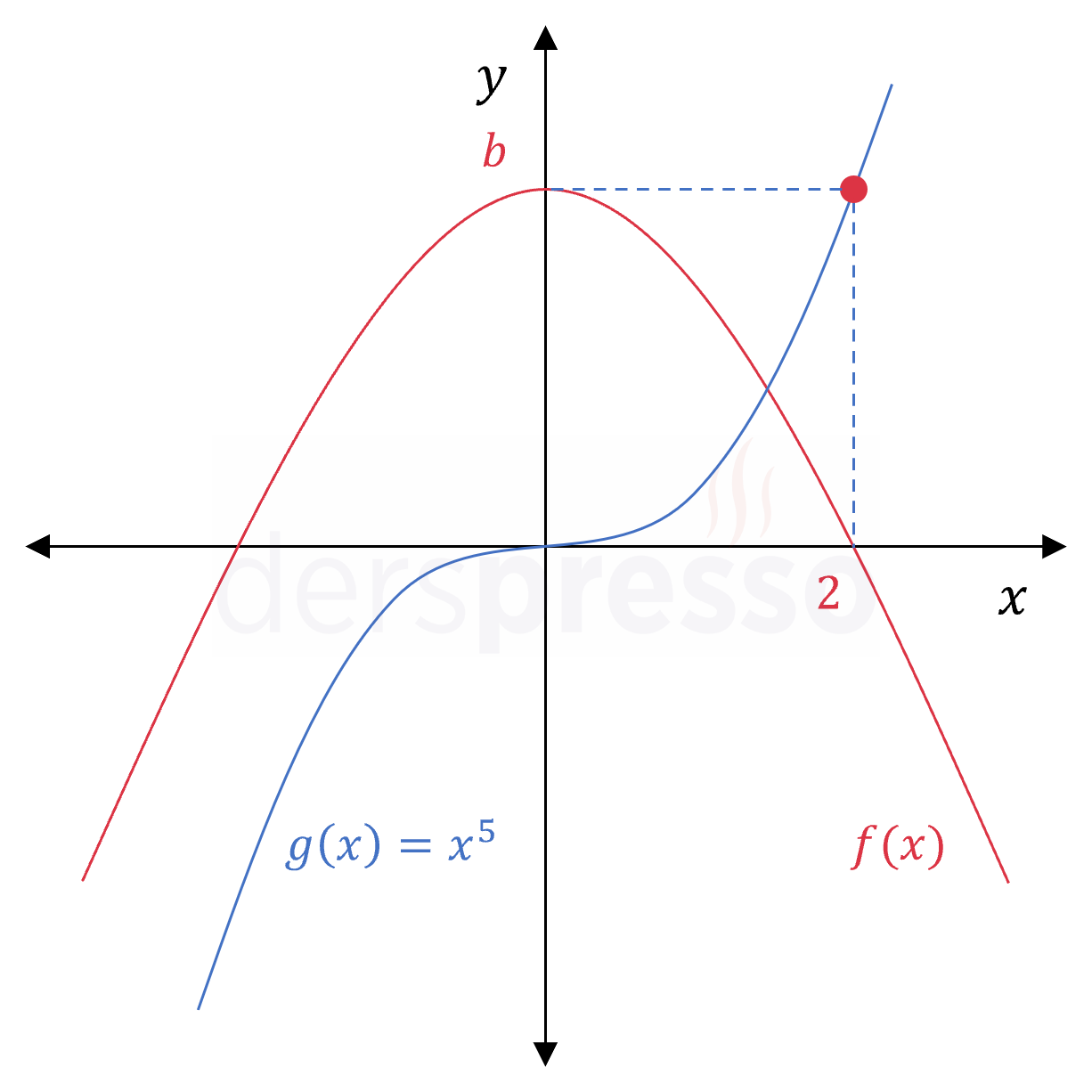
Yukarıda \( f(x) \) ve \( g(x) = x^5 \) fonksiyonlarının grafikleri verilmiştir.
Buna göre \( (f \circ g^{-1} \circ f)(0) \) ifadesinin değeri kaçtır?
Çözümü Göster\( b = g(2) = 2^5 = 32 \)
\( (f \circ g^{-1} \circ f)(0) = f(g^{-1}(f(0))) \)
Fonksiyon değerlerini içten dışa doğru bulalım.
\( f(0) = b = 32 \)
\( g^{-1}(32) = 2 \)
\( f(2) = 0 \) bulunur.
\( f\left( \dfrac{3}{7x + 5} \right) = \dfrac{1}{3 - 7x} \) olduğuna göre, \( f(x) \) fonksiyonunu bulunuz.
Çözümü GösterVerilen eşitlikte \( x \) yerine \( \frac{3}{7x + 5} \) ifadesinin tersini koyduğumuzda \( f(x) \) fonksiyonunu buluruz.
Bu ifadede \( x \)'i yalnız bırakalım.
\( y = \dfrac{3}{7x + 5} \)
\( 7xy + 5y = 3 \)
\( 7yx = 3 - 5y \)
\( x = \dfrac{3 - 5y}{7y} \)
Verilen eşitlikte \( x \) yerine \( \frac{3 - 5x}{7x} \) yazalım.
\( f\left( \dfrac{3}{7x + 5} \right) = \dfrac{1}{3 - 7x} \)
\( f\left( \dfrac{3}{7(\frac{3 - 5x}{7x}) + 5} \right) = \dfrac{1}{3 - 7(\frac{3 - 5x}{7x})} \)
\( f\left( \dfrac{3}{\frac{3 - 5x}{x} + 5} \right) = \dfrac{1}{3 - \frac{3 - 5x}{x}} \)
\( f\left( \dfrac{3}{\frac{3 - 5x + 5x}{x}} \right) = \dfrac{1}{\frac{3x - 3 + 5x}{x}} \)
\( f(x) = \dfrac{x}{8x - 3} \) bulunur.
Eşitliğin sol tarafında parantez içinin \( f(x) \) olacağını bildiğimiz için sadece eşitliğin sağ tarafındaki işlemleri yapmamız da yeterli olacaktır.
\( f\left( \dfrac{x - 1}{x + 1} \right) = x + 2 \) olduğuna göre, \( f(x) \) fonksiyonunu bulunuz.
Çözümü GösterVerilen eşitlikte \( x \) yerine \( \frac{x - 1}{x + 1} \) ifadesinin tersini koyduğumuzda \( f(x) \) fonksiyonunu buluruz.
\( f(x) = \frac{ax + b}{cx + d} \) formundaki bir fonksiyonun kısa yoldan tersini elde etmek için paydaki \( a \) ile paydadaki \( d \) işaret ve yer değiştirir.
\( y = \dfrac{-x - 1}{x - 1} \)
Verilen eşitlikte \( x \) yerine \( \frac{-x - 1}{x - 1} \) yazalım.
\( f\left( \dfrac{\frac{-x - 1}{x - 1} - 1}{\frac{-x - 1}{x - 1} + 1} \right) = \dfrac{-x - 1}{x - 1} + 2 \)
\( f\left( \dfrac{\frac{-x - 1 - x + 1}{x - 1}}{\frac{-x - 1 + x - 1}{x - 1}} \right) = \dfrac{-x - 1 + 2x - 2}{x - 1} \)
\( f\left( \dfrac{\frac{-2x}{x - 1}}{\frac{-2}{x - 1}} \right) = \dfrac{x - 3}{x - 1} \)
\( f(x) = \dfrac{x - 3}{x - 1} \) bulunur.
Eşitliğin sol tarafında parantez içinin \( f(x) \) olacağını bildiğimiz için sadece eşitliğin sağ tarafındaki işlemleri yapmamız da yeterli olacaktır.
\( (g \circ f^{-1})^{-1}(x) = 4x - 9 \)
\( f(x) = x - 1 \)
olduğuna göre, \( g(x) \) fonksiyonunu bulunuz.
Çözümü GösterBileşke fonksiyonun ters işlemini parantez içine dağıtalım.
\( ((f^{-1})^{-1} \circ g^{-1})(x) = 4x - 9 \)
Ters fonksiyonun tersi fonksiyonun kendisine eşittir.
\( (f \circ g^{-1})(x) = 4x - 9 \)
\( f(g^{-1}(x)) = 4x - 9 \)
Eşitliğin sol tarafını \( f \) fonksiyonunda \( x \) yerine \( g^{-1}(x) \) yazarak da elde edebiliriz.
\( g^{-1}(x) - 1 = 4x - 9 \)
\( g^{-1}(x) \) ifadesini yalnız bırakalım.
\( g^{-1}(x) = 4x - 8 \)
Eşitliğin iki tarafındaki fonksiyonların tersini alalım.
\( g(x) = \dfrac{x + 8}{4} \) bulunur.
\( f(x) = \dfrac{x + 4}{6} \)
\( (g \circ f)^{-1}(x) = 3x - 13 \)
olduğuna göre, \( g(x) \) fonksiyonunu bulunuz.
Çözümü Göster\( f \) fonksiyonunun tersini bulalım.
\( f^{-1}(x) = 6x - 4 \)
\( (g \circ f)^{-1}(x) = 3x - 13 \)
Bileşke fonksiyonun ters işlemini parantez içine dağıtalım.
\( (f^{-1} \circ g^{-1})(x) = 3x - 13 \)
\( f^{-1}(g^{-1}(x)) = 3x - 13 \)
Eşitliğin sol tarafını \( f^{-1} \) fonksiyonunda \( x \) yerine \( g^{-1}(x) \) yazarak da elde edebiliriz.
\( 6g^{-1}(x) - 4 = 3x - 13 \)
\( g^{-1}(x) \) ifadesini yalnız bırakalım.
\( g^{-1}(x) = \dfrac{3x - 9}{6} \)
\( = \dfrac{x - 3}{2} \)
Bir fonksiyonun tersinin tersi kendisine eşittir.
\( (g^{-1})^{-1}(x) = g(x) = 2x + 3 \) olarak bulunur.
\( f(x) = \dfrac{2x + 3}{4x - 2} \) olduğuna göre,
\( \underbrace{(f \circ f \circ \ldots \circ f \circ f)}_\text{999 adet}(x) \) ifadesinin değeri kaçtır?
Çözümü Göster\( f(x) = \frac{ax + b}{cx + d} \) formundaki bir fonksiyonun kısa yoldan tersini elde etmek için paydaki \( a \) ile paydadaki \( d \) işaret ve yer değiştirir.
Buna göre verilen fonksiyon tersine eşittir.
\( f(x) = f^{-1}(x) = \dfrac{2x + 3}{4x - 2} \)
Bir fonksiyonun tersi ile bileşkesi birim fonksiyonu verir.
\( (f \circ f^{-1})(x) = I = x \)
Buna göre verilen ifadeyi aşağıdaki şekilde yazabiliriz.
\( (f \circ f \circ \ldots \circ f \circ f \circ f)(x) = (f \circ f^{-1} \circ \ldots \circ f \circ f^{-1} \circ f)(x) \)
Son fonksiyon dışındaki fonksiyonların ikişerli bileşkesi birim fonksiyonu verir.
\( = (I \circ \ldots \circ I \circ f)(x) \)
\( = f(x) = \dfrac{2x + 3}{4x - 2} \) bulunur.
\( f(x) = mx + n \) ve \( f^{-1}(x) = nx + m \) olduğuna göre, \( m + n \) kaça eşittir?
Çözümü GösterBir fonksiyonun ve tersinin bileşkesi birim fonksiyona eşittir.
\( (f \circ f^{-1})(x) = f(f^{-1}(x)) = x \)
\( f(nx + m) = x \)
\( m (nx + m) + n = x \)
\( mnx + m^2 + n = x \)
İki polinomun eşitliğinde aynı dereceli terimlerin katsayıları birbirine eşit olur.
\( mn = 1 \)
\( m^2 + n = 0 \)
\( n = -m^2 \)
Bu değeri birinci eşitlikte yerine koyalım.
\( mn = m(-m^2) = 1 \)
\( m^3 = -1 \)
\( m = -1 \)
\( mn = -1(n) = 1 \Longrightarrow n = -1 \)
\( m + n = -1 + (-1) = -2 \) bulunur.
\( f \) ve \( g \) fonksiyonları birebir ve örtendir.
\( f(3x + 2) = g^{-1}\left( \dfrac{3x - 4}{1 + x} \right) \)
olduğuna göre, \( (g \circ f)(-4) \) kaçtır?
Çözümü GösterVerilen eşitliğin her iki tarafının \( g \) fonksiyonu ile bileşkesini alalım.
\( g(f(3x + 2)) = g\left( g^{-1}\left( \dfrac{3x - 4}{1 + x} \right) \right) \)
\( (g \circ f)(3x + 2) = (g \circ g^{-1})\left( \dfrac{3x - 4}{1 + x} \right) \)
\( g \circ g^{-1} \) bileşke fonksiyonu birim fonksiyona eşittir.
\( (g \circ f)(3x + 2) = I\left( \dfrac{3x - 4}{1 + x} \right) \)
Birim fonksiyonda çıktı değeri girdi değerine eşittir.
\( (g \circ f)(3x + 2) = \dfrac{3x - 4}{1 + x} \)
Bu eşitlikte \( (g \circ f)(-4) \) değerini elde etmek için \( x \) yerine yazılacak değeri bulalım.
\( 3x + 2 = -4 \)
\( x = -2 \)
Eşitlikte \( x = -2 \) yazalım.
\( (g \circ f)(3(-2) + 2) = \dfrac{3(-2) - 4}{1 + (-2)} \)
\( (g \circ f)(-4) = 10 \) bulunur.
\( f, g, h, t \) fonksiyonları tanımlı oldukları aralıklarda birebir ve örtendir.
\( (f \circ g^{-1} \circ h)(x) = 3x + 4 \)
\( (h^{-1} \circ g)(x) = 2x - 1 \) olduğuna göre,
\( f(x) \) fonksiyonu nedir?
Çözümü GösterBirinci eşitlikteki fonksiyonların ikinci eşitlikteki fonksiyonlarla bileşkesini alalım.
\( (f \circ g^{-1} \circ h \circ h^{-1} \circ g)(x) = 3(2x - 1) + 4 \)
Bir fonksiyonun tersi ile bileşkesi birim fonksiyonu verir.
\( k \circ k^{-1} = k^{-1} \circ k = I \)
\( (f \circ g^{-1} \circ I \circ g)(x) = 6x + 1 \)
Bir fonksiyonun birim fonksiyon ile bileşkesi kendisini verir.
\( k \circ I = I \circ k = k \)
\( (f \circ g^{-1} \circ g)(x) = 6x + 1 \)
\( (f \circ I)(x) = 6x + 1 \)
\( f(x) = 6x + 1 \) bulunur.
\( f: \mathbb{R} - \{ a \} \to \mathbb{R} - \{ b \} \) olmak üzere,
\( f(x) = \dfrac{3x - a}{2x - 1} \) fonksiyonu birebir ve örten olduğuna göre, \( f(b) \) kaçtır?
Çözümü GösterBir rasyonel fonksiyonda paydayı 0 yapan \( x \) değeri fonksiyonu tanımsız yapar. Tanım kümesindeki tüm elemanlar için fonksiyonun tanımlı olması gerektiği için, paydayı sıfır yapan bu \( x \) değeri tanım kümesinin dışında bırakılan \( a \) değeri olmalıdır.
\( 2a - 1 = 0 \Longrightarrow a = \dfrac{1}{2} \)
\( f(x) = \dfrac{3x - \frac{1}{2}}{2x - 1} \)
Fonksiyon birebir ve örten olduğu için tersini alabiliriz.
\( f(x) = \frac{ax + b}{cx + d} \) formundaki bir fonksiyonun kısa yoldan tersini elde etmek için paydaki \( a \) ile paydadaki \( d \) işaret ve yer değiştirir.
\( f^{-1}(x) = \dfrac{x - \frac{1}{2}}{2x - 3} \)
\( f \) fonksiyonunun görüntü kümesi \( f^{-1} \) fonksiyonunun tanım kümesi, \( f \) fonksiyonunun tanım kümesi \( f^{-1} \) fonksiyonunun görüntü kümesidir.
\( f^{-1}: \mathbb{R} - \{ b \} \to \mathbb{R} - \{ \frac{1}{2} \} \)
Yine bir rasyonel fonksiyon olan ters fonksiyonda paydayı 0 yapan değer fonksiyonu tanımsız yapar. Tanım kümesindeki tüm elemanlar için fonksiyonun tanımlı olması gerektiği için, paydayı sıfır yapan bu \( x \) değeri ters fonksiyonun tanım kümesinin dışında bırakılan \( b \) değeri olmalıdır.
\( 2b - 3 = 0 \Longrightarrow b = \dfrac{3}{2} \)
\( f(b) \) değerini bulmak için \( x = \frac{3}{2} \) yazalım.
\( f(b) = f(\frac{3}{2}) \)
\( = \dfrac{3(\frac{3}{2}) - \frac{1}{2}}{2(\frac{3}{2}) - 1} = 2 \) bulunur.
\( f: [4, \infty) \to A \) fonksiyonu örtendir.
\( f(x) = x^2 - 8x + 12 \) olduğuna göre, \( f^{-1}(x) \) fonksiyonunu bulunuz.
Çözümü GösterVerilen fonksiyon başkatsayısı pozitif ve kolları yukarı yönlü olan bir paraboldür.
Parabolün tepe noktasına \( T(r, k) \) diyelim.
\( r = -\dfrac{-8}{2} = 4 \)
\( k = f(4) = 4^2 - 8(4) + 12 = -4 \)
\( T(4, -4) \) olduğuna göre parabolün görüntü kümesi \( [-4, \infty) \) olur.
\( f: [4, \infty) \to [-4, \infty) \)
Fonksiyonun tanım kümesi parabolün tepe noktası ve daha büyük apsis değerli noktaları kapsadığı için fonksiyon yatay doğru testini geçer ve birebirdir, dolayısıyla tersi tanımlıdır.
\( x \) değişkenini yalnız bırakalım.
İfadeyi tam kareye tamamlamak için 16 ekleyip çıkaralım.
\( y = x^2 - 8x + 16 - 16 + 12 \)
\( y = (x - 4)^2 - 4 \)
\( (x - 4)^2 = y + 4 \)
\( \sqrt{(x - 4)^2} = \sqrt{y + 4} \)
\( \abs{x - 4} = \sqrt{y + 4} \)
\( f \) fonksiyonunun tanım kümesi 4'ten büyük reel sayıları kapsadığı için \( x - 4 \) ifadesi mutlak değer dışına olduğu gibi çıkar.
\( x - 4 = \sqrt{y + 4} \)
\( x = \sqrt{y + 4} + 4 \)
\( x \) ve \( y \) değişkenlerinin yerlerini değiştirdiğimizde \( y = f^{-1} \) fonksiyonunu elde ederiz.
\( y = f^{-1}(x) = \sqrt{x + 4} + 4 \)
\( f^{-1} \) fonksiyonunun tanım kümesi \( f \) fonksiyonunun görüntü kümesine, \( f^{-1} \) fonksiyonunun görüntü kümesi \( f \) fonksiyonunun tanım kümesine eşittir.
\( f^{-1}: [-4, \infty) \to [4, \infty) \)
\( f, g, h \) uygun aralıklarda tanımlı birer fonksiyon olmak üzere,
Aşağıdaki fonksiyonların tersini bulunuz.
(a) \( f(x) = 2 - \ln(x + 1) \)
(b) \( g(x) = \sqrt{e^x - 2} \)
(c) \( h(x) = 1 + 2e^{-x} \)
Çözümü GösterBir fonksiyonun tersini bulmak için fonksiyon tanımında \( x \) yalnız bırakılır, elde edilen ifadede \( x \) ve \( y \) değişkenlerinin yerleri değiştirilir.
(a) seçeneği:
\( y = 2 - \ln(x + 1) \)
\( x \)'i yalnız bırakalım.
\( \ln(x + 1) = 2 - y \)
Her iki tarafta \( e \)'nin kuvvetini alalım.
\( e^{\ln(x + 1)} = e^{2 - y} \)
\( x + 1 = e^{2 - y} \)
\( x = e^{2 - y} - 1 \)
\( x \) ve \( y \) değişkenlerinin yerlerini değiştirdiğimizde ters fonksiyonu elde ederiz.
\( y = f^{-1}(x) = e^{2 - x} - 1 \)
(b) seçeneği:
\( y = \sqrt{e^x - 2} \)
Eşitliğin her iki tarafının karesini alıp köklü ifadeden kurtulalım.
\( y^2 = e^x - 2 \)
\( e^x = y^2 + 2 \)
Her iki tarafın doğal logaritmasını alalım.
\( \ln{e^x} = \ln(y^2 + 2) \)
\( x = \ln(y^2 + 2) \)
\( x \) ve \( y \) değişkenlerinin yerlerini değiştirdiğimizde ters fonksiyonu elde ederiz.
\( y = g^{-1}(x) = \ln(x^2 + 2) \)
(c) seçeneği:
\( y = 1 + 2e^{-x} \)
\( x \)'i yalnız bırakalım.
\( 2e^{-x} = y - 1 \)
\( e^{-x} = \dfrac{y - 1}{2} \)
Her iki tarafın doğal logaritmasını alarak \( e \) ifadesinden kurtulalım.
\( \ln{e^{-x}} = \ln{\dfrac{y - 1}{2}} \)
\( -x = \ln{\dfrac{y - 1}{2}} \)
\( x = -\ln{\dfrac{y - 1}{2}} \)
\( x \) ve \( y \) değişkenlerinin yerlerini değiştirdiğimizde ters fonksiyonu elde ederiz.
\( y = h^{-1}(x) = -\ln{\dfrac{x - 1}{2}} \)
\( f(x) = \dfrac{12^x + 20^x}{3^x + 5^x} \) olduğuna göre,
\( f(2) \cdot f^{-1}(2) \) çarpımı kaçtır?
Çözümü Göster\( f(x) = \dfrac{12^x + 20^x}{3^x + 5^x} = \dfrac{3^x \cdot 4^x + 4^x \cdot 5^x}{3^x + 5^x} \)
Eşitliği \( 4^x \) parentezine alalım.
\( = \dfrac{4^x(3^x + 5^x)}{3^x + 5^x} = 4^x \)
Üstel fonksiyonun ters fonksiyonu logaritma fonksiyonudur.
\( f^{-1}(x) = \log_4{x} \)
Sorudaki ifadelerin değerini bulalım.
\( f(2) = 4^2 = 16 \)
\( f^{-1}(2) = \log_4{2} = \dfrac{1}{2} \)
Bulduğumuz değerleri yerlerine koyalım.
\( f(2) \cdot f^{-1}(2) = 16 \cdot \dfrac{1}{2} = 8 \) bulunur.
\( f: [0, 5) \to A \) olmak üzere,
\( f(x) = \sqrt{x + 4} \)
fonksiyonunun ters fonksiyonunu bularak tanım ve görüntü kümelerini belirtin.
Çözümü GösterBir fonksiyonun tersini bulmak için fonksiyon tanımında \( x \) yalnız bırakılır, elde edilen ifadede \( x \) ve \( y \) değişkenlerinin yerleri değiştirilir.
\( y = \sqrt{x + 4} \)
Her iki tarafın karesini alarak köklü ifadeden kurtaralım.
\( y^2 = x + 4 \)
\( x \)'i yalnız bırakalım.
\( x = y^2 - 4 \)
\( x \) ve \( y \) değişkenlerinin yerlerini değiştirdiğimizde \( y = f^{-1} \) fonksiyonunu elde ederiz.
\( y = f^{-1}(x) = x^2 - 4 \)
\( f^{-1} \) fonksiyonunun tanım kümesi \( f \) fonksiyonunun görüntü kümesine, \( f^{-1} \) fonksiyonunun görüntü kümesi \( f \) fonksiyonunun tanım kümesine eşittir.
\( f \) fonksiyonunun görüntü kümesini bulalım.
Karekök fonksiyonu kesin artan bir fonksiyon olduğu için görüntü kümesi tanım kümesinin sınır değerlerindeki fonksiyon değerleri arasındaki aralıktır.
\( f(0) = \sqrt{0 + 4} = 2 \)
\( f(5) = \sqrt{5 + 4} = 3 \)
Görüntü kümesi: \( f(x) \in [2, 3) \)
O halde \( f^{-1} \) fonksiyonunun tanım ve görüntü kümeleri aşağıdaki gibidir.
Tanım kümesi: \( x \in [2, 3) \)
Görüntü kümesi: \( f^{-1}(x) \in [0, 5) \)
\( f: [0, \infty) \to A \) olmak üzere,
\( f(x) = 2x^2 + 5 \)
fonksiyonunun ters fonksiyonunu bularak tanım ve görüntü kümelerini belirtin.
Çözümü GösterBir fonksiyonun tersini bulmak için fonksiyon tanımında \( x \) yalnız bırakılır, elde edilen ifadede \( x \) ve \( y \) değişkenlerinin yerleri değiştirilir.
\( y = 2x^2 + 5 \)
\( x \)'i yalnız bırakalım.
\( 2x^2 = y - 5 \)
\( x^2 = \dfrac{y - 5}{2} \)
Her iki tarafın karekökünü alalım.
\( x = \sqrt{\dfrac{y - 5}{2}} \)
\( x \) ve \( y \) değişkenlerinin yerlerini değiştirdiğimizde \( y = f^{-1} \) fonksiyonunu elde ederiz.
\( y = f^{-1}(x) = \sqrt{\dfrac{x - 5}{2}} \)
\( f^{-1} \) fonksiyonunun tanım kümesi \( f \) fonksiyonunun görüntü kümesine, \( f^{-1} \) fonksiyonunun görüntü kümesi \( f \) fonksiyonunun tanım kümesine eşittir.
\( f \) fonksiyonunun görüntü kümesini bulalım.
\( f(x) = 2x^2 + 5 \) fonksiyonu \( [0, \infty) \) aralığında kesin artan bir fonksiyon olduğu için görüntü kümesi tanım kümesinin sınır değerlerindeki fonksiyon değerleri arasındaki aralıktır.
\( f(0) = 2(0)^2 + 5 = 5 \)
\( x \to \infty \) iken \( f(x) \to \infty \) olur.
Görüntü kümesi: \( f(x) \in [5, \infty) \)
O halde \( f^{-1} \) fonksiyonunun tanım ve görüntü kümeleri aşağıdaki gibidir.
Tanım kümesi: \( x \in [5, \infty) \)
Görüntü kümesi: \( f^{-1}(x) \in [0, \infty) \)
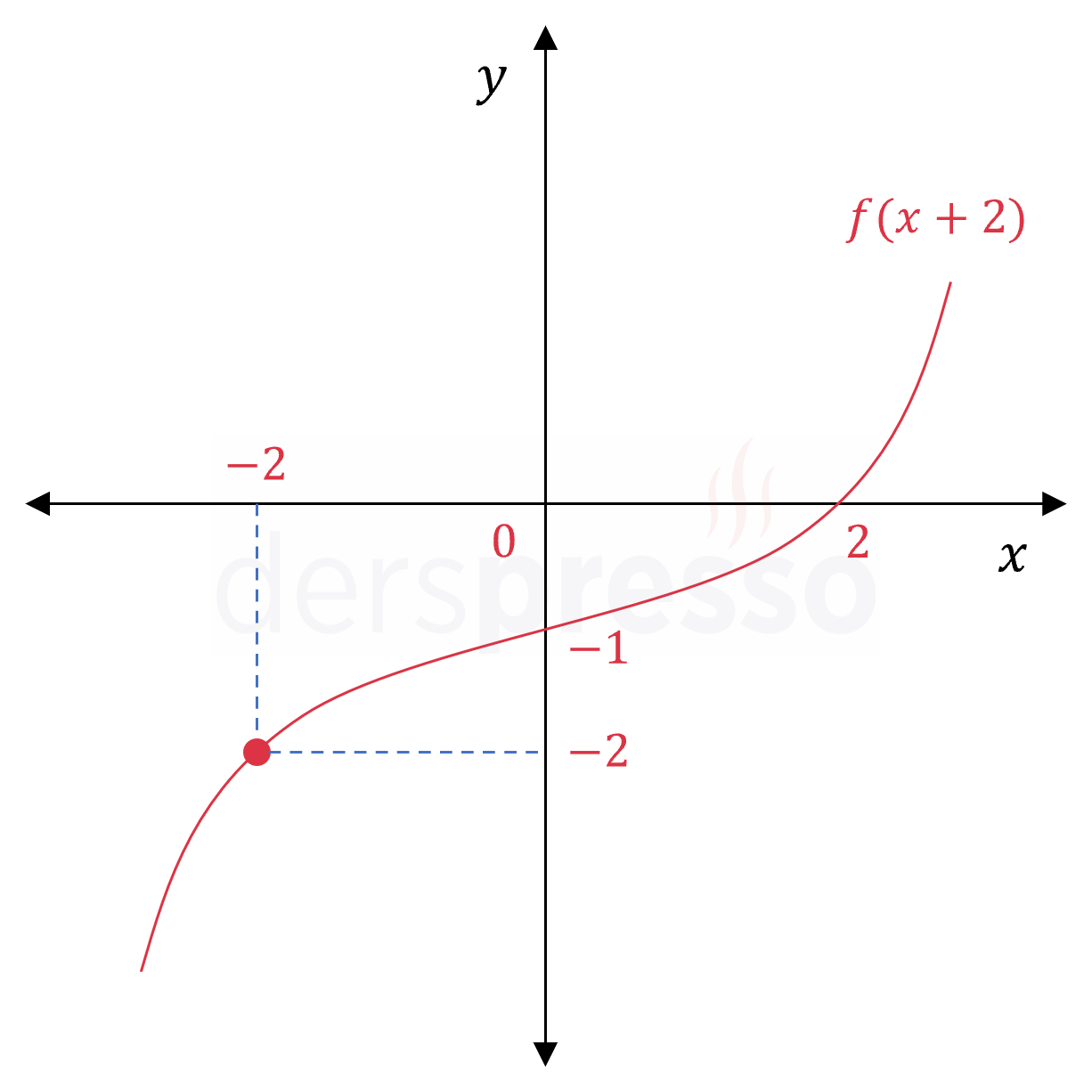
Yukarıda \( y = f(x + 2) \) fonksiyonunun grafiği verilmiştir.
\( \dfrac{f(0) + f^{-1}(-1)}{f(2)} \) ifadesinin değeri kaçtır?
Çözümü Göster\( f(2) \) değerini bulmak için \( f(x + 2) \) grafiğinde \( x = 0 \) noktasına bakılır.
\( f(0 + 2) = f(2) = -1 \)
\( f(0) \) değerini bulmak için \( f(x + 2) \) grafiğinde \( x = -2 \) noktasına bakılır.
\( f(-2 + 2) = f(0) = -2 \)
\( f(2) = -1 \) olarak bulduğumuz için \( f^{-1}(-1) = 2 \) olur.
Bu değerleri sorudaki ifadede yerlerine koyalım.
\( \dfrac{f(0) + f^{-1}(-1)}{f(2)} = \dfrac{-2 + 2}{-1} = 0 \) bulunur.

Yukarıda \( f \) ve \( g \) fonksiyonlarının grafikleri verilmiştir.
\( g \) fonksiyonu doğrusal, her iki fonksiyon da birebir ve artandır.
\( (g^{-1} \circ f)(k) = -3 \) olduğuna göre, \( k \) kaçtır?
Çözümü GösterEksenleri \( (x_1, 0) \) ve \( (0, y_2) \) noktalarında kesen doğrunun denklemi aşağıdaki formülle bulunur.
\( \dfrac{x}{x_1} + \dfrac{y}{y_1} = 1 \)
\( \dfrac{x}{-6} + \dfrac{y}{2} = 1 \)
\( -x + 3y = 6 \)
\( y = g(x) = \dfrac{x}{3} + 2 \)
\( f \) ve \( g \) fonksiyonları \( x = k \) noktasında kesiştiklerine göre, bu noktada iki fonksiyonun değeri eşittir.
\( f(k) = g(k) = \dfrac{k}{3} + 2 \)
Soruda verilen ifadeyi düzenleyelim.
\( (g^{-1} \circ f)(k) = g^{-1}(f(k)) = -3 \)
\( g(-3) = f(k) \)
\( \dfrac{-3}{3} + 2 = f(k) \)
\( f(k) = 1 \)
\( f(k) = g(k) \) eşitliğini kullanalım.
\( g(k) = 1 \)
\( \dfrac{k}{3} + 2 = 1 \)
\( k = -3 \) bulunur.
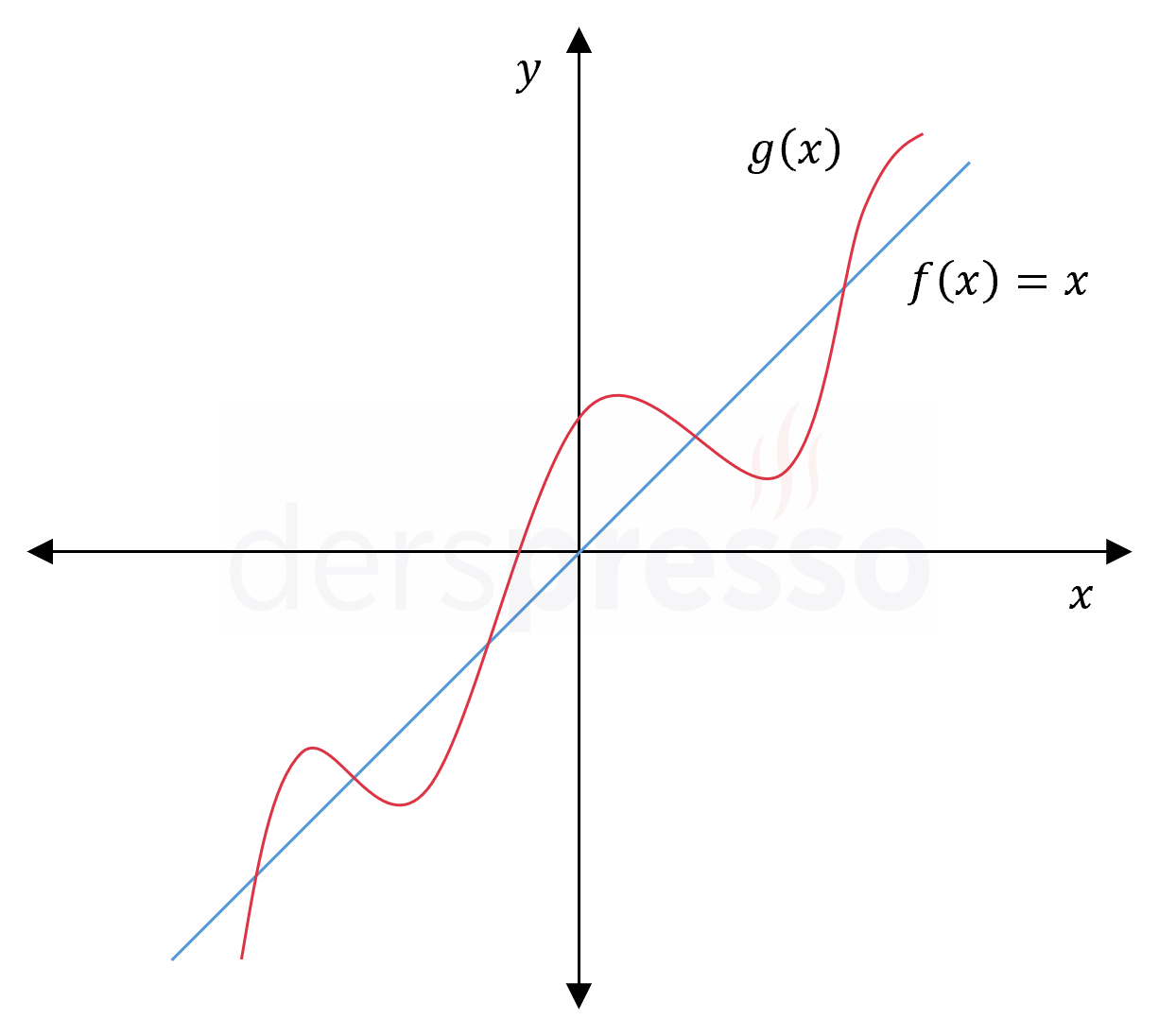
Verilen aralıkta tanımlı \( f \) ve \( g \) fonksiyonlarının grafikleri yukarıdaki gibidir.
Buna göre \( g(x) = g^{-1}(x) \) eşitliğini sağlayan kaç reel sayı vardır?
Çözümü Göster\( g(x) = g^{-1}(x) \) eşitliği, \( g(x) \) ve \( g^{-1}(x) \) fonksiyonlarının kesişim noktalarını ifade eder.
Bir fonksiyonun ve tersinin grafikleri \( y = x \) doğrusuna göre simetriktir, dolayısıyla iki fonksiyonun grafiklerinin kesişim noktaları \( y = x \) doğrusu üzerinde bulunur.
Buna göre, \( g(x) = g^{-1}(x) \) eşitliğini sağlayan noktalar, \( f(x) \) ve \( g(x) \) fonksiyonlarının grafiklerinin kesişim noktaları ile aynıdır.
Grafiği incelediğimizde \( f(x) \) ve \( g(x) \) fonksiyonları 5 noktada kesişir, dolayısıyla \( g(x) = g^{-1}(x) \) eşitliğini sağlayan 5 reel sayı vardır.
\( f(\log_2{x}) = \sqrt{x} + 5 \) olduğuna göre, \( f^{-1}(x) \) fonksiyonunu bulunuz.
Çözümü GösterFonksiyonun içini \( x \) yapabilmek için \( x \) yerine \( \log_2{x} \) ifadesinin tersi olan \( 2^x \) yazalım.
\( f(\log_2{2^x}) = \sqrt{2^x} + 5 \)
\( f(x) = \sqrt{2^x} + 5 = y \)
\( x \) değişkenini yalnız bırakalım.
\( y - 5 = \sqrt{2^x} \)
Tarafların karesini alalım.
\( (y - 5)^2 = 2^x \)
Tarafların 2 tabanında logaritmasını alalım.
\( \log_2{(y - 5)^2} = \log_2{2^x} \)
\( x = 2\log_2(y - 5) \)
\( x \) ve \( y \) değişkenlerinin yerlerini değiştirdiğimizde \( y = f^{-1} \) fonksiyonunu elde ederiz.
\( y = f^{-1}(x) = 2\log_2(x - 5) \)