Bir Faktöriyelde Bulunan Çarpan Sayısı
10! içinde belirli bir asal çarpanın kaç kez bulunduğunu sayıyı asal çarpanlarının kuvvetleri biçiminde yazarak bulabiliriz.
\( 10! = 1 \cdot 2 \cdot 3 \cdot 4 \cdot 5 \cdot 6 \cdot 7 \cdot 8 \cdot 9 \cdot 10 \)
İfadedeki bileşik sayıları asal çarpanlarına ayıralım.
\( 10! = 1 \cdot 2 \cdot 3 \cdot (2 \cdot 2) \cdot 5 \cdot (2 \cdot 3) \cdot \) \( 7 \cdot \) \( (2 \cdot 2 \cdot 2) \cdot \) \( (3 \cdot 3) \cdot \) \( (2 \cdot 5) \)
Şimdi de her bir asal çarpanın kaç kez tekrarladığını sayarak ifadeyi asal çarpanların kuvvetleri biçiminde yazalım.
\( 10! = 2^8 \cdot 3^4 \cdot 5^2 \cdot 7^1 \)
10! için bu işlemi asal çarpanlara ayırarak yapabilmiş olsak da, daha büyük bir sayının faktöriyeli için bu işlem çok uzun sürecektir. Bir sayının faktöriyelinin içinde belirli bir çarpanın kaç kez bulunduğunu aşağıda detaylandıracağımız yöntemle hızlı bir şekilde bulabiliriz.
Örnek olarak 85! içinde 3 çarpanının kaç kez geçtiğini bulalım. 85!'in açılımı 1'den 85'e kadar sayıların çarpımı şeklinde aşağıdaki tabloda listelenmiştir.
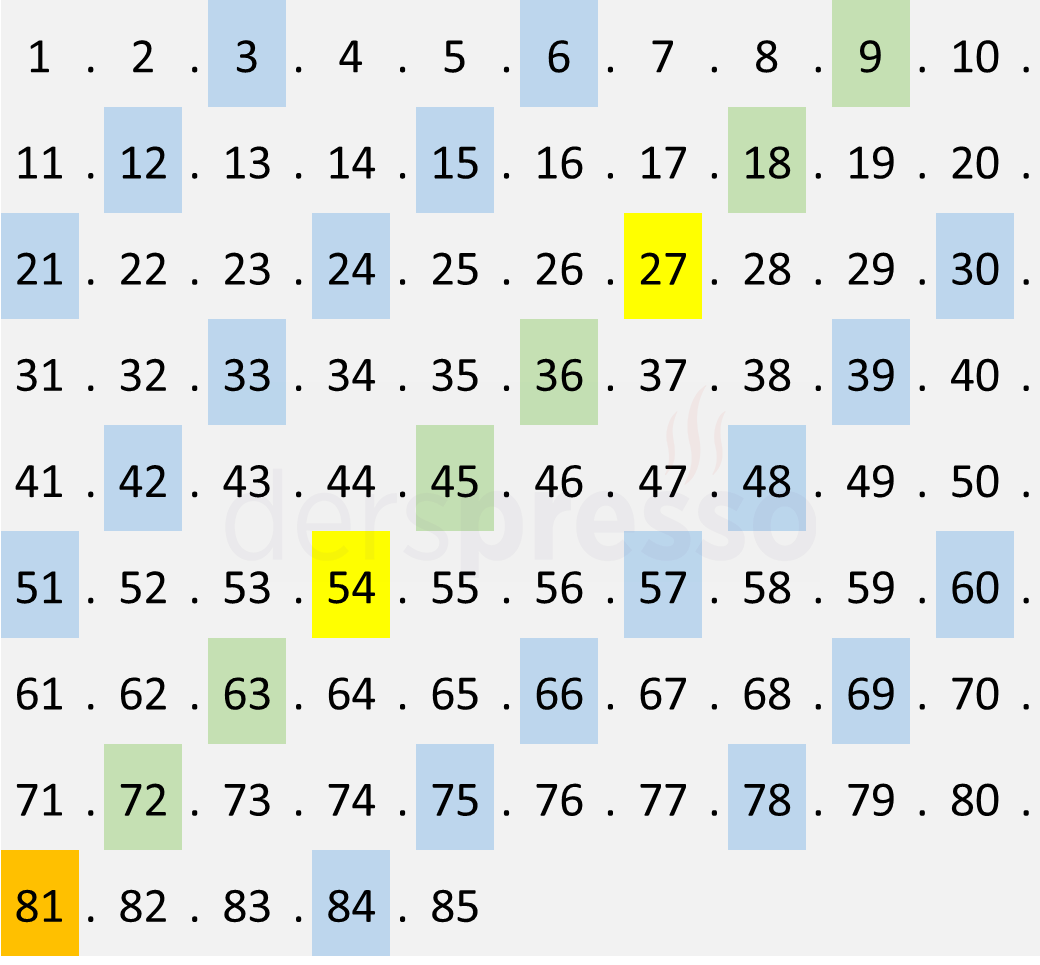
Tablodaki her bir sayıyı asal çarpanları açısından düşündüğümüzde şu çıkarımları yapabiliriz.
- Mavi kutular: Bu sayıların içinde bir tane \( 3 \) çarpanı bulunmaktadır (\( 3^1 = 3 \)).
- Yeşil kutular: Bu sayıların içinde iki tane \( 3 \) çarpanı bulunmaktadır (\( 3^2 = 3 \cdot 3 \)).
- Sarı kutular: Bu sayıların içinde üç tane \( 3 \) çarpanı bulunmaktadır (\( 3^3 = 3 \cdot 3 \cdot 3 \)).
- Turuncu kutular: Bu sayıların içinde dört tane \( 3 \) çarpanı bulunmaktadır (\( 3^4 = 3 \cdot 3 \cdot 3 \cdot 3 \)).
- Gri kutular: Bu sayıların içinde \( 3 \) asal çarpan olarak bulunmaz.
Bu bilgiyi kullanarak 85! içinde 3 çarpanının kaç kez geçtiğini bulmak için aşağıdaki yöntemi kullanabiliriz.
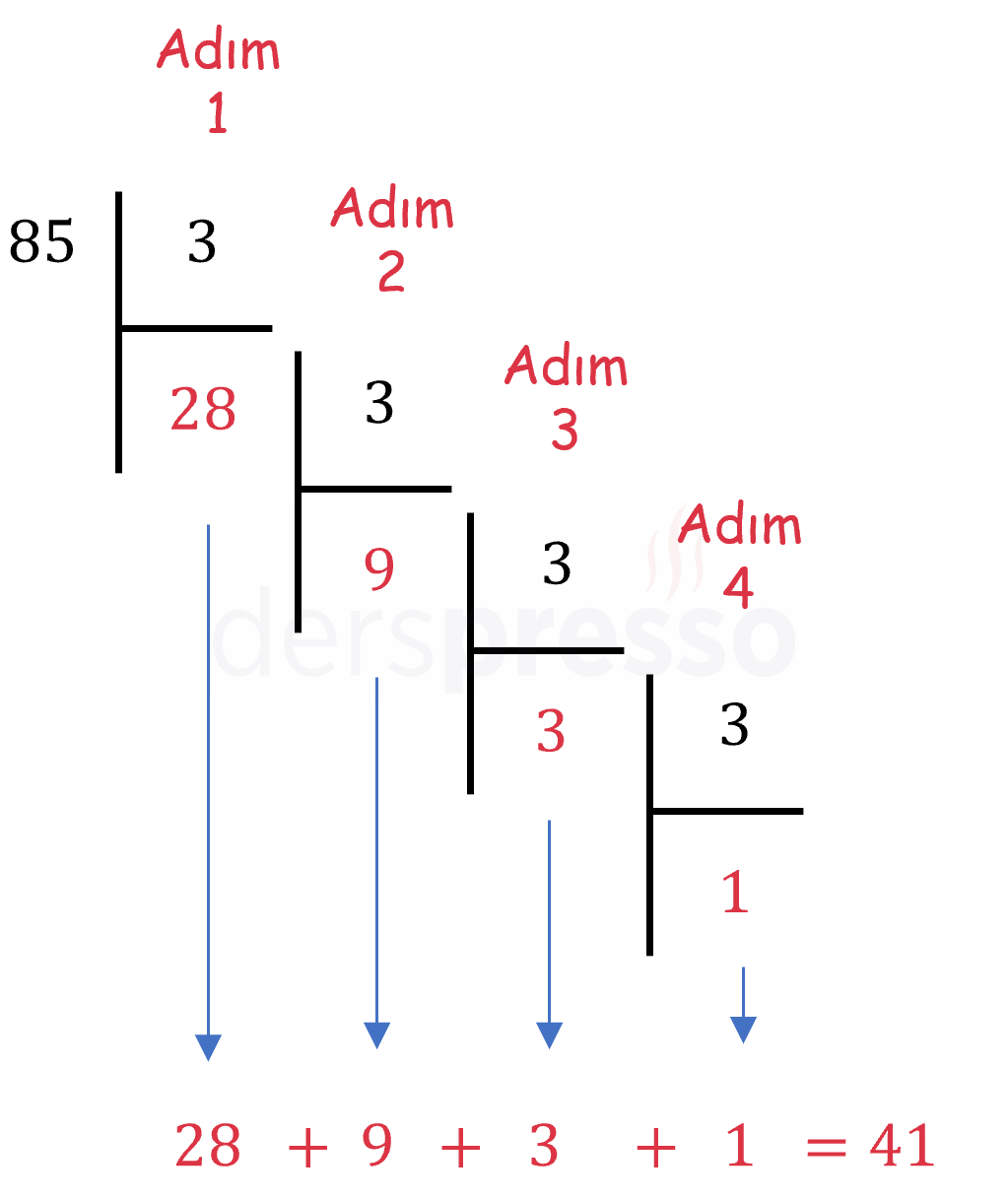
- Adım 1: Önce faktöriyeli verilen sayı olan \( 85 \)'i \( 3 \)'e böleriz. Kalanı dikkate almadan elde ettiğimiz bölüm (\( 28 \)) bize en azından bir tane \( 3 \) çarpanı içeren kutu sayısını verir (gri dışındaki tüm renkli kutular).
- Adım 2: İlk adımda elde ettiğimiz bölümü (\( 28 \)) tekrar \( 3 \)'e böleriz. Bu işlemin sonucu bize kutuların kaçının ikinci bir \( 3 \) çarpanı içerdiğini verir (yeşil, sarı ve turuncu kutular).
- Adım 3: İkinci adımda elde ettiğimiz bölümü (\( 9 \)) tekrar \( 3 \)'e böleriz. Bu işlemin sonucu bize kutuların kaçının üçüncü bir \( 3 \) çarpanı içerdiğini verir (sarı ve turuncu kutular).
- Adım 4: Üçüncü adımda elde ettiğimiz bölüm (\( 3 \)) içinde en az bir \( 3 \) bulundurduğu için bölme işlemini tekrar yaparız. Bu işlemin sonucu bize renkli kutuların kaçının dördüncü bir \( 3 \) çarpanı içerdiğini verir (turuncu kutular).
- Dördüncü adımın işlem sonucu olan \( 1 \) içinde başka bir \( 3 \) bulunmadığı için işlemi sonlandırırız. Her bir adımın bölümlerinin toplamı bize \( 85! \) sayısının içindeki \( 3 \) asal çarpanlarının toplam sayısını verir (\( 28 + 9 + 3 + 1 = 41 \)).
\( 85! = 2^a \cdot 3^{41} \cdot 5^c \cdot \ldots \)
Bir Faktöriyelde Asal Çarpanların Kuvvetleri
Bir sayının faktöriyelinin asal çarpanlarının kuvvetleri biçiminde yazılışında asal çarpanlar büyüdükçe çarpanların kuvvetleri azalır ya da aynı kalır.
\( n \in \mathbb{Z^+} \) olmak üzere,
\( n! = 2^a \cdot 3^b \cdot 5^c \cdot 7^d \cdot \ldots \) ise,
\( a \ge b \ge c \ge d \)
\( 100! \) sayısı arka arkaya kaç kez kalansız \( 3 \)'e bölünebilir?
Çözümü GösterBir sayı belirli bir çarpanı içerdiği sayıda o çarpana kalansız bölünebilir, bunun sebebi sayıyı o çarpana her böldüğümüzde sayının asal çarpanları biçiminde yazılışında o çarpanın kuvvetinin bir azalacak olmasıdır.
Buna göre \( 100! \) sayısının içinde:
3'ün her katı için \( \floor{100 / 3} = 33 \) tane
9'un her katı için \( \floor{33 / 3} = 11 \) tane daha
27'nin her katı için \( \floor{11 / 3} = 3 \) tane daha
81'in her katı için \( \floor{3 / 3} = 1 \) tane daha
Toplamda \( 33 + 11 + 3 + 1 = 48 \) tane 3 çarpanı vardır.
Dolayısıyla \( 100! \) sayısı arka arkaya 48 kez 3'e kalansız bölünebilir.
\( x, y \in \mathbb{N} \) olmak üzere,
\( 30! = 6^x \cdot y \)
eşitliğini sağlayan \( x \) değeri en çok kaç olabilir?
Çözümü Göster\( 30! = 6^x \cdot y \)
\( 6 = 2 \cdot 3 \)
Her 6 çarpanı birer tane 2 ve 3 çarpanından oluştuğu için, \( 30! \) sayısı içindeki 2 ve 3 çarpanlarından hangisi daha az sayıda ise o sayıda 6 çarpanı içerir.
Bir faktöriyelin içinde daha büyük bir sayı olan 3 çarpanı 2 çarpanından daha az sayıda bulunur.
Buna göre, \( 30! \) sayısının içinde:
3'ün her katı için \( \floor{30 / 3} = 10 \) tane
9'un her katı için \( \floor{10 / 3} = 3 \) tane daha
27'nin her katı için \( \floor{3 / 3} = 1 \) tane daha
Toplamda \( 10 + 3 + 1 = 14 \) tane 3 çarpanı vardır.
Buna göre, \( 30! \) sayısının içinde 14 tane 3 çarpanı, dolayısıyla 14 tane 6 çarpanı vardır.
O halde, verilen eşitlikte \( x \) doğal sayısı en çok 14 olabilir.
\( n, A \in \mathbb{Z^+} \) olmak üzere,
\( 88! = 24^n \cdot A \)
denkleminde \( n \)'nin alabileceği en büyük değer kaçtır?
Çözümü GösterBu soru \( 88! \) sayısı \( 24 \)'e en çok kaç kez kalansız bölünebilir sorusu ile özdeştir, çünkü \( n \)'nin alabileceği en büyük değer \( 88! \) içindeki \( 24 \) çarpan sayısına eşittir.
\( 24 \)'ü asal çarpanlarına ayıralım.
\( 24 = 2^3 \cdot 3^1 \)
\( 88! \) içinde 3 adet 2 çarpanı ve 1 adet 3 çarpanı grup olarak kaç adet bulunuyorsa o kadar 24 çarpanı bulunuyordur. Buna göre önce \( 88! \) içindeki 2 ve 3 çarpan sayılarını bulalım.
\( 88! \) içindeki \( 2 \) çarpanı sayısı \( = 44 + 22 + 11 + 5 + 2 + 1 = 85 \)
\( 88! \) içindeki \( 3 \) çarpanı sayısı \( = 29 + 9 + 3 + 1 = 42 \)
Verilen eşitlikte 24'ü çarpanları cinsinden yazalım.
\( 88! = (2^3 \cdot 3^1)^n \cdot A \)
\( 88! \) içindeki 85 adet 2 çarpanı ve 42 adet 3 çarpanını aşmayacak şekilde \( n \)'ye verebileceğimiz en büyük değer 28 olur. Bu durumda, kalan 1 adet 2 çarpanı ve 14 adet 3 çarpanı \( A \) değişkenine dahil olur.
\( 88! = (2^3 \cdot 3^1)^{28} \cdot A \)
\( 88! = 2^{84} \cdot 3^{28} \cdot A \)
Buna göre, \( n = 28 \) olarak bulunur.
\( M \in \mathbb{Z^+} \) olmak üzere,
\( 5! \cdot 9! \cdot M \)
ifadesinin bir tam kare sayı olması için \( M \) sayısının alabileceği en küçük değer kaçtır?
Çözümü GösterBir sayının tam kare olabilmesi için (1, 4, 9, 16, ...) asal çarpanları biçiminde yazılışında tüm asal çarpanlarının kuvveti çift sayı olmalıdır.
\( A = (x^a \cdot y^b \cdot z^c)^2 \)
\( = x^{2a} \cdot y^{2b} \cdot z^{2c} \)
\( 5! \) ve \( 9! \) sayılarını asal çarpanlarına ayıralım.
\( 5! = 1 \cdot 2 \cdot 3 \cdot 4 \cdot 5 \)
\( = 2^3 \cdot 3^1 \cdot 5^1 \)
\( 9! = 1 \cdot 2 \cdot 3 \cdot 4 \cdot 5 \cdot 6 \cdot 7 \cdot 8 \cdot 9 \)
\( = 2^7 \cdot 3^4 \cdot 5^1 \cdot 7^1 \)
Bu iki sayının çarpımını alalım.
\( 5! \cdot 9! = 2^{10} \cdot 3^5 \cdot 5^2 \cdot 7^1 \)
Bu çarpımda 2 ve 5'in kuvvetlerinin çift, 3 ve 7'nin kuvvetlerinin tek olduğunu görüyoruz, dolayısıyla ifadenin bir tam kare olması için ihtiyacımız olan en azından 1'er adet 3 ve 7 çarpanıdır.
Buna göre, \( M \)'nin alması gereken en küçük değer \( M = 3 \cdot 7 = 21 \) olur.
\( 5! \cdot 9! \cdot M \)
\( = (2^{10} \cdot 3^5 \cdot 5^2 \cdot 7^1) \cdot (3 \cdot 7) \)
\( = 2^{10} \cdot 3^6 \cdot 5^2 \cdot 7^2 \)
\( = (2^5 \cdot 3^3 \cdot 5^1 \cdot 7^1)^2 \)
\( k \in \mathbb{Z^+} \) olmak üzere,
\( k^2 \) sayısının \( 15! \) sayısının bir böleni olması şartını sağlayan en büyük \( k \) sayısı kaçtır?
Çözümü Göster\( 15! \) sayısını asal çarpanlarına ayıralım.
Örnek olarak; 2, 6, 10, 14 birer tane, 4 ve 12 ikişer tane, 8 üç tane olmak üzere \( 15! \) sayısı toplam 11 tane 2 çarpanı içerir.
\( 15! = 2^{11} \cdot 3^6 \cdot 5^3 \cdot 7^2 \cdot 11^1 \cdot 13^1 \)
İstenen koşulun sağlanması için; \( k^2 \) sayısının her bir asal çarpanının kuvveti, \( 15! \) sayısının aynı çarpanının kuvvetine eşit ya da ondan küçük en büyük çift sayı olmalıdır.
Bu koşulu sağlayan en büyük \( k^2 \) sayısını yazalım.
\( k^2 = 2^{10} \cdot 3^6 \cdot 5^2 \cdot 7^2 \cdot 11^0 \cdot 13^0 \)
\( k = 2^5 \cdot 3^3 \cdot 5 \cdot 7 \)
\( = 30240 \) bulunur.
\( 12! \cdot 11! \cdot 10! \) çarpımının pozitif bölenlerinin kaç tanesi tam karedir?
Çözümü Göster\( 12! \cdot 11! \cdot 10! = A \) diyelim.
\( 10! \) sayısını asal çarpanlarına ayıralım.
Bir faktöriyelde bulunan çarpan sayısını bulma yöntemini kullanalım.
\( 10! \) içinde \( 5 + 2 + 1 = 8 \) tane 2 çarpanı, \( 3 + 1 = 4 \) tane 3 çarpanı, \( 2 \) tane 5 çarpanı, \( 1 \) tane de 7 çarpanı vardır.
\( 10! = 2^8 \cdot 3^4 \cdot 5^2 \cdot 7 \)
\( A \) sayısını aşağıdaki şekilde yazabiliriz.
\( A = (12 \cdot 11 \cdot 10!) \cdot (11 \cdot 10!) \cdot 10! \)
\( = 12 \cdot 11^2 \cdot (10!)^3 \)
\( = 2^2 \cdot 3 \cdot 11^2 \cdot (10!)^3 \)
\( 10! \) yerine yukarıda bulduğumuz eşitini yazalım.
\( = 2^2 \cdot 3 \cdot 11^2 \cdot (2^8 \cdot 3^4 \cdot 5^2 \cdot 7)^3 \)
\( = 2^2 \cdot 3 \cdot 11^2 \cdot 2^{24} \cdot 3^{12} \cdot 5^6 \cdot 7^3 \)
\( = 2^{26} \cdot 3^{13} \cdot 5^6 \cdot 7^3 \cdot 11^2 \)
İfadeyi en küçük tam kare sayıların kuvvetleri şeklinde yazalım.
\( = (2^2)^{13} \cdot (3^2)^{6} \cdot 3 \cdot (5^2)^3 \cdot (7^2)^1 \cdot 7 \cdot (11^2)^1 \)
Tam kare pozitif bölen sayısını bulmak için \( 2^2 \), \( 3^2 \), \( 5^2 \), \( 7^2 \) ve \( 11^2 \) çarpanlarını daha fazla çarpanlarına ayrılmayan birer çarpan olarak düşünmeliyiz.
Çift sayı kuvvetleri ile bulunmayan \( 3 \) ve \( 7 \) çarpanları ise tam kare sayılarda bulunmamalıdır.
Buna göre sadece \( 2^2 \), \( 3^2 \), \( 5^2 \), \( 7^2 \) ve \( 11^2 \) çarpanlarını asal çarpan olarak kabul ederek tam kare pozitif bölen sayısını bulalım.
\( (13 + 1)(6 + 1)(3 + 1)(1 + 1)(1 + 1) = 1568 \) bulunur.