Asal Sayılar
1 ve kendisi dışında iki doğal sayının çarpımı olarak yazılamayan ve 1'den büyük olan tam sayılara asal sayı denir.
1 ve kendisi dışında iki doğal sayının çarpımı olarak yazılabilen ve 1'den büyük olan tam sayılara bileşik sayı denir.
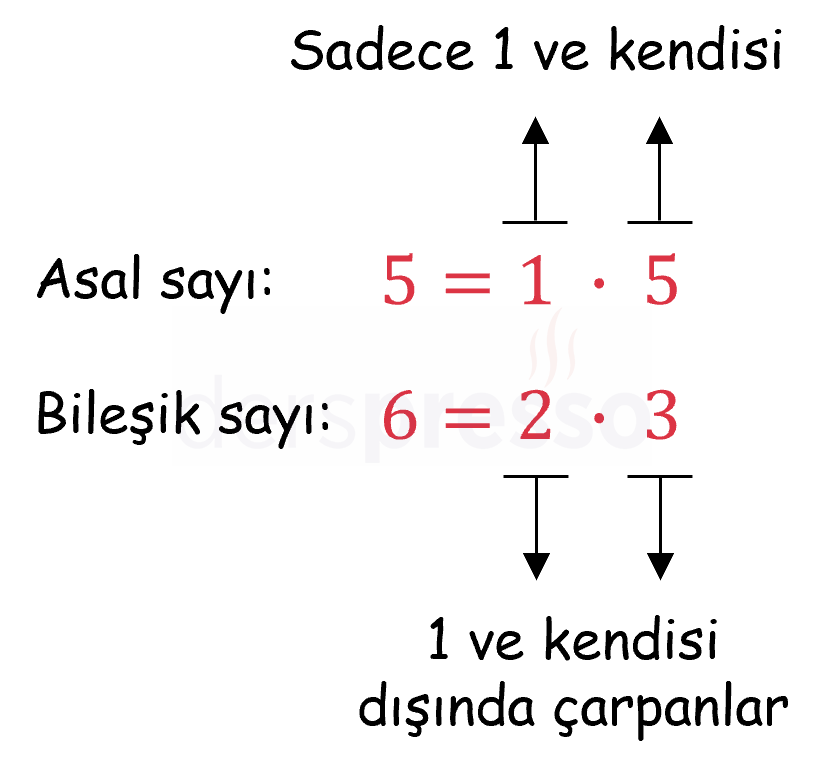
0 ve 1 sayıları ne asaldır ne de bileşiktir. En küçük asal sayı 2, en küçük bileşik sayı 4'tür. 1'den büyük her tam sayı ya asal ya da bileşiktir.
1'in asal sayı olarak kabul edilmemesi tanım gereğidir ve bir ispata dayanmamaktadır. 1'in asal sayıldığı dönemler olmuş olsa da 20. yüzyılın ortalarından itibaren matematikçilerin genel kabulü 1'in asal olmadığı yönündedir.
1'in asal sayı olarak kabul edilmemesinin sebeplerinden biri olan aritmetiğin temel teoreminden önümüzdeki bölümde bahsedeceğiz.
Aşağıda bazı sayıların asal/bileşik olma durumları ve bileşik ise 1 ve kendisi dışındaki çarpanları verilmiştir:
| Sayı | Asal/Bileşik | Çarpanlar |
|---|---|---|
| 0 | İkisi de değil | |
| 1 | İkisi de değil | |
| 2 | Asal | |
| 3 | Asal | |
| 4 | Bileşik | \( 4 = 2 \cdot 2 \) |
| 6 | Bileşik | \( 6 = 2 \cdot 3 \) |
| 13 | Asal | |
| 21 | Bileşik | \( 21 = 3 \cdot 7 \) |
| 53 | Asal | |
| 91 | Bileşik | \( 91 = 7 \cdot 13 \) |
Asal ve bileşik sayılarla ilgili diğer bazı önemli bilgiler aşağıda verilmiştir.
- Asal ve bileşik sayı kavramı sadece 1'den büyük tam sayılar için geçerlidir. Negatif sayıların asallığına bakılmaz.
- Tüm çift sayılar 2 çarpanına ayrılabildikleri için 2 hariç tüm pozitif çift sayılar bileşik sayıdır. Bir diğer deyişle, 2 hariç tüm asal sayılar tek sayıdır.
- Ardışık tam sayı olan asal sayılar sadece 2 ve 3'tür. 2 hariç tüm asal sayılar tek oldukları için ardışık iki asal sayı arasındaki fark en az iki olabilir.
- Asal sayılar içinde sadece 2 çift sayı olduğu için 2 hariç iki asal sayının toplamı ve farkı her zaman çift sayıdır, çarpımları da tek sayıdır. Buna göre, birbirinden farklı iki asal sayının toplamının/farkının tek sayı ya da çarpımının çift sayı olduğunu biliyorsak bu asal sayılardan biri 2 olmalıdır.
Sonsuz sayıda asal sayı vardır.
Sonsuz sayıda asal sayı olduğunu ispatlayabilmek için önce sonlu sayıda ve \( n \) adet asal sayı olduğunu varsayalım ve tüm asal sayılardan oluşan kümeye \( A \) diyelim.
\( A = \{ p_1, p_2, p_3, \cdots, p_n \} \)
Tüm bu asal sayıların çarpımının bir fazlasına eşit olan bir \( P \) sayısı tanımlayalım.
\( P = p_1 \cdot p_2 \cdot p_3 \cdots p_n + 1 \)
\( A \) kümesini tüm asal sayıların kümesi olarak tanımladığımız için yeni elde ettiğimiz \( P \) sayısının bir asal sayı olmaması gerekir, bu da \( P \) sayısının \( A \) kümesinin elemanı olan asal sayılardan en az birine tam bölünmesi anlamına gelir. Ancak yukarıdaki \( P \) sayısını tanımlı asal sayılardan herhangi birine bölersek 1 kalanını elde edeceğimizi görebiliriz, bu da \( P \) sayısının asal sayılardan hiçbirine tam bölünmemesi, dolayısıyla kendisinin bir asal sayı olması anlamına gelir.
İspatın başında tüm asal sayılar kümesini \( A \) olarak tanımlamıştık, ancak \( A \) kümesinin elemanlarını kullanarak elde ettiğimiz \( P \) sayısının bir asal sayı olduğunu göstermiş olduk, dolayısıyla asal sayılar kümesini sonlu bir küme olarak varsaydığımız her durum için yukarıdaki yöntemle yeni bir asal sayı türetebileceğimizi söyleyebiliriz, bu şekilde elde edeceğimiz her yeni \( P \) asal sayısını \( A \) kümesine eklediğimizde de sonsuz elemanlı bir küme elde ederiz.
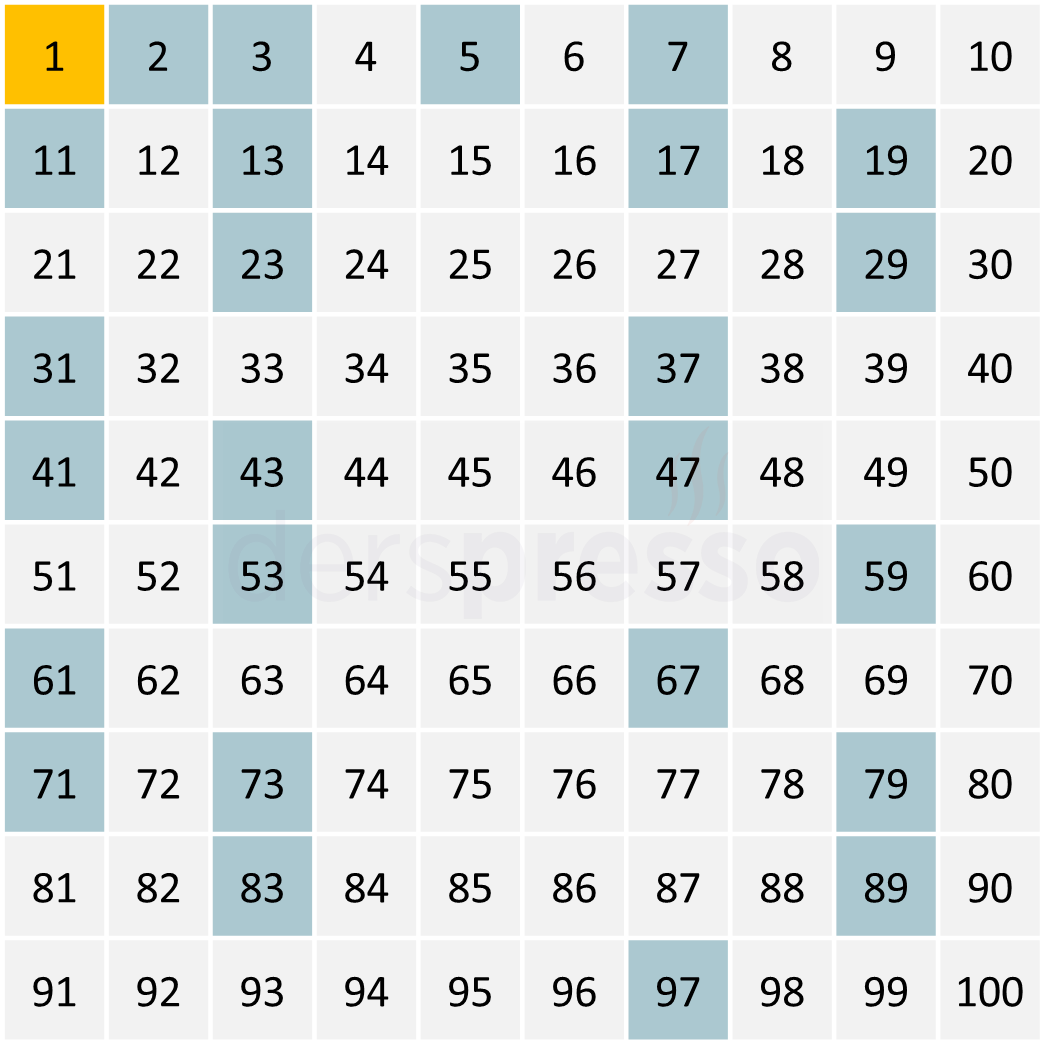
100'e kadar olan ilk 25 asal sayı aşağıdaki tabloda renkli işaretlenmiştir. Asal sayıların 1 ve kendisi dışında iki doğal sayının çarpımı şeklinde yazılamadığı, bileşik sayıların ise yazılabildiği bilgisi doğrultusunda tablodaki sayıların incelenmesinde bu önemli konuyu pekiştirmek adına fayda görüyoruz.
\( a, b \in \mathbb{N} \) olmak üzere,
\( a^2 - b^2 = 13 \) olduğuna göre, \( ab \) çarpımı kaçtır?
Çözümü Gösterİki kare farkı özdeşliğini kullanalım.
\( (a - b)(a + b) = 13 \)
\( a \) ve \( b \) birer doğal sayı olduğu için, toplamları doğal sayı, farkları tam sayı olur.
Sayıların çarpımı bir asal sayı olan 13 olduğuna göre, farkları 1, toplamları 13 olmak zorundadır.
\( a - b = 1 \)
\( a + b = 13 \)
Bu iki denklemi ortak çözdüğümüzde aşağıdaki değerleri buluruz.
\( a = 7, \quad b = 6 \)
\( ab = 7 \cdot 6 = 42 \) bulunur.
236460 ve 236466 sayıları arasında sadece bir asal sayı olduğuna göre, bu sayı kaçtır?
Çözümü Göster23646x sayısı birler basamağı \( \{0, 2, 4, 6\} \) olduğunda 2'ye bölünür.
23646x sayısı birler basamağı \( \{0, 5\} \) olduğunda 5'e bölünür.
23646x sayısı birler basamağı \( \{3, 6\} \) olduğunda (rakamların toplamı 3'ün katı olduğu için) 3'e bölünür.
Buna göre geriye kalan tek seçenek olan 236461 sayısı asal olmalıdır.
\( a \) ve \( b \) asal sayılardır.
\( a + b = 199 \) olduğuna göre, bu sayılardan büyük olan kaçtır?
Çözümü Göster2 dışındaki tüm asal sayılar tek sayıdır, dolayısıyla iki asal sayının toplamı tek sayı ise sayılardan biri 2 olmalıdır.
Sayılardan biri 2 olduğuna göre, diğeri (büyük olanı) 197 olur.
\( a \) ve \( b \) asal sayılardır.
\( a - b = 2999 \) olduğuna göre, \( a + b \) kaçtır?
Çözümü Göster2 dışındaki tüm asal sayılar tek sayıdır, dolayısıyla iki asal sayının toplamı tek sayı ise sayılardan biri 2 olmalıdır.
Buna göre \( a = 3001 \) ve \( b = 2 \) olur.
\( a + b = 3001 + 2 = 3003 \) bulunur.
\( a \) bir asal sayı olmak üzere,
\( \dfrac{3a + 369}{a} \) ifadesinin sonucu bir tam sayı olduğuna göre, \( a \)'nın alabileceği değerlerin toplamı kaçtır?
Çözümü Göster\( \dfrac{3a + 369}{a} = \dfrac{3a}{a} + \dfrac{369}{a} = 3 + \dfrac{369}{a} \)
İlk terim tam sayı olduğu için ikinci terimi tam sayı yapan \( a \) değerlerini bulalım.
Payı asal çarpanlarına ayıralım.
\( \dfrac{369}{a} = \dfrac{3^2 \cdot 41}{a} \)
Bu kesrin bir tam sayı olması için \( a \in \{3, 41\} \) asal sayı değerlerini alabilir.
\( 3 + 41 = 44 \) bulunur.
Atakan, altı basamaklı bir asal sayının bir rakamını siliyor ve 21042 sayısını elde ediyor.
Buna göre Atakan'ın bir rakamını sildiği asal sayı nedir?
Çözümü Göster2 dışında hiçbir çift sayı asal olamayacağı için Atakan'ın sildiği rakam birler basamağındaki rakam olmalıdır.
\( 21042x \)
\( x \) tek sayı olmalıdır.
\( x \) rakamını eleme yöntemiyle bulalım.
Birler basamağı 5 olan sayılar 5'e bölündüğü için \( x = 5 \) olamaz.
21042 sayısının rakamları toplamı 9'dur yani 3'e bölünebilir. Buna göre birler basamağı 3 ya da 9 da olamaz, aksi durumda sayı 3'e bölünebilir.
21042 sayısı 7'ye bölünebilir, dolayısıyla 210427 sayısı da 7'ye bölünebilir. Buna göre \( x = 7 \) de olamaz.
Geriye tek rakamlardan sadece 1 kalır ve 210421 bir asal sayıdır.
Atakan'ın bir rakamını sildiği asal sayı 210421 olarak bulunur.
\( x \) bir asal sayı olmak üzere,
\( \dfrac{222^2 + 333^2}{x} \) kesrini tam sayı yapan farklı \( x \) sayılarının toplamı kaçtır?
Çözümü GösterPaydaki ifadeyi asal çarpanlarına ayıralım.
\( \dfrac{222^2 + 333^2}{x} = \dfrac{(2 \cdot 111)^2 + (3 \cdot 111)^2}{x} \)
\( = \dfrac{4 \cdot 111^2 + 9 \cdot 111^2}{x} \)
\( = \dfrac{13 \cdot 111^2}{x} \)
\( = \dfrac{13 \cdot (3 \cdot 37)^2}{x} \)
\( = \dfrac{13 \cdot 3^2 \cdot 37^2}{x} \)
Bu kesrin tam sayı olması için \( x \in \{ 3, 13, 37 \} \) asal sayı değerlerini alabilir.
\( 3 + 13 + 37 = 53 \) bulunur.
\( p \) ve \( q \) asal sayılar olmak üzere,
\( p^2 \cdot q = p \cdot q^2 - 520 \) olduğuna göre, \( q \) kaçtır?
Çözümü Göster\( p^2 \cdot q = p \cdot q^2 - 520 \)
\( p \cdot q^2 - p^2 \cdot q = 520 \)
\( p \cdot q \cdot (q - p) = 2^3 \cdot 5 \cdot 13 \)
\( p \) ve \( q \) asal sayılar olduğu için 2, 5 ya da 13'ten ikisi olabilirler.
Bulduğumuz eşitlik sadece \( p = 5 \) ve \( q = 13 \) olduğunda sağlanır.
\( q - p = 13 - 5 = 8 = 2^3 \)
\( q = 13 \) bulunur.
\( x, y, z \) asal sayılar olmak üzere,
\( x = (y - z)(y^2 + z^2) \) olduğuna göre, \( x + y + z\) kaçtır?
Çözümü Göster\( x \) asal sayı olduğuna göre, verilen eşitlikteki çarpanlardan biri 1 olmalıdır, aksi takdirde \( x \) 1'den farklı iki sayının çarpımı olacağı için bileşik sayı olur.
\( y \) ve \( z \) asal oldukları için \( y^2 + z^2 \) ifadesi 1'den büyük olur, dolayısıyla \( y - z = 1 \) olmalıdır.
2 dışındaki tüm asal sayılar tek sayıdır, dolayısıyla iki asal sayının farkı tek sayı ise sayılardan biri 2'dir.
Buna göre \( y = 3 \) ve \( z = 2 \) olmalıdır.
\( x = (y - z)(y^2 + z^2) \)
\( x = (3 - 2)(3^2 + 2^2) = 13 \)
\( x + y + z = 13 + 3 + 2 = 18 \) bulunur.
\( a, b, c \) asal sayılar olmak üzere,
\( a^3 - b^3 = c \) olduğuna göre, \( c \) kaçtır?
Çözümü Gösterİki küp farkı özdeşliğini kullanalım.
\( a^3 - b^3 = c \)
\( (a - b)(a^2 + ab + b^2) = c \)
\( c \) bir asal sayı olduğu için çarpanları sadece 1 ve kendisi olabilir.
Üç sayı da asal (dolayısıyla pozitif) olduğu için, fark ifadesi 1'e eşit olmalıdır.
\( a - b = 1 \)
Farkı 1 olan asal sayılar sadece 3 ve 2 olabilir.
\( a = 3, \quad b = 2 \)
\( c \) sayısının değerini bulalım.
\( c = a^3 - b^3 \)
\( = 3^3 - 2^3 = 19 \) bulunur.
\( \dfrac{x}{3} \) ve \( \dfrac{y}{3} \) asal sayılar olduğuna göre, aşağıdakilerden hangileri asal sayı olabilir?
I. \( \dfrac{xy}{3} \)
II. \( \dfrac{x^2 + y^2}{9} \)
III. \( \dfrac{x - y}{3} \)
Çözümü Göster\( \dfrac{x}{3} \) ve \( \dfrac{y}{3} \) asal sayılar olduğuna göre, \( x \) ve \( y \) sayılarını aşağıdaki şekilde yazabiliriz.
\( p, q \) asal sayılar olmak üzere,
\( x = 3p, \quad y = 3q \)
Bu değerleri kullanarak verilen öncülleri inceleyelim.
I. öncül:
\( \dfrac{xy}{3} = \dfrac{(3p)(3q)}{3} \)
\( = 3pq \)
Bu ifade birden fazla asal çarpan içerdiği için asal olamaz.
II. öncül:
\( \dfrac{x^2 + y^2}{9} = \dfrac{(3p)^2 + (3q)^2}{9} \)
\( = \dfrac{9p^2 + 9q^2}{9} \)
\( = p^2 + q^2 \)
Bu ifade örneğin \( p = 3 \) ve \( q = 2 \) için asal olabilir.
III. öncül:
\( \dfrac{x - y}{3} = \dfrac{3p - 3q}{3} \)
\( = p - q \)
Bu ifade örneğin \( p = 5 \) ve \( q = 3 \) için asal olabilir.
Buna göre II. ve III. öncüller asal olabilir.
Güney aklından bir sayı tutuyor. Arkadaşı Burak hangi sayıyı tuttuğunu sorunca Güney aşağıdaki cevabı veriyor.
"Tuttuğum sayı 0'dan büyük 30'dan küçük ve iki farklı asal sayının çarpımından oluşuyor."
Buna göre Güney'in aklından tuttuğu sayının alabileceği değerlerin toplamı kaçtır?
Çözümü Göster20'den küçük asal sayılar aşağıdaki gibidir.
2, 3, 5, 7, 11, 13, 17, 19
0 ve 30 arasında olan ve bu listedeki iki sayının çarpımına eşit olan sayılar aşağıdaki gibidir.
\( 2 \cdot 3 = 6 \)
\( 2 \cdot 5 = 10 \)
\( 2 \cdot 7 = 14 \)
\( 2 \cdot 11 = 22 \)
\( 2 \cdot 13 = 26 \)
\( 3 \cdot 5 = 15 \)
\( 3 \cdot 7 = 21 \)
Bu sayıların toplamını bulalım.
\( 6 + 10 + 14 + 22 + 26 + 15 + 21 = 114 \) bulunur.
Tanım: Aynı ya da farklı iki tane asal sayının çarpımı şeklinde yazılabilen bileşik sayılara yarı asal sayı denir.
Buna göre 30'dan küçük kaç tane yarı asal sayı vardır?
Çözümü Gösterİlk birkaç asal sayıyı listeleyelim.
\( 2, 3, 5, 7, 11, 13, 17, ... \)
Bu listeden aynı ya da farklı iki asal sayının çarpımını alarak verilen tanımı sağlayan yarı asal sayıları bulalım.
\( 4, 6, 9, 10, 14, 15, 21, 22, 25, 26 \)
Buna göre verilen koşulu sağlayan 10 tane yarı asal sayı vardır.
\( n \in \mathbb{Z^+} \) ve \( n \gt 3 \) olmak üzere,
\( n! + 2 \) ve \( n! + n \) sayıları arasındaki asal sayıların toplamı kaçtır?
Çözümü Göster\( 2 \le k \le n \) olmak üzere bir \( k \) tam sayı değeri seçelim.
\( n! \) ifadesi 1'den \( n \)'ye kadar tüm sayıların çarpımından oluştuğu için \( k \) sayısını da içerir.
\( n! = 1 \cdot 2 \cdot \ldots \cdot k \cdot \ldots \cdot (n - 1) \cdot n \)
Bu yüzden \( n! + k \) şeklindeki ifadelerin tümü \( k \) parantezine alınabilir, dolayısıyla \( k \) çarpanı içerir ve bileşik sayıdır.
Buna göre verilen aralıkta asal sayı bulunmaz, yani toplamları sıfırdır.
\( m \in \mathbb{Z^+} \) olmak üzere,
\( m^6 + 10m^3 + 9 \) ifadesi hangi \( m \) değerleri için asal olur?
Çözümü Gösterİfadeyi tam kareye tamamlamak için 16 ekleyelim ve çıkaralım.
\( m^6 + 10m^3 + 9 + 16 - 16 = m^6 + 10m^3 + 25 - 16 \)
\( = (m^3 + 5)^2 - 16 = (m^3 + 5)^2 - 4^2 \)
İki kare farkı özdeşliğini kullanalım.
\( = (m^3 + 5 - 4)(m^3 + 5 + 4) \)
\( = (m^3 + 1)(m^3 + 9) \)
\( m \) pozitif tam sayı olduğu için bu iki çarpan birbirinden ve birden farklı iki tam sayı olur.
Verilen ifadeyi birbirinden ve birden farklı iki pozitif tam sayının çarpımı şeklinde yazabildiğimiz için ifade hiçbir \( m \) değeri için asal olmaz.
\( a \in \mathbb{Z} \) olmak üzere,
\( 2a^2 + 17a + 21 \) bir asal sayı olduğuna göre, \( a \)'nın alabileceği değerlerin çarpımı kaçtır?
Çözümü Göster\( 2a^2 + 17a + 21 = b \) diyelim.
Eşitliğin solundaki ifadeyi çarpanlarına ayıralım.
\( (2a + 3)(a + 7) = b \)
\( a \) tam sayı olduğu için eşitliğin solundaki iki çarpan da tam sayı olur. İki tam sayının çarpımının asal sayı olduğu dört durum vardır.
Durum 1:
\( 1 \cdot b = b \)
\( 2a + 3 = 1 \Longrightarrow a = -1 \)
\( a + 7 = -1 + 7 = 6 = b \)
Bulduğumuz \( b = 6 \) değeri asal olmadığı için \( a = -1 \) geçerli bir çözüm değildir.
Durum 2:
\( -1 \cdot (-b) = b \)
\( 2a + 3 = -1 \Longrightarrow a = -2 \)
\( a + 7 = -2 + 7 = 5 = -b \)
Bulduğumuz \( b = -5 \) değeri asal olmadığı için \( a = -2 \) geçerli bir çözüm değildir.
Durum 3:
\( b \cdot 1 = b \)
\( a + 7 = 1 \Longrightarrow a = -6 \)
\( 2a + 3 = -12 + 3 = -9 = b \)
Bulduğumuz \( b = -9 \) değeri asal olmadığı için \( a = -6 \) geçerli bir çözüm değildir.
Durum 4:
\( -b \cdot (-1) = b \)
\( a + 7 = -1 \Longrightarrow a = -8 \)
\( 2a + 3 = -16 + 3 = -13 = -b \)
Bulduğumuz \( b = 13 \) değeri asal olduğu için \( a = -8 \) geçerli bir çözümdür.
Buna göre \( a \)'nın alabileceği tek değer \( -8 \)'dir.