Noktanın Simetriği
Bir noktanın eksenlere, bir doğruya ya da bir noktaya göre simetriğini bulmak için o noktanın apsis ve ordinat değerlerine belirli dönüşümler uygulanır. Bir noktanın simetriğini bulurken aşağıdaki temel kurallar akılda tutulmalıdır.
\( A \) noktasının \( S \) noktasına göre simetriği \( A' \) ise \( S \) noktası \( [AA'] \) doğru parçasının orta noktası olur.

\( A \) noktasının \( d \) doğrusuna göre simetriği olan \( A' \) noktası için aşağıdaki iki koşul sağlanır.
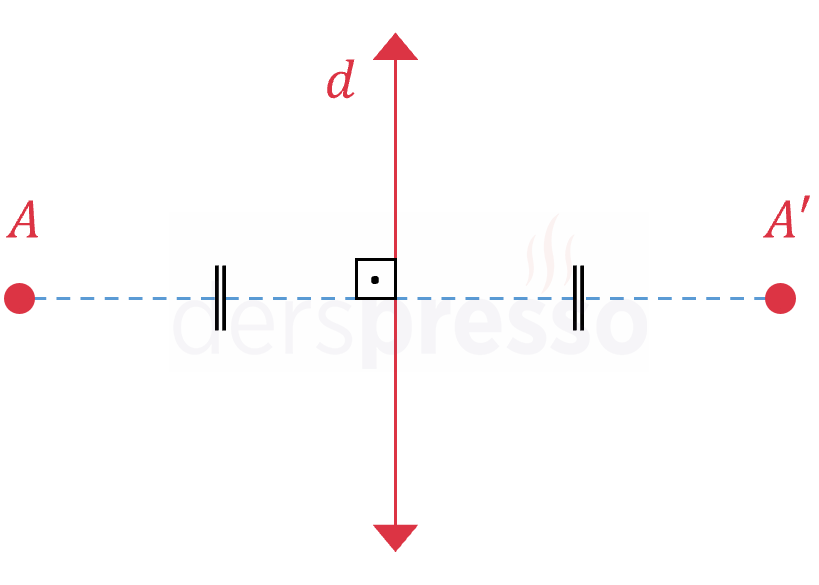
- \( [AA'] \) doğru parçası \( d \) doğrusunu dik keser.
- \( [AA'] \) doğru parçasının orta noktası \( d \) doğrusu ile kesişim noktasıdır.
Bir noktanın bir doğruya ya da noktaya göre simetriğinin aynı doğru ya da noktaya göre simetriği yine kendisi olur.
Bir noktanın farklı simetrileri için uygulanması gereken dönüşümler aşağıdaki tabloda belirtilmiştir.
| Grafik | Simetri |
|---|---|
|
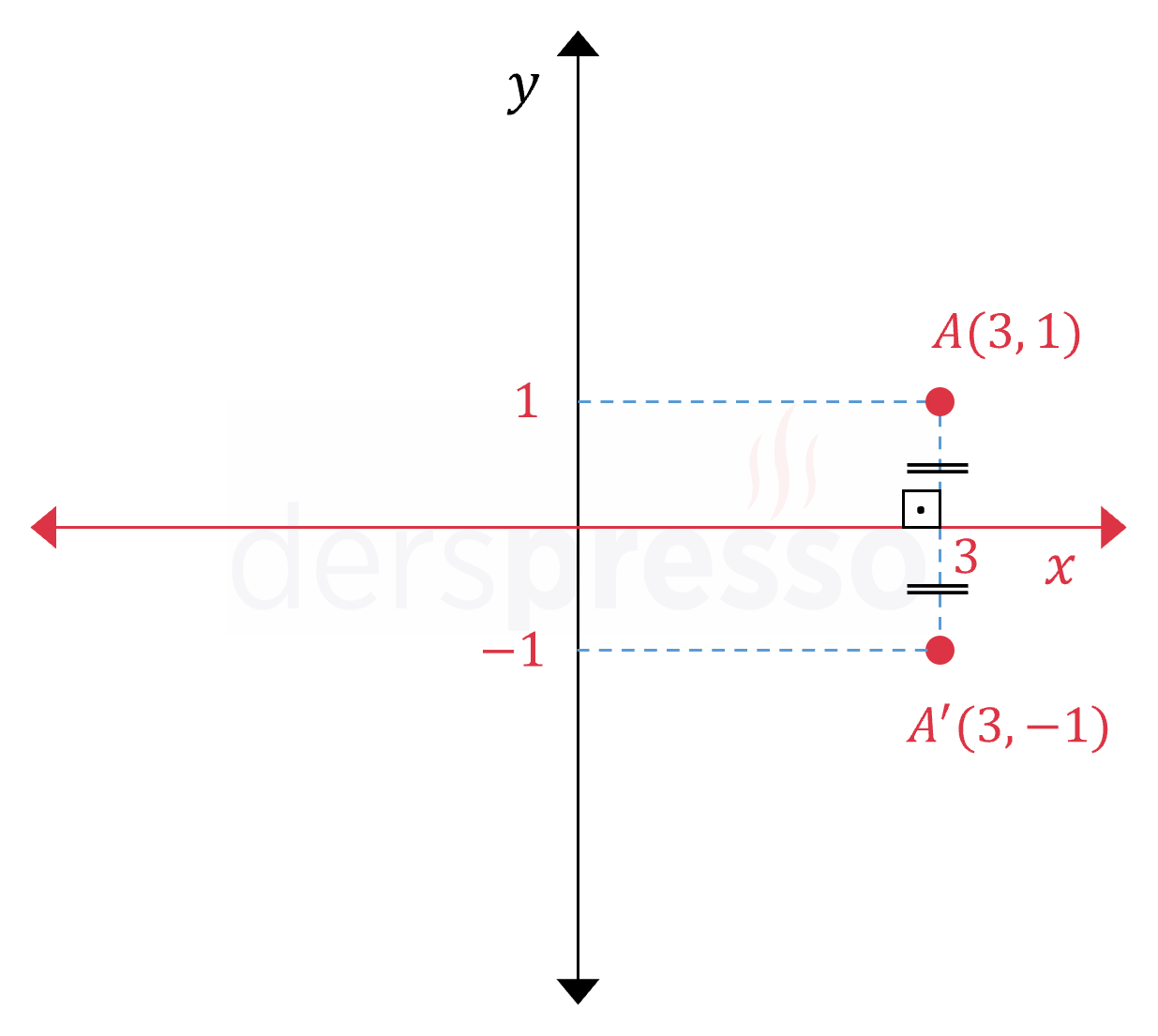
\( x \) eksenine göre: \( A(a, b) \longmapsto A'(a, -b) \) Apsis aynı kalır, ordinat işaret değiştirir. |
|
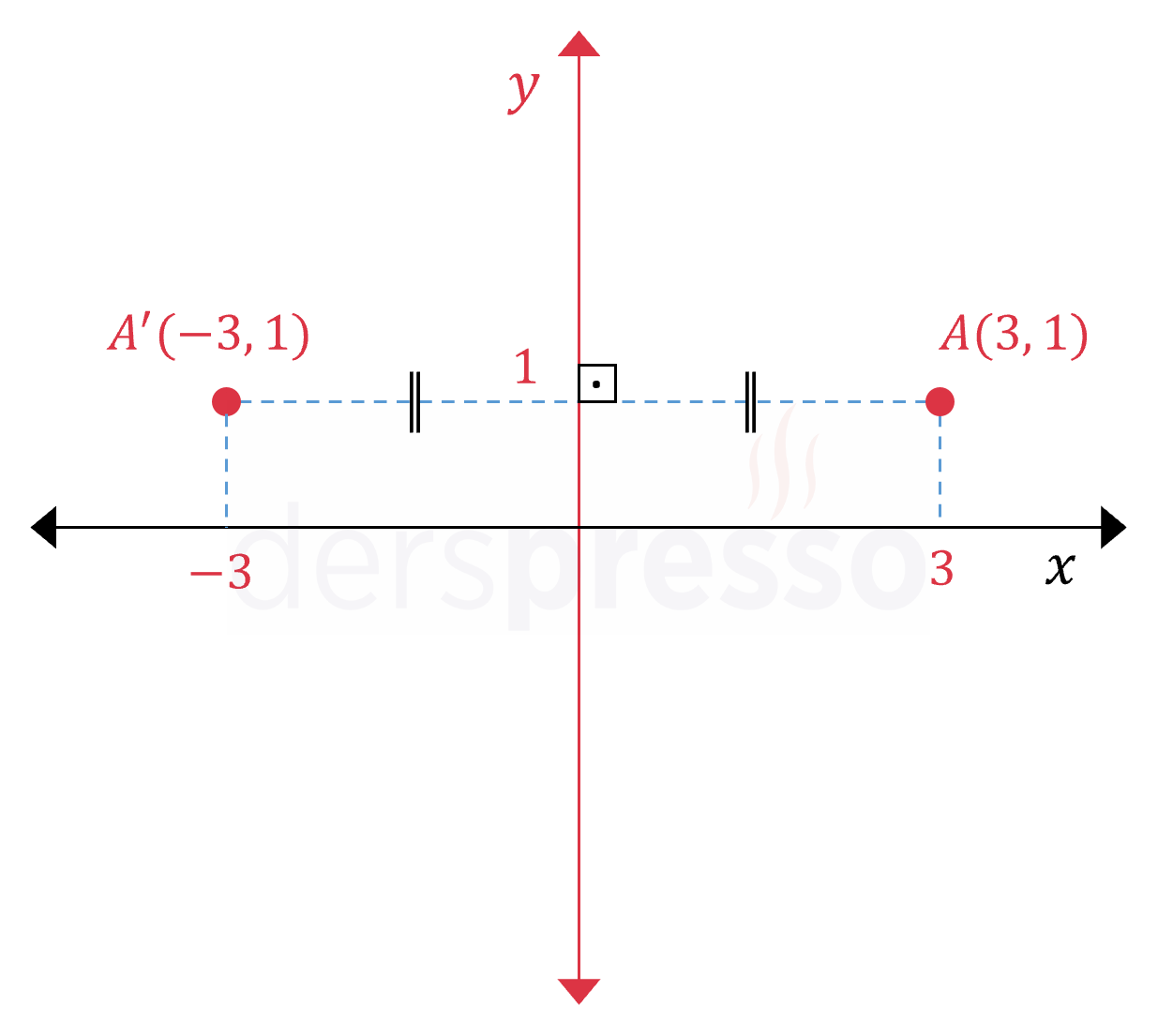
\( y \) eksenine göre: \( A(a, b) \longmapsto A'(-a, b) \) Ordinat aynı kalır, apsis işaret değiştirir. |

|
Orijine göre: \( A(a, b) \longmapsto A'(-a, -b) \) Apsis ve ordinat işaret değiştirir. |

|
\( y = x \) doğrusuna göre: \( A(a, b) \longmapsto A'(b, a) \) Apsis ve ordinat yer değiştirir. |

|
\( y = -x \) doğrusuna göre: \( A(a, b) \longmapsto A'(-b, -a) \) Apsis ve ordinat işaret ve yer değiştirir. |
|
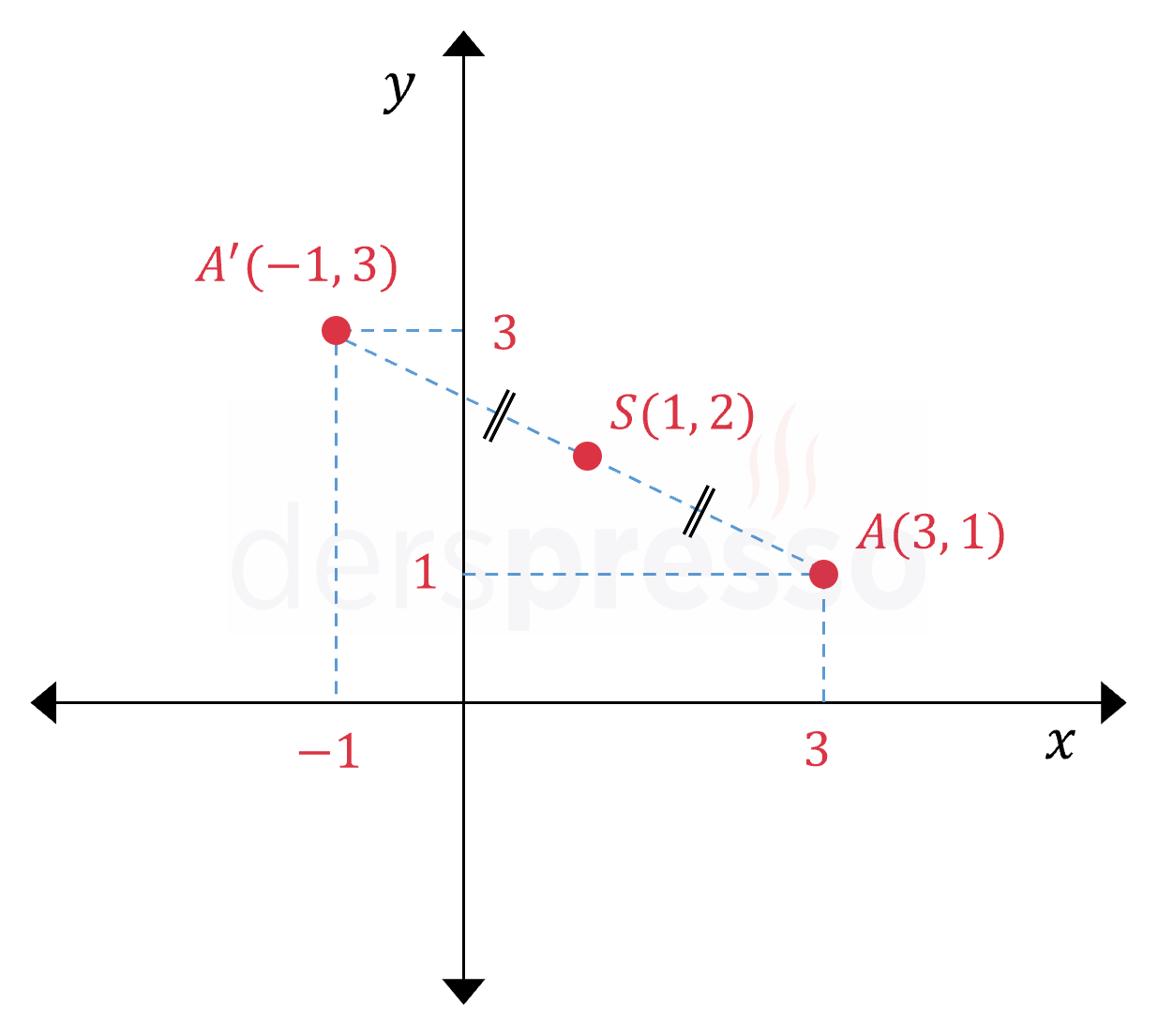
Bir noktaya göre: Simetri noktası \( S(m, n) \) olmak üzere, \( A(a, b) \longmapsto A'(2m - a, 2n - b) \) Simetri noktası \( A \) ve \( A' \) noktalarının orta noktası olur. Örnek: \( A(3, 1) \) noktasının \( S(1, 2) \) noktasına göre simetriği: \( A'(2(1) - 3, 2(2) - 1) = A'(-1, 3) \) |
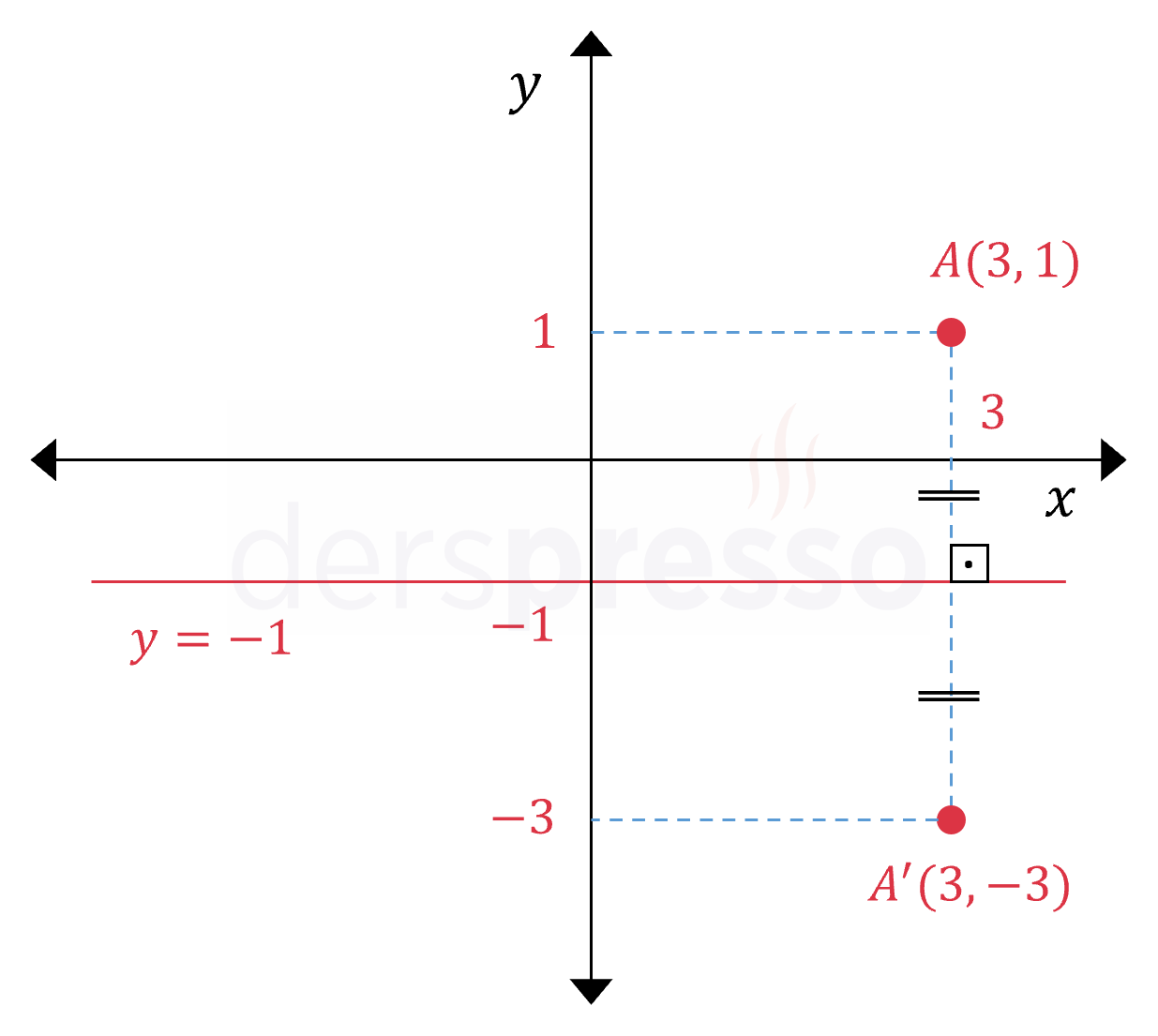
|
\( y = n \) doğrusuna göre: \( A(a, b) \longmapsto A'(a, 2n - b) \) Noktanın simetri doğrusu üzerinde aynı apsis değerli noktaya göre simetriği alınır. Örnek: \( A(3, 1) \) noktasının \( y = -1 \) doğrusuna göre simetriği: \( A'(3, 2(-1) - 1) = A'(3, -3) \) |
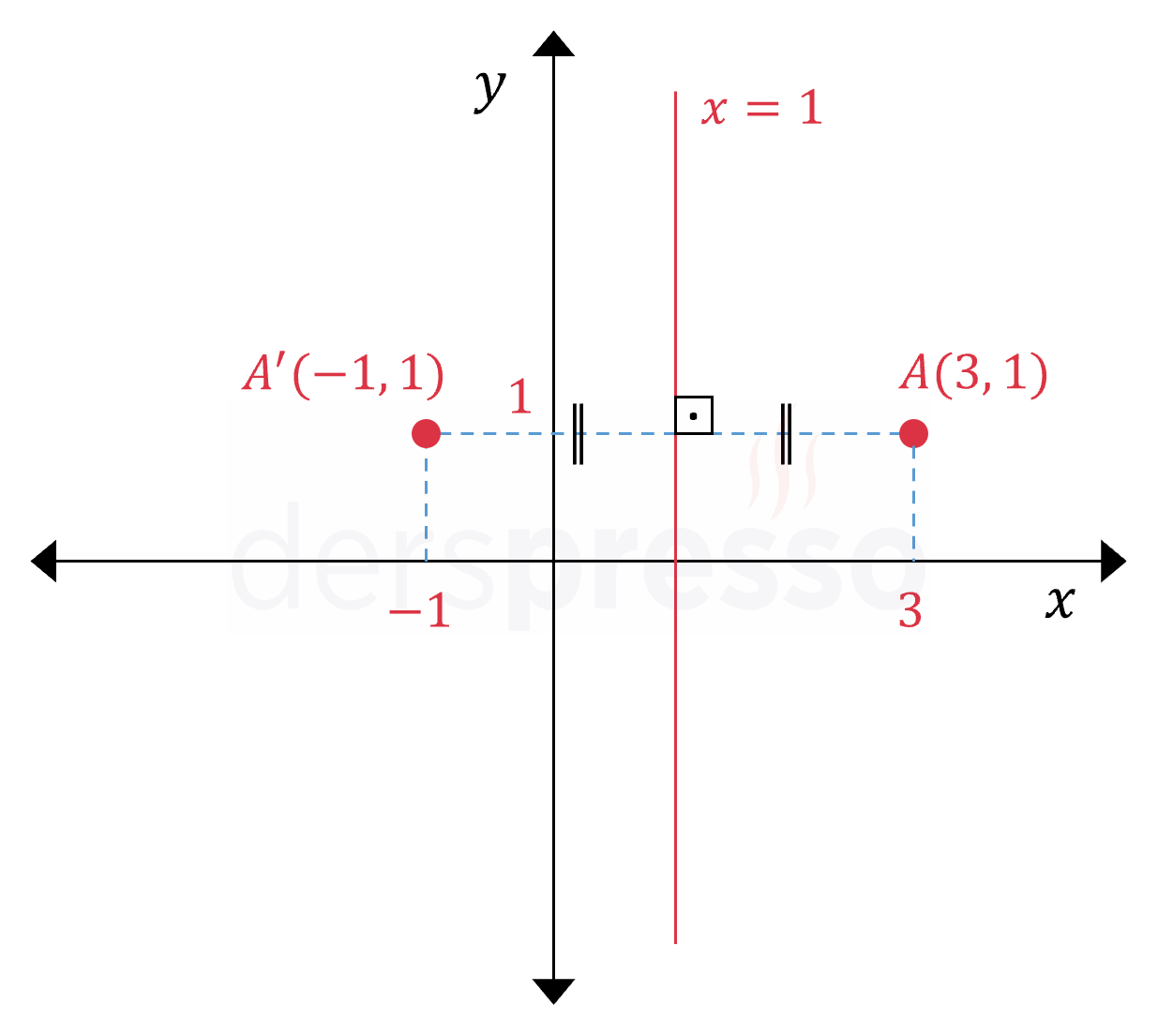
|
\( x = m \) doğrusuna göre: \( A(a, b) \longmapsto A'(2m - a, b) \) Noktanın simetri doğrusu üzerinde aynı ordinat değerli noktaya göre simetriği alınır. Örnek: \( A(3, 1) \) noktasının \( x = 1 \) doğrusuna göre simetriği: \( A'(2(1) - 3, 1) = A'(-1, 1) \) |

|
\( ax + by + c = 0 \) doğrusuna göre: \( A(x_1, y_1) \longmapsto A'(x_2, y_2) \) Simetrik noktanın koordinatları aşağıdaki iki formülle belirlenir. \( \dfrac{x_2 - x_1}{a} = \dfrac{-2(ax_1 + by_1 + c)}{a^2 + b^2} \) \( \dfrac{y_2 - y_1}{b} = \dfrac{-2(ax_1 + by_1 + c)}{a^2 + b^2} \) Örnek: \( A(2, 1) \) noktasının \( 2x + y + 5 = 0 \) doğrusuna göre simetriği: \( \dfrac{x_2 - 2}{2} = \dfrac{-2(2(2) + 1(1) + 5)}{2^2 + 1^2} \) \( \dfrac{y_2 - 1}{1} = \dfrac{-2(2(2) + 1(1) + 5)}{2^2 + 1^2} \) \( (x_2, y_2) = (-6, -3) \) |
\( A(2, -3) \) noktasının aşağıdaki eksen, doğru ve noktalara göre simetriğini bulunuz.
(a) \( x \) eksenine göre
(b) \( y \) eksenine göre
(c) orijine göre
(d) \( y = x \) doğrusuna göre
(e) \( y = -x \) doğrusuna göre
(f) \( S(-4, 1) \) noktasına göre
(g) \( y = 3 \) doğrusuna göre
(h) \( x = -7 \) doğrusuna göre
Çözümü Göster(a) seçeneği:
Bir noktanın \( x \) eksenine göre simetriğinde apsis aynı kalır, ordinat işaret değiştirir.
\( A(2, -3) \longmapsto A'(2, 3) \)
(b) seçeneği:
Bir noktanın \( y \) eksenine göre simetriğinde ordinat aynı kalır, apsis işaret değiştirir.
\( A(2, -3) \longmapsto A'(-2, -3) \)
(c) seçeneği:
Bir noktanın orijine göre simetriğinde apsis ve ordinat işaret değiştirir.
\( A(2, -3) \longmapsto A'(-2, 3) \)
(d) seçeneği:
Bir noktanın \( y = x \) doğrusuna göre simetriğinde apsis ve ordinat yer değiştirir.
\( A(2, -3) \longmapsto A'(-3, 2) \)
(e) seçeneği:
Bir noktanın \( y = -x \) doğrusuna göre simetriğinde apsis ve ordinat işaret ve yer değiştirir.
\( A(2, -3) \longmapsto A'(3, -2) \)
(f) seçeneği:
Bir noktanın \( S(m, n) \) noktasına göre simetriğinde aşağıdaki dönüşüm uygulanır.
\( A(a, b) \longmapsto A'(2m - a, 2n - b) \)
Simetri noktası \( S(-4, 1) \) olmak üzere,
\( A(2, -3) \longmapsto A'(2(-4) - 2, 2(1) - (-3)) \)
\( = A'(-10, 5) \)
(g) seçeneği:
Bir noktanın \( y = n \) doğrusuna göre simetriğinde aşağıdaki dönüşüm uygulanır.
\( A(a, b) \longmapsto A'(a, 2n - b) \)
Simetri doğrusu \( y = 3 \) olmak üzere,
\( A(2, -3) \longmapsto A'(2, 2(3) - (-3)) \)
\( = A'(2, 9) \)
(h) seçeneği:
Bir noktanın \( x = m \) doğrusuna göre simetriğinde aşağıdaki dönüşüm uygulanır.
\( A(a, b) \longmapsto A'(2m - a, b) \)
Simetri doğrusu \( x = -7 \) olmak üzere,
\( A(2, -3) \longmapsto A'(2(-7) - 2, -3) \)
\( = A'(-16, -3) \)
\( A(3a, 6) \) noktasının orijine göre simetriği olan nokta \( A'(-12, 2b) \) olduğuna göre, \( ab \) çarpımı kaçtır?
Çözümü Göster\( A(3a, 6) \) noktasının orijine göre simetriği \( A'(-3a, -6) \) noktasıdır.
\( A'(-3a, -6) = A'(-12, 2b) \)
\( -3a = -12 \Longrightarrow a = 4 \)
\( -6 = 2b \Longrightarrow b = -3 \)
\( ab = 4(-3) = -12 \) bulunur.
\( A(3, 4) \) noktasının \( x \) eksenine göre yansıması \( A' \) noktası, \( B(4, 3) \) noktasının \( y \) eksenine göre yansıması \( B' \) noktası olduğuna göre, \( \abs{A'B'} \) uzaklığı kaç birimdir?
Çözümü Göster\( A(3, 4) \) noktasının \( x \) eksenine göre yansıması \( A'(3, -4) \) noktasıdır.
\( B(4, 3) \) noktasının \( y \) eksenine göre yansıması \( B'(-4, 3) \) noktasıdır.
\( \abs{A'B'} \) değerini iki nokta arasındaki uzaklık formülü ile bulalım.
\( \abs{A'B'} = \sqrt{(3 - (-4))^2 + (-4 - 3)^2} \)
\( = \sqrt{7^2 + (-7)^2} \)
\( = 7\sqrt{2} \) bulunur.
\( A(n, 4) \) noktasının \( 3x + y - 8 = 0 \) doğrusuna göre simetriği yine kendisi olduğuna göre, \( n \) kaçtır?
Çözümü GösterBir noktanın bir doğruya göre simetriği noktanın kendisi ise nokta o doğrunun üzerindedir.
\( A(n, 4) \) noktası \( 3x + y - 8 = 0 \) doğrusunun üzerinde ise koordinatları doğru denklemini sağlar.
\( 3n + 4 - 8 = 0 \)
\( n = \dfrac{4}{3} \) bulunur.
Dik koordinat düzlemindeki \( d_1 \) ve \( d_2 \) doğruları \( A(2, 5) \) noktasında dik kesişmektedir.
Düzlemdeki \( B \) noktasının \( d_1 \) doğrusuna göre yansıması ile \( C \) noktası, \( d_2 \) doğrusuna göre yansıması ile \( D \) noktası elde edildiğine göre, \( C \) ve \( D \) noktalarının koordinatları toplamı kaçtır?
Çözümü GösterBir noktanın birbirini dik kesen iki doğruya göre yansımaları ile elde edilen iki nokta, birbirinin doğruların kesişim noktasına göre yansıması olur.

Bu nedenle \( [CD] \) doğru parçasının orta noktası, \( d_1 \) ve \( d_2 \) doğrularının kesişim noktası olan \( A(2, 5) \) olur.
\( C \) noktasının koordinatlarına \( C(x_c, y_c) \), D noktasının koordinatlarına \( D(x_d, y_d) \) diyelim.
\( A(2, 5) = \left( \dfrac{x_c + x_d}{2}, \dfrac{y_c + y_d}{2} \right) \)
\( \dfrac{x_c + x_d}{2} = 2 \)
\( x_c + x_d = 4 \)
\( \dfrac{y_c + y_d}{2} = 5 \)
\( y_c + y_d = 10 \)
\( C \) ve \( D \) noktalarının koordinatları toplamı \( x_c + x_d + y_c + y_d = 4 + 10 = 14 \) olarak bulunur.
Analitik düzlemde \( A \) noktasının \( y = 2 \) doğrusuna göre simetriği \( B \) noktası, \( B \) noktasının \( x = 1 \) doğrusuna göre simetriği \( C \) noktası, \( C \) noktasının \( y = -x \) doğrusuna göre simetriği \( D(-8, 1) \) noktası olduğuna göre, \( A \) noktasının koordinatları çarpımı kaçtır?
Çözümü Göster\( A \) noktasının koordinatlarını bulmak için \( D \) noktasından başlayarak yansıma işlemlerini geriye doğru uygulayalım.
Bir noktanın \( y = -x \) doğrusuna göre yansımasında apsis ve ordinat işaret ve yer değiştirir.
\( D(-8, 1) \longmapsto C(-1, 8) \)
Bir noktanın \( x = m \) doğrusuna göre simetriğinde aşağıdaki dönüşüm uygulanır.
\( (a, b) \longmapsto (2m - a, b) \)
Simetri doğrusu \( x = 1 \) olmak üzere,
\( C(-1, 8) \longmapsto B(2(1) - (-1), 8) \)
\( = B(3, 8) \)
Bir noktanın \( y = n \) doğrusuna göre simetriğinde aşağıdaki dönüşüm uygulanır.
\( (a, b) \longmapsto (a, 2n - b) \)
Simetri doğrusu \( y = 2 \) olmak üzere,
\( B(3, 8) \longmapsto A(3, 2(2) - 8) \)
\( = A(3, -4) \)
\( A \) noktasının koordinatları çarpımı \( 3 \cdot (-4) = -12 \) olarak bulunur.
\( K(2, 1) \) noktasının \( L \) noktasına göre simetriği ile \( P(2, 5) \) noktasının \( x = 4 \) doğrusuna göre simetriği aynı nokta olduğuna göre, \( L \) noktasının koordinatları toplamı kaçtır?
Çözümü Göster\( L \) noktasının koordinatlarına \( L(m, n) \) diyelim.
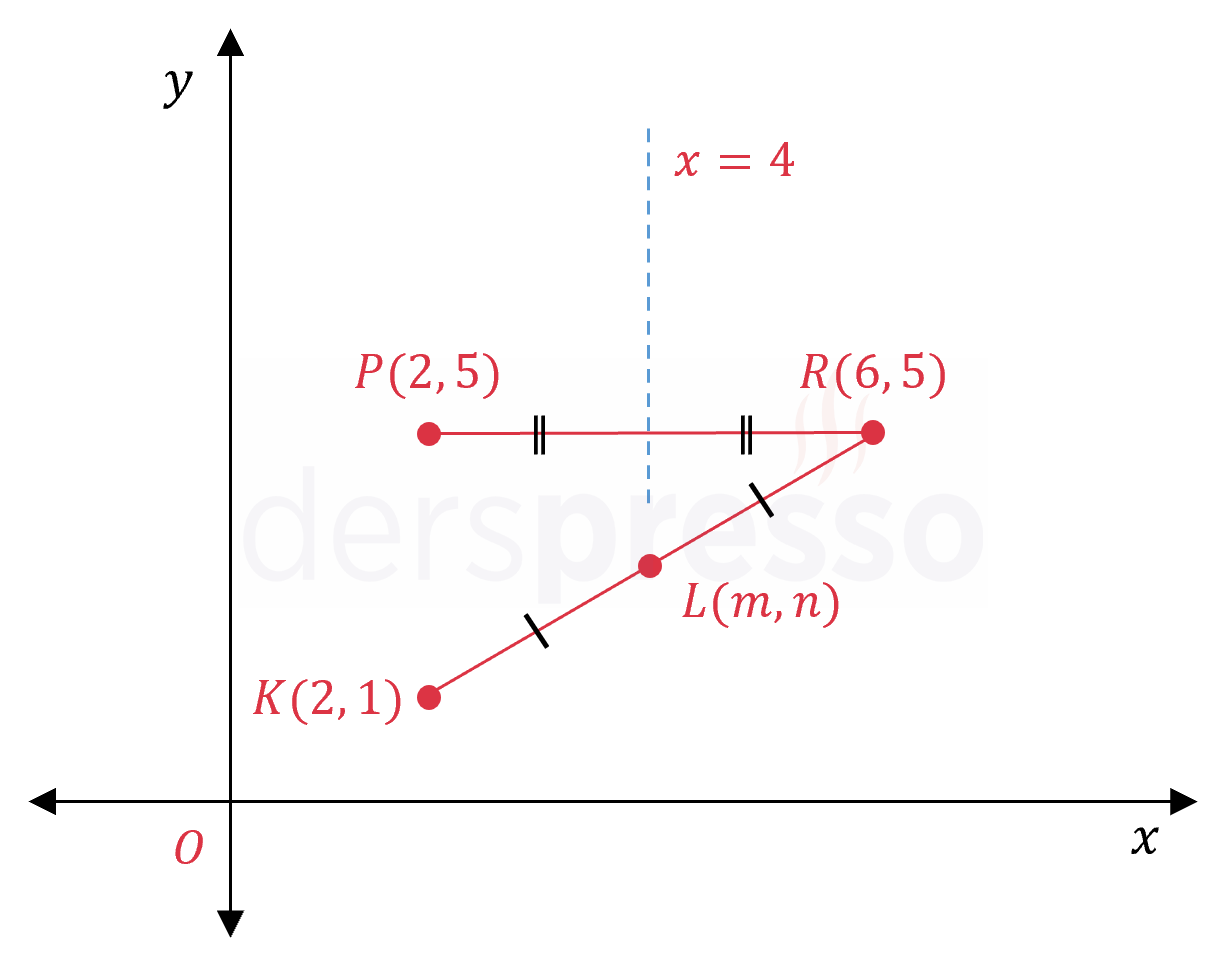
\( K \) noktasının \( L \) noktasına göre simetriğine \( R \) diyelim.
\( A(a, b) \) noktasının \( S(m, n) \) noktasına göre simetriğinde aşağıdaki dönüşüm uygulanır.
\( A(a, b) \longmapsto A'(2m - a, 2n - b) \)
\( K(2, 1) \) noktasının \( L(m, n) \) noktasına göre simetriğini bulalım.
\( K(2, 1) \longmapsto R(2m - 2, 2n - 1) \)
\( P \) noktasının \( x = 4 \) doğrusuna göre simetriği de \( R \) noktasıdır.
Bir noktanın \( x = m \) doğrusuna göre simetriğinde aşağıdaki dönüşüm uygulanır.
\( A(a, b) \longmapsto A'(2m - a, b) \)
Simetri doğrusu \( x = 4 \) olmak üzere,
\( P(2, 5) \longmapsto R(2(4) - 2, 5) \)
\( = R(6, 5) \)
\( R \) noktası için iki durumda bulduğumuz koordinatları birbirine eşitleyelim.
\( R(2m - 2, 2n - 1) = R(6, 5) \)
\( 2m - 2 = 6 \Longrightarrow m = 4 \)
\( 2n - 1 = 5 \Longrightarrow n = 3 \)
\( L(m, n) = L(4, 3) \)
\( L \) noktasının koordinatları toplamı \( 4 + 3 = 7 \) olarak bulunur.
Analitik düzlemdeki \( A(-2, 5) \) noktasının \( y \) eksenine göre yansıması ile \( B \) noktası, \( B \) noktasının \( y = x \) doğrusuna göre yansıması ile \( C \) noktası, \( C \) noktasının da \( x \) eksenine göre yansıması ile \( D \) noktası elde ediliyor.
Bu noktaların oluşturduğu \( ABCD \) dörtgeninin alanı kaçtır?
Çözümü GösterBir noktanın \( y \) eksenine göre simetriğinde ordinat aynı kalır, apsis işaret değiştirir.
\( A(-2, 5) \longmapsto B(2, 5) \)
Bir noktanın \( y = x \) doğrusuna göre simetriğinde apsis ve ordinat yer değiştirir.
\( B(2, 5) \longmapsto C(5, 2) \)
Bir noktanın \( x \) eksenine göre simetriğinde apsis aynı kalır, ordinat işaret değiştirir.
\( C(5, 2) \longmapsto D(5, -2) \)
Tüm bu noktaları analitik düzlemde gösterelim.
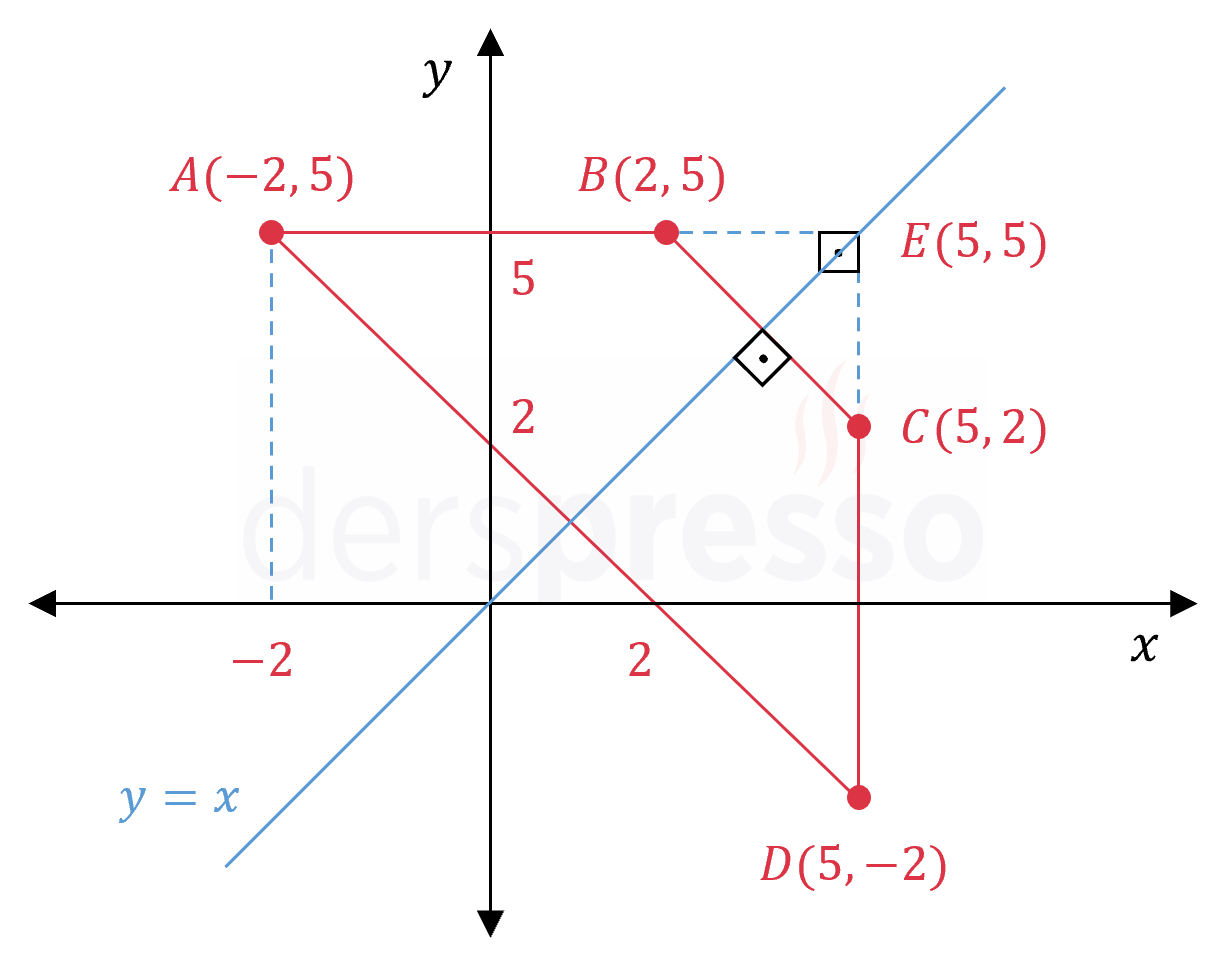
Alan hesaplamasında kullanmak için \( E(5, 5) \) noktasını işaretleyelim.
\( ABCD \) dörtgeninin alanını bulmak için büyük üçgenin alanından küçük üçgenin alanını çıkartabiliriz.
\( A(ABCD) = A(AED) - A(BEC) \)
\( A(AED) = \dfrac{\abs{AE} \cdot \abs{ED}}{2} \)
\( = \dfrac{7 \cdot 7}{2} = \dfrac{49}{2} \)
\( A(AED) = \dfrac{\abs{BE} \cdot \abs{EC}}{2} \)
\( = \dfrac{3 \cdot 3}{2} = \dfrac{9}{2} \)
Bulduğumuz alan değerlerini denklemde yerine koyalım.
\( A(ABCD) = A(AED) - A(BEC) \)
\( = \dfrac{49}{2} - \dfrac{9}{2} \)
\( = 20 \) bulunur.