Dahil Etme - Hariç Tutma Prensibi
Dahil etme - hariç tutma prensibi (bir diğer adıyla içerme - dışlama prensibi); iki ya da daha fazla kümenin birleşim kümesinin eleman sayısını, bu kümelerin kesişim kümelerindeki elemanların birden fazla kez sayılmasının önüne geçerek hesaplayan bir sayma yöntemidir.
İki Kümenin Birleşimi
Ayrık olmayan iki kümenin birleşiminin eleman sayısı, dahil etme - hariç tutma prensibi ile aşağıdaki şekilde hesaplanır.
- Kümelerin eleman sayılarının toplamı alınır (dahil et).
- Kümelerin kesişimi birinci adımda toplama iki kez dahil edildiği için toplamdan çıkarılır (hariç tut).
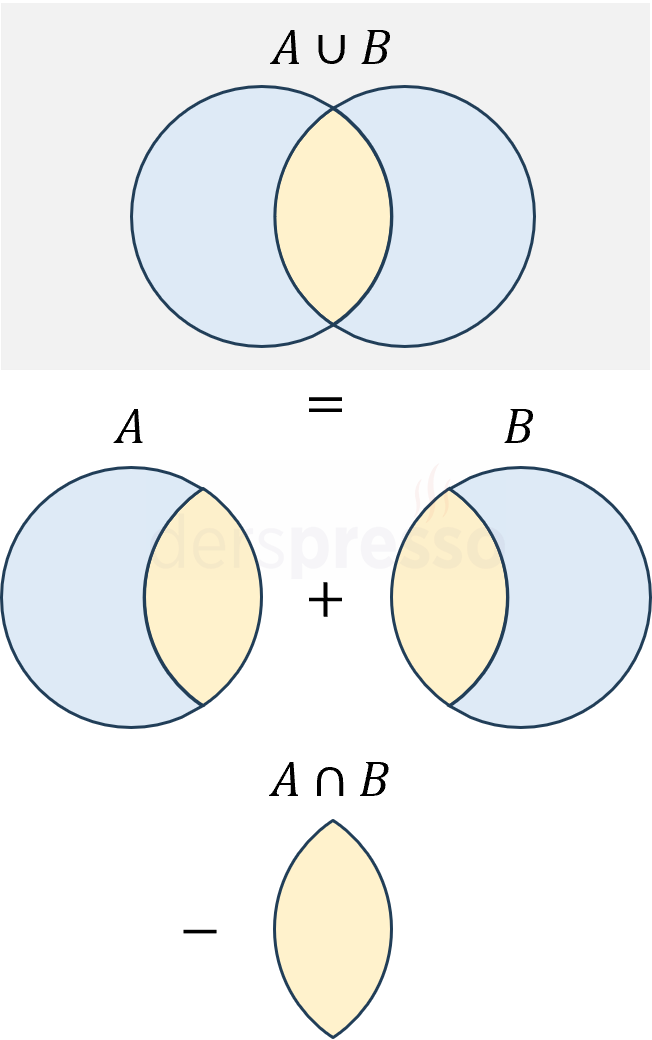
\( s(A \cup B) = s(A) + s(B) \textcolor{red}{- s(A \cap B)} \)
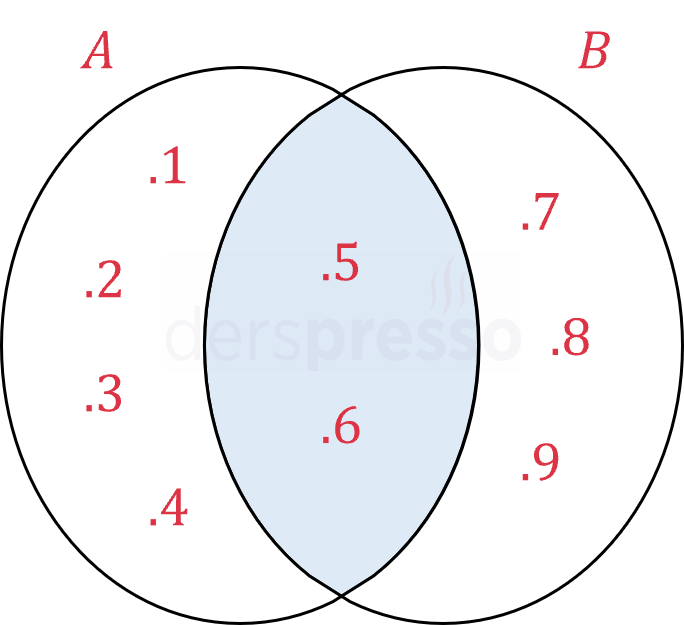
\( A = \{ 1, 2, 3, 4, 5, 6 \} \)
\( B = \{ 5, 6, 7, 8, 9 \} \)
\( A \cap B = \{ 5, 6 \} \)
\( A \cup B = \{ 1, 2, 3, 4, 5, 6, 7, 8, 9 \} \)
\( s(A) = 6, \quad s(B) = 5 \)
\( s(A \cap B) = 2 \)
\( s(A \cup B) = 6 + 5 \textcolor{red}{- 2} = 9 \)
\( A = \{1, 2, 3 , \ldots, 155\} \) olmak üzere,
\( A \) kümesinin elemanlarından kaçı 2 ve 3 sayılarından hiçbirine tam bölünmez?
Çözümü Göster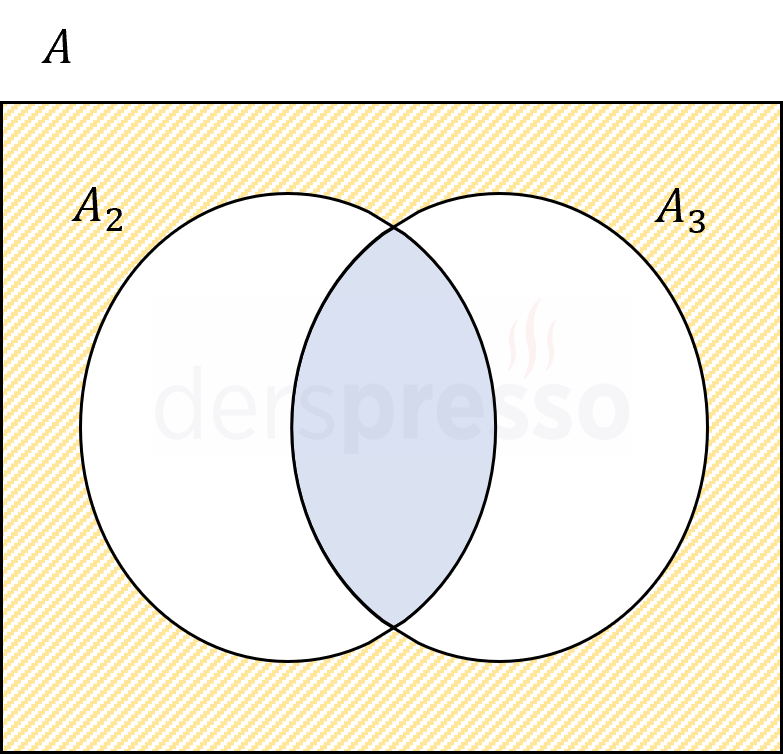
\( A \) kümesinin elemanlarından 2'ye tam bölünen sayıların kümesine \( A_2 \) diyelim.
2, 4, 6, ..., 154
\( s(A_2) = \dfrac{154 - 2}{2} + 1 = 77 \)
\( A \) kümesinin elemanlarından 3'e tam bölünen sayıların kümesine \( A_3 \) diyelim.
3, 6, 9, ..., 153
\( s(A_3) = \dfrac{153 - 3}{3} + 1 = 51 \)
Hem 2'ye hem de 3'e bölünen sayılar 6'ya da bölünür.
\( A \) kümesinin elemanlarından 6'ya tam bölünen sayıların kümesi \( A_2 \cap A_3 \) olur (mavi bölge).
6, 12, 18, ..., 150
\( s(A_2 \cap A_3) = \dfrac{150 - 6}{6} + 1 = 25 \)
Soruda istenen \( A_2 \) ve \( A_3 \) kümeleri dışında kalan ve turuncu alana karşılık gelen kümenin eleman sayısıdır. Bu kümeye \( A_x \) diyelim.
\( A_x \) kümesinin eleman sayısını bulmak için \( A \) kümesinin eleman sayısından \( A_2 \cup A_3 \) kümesinin eleman sayısını çıkaralım.
\( s(A_x) = s(A) - s(A_2 \cup A_3) \)
Dahil etme - hariç tutma prensibine göre, \( s(A_2 \cup A_3) \) açılımını yazalım.
\( = s(A) - (s(A_2) + s(A_3) - s(A_2 \cap A_3)) \)
\( = 155 - (77 + 51 - 25) = 52 \) bulunur.
\( 185^8 \) sayısının karekökü veya küpkökü tam sayı olan kaç tane pozitif böleni vardır?
Çözümü GösterBir sayı, karekökü tam sayı ise tam kare, küpkökü tam sayı ise tam küp bir sayıdır.
Aşağıdaki kümeleri tanımlayalım.
\( A \): \( 185^8 \) sayısının tüm pozitif bölenlerinin kümesi
\( A_2 \): \( 185^8 \) sayısının tam kare bölenlerinin kümesi
\( A_3 \): \( 185^8 \) sayısının tam küp pozitif bölenlerinin kümesi
Bu kümeleri bir Venn şemasında gösterelim.

\( 185^8 \) sayısının tam kare veya tam küp pozitif bölenlerinin sayısı, \( A_2 \cup A_3 \) birleşim kümesinin eleman sayısına eşittir.
\( 185^8 \) sayısını asal çarpanlarına ayıralım.
\( 185^8 = 5^8 \cdot 37^8 \)
Bir sayının tam kare olması için asal çarpanlarının tümünün üsleri çift sayı olmalıdır.
\( 185^8 = (5^2)^4 \cdot (37^2)^4 \)
Buna göre \( 185^8 \) sayısının \( (4 + 1)(4 + 1) = 25 \) tane tam kare böleni vardır.
\( s(A_2) = 25 \)
Bir sayının tam küp olması için asal çarpanlarının tümünün üsleri 3'ün birer tam sayı katı olmalıdır.
\( 185^8 = (5^3)^2 \cdot (37^3)^2 \cdot x \)
Buna göre \( 185^8 \) sayısının \( (2 + 1)(2 + 1) = 9 \) tane tam küp böleni vardır.
\( s(A_3) = 9 \)
6 hem 2'ye hem de 3'e bölündüğü için asal çarpanların 6 olduğu durumda oluşan bölenler hem tam kare hem de tam küptür ve yukarıda tanımladığımız iki kümenin de elemanıdır.
\( 185^8 = (5^6)^1 \cdot (37^6)^1 \cdot y \)
Buna göre \( 185^8 \) sayısının \( (1 + 1)(1 + 1) = 4 \) tane böleni hem tam kare hem de tam küptür.
\( s(A_2 \cap A_3) = 4 \)
Hem tam kare hem de tam küp olan bölenler: \( 5^0 \cdot 37^0, 5^0 \cdot 37^6, 5^6 \cdot 37^0, 5^6 \cdot 37^6 \)
\( A_2 \cup A_3 \) kümesinin eleman sayısını bulmak için iki kümenin birleşiminin eleman sayısı formülünü kullanalım.
\( s(A_2 \cup A_3) = s(A_2) + s(A_3) - s(A_2 \cap A_3) \)
\( = 25 + 9 - 4 = 30 \) bulunur.
Üç Kümenin Birleşimi
İkişerli ayrık olmayan üç kümenin birleşiminin eleman sayısı, dahil etme - hariç tutma prensibi ile aşağıdaki şekilde hesaplanır.
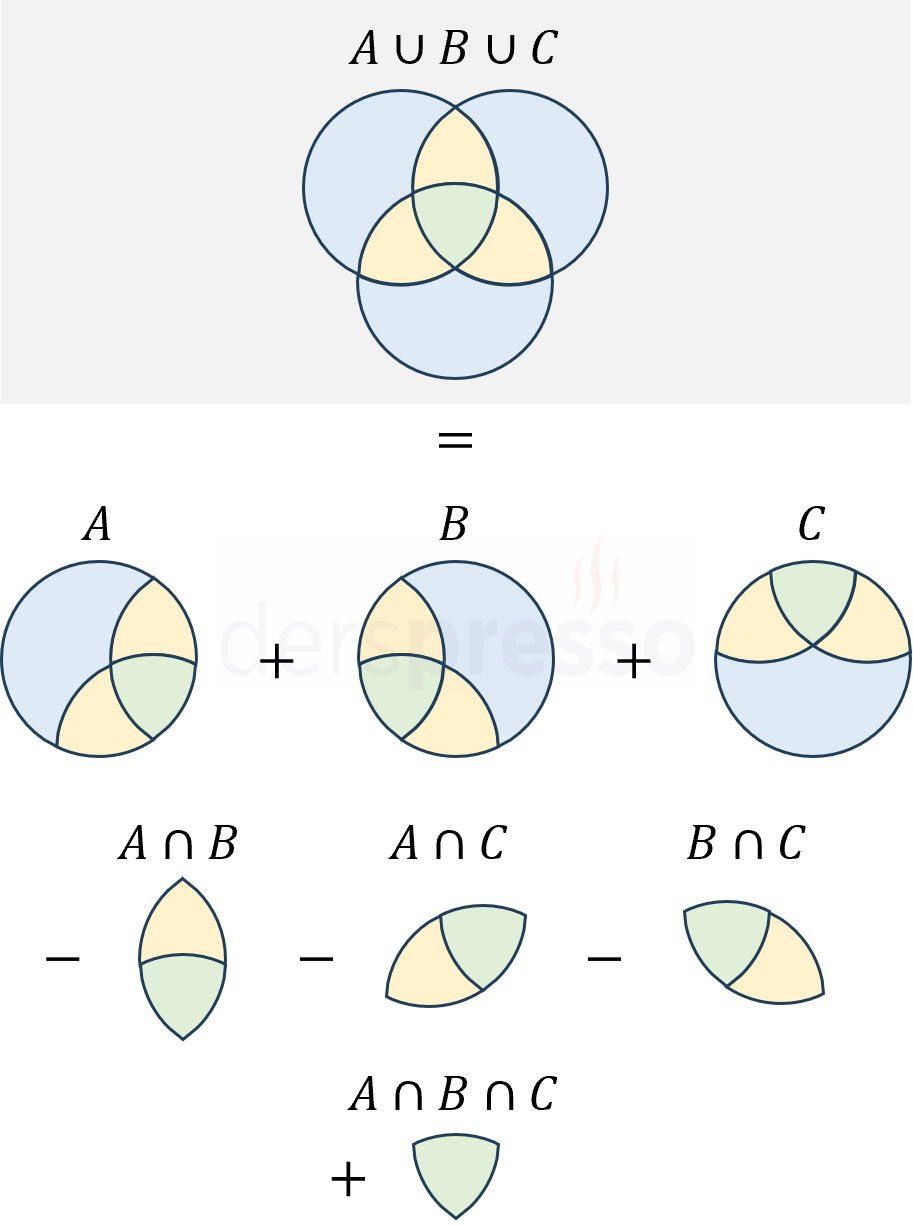
- Kümelerin eleman sayılarının toplamı alınır (dahil et).
- Kümelerin ikili kesişimleri birinci adımda toplama ikişer kez dahil edildiği için toplamdan birer kez çıkarılır (hariç tut).
- Kümelerin üçlü kesişimi birinci adımda toplama üç kez dahil edilip ikinci adımda toplamdan üç kez çıkarıldığı için toplama tekrar eklenir (dahil et).
\( s(A \cup B \cup C) = s(A) + s(B) + s(C) \)
\( \quad \textcolor{red}{- s(A \cap B) - s(A \cap C) - s(B \cap C)} \)
\( \quad \textcolor{blue}{+ s(A \cap B \cap C)} \)
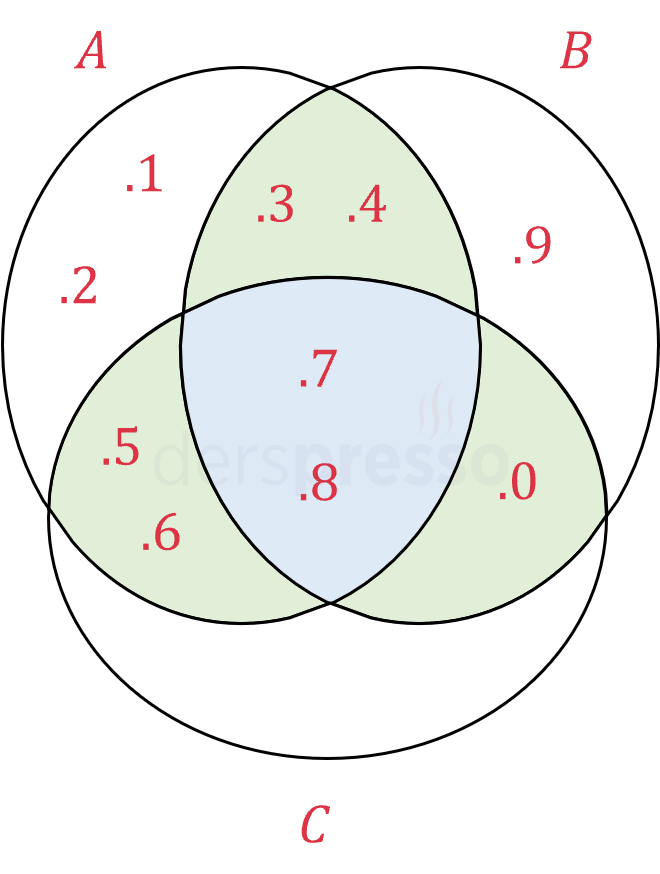
\( A = \{ 1, 2, 3, 4, 5, 6, 7, 8 \} \)
\( B = \{ 3, 4, 7, 8, 9, 0 \} \)
\( C = \{ 5, 6, 7, 8, 0 \} \)
\( A \cap B = \{ 3, 4, 7, 8 \} \)
\( A \cap C = \{ 5, 6, 7, 8 \} \)
\( B \cap C = \{ 7, 8, 0 \} \)
\( A \cap B \cap C = \{ 7, 8 \} \)
\( A \cup B = \{ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 \} \)
\( s(A) = 8, \quad s(B) = 6, \quad s(C) = 5 \)
\( s(A \cap B) = 4, \quad s(A \cap C) = 4, \quad s(B \cap C) = 3 \)
\( s(A \cap B \cap C) = 2 \)
\( s(A \cup B \cup C) = 8 + 6 + 5 \textcolor{red}{- 4 - 4 - 3} \textcolor{blue}{+ 2} = 10 \)
Futbol, voleybol ve tenis oyunlarının bulunduğu bir sporcu grubunda futbol oynayan 18, voleybol oynayan 13, tenis oynayan 10 kişi vardır.
Grupta futbol ve voleybol oynayan 7, voleybol ve tenis oynayan 5, futbol ve tenis oynayan 4 ve bu üç sporu da yapan 2 kişi olduğuna göre, bu grup kaç kişiden oluşmaktadır?
Çözümü Göster\( F \): Futbol oynayanların kümesi
\( V \): Voleybol oynayanların kümesi
\( T \): Tenis oynayanların kümesi
Her küme ve kesişimleri için verilen kişi sayılarını yazalım.
\( s(F) = 18 \)
\( S(V) = 13 \)
\( s(T) = 10 \)
\( s(F \cap V) = 7 \)
\( s(V \cap T) = 5 \)
\( s(F \cap T) = 4 \)
\( s(F \cap V \cap T) = 2 \)
Üç küme için birleşim kümesi eleman sayısı formülünü yazalım.
\( s(F \cup V \cup T) = s(F) + s(V) + s(T) \color{red}{- s(F \cap V) - s(V \cap T) - s(F \cap T)} \color{blue}{+ s(F \cap V \cap T)} \)
\( = 18 + 13 + 10 \color{red}{- 7 - 5 - 4} \color{blue}{+ 2} \)
\( = 27 \) bulunur.
3 evli çift yan yana fotoğraf çektirecektir. Çiftler hiçbir karı - koca yan yana olmamak koşuluyla kaç farklı şekilde dizilebilirler?
Çözümü GösterAşağıdaki kümeleri tanımlayalım.
\( E \): 6 kişinin tüm farklı dizilişlerinin kümesi
\( A \): Birinci çiftin yan yana olduğu dizilişlerin kümesi
\( B \): İkinci çiftin yan yana olduğu dizilişlerin kümesi
\( C \): Üçüncü çiftin yan yana olduğu dizilişlerin kümesi
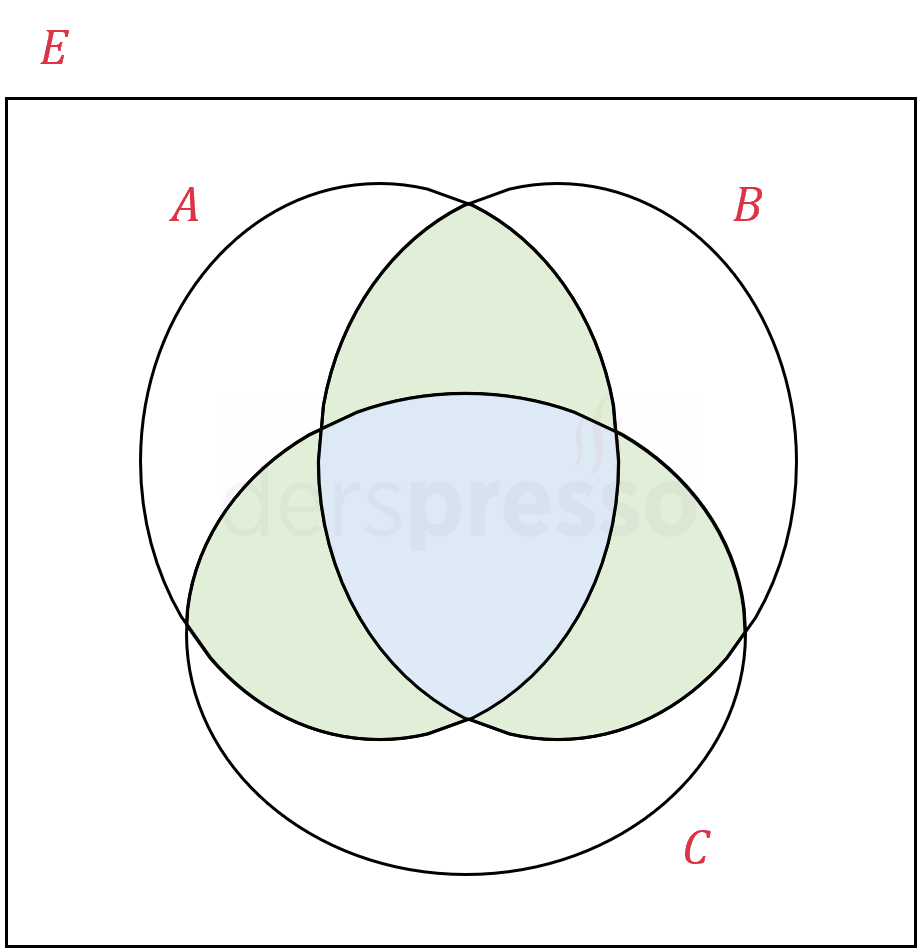
Buna göre soruda istenen aşağıdaki kümenin eleman sayısıdır.
\( E - (A \cup B \cup C) \)
Evrensel küme 6 kişinin tüm farklı dizilişlerinden oluşur.
\( s(E) = 6! = 720 \)
\( A \cup B \cup C \) kümesinin eleman sayısını dahil etme - hariç tutma prensibini kullanarak hesaplayalım.
Durum 1: \( A, B, C \) kümeleri
\( A \) kümesi birinci çiftin yan yana olduğu dizilişlerden oluşur.
Birinci çifti tek bir kişi olarak düşünelim.
Biri birinci çift olmak üzere, 5 kişi aralarında \( 5! \) farklı şekilde dizilebilir, her dizilişte birinci çift kendi aralarında \( 2! \) farklı şekilde yer değiştirebilir.
\( s(A) = 5! \cdot 2! = 240 \)
Bu sayının içinde ikinci ve üçüncü çiftlerin yan yana olduğu bazı dizilişlerin de bulunduğu unutulmamalıdır.
Aynı yaklaşımı \( B \) ve \( C \) kümelerine uyguladığımızda aynı sonuçları elde ederiz.
\( s(B) = s(C) = 240 \)
Durum 2: İkili kesişim kümeleri
\( A \cap B \) kümesi birinci ve ikinci çiftlerin ayrı ayrı yan yana olduğu dizilişlerden oluşur.
Birinci ve ikinci çiftleri ayrı ayrı tek birer kişi olarak düşünelim.
Biri birinci, diğeri ikinci çift olmak üzere, 4 kişi aralarında \( 4! \) farklı şekilde dizilebilir, her dizilişte birinci ve ikinci çiftler kendi aralarında \( 2! \) farklı şekilde yer değiştirebilir.
\( s(A \cap B) = 4! \cdot 2! \cdot 2! = 96 \)
Bu sayının içinde üçüncü çiftin yan yana olduğu bazı dizilişlerin de bulunduğu unutulmamalıdır.
Aynı yaklaşımı \( A \cap C \) ve \( B \cap C \) kümelerine uyguladığımızda aynı sonuçları elde ederiz.
\( s(A \cap C) = s(B \cap C) = 96 \)
Durum 3: Üçlü kesişim kümesi
\( A \cap B \cap C \) kümesi tüm çiftlerin ayrı ayrı yan yana olduğu dizilişlerden oluşur.
Tüm çiftleri ayrı ayrı tek birer kişi olarak düşünelim.
Biri birinci, diğeri ikinci, diğeri üçüncü çift olmak üzere, 3 kişi aralarında \( 3! \) farklı şekilde dizilebilir, her dizilişte birinci, ikinci ve üçüncü çiftler kendi aralarında \( 2! \) farklı şekilde yer değiştirebilir.
\( s(A \cap B \cap C) = 3! \cdot 2! \cdot 2! \cdot 2! = 48 \)
Üç küme için dahil etme - hariç tutma prensibi formülünü kullanalım.
\( s(A \cup B \cup C) = s(A) + s(B) + s(C) \)
\( \quad - s(A \cap B) - s(A \cap C) - s(B \cap C) \)
\( \quad + s(A \cap B \cap C) \)
\( = 240 + 240 + 240 \)
\( \quad - 96 - 96 - 96 \)
\( \quad + 48 = 480 \)
Bulduğumuz sayı, en az bir çiftin yan yana olduğu birleşim kümesinin eleman sayısıdır.
Soruda istenen hiçbir çiftin yan yana olmadığı dizilişlerin sayısıdır.
\( s(E) - s(A \cup B \cup C) = 720 - 480 = 240 \) bulunur.
Türk alfabesindeki 29 harfin tamamının yan yana yazılmasıyla oluşan tüm dizilişlerde, KALEM, OMUZ, SIR kelimelerinin hiçbirinin bulunmadığı diziliş sayısı kaçtır?
Çözümü GösterBir \( A \) kümesinin elemanlarının bir sıra gözetilerek farklı dizilişlerinin her birine \( A \) kümesinin bir permütasyonu denir.
\( n \) elemanlı \( A \) kümesinin permütasyonlarının sayısı \( n! \) formülü ile hesaplanır.
Aşağıdaki dört kümeyi tanımlayalım.
\( E \): 29 harf için tüm dizilişlerin kümesi
\( K \): İçinde KALEM geçen dizilişlerin kümesi
\( O \): İçinde OMUZ geçen dizilişlerin kümesi
\( S \): İçinde SIR geçen dizilişlerin kümesi
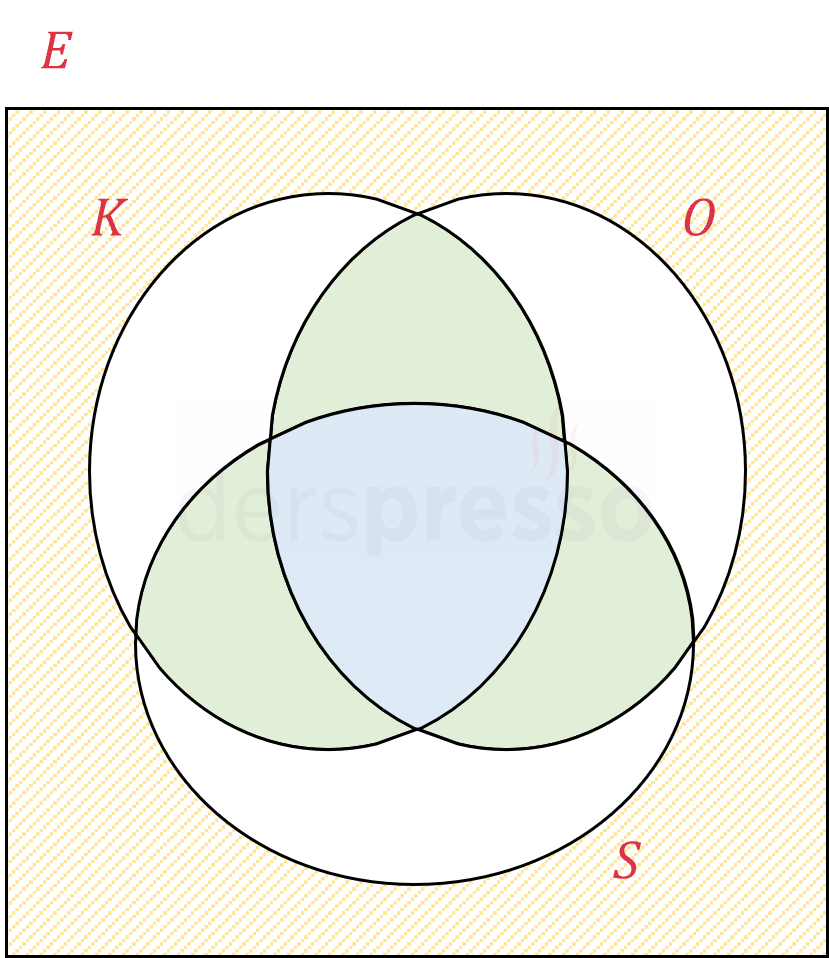
Soruda istenen \( E \) kümesinin elemanı olup \( K \), \( O \) veya \( S \) kümelerinin elemanı olmayan dizilişlerin sayısıdır (turuncu taralı alan).
Bu amaçla önce üç kümenin birleşim kümesinin eleman sayısını bulalım.
İçinde KALEM kelimesinin geçtiği diziliş sayısını bulalım.
5 harfli KALEM kelimesini tek bir harf olarak düşünelim. Buna göre geriye kalan 24 harf ve KALEM kelimesi için \( 29 - 5 + 1 = 25! \) farklı diziliş vardır.
\( s(K) = 25! \)
Benzer yaklaşımla 4 harfli OMUZ kelimesi için \( 29 - 4 + 1 = 26! \) ve 3 harfli SIR kelimesi için \( 29 - 3 + 1 = 27! \) farklı diziliş vardır.
\( s(O) = 26! \)
\( s(S) = 27! \)
Yukarıda hesapladığımız dizilişlerin bir kısmı KALEM, OMUZ ve SIR kelimelerini birlikte içerdiği için bazı dizilişleri birden fazla kez saymış olduk.
Şimdi bu kelimelerin ikişerli bulunduğu dizilişlerin sayısını bulalım.
İçinde KALEM ve OMUZ kelimelerinin geçtiği diziliş sayısını bulalım.
Bu iki kelimede "M" harfi ortak olduğu için hiçbir durumda bir dizilişte birlikte yer almazlar.
\( s(K \cap O) = 0 \)
İçinde OMUZ ve SIR kelimelerinin geçtiği diziliş sayısını bulalım.
4 harfli OMUZ ve 3 harfli SIR kelimelerini birer harf olarak düşünelim. Buna göre geriye kalan 22 harf ve bu iki kelime için \( 29 - (4 + 3) + 1 + 1 = 24! \) farklı diziliş vardır.
\( s(O \cap S) = 24! \)
İçinde KALEM ve SIR kelimelerinin geçtiği diziliş sayısını bulalım.
5 harfli KALEM ve 3 harfli SIR kelimelerini birer harf olarak düşünelim. Buna göre geriye kalan 21 harf ve bu iki kelime için \( 29 - (5 + 3) + 1 + 1 = 23! \) farklı diziliş vardır.
\( s(K \cap S) = 23! \)
Şimdi bu kelimelerin üçerli bulunduğu dizilişlerin sayısını bulalım.
KALEM ve OMUZ kelimelerinde "M" harfi ortak olduğu için bu üç kelime hiçbir durumda bir dizilişte birlikte yer almazlar.
\( s(K \cap O \cap S) = 0 \)
KALEM, OMUZ, SIR kelimelerinin en az birinin bulunduğu diziliş sayısını bulmak için dahil etme - hariç bırakma yöntemini kullanarak üç kümenin birleşim kümesinin eleman sayısını bulalım.
\( s(K \cup O \cup S) = s(K) + s(O) + s(S) \color{red}{- s(K \cap O) - s(O \cap S) - s(K \cap S)} \color{blue}{+ s(K \cap O \cap S)} \)
\( = 25! + 26! + 27! \color{red}{- 0 - 24! - 23!} \color{blue}{+ 0} \)
\( = 25! + 26! + 27! - 24! - 23! \)
Tüm dizilişlerden bu sayıyı çıkarırsak bu üç kelimenin hiçbirinin bulunmadığı diziliş sayısını buluruz.
29 harfin tamamının yan yana yazılmasıyla oluşan farklı dizilişlerin sayısı \( 29! \) olur.
\( s(E) = 29! \)
KALEM, OMUZ, SIR kelimelerinin hiçbirinin bulunmadığı diziliş sayısı:
\( = s(E) - s(K \cup O \cup S) \)
\( = 29! - (25! + 26! + 27! - 24! - 23!) \) bulunur.
n Kümenin Birleşimi
\( n \) kümenin birleşiminin eleman sayısı, dahil etme - hariç tutma prensibi ile aşağıdaki şekilde hesaplanır.
- \( (+) \) Kümelerin eleman sayılarının toplamı alınır (dahil et).
- \( (-) \) Kümelerin ikili kesişimleri toplamdan çıkarılır (hariç tut).
- \( (+) \) Kümelerin üçlü kesişimleri toplama eklenir (dahil et).
- \( (-) \) Kümelerin dörtlü kesişimleri toplamdan çıkarılır (hariç tut).
- \( (+) \) Kümelerin beşli kesişimleri toplama eklenir (dahil et).
- \( \vdots \)
- \( (\pm) \) Bu işlem kümelerin \( n \)'li kesişimine kadar tekrarlanır.
Yöntemi özetlemek gerekirse, \( n \) tane kümenin birleşim kümesinin eleman sayısını bulmak için kümelerin eleman sayılarının toplamı alınır, tek sayıda kümeden oluşan kesişim kümelerinin eleman sayıları bu toplama eklenir, çift sayıda kümeden oluşan kesişim kümelerinin eleman sayıları bu toplamdan çıkarılır.
Bu yöntemin \( n \) küme için genel formülü aşağıdaki gibidir.
\( A_1, A_2, \ldots, A_n \) birer küme ve,
\( \emptyset \ne J \subseteq \{ 1, 2, 3, \ldots, n \} \) olmak üzere,
\( s(\displaystyle\bigcup_{i=1}^{n} A_i) = \displaystyle\sum_{J} (-1)^{s(J) + 1} \cdot s(\displaystyle\bigcap_{j \in J} A_j) \)
Dahil Etme - Hariç Tutma Prensibinin Uygulamaları
Bu bölümde bu prensibin üç uygulamasını birer örnek üzerinden inceleyeceğiz.
Birleşim Kümesinin Eleman Sayısı
Her öğrencinin en azından bir yabancı dil konuştuğu bir sınıfta İngilizce bilen öğrencilerin sayısı 25, Almanca bilen öğrencilerin sayısı 16, her iki dili de bilen öğrencilerin sayısı da 9 ise sınıfta öğrenci vardır?
Dahil etme - hariç tutma prensibini iki kümeli duruma uygulayarak soruyu çözebiliriz.
\( I \): İngilizce konuşan öğrencilerin kümesi
\( A \): Almanca konuşan öğrencilerin kümesi
\( s(I) = 25 \)
\( s(A) = 16 \)
\( s(I \cap A) = 9 \)
Bu bilgileri iki kümeli durum için dahil etme - hariç tutma formülünde yerine koyalım.
\( s(I \cup A) = s(I) + s(A) - s(I \cap A) \)
\( = 25 + 16 - 9 = 32 \) bulunur.
Bölünebilme Problemleri
1-1000 arasındaki pozitif tam sayılar içinde 2'ye, 3'e veya 5'e tam bölünen kaç sayı vardır?
Dahil etme - hariç tutma prensibini üç kümeli duruma uygulayarak soruyu çözebiliriz.
2'ye, 3'e ve 5'e tam bölünen sayıları birer küme olarak tanımlayalım.
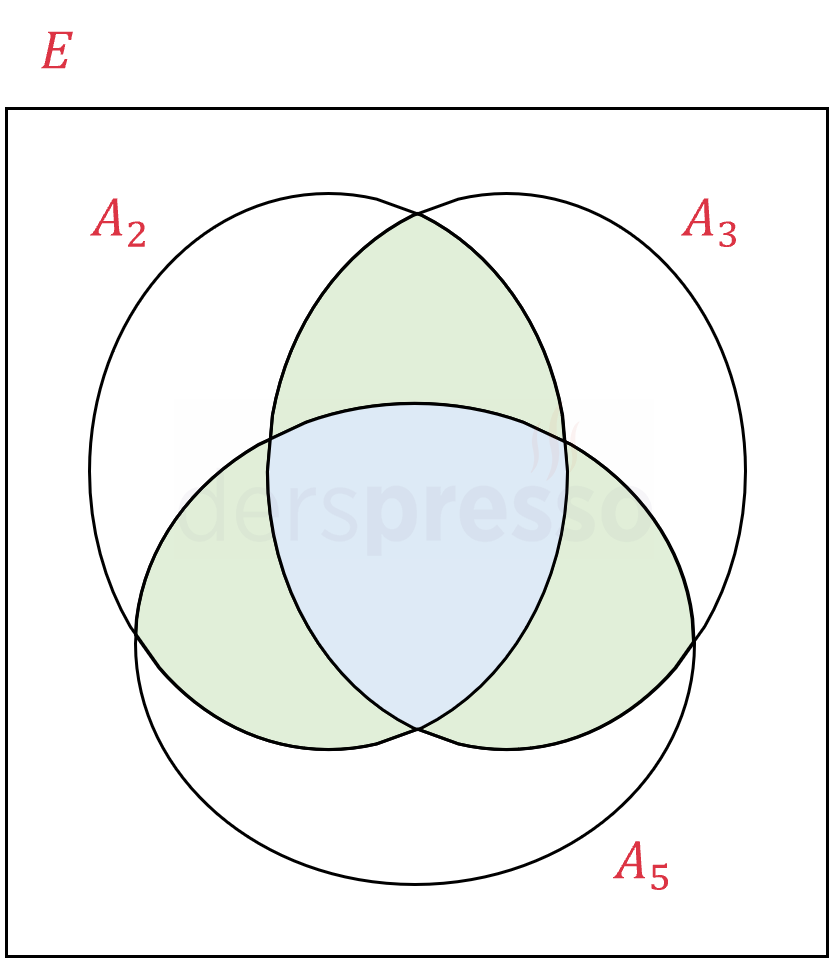
\( E \): 1-1000 arasındaki pozitif tam sayılar (1-1000)
\( A_2 \): 2'ye tam bölünen sayılar kümesi
\( A_3 \): 3'e tam bölünen sayılar kümesi
\( A_5 \): 5'e tam bölünen sayılar kümesi
\( A_2 \cap A_3 \): 2'ye VE 3'e tam bölünen sayılar (5'e bölünebilmesinden bağımsız)
\( A_2 \cap A_5 \): 2'ye VE 5'e tam bölünen sayılar (3'e bölünebilmesinden bağımsız)
\( A_3 \cap A_5 \): 3'e VE 5'e tam bölünen sayılar (2'ye bölünebilmesinden bağımsız)
\( A_2 \cap A_3 \cap A_5 \): 2'ye VE 3'e VE 5'e tam bölünen sayılar
1-1000 arasında 2'ye bölünen \( \floor{\frac{1000}{2}} = 500 \) sayı vardır.
\( s(A_2) = 500 \)
1-1000 arasında 3'e bölünen \( \floor{\frac{1000}{3}} = 333 \) sayı vardır.
\( s(A_3) = 333 \)
1-1000 arasında 5'e bölünen \( \floor{\frac{1000}{5}} = 200 \) sayı vardır.
\( s(A_5) = 200 \)
2'ye ve 3'e birlikte bölünen sayılar \( \text{EKOK}(2, 3) = 6 \)'ya da bölünür. 1-1000 arasında 6'ya tam bölünen \( \floor{\frac{1000}{6}} = 166 \) sayı vardır.
\( s(A_2 \cap A_3) = 166 \)
2'ye ve 5'e birlikte bölünen sayılar \( \text{EKOK}(2, 5) = 10 \)'a da bölünür. 1-1000 arasında 10'a tam bölünen \( \floor{\frac{1000}{10}} = 100 \) sayı vardır.
\( s(A_2 \cap A_5) = 100 \)
3'e ve 5'e birlikte bölünen sayılar \( \text{EKOK}(3, 5) = 15 \)'e de bölünür. 1-1000 arasında 15'e tam bölünen \( \floor{\frac{1000}{15}} = 66 \) sayı vardır.
\( s(A_3 \cap A_5) = 66 \)
2'ye, 3'e ve 5'e birlikte bölünen sayılar \( \text{EKOK}(2, 3, 5) = 30 \)'a da bölünür. 1-1000 arasında 30'a tam bölünen \( \floor{\frac{1000}{30}} = 33 \) sayı vardır.
\( s(A_2 \cap A_3 \cap A_5) = 33 \)
Bu bilgileri üç kümeli durum için dahil etme - hariç tutma formülünde yerine koyalım.
\( s(A_2 \cup A_3 \cup A_5) = s(A_2) + s(A_3) + s(A_5) - s(A_2 \cap A_3) - s(A_2 \cap A_5) - s(A_3 \cap A_5) + s(A_2 \cap A_3 \cap A_5) \)
\( = 500 + 333 + 200 - 166 - 100 - 66 + 33 = 734 \) bulunur.
Örten Fonksiyon Sayısı
İki küme arasında tanımlanabilecek örten fonksiyon sayısını dahil etme - hariç tutma prensibi ile nasıl hesaplayabileceğimizi önümüzdeki bölümde inceleyeceğiz.
\( x \in \mathbb{Z^+} \) olmak üzere,
\( (0, 1) \) açık aralığında ve en sade hali \( \frac{x}{2023} \) formunda olan kaç farklı kesir vardır?
Çözümü Göster\( \frac{x}{2023} \) formundaki kesirler iki koşulu sağlamalıdır.
\( 1 \le x \le 2022 \) olmalıdır, aksi takdirde kesir 0 ile 1 açık aralığında olmaz.
\( x \) ve 2023 sayıları aralarında asal sayılar olmalıdır, aksi takdirde kesrin daha sade hali bulunabilir.
Öncelikle 2023 sayısını asal çarpanlarına ayıralım.
\( 2023 = 7 \cdot 17^2 \)
2023 ile aralarında asal sayıları bulmak için \( x \)'in alabileceği 2022 adet değerden 7'nin ve 17'nin katlarını çıkaralım.
\( E \): 1-2022 arasındaki tam sayılar kümesi
\( A_7 \): 7'ye tam bölünen sayılar kümesi
\( A_{17} \): 17'ye tam bölünen sayılar kümesi
\( A_7 \cap A_{17} \): 7'ye VE 17'ye tam bölünen sayılar
1-2022 arasında 7'ye bölünen \( \floor{\frac{2022}{7}} = 288 \) sayı vardır.
\( s(A_7) = 288 \)
1-2022 arasında 17'ye bölünen \( \floor{\frac{2022}{17}} = 118 \) sayı vardır.
\( s(A_{17}) = 118 \)
Hem 7'ye hem de 17'ye bölünen sayılar \( \text{EKOK}(7, 17) = 119 \)'a da bölünür.
1-2022 arasında 119'a bölünen \( \floor{\frac{2022}{119}} = 16 \) sayı vardır.
\( s(A_7 \cap A_{17}) = 16 \)
Bu bilgileri iki kümeli durum için dahil etme - hariç tutma formülünde yerine koyalım.
\( s(A_7 \cup A_{17}) = s(A_7) + s(A_{17}) - s(A_7 \cap A_{17}) \)
\( = 288 + 118 - 16 = 390 \)
Buna göre 1-2022 aralığındaki tam sayılar içinde 7'ye veya 17'ye tam bölünmeyen \( 2022 - 390 = 1632 \) farklı \( x \) tam sayısı vardır, dolayısıyla istenen koşulları sağlayan 1632 farklı kesir yazılabilir.