Trigonometrik Fonksiyonların Periyodu
Konu tekrarı için: Periyodik Fonksiyon | Fonksiyonların Dönüşümü | Trigonometrik Fonksiyon Grafikleri
Trigonometrik fonksiyonlar birer periyodik fonksiyondur ve her fonksiyon için aşağıdaki eşitlik sağlanır.
\( T \) fonksiyonun esas periyodu ve \( T \in \mathbb{R^+} \) olmak üzere,
\( f(x + T) = f(x) \)
Trigonometrik fonksiyonların ve farklı dönüşümlerinin periyotları aşağıdaki formüllerle bulunabilir.
Sinüs ve Kosinüs Periyodu
Trigonometrik fonksiyon grafikleri bölümünde gördüğümüz gibi, sinüs ve kosinüs fonksiyonlarının periyodu \( 2\pi \) radyandır.
\( f(x) = \sin(x) \)
\( g(x) = \cos(x) \)
\( T_f = T_g = 2\pi \)
Sinüs ve kosinüs fonksiyonlarının farklı dönüşümlerinin periyodu aşağıdaki formülle bulunur.
\( f(x) = a\sin^n(cx + d) + b \)
\( g(x) = a\cos^n(cx + d) + b \)
\( n \) tek sayı ise \( T_f = T_g = \dfrac{2\pi}{\abs{c}} \)
\( n \) çift sayı ise \( T_f = T_g = \dfrac{\pi}{\abs{c}} \)
\( f(x) = 2\sin^2(3x) + 1 \) ise,
\( T_f = \dfrac{\pi}{3} \)
\( g(x) = -\cos^3(5x - \frac{\pi}{3}) \) ise,
\( T_g = \dfrac{2\pi}{5} \)
Bu formüllerin mantığı şu şekilde açıklanabilir.
- \( a \) katsayısı fonksiyon grafiğinde dikey genişleme/daralmaya yol açar, dolayısıyla \( x \) ekseni boyunca olan tekrarlama periyoduna bir etkisi yoktur.
- \( b \) değeri fonksiyon grafiğinde dikey ötelemeye yol açar ve grafiğin şeklini değiştirmeden sadece konumunu değiştirir, dolayısıyla periyoda bir etkisi yoktur.
- \( c \) katsayısı fonksiyon grafiğinde yatay genişleme/daralmaya yol açar, dolayısıyla periyot bu katsayı ile ters orantılı şekilde değişir.
- \( d \) değeri fonksiyon grafiğinde yatay ötelemeye yol açar ve grafiğin şeklini değiştirmeden sadece konumunu değiştirir, dolayısıyla periyoda bir etkisi yoktur.
- \( n \) tek sayı olduğunda, \( y \) değerlerinin işareti değişmediği için periyotta bir değişiklik olmaz.
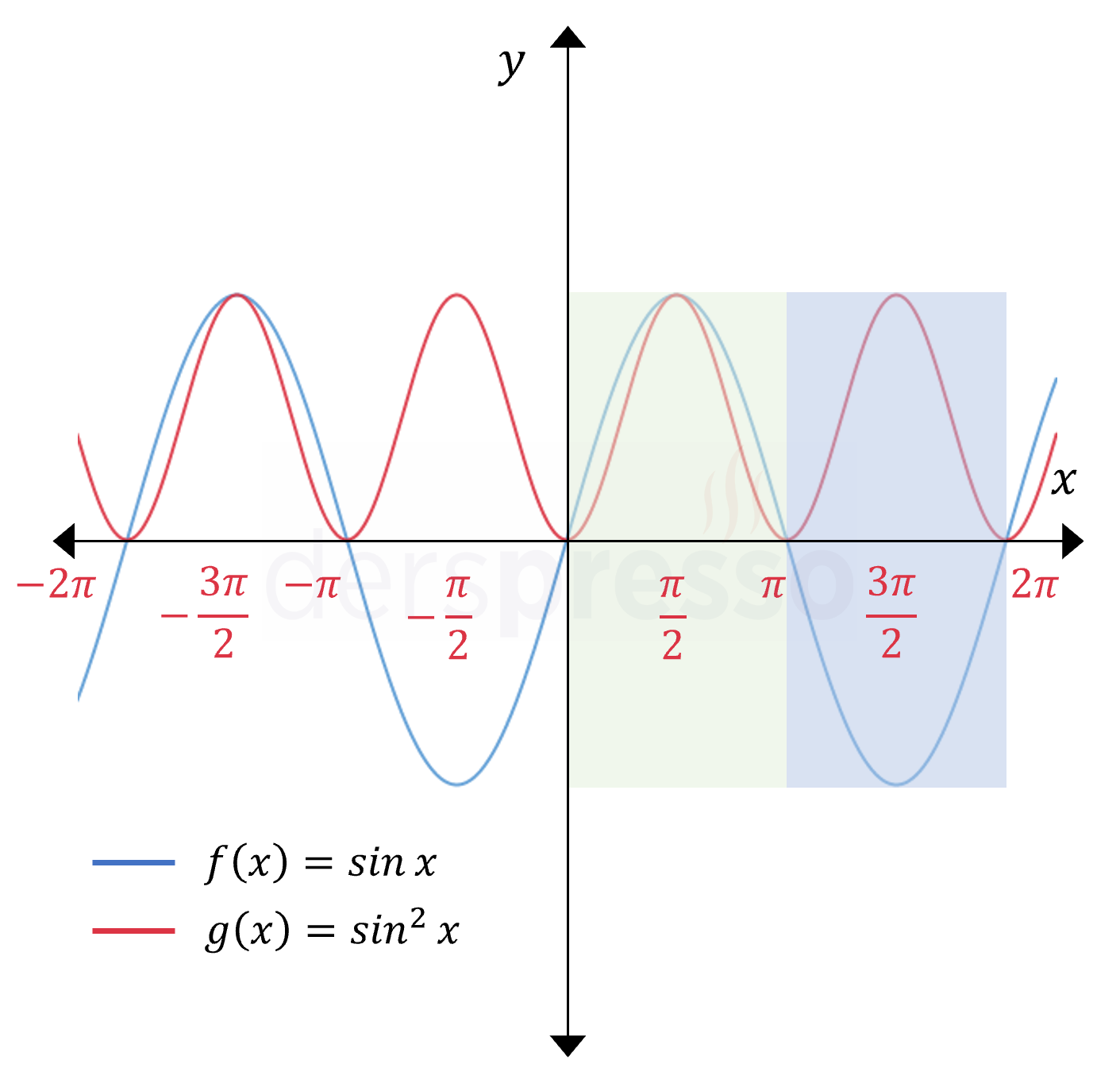
- \( n \) çift sayı olduğunda, fonksiyonun negatif değerleri pozitife döner ve aşağıdaki şekilde gibi grafiğin \( [0, \pi] \) ve \( [\pi, 2\pi] \) aralıkları birbirinin tekrarı olur, bunun sonucu olarak grafiğin periyodu \( \pi \) radyana iner.
Tanjant ve Kotanjant Periyodu
Trigonometrik fonksiyon grafikleri bölümünde gördüğümüz gibi, tanjant ve kotanjant fonksiyonlarının periyodu \( \pi \) radyandır.
\( f(x) = \tan(x) \)
\( g(x) = \cot(x) \)
\( T_f = T_g = \pi \)
Tanjant ve kotanjant fonksiyonlarının farklı dönüşümlerinin periyodu aşağıdaki formülle bulunur.
\( f(x) = a\tan^n(cx + d) + b \)
\( g(x) = a\cot^n(cx + d) + b \)
\( T_f = T_g = \dfrac{\pi}{\abs{c}} \)
\( f(x) = -\tan^2(4x) + 1 \) ise,
\( T_f = \dfrac{\pi}{4} \)
\( g(x) = 5\cot^3(2x - \frac{\pi}{4}) \) ise,
\( T_g = \dfrac{\pi}{2} \)
Bu formüllerin mantığı ile ilgili olarak, yukarıda sinüs/kosinüs fonksiyonları için paylaştığımız ilk beş madde tanjant/kotanjant fonksiyonları için de geçerlidir.
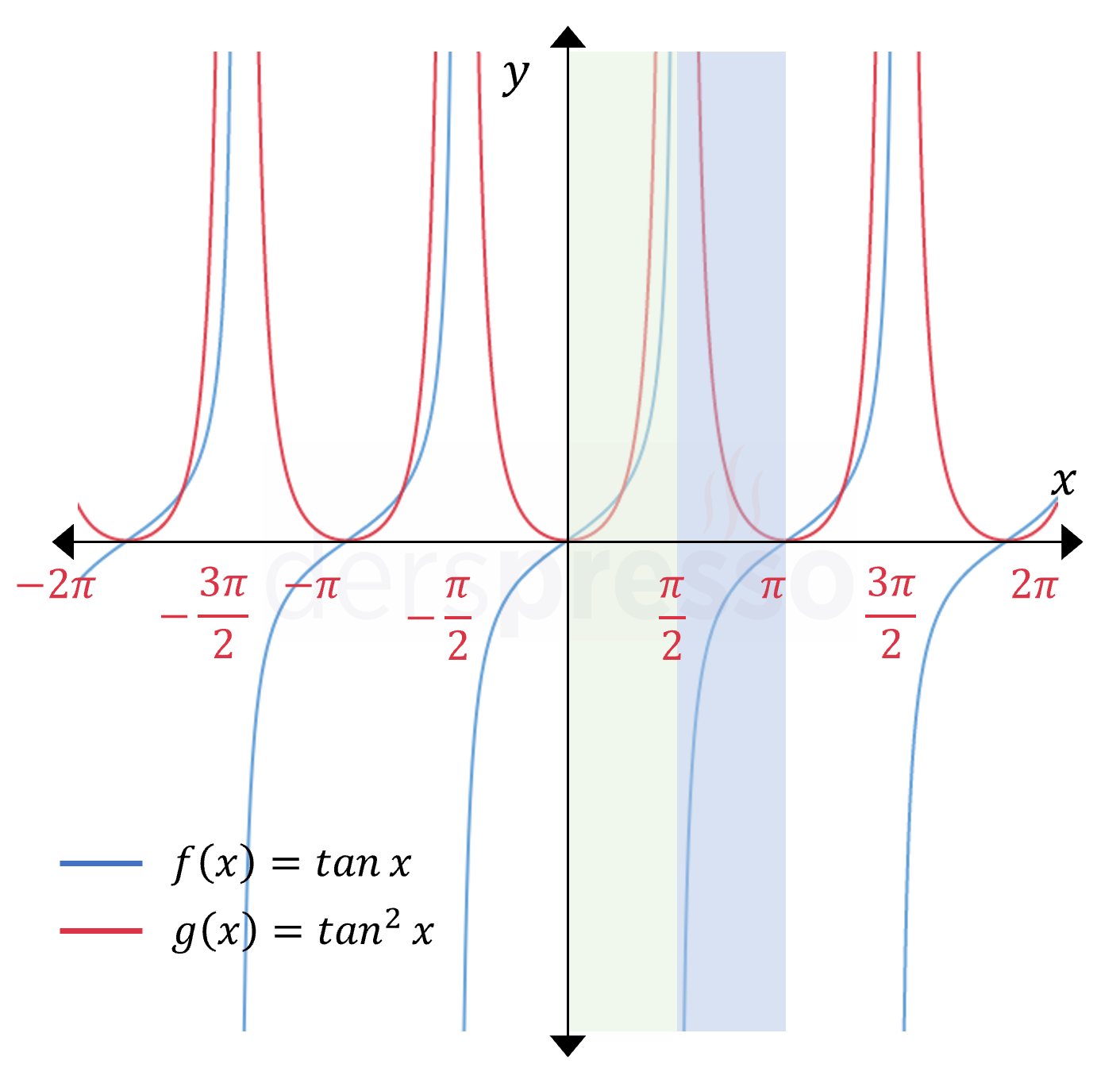
Bu maddelere ek olarak, \( n \) değeri çift sayı olduğunda fonksiyonun negatif değerleri pozitife döner, ancak aşağıdaki şekilde gibi grafiğin \( [0, \frac{\pi}{2}] \) ve \( [\frac{\pi}{2}, \pi] \) aralıkları birbirinin tekrarı değil, dikey bir doğruya göre simetriği olur, bu yüzden grafiğin periyodu değişmez.
Fonksiyonların Toplamının/Farkının Periyodu
\( f \) ve \( g \) iki periyodik fonksiyon olmak üzere, \( f \pm g \) fonksiyonunun esas periyodu, bu fonksiyonların esas periyotlarının EKOK'una (ortak katlarının en küçüğüne) eşittir.
\( T_f = \dfrac{a}{b} \)
\( T_g = \dfrac{c}{d} \) olmak üzere,
\( T_{f \pm g} = EKOK \left( \dfrac{a}{b}, \dfrac{c}{d} \right) = \dfrac{EKOK(a, c)}{EBOB(b, d)} \)
\( T_f = \dfrac{3\pi}{4} \)
\( T_g = \dfrac{2\pi}{5} \) ise,
\( T_{f + g} = \dfrac{EKOK(3, 2)}{EBOB(4, 5)}\pi \)
\( = \dfrac{6}{1}\pi = 6\pi \)
Aşağıdaki fonksiyonların esas periyodunu bulunuz.
(a) \( f(x) = 5 - 4\tan{\frac{3 - 2x}{3}} \)
(b) \( g(x) = 7 + \cos^6(6 - 2x) \)
(c) \( h(x) = 4\cot^5(8x - 2) \)
(d) \( k(x) = 18 - 3\sin^3(\frac{x}{2} - 4) \)
Çözümü Göster(a) seçeneği:
\( f(x) = 5 - 4\tan{\frac{3 - 2x}{3}} \)
\( = 5 - 4\tan(-\frac{2}{3}x + 1) \)
\( a\tan^n(cx + d) + b \) formundaki tanjant fonksiyonunun esas periyodu aşağıdaki formülle bulunur.
\( T = \dfrac{\pi}{\abs{c}} \)
Bu formülü verilen fonksiyona uygulayalım.
\( T_f = \dfrac{\pi}{\abs{-\frac{2}{3}}} = \dfrac{3\pi}{2} \)
(b) seçeneği:
\( g(x) = 7 + \cos^6(6 - 2x) \)
\( n \) çift sayı olmak üzere, \( a\cos^n(cx + d) + b \) formundaki kosinüs fonksiyonunun esas periyodu aşağıdaki formülle bulunur.
\( T = \dfrac{\pi}{\abs{c}} \)
Bu formülü verilen fonksiyona uygulayalım.
\( T_g = \dfrac{\pi}{\abs{-2}} = \dfrac{\pi}{2} \)
(c) seçeneği:
\( h(x) = 4\cot^5(8x - 2) \)
\( a\cot^n(cx + d) + b \) formundaki kotanjant fonksiyonunun esas periyodu aşağıdaki formülle bulunur.
\( T = \dfrac{\pi}{\abs{c}} \)
Bu formülü verilen fonksiyona uygulayalım.
\( T_h = \dfrac{\pi}{\abs{8}} = \dfrac{\pi}{8} \)
(d) seçeneği:
\( k(x) = 18 - 3\sin^3(\frac{x}{2} - 4) \)
\( n \) tek sayı olmak üzere, \( a\sin^n(cx + d) + b \) formundaki sinüs fonksiyonunun esas periyodu aşağıdaki formülle bulunur.
\( T = \dfrac{2\pi}{\abs{c}} \)
Bu formülü verilen fonksiyona uygulayalım.
\( T_k = \dfrac{2\pi}{\abs{\frac{1}{2}}} = 4\pi \)
Aşağıdaki fonksiyonların esas periyodunu bulunuz.
(a) \( f(x) = \sin(8x) + 3\cos(5x) \)
(b) \( g(x) = 4\sin^2(\frac{2 - x}{3}) + \sin^3(3x + 1) \)
(c) \( h(x) = 4\tan(3x) + \cot(5x + \frac{\pi}{2}) \)
(d) \( k(x) = \sqrt{5}\cos^4(-\frac{2x}{5} + 40) + \tan^2(4x - 20) \)
Çözümü Göster(a) seçeneği:
\( f(x) = \sin(8x) + 3\cos(5x) \)
\( \sin(8x) \) fonksiyonunun esas periyodu:
\( T_1 = \dfrac{2\pi}{8} = \dfrac{\pi}{4} \)
\( \cos(5x) \) fonksiyonunun esas periyodu:
\( T_2 = \dfrac{2\pi}{5} \)
İki fonksiyonunun toplamının esas periyodu fonksiyonların esas periyotlarının EKOK'una eşittir.
\( T_f = EKOK\left( \dfrac{\pi}{4}, \dfrac{2\pi}{5} \right) \)
\( = \dfrac{EKOK(\pi, 2\pi)}{EBOB(4, 5)} \)
\( = \dfrac{2\pi}{1} = 2\pi \)
(b) seçeneği:
\( g(x) = 4\sin^2(\frac{2 - x}{3}) + \sin^3(3x + 1) \)
Fonksiyon tanımını düzenleyelim.
\( g(x) = 4\sin^2(\frac{2}{3} - \frac{1}{3}x) + \sin^3(3x + 1) \)
\( \sin^2(\frac{2}{3} - \frac{1}{3}x) \) fonksiyonunun esas periyodu:
\( T_1 = \dfrac{\pi}{\abs{-\frac{1}{3}}} = 3\pi \)
\( \sin^3(3x + 1) \) fonksiyonunun esas periyodu:
\( T_2 = \dfrac{2\pi}{\abs{3}} = \dfrac{2\pi}{3} \)
İki fonksiyonunun toplamının esas periyodu fonksiyonların esas periyotlarının EKOK'una eşittir.
\( T_g = EKOK\left( 3\pi, \dfrac{2\pi}{3} \right) \)
\( = \dfrac{EKOK(3\pi, 2\pi)}{EBOB(1, 3)} \)
\( = \dfrac{6\pi}{1} = 6\pi \)
(c) seçeneği:
\( h(x) = 4\tan(3x) + \cot(5x + \frac{\pi}{2}) \)
\( \tan(3x) \) fonksiyonunun esas periyodu:
\( T_1 = \dfrac{\pi}{\abs{3}} = \dfrac{\pi}{3} \)
\( \cot(5x + \frac{\pi}{2}) \) fonksiyonunun esas periyodu:
\( T_2 = \dfrac{\pi}{\abs{5}} = \dfrac{\pi}{5} \)
İki fonksiyonunun toplamının esas periyodu fonksiyonların esas periyotlarının EKOK'una eşittir.
\( T_h = EKOK\left( \dfrac{\pi}{3}, \dfrac{\pi}{5} \right) \)
\( = \dfrac{EKOK(\pi, \pi)}{EBOB(3, 5)} \)
\( = \dfrac{\pi}{1} = \pi \)
(d) seçeneği:
\( k(x) = \sqrt{5}\cos^4(-\frac{2x}{5} + 40) + \tan^2(4x - 20) \)
\( \cos^4(-\frac{2x}{5} + 40) \) fonksiyonunun esas periyodu:
\( T_1 = \dfrac{\pi}{\abs{-\frac{2}{5}}} = \dfrac{5\pi}{2} \)
\( \tan^2(4x - 20) \) fonksiyonunun esas periyodu:
\( T_2 = \dfrac{\pi}{\abs{4}} = \dfrac{\pi}{4} \)
İki fonksiyonunun toplamının esas periyodu fonksiyonların esas periyotlarının EKOK'una eşittir.
\( T_k = EKOK\left( \dfrac{5\pi}{2}, \dfrac{\pi}{4} \right) \)
\( = \dfrac{EKOK(5\pi, \pi)}{EBOB(2, 4)} \)
\( = \dfrac{5\pi}{2} \)
\( f(x) = 6\pi - 4\cot^4\left( \dfrac{3x - 1}{m} \right) \)
fonksiyonunun esas periyodu \( 2\pi \) olduğuna göre, \( m \)'nin alabileceği değerlerin çarpımı kaçtır?
Çözümü GösterFonksiyon tanımını düzenleyelim.
\( f(x) = 6\pi - 4\cot^4\left( \dfrac{3}{m}x - \frac{1}{m} \right) \)
\( f(x) = a\cot^n(cx + d) + b \) formundaki kotanjant fonksiyonunun esas periyodu aşağıdaki formülle bulunur.
\( T_f = \dfrac{\pi}{\abs{c}} \)
Bu formülü verilen fonksiyona uygulayalım.
\( T_f = \dfrac{\pi}{\abs{\frac{3}{m}}} = 2\pi \)
\( \abs{\dfrac{3}{m}} = \dfrac{1}{2} \)
\( \dfrac{3}{m} = \pm \dfrac{1}{2} \)
\( m = -6 \) ya da \( m = 6 \)
\( m \)'nin alabileceği değerlerin çarpımı \( -6 \cdot 6 = -36 \) olur.
\( f(x) = -\tan^2(3x + 5) + 5 \)
\( g(x) = 2\cot^3(-6x + 2) - 2 \)
\( h(x) = 3\sin^5(-9x + 8) \)
olduğuna göre, \( f + g + h \) fonksiyonunun periyodu kaçtır?
Çözümü Göster\( a\tan^n(cx + d) + b \) formundaki tanjant fonksiyonunun esas periyodu aşağıdaki formülle bulunur.
\( T = \dfrac{\pi}{\abs{c}} \)
Buna göre \( f \) fonksiyonunun periyodu \( \frac{\pi}{\abs{3}} = \frac{\pi}{3} \) olur.
\( a\cot^n(cx + d) + b \) formundaki kotanjant fonksiyonunun esas periyodu aşağıdaki formülle bulunur.
\( T = \dfrac{\pi}{\abs{c}} \)
Buna göre \( g \) fonksiyonunun periyodu \( \frac{\pi}{\abs{-6}} = \frac{\pi}{6} \) olur.
\( n \) tek sayı olmak üzere, \( a\sin^n(cx + d) + b \) formundaki sinüs fonksiyonunun esas periyodu aşağıdaki formülle bulunur.
\( T = \dfrac{2\pi}{\abs{c}} \)
Buna göre \( h \) fonksiyonunun periyodu \( \frac{2\pi}{\abs{-9}} = \frac{2\pi}{9} \) olur.
İki ya da daha fazla fonksiyonun toplamının esas periyodu fonksiyonların esas periyotlarının EKOK'una eşittir.
\( T = EKOK\left( \dfrac{\pi}{3}, \dfrac{\pi}{6}, \dfrac{2\pi}{9} \right) \)
\( = \dfrac{EKOK(\pi, \pi, 2\pi)}{EBOB(3, 6, 9)} \)
\( = \dfrac{2\pi}{3} \) bulunur.
\( f(x) = k\cos^k(kx + k) + k \) fonksiyonunun esas periyodu \( \frac{\pi}{4} \) olduğuna göre, \( k \)'nın alabileceği değerlerin çarpımı kaçtır?
Çözümü Göster\( k \) sayısının tek ve çift sayı olduğu durumları ayrı ayrı inceleyelim.
Durum 1: \( k \) tek sayı
\( n \) tek sayı olmak üzere, \( a\cos^n(cx + d) + b \) formundaki kosinüs fonksiyonunun esas periyodu aşağıdaki formülle bulunur.
\( T = \dfrac{2\pi}{\abs{c}} \)
\( \dfrac{2\pi}{\abs{k}} = \dfrac{\pi}{4} \)
\( k \in \{ -8, 8 \} \)
Bulduğumuz \( k \) değerleri çift sayı olduğu için incelediğimiz durum için geçerli çözüm değildir.
Durum 2: \( k \) çift sayı
\( n \) çift sayı olmak üzere, \( a\cos^n(cx + d) + b \) formundaki kosinüs fonksiyonunun esas periyodu aşağıdaki formülle bulunur.
\( T = \dfrac{\pi}{\abs{c}} \)
\( \dfrac{\pi}{\abs{k}} = \dfrac{\pi}{4} \)
\( k \in \{ -4, 4 \} \)
\( k \)'nın alabileceği değerlerin çarpımı \( -4 \cdot 4 = -16 \) bulunur.
\( 0 \le x \le 2\pi \) olmak üzere,
\( \sin^2(kx) = \dfrac{7}{11} \)
denklemini sağlayan 16 tane \( x \) değeri olduğuna göre, \( k \) kaçtır?
Çözümü Göster\( \sin{x} \) fonksiyonunun periyodu \( 2\pi \)'dir, dolayısıyla \( [0, 2\pi] \) aralığında kendini 1 kez tekrarlar. Fonksiyon bu aralıkta \( (0, 1) \) aralığındaki bir değeri 2 kez alır.
\( \sin^2{x} \) fonksiyonunun periyodu \( \pi \)'dir, dolayısıyla \( [0, 2\pi] \) aralığında kendini 2 kez tekrarlar. Fonksiyon bu aralıkta \( (0, 1) \) aralığındaki bir değeri 4 kez alır.
\( \sin^2(kx) \) fonksiyonunun periyodu \( \frac{\pi}{k} \)'dır, dolayısıyla \( [0, 2\pi] \) aralığında kendini \( 2k \) kez tekrarlar. Fonksiyon bu aralıkta \( (0, 1) \) aralığındaki bir değeri \( 4k \) kez alır.
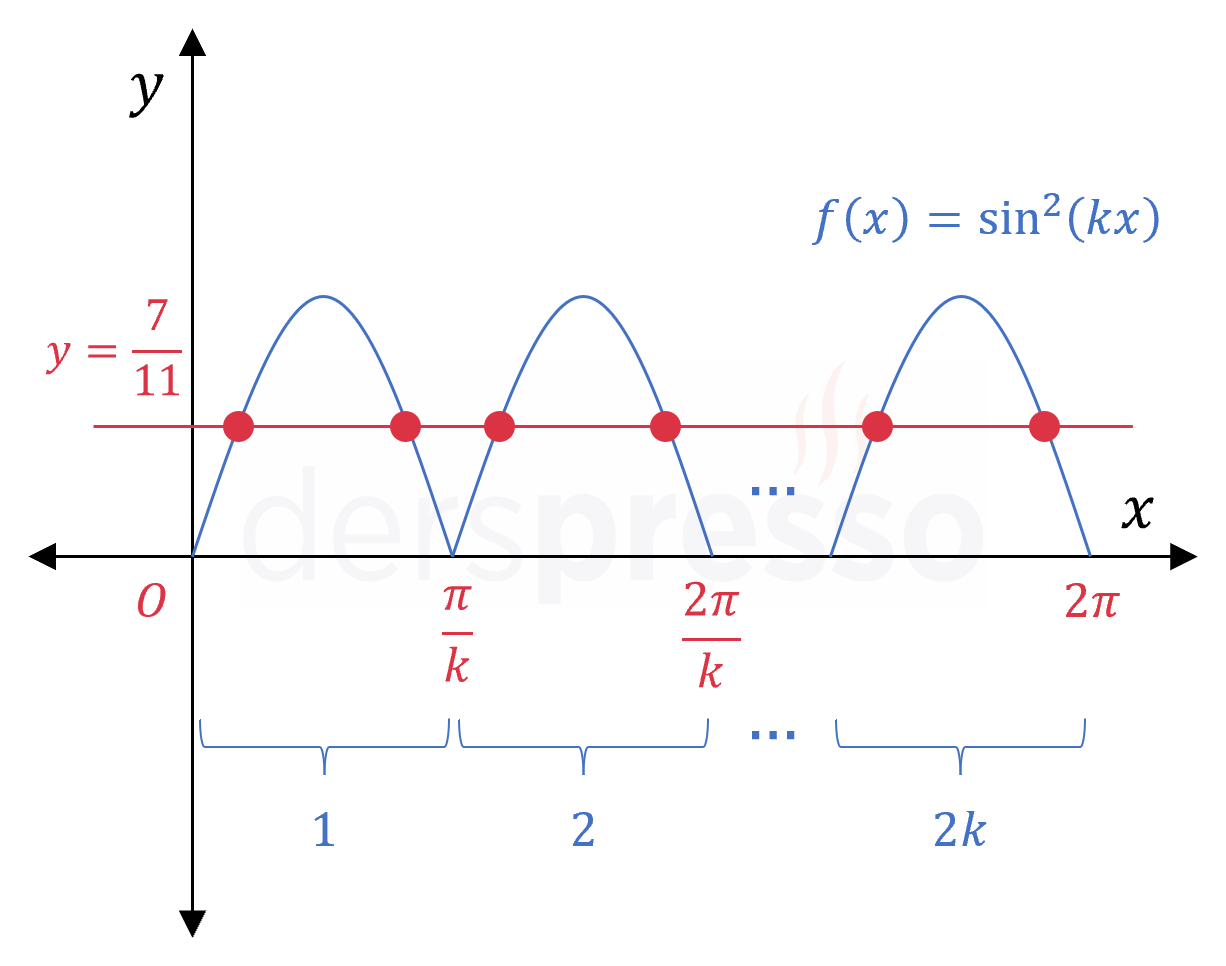
\( 4k = 16 \)
\( k = 4 \) bulunur.
\( \cos(\sin{x}) \) fonksiyonunun periyodu kaçtır?
Çözümü GösterSinüs ve kosinüs fonksiyonlarının grafikleri aşağıdaki gibidir.
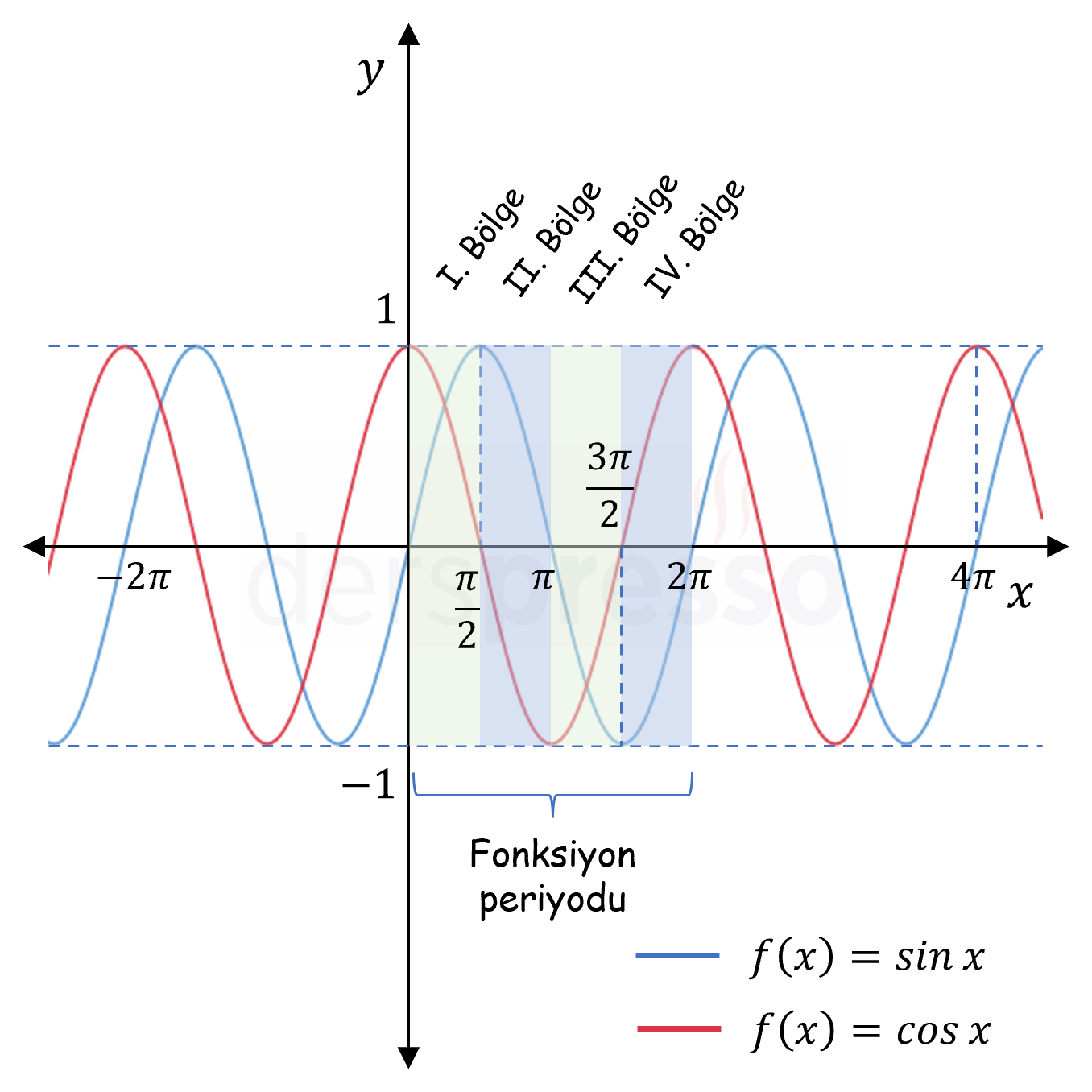
Buna göre her iki fonksiyonun da periyodu \( 2\pi \)'dir.
Verilen fonksiyonun periyoduna \( T \) diyelim.
Fonksiyonun periyodu aşağıdaki eşitliği sağlayan en küçük \( T \) değeridir.
\( \cos(\sin{x}) = \cos(\sin(x + T)) \)
Bu eşitlik \( T = 2\pi \) için sağlanır.
\( \cos(\sin{x}) = \cos(\sin(x + 2\pi)) = \cos(\sin{x}) \)
Her ne kadar sinüs fonksiyonunun periyodu \( 2\pi \) olsa da, fonksiyonun grafiği ikinci bir simetri daha içerir ve fonksiyonun mutlak değeri her \( \pi \) periyotta bir kendini tekrarlar.
Bu eşitliğin \( T = \pi \) için de sağlanıp sağlanmadığını kontrol edelim.
\( \cos(\sin{x}) = \cos(\sin(x + \pi)) \)
Sinüs III. bölgede negatiftir.
\( = \cos(-\sin{x}) \)
Kosinüs fonksiyonu çift fonksiyondur.
\( \cos(-x) = \cos{x} \)
\( = \cos(\sin{x}) \)
Dolayısıyla \( T = \pi \) de fonksiyonun bir periyodudur.
Daha küçük bir \( T \) değeri için yukarıdaki eşitlik sağlanamayacağı için fonksiyonun periyodu \( \pi \) olur.