Kosinüs ve Sinüs Teoremleri
Kosinüs ve sinüs teoremleri üçgenlerde köşe açıları ve kenar uzunlukları arasında ilişki kurmamızı sağlar. Bu iki teorem sadece dik üçgenlerde değil tüm üçgenlerde kullanılabilir.
Kosinüs Teoremi
Kosinüs teoremi kullanılarak bir üçgende iki kenar uzunluğu biliniyorsa ya bu iki kenarın arasındaki açının kosinüs değeri kullanılarak üçüncü kenarın uzunluğu bulunabilir, ya da üçüncü kenarın uzunluğu kullanılarak iki kenar arasındaki açının kosinüs değeri bulunabilir.

Yukarıdaki şekildeki gibi bir üçgen için kosinüs teoremi formülleri aşağıdaki gibidir.
\( a^2 = b^2 + c^2 - 2bc\cos(\hat{A}) \)
\( b^2 = a^2 + c^2 - 2ac\cos(\hat{B}) \)
\( c^2 = a^2 + b^2 - 2ab\cos(\hat{C}) \)
Uzunlukları 6 ve 10 br, aralarındaki açı 120° olan iki kenarın karşı kenar uzunluğu:
\( a^2 = 6^2 + 10^2 - 2(6)(10)\cos{120°} \)
\( = 36 + 100 - 120(-\frac{1}{2}) = 196 \)
\( a = 14 \text{ br} \)
İSPATI GÖSTER
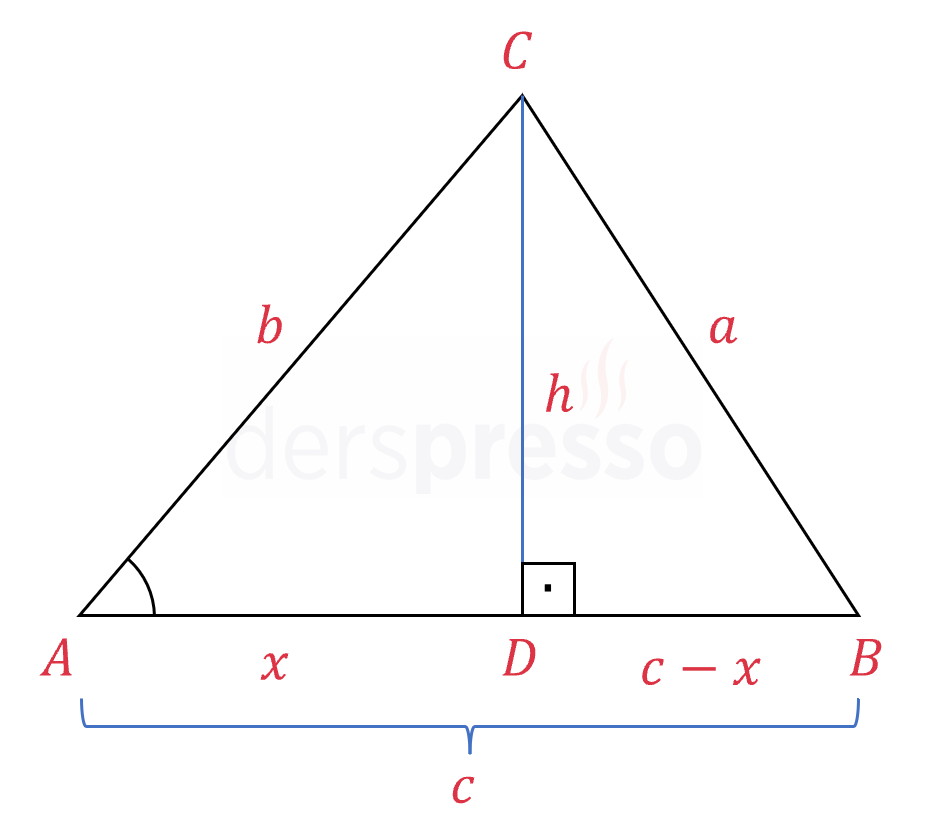
\( C \) köşesinden yükseklik indirelim ve uzunluğuna \( h \) diyelim.
\( \overset{\triangle}{ADC} \) üçgeni için Pisagor teoremini yazalım.
\( b^2 = x^2 + h^2 \)
\( \overset{\triangle}{BDC} \) üçgeni için Pisagor teoremini yazalım.
\( a^2 = (c - x)^2 + h^2 \)
\( a^2 = c^2 - 2cx + \textcolor{red}{x^2 + h^2} \)
Son satırdaki kırmızı ile işaretli terimlerin yerine, birinci üçgenden elde ettiğimiz eşitliği yazalım.
\( a^2 = c^2 - 2cx + \textcolor{red}{b^2} \)
Bu ifadedeki \( x \)'i \( A \) açısı ve üçgenin bir kenar uzunluğu cinsinden yazalım.
\( \cos(\hat{A}) = \dfrac{x}{b} \Longrightarrow x = b\cos(\hat{A}) \)
\( x \)'i yukarıdaki ifadede yerine koyduğumuzda kosinüs teoremi formülünü elde ederiz.
\( a^2 = b^2 + c^2 - 2bc\cos(\hat{A}) \)
Aynı ispatı üçgenin diğer kenarları için de yapabiliriz.
Sinüs Teoremi
Sinüs teoremine göre bir üçgende her kenarın uzunluğu ile bu kenarın karşısındaki açının sinüs değeri arasındaki oran üç kenar için de aynıdır.

Yukarıdaki şekildeki gibi bir üçgen için sinüs teoremi formülü aşağıdaki gibidir.
\( \dfrac{a}{\sin(\hat{A})} = \dfrac{b}{\sin(\hat{B})} = \dfrac{c}{\sin(\hat{C})} = 2R \)
Bir kenarın uzunluğu 8 br ve karşı açısı 45° ise karşı açısı 30° olan kenarın uzunluğu:
\( \dfrac{8}{\sin{45°}} = \dfrac{b}{\sin{30°}} \)
\( \dfrac{8}{\frac{\sqrt{2}}{2}} = \dfrac{b}{\frac{1}{2}} \)
\( b = 4\sqrt{2} \text{ br} \)
İSPATI GÖSTER
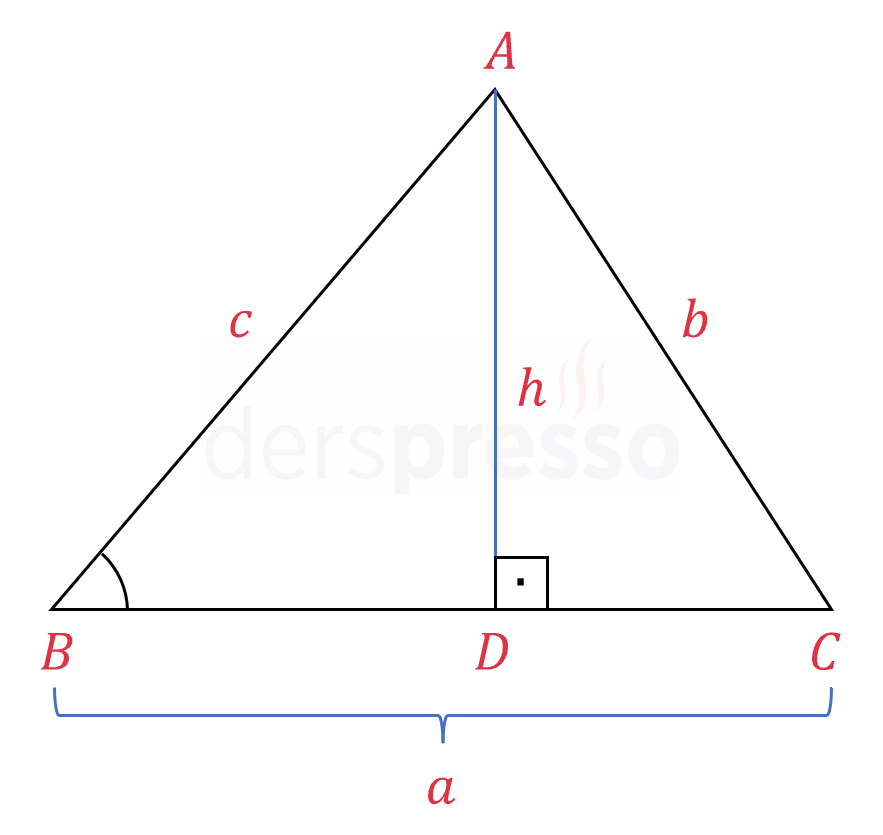
\( A \) köşesinden yükseklik indirelim ve uzunluğuna \( h \) diyelim.
\( B \) ve \( C \) köşeleri için sinüs oranlarını yazalım.
\( \sin(\hat{B}) = \dfrac{h}{c} \Longrightarrow h = c\sin(\hat{B}) \)
\( \sin(\hat{C}) = \dfrac{h}{b} \Longrightarrow h = b\sin(\hat{C}) \)
İki eşitlikteki \( h \) değişkenlerini eşitleyelim.
\( c\sin(\hat{B}) = b\sin(\hat{C}) \)
\( \dfrac{b}{\sin(\hat{B})} = \dfrac{c}{\sin(\hat{C})} \)
Sinüs teoremindeki ilk eşitliği elde etmiş olduk. Şimdi farklı bir kenar için aynı işlemi yapalım.
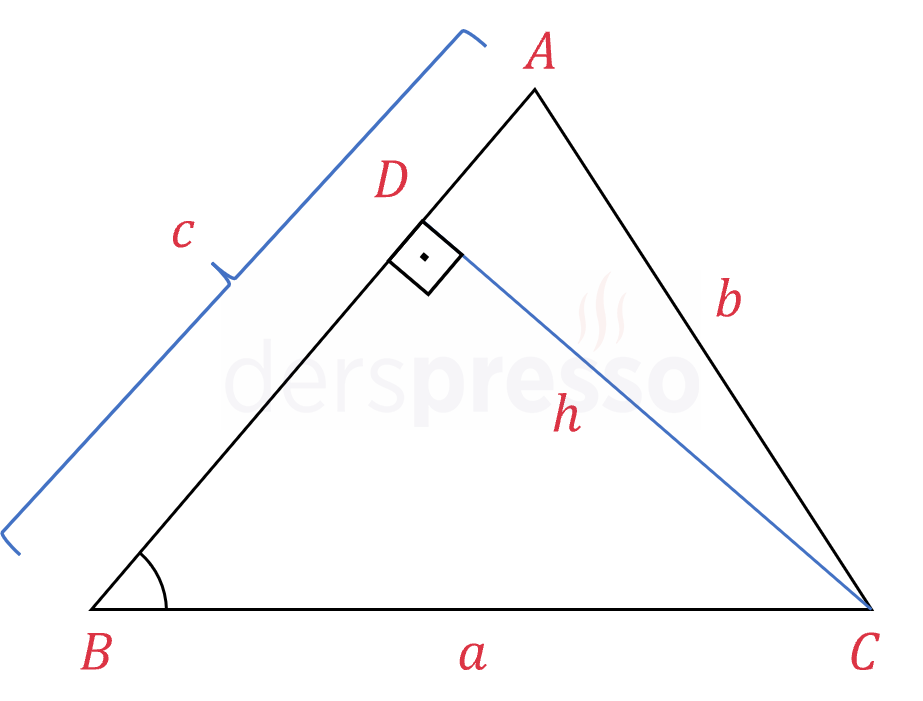
\( C \) köşesinden yükseklik indirelim ve uzunluğuna \( h \) diyelim.
\( A \) ve \( B \) köşeleri için sinüs oranlarını yazalım.
\( \sin(\hat{A}) = \dfrac{h}{b} \Longrightarrow h = b\sin(\hat{A}) \)
\( \sin(\hat{B}) = \dfrac{h}{a} \Longrightarrow h = a\sin(\hat{B}) \)
İki eşitlikteki \( h \) değişkenlerini eşitleyelim.
\( b\sin(\hat{A}) = a\sin(\hat{B}) \)
\( \dfrac{a}{\sin(\hat{A})} = \dfrac{b}{\sin(\hat{B})} \)
Elde ettiğimiz her iki orantıdaki birer oran eşit olduğu için tüm ifadeyi tek eşitlikte birleştirebiliriz.
\( \dfrac{a}{\sin(\hat{A})} = \dfrac{b}{\sin(\hat{B})} = \dfrac{c}{\sin(\hat{C})} \)
Sinüs teoremi formülünün orantı katsayısı (\( 2R \)) o üçgenin çevrel çemberinin yarıçapının iki katına eşittir.
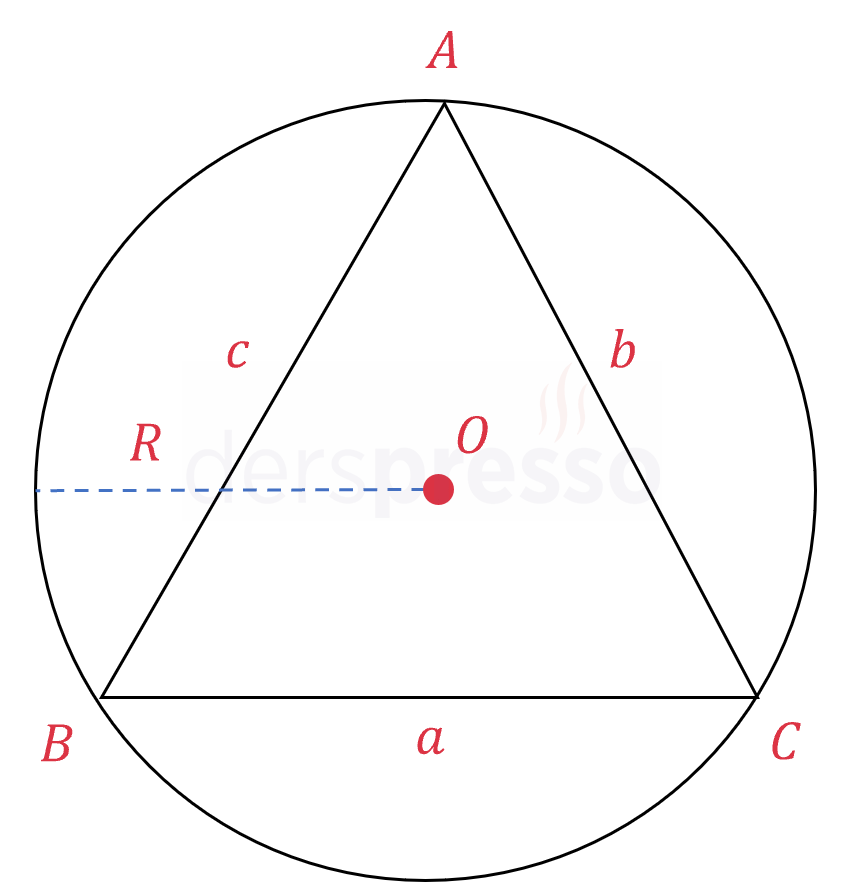
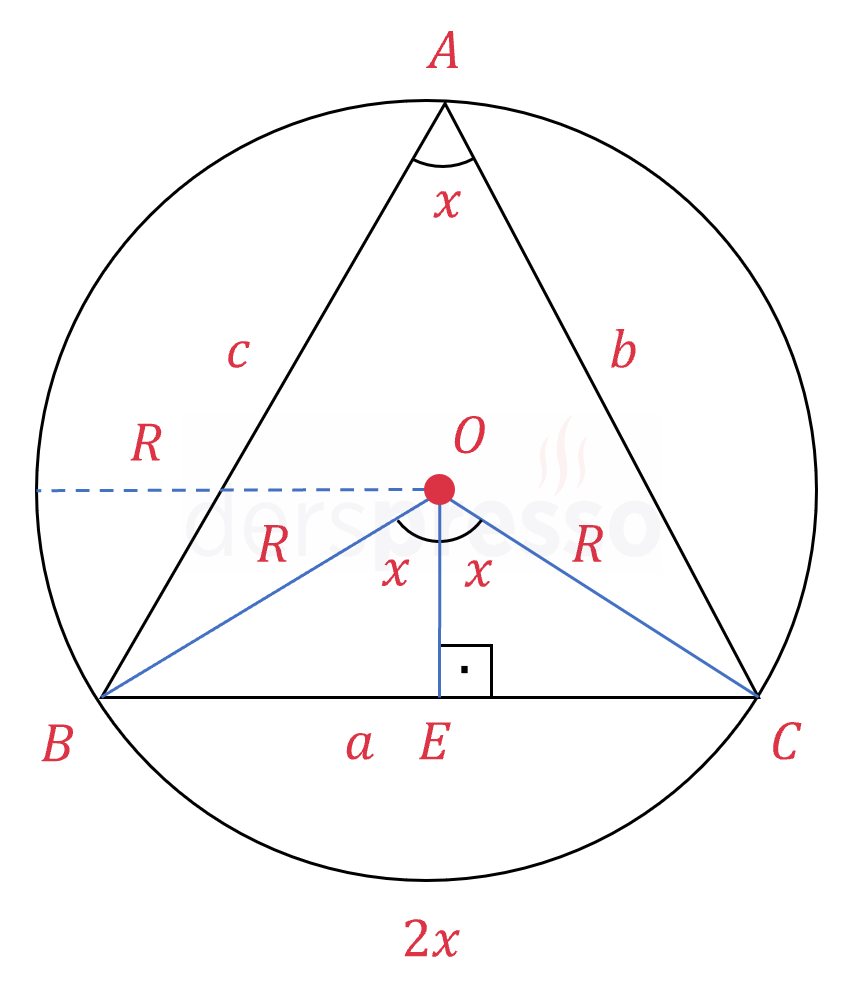
Çemberin merkezinden \( [BC] \) kirişini dik kesen \( [OE] \) doğru parçası çizelim.
Bir çemberin kirişinin orta dikmesi çemberin merkezinden geçtiği için \( [OE] \) \( [BC] \) kirişinin orta dikmesidir.
\( \abs{BE} = \abs{EC} \)
\( OEB \) ve \( OEC \) üçgenlerinin dik köşelerine komşu kenarlar eşit uzunlukta olduğu için bu iki üçgen eş üçgenlerdir.
\( \overset{\triangle}{OEB} \cong \overset{\triangle}{OEC} \)
\( m(\widehat{BOE}) = m(\widehat{COE}) = x \)
\( \widehat{BOC} \) merkez açısının gördüğü \( \overgroup{BC} \) yayının ölçüsü \( 2x \) olur, bu yayı gören \( \widehat{BAC} \) çevre açısının ölçüsü de \( \frac{2x}{2} = x \) olur.
\( BOC \) üçgeninin alanını yazalım.
\( A(BOC) = \frac{1}{2}a\abs{OE} \)
\( \cos{x} = \dfrac{\abs{OE}}{R} \)
\( \abs{OE} = R\cos{x} \)
\( \abs{OE} \) uzunluğunu alan formülünde yerine koyalım.
\( A(BOC) = \frac{1}{2}aR\cos{x} \)
\( BOC \) üçgeninin alanını şimdi de sinüs alan formülü ile yazalım.
\( A(BOC) = \frac{1}{2}RR\sin(2x) \)
\( \sin(2x) \) ifadesini sinüs iki kat açı formülü ile yeniden yazalım.
\( \sin(2x) = 2\sin{x}\cos{x} \)
\( A(BOC) = \frac{1}{2}RR(2\sin{x}\cos{x}) \)
Bulduğumuz iki alan formülünü eşitleyelim ve ortak çarpanları sadeleştirelim.
\( \frac{1}{2}aR\cos{x} = \frac{1}{2}RR(2\sin{x}\cos{x}) \)
\( a = 2R\sin{x} \)
\( \dfrac{a}{\sin{x}} = 2R \)
Bu oran sinüs teoreminin oranlarından biri olduğu için teoremdeki orantıyı çevrel çemberin yarıçapının iki katına eşitleyebiliriz.
\( \dfrac{a}{\sin{\hat{A}}} = \dfrac{b}{\sin{\hat{B}}} = \dfrac{c}{\sin{\hat{C}}} = 2R \)
Sinüs Alan Formülü
Bir üçgende iki kenar uzunluğu ve bu iki kenar arasındaki açının sinüs değeri biliniyorsa üçgenin alanı aşağıdaki formülle hesaplanabilir.

\( A(ABC) = \dfrac{1}{2}bc\sin{\hat{A}} \)
İki kenar uzunluğu 8 ve 7 br, aralarındaki açı 30° ise üçgenin alanı:
\( A(ABC) = \dfrac{1}{2} \cdot 8 \cdot 7 \cdot \sin{30°} \)
\( = 14 \text{ br}^2 \)
İSPATI GÖSTER

\( B \) köşesinden yükseklik indirelim ve uzunluğuna \( h \) diyelim.
\( A(ABC) = \dfrac{1}{2}bh \)
\( h \) yüksekliğini \( \hat{A} \) açısı cinsinden aşağıdaki gibi yazabiliriz.
\( \sin{\hat{A}} = \dfrac{h}{c} \)
\( h = c\sin{\hat{A}} \)
\( h \) değerini alan formülünde yerine koyduğumuzda sinüs alan formülünü elde ederiz.
\( A(ABC) = \dfrac{1}{2}bc\sin{\hat{A}} \)
İki kenar uzunluğu ve bir açısı verilen aşağıdaki üçgenlerin üçüncü kenar uzunluğunu bulunuz.
(a) \( \abs{AC} = 3, \abs{BC} = 7, m(\hat{A}) = 120° \)
(b) \( \abs{AB} = 4\sqrt{3}, \abs{BC} = 4, m(\hat{B}) = 30° \)
(c) \( \abs{AC} = 3\sqrt{2}, \abs{AB} = 3\sqrt{10}, m(\hat{C}) = 45° \)
Çözümü Gösterİstenen uzunluğu bulmak için kosinüs teoremini kullanalım.
(a) seçeneği:
\( \abs{AC} = 3, \abs{BC} = 7, m(\hat{A}) = 120° \)
Verilen kenarları/açıları ve bilinmeyen kenarı bir üçgen üzerinde gösterelim.

\( \abs{BC}^2 = \abs{AC}^2 + \abs{AB}^2 - 2\abs{AC}\abs{AB}\cos{\hat{A}} \)
\( 7^2 = 3^2 + \abs{AB}^2 - 2(3)\abs{AB}\cos{120°} \)
\( 49 = 9 + \abs{AB}^2 - 2(3)\abs{AB}(-\frac{1}{2}) \)
\( \abs{AB}^2 + 3\abs{AB} - 40 = 0 \)
\( (\abs{AB} + 8)(\abs{AB} - 5) = 0 \)
Denklemin kökleri her bir çarpanı sıfır yapan değerlerdir.
Uzunluk negatif olamaz.
\( \abs{AB} = 5 \)
(b) seçeneği:
\( \abs{AB} = 4\sqrt{3}, \abs{BC} = 4, m(\hat{B}) = 30° \)
Verilen kenarları/açıları ve bilinmeyen kenarı bir üçgen üzerinde gösterelim.

\( \abs{AC}^2 = \abs{BC}^2 + \abs{AB}^2 - 2\abs{BC}\abs{AB}\cos{\hat{B}} \)
\( \abs{AC}^2 = 4^2 + (4\sqrt{3})^2 - 2(4)(4\sqrt{3})\cos{30°} \)
\( \abs{AC}^2 = 16 + 48 - 2(4)(4\sqrt{3})(\dfrac{\sqrt{3}}{2}) \)
\( \abs{AC}^2 = 16 \)
Uzunluk negatif olamaz.
\( \abs{AC} = 4 \)
(c) seçeneği:
\( \abs{AC} = 3\sqrt{2}, \abs{AB} = 3\sqrt{10}, m(\hat{C}) = 45° \)
Verilen kenarları/açıları ve bilinmeyen kenarı bir üçgen üzerinde gösterelim.

\( \abs{AB}^2 = \abs{BC}^2 + \abs{AC}^2 - 2\abs{BC}\abs{AC}\cos{\hat{C}} \)
\( (3\sqrt{10})^2 = \abs{BC}^2 + (3\sqrt{2})^2 - 2\abs{BC}(3\sqrt{2})\cos{45°} \)
\( 90 = \abs{BC}^2 + 18 - 2\abs{BC}(3\sqrt{2})(\dfrac{\sqrt{2}}{2}) \)
\( 90 = \abs{BC}^2 + 18 - 6\abs{BC} \)
\( \abs{BC}^2 - 6\abs{BC} - 72 = 0 \)
\( (\abs{BC} + 6)(\abs{BC} - 12) = 0 \)
Denklemin kökleri her bir çarpanı sıfır yapan değerlerdir.
Uzunluk negatif olamaz.
\( \abs{BC} = 12 \)
\( ABC \) üçgeninin kenar uzunlukları arasında \( c^2 = a^2 + b^2 - ab \) bağıntısı olduğuna göre,
\( m(\hat{C}) \) kaç derecedir?
Çözümü Göster\( c \) kenarı için kosinüs teoremi formülünü yazalım.
\( c^2 = a^2 + b^2 - 2ab\cos{\hat{C}} \)
Bu formül ve verilen bağıntıdaki \( c^2 \) terimlerini eşitleyelim.
\( a^2 + b^2 - 2ab\cos{\hat{C}} = a^2 + b^2 - ab \)
\( 2ab\cos{\hat{C}} = ab \)
\( \cos{\hat{C}} = \dfrac{1}{2} \)
\( m(\hat{C}) = 60° \) bulunur.

Yukarıdaki \( ABC \) üçgeninin çevresi 12 birimdir.
\( \sin{\hat{A}} + \sin{\hat{B}} + \sin{\hat{C}} = \dfrac{6}{5} \)
\( \sin{\hat{A}} = \dfrac{3}{10} \) olduğuna göre, \( [BC] \) kenarının uzunluğunu bulunuz.
Çözümü GösterÜçgene sinüs teoremini uygulayalım.
\( \dfrac{a}{\sin{\hat{A}}} = \dfrac{b}{\sin{\hat{B}}} = \dfrac{c}{\sin{\hat{C}}} = 2R \)
Bir orantıda oranların paylarının toplamının paydalarının toplamına oranı aynı orantı sabitine eşittir.
\( \dfrac{a + b + c}{\sin{\hat{A}} + \sin{\hat{B}} + \sin{\hat{C}}} = 2R \)
\( a + b + c = 12 \)
\( \dfrac{12}{\frac{6}{5}} = 2R = 10 \)
Bulduğumuz orantı sabitini \( a \) kenarının uzunluğunu bulmak için kullanalım.
\( \dfrac{a}{\sin{\hat{A}}} = 2R \)
\( \dfrac{a}{\frac{3}{10}} = 10 \)
\( a = 3 \) birim bulunur.
Bir \( ABC \) üçgeninin kenar uzunlukları \( a, b, c \) olarak veriliyor.
\( \sin(\hat{A}) + \sin(\hat{B}) = 3 \sin(\hat{C}) \)
\( a - 2c = 4 - b \)
olduğuna göre, \( c \) kaç birimdir?
Çözümü GösterSinüs teoremi formülünü yazalım.
\( \dfrac{a}{\sin(\hat{A})} = \dfrac{b}{\sin(\hat{B})} = \dfrac{c}{\sin(\hat{C})} \)
Orantı kurallarına göre, orantıdaki iki oranın pay ve paydalarının toplamlarının oranı aynı orantı sabitine eşittir.
\( \dfrac{a + b}{\sin(\hat{A}) + \sin(\hat{B})} = \dfrac{c}{\sin(\hat{C})} \)
Verilen diğer eşitlikteki terimleri düzenleyelim.
\( a + b = 2c + 4 \)
Bu eşitlikleri elde ettiğimiz yeni orantıda yerine koyalım.
\( \dfrac{a + b}{\sin(\hat{A}) + \sin(\hat{B})} = \dfrac{c}{\sin(\hat{C})} \)
\( \dfrac{2c + 4}{3 \sin(\hat{C})} = \dfrac{c}{\sin(\hat{C})} \)
\( 2c + 4 = 3c \)
\( c = 4 \) bulunur.
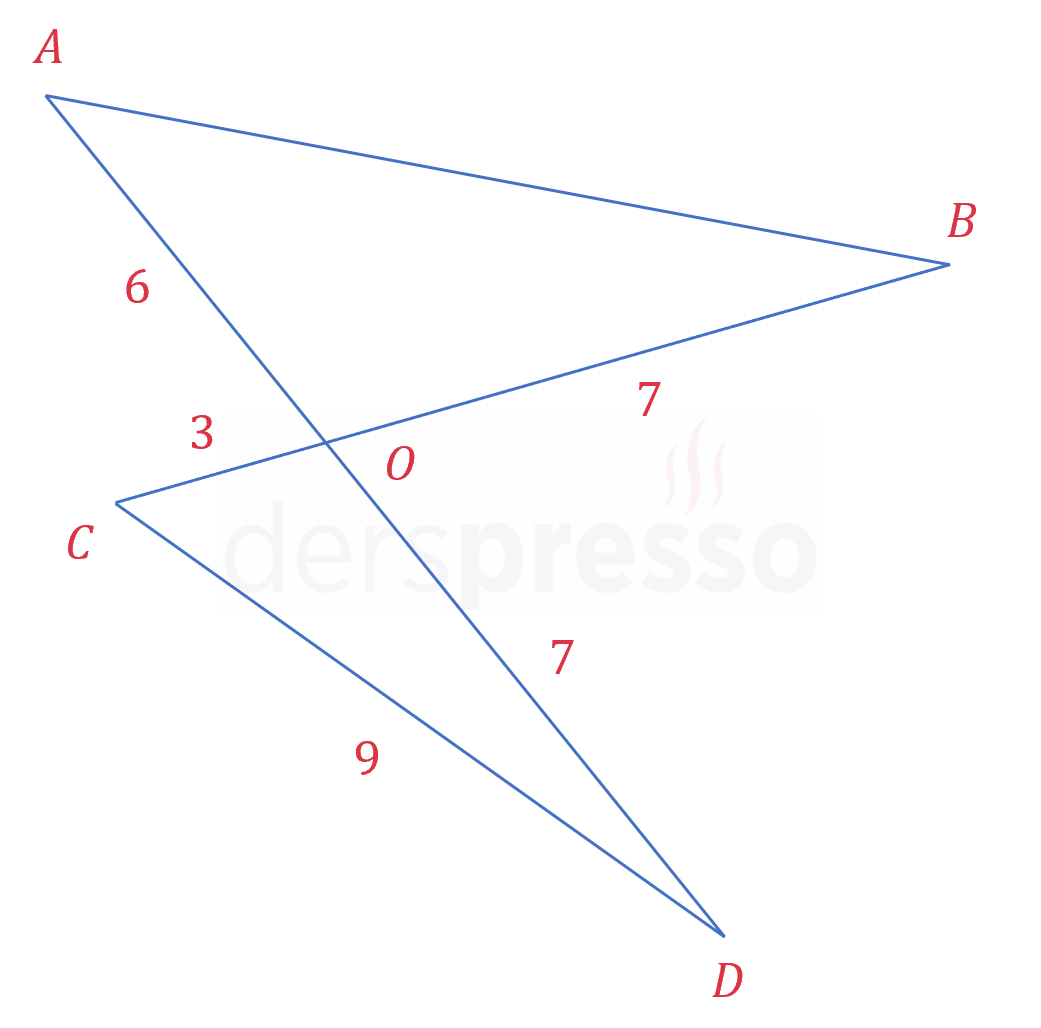
\( \abs{AD} \) ve \( \abs{BC} \) doğru parçaları şekildeki gibi \( O \) noktasında kesişmektedir.
Buna göre, \( \abs{AB} \) uzunluğu kaçtır?
Çözümü Göster\( \widehat{AOB} \) açısı ile \( \widehat{COD} \) ters açılar olduğu için ölçüleri eşittir.
Bu açıya \( \theta \) diyelim.
\( m(\widehat{AOB}) = m(\widehat{COD}) = \theta \)
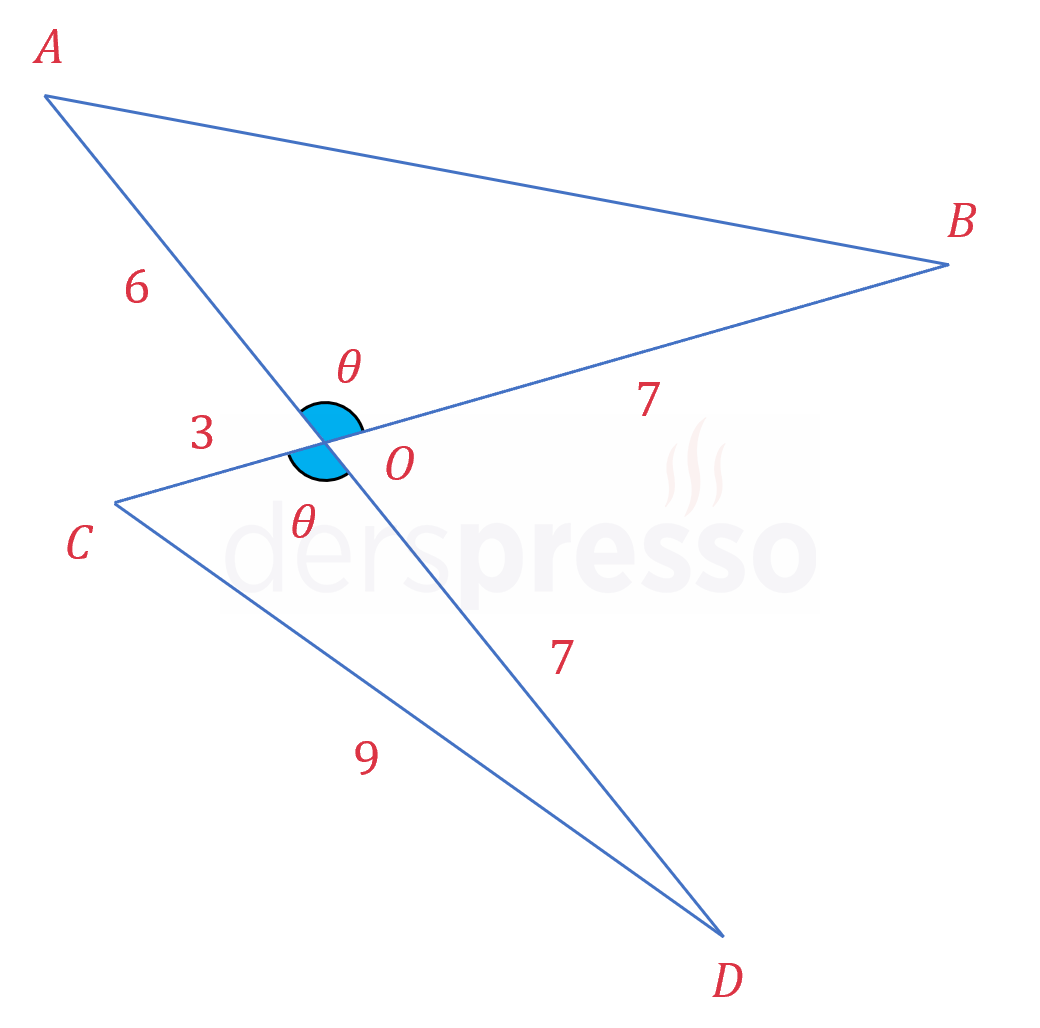
\( \theta \) açısının kosinüsünü bulmak için \( COD \) üçgenine kosinüs teoremini uygulayalım.
\( \abs{CD}^2 = \abs{OC}^2 + \abs{OD}^2 - 2\abs{OC}\abs{OD}\cos{\theta} \)
\( 9^2 = 3^2 + 7^2 - 2 \cdot 3 \cdot 7\cos{\theta} \)
\( \cos{\theta} = -\dfrac{23}{42} \)
\( \abs{AB} \) uzunluğunu bulmak için \( AOB \) üçgenine kosinüs teoremini uygulayalım.
\( \abs{AB}^2 = \abs{OA}^2 + \abs{OB}^2 - 2\abs{OA}\abs{OB}\cos{\theta} \)
\( = 6^2 + 7^2 - 2 \cdot 6 \cdot 7\cos{\theta} \)
\( = 85 - 84(-\dfrac{23}{42}) = 131 \)
\( \abs{AB} = \sqrt{131} \) bulunur.
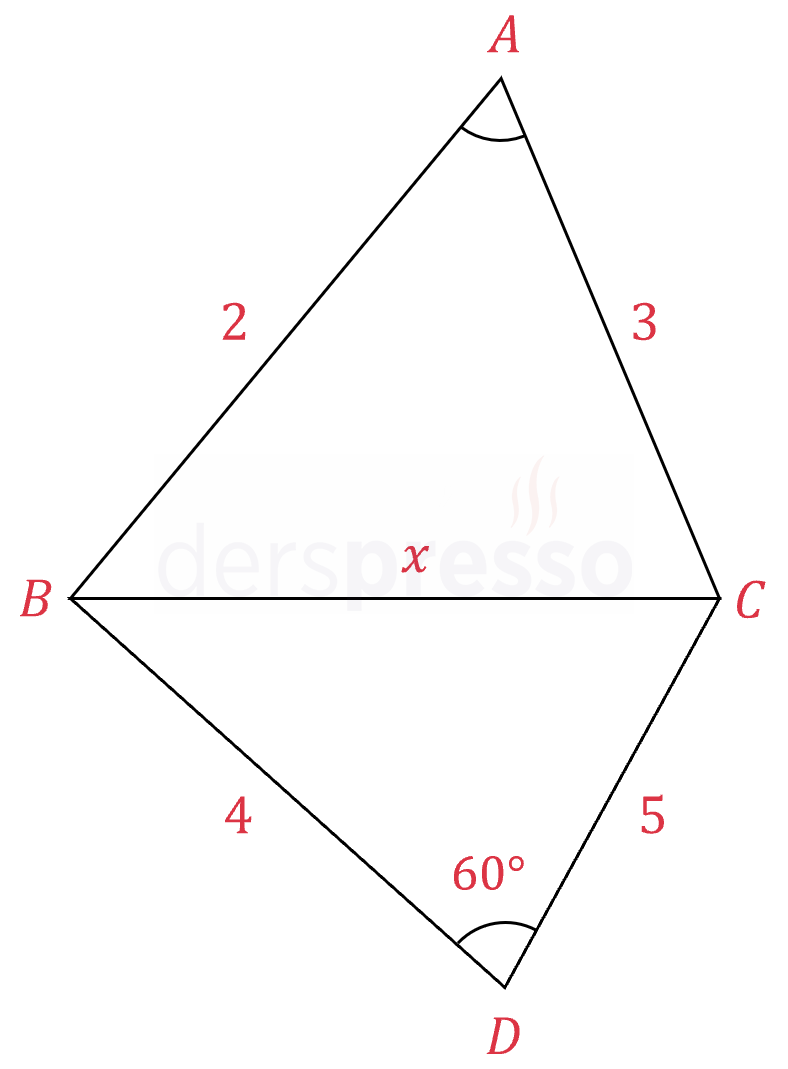
\( ABCD \) bir dörtgendir.
\( \abs{AB} = 2, \quad \abs{BD} = 4 \)
\( \abs{DC} = 5, \quad \abs{AC} = 3 \)
\( m(\widehat{BDC}) = 60° \)
olduğuna göre, \( \cos{\widehat{A}} \) kaçtır?
Çözümü Göster\( BCD \) üçgenine kosinüs teoremi uygulayarak \( x \) uzunluğunu bulalım.
\( x^2 = 4^2 + 5^2 - 2 \cdot 5 \cdot 4\cos{60°} \)
\( = 41 - 40 \cdot \dfrac{1}{2} = 21 \)
\( BAC \) üçgenine kosinüs teoremi uygulayarak \( \cos{\widehat{A}} \) değerini bulalım.
\( x^2 = 21 = 2^2 + 3^2 - 2 \cdot 2 \cdot 3\cos{\widehat{A}} \)
\( 21 = 13 - 12 \cos{\widehat{A}} \)
\( \cos{\widehat{A}} = -\dfrac{2}{3} \) bulunur.

\( ABC \) bir üçgendir.
\( \dfrac{\abs{AB}}{\abs{AC}} = \dfrac{2}{5} \)
\( \sin(\widehat{BAD}) = \dfrac{1}{4}, \sin(\widehat{DAC}) = \dfrac{1}{5} \)
olduğuna göre, \( \frac{A(ABD)}{A(ADC)} \) kaçtır?
Çözümü Göster\( \abs{AB} = 2k, \quad \abs{AC} = 5k \)
\( \abs{AD} = x \) diyelim.
İstenen oranı sinüs teoremini kullanarak bulalım.
\( \dfrac{A(\widehat{ABD})}{A(\widehat{ADC})} = \dfrac{\frac{1}{2}\abs{AB}\abs{AD}\sin(\widehat{BAD})}{\frac{1}{2}\abs{AD}\abs{AC}\sin(\widehat{DAC})} \)
\( = \dfrac{\frac{1}{2} \cdot 2k \cdot x \cdot \frac{1}{4}}{\frac{1}{2} \cdot x \cdot 5k \cdot \frac{1}{5}} \)
\( = \dfrac{1}{2} \) bulunur.

\( ABC \) ve \( EBD \) üçgenlerinin alanları eşit olduğuna göre, \( x \) uzunluğu kaç birimdir?
Çözümü Göster\( B \) köşesi üzerinden iki üçgen için sinüs alan formülünü yazarak birbirine eşitleyelim.
\( A(ABC) = A(EBD) \)
\( \dfrac{1}{2} \cdot (3 + x) \cdot 4 \cdot \sin{\hat{B}} = \dfrac{1}{2} \cdot 3 \cdot (4 + 2) \cdot \sin{\hat{B}} \)
\( 12 + 4x = 18 \)
\( x = \dfrac{3}{2} \) birim bulunur.
\( ABC \) üçgeninde \( a = 10 \), \( b = 8 \) ve \( c = 6 \) birim olduğuna göre, üçgenin çevrel çemberinin yarıçapı kaç birimdir?
Çözümü GösterKenar oranlarına göre \( ABC \) üçgeni 3-4-5 özel üçgenidir, dolayısıyla bir dik üçgendir.
\( m(\hat{A}) = 90° \)
Üçgenin alanını hesaplayalım.
\( A(ABC) = \dfrac{6 \cdot 8}{2} = 24 \text{ br}^2 \) olur.
Üçgenin alanı aynı zamanda çevrel çemberinin yarıçapı kullanılarak da hesaplanabilir.
\( A(ABC) = \dfrac{abc}{4R} \)
\( 24 = \dfrac{6 \cdot 8 \cdot 10}{4R} \)
\( R = 5 \) birim bulunur.
\( ABC \) üçgeninde \( a = 10 \), \( b = 8 \) ve \( c = 6 \) birim olduğuna göre, üçgenin iç teğet çemberinin yarıçapı kaç birimdir?
Çözümü GösterKenar oranlarına göre \( ABC \) üçgeni 3-4-5 özel üçgenidir, dolayısıyla bir dik üçgendir.
\( m(\hat{A}) = 90° \)
Üçgenin alanını hesaplayalım.
\( A(ABC) = \dfrac{6 \cdot 8}{2} = 24 \text{ br}^2 \)
Üçgenin alanı aynı zamanda iç teğet çemberinin yarıçapı kullanılarak da hesaplanabilir.
\( u = \dfrac{a + b + c}{2} \) olmak üzere,
\( A(ABC) = ur \)
\( u = \dfrac{6 + 8 + 10}{2} = 12 \)
\( A(ABC) = ur \)
\( 24 = 12r \)
\( r = 2 \) birim bulunur.

\( \abs{AB} = 9, \quad \abs{BC} = 4 \)
\( m(\widehat{BAC}) = x, \quad m(\widehat{ACB}) = 90° + x \)
olduğuna göre, \( \cot{x} \) kaçtır?
Çözümü GösterSinüs teoremini kullanalım.
\( \dfrac{4}{\sin{x}} = \dfrac{9}{\sin(90° + x)} \)
İçler - dışlar çarpımı yapalım.
\( 4\sin(90° + x) = 9\sin{x} \)
\( \sin(90° + x) = \cos{x} \) özdeşliğini kullanalım.
\( 4\cos{x} = 9\sin{x} \)
\( \dfrac{\cos{x}}{\sin{x}} = \cot{x} = \dfrac{9}{4} \) bulunur.

Yukarıdaki şekilde \( ABC \) üçgeni verilmiştir.
\( \abs{AB} = 4, \quad \abs{AC} = 5 \)
\( m(\widehat{BAC}) = 60° \)
olduğuna göre, \( [BC] \) kenarına ait yükseklik kaç birimdir?
Çözümü GösterYüksekliği bulmak için üçgenin alanını ve \( [BC] \) kenarınının uzunluğunu bulalım.
Üçgenin alanını bulmak için \( ABC \) üçgenine sinüs alan teoremini uygulayalım.
\( A(ABC) = \dfrac{1}{2}\abs{AB}\abs{AC}\sin{\hat{A}} \)
\( = \dfrac{1}{2} \cdot 4 \cdot 5\sin{60°} = 5\sqrt{3} \)
\( \abs{BC} \) uzunluğunu bulmak için kosinüs teoremi formülünü kullanalım.
\( \abs{BC}^2 = \abs{AB}^2 + \abs{AC}^2 - 2\abs{AB}\abs{AC}\cos{\hat{A}} \)
\( = 4^2 + 5^2 - 2 \cdot 4 \cdot 5\cos{60°} \)
\( = 16 + 25 - 20 = 21 \)
\( \abs{BC} = \sqrt{21} \)
\( [BC] \) kenarına ait yüksekliğe \( h \) diyelim.
\( A(ABC) = \dfrac{\abs{BC} \cdot h}{2} \)
\( 5\sqrt{3} = \dfrac{\sqrt{21}h}{2} \)
\( h = \dfrac{10\sqrt{3}}{\sqrt{21}} \)
\( = \dfrac{10}{\sqrt{7}} = \dfrac{10\sqrt{7}}{7} \) olarak bulunur.

\( ABCD \) bir yamuktur.
\( \abs{AB} = 4, \quad \abs{BD} = 1 \)
\( \abs{CD} = 2\sqrt{3} + 4 \)
\( m(\widehat{BDC}) = 30° \)
olduğuna göre, \( \abs{AC} = x \) kaç birimdir?
Çözümü Göster\( \abs{AC} \) doğrusuna paralel bir \( \abs{BE} \) doğrusu çizelim.

\( ABCE \) paralelkenarında karşılıklı kenar uzunlukları birbirine eşittir.
\( \abs{BE} = \abs{AC} = x \)
\( \abs{AB} = \abs{CE} \)
\( \abs{ED} = 2\sqrt{3} + 4 - 4 = 2\sqrt{3} \)
\( BDE \) üçgenine kosinüs teoremi uygulayalım.
\( x^2 = 1^2 + (2\sqrt{3})^2 - 2 \cdot 1 \cdot 2\sqrt{3}\cos{30°} \)
\( = 1 + 12 - 2 \cdot 2\sqrt{3} \cdot \dfrac{\sqrt{3}}{2} \)
\( = 13 - 6 = 7 \)
\( x = \sqrt{7} \) birim bulunur.

\( ABCD \) bir paralelkenardır.
\( \abs{AE} = 2\sqrt{3}, \quad \abs{AB} = \sqrt{6}, \quad \abs{BF} = 5\sqrt{3} \)
\( m(\widehat{ABF}) = 45° \)
olduğuna göre, \( \abs{EF} = x \) kaç birimdir?
Çözümü Göster
\( [AB] \) kenarına paralel \( [EG] \) doğrusu çizelim.
\( ABGE \) paralelkenarında karşılıklı kenar uzunlukları birbirine eşittir.
\( \abs{EG} = \abs{AB} = \sqrt{6} \)
\( \abs{BG} = \abs{AE} = 2\sqrt{3} \)
\( \abs{GF} = 5\sqrt{3} - 2\sqrt{3} = 3\sqrt{3} \)
Oluşan \( EGF \) üçgenine kosinüs teoremi uygulayalım.
\( x^2 = (\sqrt{6})^2 + (3\sqrt{3})^2 - 2 \cdot \sqrt{6} \cdot 3\sqrt{3}\cos{45°} \)
\( = 6 + 27 - 2\sqrt{6} \cdot 3\sqrt{3} \cdot \dfrac{\sqrt{2}}{2} \)
\( = 15 \)
\( x = \sqrt{15} \) birim bulunur.

\( ABCD \) bir eşkenar dörtgendir.
\( \abs{AB} = 5, \quad 2\abs{BE} = 3\abs{ED}\)
\( \tan(\widehat{ABD}) = \dfrac{3}{4} \)
olduğuna göre, \( \abs{CE} = x \) kaçtır?
Çözümü GösterEşkenar dörtgenin tüm kenar uzunlukları birbirine eşittir.
Soruda verilen oranlara göre kenar uzunluklarını yazalım.

\( \tan(\widehat{ABD}) = \frac{3}{4} \) olduğuna göre, bir dik üçgende \( \widehat{ABD} \) açısının karşı kenarı \( 3k \), komşu kenarı \( 4k \) ve hipotenüs \( 5k \) olur.
\( \tan(\widehat{ABD}) \) değeri pozitif olduğu için bu açı bir dar açıdır.
\( \cos(\widehat{ABD}) = \dfrac{4}{5} \)
Eşkenar dörtgen bir paralelkenar olduğu için \( \widehat{ABD} \) ve \( \widehat{CDB} \) bütünler açılardır.
\( \cos(\widehat{CDB}) = \cos(180° - \widehat{ABD}) \)
\( = - \cos(\widehat{ABD}) = -\dfrac{4}{5} \)
\( CDE \) üçgenine kosinüs teoremini uygulayalım.
\( x^2 = 2^2 + 5^2 - 2 \cdot 2 \cdot 5 \cdot (-\dfrac{4}{5}) \)
\( = 4 + 25 + 16 = 45 \)
\( x = 3\sqrt{5} \) bulunur.
Bir üçgenin iki kenar uzunluğu 7 cm'dir. Bu üçgenin alanının en büyük olması için üçüncü kenar uzunluğu kaç cm olmalıdır?
Çözümü GösterVerilen üçgenin alanını bulmak için sinüs teoremini kullanalım.
Uzunlukları verilen kenarlara \( a \) ve \( b \), bu kenarların arasında kalan açıya \( \alpha \) diyelim.
\( A = \dfrac{1}{2}ab\sin{\alpha} \)
Üçgenin alanının en büyük olması için \( \sin{\alpha} \) en büyük değerini almalıdır, dolayısıyla \( \alpha \) açısı 90° olmalıdır.
Üçgenin üçüncü kenarına \( c \) diyelim.
Üçüncü kenar (hipotenüs) uzunluğunu bulmak için Pisagor teoremini kullanalım.
\( c^2 = 7^2 + 7^2 \)
\( c = 7\sqrt{2} \) olarak bulunur.

Şekilde verilenlere göre \( \sin{x} \) kaçtır?
Çözümü Gösterİki üçgenin yükseklikleri eşit olduğu için alanları oranı taban uzunlukları oranına eşittir.
\( \dfrac{A(ABC)}{A(ACD)} = \dfrac{\frac{1}{2} \cdot 3\abs{AC} \sin{60°}}{\frac{1}{2} \cdot 4\abs{AC}\sin{x}} = \dfrac{2k}{k} \)
\( \dfrac{3 \cdot \frac{\sqrt{3}}{2}}{4\sin{x}} = 2 \)
\( 8 \sin{x} = \dfrac{3 \sqrt{3}}{2} \)
\( \sin{x} = \dfrac{3 \sqrt{3}}{16} \) bulunur.

Yukarıdaki şekilde bir çember ve bu çemberin \( ABCD \) kirişler dörtgeni verilmiştir.
\( m(\widehat{ADC}) = x \) olduğuna göre, \( \cos{x} \) değerini bulunuz.
Çözümü Göster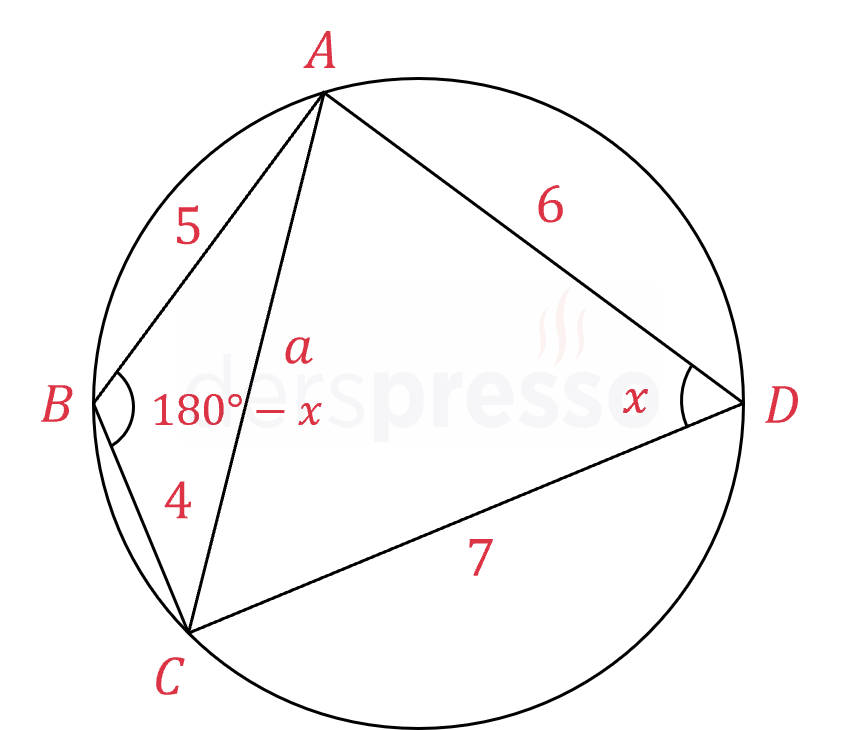
Kirişler dörtgeninde karşılıklı açıların ölçüleri toplamı \( 180° \)'dir ve gördükleri yayların uzunlukları toplamı \( 360° \)'dir.
\( m(\widehat{ABC}) = 180° - x \)
\( \abs{AC} = a \)
\( ADC \) üçgenine kosinüs teoremini uygulayalım.
\( a^2 = 6^2 + 7^2 - 2 \cdot 6 \cdot 7\cos{x} \)
\( = 85 - 84\cos{x} \)
\( ABC \) üçgenine kosinüs teoremini uygulayalım.
\( a^2 = 4^2 + 5^2 - 2 \cdot 4 \cdot 5\cos(180° - x) \)
\( = 41 - 40\cos(180° - x) \)
Kosinüs fonksiyonu II. bölgede negatiftir.
\( = 41 + 40\cos{x} \)
İki \( a^2 \) ifadesini birbirine eşitleyelim.
\( 85 - 84\cos{x} = 41 + 40\cos{x} \)
\( 124\cos{x} = 44 \)
\( \cos{x} = \dfrac{44}{124} = \dfrac{11}{31} \) bulunur.
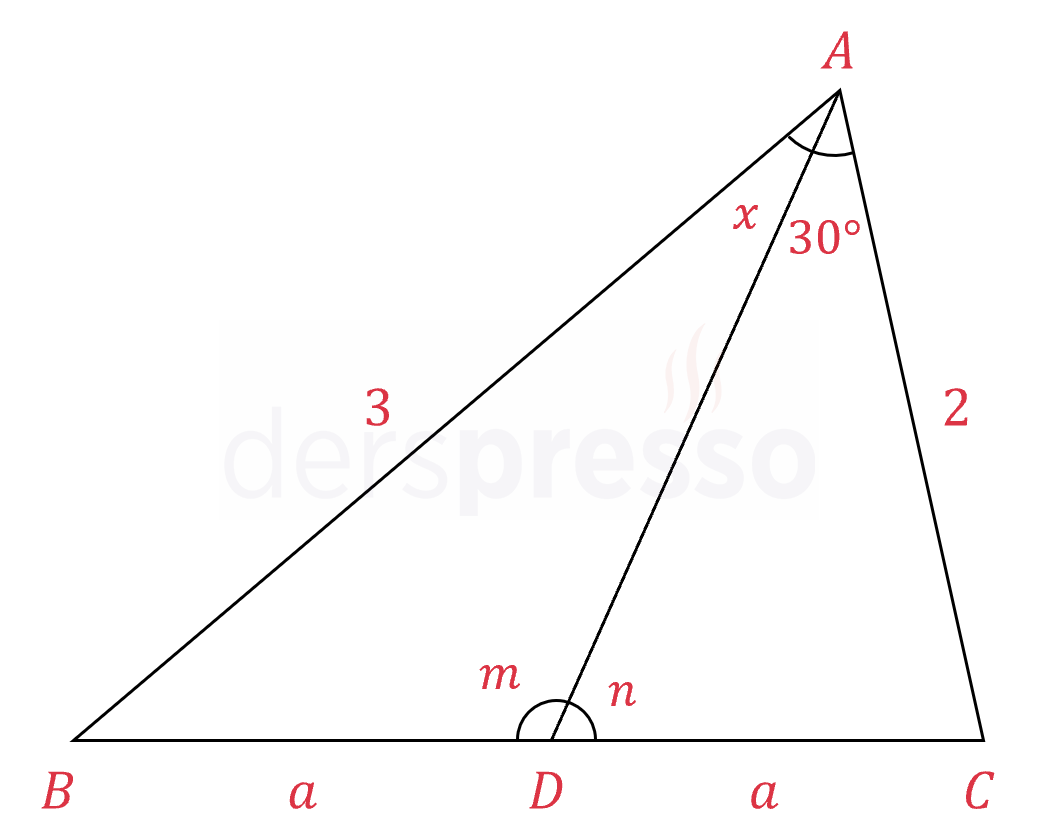
Yukarıda \( ABC \) üçgeni verilmiştir.
\( \abs{AB} = 3, \quad \abs{AC} = 2 \)
\( \abs{BD} = \abs{DC} = a \)
\( m(\widehat{BAD}) = x \)
\( m(\widehat{DAC}) = 30° \)
olduğuna göre, \( \sin{x} \) değerini bulunuz.
Çözümü Göster\( ABD \) üçgenine sinüs teoremini uygulayalım.
\( \dfrac{\abs{BD}}{\sin{x}} = \dfrac{\abs{AB}}{\sin{m}} \)
\( \dfrac{a}{\sin{x}} = \dfrac{3}{\sin{m}} \)
\( \sin{m} = \dfrac{3\sin{x}}{a} \)
\( ACD \) üçgenine sinüs teoremini uygulayalım.
\( \dfrac{\abs{DC}}{\sin{30°}} = \dfrac{\abs{AC}}{\sin{n}} \)
\( \dfrac{a}{\frac{1}{2}} = \dfrac{2}{\sin{n}} \)
\( \sin{n} = \dfrac{1}{a} \)
\( m \) ve \( n \) açıları bütünler açılar oldukları için sinüs değerleri birbirine eşittir.
\( \sin{m} = \sin{n} \)
\( \dfrac{3\sin{x}}{a} = \dfrac{1}{a} \)
\( \sin{x} = \dfrac{1}{3} \) bulunur.

Yukarıda birer kenarı ortak düzgün bir altıgen ve kare verilmiştir.
\( \abs{GH} = 6 \)
olduğuna göre, \( GAF \) üçgeninin alanı kaç birimkaredir?
Çözümü GösterDüzgün \( n \) kenarlı çokgenin bir iç açısının ölçüsü \( = \dfrac{(n - 2) \cdot 180°}{n} \)
Düzgün altıgenin bir iç açısının ölçüsü \( = \dfrac{(6 - 2) \cdot 180°}{6} = 120° \)

\( m(\widehat{BAF}) = 120° \)
Karenin bir köşe açısı 90°'dir.
\( \widehat{GAF} \) açısının ölçüsünü bulalım.
\( m(\widehat{GAF}) = 360° - 120° - 90° = 150° \)
\( GAF \) ikizkenar üçgeninin alanını sinüs teoremi ile bulalım.
\( A(GAF) = \dfrac{1}{2} \cdot 6 \cdot 6\sin{150°} \)
\( = 18 \cdot \dfrac{1}{2} = 9 \) bulunur.

\( ABCD \) bir dik yamuktur.
\( \abs{CB} = 4, \quad \abs{CD} = 6 \)
\( m(\widehat{ACB}) = x, \quad \cos{x} = \dfrac{\sqrt{5}}{3} \)
olduğuna göre, \( \abs{BD} = a \) kaç birimdir?
Çözümü Göster\( m(\widehat{ACD}) = 90° \) olduğu için \( m(\widehat{BCD}) = 90° - x \) olur.
\( BCD \) üçgenine kosinüs teoremi uygulayalım.
\( a^2 = 4^2 + 6^2 - 2 \cdot 4 \cdot 6\cos(90° - x) \)
\( a^2 = 52 - 48\cos(90° - x) \)
Tümler açıların sinüs ve kosinüs değerleri birbirine eşittir.
\( \cos(90° - x) = \sin{x} \)
\( = 52 - 48\sin{x} \)
\( \cos{x} = \frac{\sqrt{5}}{3} \) olduğuna göre, bir dik üçgende \( x \) açısının komşu kenarına \( \sqrt{5}k \) ve hipotenüse \( 3k \) dersek karşı kenar \( 2k \) olur.
\( \sin{x} = \dfrac{2k}{3k} = \dfrac{2}{3} \)
\( a^2 = 52 - 48 \cdot \dfrac{2}{3} = 20 \)
\( a = 2\sqrt{5} \) birim bulunur.

Şekilde \( ABC \) üçgeni verilmiştir.
\( 3\abs{AD} = 5\abs{DB}, \quad 3\abs{AE} = 2\abs{EC} \)
olduğuna göre, \( BCED \) dörtgeninin alanının \( ADE \) üçgeninin alanına oranı kaçtır?
Çözümü Göster\( \abs{AD} = 5a \) ve \( \abs{DB} = 3a \) diyelim.
\( \abs{AE} = 2b \) ve \( \abs{EC} = 3b \) diyelim.

Sinüs alan formülünü kullanarak \( ADE \) üçgeninin alanını bulalım.
\( A(ADE) = \dfrac{1}{2} \cdot 5a \cdot 2b \cdot \sin{x} \)
\( = 5ab\sin{x} \)
Sinüs alan formülünü kullanarak \( ABC \) üçgeninin alanını bulalım.
\( A(ABC) = \dfrac{1}{2} \cdot 8a \cdot 5b \cdot \sin{x} \)
\( = 20ab\sin{x} \)
\( BCED \) dörtgeninin alanını bulmak için iki üçgenin alanlarının farkını alalım.
\( A(BCED) = A(ABC) - A(ADE) \)
\( = 20ab\sin{x} - 5ab\sin{x} = 15ab\sin{x} \)
\( BCED \) dörtgeninin alanının \( ADE \) üçgeninin alanına oranını alalım.
\( \dfrac{A(BCED)}{A(ADE)} = \dfrac{15ab\sin{x}}{5ab\sin{x}} = 3 \) bulunur.
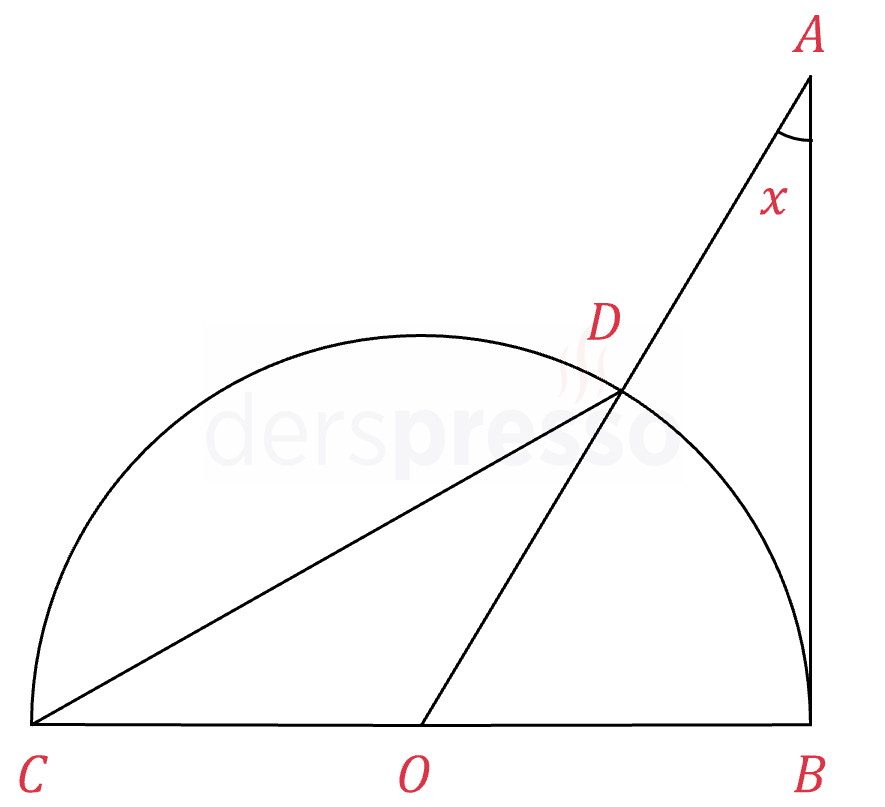
\( [AB] \) doğru parçası, \( O \) merkezli ve yarıçapı 2 birim olan çembere \( B \) noktasına teğettir.
\( \sin{x} = \dfrac{2\sqrt{6}}{5} \)
olduğuna göre, \( COD \) üçgeninin alanı kaç birimkaredir?
Çözümü Göster\( [AB] \) doğru parçası çembere teğet olduğuna göre oluşan \( \widehat{ABO} \) açısı dik açıdır.
\( m(\widehat{ABO}) = 90° \)
\( m(\widehat{AOB}) = 90° - x \)
\( m(\widehat{COD}) = 90° + x \)
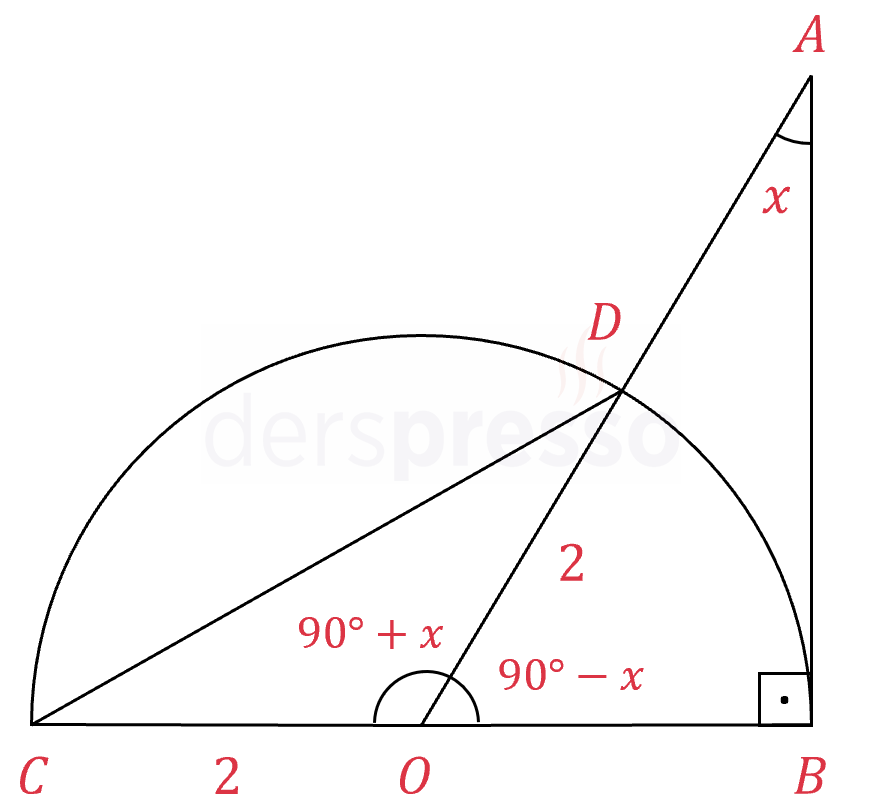
\( COD \) üçgeninin alanını bulmak için sinüs teoremini kullanalım.
\( A(COD) = \dfrac{1}{2}\abs{CO}\abs{OD}\sin(90° + x) \)
\( \sin(90° + x) = \cos{x} \)
\( \sin{x} = \frac{2\sqrt{6}}{5} \) olduğuna göre, bir dik üçgende \( x \) açısının karşı kenarına \( 2\sqrt{6}k \), hipotenüse \( 5k \) dersek komşu kenar Pisagor teoreminden \( k \) olarak bulunur.
\( \cos{x} = \dfrac{k}{5k} = \dfrac{1}{5} \)
\( A(COD) = \dfrac{1}{2} \cdot 2 \cdot 2 \cdot \dfrac{1}{5} \)
\( = \dfrac{2}{5} \) bulunur.

Yukarıda bir dik kare piramit verilmiştir.
\( \abs{AC} = \abs{EC} = 4 \)
\( [DE] \perp [BA] \)
\( m(\widehat{BAC}) = x \) olduğuna göre, \( \cos{x} \) kaçtır?
Çözümü GösterPiramit dik olduğu için yan kenar uzunlukları eşittir.
\( \abs{AD} = \abs{AE} = \abs{AC} = 4 \)
\( ADE \) üçgeni ikizkenar olduğu için tabana ait yükseklik tabanı ortalar.
\( \abs{DB} = \abs{BE} = 2 \)
Bu uzunlukları şekil üzerinde işaretleyelim.
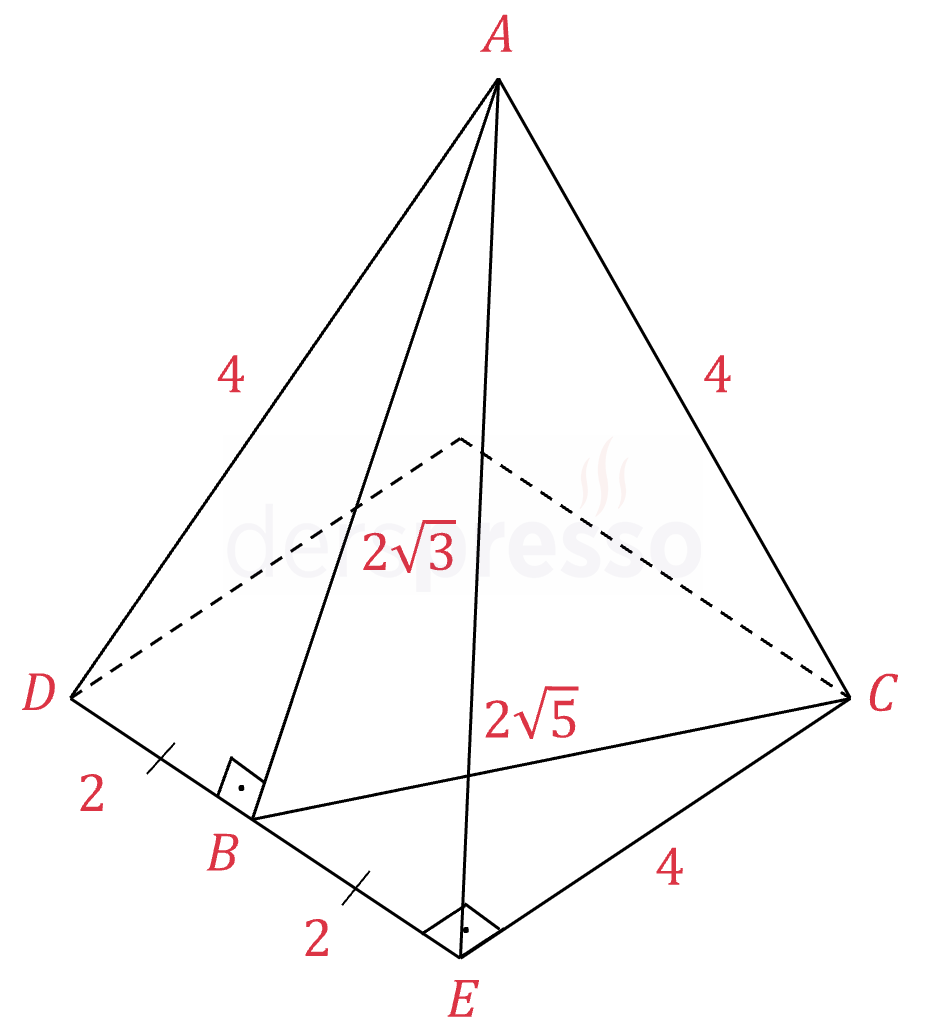
Prizmanın tabanı karedir.
\( [DE] \perp [EC] \)
\( [BC] \) kenarı \( BEC \) dik üçgeninin hipotenüsüdür.
\( \abs{BC}^2 = \abs{BE}^2 + \abs{EC}^2 \)
\( \abs{BC}^2 = 2^2 + 4^2 \)
\( \abs{BC} = 2\sqrt{5} \)
\( [BA] \) yüksekliği \( DBA \) dik üçgeninin bir dik kenarıdır.
\( \abs{DA}^2 = \abs{DB}^2 + \abs{BA}^2 \)
\( 4^2 = 2^2 + \abs{BA}^2 \)
\( \abs{BA} = 2\sqrt{3} \)
\( BAC \) üçgeninde kosinüs teoremini uygulayalım.
\( (2\sqrt{5})^2 = 4^2 + (2\sqrt{3})^2 - 2 \cdot 4 \cdot 2\sqrt{3}\cos{x} \)
\( 20 = 16 + 12 - 16\sqrt{3}\cos{x} \)
\( -8 = -16\sqrt{3}\cos{x} \)
\( \cos{x} = \dfrac{1}{2\sqrt{3}} = \dfrac{\sqrt{3}}{6} \) bulunur.

Yukarıdaki şekildeki \( ABCD \) bir karedir.
\( \abs{EB} = 2\abs{AE}, \quad \abs{BF} = \abs{FC} \)
olduğuna göre, \( \tan{x} \) kaçtır?
Çözümü Göster1. yöntem: Kosinüs teoremi
\( E \) ve \( F \) noktalarını birleştirelim.
Karenin bir kenar uzunluğuna 6 birim diyelim.
\( \abs{AE} = 2 \)
\( \abs{EB} = 4 \)
\( \abs{BF} = \abs{FC} = 3 \)
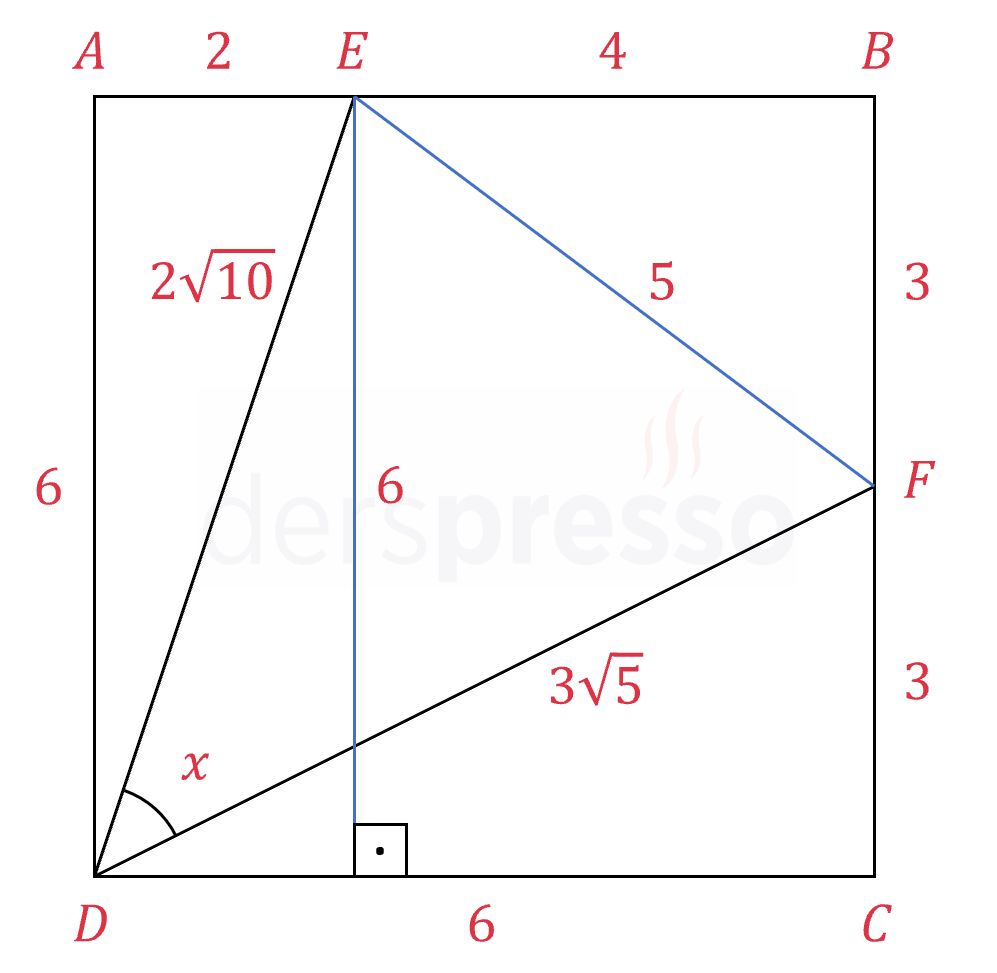
Pisagor teoremi ile \( [DE] \) uzunluğunu bulalım.
\( \abs{DE} = \sqrt{6^2 + 2^2} = 2\sqrt{10} \)
Pisagor teoremi ile \( [DF] \) uzunluğunu bulalım.
\( \abs{DF} = \sqrt{6^2 + 3^2} = 3\sqrt{5} \)
Pisagor teoremi ile \( [EF] \) uzunluğunu bulalım.
\( \abs{EF} = \sqrt{3^2 + 4^2} = 5 \)
\( DEF \) üçgenine kosinüs teoremini uygulayalım.
\( 5^2 = (2\sqrt{10})^2 + (3\sqrt{5})^2 - 2 \cdot 2\sqrt{10} \cdot 3\sqrt{5}\cos{x} \)
\( 25 = 40 + 45 - 60\sqrt{2}\cos{x} \)
\( \cos{x} = \dfrac{1}{\sqrt{2}} = \dfrac{\sqrt{2}}{2} \)
Kosinüs değeri \( \frac{\sqrt{2}}{2} \) olan dar açı 45°'dir.
\( \tan{45°} = 1 \) bulunur.
2. yöntem: Tanjant fark formülü
\( E \) noktasından karenin tabanına bir dikme çizelim.
Aşağıdaki iki açıyı tanımlayalım.
\( m(\widehat{EDC}) = y \)
\( m(\widehat{FDC}) = z \)
\( x \) açısını bu iki açının farkı şeklinde yazalım.
\( x = y - z \)
İki tarafın tanjantını alalım.
\( \tan{x} = \tan(y - z) \)
Tanjant fark formülünü kullanalım.
\( = \dfrac{\tan{y} - \tan{z}}{1 + \tan{y}\tan{z}} \)
Şekilde oluşan üçgenleri kullanarak trigonometrik değerleri yerine koyalım.
\( = \dfrac{\frac{6}{2} - \frac{3}{6}}{1 + \frac{6}{2} \cdot \frac{3}{6}} \)
\( = \dfrac{\frac{15}{6}}{1 + \frac{3}{2}} \)
\( = 1 \) bulunur.