Trigonometrik Fonksiyonların Tanım ve Görüntü Kümesi
Trigonometrik fonksiyonların tanım ve görüntü kümelerini aşağıdaki gibi özetleyebiliriz:
| Fonksiyon | Tanım Kümesi | Görüntü Kümesi |
|---|---|---|
|
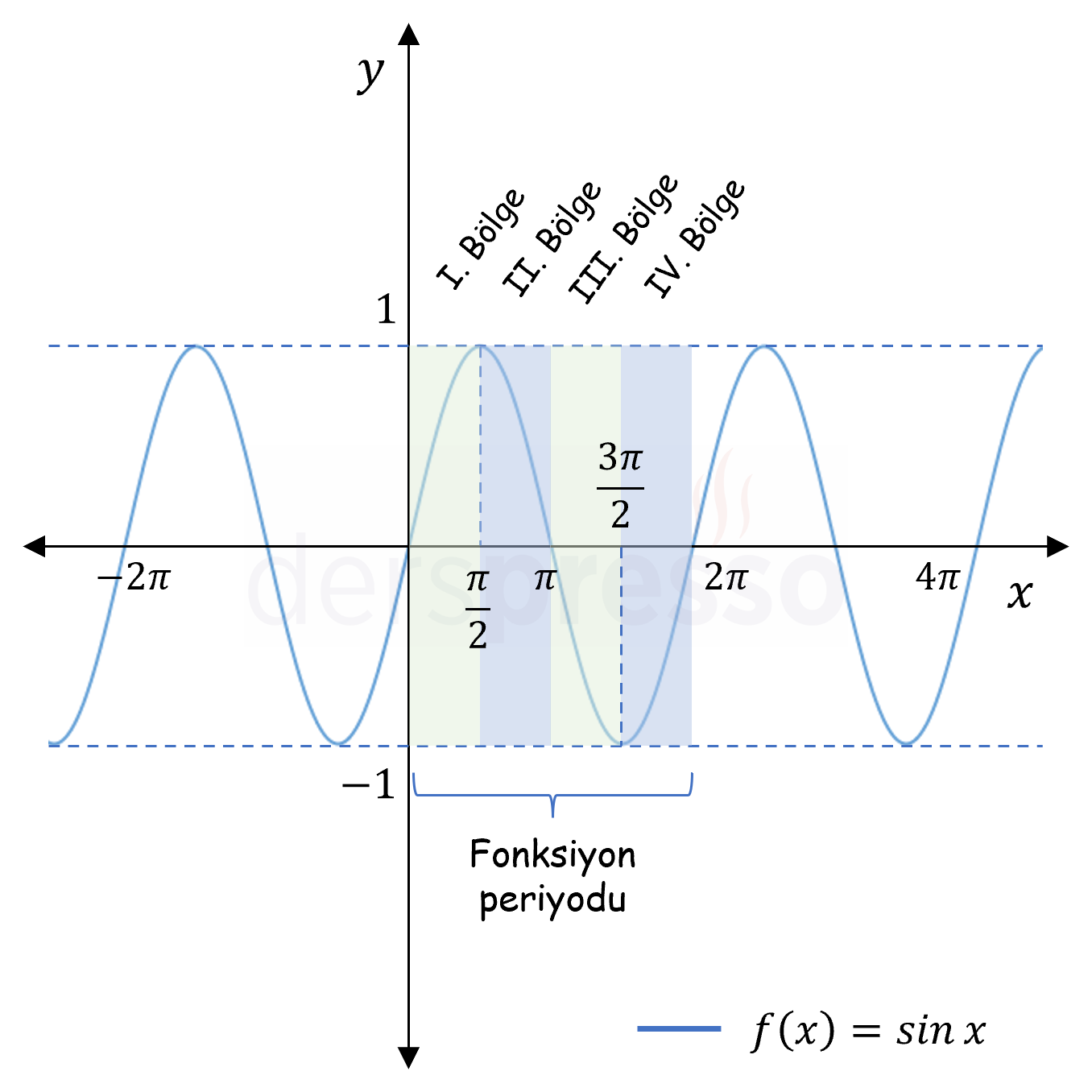
\( \sin{x} \) Grafik |
\( \mathbb{R} \) | \( [-1, 1] \) |
|
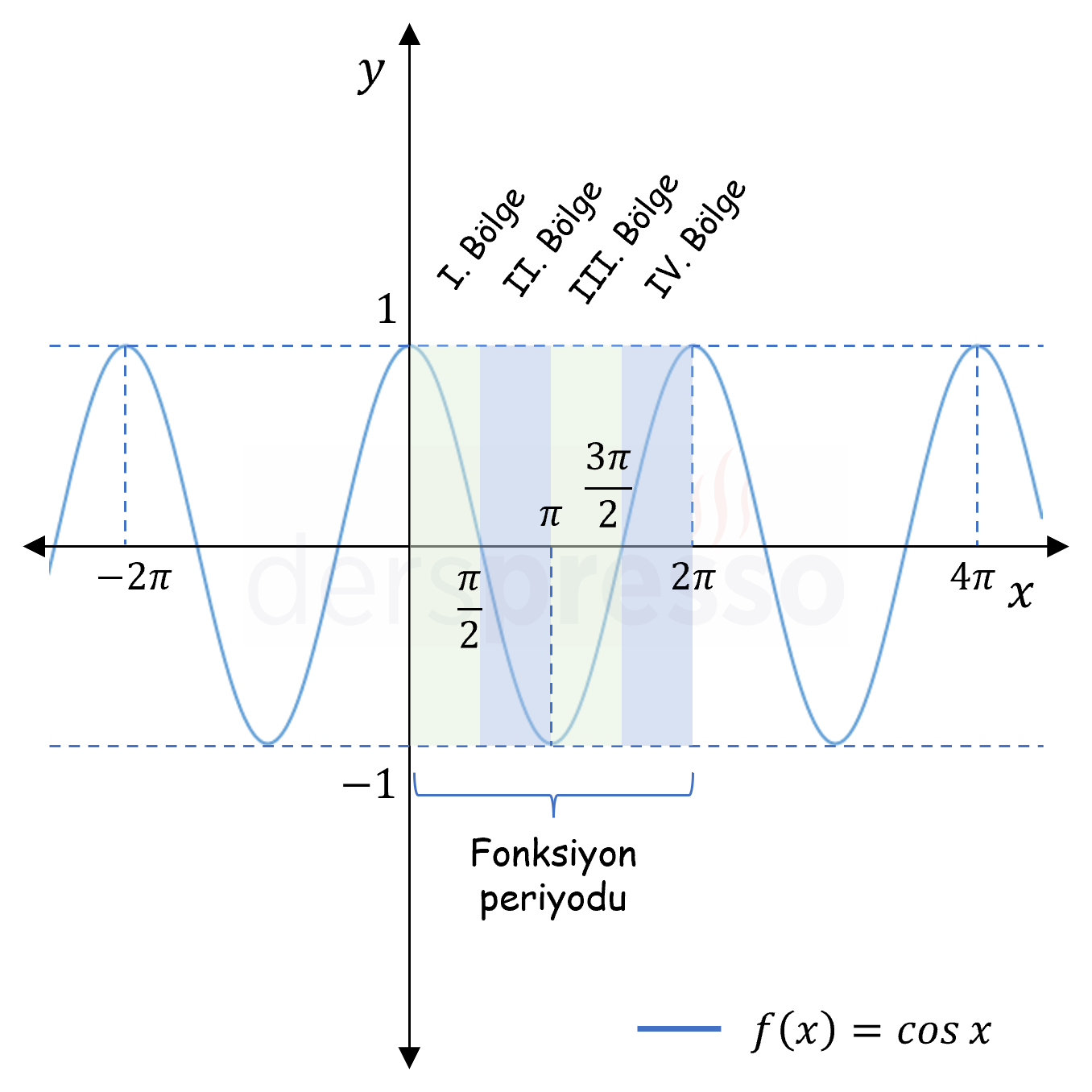
\( \cos{x} \) Grafik |
\( \mathbb{R} \) | \( [-1, 1] \) |
|
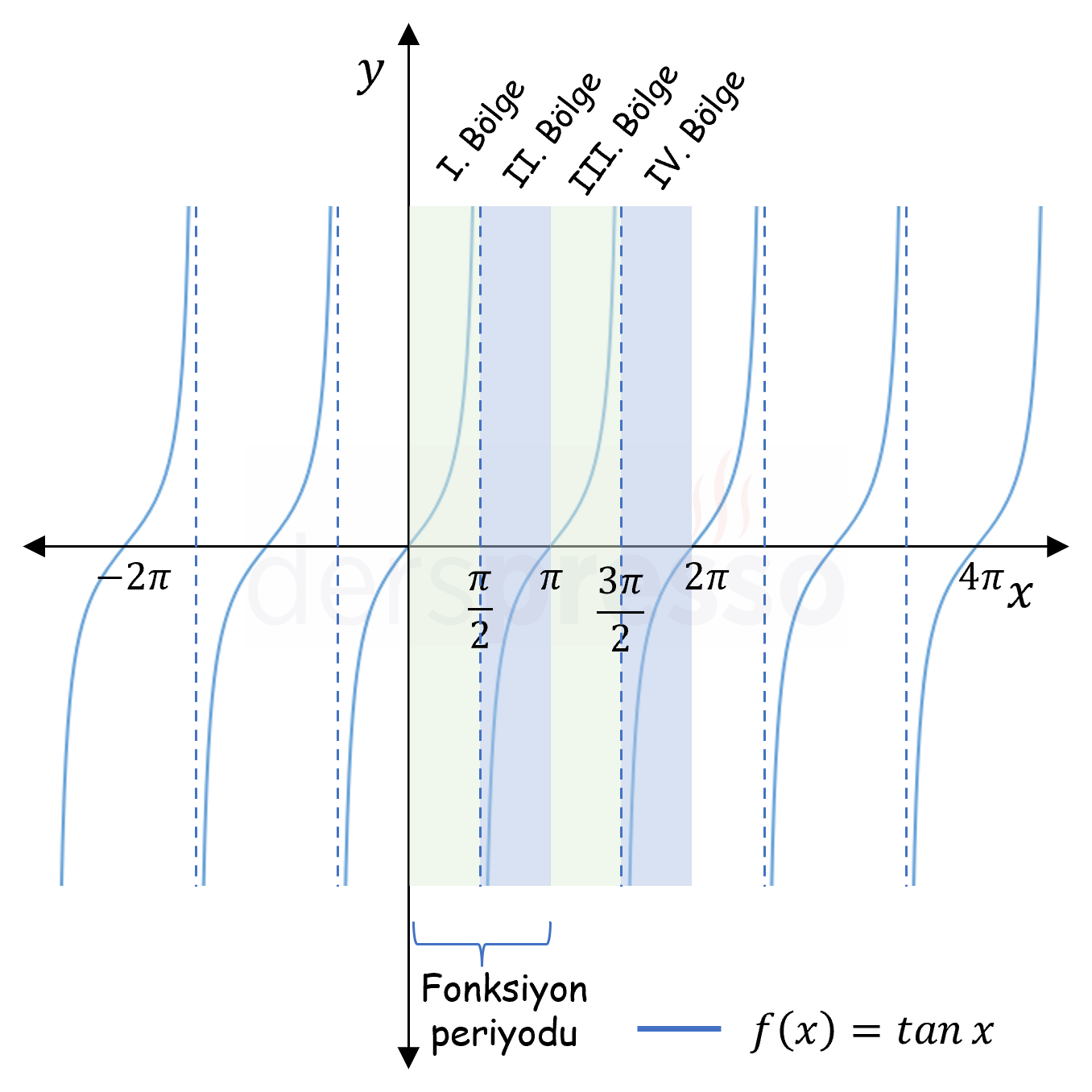
\( \tan{x} \) Grafik |
\( \mathbb{R} - \{ \frac{\pi}{2} + k\pi, k \in \mathbb{Z} \} \) | \( \mathbb{R} \) |
|
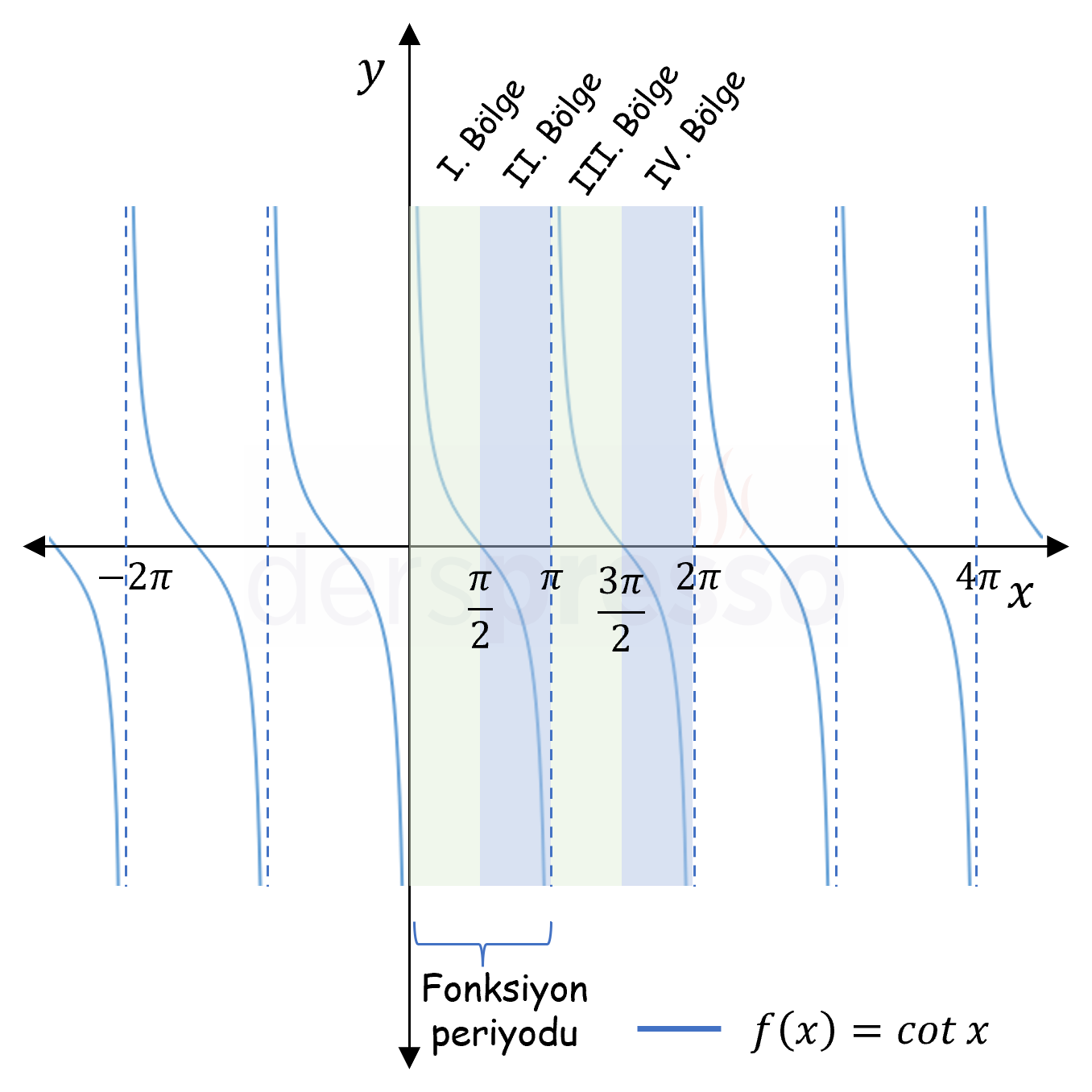
\( \cot{x} \) Grafik |
\( \mathbb{R} - \{ k\pi, k \in \mathbb{Z} \} \) | \( \mathbb{R} \) |
|
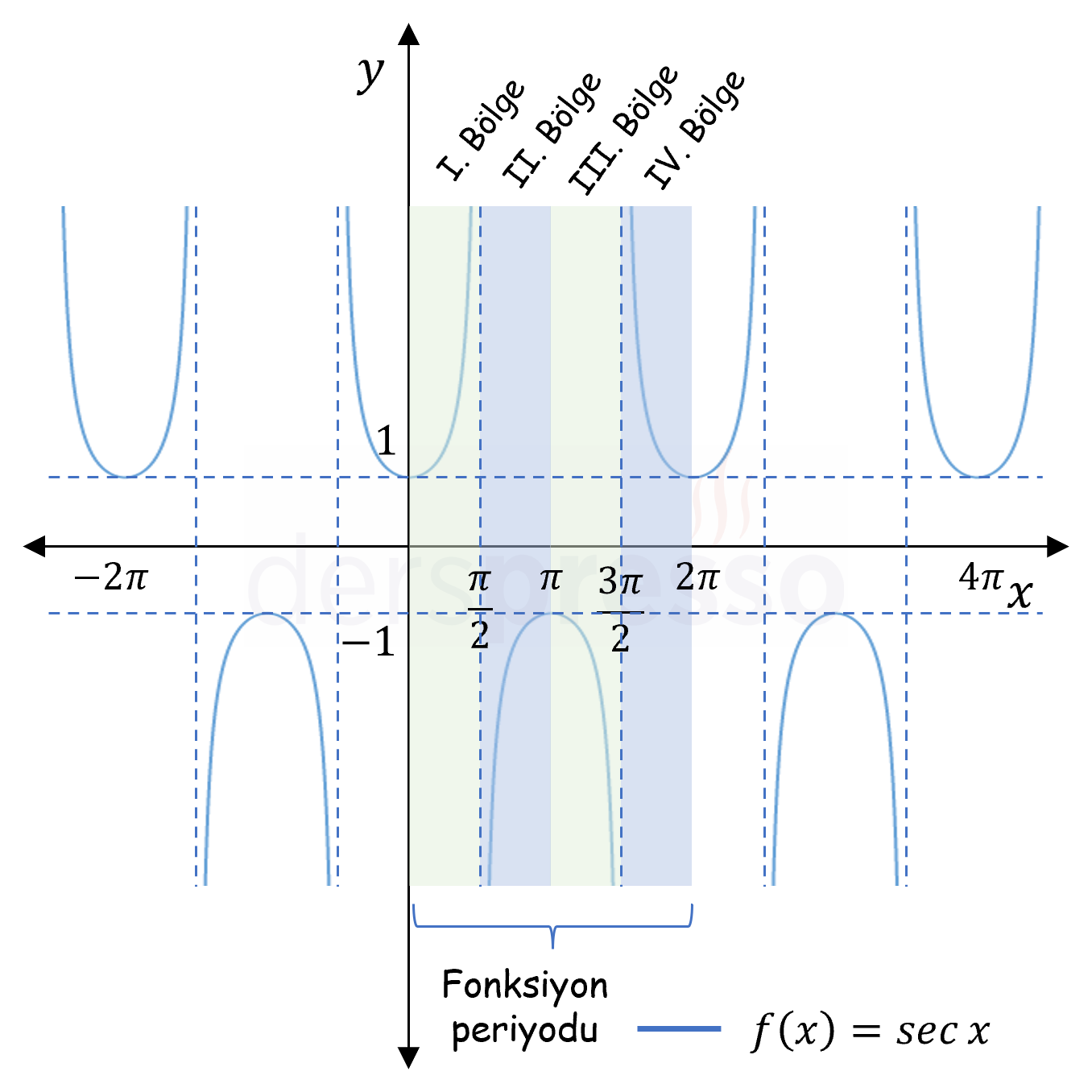
\( \sec{x} \) Grafik |
\( \mathbb{R} - \{ \frac{\pi}{2} + k\pi, k \in \mathbb{Z} \} \) | \( \mathbb{R} - (-1, 1) \) |
|
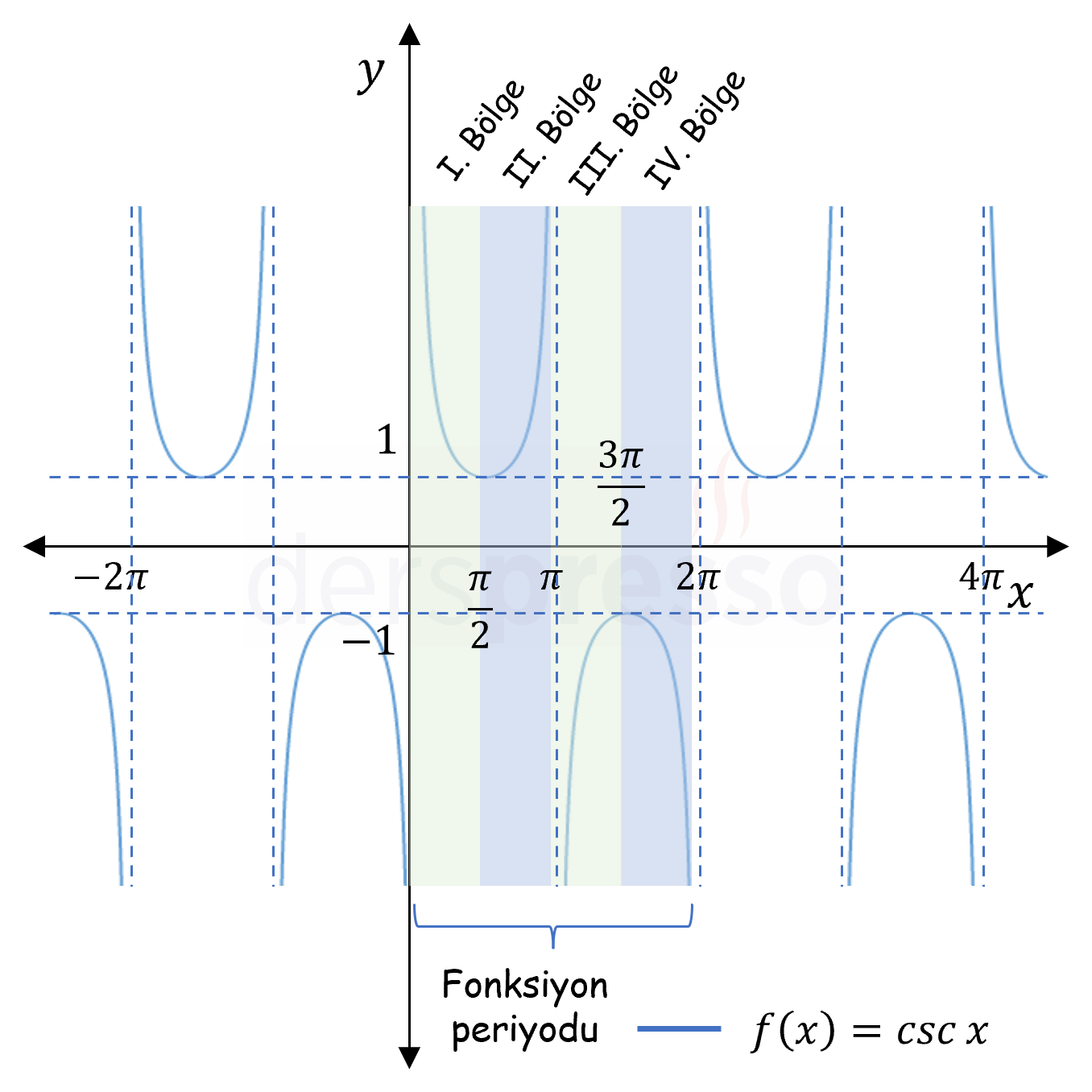
\( \csc{x} \) Grafik |
\( \mathbb{R} - \{ k\pi, k \in \mathbb{Z} \} \) | \( \mathbb{R} - (-1, 1) \) |
Burada vurgulayabileceğimiz birkaç nokta şunlardır:
- Trigonometrik fonksiyonlar periyodik fonksiyonlar oldukları için, tanım kümeleri sadece \( [0 - 2\pi) \) aralığını değil tanımsız oldukları değerler hariç tüm reel sayıları kapsar.
- Tanjant, kotanjant, sekant ve kosekant fonksiyonlarının tanımsız oldukları değerler fonksiyonun her periyodunda tekrar eder.
SORU:
\( 2A - 3 \cos{x} + 4 = 0 \) olmak üzere, \( A \)'nın değer aralığı nedir?
Çözümü Göster
« Önceki
Trigonometrik Fonksiyonların Grafiklerinin Periyodu
Sonraki »
Toplam, Fark ve İki Kat Açı Formülleri