Trigonometrik Fonksiyonların Grafikleri
Bu bölümde altı trigonometrik fonksiyonun grafiklerini ve periyotlarını inceleyeceğiz.
Sinüs Fonksiyon Grafiği
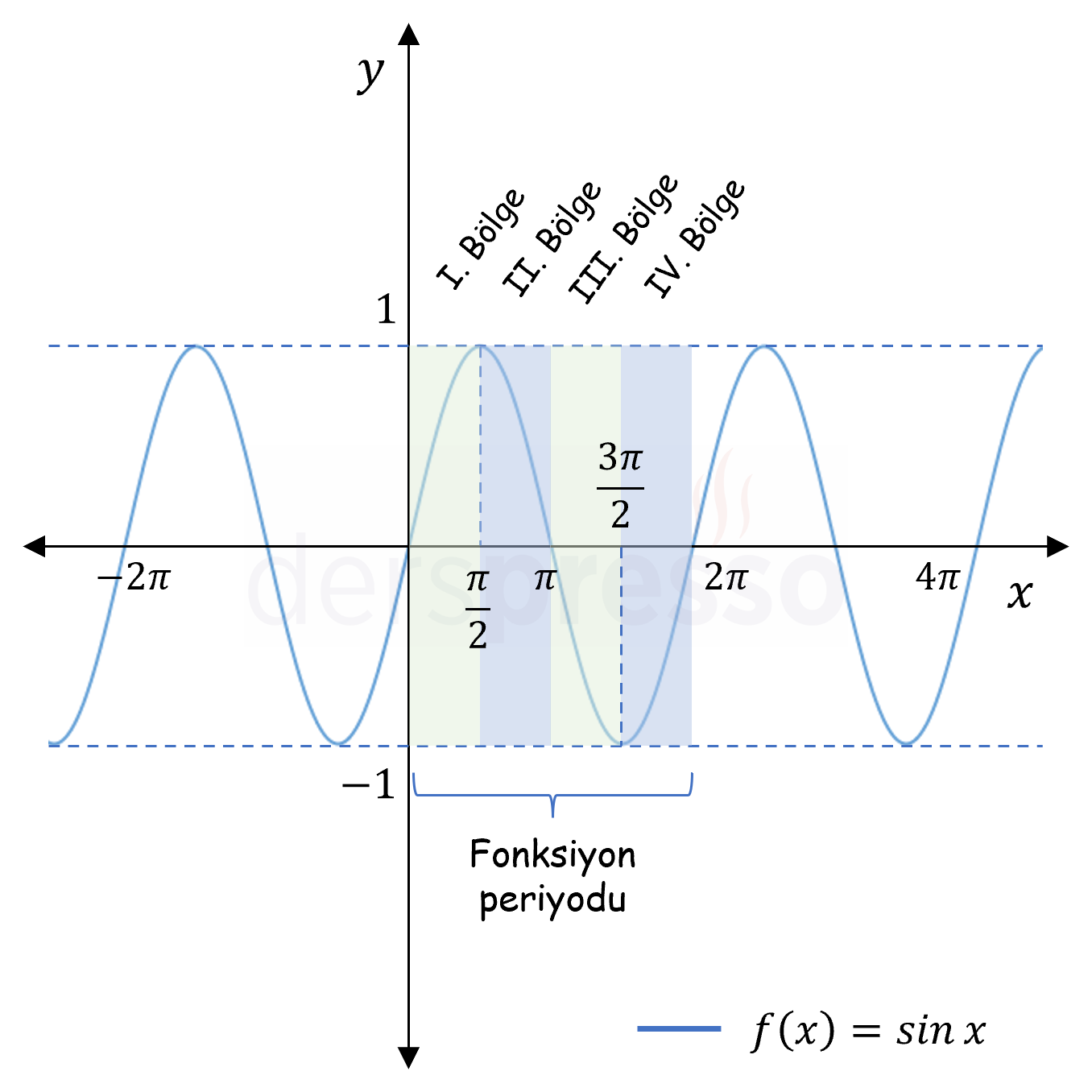
Yukarıdaki şekildeki sinüs fonksiyon grafiği ile ilgili önemli bazı noktalar aşağıdaki gibidir.
- Sık kullanılan bazı açıların sinüs değerleri bu grafik üzerinde teyit edilebilir (\( \sin{0} = \sin{\pi} = 0 \); \( \sin{\frac{\pi}{2}} = 1 \); \( \sin{\frac{3\pi}{2}} = -1 \)).
- Sinüs fonksiyonunun her bölgedeki işareti de bu grafik üzerinde teyit edilebilir (I. ve II. bölgelerde pozitif, III. ve IV. bölgelerde negatif).
- Sinüs fonksiyonunun grafiği her \( 2\pi \) radyanda bir kendini tekrarladığı için periyodu \( 2\pi \) radyandır.
- Sinüs fonksiyonunun tanımsız olduğu bir \( x \) değeri olmadığı için tanım kümesi tüm reel sayılardır.
- Sinüs fonksiyonunun görüntü kümesi \( [-1, 1] \) aralığıdır.
- Sinüs fonksiyonu \( \sin(-x) = -\sin{x} \) eşitliği sağlandığı için bir tek fonksiyondur ve grafiği orijine göre simetriktir.
| Fonksiyon | Tanım Kümesi | Görüntü Kümesi |
|---|---|---|
| \( \sin{x} \) | \( \mathbb{R} \) | \( [-1, 1] \) |
Kosinüs Fonksiyon Grafiği
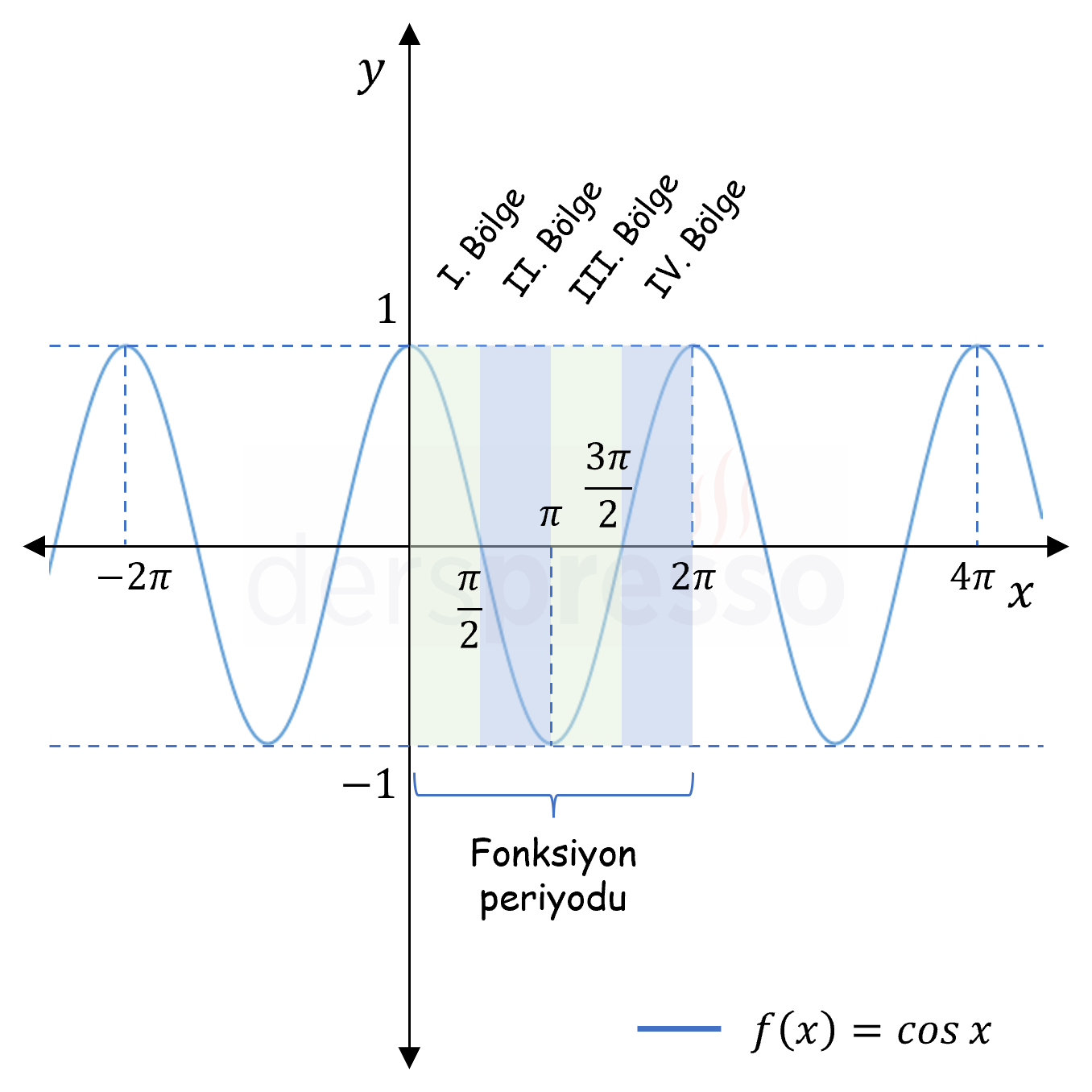
Yukarıdaki şekildeki kosinüs fonksiyon grafiği ile ilgili önemli bazı noktalar aşağıdaki gibidir.
- Sık kullanılan bazı açıların kosinüs değerleri bu grafik üzerinde teyit edilebilir (\( \cos{0} = 1 \); \( \cos{\frac{\pi}{2}} = \cos{\frac{3\pi}{2}} = 0 \); \( \cos{\pi} = -1 \)).
- Kosinüs fonksiyonunun her bölgedeki işareti de bu grafik üzerinde teyit edilebilir (I. ve IV. bölgelerde pozitif, II. ve III. bölgelerde negatif).
- Kosinüs fonksiyonunun grafiği her \( 2\pi \) radyanda bir kendini tekrarladığı için periyodu \( 2\pi \) radyandır.
- Kosinüs fonksiyonunun tanımsız olduğu bir \( x \) değeri olmadığı için tanım kümesi tüm reel sayılardır.
- Kosinüs fonksiyonunun görüntü kümesi \( [-1, 1] \) aralığıdır.
- Kosinüs fonksiyonu \( \cos(-x) = \cos{x} \) eşitliği sağlandığı için bir çift fonksiyondur ve grafiği \( y \) eksenine göre simetriktir.
| Fonksiyon | Tanım Kümesi | Görüntü Kümesi |
|---|---|---|
| \( \cos{x} \) | \( \mathbb{R} \) | \( [-1, 1] \) |
Aşağıdaki şekilde sinüs ve kosinüs fonksiyon grafikleri birlikte verilmiştir. Görülebileceği gibi, kosinüs grafiği \( \frac{\pi}{2} \) birim sağa ötelenerek sinüs grafiği elde edilebilir. Bu durum temel özdeşlikler bölümünde gördüğümüz iki fonksiyon arasındaki tümler açı özdeşliği ile de tutarlıdır.
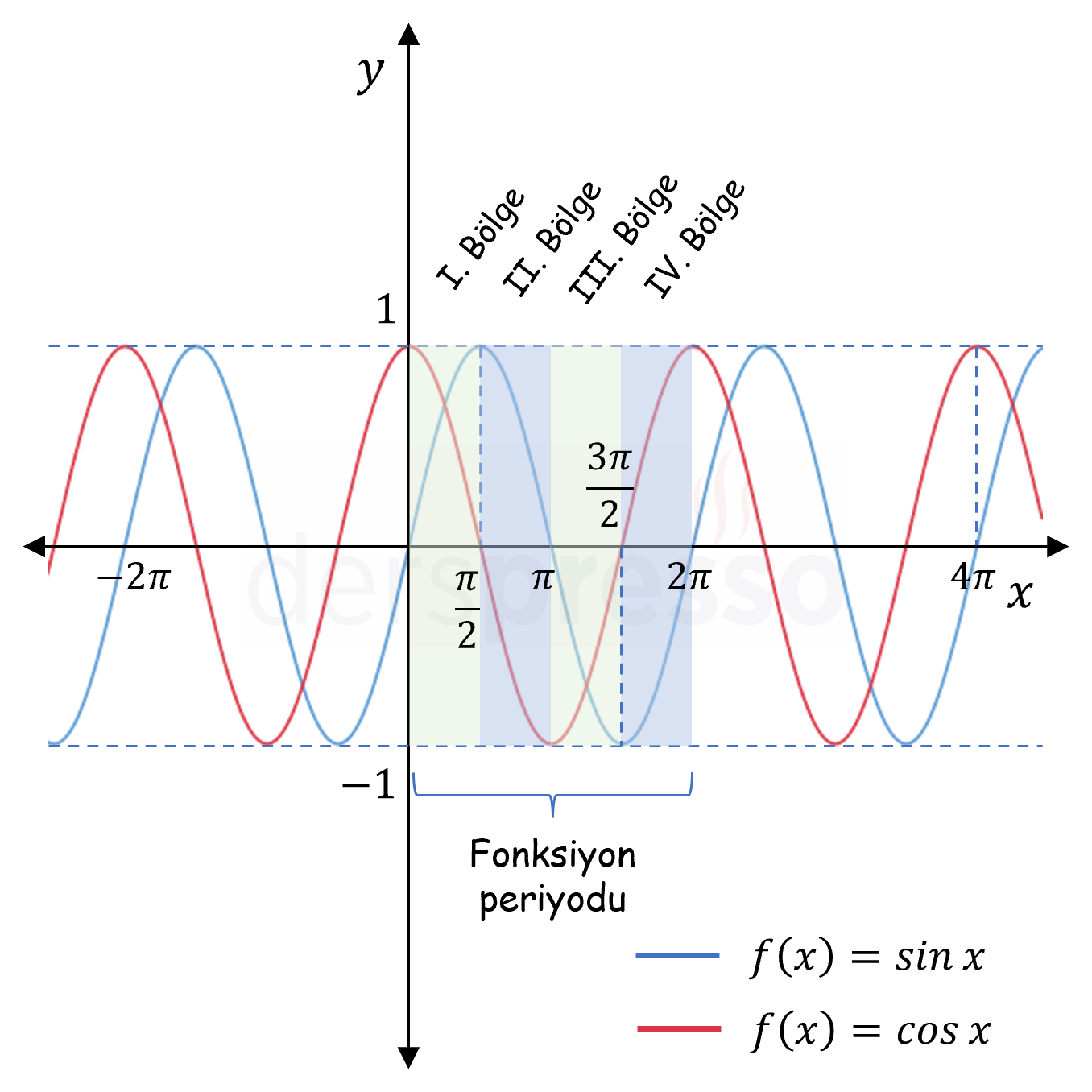
\( \sin{x} = \cos(x - \frac{\pi}{2}) = \cos(\frac{\pi}{2} - x) \)
Tanjant Fonksiyon Grafiği
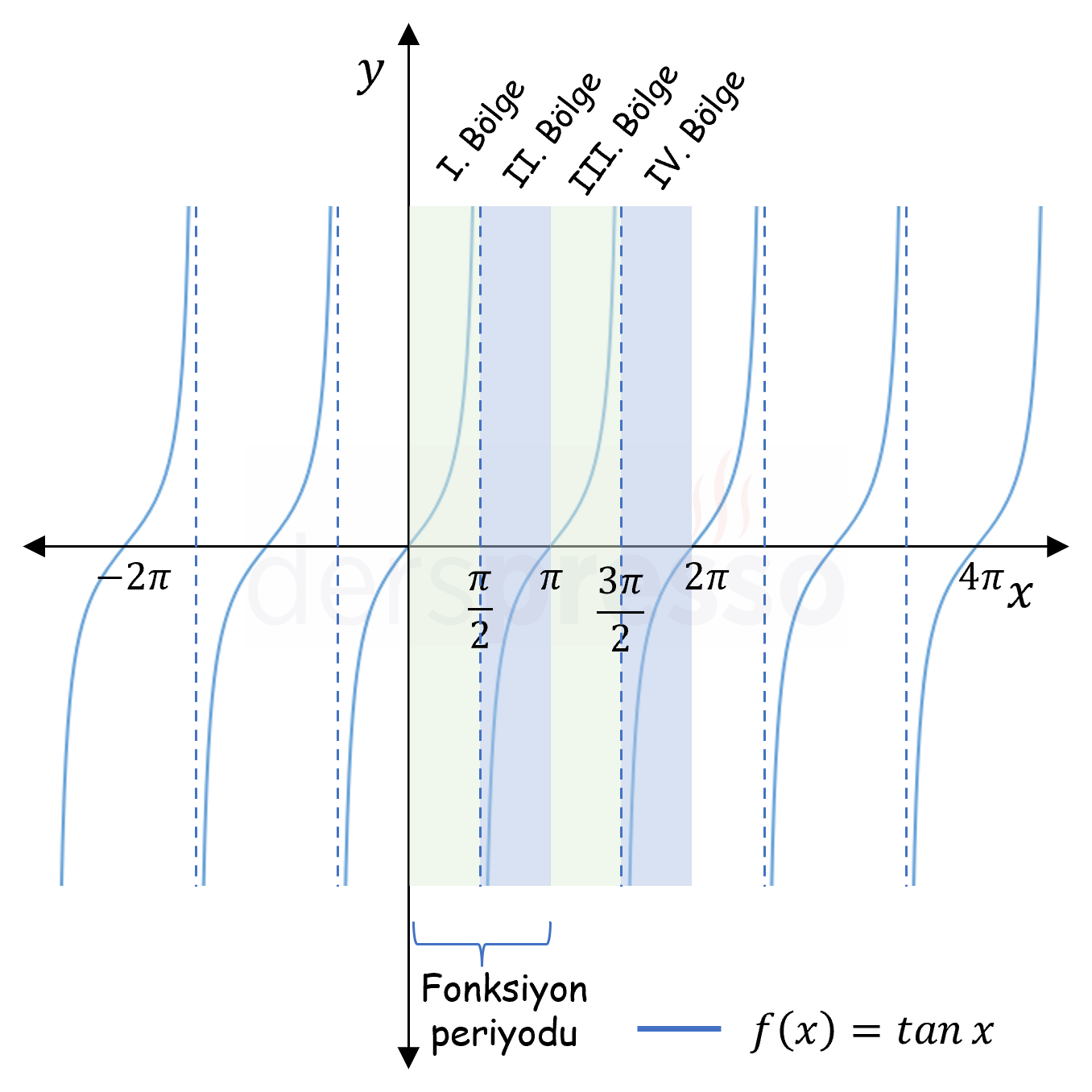
Yukarıdaki şekildeki tanjant fonksiyon grafiği ile ilgili önemli bazı noktalar aşağıdaki gibidir.
- Sık kullanılan bazı açıların tanjant değerleri bu grafik üzerinde teyit edilebilir (\( \tan{0} = 0 \); \( \tan(-\frac{\pi}{2}) = \tan{\frac{\pi}{2}} = \) Tanımsız).
- Tanjant fonksiyonunun her bölgedeki işareti de bu grafik üzerinde teyit edilebilir (I. ve III. bölgelerde pozitif, II. ve IV. bölgelerde negatif).
- Tanjant fonksiyonunun grafiği her \( \pi \) radyanda bir kendini tekrarladığı için periyodu \( \pi \) radyandır.
- Tanjant fonksiyonu \( x \in \{\frac{\pi}{2}, \frac{3\pi}{2}, \frac{5\pi}{2}, \ldots\} \) değerleri için tanımsız olduğu için tanım kümesi bu değerler hariç tüm reel sayılardır.
- Tanjant fonksiyonunun görüntü kümesi tüm reel sayılardır.
- Tanjant fonksiyonu \( \tan(-x) = -\tan{x} \) eşitliği sağlandığı için bir tek fonksiyondur ve grafiği orijine göre simetriktir.
| Fonksiyon | Tanım Kümesi | Görüntü Kümesi |
|---|---|---|
| \( \tan{x} \) | \( \mathbb{R} - \{ \frac{\pi}{2} + k\pi, k \in \mathbb{Z} \} \) | \( \mathbb{R} \) |
Kotanjant Fonksiyon Grafiği
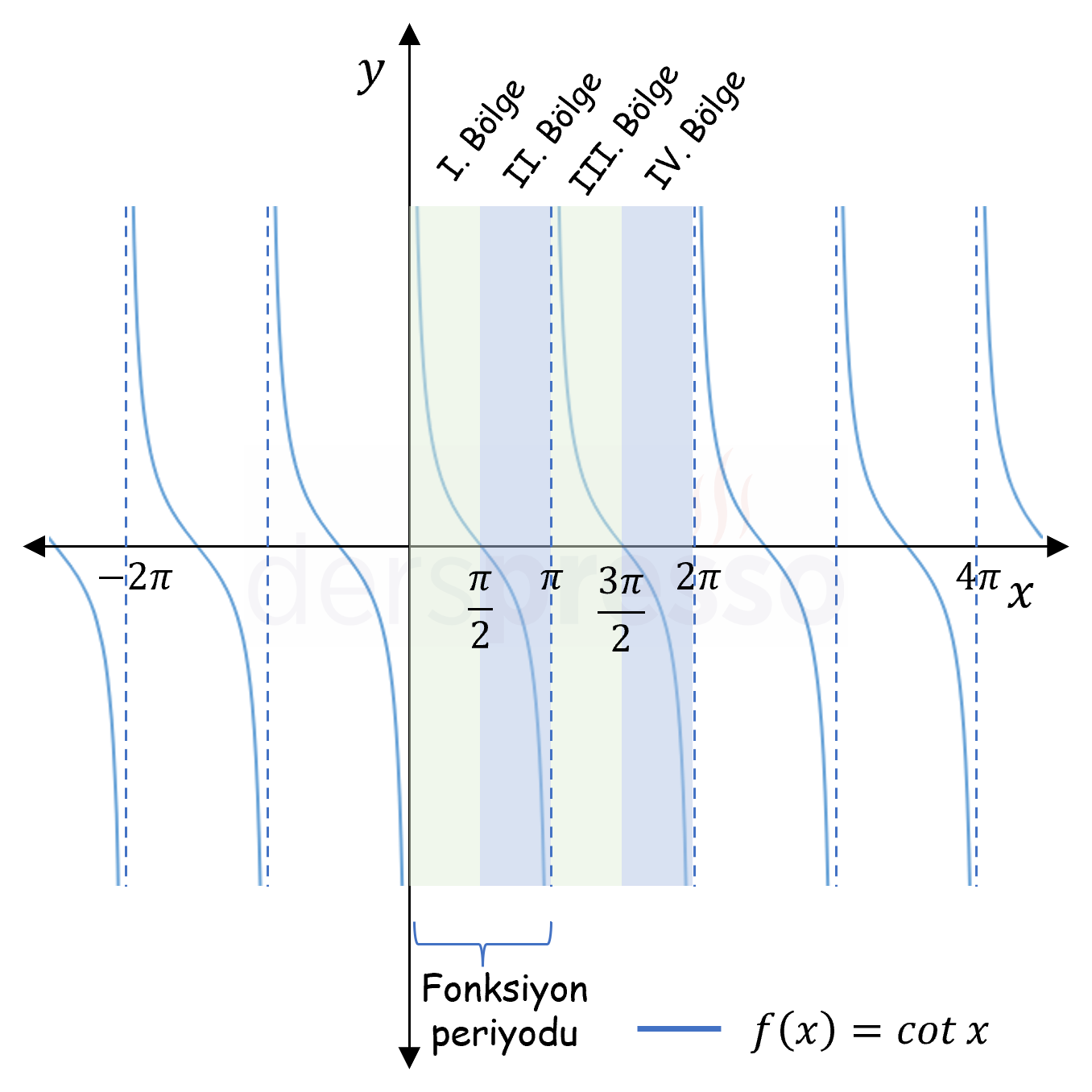
Yukarıdaki şekildeki kotanjant fonksiyon grafiği ile ilgili önemli bazı noktalar aşağıdaki gibidir.
- Sık kullanılan bazı açıların kotanjant değerleri bu grafik üzerinde teyit edilebilir (\( \cot{\frac{\pi}{2}} = 0 \); \( \cot{0} = \cot{\pi} = \) Tanımsız).
- Kotanjant fonksiyonunun her bölgedeki işareti de bu grafik üzerinde teyit edilebilir (I. ve III. bölgelerde pozitif, II. ve IV. bölgelerde negatif).
- Kotanjant fonksiyonunun grafiği her \( \pi \) radyanda bir kendini tekrarladığı için periyodu \( \pi \) radyandır.
- Kotanjant fonksiyonu \( x \in \{0, \pi, 2\pi, \ldots\} \) değerleri için tanımsız olduğu için tanım kümesi bu değerler hariç tüm reel sayılardır.
- Kotanjant fonksiyonunun görüntü kümesi tüm reel sayılardır.
- Kotanjant fonksiyonu \( \cot(-x) = -\cot{x} \) eşitliği sağlandığı için bir tek fonksiyondur ve grafiği orijine göre simetriktir.
| Fonksiyon | Tanım Kümesi | Görüntü Kümesi |
|---|---|---|
| \( \cot{x} \) | \( \mathbb{R} - \{ k\pi, k \in \mathbb{Z} \} \) | \( \mathbb{R} \) |
Aşağıdaki şekilde tanjant ve kotanjant fonksiyon grafikleri birlikte verilmiştir.
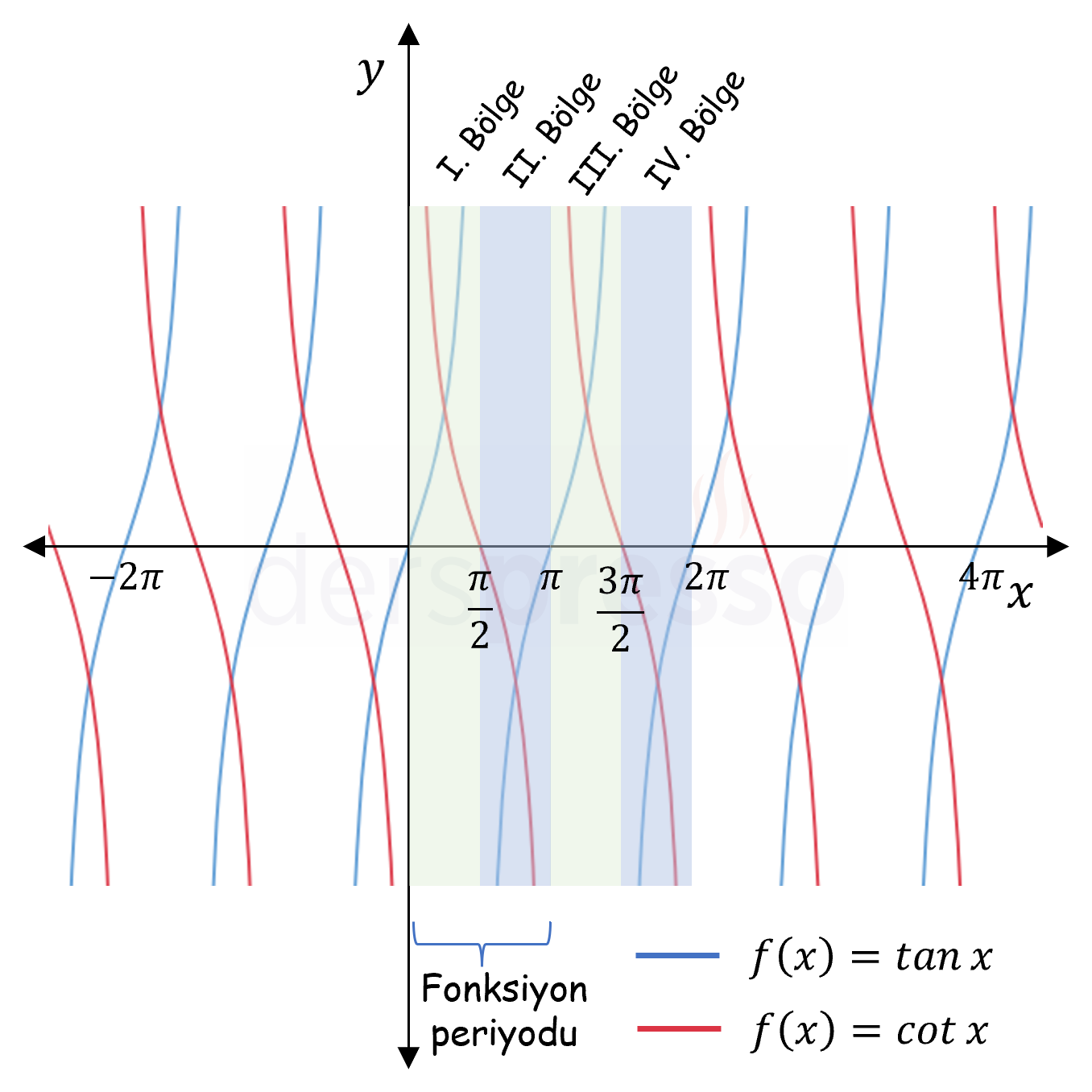
Sekant Fonksiyon Grafiği
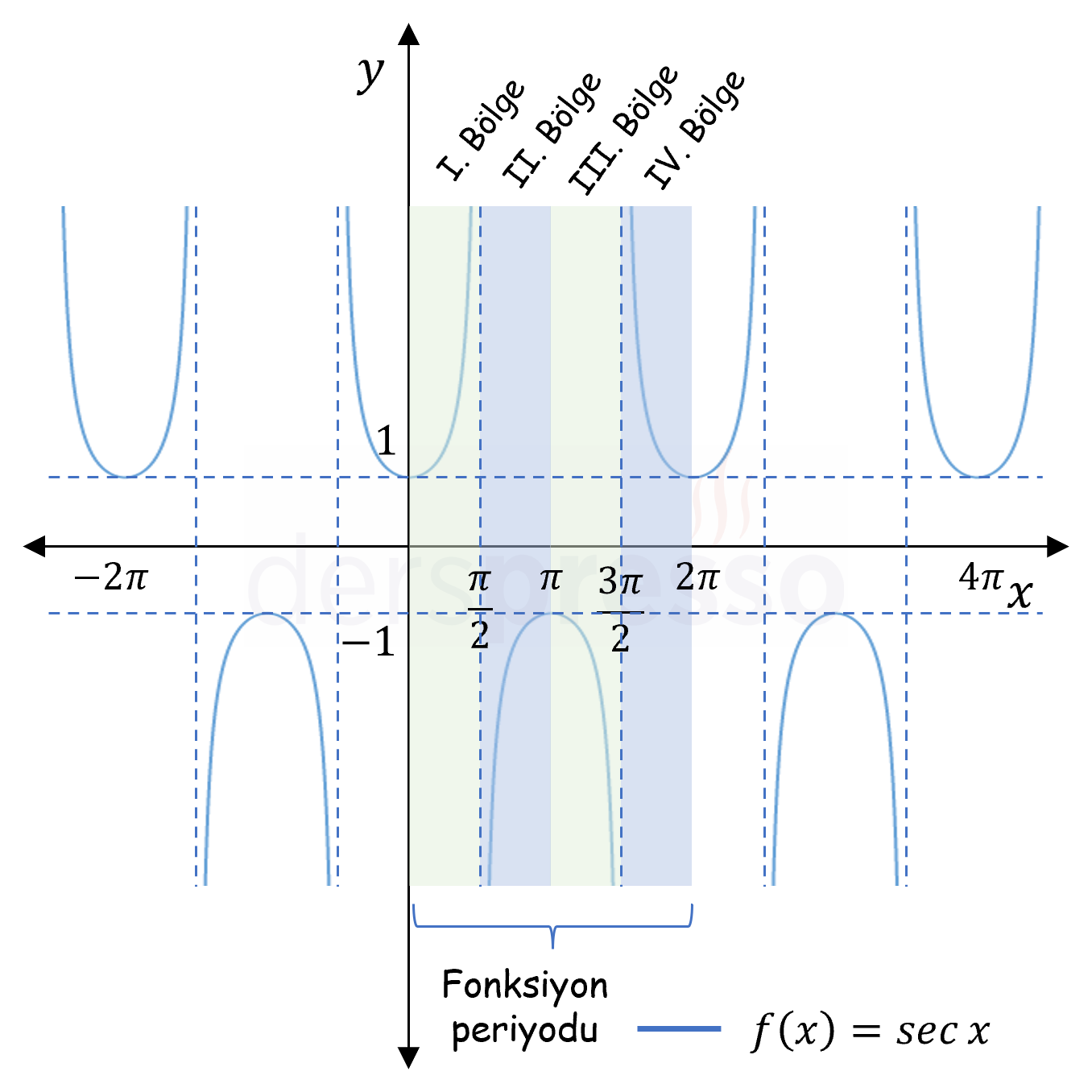
Yukarıdaki şekildeki sekant fonksiyon grafiği ile ilgili önemli bazı noktalar aşağıdaki gibidir.
- Sekant fonksiyonunun grafiği her \( 2\pi \) radyanda bir kendini tekrarladığı için periyodu \( 2\pi \) radyandır.
- Sekant fonksiyonu \( x \in \{\frac{\pi}{2}, \frac{3\pi}{2}, \ldots\} \) değerleri için tanımsız olduğu için tanım kümesi bu değerler hariç tüm reel sayılardır.
- Sekant fonksiyonunun görüntü kümesi \( (-1, 1) \) açık aralığı hariç tüm reel sayılardır.
- Sekant fonksiyonu \( \sec(-x) = \sec{x} \) eşitliği sağlandığı için bir çift fonksiyondur ve grafiği \( y \) eksenine göre simetriktir.
| Fonksiyon | Tanım Kümesi | Görüntü Kümesi |
|---|---|---|
| \( \sec{x} \) | \( \mathbb{R} - \{ \frac{\pi}{2} + k\pi, k \in \mathbb{Z} \} \) | \( \mathbb{R} - (-1, 1) \) |
Kosekant Fonksiyon Grafiği
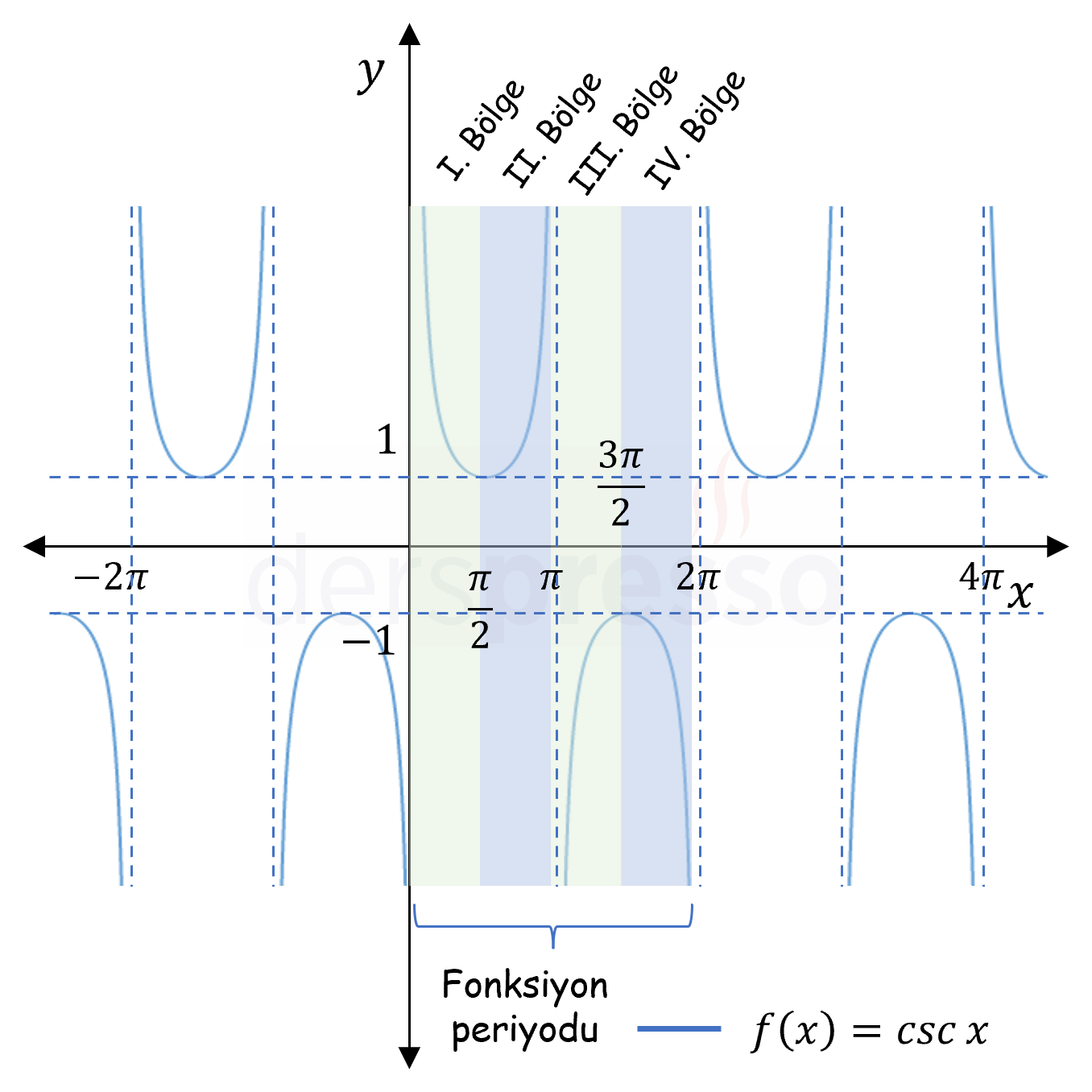
Yukarıdaki şekildeki kosekant fonksiyon grafiği ile ilgili önemli bazı noktalar aşağıdaki gibidir.
- Kosekant fonksiyonunun grafiği her \( 2\pi \) radyanda bir kendini tekrarladığı için periyodu \( 2\pi \) radyandır.
- Kosekant fonksiyonu \( x \in \{0 , \pi, 2\pi, \ldots\} \) değerleri için tanımsız olduğu için tanım kümesi bu değerler hariç tüm reel sayılardır.
- Kosekant fonksiyonunun görüntü kümesi \( (-1, 1) \) açık aralığı hariç tüm reel sayılardır.
- Kosekant fonksiyonu \( \csc(-x) = -\csc{x} \) eşitliği sağlandığı için bir tek fonksiyondur ve grafiği orijine göre simetriktir.
| Fonksiyon | Tanım Kümesi | Görüntü Kümesi |
|---|---|---|
| \( \csc{x} \) | \( \mathbb{R} - \{ k\pi, k \in \mathbb{Z} \} \) | \( \mathbb{R} - (-1, 1) \) |
Birim Çember - Grafik İlişkisi
Aşağıdaki şekilde birim çember üzerindeki bazı noktaların sinüs (mavi) ve kosinüs (kırmızı) grafikleri üzerinde karşılık geldiği noktalar gösterilmiştir.
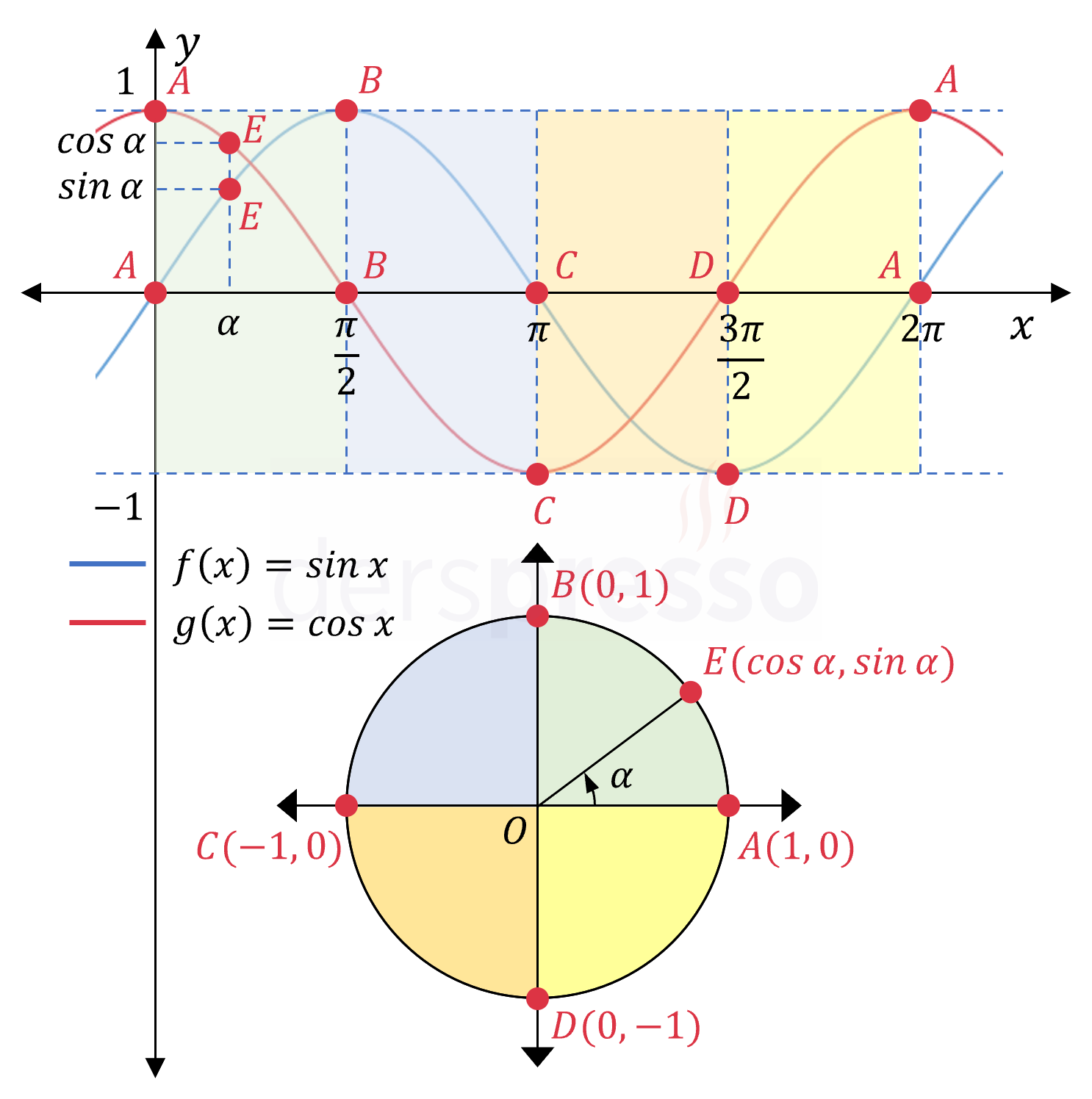
Bu şekilden aşağıdaki çıkarımları yapabiliriz.
- Birim çember üzerindeki bir noktanın apsisi, o noktanın \( x \) ekseni ile yaptığı açının kosinüs grafiğindeki değerine karşılık gelir.
- Birim çember üzerindeki bir noktanın ordinatı, o noktanın \( x \) ekseni ile yaptığı açının sinüs grafiğindeki değerine karşılık gelir.
- Birim çember üzerindeki noktaların apsis değerinin pozitif olduğu bölgelerde (I. ve IV. bölgeler) kosinüs değeri pozitiftir, negatif olduğu bölgelerde de (II. ve III. bölgeler) negatiftir.
- Birim çember üzerindeki noktaların ordinat değerinin pozitif olduğu bölgelerde (I. ve II. bölgeler) sinüs değeri pozitiftir, negatif olduğu bölgelerde de (III. ve IV. bölgeler) negatiftir.
- Birim çember üzerindeki bir noktanın karşılık geldiği açı \( [0, \frac{\pi}{2}] \) aralığında arttıkça apsisi (kosinüs değeri) azalır, ordinatı (sinüs değeri) artar.
- Aynı açı \( [\frac{\pi}{2}, \pi] \) aralığında arttıkça apsisi (kosinüs değeri) ve ordinatı (sinüs değeri) azalır.
- Aynı açı \( [\pi, \frac{3\pi}{2}] \) aralığında arttıkça apsisi (kosinüs değeri) artar, ordinatı (sinüs değeri) azalır.
- Aynı açı \( [\frac{3\pi}{2}, 2\pi] \) aralığında arttıkça apsisi (kosinüs değeri) ve ordinatı (sinüs değeri) artar.
\( a = \sin{50°}, b = \cos{72°}, c = \tan{50°} \)
Yukarıdaki ifadeleri değerlerine göre küçükten büyüğe doğru sıralayın.
Çözümü Göster\( b = \cos{72°} = \sin{18°} \)
Sinüs grafiği I. bölgede artandır.
\( \sin{18°} \lt \sin{50°} \Longrightarrow b \lt a \)
Tanjant grafiği \( [0°, 90°) \) aralığında artandır ve \( \tan{45°} = 1 \)'dir.
Buna göre \( \tan{50°} \gt 1 \) olur.
Sinüs görüntü kümesi \( [-1, 1] \) olduğu için \( c \) diğer iki değerden büyüktür.
\( b \lt a \lt c \) bulunur.
\( 0° \lt x \lt 45° \) olmak üzere,
\( \sin{x} + \cos{x} = \dfrac{7}{5} \) olduğuna göre,
\( \sin{x} - \cos{x} \) ifadesinin değeri kaçtır?
Çözümü GösterEşitliğin iki tarafının karesini alalım.
\( (\sin{x} + \cos{x})^2 = (\dfrac{7}{5})^2 \)
\( \sin^2{x} + 2\sin{x}\cos{x} + \cos^2{x} = \dfrac{49}{25} \)
\( 1 + 2\sin{x}\cos{x} = \dfrac{49}{25} \)
\( 2\sin{x}\cos{x} = \dfrac{24}{25} \)
Değeri sorulan ifadenin sonucuna \( t \) diyelim.
\( \sin{x} - \cos{x} = t \)
İki tarafın karesini alalım.
\( \sin^2{x} - 2\sin{x}\cos{x} + \cos^2{x} = t^2 \)
\( 1 - \dfrac{24}{25} = t^2 \)
\( \dfrac{1}{25} = t^2 \)
\( t \in \{-\dfrac{1}{5}, \dfrac{1}{5}\} \)
\( (0°, 45°) \) aralığında \( \sin{x} \lt \cos{x} \) olduğu için \( \sin{x} - \cos{x} = t \) negatif olmalıdır.
\( \sin{x} - \cos{x} = t = -\dfrac{1}{5} \) olarak bulunur.
\( f(x) = \cos(\frac{x}{2} + \frac{2\pi}{3}) \) eğrisi \( x = a \) doğrusuna göre simetrik olduğuna göre \( a \)'nın en büyük negatif değeri nedir?
Çözümü GösterAşağıdaki \( y = \cos{x} \) grafiğini incelediğimizde, grafiğin \( y = 1 \) ve \( y = -1 \) değerini aldığı \( x \) değerlerinde çizilen dikey doğrulara göre simetrik olduğunu görürüz.
\( y = \cos(\frac{x}{2} + \frac{2\pi}{3}) \) fonksiyonunun 1 ve -1'e eşit olduğu \( x \) değerlerini ayrı ayrı bulalım.
\( y = \cos(\frac{x}{2} + \frac{2\pi}{3}) = 1 \)
\( k \in \mathbb{Z} \) olmak üzere,
\( \dfrac{x}{2} + \dfrac{2\pi}{3} = 0 + 2k \pi \)
\( \dfrac{x}{2} = -\dfrac{2\pi}{3} + 2k \pi \)
\( x = -\dfrac{4\pi}{3} + 4k \pi \)
Bu eşitlikte \( x \)'in alabileceği en büyük negatif değer \( k = 0 \) için \( x = -\frac{4\pi}{3} \) olur.
\( y = \cos(\frac{x}{2} + \frac{2\pi}{3}) = -1 \)
\( \dfrac{x}{2} + \dfrac{2\pi}{3} = \pi + 2k \pi \)
\( \dfrac{x}{2} = \dfrac{\pi}{3} + 2k \pi \)
\( x = \dfrac{2\pi}{3} + 4k \pi \)
Bu eşitlikte \( x \)'in alabileceği en büyük negatif değer \( k = -1 \) için \( x = -\frac{10\pi}{3} \) olur.
\( -\frac{4\pi}{3} \gt -\frac{10\pi}{3} \) olduğundan \( a \)'nın alabileceği en büyük negatif değer \( -\frac{4\pi}{3} \) olur.
\( 4\pi \sin{x} = x \) denkleminin kaç reel çözümü vardır?
Çözümü GösterVerilen denklemin sol ve sağ tarafındaki fonksiyonları ayrı ayrı inceleyelim.
\( f(x) = 4\pi \sin{x} \)
Sinüs fonksiyonu \( [-1, 1] \) aralığında, \( f \) fonksiyonu \( [-4\pi, 4\pi] \) aralığında değer alır.
Sinüs fonksiyonunun periyodu \( 2\pi \) radyandır.
\( g(x) = x \)
Birim fonksiyon orijinden geçen ve eğimi 1 olan doğrusal bir fonksiyondur.
Verilen denklemin çözüm kümesi bu iki fonksiyonun grafiklerinin kesişim noktalarıdır.
\( f \) ve \( g \) fonksiyonlarının kesişim noktalarını sinüs fonksiyon grafiği bilgimizi kullanarak bulalım.
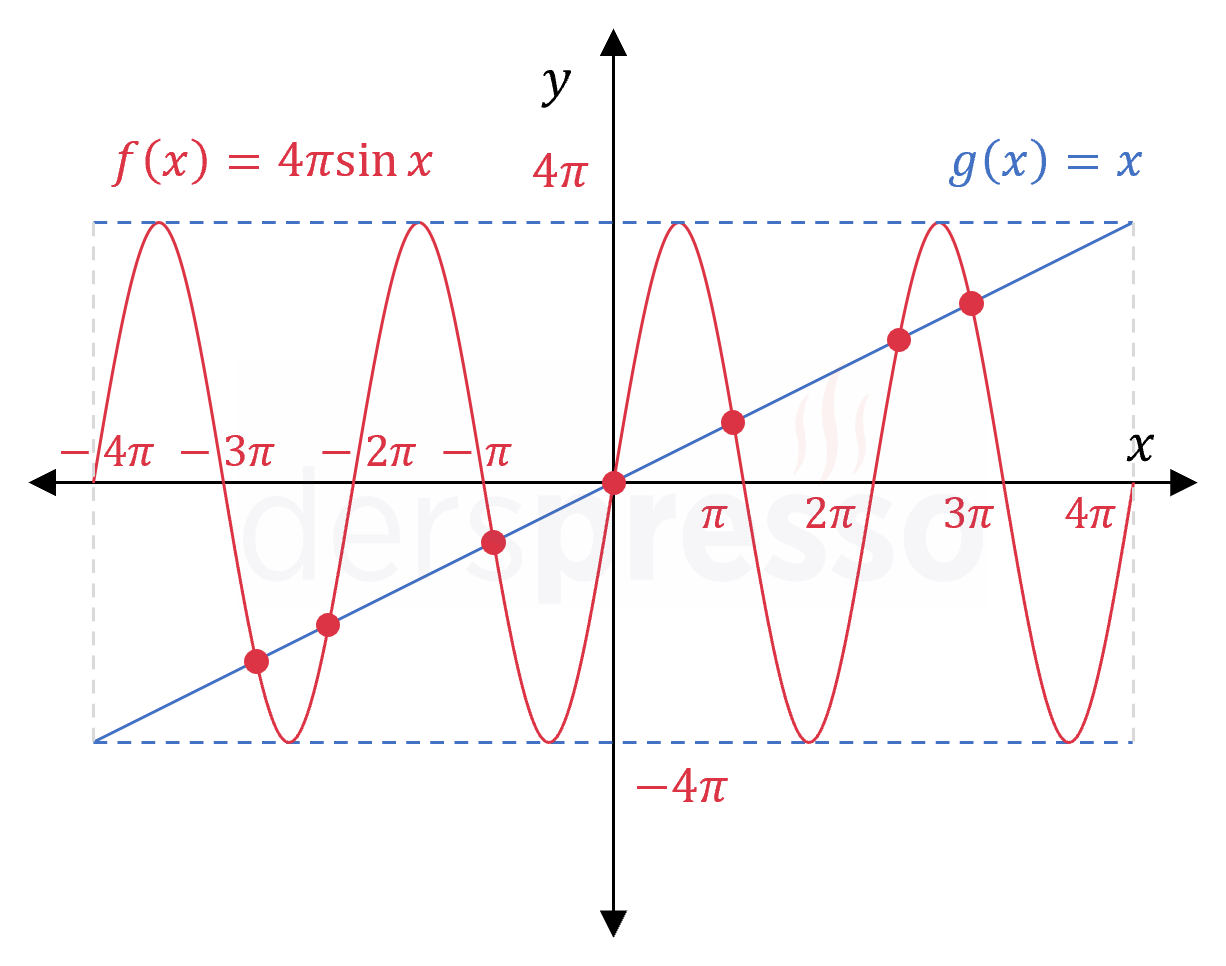
İki grafiğin kesişim noktaları \( x \in [-4\pi, 4\pi] \) aralığında olmalıdır, çünkü bu aralığın dışında \( g \) fonksiyonunun değeri \( f \) fonksiyonunun değer aralığının dışında olmaktadır (\( g(x) \gt 4\pi \) ya da \( g(x) \lt -4\pi \)).
Birim fonksiyon grafiği \( f \) fonksiyon grafiğini \( 0 \le x \le 4\pi \) aralığında her periyotta iki kez olmak üzere toplam 4 kez keser.
Birim fonksiyon grafiği \( f \) fonksiyon grafiğini \( -4\pi \le x \le 0 \) aralığında her periyotta iki kez olmak üzere toplam 4 kez keser.
Bu noktalardan orijin yukarıdaki iki gruba da dahil olduğu için toplam kesişim noktası sayısından çıkarmamız gerekir.
Buna göre iki fonksiyon \( 4 + 4 - 1 = 7 \) noktada kesişirler.
Dolayısıyla verilen denklemin 7 reel çözümü vardır.