Trigonometrik Fonksiyonlar
Trigonometri üçgenlerin kenarları ve açıları arasındaki oranları inceler ve bu oranları hesaplamak için trigonometrik fonksiyon adı verilen fonksiyonlar kullanılır. Bir dik üçgenin üç kenarı arasında yazılabilecek altı farklı oran vardır ve bunların her biri için birer fonksiyon tanımlanmıştır.

Sinüs Fonksiyonu
Bir dik üçgende dik olmayan bir köşeye ait \( x \) açısının karşı kenar uzunluğunun hipotenüs uzunluğuna oranına o açının sinüs değeri denir. Belirli bir açı ölçüsü için sinüs değerini hesaplayan fonksiyona sinüs fonksiyonu denir ve \( \sin{x} \) şeklinde gösterilir.
\( \sin{x} = \dfrac{\text{karşı kenar}}{\text{hipotenüs}} = \dfrac{b}{a} \)

\( \sin{x} = \dfrac{3}{5} \)
Bu orana göre, bir dik üçgende ölçüsü \( x \) olan bir açının karşı kenar uzunluğu 3 birim ise üçgenin hipotenüs uzunluğu 5 birimdir.
Bir diğer dik üçgende ölçüsü yine \( x \) olan bir açının karşı kenar uzunluğu 6 birim ise üçgenin hipotenüs uzunluğu 10 birimdir.
Bir diğer dik üçgende ölçüsü yine \( x \) olan bir açının karşı kenar uzunluğu 300 birim ise üçgenin hipotenüs uzunluğu 500 birimdir.
Buna göre açılarından birinin ölçüsü \( x \) olan dik üçgenlerde kenar uzunlukları farklı olabilir, ama karşı kenarın hipotenüse oranı her zaman \( \frac{3}{5} \) olur.
Kosinüs Fonksiyonu
Bir dik üçgende dik olmayan bir köşeye ait \( x \) açısının komşu kenar uzunluğunun hipotenüs uzunluğuna oranına o açının kosinüs değeri denir. Belirli bir açı ölçüsü için kosinüs değerini hesaplayan fonksiyona kosinüs fonksiyonu denir ve \( \cos{x} \) şeklinde gösterilir.
\( \cos{x} = \dfrac{\text{komşu kenar}}{\text{hipotenüs}} = \dfrac{c}{a} \)

\( \cos{x} = \dfrac{4}{5} \)
Tanjant Fonksiyonu
Bir dik üçgende dik olmayan bir köşeye ait \( x \) açısının karşı kenar uzunluğunun komşu kenar uzunluğuna oranına o açının tanjant değeri denir. Belirli bir açı ölçüsü için tanjant değerini hesaplayan fonksiyona tanjant fonksiyonu denir ve \( \tan{x} \) şeklinde gösterilir.
\( \tan{x} = \dfrac{\text{karşı kenar}}{\text{komşu kenar}} = \dfrac{b}{c} \)
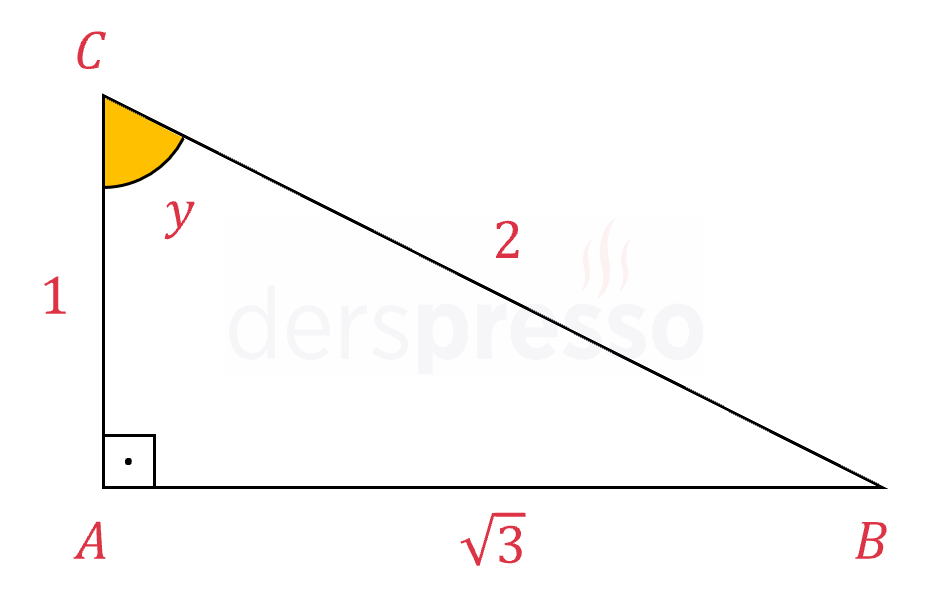
\( \tan{y} = \dfrac{\sqrt{3}}{1} = \sqrt{3} \)
Belirli bir açı için tanjant fonksiyonu, aynı açı için sinüs ve kosinüs fonksiyonlarının oranına eşittir.
\( \tan{x} = \dfrac{\sin{x}}{\cos{x}} = \dfrac{\frac{b}{a}}{\frac{c}{a}} = \dfrac{b}{c} \)
Kotanjant Fonksiyonu
Bir dik üçgende dik olmayan bir köşeye ait \( x \) açısının komşu kenar uzunluğunun karşı kenar uzunluğuna oranına o açının kotanjant değeri denir. Belirli bir açı ölçüsü için kotanjant değerini hesaplayan fonksiyona kotanjant fonksiyonu denir ve \( \cot{x} \) şeklinde gösterilir.
\( \cot{x} = \dfrac{\text{komşu kenar}}{\text{karşı kenar}} = \dfrac{c}{b} \)
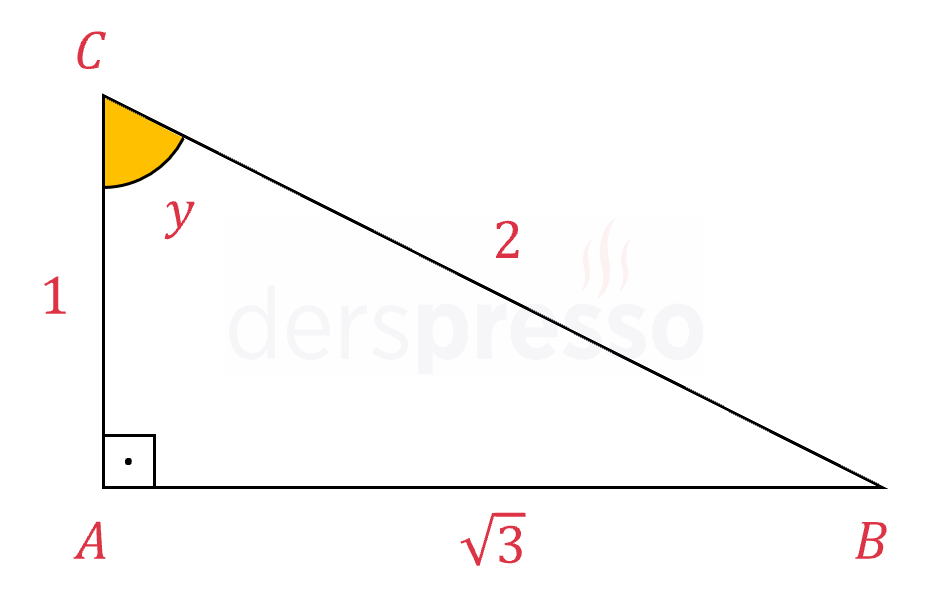
\( \cot{y} = \dfrac{1}{\sqrt{3}} = \dfrac{\sqrt{3}}{3} \)
Belirli bir açı için kotanjant fonksiyonu, aynı açı için kosinüs ve sinüs fonksiyonlarının oranına eşittir.
\( \cot{x} = \dfrac{\cos{x}}{\sin{x}} = \dfrac{\frac{c}{a}}{\frac{b}{a}} = \dfrac{c}{b} \)
Tanjant ve kotanjant fonksiyonları birbirlerinin çarpmaya göre tersidir.
\( \tan{x}\cot{x} = \dfrac{b}{c} \cdot \dfrac{c}{b} = 1 \)
\( \cot{x} = \dfrac{1}{\tan{x}} \)
\( \tan{x} = \dfrac{1}{\cot{x}} \)
Sekant Fonksiyonu
Bir dik üçgende dik olmayan bir köşeye ait \( x \) açısının hipotenüs uzunluğunun komşu kenar uzunluğuna oranına o açının sekant değeri denir. Belirli bir açı ölçüsü için sekant değerini hesaplayan fonksiyona sekant fonksiyonu denir ve \( \sec{x} \) şeklinde gösterilir.
\( \sec{x} = \dfrac{\text{hipotenüs}}{\text{komşu kenar}} = \dfrac{a}{c} \)

\( \sec{x} = \dfrac{5}{4} \)
Kosinüs ve sekant fonksiyonları birbirlerinin çarpmaya göre tersidir.
\( \cos{x}\sec{x} = \dfrac{c}{a} \cdot \dfrac{a}{c} = 1 \)
\( \sec{x} = \dfrac{1}{\cos{x}} \)
\( \cos{x} = \dfrac{1}{\sec{x}} \)
Kosekant Fonksiyonu
Bir dik üçgende dik olmayan köşeye ait bir \( x \) açısının hipotenüs uzunluğunun karşı kenar uzunluğuna oranına o açının kosekant değeri denir. Belirli bir açı ölçüsü için kosekant değerini hesaplayan fonksiyona kosekant fonksiyonu denir ve \( \csc{x} \) şeklinde gösterilir.
\( \csc{x} = \dfrac{\text{hipotenüs}}{\text{karşı kenar}} = \dfrac{a}{b} \)

\( \csc{x} = \dfrac{5}{3} \)
Sinüs ve kosekant fonksiyonları birbirlerinin çarpmaya göre tersidir.
\( \sin{x}\csc{x} = \dfrac{b}{a} \cdot \dfrac{a}{b} = 1 \)
\( \csc{x} = \dfrac{1}{\sin{x}} \)
\( \sin{x} = \dfrac{1}{\csc{x}} \)
Dik üçgenin bir dar açısı üzerinden yaptığımız bu tanımlamalar \( 0° \lt x \lt 90° \) aralığında geçerli olsa da, önümüzdeki bölümlerde trigonometrik fonksiyonların bu aralığın dışında da tanımlı olduğunu göreceğiz.
Trigonometrik Oranlar
Bir dik üçgende kenar uzunlukları arasındaki oranlar sadece \( x \) açısına bağlı olarak değişir ve üçgenin büyüklüğünden bağımsızdır. Bir diğer deyişle, üçgenin açıları aynı kalmak koşuluyla kenar uzunlukları artırıldığında/azaltıldığında uzunluklar arasındaki oranlar değişmez.
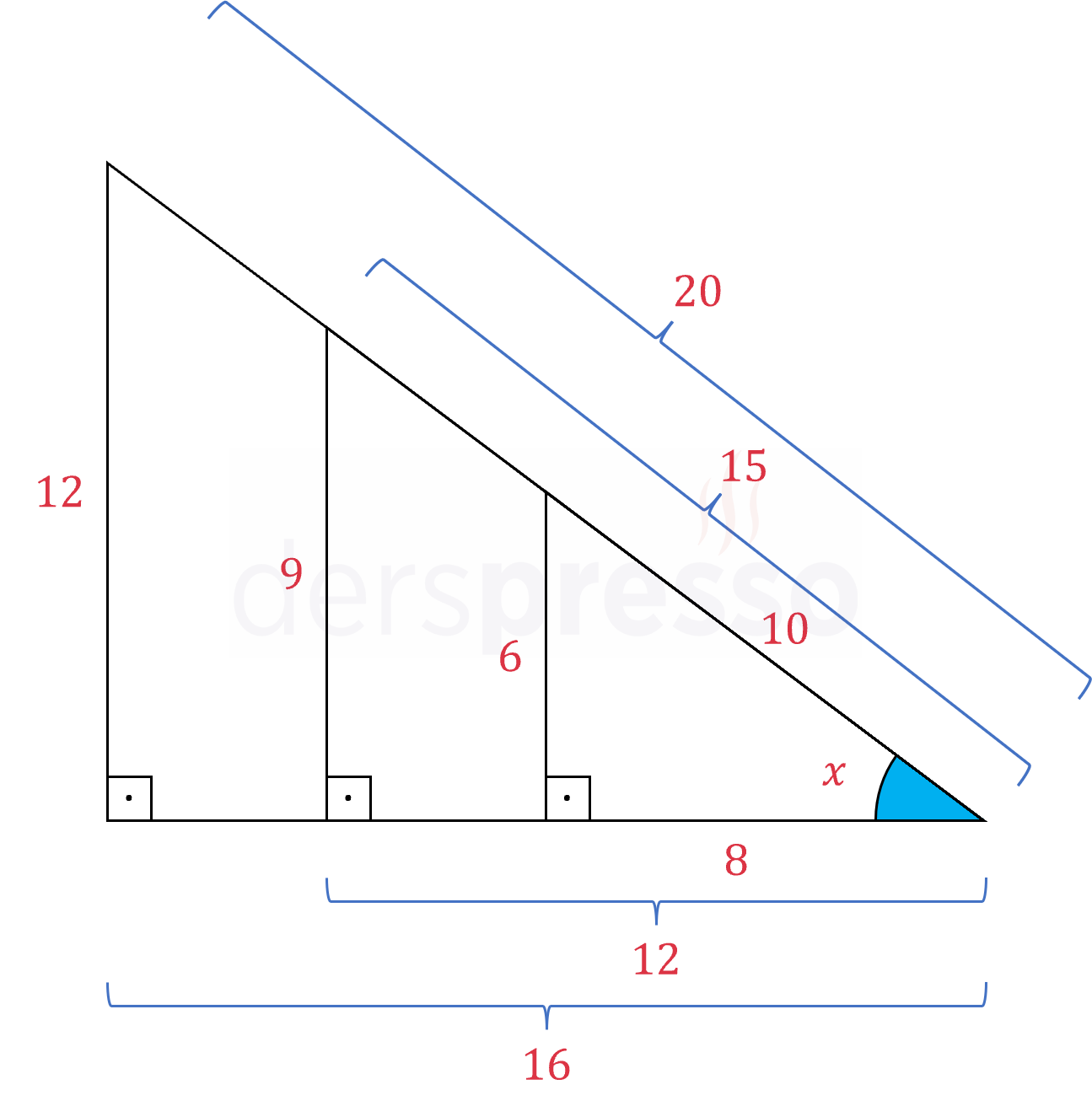
\( \sin{x} = \dfrac{6}{10} = \dfrac{9}{15} = \dfrac{12}{20} \)
\( \cos{x} = \dfrac{8}{10} = \dfrac{12}{15} = \dfrac{16}{20} \)
\( \tan{x} = \dfrac{6}{8} = \dfrac{9}{12} = \dfrac{12}{16} \)
\( \widehat{A} \) açısı dik açı olan \( ABC \) üçgeninde \( \widehat{B} \) açısının sinüs değeri \( \frac{1}{3} \) olduğuna göre, \( \widehat{C} \) açısı için altı trigonometrik fonksiyonun değerini bulalım.
\( \sin{\widehat{B}} = \dfrac{1}{3} \)
Buna göre \( \widehat{B} \) açısının karşı kenar uzunluğuna \( b = k \) birim, hipotenüs uzunluğuna \( a = 3k \) birim diyebiliriz.
Komşu kenar uzunluğunu Pisagor teoremi ile bulalım.
\( a^2 = b^2 + c^2 \)
\( c = \sqrt{a^2 - b^2} \)
\( = \sqrt{(3k)^2 - k^2} = 2\sqrt{2}k \)
Buna göre \( ABC \) üçgeni aşağıdaki gibi olur.
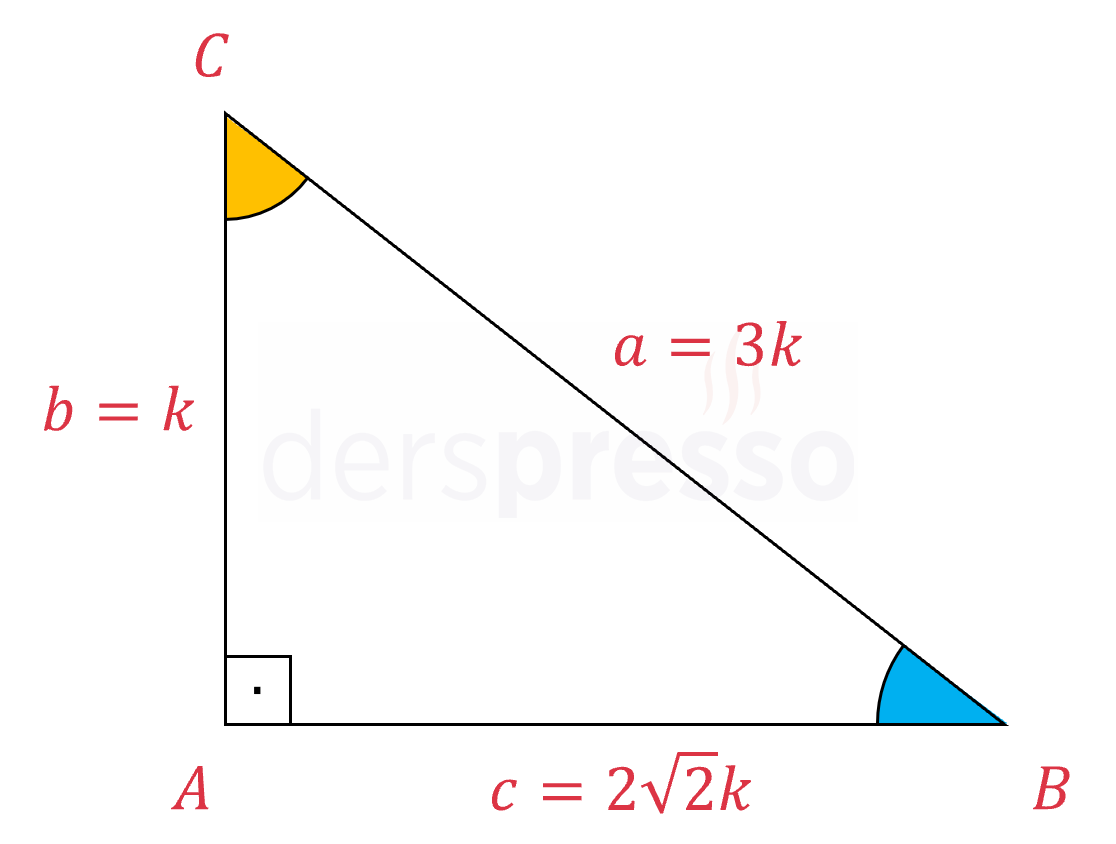
\( \widehat{C} \) açısı için fonksiyon değerlerini hesaplayalım.
\( \sin{\widehat{C}} = \dfrac{2\sqrt{2}k}{3k} = \dfrac{2\sqrt{2}}{3} \)
\( \cos{\widehat{C}} = \dfrac{k}{3k} = \dfrac{1}{3} \)
\( \tan{\widehat{C}} = \dfrac{2\sqrt{2}k}{k} = 2\sqrt{2} \)
\( \cot{\widehat{C}} = \dfrac{k}{2\sqrt{2}k} = \dfrac{\sqrt{2}}{4} \)
\( \sec{\widehat{C}} = \dfrac{3k}{k} = 3 \)
\( \csc{\widehat{C}} = \dfrac{3k}{2\sqrt{2}k} = \dfrac{3\sqrt{2}}{4} \)
Fonksiyonlarda Açı Ölçü Birimi
Trigonometrik fonksiyonlarda açı ölçü birimi olarak derece ya da radyan kullanılabilir. Kullanılan birimin net bir şekilde belirtilmediği durumlarda aşağıdaki noktalara dikkat edilmelidir.
- \( \sin{30°} \): Derece işareti kullanıldığı durumlarda birim derecedir.
- \( \cos{\pi} \): Derece işareti kullanılmadığı durumlarda birim radyan olarak kabul edilebilir.
- \( \tan{x} \): Bir değişkenin kullanıldığı ve birimle ilgili bir bilgi verilmediği durumlarda birimin radyan olduğu kabul edilmelidir.

Yukarıdaki üçgenin \( x \) açısı için 6 trigonometrik fonksiyonun değerini bulunuz.
Çözümü GösterPisagor teoremini kullanarak hipotenüs uzunluğunu bulalım.
\( c^2 = 2^2 + 4^2 = 20 \)
\( c = \sqrt{20} = 2\sqrt{5} \)
\( x \) açısı için trigonometrik fonksiyonların değerlerini bulalım.
\( \sin{x} = \dfrac{\text{karşı kenar}}{\text{hipotenüs}} = \dfrac{2}{2\sqrt{5}} = \dfrac{\sqrt{5}}{5} \)
\( \cos{x} = \dfrac{\text{komşu kenar}}{\text{hipotenüs}} = \dfrac{4}{2\sqrt{5}} = \dfrac{2\sqrt{5}}{5} \)
\( \tan{x} = \dfrac{\text{karşı kenar}}{\text{komşu kenar}} = \dfrac{2}{4} = \dfrac{1}{2} \)
\( \cot{x} = \dfrac{\text{komşu kenar}}{\text{karşı kenar}} = \dfrac{4}{2} = 2 \)
\( \sec{x} = \dfrac{\text{hipotenüs}}{\text{komşu kenar}} = \dfrac{2\sqrt{5}}{4} = \dfrac{\sqrt{5}}{2} \)
\( \csc{x} = \dfrac{\text{hipotenüs}}{\text{karşı kenar}} = \dfrac{2\sqrt{5}}{2} = \sqrt{5} \)
Aşağıda bir trigonometrik oranı verilen açı için diğer trigonometrik oranları hesaplayın.
(a) \( \cos{x} = \dfrac{2}{3} \)
(b) \( \cot{y} = 3 \)
(c) \( \sec{z} = \dfrac{\sqrt{7}}{2} \)
Çözümü Göster(a) seçeneği:
\( \cos{x} = \dfrac{2}{3} \)
\( x \) açısının komşu kenar uzunluğuna 2 birim, hipotenüs uzunluğuna 3 birim diyelim.
Pisagor teoremi ile karşı kenar uzunluğunu bulalım.
\( a^2 = b^2 + c^2 \)
\( 3^2 = 2^2 + c^2 \)
\( c = \sqrt{5} \)

Diğer trigonometrik oranları bulalım.
\( \sin{x} = \dfrac{\sqrt{5}}{3} \)
\( \tan{x} = \dfrac{\sqrt{5}}{2} \)
\( \cot{x} = \dfrac{2}{\sqrt{5}} = \dfrac{2\sqrt{5}}{5} \)
\( \sec{x} = \dfrac{3}{2} \)
\( \csc{x} = \dfrac{3}{\sqrt{5}} = \dfrac{3\sqrt{5}}{5} \)
(b) seçeneği:
\( \cot{y} = 3 \)
\( y \) açısının komşu kenar uzunluğuna 3 birim, karşı kenar uzunluğuna 1 birim diyelim.
Pisagor teoremi ile hipotenüs uzunluğunu bulalım.
\( a^2 = b^2 + c^2 \)
\( a^2 = 3^2 + 1^2 \)
\( a = \sqrt{10} \)

Diğer trigonometrik oranları bulalım.
\( \sin{y} = \dfrac{1}{\sqrt{10}} = \dfrac{\sqrt{10}}{10} \)
\( \cos{y} = \dfrac{3}{\sqrt{10}} = \dfrac{3\sqrt{10}}{10} \)
\( \tan{y} = \dfrac{1}{3} \)
\( \sec{y} = \dfrac{\sqrt{10}}{3} \)
\( \csc{y} = \dfrac{\sqrt{10}}{1} = \sqrt{10} \)
(c) seçeneği:
\( \sec{z} = \dfrac{\sqrt{7}}{2} \)
\( z \) açısının hipotenüs uzunluğuna \( \sqrt{7} \) birim, komşu kenar uzunluğuna 2 birim diyelim.
Pisagor teoremi ile karşı kenar uzunluğunu bulalım.
\( (\sqrt{7})^2 = b^2 + 2^2 \)
\( b = \sqrt{3} \)

Diğer trigonometrik oranları bulalım.
\( \sin{z} = \dfrac{\sqrt{3}}{\sqrt{7}} = \dfrac{\sqrt{21}}{7} \)
\( \cos{z} = \dfrac{2}{\sqrt{7}} = \dfrac{2\sqrt{7}}{7} \)
\( \tan{z} = \dfrac{\sqrt{3}}{2} \)
\( \cot{z} = \dfrac{2}{\sqrt{3}} = \dfrac{2\sqrt{3}}{3} \)
\( \csc{z} = \dfrac{\sqrt{7}}{\sqrt{3}} = \dfrac{\sqrt{21}}{3} \)
Aşağıda farklı iki kenar uzunluğu verilen dik üçgenlerde ilgili açı için altı trigonometrik oranı hesaplayın.
(a) Karşı kenar: 3, komşu kenar: 9
(b) Karşı kenar: \( 6\sqrt{3} \), hipotenüs: \( 8\sqrt{2} \)
(c) Komşu kenar: \( \frac{1}{10} \), hipotenüs: \( \frac{1}{9} \)
Çözümü Göster(a) seçeneği:
Karşı kenar: 3, komşu kenar: 9
Pisagor teoremi ile hipotenüs uzunluğunu bulalım.
\( a^2 = b^2 + c^2 \)
\( a^2 = 3^2 + 9^2 \)
\( a = 3\sqrt{10} \)

Altı trigonometrik oranı bulalım.
\( \sin{x} = \dfrac{3}{3\sqrt{10}} = \dfrac{\sqrt{10}}{10} \)
\( \cos{x} = \dfrac{9}{3\sqrt{10}} = \dfrac{3\sqrt{10}}{10} \)
\( \tan{x} = \dfrac{3}{9} = \dfrac{1}{3} \)
\( \cot{x} = \dfrac{9}{3} = 3 \)
\( \sec{x} = \dfrac{3\sqrt{10}}{9} = \dfrac{\sqrt{10}}{3} \)
\( \csc{x} = \dfrac{3\sqrt{10}}{3} = \sqrt{10} \)
(b) seçeneği:
Karşı kenar: \( 6\sqrt{3} \), hipotenüs: \( 8\sqrt{2} \)
Pisagor teoremi ile komşu kenar uzunluğunu bulalım.
\( a^2 = b^2 + c^2 \)
\( (8\sqrt{2})^2 = (6\sqrt{3})^2 + c^2 \)
\( c = 2\sqrt{5} \)

Altı trigonometrik oranı bulalım.
\( \sin{x} = \dfrac{6\sqrt{3}}{8\sqrt{2}} = \dfrac{3\sqrt{6}}{8} \)
\( \cos{x} = \dfrac{2\sqrt{5}}{8\sqrt{2}} = \dfrac{\sqrt{10}}{8} \)
\( \tan{x} = \dfrac{6\sqrt{3}}{2\sqrt{5}} = \dfrac{3\sqrt{15}}{5} \)
\( \cot{x} = \dfrac{2\sqrt{5}}{6\sqrt{3}} = \dfrac{\sqrt{15}}{9} \)
\( \sec{x} = \dfrac{8\sqrt{2}}{2\sqrt{5}} = \dfrac{4\sqrt{10}}{5} \)
\( \csc{x} = \dfrac{8\sqrt{2}}{6\sqrt{3}} = \dfrac{4\sqrt{6}}{9} \)
(c) seçeneği:
Komşu kenar: \( \dfrac{1}{10} \), hipotenüs: \( \dfrac{1}{9} \)
Pisagor teoremi ile karşı kenar uzunluğunu bulalım.
\( a^2 = b^2 + c^2 \)
\( (\dfrac{1}{9})^2 = b^2 + (\dfrac{1}{10})^2 \)
\( b = \dfrac{\sqrt{19}}{90} \)

Altı trigonometrik oranı bulalım.
\( \sin{x} = \dfrac{\frac{\sqrt{19}}{90}}{\frac{1}{9}} = \dfrac{\sqrt{19}}{10} \)
\( \cos{x} = \dfrac{\frac{1}{10}}{\frac{1}{9}} = \dfrac{9}{10} \)
\( \tan{x} = \dfrac{\frac{\sqrt{19}}{90}}{\frac{1}{10}} = \dfrac{\sqrt{19}}{9} \)
\( \cot{x} = \dfrac{\frac{1}{10}}{\frac{\sqrt{19}}{90}} = \dfrac{9\sqrt{19}}{19} \)
\( \sec{x} = \dfrac{\frac{1}{9}}{\frac{1}{10}} = \dfrac{10}{9} \)
\( \csc{x} = \dfrac{\frac{1}{9}}{\frac{\sqrt{19}}{90}} = \dfrac{10\sqrt{19}}{19} \)
\( \dfrac{3 \sin{x} - 2 \cos{x}}{2 \cos{x} + 2 \sin{x}} = \dfrac{1}{3} \)
olduğuna göre, \( \tan{x} \) kaçtır?
Çözümü Gösterİçler - dışlar çarpımı yapalım.
\( 9\sin{x} - 6\cos{x} = 2\cos{x} + 2\sin{x} \)
\( 7\sin{x} = 8\cos{x} \)
\( \dfrac{\sin{x}}{\cos{x}} = \dfrac{8}{7} \)
Sinüs/kosinüs oranı tanjanta eşittir.
\( \tan{x} = \dfrac{8}{7} \) bulunur.
\( \sin{x} = 4\cos{x} \) olduğuna göre,
\( \sec{x}\csc{x} \) ifadesi kaça eşittir?
Çözümü Göster\( \cos{x} \) ifadesini eşitliğin sol tarafına alalım.
\( \dfrac{\sin{x}}{\cos{x}} = 4 \)
\( \tan{x} = 4 \)
Bir açısının tanjant değeri 4 olan bir dik üçgen çizelim.

Yukarıdaki üçgeni kullanarak değeri istenen trigonometrik oranları bulalım.
\( \sec{x} = \dfrac{\sqrt{17}}{1} = \sqrt{17} \)
\( \csc{x} = \dfrac{\sqrt{17}}{4} \)
Bu değerleri sorudaki ifadede yerine koyalım.
\( \sec{x}\csc{x} = \sqrt{17} \cdot \dfrac{\sqrt{17}}{4} \)
\( = \dfrac{17}{4} \) bulunur.
\( x \in (0, \frac{\pi}{2}) \) olmak üzere,
\( \dfrac{1 + \cot{x}}{1 + \tan{x}} = 3 \) olduğuna göre, \( \cos{x} \) kaçtır?
Çözümü GösterTanjant ve kotanjant ifadelerini sinüs ve kosinüs cinsinden yazalım.
\( \dfrac{1 + \frac{\cos{x}}{\sin{x}}}{1 + \frac{\sin{x}}{\cos{x}}} = 3 \)
\( \dfrac{\frac{\sin{x} + \cos{x}}{\sin{x}}}{\frac{\cos{x + \sin{x}}}{\cos{x}}} = 3 \)
\( \dfrac{\cos{x}}{\sin{x}} = 3 \)
\( \cot{x} = 3 \)
Bir açının kotanjantı 3 ise komşu kenara \( 3k \), karşı kenara \( k \) diyebiliriz.
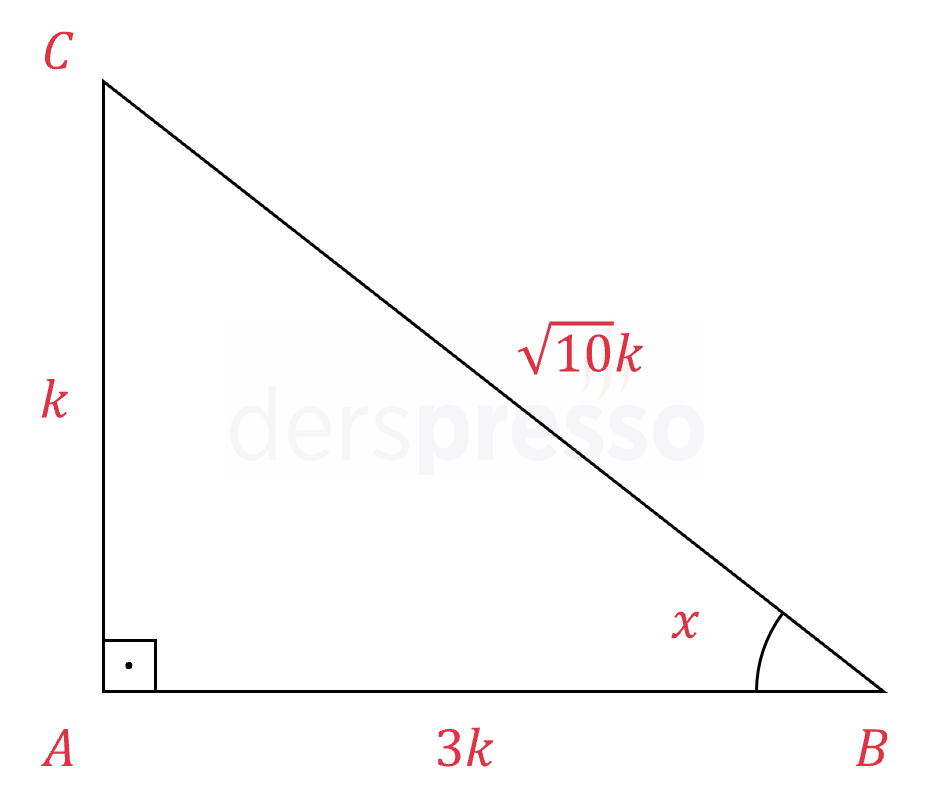
Pisagor teoremi ile dik üçgenin hipotenüs uzunluğunu bulalım.
\( \abs{BC}^2 = k^2 + (3k)^2 \)
\( \abs{BC} = \sqrt{10}k \)
\( \cos{x} = \dfrac{3k}{\sqrt{10}k} \)
\( = \dfrac{3\sqrt{10}}{10} \) bulunur.
\( \csc{x}(\sin{x} - \tan{x}) = -2 \) olduğuna göre,
\( \sec{x} \) ifadesinin değeri kaçtır?
Çözümü Gösterİfadeleri sinüs ve kosinüs cinsinden yazalım.
\( \dfrac{1}{\sin{x}}\left( \sin{x} - \dfrac{\sin{x}}{\cos{x}} \right) = -2 \)
Parantezi genişletelim.
\( 1 - \dfrac{1}{\cos{x}} = -2 \)
\( \dfrac{1}{\cos{x}} = 3 \)
Kosinüs fonksiyonunun çarpmaya göre tersi sekant fonksiyonudur.
\( \dfrac{1}{\cos{x}} = \sec{x} = 3 \) bulunur.
\( 0° \lt x \lt 90° \) olmak üzere,
\( \cot{x} = \dfrac{15}{8} \) olduğuna göre,
\( \sqrt{\sec{x} + \tan{x}} \) ifadesinin değeri kaçtır?
Çözümü Göster\( x \) açısının komşu kenar uzunluğuna \( 15k \), karşı kenar uzunluğuna da \( 8k \) dersek Pisagor teoremi ile hipotenüs uzunluğu \( 17k \) olarak bulunur.
\( (15k)^2 + (8k)^2 = (17k)^2 \)
Bu değerleri bir dik üçgen çizerek kenarlar üzerinde gösterelim.

Üçgeni kullanarak sorudaki ifadedeki değerleri bulalım.
\( \sec{x} = \dfrac{17k}{15k} = \dfrac{17}{15} \)
\( \tan{x} = \dfrac{8k}{15k} = \dfrac{8}{15} \)
Değerleri yerine koyalım.
\( \sqrt{\sec{x} + \tan{x}} = \sqrt{\dfrac{17}{15} + \dfrac{8}{15}} \)
\( = \sqrt{\dfrac{5}{3}} = \dfrac{\sqrt{15}}{3} \) bulunur.
\( \tan{x} = \dfrac{k}{t} \) olduğuna göre,
\( \sin{x} - \cos{x} \) ifadesinin \( k \) ve \( t \) cinsinden eşiti nedir?
Çözümü GösterVerilen tanjant değerini bir üçgen üzerinde karşı kenar uzunluğunun komşu kenar uzunluğuna oranı şeklinde gösterelim.

Hipotenüs uzunluğunu Pisagor teoremi ile \( k \) ve \( t \) cinsinden bulalım.
\( \abs{BC} = \sqrt{k^2 + t^2} \)
Sinüs değeri karşı kenar uzunluğunun hipotenüs uzunluğuna oranına eşittir.
\( \sin{x} = \dfrac{k}{\sqrt{k^2 + t^2}} \)
Kosinüs değeri komşu kenar uzunluğunun hipotenüs uzunluğuna oranına eşittir.
\( \cos{x} = \dfrac{t}{\sqrt{k^2 + t^2}} \)
Bu iki değeri istenen ifadede yerine koyalım.
\( \sin{x} - \cos{x} = \dfrac{k}{\sqrt{k^2 + t^2}} - \dfrac{t}{\sqrt{k^2 + t^2}} \)
\( = \dfrac{k - t}{\sqrt{k^2 + t^2}} \) bulunur.
\( m \in \mathbb{R} - \{ -1, 1 \} \) olmak üzere,
\( \dfrac{\sin{x} + \cos{x}}{\sin{x} - \cos{x}} = m \) veriliyor.
Buna göre, \( \cot{x} \)'in \( m \) cinsinden değeri nedir?
Çözümü Gösterİçler - dışlar çarpımı yapalım.
\( \sin{x} + \cos{x} = m(\sin{x} - \cos{x}) \)
\( \sin{x} + \cos{x} = m\sin{x} - m\cos{x} \)
\( m\sin{x} - \sin{x} = m\cos{x} + \cos{x} \)
\( \sin{x}(m - 1) = \cos{x}(m + 1) \)
\( \dfrac{\cos{x}}{\sin{x}} = \dfrac{m - 1}{m + 1} \)
\( \cot{x} = \dfrac{m - 1}{m + 1} \) bulunur.

\( ABC \) üçgeninde verilenlere göre, \( \cot{x} \) değeri kaçtır?
Çözümü Göster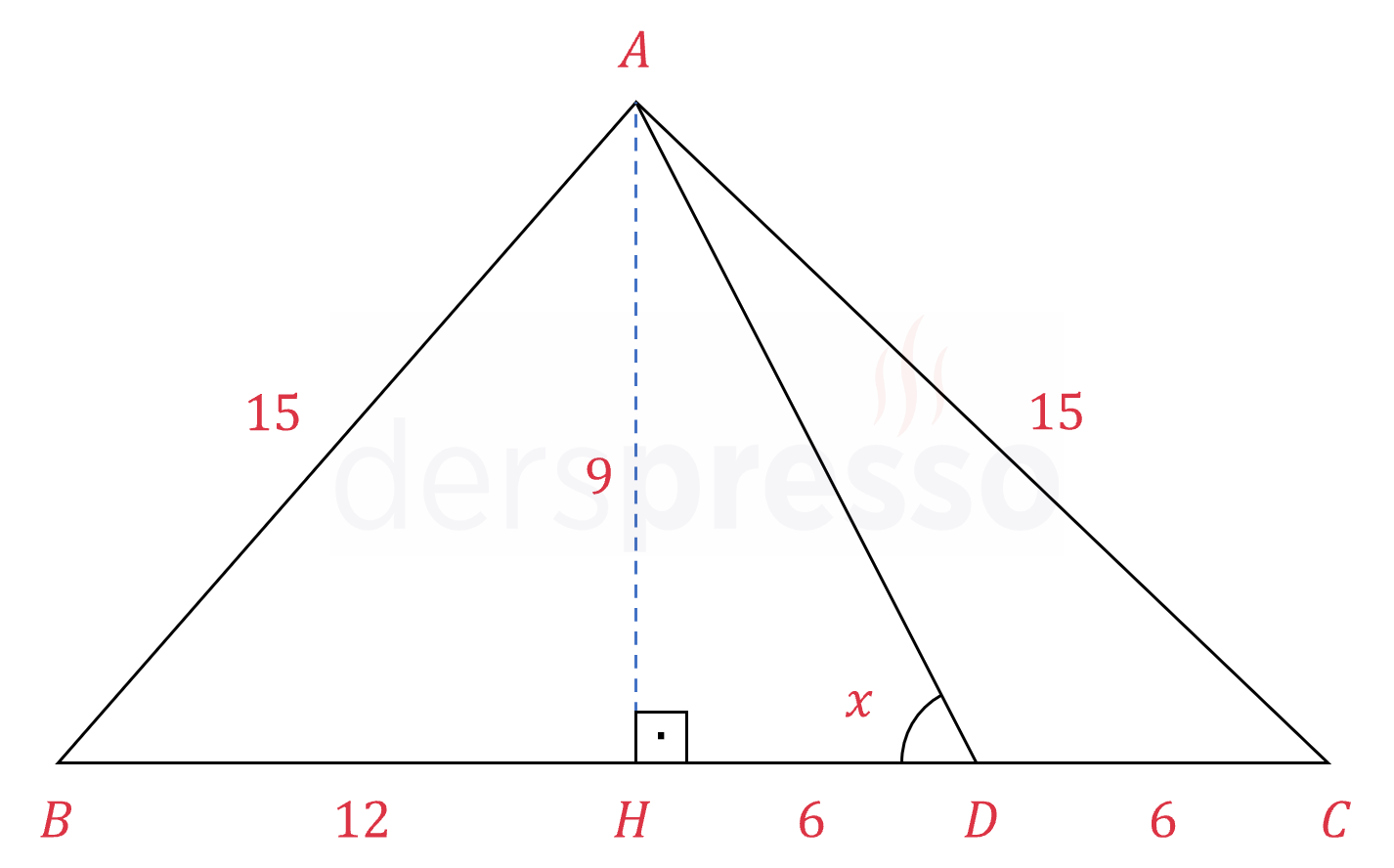
\( A \) köşesinden tabana bir dikme çizelim (mavi kesikli çizgi) ve tabanı kestiği noktaya \( H \) diyelim.
Çizdiğimiz bu doğru parçası tabana ait yüksekliktir.
\( [AH] \perp [BC] \)
\( ABC \) ikizkenar üçgen olduğu için bu yükseklik aynı zamanda kenarortaydır.
\( \abs{BH} = \abs{HC} = \dfrac{18 + 6}{2} = 12 \)
\( \abs{HD} = 6 \)
Kotanjant değeri komşu kenar uzunluğunun karşı kenar uzunluğuna oranına eşittir.
\( \cot{x} = \dfrac{\abs{HD}}{\abs{AH}} = \dfrac{6}{9} = \dfrac{2}{3} \) bulunur.
\( 0 \lt x \lt \frac{\pi}{2} \) olmak üzere,
\( \sqrt{5}^{\sin{x}} = 125^{\cos{x}} \)
olduğuna göre, \( \tan{x} \) değeri kaçtır?
Çözümü Göster\( (5^{\frac{1}{2}})^{\sin{x}} = (5^3)^{\cos{x}} \)
\( 5^{\frac{\sin{x}}{2}} = 5^{3\cos{x}} \)
İki üslü ifadenin eşitliğinde tabanlar aynı ve 0, 1 ve -1'den farklıysa üsler birbirine eşittir.
\( \dfrac{\sin{x}}{2} = 3\cos{x} \)
\( \sin{x} = 6\cos{x} \)
\( \dfrac{\sin{x}}{\cos{x}} = 6 \)
\( \tan{x} = 6 \) bulunur.
Aşağıda bir merdivenin bir duvar ve zemindeki iki farklı konumu verilmiştir.
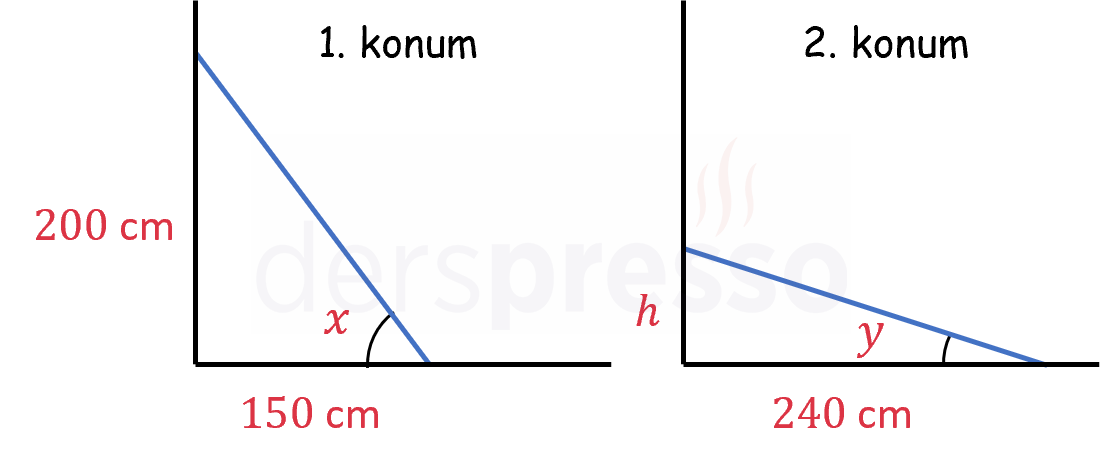
Merdivenin zemin ile yaptığı açı 1. konumda \( x \), 2. konumda \( y \) olmaktadır.
Buna göre, \( \sin{x}\tan{y} \) çarpımı kaçtır?
Çözümü GösterMerdivenin uzunluğuna \( a \) diyelim.
\( a \) uzunluğunu 1. konumu kullanarak Pisagor Teoremi ile bulalım.
\( 150^2 + 200^2 = a^2 \)
\( a = 250 \) cm
Merdivenin uzunluğu 2. konumda da aynı olur. Yine Pisagor Teoremi'ni kullanarak 2. konumda merdivenin yerden yüksekliğini bulalım.
\( h^2 + 240^2 = a^2 = 250^2 \)
\( h = \sqrt{250^2 - 240^2} = 70 \) cm
Oluşan üçgenlerin kenar uzunluklarını kullanarak istenen trigonometrik oranları bulalım.
\( \sin{x} = \dfrac{200}{250} = \dfrac{4}{5} \)
\( \tan{y} = \dfrac{70}{240} = \dfrac{7}{24} \)
\( \sin{x}\tan{y} = \dfrac{4}{5} \cdot \dfrac{7}{24} \)
\( = \dfrac{7}{30} \) bulunur.

Yukarıdaki gibi dar açılı bir \( ABC \) üçgeninde her zaman \( b\cos{\hat{A}} + a\cos{\hat{B}} = c \) olduğunu gösterin.
Çözümü Göster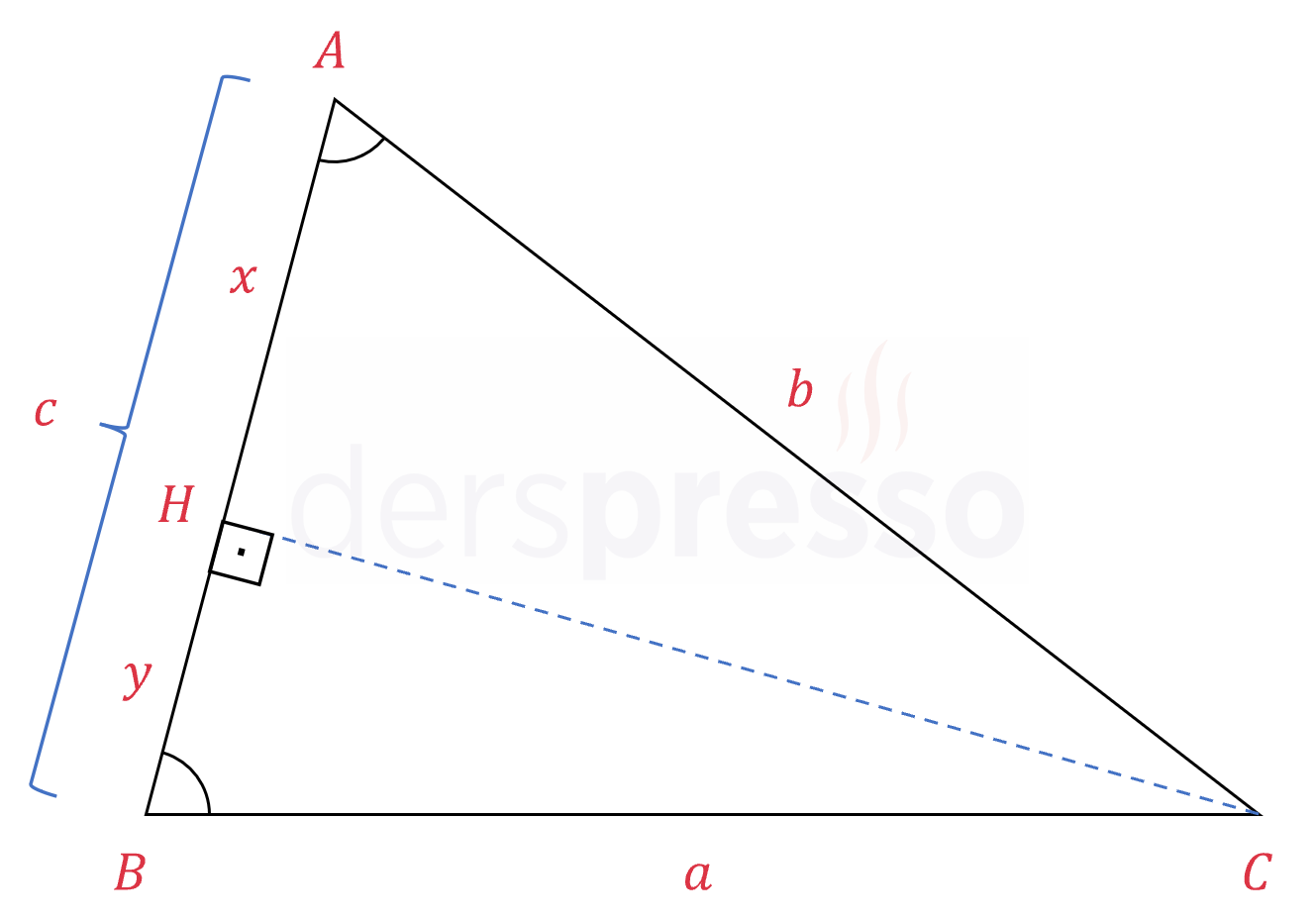
\( C \) köşesinden \( [AB] \) kenarına bir dikme çizelim (mavi kesikli çizgi) ve kenarı kestiği noktaya \( H \) diyelim.
\( [CH] \perp [AB] \)
\( [AH] = x \) ve \( [HB] = y \) diyelim.
\( \hat{A} \) ve \( \hat{B} \) açılarına ait kosinüs oranlarını yazalım.
\( \cos{\hat{A}} = \dfrac{x}{b} \Longrightarrow x = b\cos{\hat{A}} \)
\( \cos{\hat{B}} = \dfrac{y}{a} \Longrightarrow y = a\cos{\hat{B}} \)
\( x + y = c \)
\( x \) ve \( y \) değerlerini yerine koyalım.
\( b\cos{\hat{A}} + a\cos{\hat{B}} = c \) bulunur.

Kenar uzunlukları 16 ve 20 birim olan \( ABCD \) dikdörtgeni \( [DE] \) doğru parçası boyunca şekildeki gibi katlandığında \( A \) noktası \( F \) noktasına gelmektedir.
Buna göre, \( \sec{x} \) kaçtır?
Çözümü Göster\( \abs{DA} = \abs{DF} = 20 \)
Pisagor Teoremi ile \( \abs{CF} \) uzunluğunu bulalım.
\( \abs{DC}^2 + \abs{CF}^2 = \abs{DF}^2 \)
\( \abs{CF} = \sqrt{20^2 - 16^2} = 12 \)

\( \widehat{FEB} \) ve \( \widehat{EFB} \) açıları kendi aralarında, \( \widehat{EFB} \) ve \( \widehat{DFC} \) açıları da kendi aralarında tümler açılar oldukları için, \( \widehat{FEB} \) ve \( \widehat{DFC} \) açılarının ölçüleri eşittir.
\( m(\widehat{DFC}) = m(\widehat{FEB}) = x \)
\( x \) açısının sekant değerini hesaplayalım.
\( \sec{x} = \dfrac{\abs{DF}}{\abs{CF}} \)
\( = \dfrac{20}{12} = \dfrac{5}{3} \) bulunur.

\( ABCD \) bir yamuktur.
Şekilde verilen bilgilere göre \( \sin{x} + \cos{x} \) ifadesinin sonucu kaçtır?
Çözümü Göster\( [AD] \) kenarına paralel bir \( [EC] \) doğrusu çizelim.

\( AECD \) dörtgeni bir paralelkenar olur.
\( \abs{EC} = \abs{AD} = 8 \)
\( \abs{AE} = \abs{DC} = 2 \)
\( m(\widehat{DAE}) = m(\widehat{CEB}) = x \)
Buna göre \( \abs{EB} = 10 \) olur.
Oluşan \( ECB \) üçgeni 6-8-10 özel üçgeni olduğu için \( m(\widehat{ECB}) = 90° \) olur.
\( ECB \) dik üçgeninde \( \widehat{CEB} \) açısını kullanarak istenen sinüs ve kosinüs değerlerini bulalım.
\( \sin{x} + \cos{x} = \dfrac{6}{10} + \dfrac{8}{10} \)
\( = \dfrac{7}{5} \) bulunur.