Bölgeler Arası Dönüşümler
II., III. ya da IV. bölgedeki bir açının trigonometrik değerlerini I. bölgedeki, yani dar bir açı cinsinden bulmamızı sağlayan formüllere indirgeme formülleri denir.
Bölgeler ve İşaretler
Önceki bölümde birim çember üzerindeki bir \( A \) noktasının apsisinin o noktanın karşılık geldiği \( \alpha \) açısının kosinüs değerine, ordinatının da aynı açının sinüs değerine eşit olduğunu gördük.
Buna göre analitik düzlemin farklı bölgelerindeki noktaların apsis ve ordinat değerlerinin işareti, o bölgelerdeki açıların sinüs ve kosinüs değerlerinin işaretini de belirler. Apsis değerlerinin I. ve IV. bölgelerde pozitif, II. ve III. bölgelerde negatif, ordinat değerlerinin de I. ve II. bölgelerde pozitif, III. ve IV. bölgelerde negatif olduğunu düşünürsek sinüs ve kosinüs değerlerinin farklı bölgelerdeki işareti aşağıdaki gibi olur.
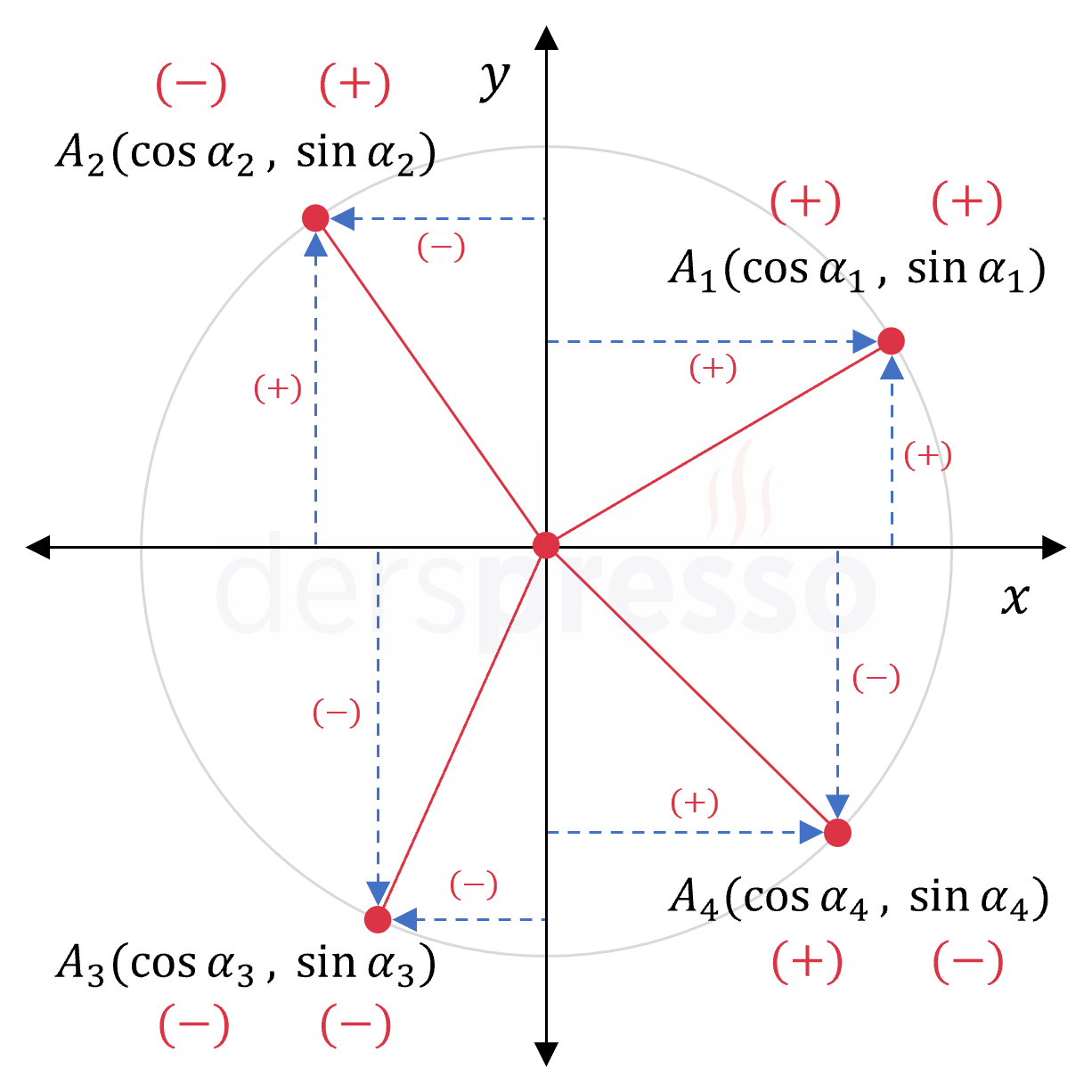
Sinüs ve kosinüs fonksiyonlarının işaretlerini kullanarak diğer 4 trigonometrik fonksiyonun farklı bölgelerdeki işaretlerini aşağıdaki şekilde belirleyebiliriz.
- Tanjant ve kotanjant fonksiyonları sinüs ve kosinüs fonksiyonlarının oranı şeklinde yazılabildiği için işaretleri bu fonksiyonların her bölgedeki oranının işareti ile aynıdır.
- Sekant ve kosekant fonksiyonları sırasıyla kosinüs ve sinüs fonksiyonlarının çarpmaya göre tersi olduğu için işaretleri bu fonksiyonların her bölgedeki işareti ile aynıdır.
Buna göre 6 trigonometrik fonksiyonun analitik düzlemin 4 bölgesindeki işaretleri aşağıdaki şekilde özetlenebilir.
Fonksiyonların farklı bölgelerdeki işaretlerini inceledikten sonra şimdi II., III. ve IV. bölgedeki açıların trigonometrik değerlerini I. bölgedeki bir açı cinsinden nasıl ifade edebileceğimizi görelim.
\( \pi \pm \alpha \) ve \( 2\pi - \alpha \) Formülleri
\( \alpha \) bir dar açı olmak üzere, dar olmayan bir açıyı \( \pi \pm \alpha \) ya da \( 2\pi - \alpha \) şeklinde yazarak bu açının trigonometrik değerlerini \( \alpha \) açısı cinsinden ifade edebiliriz. Bu yöntemde;
- Trigonometrik fonksiyon aynı kalır.
- Fonksiyonun açının bulunduğu bölgedeki işareti ifadenin önüne eklenir.
\( \sin{150°} = \sin(180° - 30°) \)
Sinüs II. bölgede pozitiftir.
\( = \sin{30°} \)
\( \cos{220°} = \cos(180° + 40°) \)
Kosinüs III. bölgede negatiftir.
\( = -\cos{40°} \)
\( \tan{310°} = \tan(360° - 50°) \)
Tanjant IV. bölgede negatiftir.
\( = -\tan{50°} \)
\( \csc{100°} = \csc(180° - 80°) \)
Kosekant II. bölgede pozitiftir.
\( = \csc{80°} \)
Şimdi bu formüllerin farklı bölgelerdeki noktaların eksenlere ve orijine göre simetri özelliklerini kullanarak nasıl türetildiğini inceleyelim.
II. Bölgeki Açılar
\( \alpha \) bir dar açı olmak üzere, II. bölgedeki \( \pi - \alpha \) açısı için sinüs ve kosinüs değerlerini bu açının I. bölgede \( y \) eksenine göre simetriği olan noktanın sinüs ve kosinüs değerleri cinsinden aşağıdaki şekilde yazabiliriz.
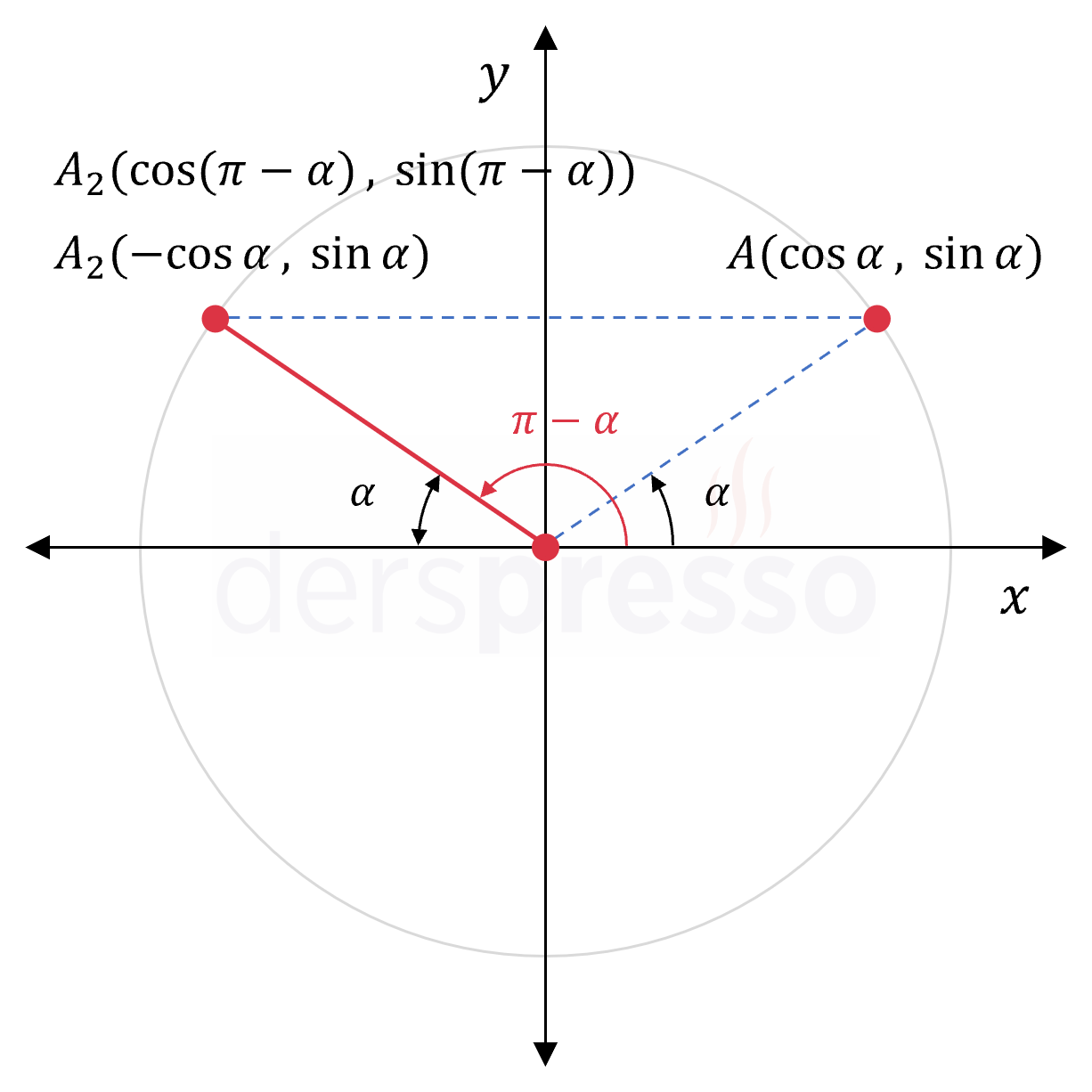
\( \sin(\pi - \alpha) = \sin{\alpha} \)
\( \cos(\pi - \alpha) = -\cos{\alpha} \)
\( \sin{160°} = \sin(180° - 20°) = \sin{20°} \)
\( \cos{\frac{5\pi}{6}} = \cos(\pi - \frac{\pi}{6}) = -\cos{\frac{\pi}{6}} \)
Bu iki oranı kullanarak diğer 4 fonksiyon için de benzer formülleri yazabiliriz.
\( \tan(\pi - \alpha) = \dfrac{\sin(\pi - \alpha)}{\cos(\pi - \alpha)} = -\tan{\alpha} \)
\( \cot(\pi - \alpha) = \dfrac{\cos(\pi - \alpha)}{\sin(\pi - \alpha)} = -\cot{\alpha} \)
\( \sec(\pi - \alpha) = \dfrac{1}{\cos(\pi - \alpha)} = -\sec{\alpha} \)
\( \csc(\pi - \alpha) = \dfrac{1}{\sin(\pi - \alpha)} = \csc{\alpha} \)
III. Bölgeki Açılar
\( \alpha \) bir dar açı olmak üzere, III. bölgedeki \( \pi + \alpha \) açısı için sinüs ve kosinüs değerlerini bu açının I. bölgede orijine göre simetriği olan noktanın sinüs ve kosinüs değerleri cinsinden aşağıdaki şekilde yazabiliriz.
\( \sin(\pi + \alpha) = -\sin{\alpha} \)
\( \cos(\pi + \alpha) = -\cos{\alpha} \)
\( \sin{250°} = \sin(180° + 70°) = -\sin{70°} \)
\( \cos{\frac{4\pi}{3}} = \cos(\pi + \frac{\pi}{3}) = -\cos{\frac{\pi}{3}} \)
Bu iki oranı kullanarak diğer 4 fonksiyon için de benzer formülleri yazabiliriz.
\( \tan(\pi + \alpha) = \dfrac{\sin(\pi + \alpha)}{\cos(\pi + \alpha)} = \tan{\alpha} \)
\( \cot(\pi + \alpha) = \dfrac{\cos(\pi + \alpha)}{\sin(\pi + \alpha)} = \cot{\alpha} \)
\( \sec(\pi + \alpha) = \dfrac{1}{\cos(\pi + \alpha)} = -\sec{\alpha} \)
\( \csc(\pi + \alpha) = \dfrac{1}{\sin(\pi + \alpha)} = -\csc{\alpha} \)
IV. Bölgeki Açılar
\( \alpha \) bir dar açı olmak üzere, IV. bölgedeki \( 2\pi - \alpha \) açısı için sinüs ve kosinüs değerlerini bu açının I. bölgede \( x \) eksenine göre simetriği olan noktanın sinüs ve kosinüs değerleri cinsinden aşağıdaki şekilde yazabiliriz.
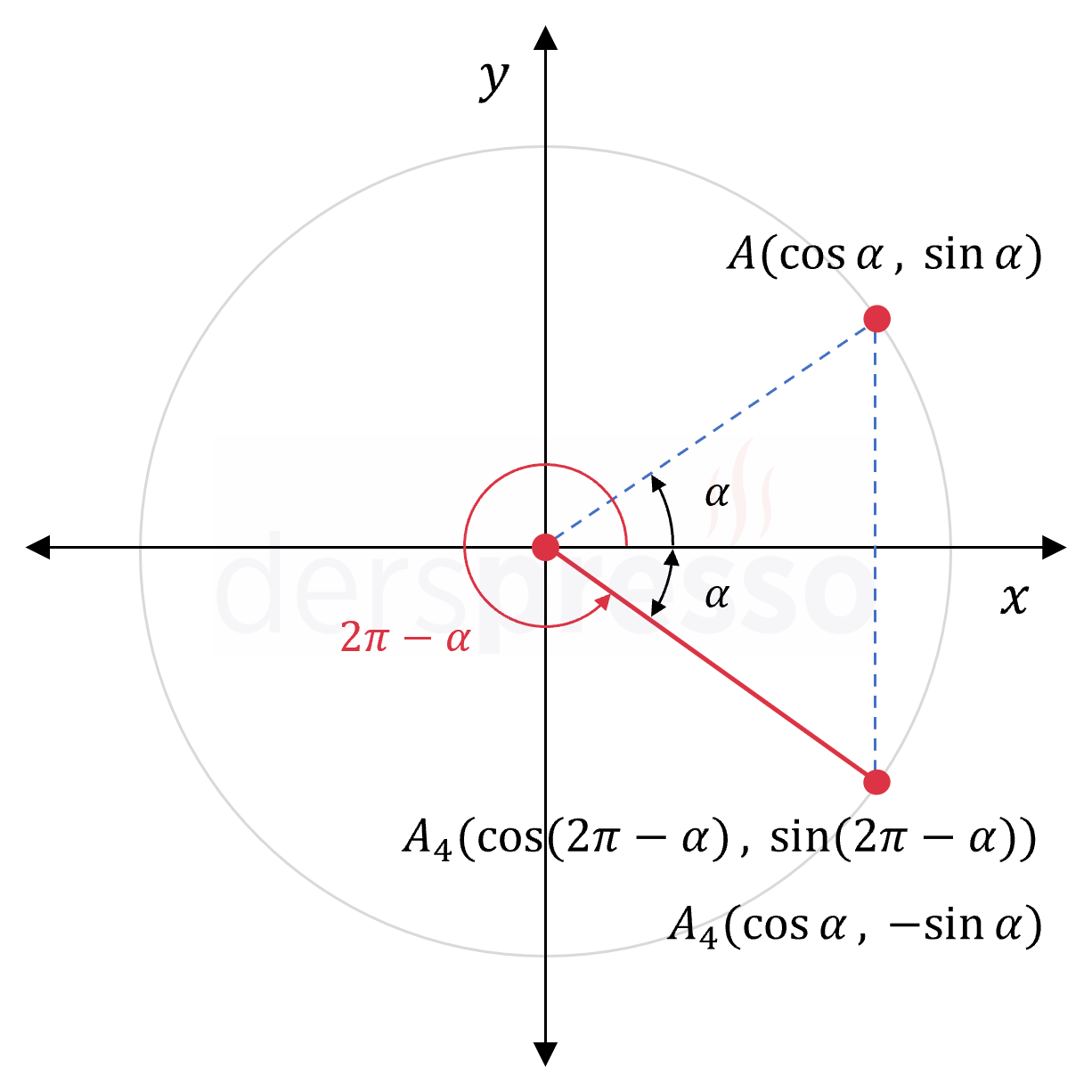
\( \sin(2\pi - \alpha) = -\sin{\alpha} \)
\( \cos(2\pi - \alpha) = \cos{\alpha} \)
\( \sin{350°} = \sin(360° - 10°) = -\sin{10°} \)
\( \cos{\frac{11\pi}{6}} = \cos(2\pi - \frac{\pi}{6}) = \cos{\frac{\pi}{6}} \)
Bu iki oranı kullanarak diğer 4 fonksiyon için de benzer formülleri yazabiliriz.
\( \tan(2\pi - \alpha) = \dfrac{\sin(2\pi - \alpha)}{\cos(2\pi - \alpha)} = -\tan{\alpha} \)
\( \cot(2\pi - \alpha) = \dfrac{\cos(2\pi - \alpha)}{\sin(2\pi - \alpha)} = -\cot{\alpha} \)
\( \sec(2\pi - \alpha) = \dfrac{1}{\cos(2\pi - \alpha)} = \sec{\alpha} \)
\( \csc(2\pi - \alpha) = \dfrac{1}{\sin(2\pi - \alpha)} = -\csc{\alpha} \)
\( \frac{\pi}{2} \pm \alpha \) ve \( \frac{3\pi}{2} \pm \alpha \) Formülleri
\( \alpha \) bir dar açı olmak üzere, dar olmayan bir açıyı \( \frac{\pi}{2} + \alpha \) ya da \( \frac{3\pi}{2} \pm \alpha \) şeklinde yazarak bu açının trigonometrik değerlerini \( \alpha \) açısı cinsinden ifade edebiliriz. Bu yöntemde;
- Trigonometrik fonksiyon sin - cos, tan - cot ve sec - csc olacak şekilde kendi aralarında yer değiştirir.
- Orijinal fonksiyonun (ilk maddede değiştirildiği fonksiyon değil) açının bulunduğu bölgedeki işareti ifadenin önüne eklenir.
\( \sin{150°} = \sin(90° + 60°) \)
Sinüs II. bölgede pozitiftir.
\( = \cos{60°} \)
\( \cos{220°} = \cos(270° - 50°) \)
Kosinüs III. bölgede negatiftir.
\( = -\sin{50°} \)
\( \tan{310°} = \tan(270° + 40°) \)
Tanjant IV. bölgede negatiftir.
\( = -\cot{40°} \)
\( \csc{100°} = \csc(90° + 10°) \)
Kosekant II. bölgede pozitiftir.
\( = \sec{10°} \)
Şimdi bu formüllerin farklı bölgelerdeki noktaların eksenlere ve orijine göre simetri özelliklerini kullanarak nasıl türetildiğini inceleyelim.
I. Bölge Dönüşümleri
\( A \) noktasının \( y = x \) doğrusuna göre simetriği olan \( A_1 \) noktasının \( x \) ekseni ile yaptığı yönlü açı \( \frac{\pi}{2} - \alpha \) olur. Noktanın \( y = x \) doğrusuna göre simetrisinden bu noktanın koordinatları \( A_1(\sin{\alpha}, \cos{\alpha}) \) olur.
\( \sin(\frac{\pi}{2} - \alpha) = \cos{\alpha} \)
\( \cos(\frac{\pi}{2} - \alpha) = \sin{\alpha} \)
\( \sin{75°} = \sin(90° - 15°) = \cos{15°} \)
\( \cos{\frac{\pi}{6}} = \cos(\frac{\pi}{2} - \frac{\pi}{3}) = \sin{\frac{\pi}{3}} \)
Bu iki oranı kullanarak diğer 4 fonksiyon için de benzer formülleri yazabiliriz.
\( \tan(\frac{\pi}{2} - \alpha) = \dfrac{\sin(\frac{\pi}{2} - \alpha)}{\cos(\frac{\pi}{2} - \alpha)} = \cot{\alpha} \)
\( \cot(\frac{\pi}{2} - \alpha) = \dfrac{\cos(\frac{\pi}{2} - \alpha)}{\sin(\frac{\pi}{2} - \alpha)} = \tan{\alpha} \)
\( \sec(\frac{\pi}{2} - \alpha) = \dfrac{1}{\cos(\frac{\pi}{2} - \alpha)} = \csc{\alpha} \)
\( \csc(\frac{\pi}{2} - \alpha) = \dfrac{1}{\sin(\frac{\pi}{2} - \alpha)} = \sec{\alpha} \)
II. Bölge Dönüşümleri
\( \alpha \) bir dar açı olmak üzere, II. bölgedeki \( \frac{\pi}{2} + \alpha \) açısı için sinüs ve kosinüs değerlerini bu açının I. bölgede \( y \) eksenine göre simetriği olan noktanın sinüs ve kosinüs değerleri cinsinden aşağıdaki şekilde yazabiliriz.
\( \sin(\frac{\pi}{2} + \alpha) = \cos{\alpha} \)
\( \cos(\frac{\pi}{2} + \alpha) = -\sin{\alpha} \)
\( \sin{125°} = \sin(90° + 35°) = \cos{35°} \)
\( \cos{\frac{3\pi}{4}} = \cos(\frac{\pi}{2} + \frac{\pi}{4}) = -\sin{\frac{\pi}{4}} \)
Bu iki oranı kullanarak diğer 4 fonksiyon için de benzer formülleri yazabiliriz.
\( \tan(\frac{\pi}{2} + \alpha) = \dfrac{\sin(\frac{\pi}{2} + \alpha)}{\cos(\frac{\pi}{2} + \alpha)} = -\cot{\alpha} \)
\( \cot(\frac{\pi}{2} + \alpha) = \dfrac{\cos(\frac{\pi}{2} + \alpha)}{\sin(\frac{\pi}{2} + \alpha)} = -\tan{\alpha} \)
\( \sec(\frac{\pi}{2} + \alpha) = \dfrac{1}{\cos(\frac{\pi}{2} + \alpha)} = -\csc{\alpha} \)
\( \csc(\frac{\pi}{2} + \alpha) = \dfrac{1}{\sin(\frac{\pi}{2} + \alpha)} = \sec{\alpha} \)
III. Bölge Dönüşümleri
\( \alpha \) bir dar açı olmak üzere, III. bölgedeki \( \frac{3\pi}{2} - \alpha \) açısı için sinüs ve kosinüs değerlerini bu açının I. bölgede orijine göre simetriği olan noktanın sinüs ve kosinüs değerleri cinsinden aşağıdaki şekilde yazabiliriz.
\( \sin(\frac{3\pi}{2} - \alpha) = -\cos{\alpha} \)
\( \cos(\frac{3\pi}{2} - \alpha) = -\sin{\alpha} \)
\( \sin{220°} = \sin(270° - 50°) = -\cos{50°} \)
\( \cos{\frac{17\pi}{12}} = \cos(\frac{3\pi}{2} - \frac{\pi}{12}) = -\sin{\frac{\pi}{12}} \)
Bu iki oranı kullanarak diğer 4 fonksiyon için de benzer formülleri yazabiliriz.
\( \tan(\frac{3\pi}{2} - \alpha) = \dfrac{\sin(\frac{3\pi}{2} - \alpha)}{\cos(\frac{3\pi}{2} - \alpha)} = \cot{\alpha} \)
\( \cot(\frac{3\pi}{2} - \alpha) = \dfrac{\cos(\frac{3\pi}{2} - \alpha)}{\sin(\frac{3\pi}{2} - \alpha)} = \tan{\alpha} \)
\( \sec(\frac{3\pi}{2} - \alpha) = \dfrac{1}{\cos(\frac{3\pi}{2} - \alpha)} = -\csc{\alpha} \)
\( \csc(\frac{3\pi}{2} - \alpha) = \dfrac{1}{\sin(\frac{3\pi}{2} - \alpha)} = -\sec{\alpha} \)
IV. Bölge Dönüşümleri
\( \alpha \) bir dar açı olmak üzere, III. bölgedeki \( \frac{3\pi}{2} + \alpha \) açısı için sinüs ve kosinüs değerlerini bu açının I. bölgede \( x \) eksenine göre simetriği olan noktanın sinüs ve kosinüs değerleri cinsinden aşağıdaki şekilde yazabiliriz.
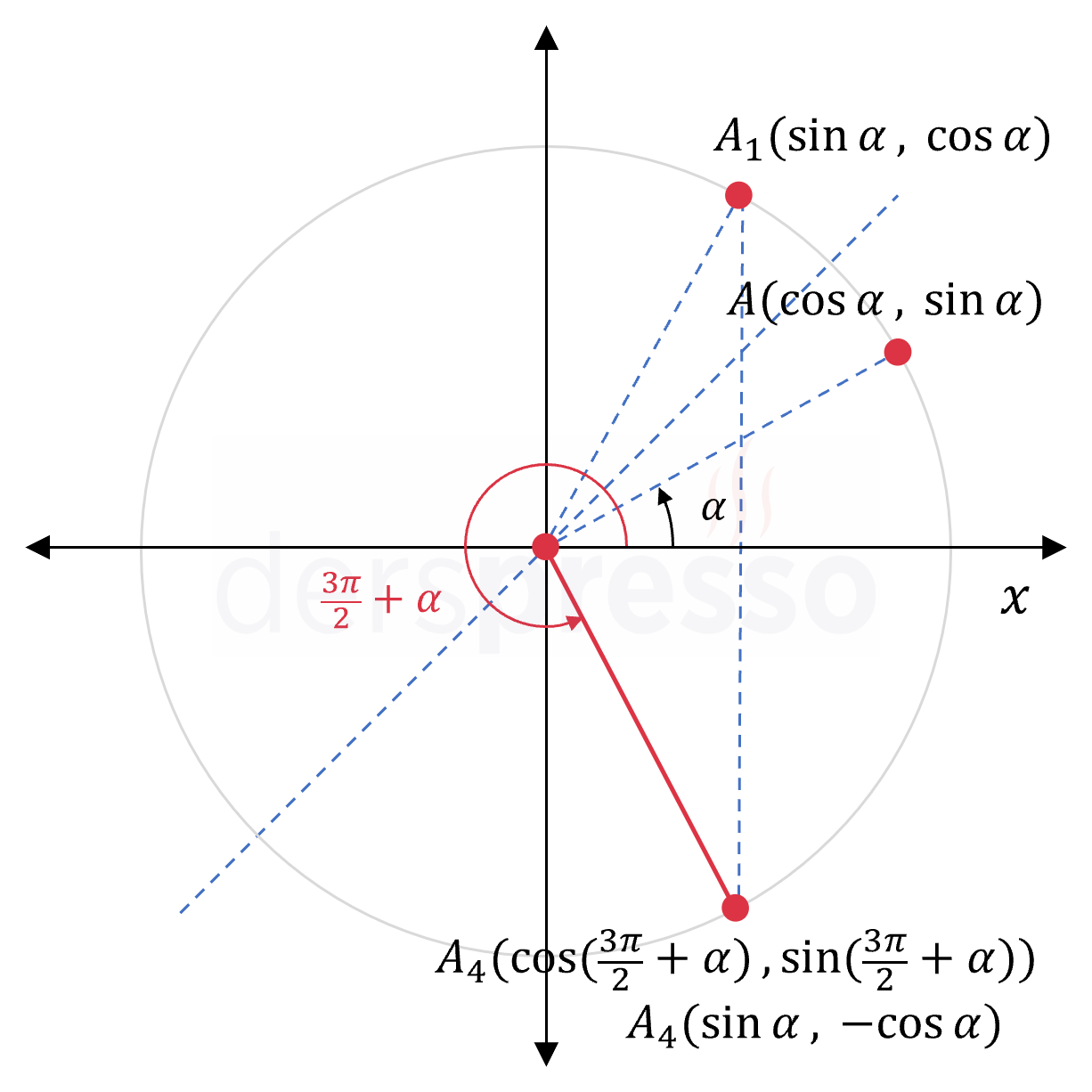
\( \sin(\frac{3\pi}{2} + \alpha) = -\cos{\alpha} \)
\( \cos(\frac{3\pi}{2} + \alpha) = \sin{\alpha} \)
\( \sin{305°} = \sin(270° + 35°) = -\cos{35°} \)
\( \cos{\frac{5\pi}{3}} = \cos(\frac{3\pi}{2} + \frac{\pi}{6}) = \sin{\frac{\pi}{6}} \)
Bu iki oranı kullanarak diğer 4 fonksiyon için de benzer formülleri yazabiliriz.
\( \tan(\frac{3\pi}{2} + \alpha) = \dfrac{\sin(\frac{3\pi}{2} + \alpha)}{\cos(\frac{3\pi}{2} + \alpha)} = -\cot{\alpha} \)
\( \cot(\frac{3\pi}{2} + \alpha) = \dfrac{\cos(\frac{3\pi}{2} + \alpha)}{\sin(\frac{3\pi}{2} + \alpha)} = -\tan{\alpha} \)
\( \sec(\frac{3\pi}{2} + \alpha) = \dfrac{1}{\cos(\frac{3\pi}{2} + \alpha)} = \csc{\alpha} \)
\( \csc(\frac{3\pi}{2} + \alpha) = \dfrac{1}{\sin(\frac{3\pi}{2} + \alpha)} = -\sec{\alpha} \)
Birbirini Tamamlayan Açılar
Birbirini belirli bir açıya tamamlayan açılar arasında aşağıdaki özdeşlikleri yazabiliriz.
Birbirini 90°'ye Tamamlayan Açılar
Birbirini 90°'ye tamamlayan (tümler) açılar arasında aşağıdaki dönüşümler geçerlidir.
\( \alpha + \beta =\dfrac{\pi}{2} \) olmak üzere,
\( \sin{\alpha} = \cos{\beta} \)
\( \tan{\alpha} = \cot{\beta} \)
\( \tan{55°} = \cot{35°} \)
Birbirini 180°'ye Tamamlayan Açılar
Birbirini 180°'ye tamamlayan (bütünler) açılar arasında aşağıdaki dönüşümler geçerlidir.
\( \alpha + \beta = \pi \) olmak üzere,
\( \sin{\alpha} = \sin{\beta} \)
\( \cos{\alpha} = -\cos{\beta} \)
\( \tan{\alpha} = -\tan{\beta} \)
\( \cot{\alpha} = -\cot{\beta} \)
\( \cos{130°} = -\cos{50°} \)
Birbirini 360°'ye Tamamlayan Açılar
Birbirini 360°'ye tamamlayan açılar arasında aşağıdaki dönüşümler geçerlidir.
\( \alpha + \beta = 2\pi \) olmak üzere,
\( \sin{\alpha} = -\sin{\beta} \)
\( \cos{\alpha} = \cos{\beta} \)
\( \tan{\alpha} = -\tan{\beta} \)
\( \cot{\alpha} = -\cot{\beta} \)
\( \sin{220°} = -\sin{140°} \)
Aşağıdaki trigonometrik fonksiyonların değerlerini bulunuz.
(a) \( \sin{225°} \)
(b) \( \cos{210°} \)
(c) \( \cot{300°} \)
Çözümü Göster(a) seçeneği:
225° III. bölgededir ve sinüs bu bölgede negatiftir.
\( \sin{225°} = \sin(180° + 45°) \)
\( = -\sin{45°} = -\dfrac{\sqrt{2}}{2} \)
(b) seçeneği:
210° III. bölgededir ve kosinüs bu bölgede negatiftir.
\( \cos{210°} = -\cos(180° + 30°) \)
\( = -\cos{30°} = -\dfrac{\sqrt{3}}{2} \)
(c) seçeneği:
300° IV. bölgededir ve kotanjant bu bölgede negatiftir.
\( \cot{300°} = \cot(360° - 60°) \)
\( = -\cot{60°} = -\dfrac{\sqrt{3}}{3} \)
Aşağıdaki trigonometrik fonksiyonların değerlerini bulunuz.
(a) \( \tan{\dfrac{11\pi}{6}} \)
(b) \( \cos{\dfrac{5\pi}{4}} \)
(c) \( \sin{\dfrac{5\pi}{6}} \)
Çözümü Göster(a) seçeneği:
\( \frac{11\pi}{6} \) IV. bölgededir ve tanjant bu bölgede negatiftir.
\( \tan{\dfrac{11\pi}{6}} = \tan(2\pi - \dfrac{\pi}{6}) \)
\( = -\tan{\dfrac{\pi}{6}} = -\dfrac{\sqrt{3}}{3} \)
(b) seçeneği:
\( \frac{5\pi}{4} \) III. bölgededir ve kosinüs bu bölgede negatiftir.
\( \cos{\dfrac{5\pi}{4}} = \cos(\pi + \dfrac{\pi}{4}) \)
\( = -\cos{\dfrac{\pi}{4}} = -\dfrac{\sqrt{2}}{2} \)
(c) seçeneği:
\( \frac{5\pi}{6} \) II. bölgededir ve sinüs bu bölgede pozitiftir.
\( \sin{\dfrac{5\pi}{6}} = \sin(\pi - \dfrac{\pi}{6}) \)
\( = \sin{\dfrac{\pi}{6}} = \dfrac{1}{2} \)
Aşağıdaki trigonometrik fonksiyonları I. bölgedeki açılar cinsinden ifade ediniz.
(a) \( \sin{318°} \)
(b) \( \cot{265°} \)
(c) \( \cos{143°} \)
Çözümü Göster(a) seçeneği:
318° IV. bölgededir ve sinüs bu bölgede negatiftir.
\( \sin{318°} = \sin(360° - 42°) \)
\( = -\sin{42°} \)
(b) seçeneği:
265° III. bölgededir ve kotanjant bu bölgede pozitiftir.
\( \cot{265°} = \cot(180° + 85°) \)
\( = \cot{85°} \)
(c) seçeneği:
143° II. bölgededir ve kosinüs bu bölgede negatiftir.
\( \cos{143°} = \cos(180° - 37°) \)
\( = -\cos{37°} \)
Aşağıdaki trigonometrik fonksiyonları I. bölgedeki açılar cinsinden ifade ediniz.
(a) \( \tan{\dfrac{4\pi}{5}} \)
(b) \( \cos{\dfrac{17\pi}{10}} \)
(c) \( \sin{\dfrac{13\pi}{9}} \)
Çözümü Göster(a) seçeneği:
\( \frac{4\pi}{5} \) II. bölgededir ve tanjant bu bölgede negatiftir.
\( \tan{\dfrac{4\pi}{5}} = \tan(\pi - \dfrac{\pi}{5}) \)
\( = -\tan{\dfrac{\pi}{5}} \)
(b) seçeneği:
\( \frac{17\pi}{10} \) IV. bölgededir ve kosinüs bu bölgede pozitiftir.
\( \cos{\dfrac{17\pi}{10}} = \cos(2\pi - \dfrac{3\pi}{10}) \)
\( = \cos{\dfrac{3\pi}{10}} \)
(c) seçeneği:
\( \frac{13\pi}{9} \) III. bölgededir ve sinüs bu bölgede negatiftir.
\( \sin{\dfrac{13\pi}{9}} = \sin(\pi + \dfrac{4\pi}{9}) \)
\( = -\sin{\dfrac{4\pi}{9}} \)
Aşağıdaki trigonometrik fonksiyonları I. bölgedeki açılar cinsinden ifade ediniz.
(a) \( \cos{944°} \)
(b) \( \cot{2789°} \)
(c) \( \tan{3557°} \)
Çözümü GösterÖncelikle verilen trigonometrik ifadelerdeki açıların esas ölçülerini bulalım.
Ölçüsü pozitif olan açıların esas ölçüsünü bulmak için açı ölçüsü 360°'ye bölünür. Bölme işleminin kalanı açının esas ölçüsüdür.
(a) seçeneği:
\( 944° = 2 \cdot 360° + 224° \)
Buna göre 944°'nin esas ölçüsü 224° olur.
\( \cos{944°} = \cos{224°} \)
224° III. bölgededir ve kosinüs bu bölgede negatiftir.
\( = \cos(180° + 44°) \)
\( = -\cos{44°} \)
(b) seçeneği:
\( 2789° = 7 \cdot 360° + 269° \)
Buna göre 2789°'nin esas ölçüsü 269° olur.
\( \cot{2789°} = \cot{269°} \)
269° III. bölgededir ve kotanjant bu bölgede pozitiftir.
\( = \cot(180° + 89°) \)
\( = \cot{89°} \)
(c) seçeneği:
\( 3557° = 9 \cdot 360° + 317° \)
Buna göre 3557°'nin esas ölçüsü 317° olur.
\( \tan{3557°} = \tan{317°} \)
317° IV. bölgededir ve tanjant bu bölgede negatiftir.
\( = \tan(360° - 43°) \)
\( = -\tan{43°} \)
Aşağıdaki trigonometrik fonksiyonları I. bölgedeki açılar cinsinden ifade ediniz.
(a) \( \tan{\dfrac{21\pi}{5}} \)
(b) \( \cos{\dfrac{39\pi}{7}} \)
(c) \( \sin{\dfrac{107\pi}{8}} \)
Çözümü GösterÖncelikle verilen trigonometrik ifadelerdeki açıların esas ölçülerini bulalım.
Ölçüsü pozitif olan açıların esas ölçüsünü bulmak için açı ölçüsü içindeki \( 2\pi \)'nin katı olan en büyük sayı çıkarılır. Eğer açı ölçüsü kesirli ise paydaki \( \pi \)'nin katsayısı paydanın 2 katına bölünerek kalan bulunur ve bu kalan paydaki katsayının yerine yazılır.
(a) seçeneği:
Paydaki katsayı olan 21'in paydanın iki katı olan 10'a bölümünden kalan 1 olduğu için esas ölçü \( \frac{\pi}{5} \) olur.
\( \dfrac{21\pi}{5} = 2 \cdot 2\pi + \dfrac{\pi}{5} \)
\( \tan{\dfrac{21\pi}{5}} = \tan{\dfrac{\pi}{5}} \)
\( \frac{\pi}{5} \) I. bölgededir.
\( = \tan{\dfrac{\pi}{5}} \)
(b) seçeneği:
Paydaki katsayı olan 39'un paydanın iki katı olan 14'e bölümünden kalan 11 olduğu için esas ölçü \( \frac{11\pi}{7} \) olur.
\( \dfrac{39\pi}{7} = 2 \cdot 2\pi + \dfrac{11\pi}{7} \)
\( \cos{\dfrac{39\pi}{7}} = \cos{\dfrac{11\pi}{7}} \)
\( \frac{11\pi}{7} \) IV. bölgededir ve kosinüs bu bölgede pozitiftir.
\( = \cos(2\pi - \dfrac{3\pi}{7}) \)
\( = \cos{\dfrac{3\pi}{7}} \)
(c) seçeneği:
Paydaki katsayı olan 107'nin paydanın iki katı olan 16'ya bölümünden kalan 11 olduğu için esas ölçü \( \frac{11\pi}{8} \) olur.
\( \dfrac{107\pi}{8} = 6 \cdot 2\pi + \dfrac{11\pi}{8} \)
\( \sin{\dfrac{107\pi}{8}} = \sin{\dfrac{11\pi}{8}} \)
\( \frac{11\pi}{8} \) III. bölgededir ve sinüs bu bölgede negatiftir.
\( = \sin(\pi + \dfrac{3\pi}{8}) \)
\( = -\sin{\dfrac{3\pi}{8}} \)
\( \cos{20°} = x \) olduğuna göre,
\( \sin{110°} \)'nin \( x \) cinsinden değeri nedir?
Çözümü Göster\( 110° \) II. bölgededir ve sinüs bu bölgede pozitiftir.
\( \sin{110°} = \sin(180° - 70°) \)
\( = \sin{70°} \)
Tümler açıların sinüs ve kosinüs değerleri birbirine eşittir.
\( = \cos{20°} \)
\( = x \) bulunur.
\( \cos{70°} = x \) olduğuna göre,
\( \sin(-160°) \)'nin \( x \) cinsinden değeri nedir?
Çözümü Göster\( -160° \)'nin esas ölçüsü \( -160 + 360 = 200° \) olur.
\( \sin(-160°) = \sin{200°} \)
\( 200° \) III. bölgededir ve sinüs bu bölgede negatiftir.
\( = \sin(180 + 20°) = -\sin{20°} \)
Tümler açıların sinüs ve kosinüs değerleri birbirine eşittir.
\( = -\cos{70°} \)
\( = -x \) bulunur.
\( x + y = \dfrac{\pi}{2} \) olduğuna göre,
\( \tan(3x + 4y) \) ifadesinin en sade halini bulunuz.
Çözümü Göster\( \tan(3x + 4y) = \tan(3(x + y) + y) \)
\( = \tan(\frac{3\pi}{2} + y) \)
Tanjant IV. bölgede negatiftir.
\( = -\cot{y} \)
\( 0 \lt x \lt \dfrac{\pi}{2} \) olmak üzere,
Aşağıdaki ifadelerden hangileri doğrudur?
I. \( \cos{(\frac{3\pi}{2} - x) = \sin(\pi - x)} \)
II. \( -\sin{(\frac{\pi}{2} + x)} = \sin{(\frac{3\pi}{2} - x)} \)
III. \( \tan{(2\pi - x)} = \cot{(\frac{\pi}{2} - x)} \)
IV. \( \sec{(\frac{3\pi}{2} + x)} = -\csc{(\pi - x)} \)
Çözümü GösterI. öncül:
\( \cos{(\frac{3\pi}{2} - x)} = -\sin{x} \)
\( \sin{(\pi - x)} = \sin{x} \)
I. öncül yanlıştır.
II. öncül:
\( -\sin{(\frac{\pi}{2} + x)} = -\cos{x} \)
\( \sin{(\frac{3\pi}{2} - x)} = -\cos{x} \)
II. öncül doğrudur.
III. öncül:
\( \tan{(2\pi - x)} = -\tan{x} \)
\( \cot{(\frac{\pi}{2} - x)} = \tan{x} \)
III. öncül yanlıştır.
IV. öncül:
\( \sec{(\frac{3\pi}{2} + x)} = \dfrac{1}{\cos{(\frac{3\pi}{2} + x)}} = \dfrac{1}{\sin{x}} \)
\( -\csc{(\pi - x)} = \dfrac{1}{-\sin{(\pi - x)}} = -\dfrac{1}{\sin{x}} \)
IV. öncül yanlıştır.
Buna göre sadece II. öncül doğrudur.
\( 0 \lt x \lt \dfrac{\pi}{2} \) olmak üzere,
Aşağıdakilerden hangilerinin değeri \( \sin(\pi + x) \) ile aynıdır?
I. \( \sin(-\pi - x) \)
II. \( -\sin(-x) \)
III. \( -\sin(\pi - x) \)
IV. \( \cos(\dfrac{\pi}{2} + x) \)
Çözümü GösterSinüs fonksiyonu üçüncü bölgede negatiftir.
\( \sin(\pi + x) = -\sin{x} \)
I. öncül
\( \sin(-\pi - x) = \sin[-(\pi + x)] \)
Sinüs fonksiyonu tek fonksiyondur.
\( = -\sin(\pi + x) = \sin{x} \)
II. öncül
\( -\sin(-x) = -(-\sin{x}) \)
\( = \sin{x} \)
III. öncül
Sinüs fonksiyonu ikinci bölgede pozitiftir.
\( -\sin(\pi - x) = -\sin{x} \)
IV. öncül
Kosinüs fonksiyonu ikinci bölgede negatiftir.
\( \cos(\dfrac{\pi}{2} + x) = -\sin{x} \)
Buna göre III. ve IV. öncüllerin değeri verilen ifadeye eşittir.
\( \cos{155°} = x \) ise,
\( \cos{205°} + \sin{655°} \) ifadesinin \( x \) cinsinden değeri nedir?
Çözümü Göster\( 155° \) II. bölgededir ve kosinüs bu bölgede negatiftir.
\( x = \cos{155°} = \cos(180° - 25°) \)
\( = -\cos{25°} \)
Buna göre \( \cos{25°} = -x \) olur.
\( 205° \) III. bölgededir ve kosinüs bu bölgede negatiftir.
\( \cos{205°} = \cos(180° + 25°) \)
\( = -\cos{25°} = -(-x) = x \)
\( 655° \)'nin esas ölçüsü \( 655 - 360 = 295° \) olur.
\( \sin{655°} = \sin{295°} \)
\( 295° \) IV. bölgededir ve sinüs bu bölgede negatiftir.
\( \sin{295°} = \sin(270° + 25°) \)
\( = -\cos{25°} = -(-x) = x \)
Soruda istenen ifadeyi \( x \) cinsinden yazalım.
\( \cos{205°} + \sin{655°} = x + x \)
\( = 2x \) bulunur.
\( \dfrac{\sin(9\pi + x)}{\cos(\frac{43\pi}{2} + x)} + \dfrac{\tan(20\pi - x)}{\cot(x - \frac{39\pi}{2})} \) işleminin sonucu kaçtır?
Çözümü GösterTrigonometrik ifadelerin içindeki değerlerin esas ölçülerini yazalım.
\( \dfrac{\sin(\pi + x)}{\cos(\frac{3\pi}{2} + x)} + \dfrac{\tan(-x)}{\cot(x + \frac{\pi}{2})} \)
Bölgeler arası dönüşüm formüllerini kullanalım.
\( = \dfrac{-\sin{x}}{\sin{x}} + \dfrac{-\tan{x}}{-\tan{x}} \)
\( = -1 + 1 = 0 \) bulunur.
Bir \( ABC \) üçgeninin köşelerine ait açıların ölçüleri \( a, b, c \) olduğuna göre,
\( \cos(a + c) + \cos{b} \) ifadesinin eşiti nedir?
Çözümü GösterÜçgenin iç açıları toplamı 180°'dir.
\( a + b + c = 180° \)
\( a + c = 180° - b \)
Ölçüleri eşit açıların kosinüsleri de eşittir.
\( \cos(a + c) = \cos(180° - b) \)
Kosinüs II. bölgede negatiftir.
\( \cos(a + c) = -\cos{b} \)
Sorudaki ifadenin değerini bulalım.
\( \cos(a + c) + \cos{b} = -\cos{b} + \cos{b} = 0 \) bulunur.
\( 2x - 3y = \pi \) olmak üzere,
\( \dfrac{\sin(2x - 4y)}{\cos(4x - 5y)} \) ifadesinin en sade halini bulunuz.
Çözümü GösterSinüs ve kosinüs ifadelerinin içine \( y \) ekleyip çıkararak parantez içinde \( 2x - 3y \) elde etmeye çalışalım.
\( \dfrac{\sin(2x - 4y + y - y)}{\cos(4x - 5y + y - y)} \)
\( = \dfrac{\sin(2x - 3y - y)}{\cos(4x - 6y + y)} \)
\( = \dfrac{\sin(2x - 3y - y)}{\cos[2(2x - 3y) + y]} \)
\( 2x - 3y = \pi \) yazalım.
\( = \dfrac{\sin(\pi - y)}{\cos(2\pi + y)} \)
Sinüs II. bölgede pozitiftir.
\( = \dfrac{\sin{y}}{\cos{y}} = \tan{y} \) bulunur.
\( 0 \lt x \lt 2 \pi \) olmak üzere,
\( \dfrac{\cos(\frac{3\pi}{2} + x)}{\cot(x - \frac{\pi}{2})} = \dfrac{\sqrt{3}}{2} \) olduğuna göre,
\( x \)'in alabileceği değerler nelerdir?
Çözümü Göster\( \cot(x - \frac{\pi}{2}) = \cot(x - \frac{\pi}{2} + 2\pi) \)
\( = \cot(\frac{3\pi}{2} + x) \)
\( \dfrac{\cos(\frac{3\pi}{2} + x)}{\cot(\frac{3\pi}{2} + x)} = \dfrac{\sqrt{3}}{2} \)
Kosinüs IV. bölgede pozitif, kotanjant IV. bölgede negatiftir.
\( \dfrac{\sin{x}}{-\tan{x}} = \dfrac{\sqrt{3}}{2} \)
\( \dfrac{\sin{x}}{\frac{\sin{x}}{\cos{x}}} = -\dfrac{\sqrt{3}}{2} \)
\( \cos{x} = -\dfrac{\sqrt{3}}{2} \)
Kosinüs II. ve III. bölgelerde negatiftir.
\( x \in \{\frac{5\pi}{6}, \frac{7\pi}{6}\} \)
\( \dfrac{3\pi}{2} \lt x \lt 2\pi \) olmak üzere,
\( \cot(\pi + x) = -\dfrac{3}{4} \) olduğuna göre,
\( \csc(\pi + x)\cot(\pi - x) \) ifadesinin eşiti nedir?
Çözümü Göster\( \cot(\pi + x) = \cot{x} = -\dfrac{3}{4} \)
Kotanjantı \( \frac{3}{4} \) olan bir açı için dik üçgen çizersek komşu kenara \( 3k \), karşı kenara \( 4k \) diyebiliriz. Bu durumda hipotenüs Pisagor teoreminden \( 5k \) olur.
\( x \) açısı IV. bölgededir. Bu bölgede sinüs negatif, kosinüs pozitiftir.
\( \sin{x} = -\dfrac{4}{5} \)
\( \cos{x} = \dfrac{3}{5} \)
Sorudaki ifadenin değerini bulalım.
\( \csc(\pi + x)\cot(\pi - x) = \dfrac{\cot(\pi - x)}{\sin(\pi + x)} \)
Kotanjant II. bölgede, sinüs III. bölgede negatiftir.
\( = \dfrac{-\cot{x}}{-\sin{x}} \)
\( = \dfrac{\cot{x}}{\sin{x}} \)
\( = \dfrac{-\frac{3}{4}}{-\frac{4}{5}} = \dfrac{15}{16} \) bulunur.
\( \pi \lt x \lt \dfrac{3\pi}{2} \) olmak üzere,
\( \sqrt{5} + 2\sec{x} = 0 \) olduğuna göre,
\( \dfrac{\sin{x} - \cos{x}}{\cot{x}} \) ifadesinin değeri kaçtır?
Çözümü Göster\( \sqrt{5} + 2\sec{x} = 0 \)
\( \sec{x} = -\dfrac{\sqrt{5}}{2} \)
\( \cos{x} = \dfrac{1}{\sec{x}} = -\dfrac{2}{\sqrt{5}} \)
Pisagor özdeşliğini kullanarak \( x \) açısının sinüs değerini bulalım.
\( \sin^2{x} + \cos^2{x} = 1 \)
\( \sin^2{x} + (-\dfrac{2}{\sqrt{5}})^2 = 1 \)
\( \sin^2{x} = \dfrac{1}{5} \)
Sinüs III. bölgede negatiftir.
\( \sin{x} = -\dfrac{1}{\sqrt{5}} \)
\( x \) açısının kotanjant değerini bulalım.
\( \cot{x} = \dfrac{\cos{x}}{\sin{x}} \)
\( = \dfrac{-\frac{2}{\sqrt{5}}}{-\frac{1}{\sqrt{5}}} = 2 \)
Sorudaki ifadenin değerini bulalım.
\( \dfrac{\sin{x} - \cos{x}}{\cot{x}} = \dfrac{-\frac{1}{\sqrt{5}} - (-\frac{2}{\sqrt{5}})}{2} \)
\( = \dfrac{\frac{1}{\sqrt{5}}}{2} = \dfrac{1}{2\sqrt{5}} \)
Paydayı rasyonel hale getirelim.
\( = \dfrac{\sqrt{5}}{10} \) bulunur.
\( ABCD \) bir karedir.
\( \abs{AE} = 3\abs{EB} \)
\( m(\widehat{BED}) = x \)
olduğuna göre, \( \sin{x} \) kaçtır?
Çözümü Göster
\( \abs{EB} = a \) diyelim
\( \abs{AE} = 3\abs{EB} = 3a \) olur.
\( \abs{AD} = \abs{AB} = a + 3a = 4a \)
Pisagor teoremi ile \( \abs{DE} \) uzunluğunu bulalım.
\( \abs{DE} = \sqrt{(4a)^2 + (3a)^2} = 5a \)
\( m(\widehat{AED}) = y \) diyelim.
II. bölgede sinüs pozitif olduğu için bütünler açılar olan \( x \) ve \( y \)'nin sinüs değerleri eşittir.
\( \sin{x} = \sin(180° - y) = \sin{y} \)
\( = \dfrac{4a}{5a} = \dfrac{4}{5} \) bulunur.
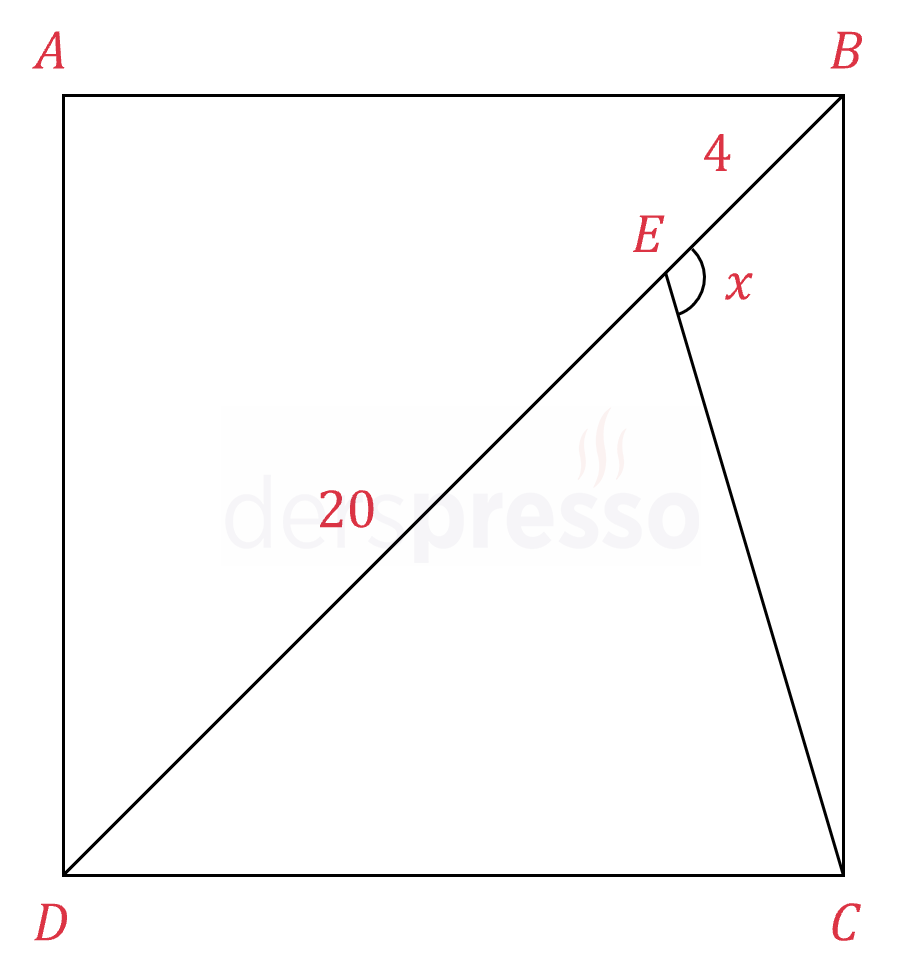
\( ABCD \) bir kare ve \( [BD] \) karenin bir köşegenidir.
\( \abs{DE} = 20, \abs{EB} = 4 \)
\( m(\widehat{BEC}) = x \) olduğuna göre, \( \cot{x} \) kaçtır?
Çözümü Göster\( C \) noktasından \( [BD] \) köşegenine bir dikme çizelim ve köşegeni kestiği noktaya \( F \) diyelim.
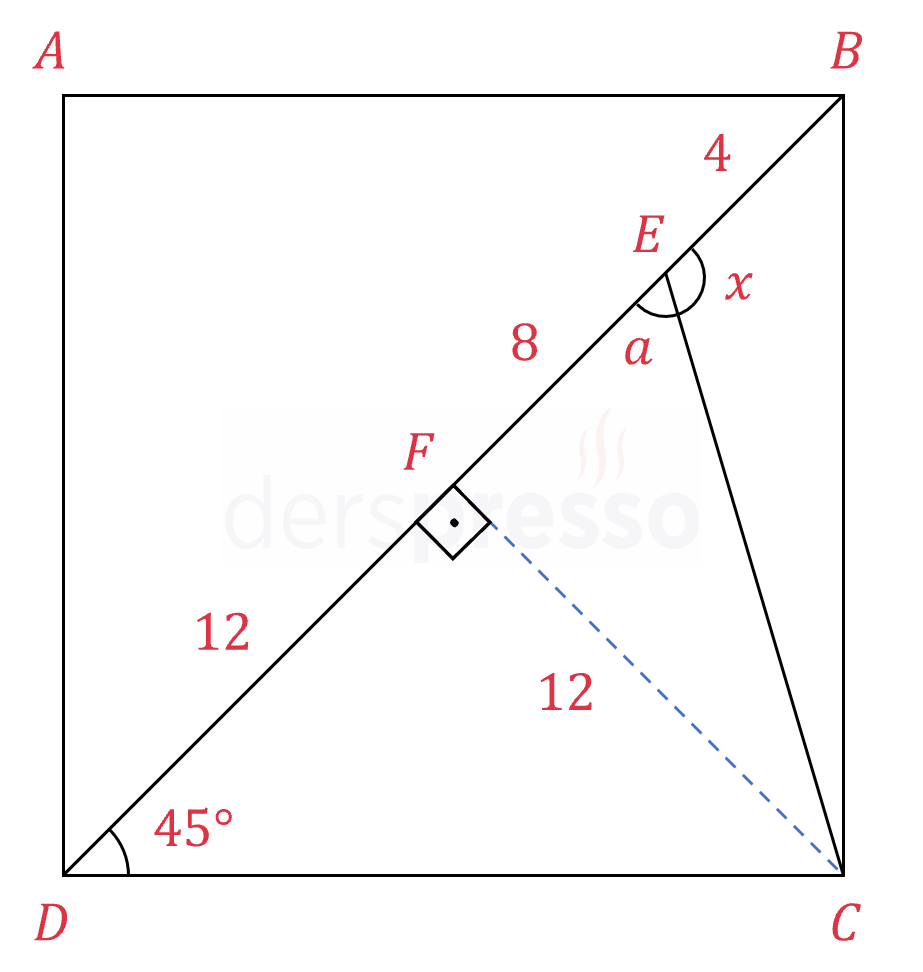
Bir karede köşegenler birbirini dik kestiği için bu dikmenin uzantısı aynı zamanda karenin \( [AC] \) köşegenidir.
Bir karede köşegenler birbirini ortalar.
\( \abs{DF} = \dfrac{20 + 4}{2} = 12 \)
\( \abs{FE} = 20 - 12 = 8 \)
\( m(\widehat{BDC}) = 45° \) olduğu için oluşan dik üçgen ikizkenar üçgendir.
\( \abs{FC} = 12 \)
\( m(\widehat{FEC}) = a \) diyelim.
\( a = 180° - x \)
Kotanjant dönüşüm formülünü kullanalım.
\( \cot{x} = \cot(180° - a) = -\cot{a} \)
\( = -\dfrac{8}{12} = -\dfrac{2}{3} \) bulunur.