Birim Çember
Analitik düzlemde merkezi orijin ve yarıçapı 1 birim olan çembere birim çember denir. Merkezi \( O(0, 0) \) noktası olan birim çember eksenleri \( A(1, 0) \), \( B(0, 1) \), \( C(-1, 0) \) ve \( D(0, -1) \) noktalarında keser.

Birim çemberin denklemi merkezi orijin ve yarıçapı 1 birim olan çember denklemidir.
\( x^2 + y^2 = 1 \)
Birim çemberin trigonometride önemli bir yerinin olmasının bazı sebepleri şunlardır.
- Açıların başlangıç kenarını sabitleyerek (aşağıdaki şekilde \( [OA \) ışını), tüm açıları ve trigonometrik değerlerini standart bir şekilde incelememizi ve karşılaştırmamızı sağlar.
- Birim çember üzerindeki noktaların koordinatları üzerinden trigonometrik fonksiyonların değerleri belirlenebilir.
- Birim çember kullanılarak dar olmayan açıların trigonometrik değerleri dar açılar cinsinden ifade edilebilir.
- Kullanılan pek çok trigonometrik özdeşlik birim çember üzerinde geometrik olarak türetilebilir.
Sinüs ve Kosinüs Değerleri
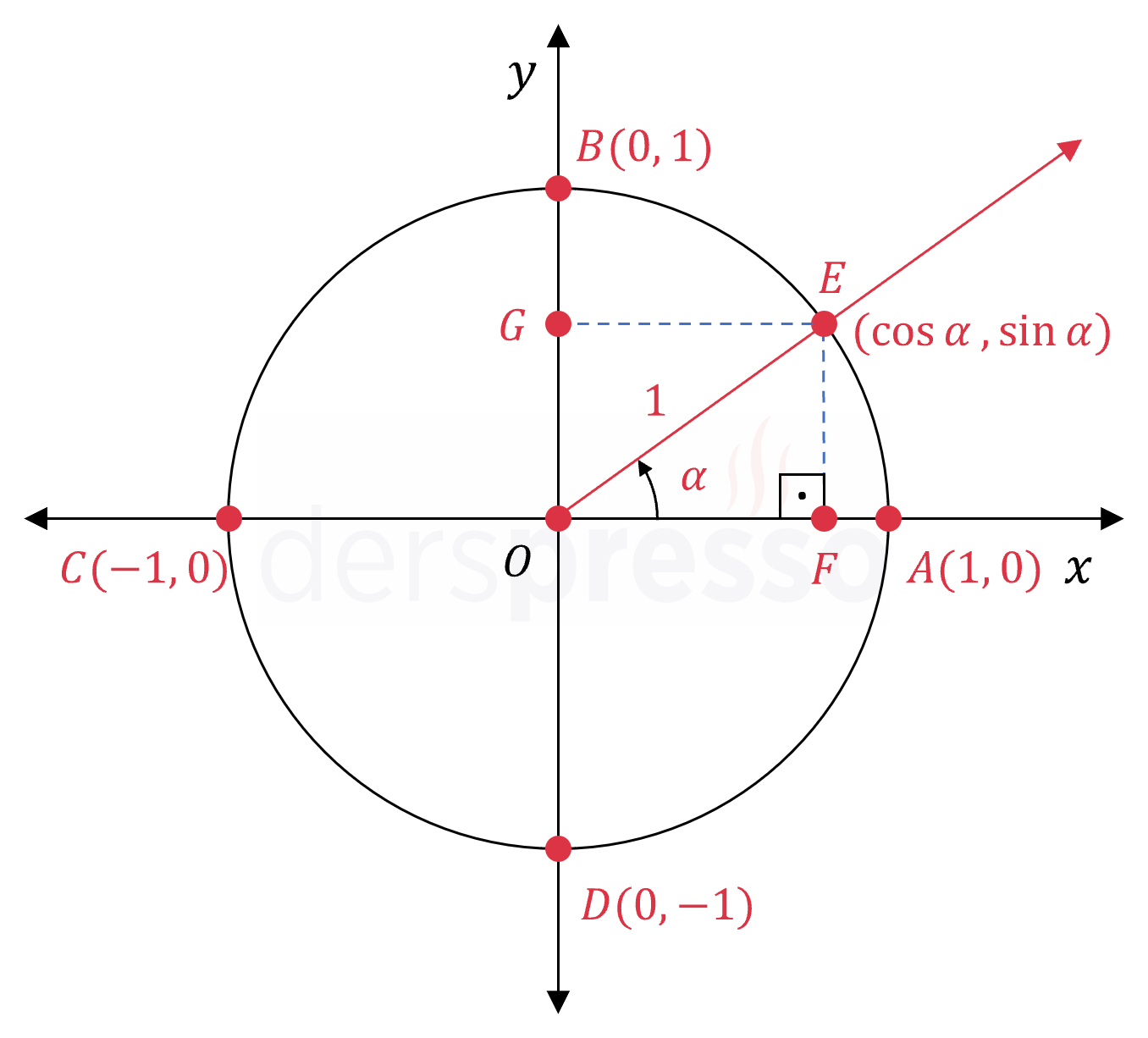
Belirli bir \(\alpha \) açısının bitim kolu olan \( [OE \) ışınının birim çemberi kestiği \( E \) noktasının koordinatları \( \alpha \) açısı cinsinden aşağıdaki şekilde yazılabilir.
\( E \) noktasının apsis ve ordinat değerleri \( \abs{OF} \) ve \( \abs{OG} \) olmak üzere,
\( \cos{\alpha} = \dfrac{\abs{OF}}{\abs{OE}} = \dfrac{\abs{OF}}{1} = \abs{OF} \)
Buna göre \( E \) noktasının apsis değeri \( \cos{\alpha} \)'ya eşit olur.
\( \sin{\alpha} = \dfrac{\abs{EF}}{\abs{OE}} = \dfrac{\abs{OG}}{1} = \abs{OG} \)
Buna göre \( E \) noktasının ordinat değeri \( \sin{\alpha} \)'ya eşit olur.
Dolayısıyla \( E \) noktasının koordinatları \( E(\cos{\alpha}, \sin{\alpha}) \) şeklinde yazılabilir.
Birim çemberin eksenleri kestiği noktaların koordinatları, bu noktaların karşılık geldiği açıların sinüs ve kosinüs değerleri cinsinden yazılarak bu formül doğrulanabilir.
\( A(\cos{0°}, \sin{0°}) = A(1, 0) \)
\( B(\cos{90°}, \sin{90°}) = B(0, 1) \)
\( C(\cos{180°}, \sin{180°}) = C(-1, 0) \)
\( D(\cos{270°}, \sin{270°}) = D(0, -1) \)
\( E \) noktasının orijin ve \( x \) ekseni ile birlikte oluşturduğu \( OFE \) dik üçgenine Pisagor bağıntısı uygulandığında Pisagor özdeşliği elde edilir.
\( \abs{EF} = \sin{\alpha} \)
\( \abs{OF} = \cos{\alpha} \)
\( \sin^2{\alpha} + \cos^2{\alpha} = 1^2 = 1 \)
Ayrıca birim çember üzerindeki herhangi bir noktanın koordinatları yukarıdaki birim çember denkleminde yerine konduğunda denklemin her zaman sağlandığı görülebilir.
\( E(\cos{\alpha}, \sin{\alpha}) \) birim çember üzerinde bir nokta olmak üzere,
Birim çemberin denklemi: \( x^2 + y^2 = 1 \)
\( (\cos{\alpha})^2 + (\sin{\alpha})^2 = 1 \)
Yarıçap uzunluğu tüm birim çember üzerinde 1 birim olduğu ve \( E \) noktasının koordinatları diğer bölgelerde negatif olsa da koordinat değerlerinin kareleri alındığı için, Pisagor özdeşliği analitik düzlemin dört bölgesindeki açılar için de geçerlidir.
Sinüs ve Kosinüs Eksenleri
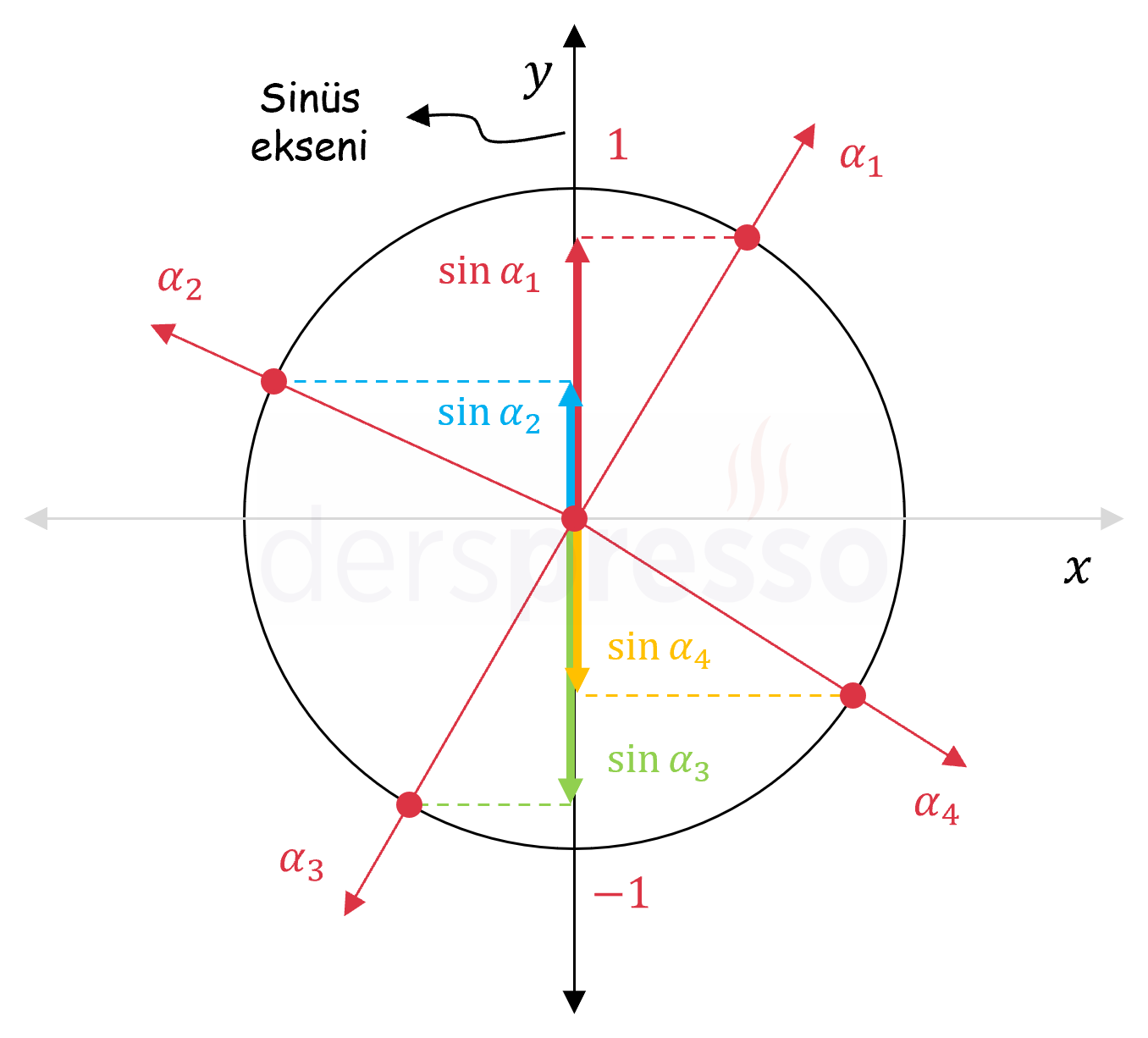
Bir açının birim çember üzerinde karşılık geldiği noktanın ordinat değeri o açının sinüs değerini verir, bu yüzden \( y \) eksenine sinüs ekseni de denir. \( \alpha \) açısı \( [0, 2\pi] \) aralığında farklı değerler aldıkça bu uzunluk \( [-1, 1] \) aralığında değer alabileceği için sinüs fonksiyonunun değer aralığı da \( [-1, 1] \) olur.
Aşağıdaki şekilde dört bölgedeki birer açı için sinüs değerleri sinüs ekseni üzerinde gösterilmiştir.
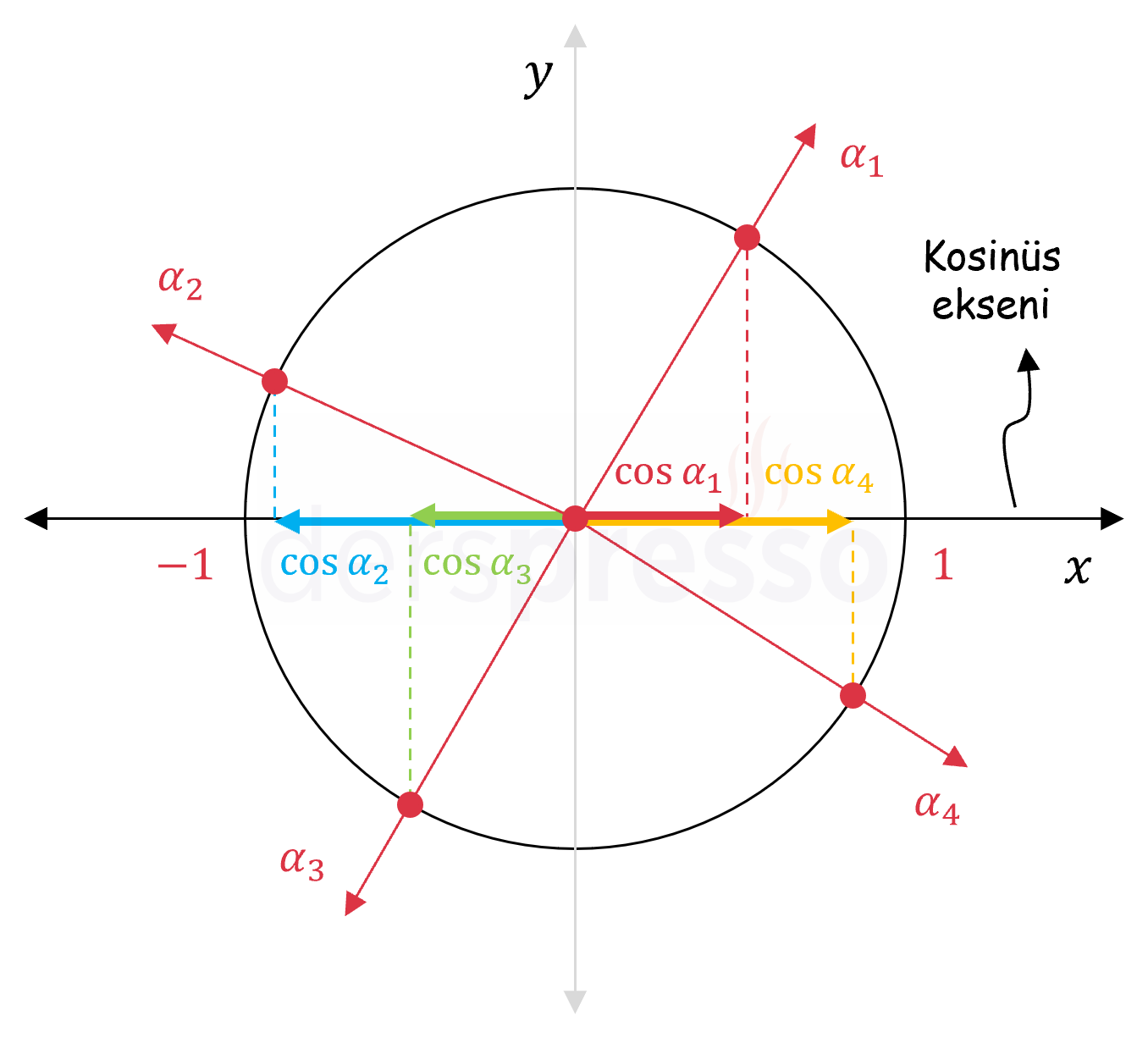
Bir açının birim çember üzerinde karşılık geldiği noktanın apsis değeri o açının kosinüs değerini verir, bu yüzden \( x \) eksenine kosinüs ekseni de denir. \( \alpha \) açısı \( [0, 2\pi] \) aralığında farklı değerler aldıkça bu uzunluk \( [-1, 1] \) aralığında değer alabileceği için kosinüs fonksiyonunun değer aralığı da \( [-1, 1] \) olur.
Aşağıdaki şekilde dört bölgedeki birer açı için kosinüs değerleri kosinüs ekseni üzerinde gösterilmiştir.
Tanjant Değeri
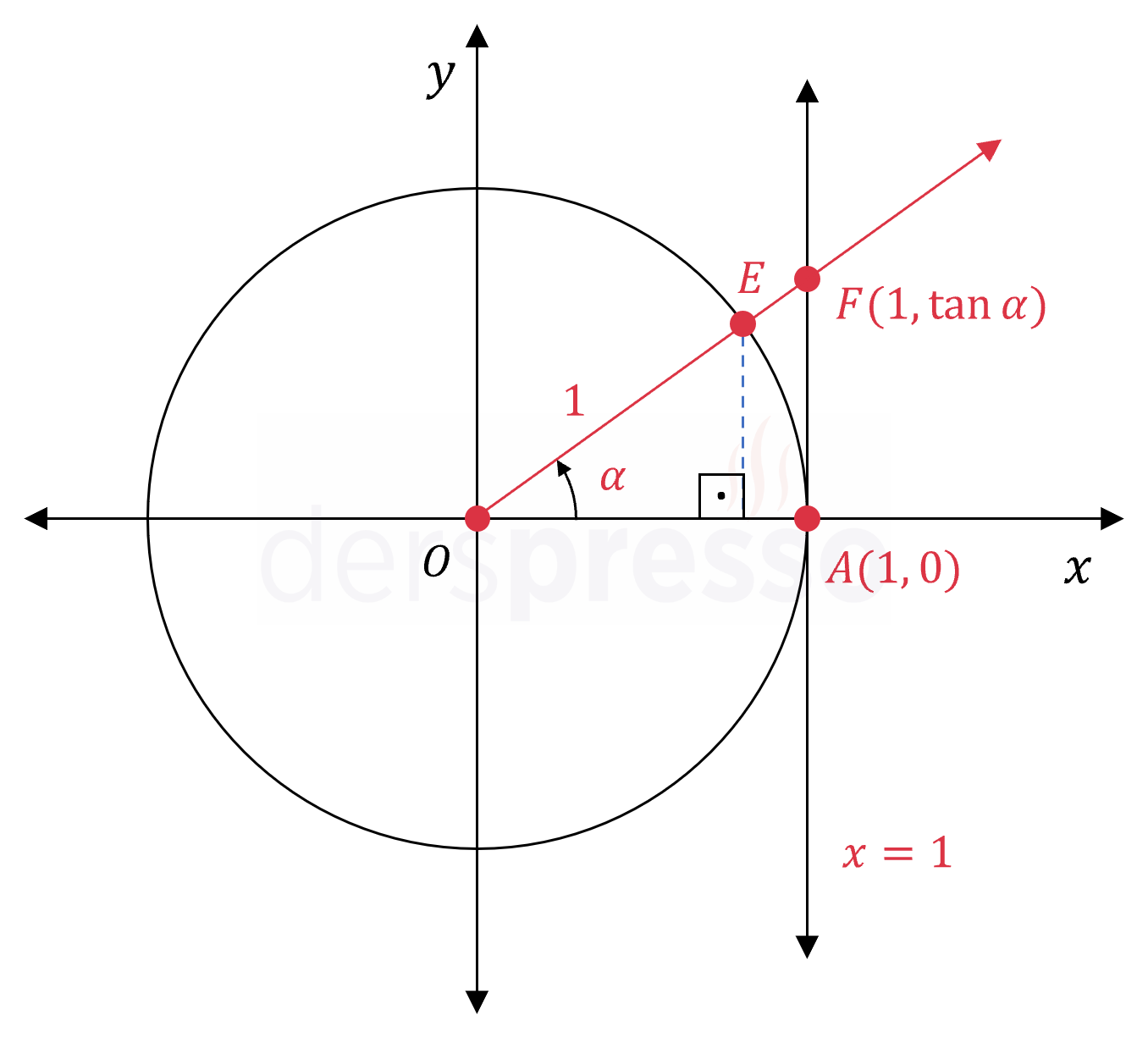
Belirli bir \(\alpha \) açısının bitim kolu olan \( [OE \) ışınının \( x = 1 \) doğrusunu kestiği \( F \) noktasının koordinatları \( \alpha \) açısı cinsinden aşağıdaki şekilde yazılabilir.
\( F \) noktasının ordinat değeri \( \abs{FA} \) olmak üzere,
\( \tan{\alpha} = \dfrac{\abs{FA}}{\abs{OA}} = \dfrac{\abs{FA}}{1} = \abs{FA} \)
Buna göre \( F \) noktasının koordinatları \( F(1, \tan{\alpha}) \) olur.
Tanjant Ekseni
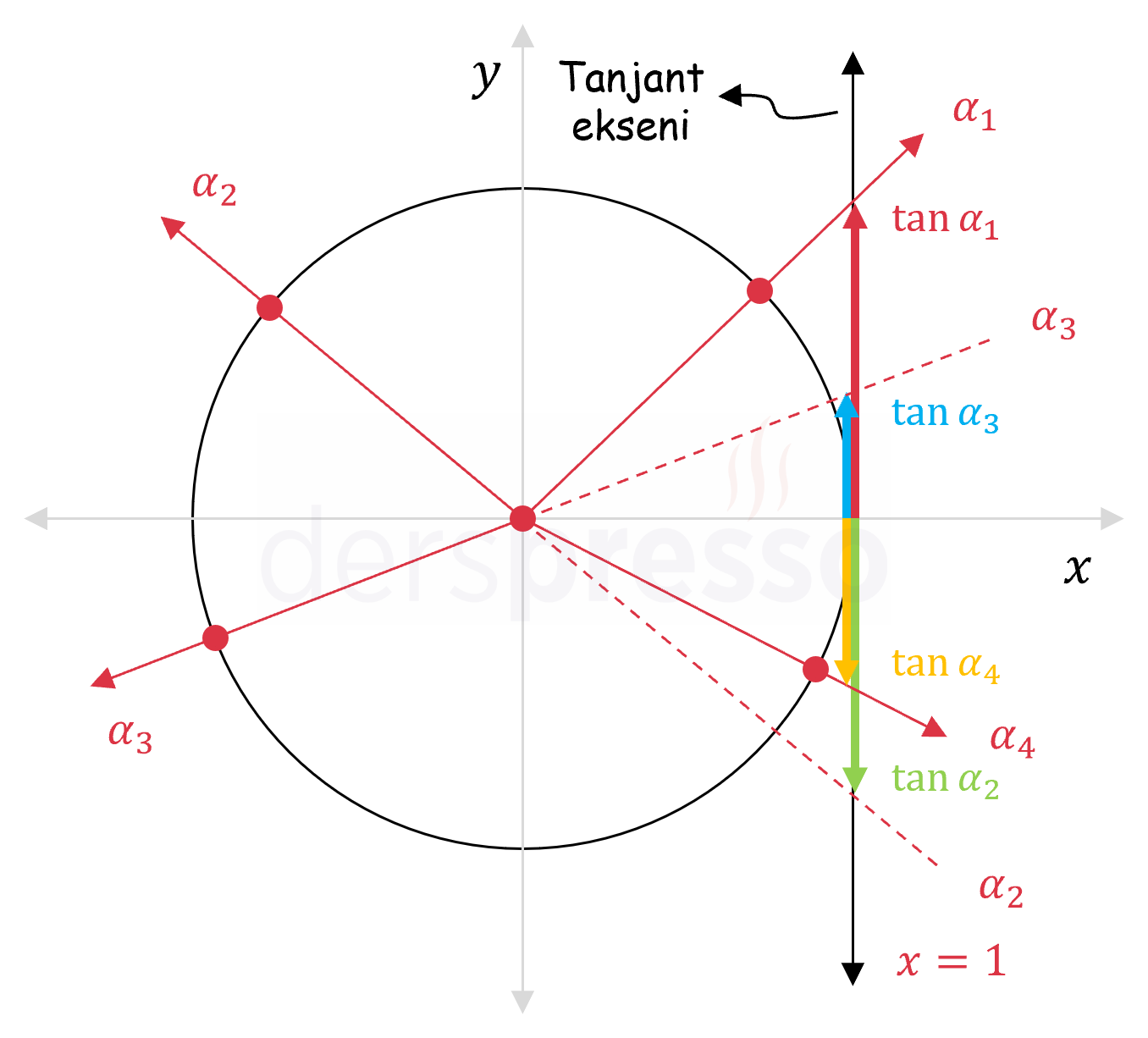
Bir açının bitim kolunun \( x = 1 \) doğrusunu kestiği noktanın \( x \) ekseninden yönlü uzaklığı o açının tanjant değerini verir, bu yüzden \( x = 1 \) doğrusuna tanjant ekseni de denir. \( \alpha \) açısı \( [0, 2\pi] \) aralığında farklı değerler aldıkça bu uzunluk \( (-\infty, \infty) \) aralığında değer alabileceği için tanjant fonksiyonunun değer aralığı da \( (-\infty, \infty) \) olur.
Aşağıdaki şekilde dört bölgedeki birer açı için tanjant değerleri tanjant ekseni üzerinde gösterilmiştir.
Kotanjant Değeri

Belirli bir \(\alpha \) açısının bitim kolu olan \( [OE \) ışınının \( y = 1 \) doğrusunu kestiği \( G \) noktasının koordinatları \( \alpha \) açısı cinsinden aşağıdaki şekilde yazılabilir.
\( G \) noktasının apsis değeri \( \abs{BG} \) olmak üzere,
\( \cot{\alpha} = \dfrac{\abs{BG}}{\abs{BO}} = \dfrac{\abs{BG}}{1} = \abs{BG} \)
Buna göre \( G \) noktasının koordinatları \(G(\cot{\alpha}, 1)\) olur.
Kotanjant Ekseni
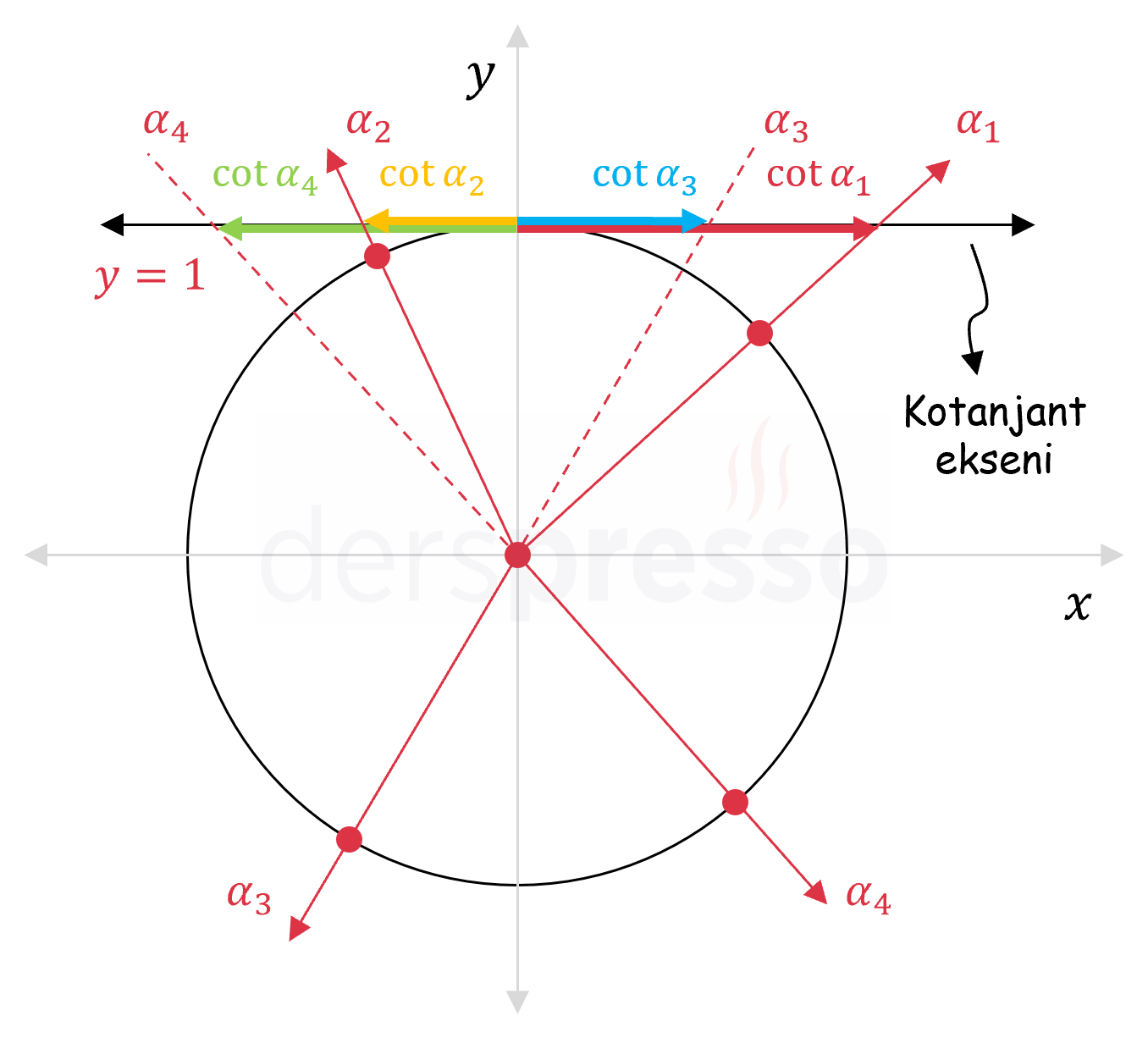
Bir açının bitim kolunun \( y = 1 \) doğrusunu kestiği noktanın \( y \) ekseninden yönlü uzaklığı o açının kotanjant değerini verir, bu yüzden \( y = 1 \) doğrusuna kotanjant ekseni de denir. \( \alpha \) açısı \( [0, 2\pi] \) aralığında farklı değerler aldıkça bu uzunluk \( (-\infty, \infty) \) aralığında değer alabileceği için kotanjant fonksiyonunun değer aralığı da \( (-\infty, \infty) \) olur.
Aşağıdaki şekilde dört bölgedeki birer açı için kotanjant değerleri kotanjant ekseni üzerinde gösterilmiştir.
Sekant ve Kosekant Değerleri

Belirli bir \(\alpha \) açısının bitim kolu olan \( [OE \) ışınının birim çemberi kestiği \( E \) noktasında çembere çizilen teğet doğrunun \( x \) eksenini kestiği \( H \) noktasının koordinatları \( \alpha \) açısı cinsinden aşağıdaki şekilde yazılabilir.
\( H \) noktasının apsis değeri \( \abs{OH} \) olmak üzere,
\( \sec{\alpha} = \dfrac{\abs{OH}}{\abs{OE}} = \dfrac{\abs{OH}}{1} = \abs{OH} \)
Buna göre \( H \) noktasının koordinatları \( H(\sec{\alpha}, 0) \) olur.
Aynı teğet doğrunun \( y \) eksenini kestiği \( K \) noktasının koordinatları \( \alpha \) açısı cinsinden aşağıdaki şekilde yazılabilir.
\( K \) noktasının ordinat değeri \( \abs{KO} \) olmak üzere,
\( \csc{\alpha} = \dfrac{\abs{KO}}{\abs{OE}} = \dfrac{\abs{KO}}{1} = \abs{KO} \)
Buna göre \( K \) noktasının koordinatları \( K(0, \csc{\alpha}) \) olur.
Birim Çember ve Sık Kullanılan Açılar
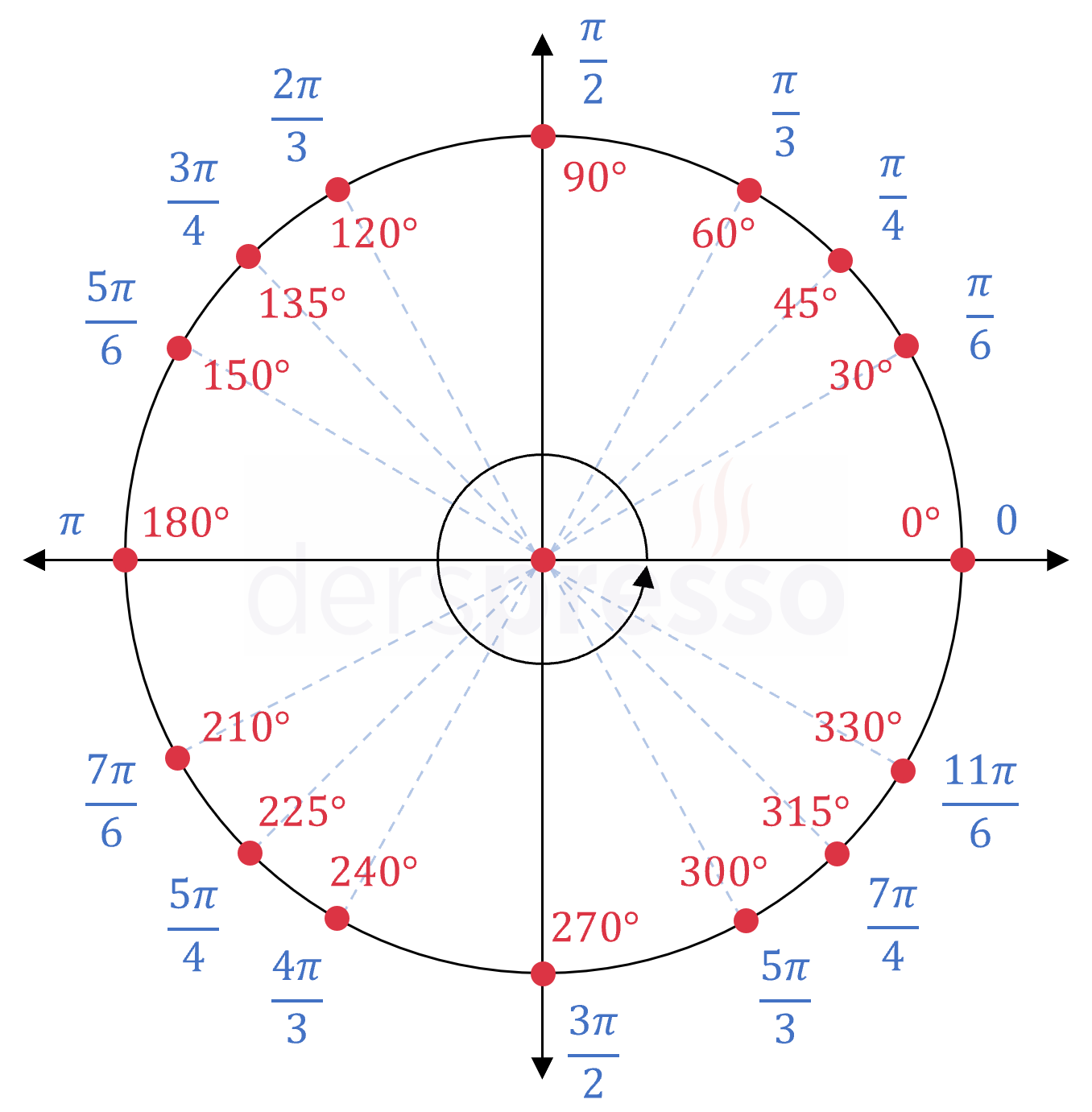
En sık kullanılan açıların derece ve radyan karşılıkları aşağıdaki şekilde birim çember üzerinde gösterilmiştir. Bu açıların derece ve radyan karşılıklarının ve her birinin trigonometrik fonksiyon değerlerinin bilinmesi ya da hızlı bir şekilde hesaplanabilmesi oldukça önemlidir.
\( (a + 4)x^2 + (3b + 6)xy + (c - 5)y^2 = 3 \)
denklemi bir birim çember belirttiğine göre, \( \dfrac{a - b}{c} \) kaçtır?
Çözümü GösterBirim çemberin denklemi aşağıdaki gibidir.
\( x^2 + y^2 = 1 \)
Verilen denklemin taraflarını 3'e bölelim.
\( \dfrac{a + 4}{3}x^2 + \dfrac{3b + 6}{3}xy + \dfrac{c - 5}{3}y^2 = 1 \)
Verilen denklem birim çember denklemine eşit olacak şekilde katsayıları eşitleyelim.
\( \dfrac{a + 4}{3} = 1 \Longrightarrow a = -1 \)
\( \dfrac{c - 5}{3} = 1 \Longrightarrow c = 8 \)
Çember denkleminde \( xy \)'li terim bulunamaz.
\( 3b + 6 = 0 \Longrightarrow b = -2 \)
Bu değerleri soruda verilen ifadede yerine yazalım.
\( \dfrac{a - b}{c} = \dfrac{-1 - (-2)}{8} \)
\( = \dfrac{1}{8} \) bulunur.
Birim çember üzerindeki \( A(-\frac{1}{2}, \frac{\sqrt{3}}{2}) \) noktasının oluşturduğu merkez açısının ölçüsü kaç derecedir?
Çözümü GösterApsis negatif, ordinat pozitif olduğu için nokta II. bölgededir.
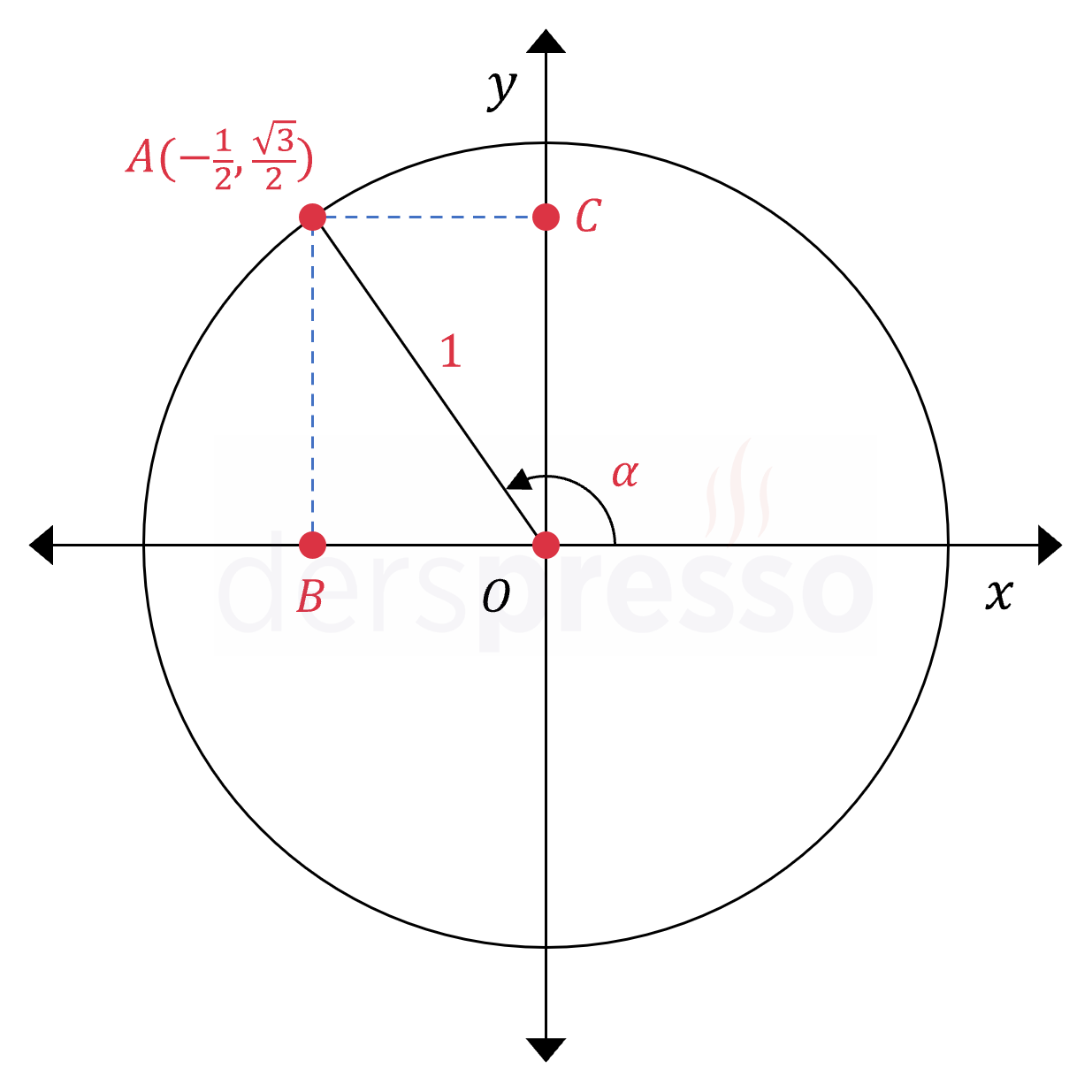
Birim çember üzerindeki bir noktanın apsis ve ordinat değerleri sırasıyla o noktanın karşılık geldiği açının kosinüs ve sinüs değerlerine eşittir.
Noktanın \( x \) ekseni ile yaptığı pozitif yönlü açı \( \alpha \) olmak üzere,
\( A(-\dfrac{1}{2}, \dfrac{\sqrt{3}}{2}) = A(\cos{\alpha}, \sin{\alpha}) \)
Kosinüs değeri \( -\frac{1}{2} \) ve sinüs değeri \( \frac{\sqrt{3}}{2} \) olan açı 120°'dir.
Birim çember üzerinde apsisi ordinatının 3 katına eşit olan noktalar nelerdir?
Çözümü Gösterİstenilen noktaların koordinatlarına \( A(3a, a) \) diyelim.
Birim çember üzerindeki bir noktanın apsis ve ordinat değerleri sırasıyla o noktanın karşılık geldiği açının kosinüs ve sinüs değerlerine eşittir.
Noktanın \( x \) ekseni ile yaptığı pozitif yönlü açı \( \alpha \) olmak üzere,
\( A(3a, a) = A(\cos{\alpha}, \sin{\alpha}) \)
Birim çember üzerindeki tüm noktalar Pisagor özdeşliğini sağlar.
\( \cos^2{\alpha} + \sin^2{\alpha} = 1 \)
\( (3a)^2 + a^2 = 1 \)
\( 10a^2 = 1 \)
\( a = \pm \dfrac{\sqrt{10}}{10} \)
O halde istenen koşulu sağlayan noktalar aşağıdaki gibi bulunur.
\( A_1(\frac{3 \sqrt{10}}{10}, \frac{\sqrt{10}}{10}) \)
\( A_2(-\frac{3 \sqrt{10}}{10}, -\frac{\sqrt{10}}{10}) \)
Dik koordinat düzleminde birim çember üzerinde \( A(-\frac{\sqrt{3}}{2}, \frac{1}{2}) \) noktası veriliyor.
Bu nokta saat yönünde 3500° hareket ettirilirse hangi bölgeye ulaşılır?
Çözümü Göster\( A \) noktası 2. bölgededir ve \( x \) ekseni ile yaptığı pozitif yönlü açı 150°'dir.
\( \cos{150°} = -\dfrac{\sqrt{3}}{2} \)
\( \sin{150°} = \dfrac{1}{2} \)

Saat yönünde hareket negatif yönlü açıya karşılık gelir.
\( 150° - 3500° = -3350° \)
\( -3350° \)'nin esas ölçüsü \( 250° \)'dir.
\( -3350° = 250° + 360° \cdot (-10) \)
250° III. bölgede bir açıdır.
\( a = \tan{34°}, b = \cot{323°}, c = \sin{146°}, d = \cos{217°} \)
ifadelerini değerlerine göre küçükten büyüğe doğru sıralayın.
Çözümü GösterVerilen ifadeleri kosinüs ve kotanjant fonksiyonları ve I. ve II. bölgede açılar cinsinden yazalım.
Tümler açıların tanjant ve kotanjant değerleri eşittir.
\( a = \tan{34°} = \cot{56°} \)
Kotanjant fonksiyonunun periyodu 180°'dir.
\( b = \cot{323°} = \cot(323° - 180°) = \cot{143°} \)
\( c = \sin{146°} = \cos{56°} \)
\( d = \cos{217°} = \cos{143°} \)
Bu trigonometrik ifadelerin değerlerini birim çember üzerinde işaretleyelim.
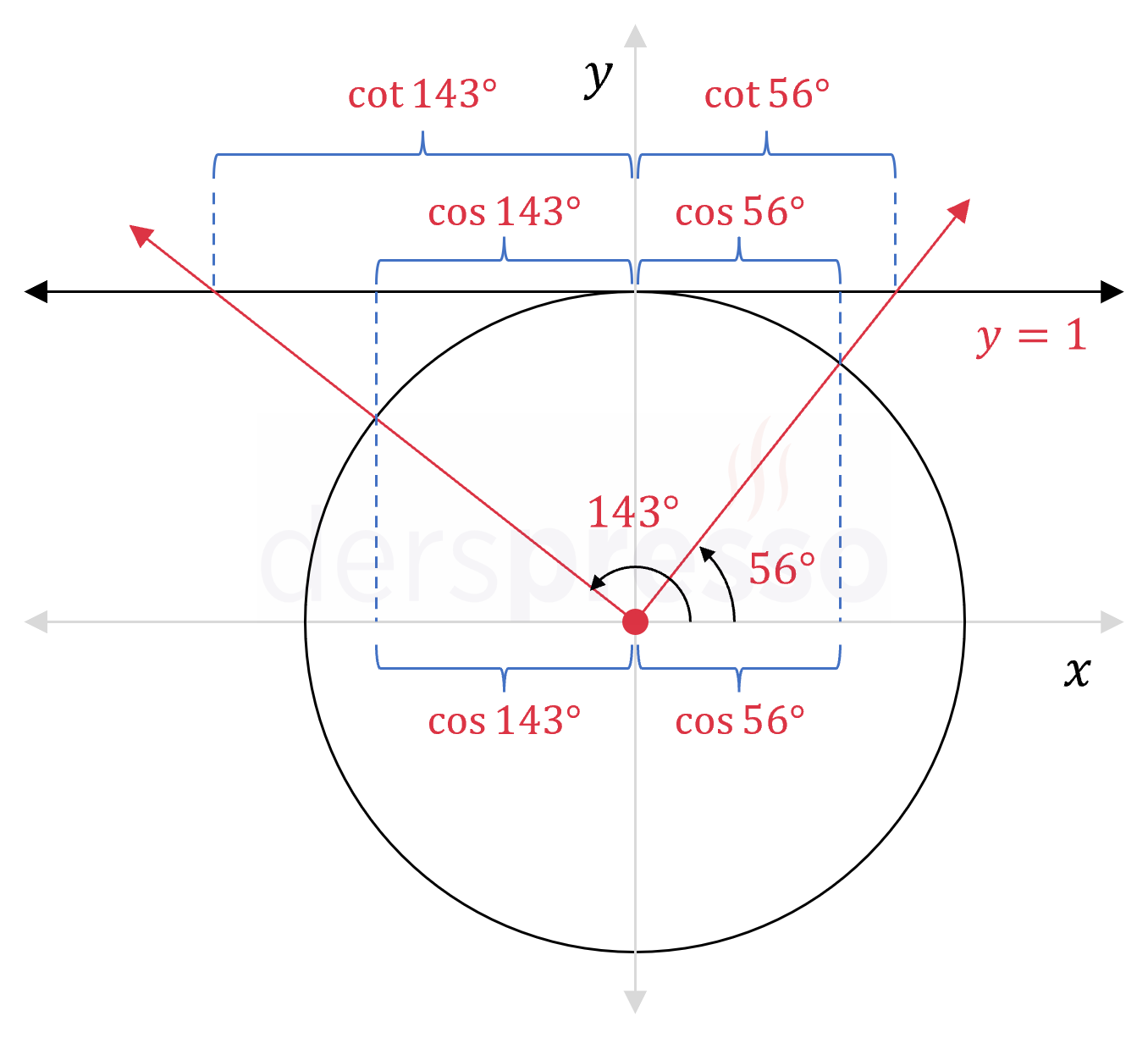
Şekilde kotanjant ifadeleri \( y = 1 \) kotanjant ekseni üzerinde işaretlenmiştir. Kosinüs ifadelerinin \( x \) ekseni üzerindeki değerlerinin kotanjant ekseni üzerindeki izdüşümleri de işaretlenmiştir.
Kotanjant ekseni üzerindeki büyüklükleri karşılaştırarak verilen ifadelerin küçükten büyüğe doğru sıralaması aşağıdaki gibi olur.
\( \cot{143°} \lt \cos{143°} \lt \cos{56°} \lt \cot{56°} \)
\( b \lt d \lt c \lt a \)