Sayı Kümeleri
Önceki bölümde bahsettiğimiz sayıların farklı sınıflandırmaları içinde en temel olanı sayı kümeleridir. Her sayı bu bölümde inceleyeceğimiz sayı kümelerinden birinin ya da birkaçının elemanı olabilir.
Sayı kümeleri birer küme oldukları için küme işlemleri ve özellikleri sayı kümeleri için de geçerlidir.
Doğal Sayılar
Doğal sayılar kümesi 0'dan pozitif sonsuza kadar olan tam sayıları kapsar ve \( \mathbb{N} \) sembolü ile gösterilir.
\( \mathbb{N} = \{0, 1, 2, 3, \ldots\} \)
0 hariç doğal sayılar kümesine sayma sayıları denir ve \( \mathbb{N^+} \) sembolü ile gösterilir.
\( \mathbb{N^+} = \{1, 2, 3, \ldots\} \)
NOT: Doğal sayılar bazı kaynaklarda 0 ile başlarken bazı kaynaklarda 1 ile başlar.
Tam Sayılar
Tam sayılar kümesi negatif sonsuzdan pozitif sonsuza kadar olan tam sayıları kapsar ve \( \mathbb{Z} \) sembolü ile gösterilir.
\( \mathbb{Z} = \{\ldots, -3, -2, -1, 0, 1, 2, 3, \ldots\} \)
Tam sayılar kümesinin birer alt kümesi olarak pozitif ve negatif tam sayılar kümeleri aşağıdaki şekilde tanımlıdır.
\(\mathbb{Z^+} = \{1, 2, 3, \ldots\} \)
\(\mathbb{Z^-} = \{\ldots, -3, -2, -1\} \)
0 (sıfır) pozitif ya da negatif değildir, işareti olmayan bir tam sayıdır.
Tam sayılar kümesi pozitif ve negatif tam sayılar kümeleri ile sıfırın birleşim kümesi şeklinde ifade edilebilir.
\( \mathbb{Z} = \mathbb{Z^-} \cup \{0\} \cup \mathbb{Z^+} \)
Rasyonel Sayılar
Paydası sıfır olmamak şartıyla, iki tam sayının birbirine oranı şeklinde yazılabilen sayılara rasyonel sayılar denir. Rasyonel sayılar kümesi \( \mathbb{Q} \) sembolü ile gösterilir.
\( \mathbb{Q} = \left\{ \dfrac{a}{b} \mid a, b \in \mathbb{Z}, b \ne 0 \right\} \)
Bu tanıma göre aşağıdaki sayılar birer rasyonel sayıdır.
\( \dfrac{1}{2}, -\dfrac{4}{3}, 2\dfrac{4}{5} \)
Bir kesre dönüştürülebilen ondalık sayı ve yüzdeli ifadeler de birer rasyonel sayıdır.
\( 1,5 = \dfrac{3}{2} \)
\( \%75 = \dfrac{3}{4} \)
Tam sayılar kesirli ifade şeklinde yazılabildikleri için birer rasyonel sayıdır.
\( 0 = \dfrac{0}{1} \)
\( 1 = \dfrac{1}{1} = \dfrac{2}{2} = \dfrac{5}{5} \)
\( -2 = -\dfrac{2}{1} = -\dfrac{4}{2} \)
Virgülden sonra sonlu sayıda basamağı olan ondalık sayılar, bir kesirli ifadeye dönüştürülebildikleri için birer rasyonel sayıdır.
\( 0,123456789 \) \( = \dfrac{123.456.789}{1.000.000.000} \)
Devirli ondalık sayılar ondalık basamakları tekrar ederek sonsuza gitse de, bir kesirli ifadeye dönüştürülebildikleri için birer rasyonel sayıdır.
\( 0,333\ldots = 0,\overline{3} = \dfrac{1}{3} \)
\( 2,272727\ldots = 2,\overline{27} = \dfrac{25}{11} \)
Özetle, bir rasyonel sayının ya virgülden sonra sonlu sayıda basamağı vardır, ya da bu basamaklar sonsuza gidiyorsa bir basamaktan sonra kendini tekrar eder.
\( \pi \) ve \( e \) sayıları, virgülden sonraki basamakları tekrar etmeden sonsuza gittiği için rasyonel sayı değildir. Bazı sorularda \( \pi \) sayısı için verilen \( 3,14 \) ve \( \frac{22}{7} \) değerleri \( \pi \) sayısının gerçek değeri olmayıp hesaplama kolaylığı açısından verilen yaklaşık değerlerdir.
\( \sqrt{2}, \sqrt[3]{15}, \sqrt[4]{95} \) gibi kökten çıkamayan ifadeler virgülden sonraki basamakları tekrar etmeden sonsuza gittiği için rasyonel sayı değildir.
\( \frac{a}{0} \) biçimindeki ifadeler tanımsızdır ve herhangi bir sayı kümesine dahil değildir. \( a \ne 0 \) olmak üzere, \( \frac{0}{a} \) biçimindeki ifadeler ise 0'a eşittir.
İrrasyonel Sayılar
İki tam sayının birbirine oranı şeklinde yazılamayan sayılara irrasyonel sayılar denir. İrrasyonel sayılar kümesi \( \mathbb{Q'} \) sembolü ile gösterilir.
İrrasyonel sayılara aşağıdaki örnekler verilebilir.
Pi sayısı: \( \pi = 3,1415926535\ldots \)
Euler sayısı: \( e = 2,7182818284\ldots \)
Altın oran: \( \phi = 1,6180339887\ldots \)
Tam kare olmayan doğal sayıların karekökleri: \( \sqrt{2}, \sqrt{3}, \sqrt{5}, \ldots \)
Çoğu logaritmik ifade: \( \log{2}, \log_2{3}, \ldots \)
Reel (Gerçel) Sayılar
Rasyonel ve irrasyonel sayılar kümelerinin birleşim kümesine reel (gerçel) sayılar denir. Reel sayılar kümesi \( \mathbb{R} \) sembolü ile gösterilir.
\( \mathbb{R} = \mathbb{Q} \cup \mathbb{Q'} \)
Bu tanıma göre rasyonel ve irrasyonel sayılar dışında bir reel sayı yoktur.
Pozitif reel sayılar kümesi \(\mathbb{R^+} \) sembolü ile, negatif reel sayılar kümesi de \(\mathbb{R^-} \) sembolü ile gösterilir.
Reel sayılar kümesi pozitif ve negatif reel sayılar kümeleri ile sıfırın birleşim kümesi şeklinde ifade edilebilir.
\( \mathbb{R} = \mathbb{R^-} \cup \{ 0 \} \cup \mathbb{R^+} \)
Sıfırın dahil olduğu aşağıdaki sayı kümeleri de belirtilen isimlerle kullanılabilir.
Negatif olmayan reel sayılar \( = \mathbb{R^+} \cup \{ 0 \} \)
Pozitif olmayan reel sayılar \( = \mathbb{R^-} \cup \{ 0 \} \)
Sanal Sayılar
Karesi bir negatif reel sayı olan, bir diğer ifadeyle bir negatif reel sayının karekökü olan sayılara sanal sayı denir.
Aşağıdaki sayılar birer sanal sayıdır.
\( \sqrt{-1}, \sqrt{-2}, \sqrt{-\frac{7}{2}} \)
\( -1 \) sayısının kareköküne sanal birim denir ve \( i \) ile gösterilir.
\( i = \sqrt{-1} \)
Sanal birimin tüm reel sayı katları sanal sayılar kümesini oluşturur.
\( i, 2i, -3i \)
Karmaşık Sayılar
Reel ve sanal bileşenlerden oluşan ve \( a + bi \) şeklinde ifade edilebilen sayılara karmaşık sayılar denir. Karmaşık sayılar kümesi \( \mathbb{C} \) sembolü ile gösterilir.
\( \mathbb{C} = \{a + bi \mid a, b \in \mathbb{R}, i = \sqrt{-1}\} \)
Tüm reel sayılar sanal bileşenleri sıfır olacak şekilde \( a + 0i \) şeklinde yazılabildikleri için aynı zamanda birer karmaşık sayıdır.
\( 3 = 3 + 0i \)
Benzer şekilde, tüm sanal sayılar reel bileşenleri sıfır olacak şekilde \( 0 + bi \) şeklinde yazılabildikleri için aynı zamanda birer karmaşık sayıdır.
\( 3i = 0 + 3i \)
Sanal ve karmaşık sayıları detaylı şekilde karmaşık sayılar konusunda inceyeceğiz.
Sayı Kümeleri Arasındaki İlişki
Sayı kümeleri arasındaki ilişkiyi aşağıdaki şekilde özetleyebiliriz.
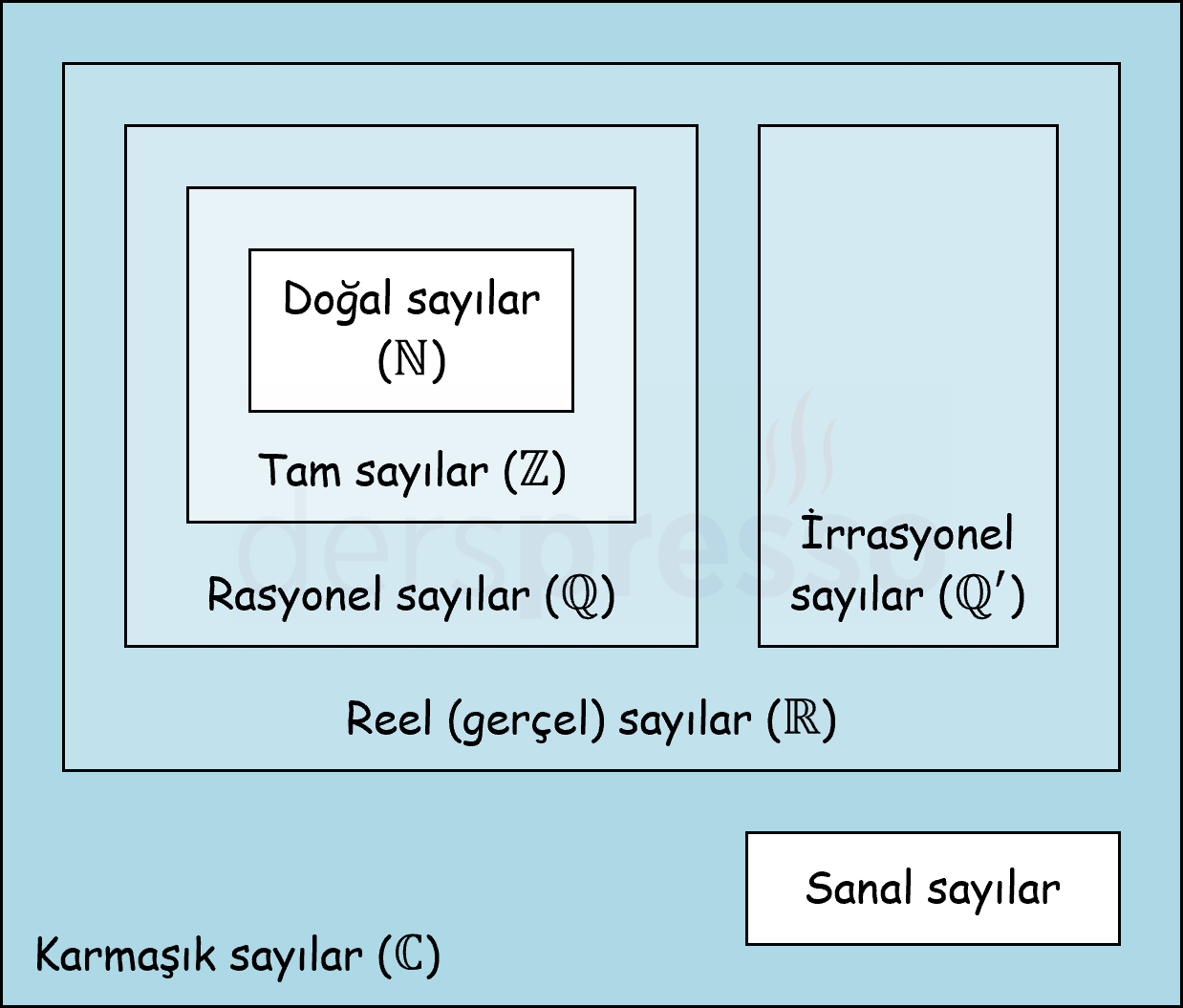
\( \mathbb{N} = \{ 0 \} \cup \mathbb{Z^+} \)
\( \mathbb{Z} = \mathbb{Z^-} \cup \{ 0 \} \cup \mathbb{Z^+} \)
\( \mathbb{R} = \mathbb{Q} \cup \mathbb{Q'} \)
\( \mathbb{N} \subset \mathbb{Z} \subset \mathbb{Q} \subset \mathbb{R} \subset \mathbb{C} \)
Aşağıdaki sayıların ait oldukları sayı kümelerini belirtin.
\( 1; \ \ -5; \ \ \sqrt{9}; \ \ \sqrt{10}; \ \ \%25 \)
Çözümü GösterAşağıdaki sayılardan kaçı hem doğal sayı, hem sayma sayısı, hem de rasyonel sayıdır?
\( -21; \ \ 68; \ \ 0; \ \ \sqrt{169} \)
\( \dfrac{2}{5}; \ \ \dfrac{24}{8}; \ \ 3,5 \)
Çözümü GösterAşağıdakilerden hangileri doğrudur?
I. Rasyonel ve irrasyonel sayıların birleşimi reel sayılar kümesini verir.
II. Pozitif ve negatif tam sayıların birleşimi tam sayılar kümesini verir.
III. Reel ve sanal sayıların birleşimi karmaşık sayılar kümesini verir.
IV. Rasyonel sayılar doğal sayıları kapsar.
Çözümü Göster\( x, y \in \mathbb{R} - \{0\} \) olmak üzere,
\( x \cdot y = 14 \) ise aşağıdakilerden hangileri doğrudur?
I. \( x \) rasyonel sayı ise \( y \) de rasyonel sayıdır.
II. \( x \) irrasyonel sayı ise \( y \) de irrasyonel sayıdır.
III. \( x \) tam sayı ise \( y \) de tam sayıdır.
Çözümü Göster