Ardışık Sayılar
Art arda gelen terimleri sabit bir fark kadar artan ya da azalan sayılara ardışık sayılar denir.
Ardışık sayılar pozitif ya da negatif olabilir. Bir ardışık sayı dizisi birden başlamak zorunda değildir, herhangi bir sayıdan başlayıp herhangi bir sayıda bitebilir.
Ardışık tam sayılar art arda gelen tam sayılardan oluşur ve terimler arası artış miktarı 1'dir.
\( 1, 2, 3, \ldots, n - 2, n - 1, n \)
\( 15, 16, 17, \ldots, 98, 99 \)
\( -35, -34, -33, \ldots, 81, 82 \)
Ardışık tam sayıların ardışık iki teriminden biri tek diğeri çift olacağı için ardışık terimlerin toplamı her zaman tek sayı, çarpımı ise çift sayıdır.
Ardışık çift sayılar art arda gelen çift sayılardan oluşur ve terimler arası artış miktarı 2'dir.
\( 2, 4, 6, \ldots, 2n - 2, 2n \)
\( 26, 28, 30, \ldots, 72, 74 \)
\( 56, 54, 52, \ldots, 4, 2 \)
Ardışık tek sayılar art arda gelen tek sayılardan oluşur ve terimler arası artış miktarı 2'dir.
\( 1, 3, 5, \ldots, 2n - 3, 2n - 1 \)
\( 45, 47, 49, \ldots, 69, 71 \)
\( 39, 37, 35, \ldots, -41, -43 \)
Ardışık sayılarda terimler arası artış miktarı herhangi bir sayı olabilir.
\( 10, 23, 36, \ldots, 140, 153 \)
\( 99, 88, 77, \ldots, -88, -99 \)
Terim Sayısı
Bir ardışık sayı dizisindeki terim sayısı aşağıdaki formülle bulunur.
\( \text{Terim sayısı} = \dfrac{\text{Son terim} - \text{İlk terim}}{\text{Artış miktarı}} + 1 \)
\( 7, 15, 23, \ldots, 199 \)
Verilen sayı dizisinde ilk terim 7, son terim 199, artış miktarı 8'dir.
\( \text{Terim sayısı} = \dfrac{199 - 7}{8} + 1 = 25 \)
\( -62, -59, -56, \ldots, 91 \)
Verilen sayı dizisinde ilk terim -62, son terim 91, artış miktarı 3'tür.
\( \text{Terim sayısı} = \dfrac{91 - (-62)}{3} + 1 = 52 \)
İSPATI GÖSTER
İlk ve son terimlerin farkının terimler arası artış miktarına oranı toplam artış sayısını verir. Bir dizideki terim sayısı artış (ok) sayısının bir fazlasıdır.

Terimler arası artış miktarı 1 olduğunda yukarıdaki formül aşağıdaki şekilde sadeleşir.
Terimler arası artış miktarı 1 ise,
\( \text{Terim sayısı} = \text{Son terim} - \text{İlk terim} + 1 \)
\( 52, 53, 54, \ldots, 1052 \)
\( \text{Terim sayısı} = 1052 - 52 + 1 = 1001 \)
\( -13, -12, -11, \ldots, 25 \)
\( \text{Terim sayısı} = 25 - (-13) + 1 = 39 \)
Terimler Toplamı
Bir ardışık sayı dizisindeki terimler toplamı aşağıdaki formülle bulunur.
\( \text{Terimler toplamı} = \dfrac{\text{İlk terim} + \text{Son terim}}{2} \cdot \text{Terim sayısı} \)
\( 1, 3, 5, \ldots, 97, 99 \)
Verilen sayı dizisinde ilk terim 1, son terim 99, artış miktarı 2'dir.
\( \text{Terim sayısı} = \dfrac{99 - 1}{2} + 1 = 50 \)
\( \text{Terimler toplamı} = \dfrac{1 + 99}{2} \cdot 50 = 2500 \)
\( 27, 33, 39, \ldots, 93 \)
Verilen sayı dizisinde ilk terim 27, son terim 93, artış miktarı 6'dır.
\( \text{Terim sayısı} = \dfrac{93 - 27}{6} + 1 = 12 \)
\( \text{Terimler toplamı} = \dfrac{27 + 93}{2} \cdot 12 = 720 \)
İSPATI GÖSTER
Ardışık sayılarda terimler arası artış miktarının sabit olmasının bir sonucu olarak, dizinin ortasına eşit uzaklıktaki terimlerin toplamları birbirine eşittir.
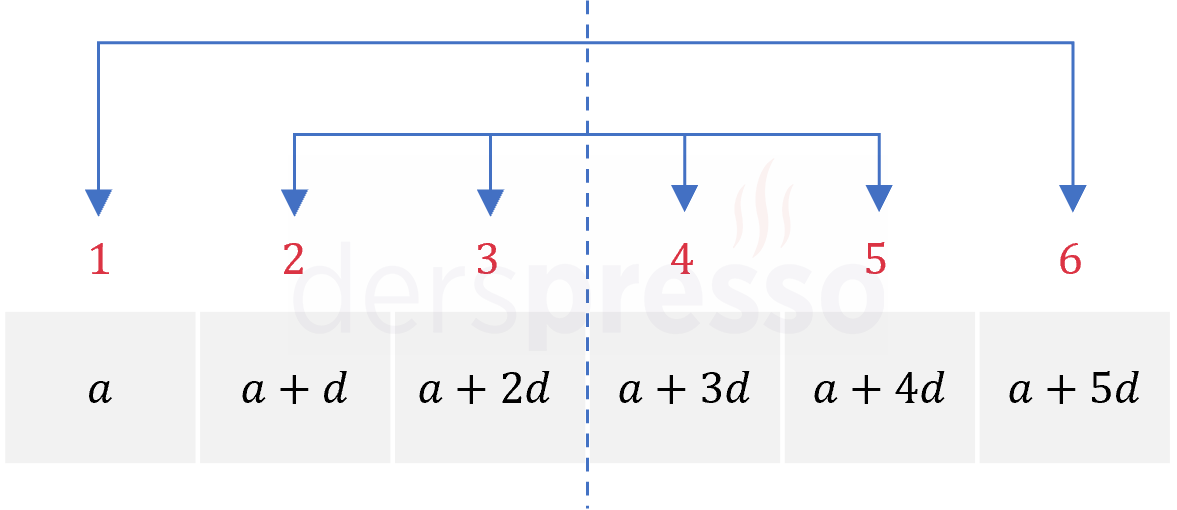
1. terim + 6. terim = 2. terim + 5. terim = 3. terim + 4. terim = ...
\( (a) + (a + 5d) = (a + d) + (a + 4d) = (a + 2d) + (a + 3d) = 2a + 5d \)
Dolayısıyla, dizinin ortasına eşit uzaklıktaki sayı ikililerinin toplamı her zaman dizinin birinci ve sonuncu terimlerinin toplamına eşit olur.
Dizinin ortasına eşit uzaklıktaki terim ikililerinin toplamı \( = \text{İlk terim} + \text{Son terim} \)
Bir dizide bu terim ikililerinden dizideki terim sayısının yarısı kadar olduğunu düşünürsek, tüm terimlerin toplamı aşağıdaki formülle bulunur.
\( \text{Terimler toplamı} = (\text{İlk terim} + \text{Son terim}) \cdot \dfrac{\text{Terim sayısı}}{2} \)
Aşağıda 1'den başlayan ve \( n \) terimli bazı ardışık sayılar için terimler toplamı formülleri verilmiştir. Bu formüllerin ezberlenmesinden ziyade yukarıdaki genel formülün mantığının ve türetilişinin anlaşılması daha önemlidir.
Ardışık Tam Sayıların Terimler Toplamı
\( 1, 2, 3, \ldots, n \)
\( \text{Terimler toplamı} = \dfrac{n(n + 1)}{2} \)
İSPATI GÖSTER
Bu sayı dizisinde ilk terim 1, son terim \( n \), artış miktarı 1'dir.
\( \text{Terim sayısı} = \dfrac{\text{Son terim} - \text{İlk terim}}{\text{Ortak fark}} + 1 \)
\( = \dfrac{n - 1}{1} + 1 = n \)
\( \text{Terimler toplamı} = \dfrac{\text{İlk terim} + \text{Son terim}}{2} \cdot \text{Terim sayısı} \)
\( = \dfrac{1 + n}{2} \cdot n \)
\( = \dfrac{n(n + 1)}{2} \)
Ardışık Çift Sayıların Terimler Toplamı
\( 2, 4, 6, \ldots, 2n \)
\( \text{Terimler toplamı} = n(n + 1) \)
İSPATI GÖSTER
Bu sayı dizisinde ilk terim 2, son terim \( 2n \), artış miktarı 2'dir.
\( \text{Terim sayısı} = \dfrac{\text{Son terim} - \text{İlk terim}}{\text{Ortak fark}} + 1 \)
\( = \dfrac{2n - 2}{2} + 1 = n \)
\( \text{Terimler toplamı} = \dfrac{\text{İlk terim} + \text{Son terim}}{2} \cdot \text{Terim sayısı} \)
\( = \dfrac{2 + 2n}{2} \cdot n \)
\( = n(n + 1) \)
Ardışık Tek Sayıların Terimler Toplamı
\( 1, 3, 5, \ldots, 2n - 1 \)
\( \text{Terimler toplamı} = n^2 \)
İSPATI GÖSTER
Bu sayı dizisinde ilk terim 1, son terim \( 2n - 1 \), artış miktarı 2'dir.
\( \text{Terim sayısı} = \dfrac{\text{Son terim} - \text{İlk terim}}{\text{Ortak fark}} + 1 \)
\( = \dfrac{2n - 1 - 1}{2} + 1 = n \)
\( \text{Terimler toplamı} = \dfrac{\text{İlk terim} + \text{Son terim}}{2} \cdot \text{Terim sayısı} \)
\( = \dfrac{1 + 2n - 1}{2} \cdot n \)
\( = n^2 \)
Ortanca Terim
Ardışık sayılarda ilk ve son terimlerin aritmetik ortalamasına ortanca terim denir.
\( \text{Ortanca terim} = \dfrac{\text{İlk terim} + \text{Son terim}}{2} \)
Tek sayıda terimi olan ardışık sayılarda ortanca terim en ortadaki terime karşılık gelirken çift sayıda terimi olan ardışık sayılarda ortadaki iki terimin ortalamasına karşılık gelir.
Tek sayıda terim: \( 3, 5, \textcolor{red}{7}, 9, 11 \)
Çift sayıda terim: \( 3, 5, \textcolor{red}{7}, \textcolor{red}{9}, 11, 13 \)
Aşağıda verilen ardışık sayılardaki terim sayılarını bulunuz.
(a) \( 15, 17, 19, \ldots, 67 \)
(b) \( 113, 105, 97, \ldots, 33 \)
(c) \( -104, -99, -94, \ldots, 106 \)
Çözümü GösterBir ardışık sayı dizisindeki terim sayısı aşağıdaki formülle bulunur.
\( \text{Terim sayısı} = \dfrac{\text{Son terim} - \text{İlk terim}}{\text{Artış miktarı}} + 1 \)
(a) seçeneği:
\( 15, 17, 19, \ldots, 67 \)
Verilen sayı dizisinde ilk terim 15, son terim 67, artış miktarı 2'dir.
Terim sayısı \( = \dfrac{67 - 15}{2} + 1 \)
\( = \dfrac{52}{2} + 1 = 27 \)
(b) seçeneği:
\( 113, 105, 97, \ldots, 33 \)
Verilen sayı dizisinde ilk terim 113, son terim 33, artış miktarı -8'dir.
Terim sayısı \( = \dfrac{33 - 113}{-8} + 1 \)
\( = \dfrac{-80}{-8} + 1 = 11 \)
(c) seçeneği:
\( -104, -99, -94, \ldots, 106 \)
Verilen sayı dizisinde ilk terim -104, son terim 106, artış miktarı 5'tir.
Terim sayısı \( = \dfrac{106 - (-104)}{5} + 1 \)
\( = \dfrac{210}{5} + 1 = 43 \)
Aşağıdaki ardışık sayı dizilerindeki ortanca terimleri bulunuz.
(a) \( 42, 49, 56, \ldots , 112 \)
(b) \( 520, 507, 494, \ldots, 0 \)
(c) \( 943, 920, 897, \ldots, 460 \)
Çözümü GösterArdışık sayılarda ilk ve son terimlerin aritmetik ortalamasına ortanca terim denir.
\( \text{Ortanca terim} = \dfrac{\text{İlk terim} + \text{Son terim}}{2} \)
(a) seçeneği:
\( 42, 49, 56, \ldots , 112 \)
Ortanca terim \( = \dfrac{42 + 112}{2} \)
\( = \dfrac{154}{2} = 77 \)
(b) seçeneği:
\( 520, 507, 494, \ldots, 0 \)
Ortanca terim \( = \dfrac{520 + 0}{2} \)
\( = 260 \)
(c) seçeneği:
\( 943, 920, 897, \ldots, 460 \)
Ortanca terim \( = \dfrac{943 + 460}{2} \)
\( = 701,5 \)
Aşağıdaki ardışık sayı dizilerindeki terimler toplamını bulunuz.
(a) \( 5, 11, 17, \ldots, 191 \)
(b) \( 20, 28, 36, \ldots, 332 \)
(c) \( 514, 500, 486, \ldots, 290 \)
Çözümü GösterBir ardışık sayı dizisindeki terim sayısı aşağıdaki formülle bulunur.
\( \text{Terim sayısı} = \dfrac{\text{Son terim} - \text{İlk terim}}{\text{Artış miktarı}} + 1 \)
Bir ardışık sayı dizisindeki terimler toplamı aşağıdaki formülle bulunur.
\( \text{Terimler toplamı} = \dfrac{\text{İlk terim} + \text{Son terim}}{2} \cdot \text{Terim sayısı} \)
(a) seçeneği:
\( 5, 11, 17, \ldots, 191 \)
Verilen sayı dizisinde ilk terim 5, son terim 191, artış miktarı 6'dır.
Terim sayısı \( = \dfrac{191 - 5}{6} + 1 = 32 \)
Terimler toplamı \( = \dfrac{5 + 191}{2} \cdot 32 \)
\( = 98 \cdot 32 = 3136 \)
(b) seçeneği:
\( 20, 28, 36, \ldots, 332 \)
Verilen sayı dizisinde ilk terim 20, son terim 332, artış miktarı 8'dir.
Terim sayısı \( = \dfrac{332 - 20}{8} + 1 = 40 \)
Terimler toplamı \( = \dfrac{20 + 332}{2} \cdot 40 \)
\( = 176 \cdot 40 = 7040 \)
(c) seçeneği:
\( 514, 500, 486, \ldots, 290 \)
Verilen sayı dizisinde ilk terim 514, son terim 290, artış miktarı -14'tür.
Terim sayısı \( = \dfrac{290 - 514}{-14} + 1 = 17 \)
Terimler toplamı \( = \dfrac{514 + 290}{2} \cdot 17 \)
\( = 402 \cdot 17 = 6834 \)
Altı ardışık tam sayının toplamı \( n \) olduğuna göre, bu sayılardan en büyüğü \( n \) cinsinden kaçtır?
Çözümü GösterSayılardan en büyüğüne \( k \) diyelim.
Sayıların toplamı \( n \)'ye eşittir.
\( k + (k - 1) + (k - 2) + (k - 3) + (k - 4) + (k - 5) = n \)
\( 6k - 15 = n \)
\( 6k = n + 15 \)
\( k = \dfrac{n + 15}{6} \) bulunur.
\( a, b, c \) ardışık doğal sayılar ve \( a \lt b \lt c \) olduğuna göre,
\( \dfrac{(b - a)(c - a)}{c - b} \) ifadesinin değeri kaçtır?
Çözümü Göster\( a, b, c \) ardışık doğal sayılar olduğu için, aralarında aşağıdaki eşitlikleri kurabiliriz.
\( b = a + 1, \quad c = b + 1 = a + 2 \)
Değeri sorulan ifadedeki tüm değişkenleri \( a \) cinsinden yazalım.
\( \dfrac{(a + 1 - a)(a + 2 - a)}{a + 2 - (a + 1)} \)
\( = \dfrac{1 \cdot 2}{1} = 2 \)
\( a \) ve \( b \) ardışık iki tek sayı ve \( a \lt b \) olmak üzere,
\( 2a + 3b = 41 \) olduğuna göre, \( a + b \) toplamı kaçtır?
Çözümü Gösterİki sayı ardışık tek sayılar olduğu için aralarındaki fark 2'dir.
\( a \lt b \) olduğuna göre \( b = a + 2 \) yazabiliriz.
\( 2a + 3b = 41 \)
\( 2a + 3(a + 2) = 41 \)
\( 5a + 6 = 41 \)
\( a = 7 \)
\( b = a + 2 = 9 \)
\( a + b = 7 + 9 = 16 \) bulunur.
Üçün katı ardışık dört tam sayıdan en büyüğü ile en küçüğünün toplamı 39 olduğuna göre, bu sayıların toplamı kaçtır?
Çözümü GösterSayılara \( a \), \( a + 3 \), \( a + 6 \) ve \( a + 9 \) diyelim.
En küçük ve en büyük sayıların toplamını bulalım.
\( a + (a + 9) = 39 \)
\( a = 15 \)
Bu durumda dört sayının toplamı aşağıdaki gibi olur:
\( 15 + 18 + 21 + 24 = 78 \) bulunur.
\( 1 + 2 + \ldots + 99 \) toplamının sonucu sayıların ortanca teriminin kaç katıdır?
Çözümü GösterBir ardışık sayı dizisindeki terimler toplamı aşağıdaki formülle bulunur.
\( \text{Terimler toplamı} = \dfrac{\text{İlk terim} + \text{Son terim}}{2} \cdot \text{Terim sayısı} \)
\( = \dfrac{1 + 99}{2} \cdot 99 \)
\( = 50 \cdot 99 \)
Ortanca terimi bulalım.
\( \text{Ortanca terim} = \dfrac{\text{İlk terim} + \text{Son terim}}{2} \)
\( = \dfrac{1 + 99}{2} = 50 \)
Buna göre terimler toplamı ortanca terimin 99 katıdır.
\( -1 - 2 - 3 - \ldots - 49 \) işleminin sonucu kaçtır?
Çözümü GösterTüm işlemi \( -1 \) parantezine alalım.
\( -(1 + 2 + 3 + \ldots + 49) \)
Bir ardışık sayı dizisindeki terimler toplamı aşağıdaki formülle bulunur.
\( \text{Terimler toplamı} = \dfrac{\text{İlk terim} + \text{Son terim}}{2} \cdot \text{Terim sayısı} \)
\( = -\dfrac{1 + 49}{2} \cdot 49 \)
\( = -25 \cdot 49 = -1225 \) bulunur.
Ardışık 9 doğal sayının toplamı 99 olduğuna göre, bu sayılardan en büyüğü kaçtır?
Çözümü Gösterİlk terime \( a \) diyelim. Bu durumda son terim \( a + 8 \) olur.
Bir ardışık sayı dizisindeki terimler toplamı aşağıdaki formülle bulunur.
\( \text{Terimler toplamı} = \dfrac{\text{İlk terim} + \text{Son terim}}{2} \cdot \text{Terim sayısı} \)
\( 99 = \dfrac{a + (a + 8)}{2} \cdot 9 \)
\( 99 = (a + 4) \cdot 9 \)
\( a = 7 \)
Ardışık sayılardan en küçüğü \( a = 7 \) olduğuna göre, en büyüğü \( a + 8 = 15 \) olur.
\( 2a + 5 \) ve \( 4a - 11 \) ardışık tek sayılar olduğuna göre, \( a \)'nın alabileceği değerlerin toplamı kaçtır?
Çözümü GösterSayılardan hangisinin büyük olduğu verilmediği için, ikisinin de diğerinden büyük olduğu durumu dikkate almamız gerekir.
Durum 1:
\( 2a + 5 \lt 4a - 11 \)
Bu durumda ikinci sayı birinciden 2 fazladır.
\( 2a + 5 + 2 = 4a - 11 \)
\( a = 9 \)
Durum 2:
\( 2a + 5 \gt 4a - 11 \)
Bu durumda birinci sayı ikinciden 2 fazladır.
\( 2a + 5 = 4a - 11 + 2 \)
\( a = 7 \)
\( a \)'nın alabileceği değerlerin toplamı \( 9 + 7 = 16 \) olur.
40 ile 420 arasındaki sonu 2 ile biten sayıların toplamı kaçtır?
Çözümü Gösterİstenen koşulu sağlayan sayılar aşağıdaki sayı dizisini oluşturur.
\( 42, 52, 62, \ldots, 402, 412 \)
Bu sayı dizisinde ilk terim 42, son terim 412, artış miktarı 10'dur.
Bu sayıların toplamını ardışık sayıların toplam formülü ile bulalım.
\( \text{Terim sayısı} = \dfrac{\text{Son terim} - \text{İlk terim}}{\text{Artış miktarı}} + 1 \)
\( = \dfrac{412 - 42}{10} + 1 = 38 \)
\( \text{Terimler toplamı} = \dfrac{\text{İlk terim} + \text{Son terim}}{2} \cdot \text{Terim sayısı} \)
\( = \dfrac{42 + 412}{2} \cdot 38 = 8626 \) bulunur.
\( A = 4 + 9 + 14 + \ldots + 99 \)
\( B = 4 + 8 + 12 + \ldots + 80 \)
olduğuna göre, \( A - B \) kaçtır?
Çözümü Göster\( A \) ifadesindeki terim sayısını bulalım.
\( n_A = \dfrac{99 - 4}{5} + 1 = 20 \)
\( B \) ifadesindeki terim sayısını bulalım.
\( n_B = \dfrac{80 - 4}{4} + 1 = 20 \)
Terim sayıları aynı olan iki sayıya ait eşitlikleri taraf tarafa çıkaralım.
\( A - B = (4 - 4) + (9 - 8) + (14 - 12) + \ldots + (99 - 80) \)
\( = 0 + 1 + 2 + \ldots + 19 \)
\( = 1 + 2 + \ldots + 19 \)
Bir ardışık sayı dizisindeki terimler toplamı aşağıdaki formülle bulunur.
\( \text{Terimler toplamı} = \dfrac{\text{İlk terim} + \text{Son terim}}{2} \cdot \text{Terim sayısı} \)
\( = \dfrac{1 + 19}{2} \cdot 19 \)
\( = 10 \cdot 19 = 190 \) bulunur.
7'ye tam bölünen iki basamaklı pozitif tam sayıların toplamı kaçtır?
Çözümü Göster7'ye tam bölünen iki basamaklı pozitif tam sayıları listeleyelim.
\( 14, 21, 28, \ldots, 98 \)
Bu sayı dizisinde ilk terim 14, son terim 98, artış miktarı 7'dir.
Bir ardışık sayı dizisindeki terim sayısı aşağıdaki formülle bulunur.
\( \text{Terim sayısı} = \dfrac{\text{Son terim} - \text{İlk terim}}{\text{Artış miktarı}} + 1 \)
\( = \dfrac{98 - 14}{7} + 1 = 13 \)
Bir ardışık sayı dizisindeki terimler toplamı aşağıdaki formülle bulunur.
\( \text{Terimler toplamı} = \dfrac{\text{İlk terim} + \text{Son terim}}{2} \cdot \text{Terim sayısı} \)
\( = \dfrac{14 + 98}{2} \cdot 13 \)
\( = 56 \cdot 13 = 728 \) bulunur.
Ardışık 32 tam sayının toplamı \( A \) olduğuna göre, bu sayılardan en büyüğü \( A \) cinsinden kaçtır?
Çözümü GösterArdışık sayı dizisindeki sayıların en küçüğüne \( a \) diyelim. Bu durumda sayıların en büyüğü \( a + 31 \) olur.
Bir ardışık sayı dizisindeki terimler toplamı aşağıdaki formülle bulunur.
\( \text{Terimler toplamı} = \dfrac{\text{İlk terim} + \text{Son terim}}{2} \cdot \text{Terim sayısı} \)
\( A = \dfrac{a + (a + 31)}{2} \cdot 32 \)
\( 2a + 31 = \dfrac{A}{16} \)
\( 2a = \dfrac{A}{16} - 31 = \dfrac{A - 496}{16} \)
\( a = \dfrac{A - 496}{32} \)
Sayıların en büyüğü olan \( a + 31 \) değeri bulalım.
\( a + 31 = \dfrac{A - 496}{32} + 31 \)
\( = \dfrac{A - 496 + 31 \cdot 32}{32} \)
\( = \dfrac{A + 496}{32} \) bulunur.
\( \{3, 6, 9, \ldots, 99\} \) kümesinin elemanlarından biri kümeden çıkarılıyor ve kalan sayıların ortalaması 51 olarak bulunuyor.
Buna göre kümeden çıkarılan sayı kaçtır?
Çözümü GösterKümedeki eleman sayısını bulalım.
\( \dfrac{\text{Son terim} - \text{İlk terim}}{\text{Artış miktarı}} + 1 = \dfrac{99 - 3}{3} + 1 = 33 \)
Kümedeki sayıların toplamını bulalım.
\( \text{Terimler toplamı} = \dfrac{\text{İlk terim} + \text{Son terim}}{2} \cdot \text{Terim sayısı} \)
\( = \dfrac{3 + 99}{2} \cdot 33 \)
\( = 51 \cdot 33 = 1683 \)
Kümeden çıkarılan sayıya \( x \) diyelim ve \( x \) çıkarıldıktan sonraki ortalamayı bulalım.
\( \dfrac{\text{Kalan toplam}}{\text{Kalan terim sayısı}} = \dfrac{1683 - x}{33 - 1} = 51 \)
\( 1683 - x = 32 \cdot 51 \)
\( 1683 - x = 1632 \)
\( x = 51 \) bulunur.
İki basamaklı tek sayıların toplamı \( a \), iki basamaklı çift sayıların toplamı \( b \) ise \( a - b \) farkı kaçtır?
Çözümü GösterBir ardışık sayı dizisindeki terim sayısı aşağıdaki formülle bulunur.
\( \text{Terim sayısı} = \dfrac{\text{Son terim} - \text{İlk terim}}{\text{Artış miktarı}} + 1 \)
Bir ardışık sayı dizisindeki terimler toplamı aşağıdaki formülle bulunur.
\( \text{Terimler toplamı} = \dfrac{\text{İlk terim} + \text{Son terim}}{2} \cdot \text{Terim sayısı} \)
İki basamaklı tek sayıların toplamını bulalım.
\( 11, 13, 15, \ldots, 99 \)
Terim sayısı \( = \dfrac{99 - 11}{2} + 1 = 45 \)
Terimler toplamı \( = \dfrac{11 + 99}{2} \cdot 45 \)
\( a = 55 \cdot 45 \)
Aynı şekilde iki basamaklı çift sayıların toplamını bulalım.
\( 10, 12, 14, \ldots, 98 \)
Terim sayısı \( = \dfrac{98 - 10}{2} + 1 = 45 \)
Terimler toplamı \( = \dfrac{10 + 98}{2} \cdot 45 \)
\( b = 54 \cdot 45 \)
İki sayının farkını bulalım.
\( a - b = 55 \cdot 45 - 54 \cdot 45 \)
\( = 45(55 - 54) = 45 \) bulunur.
11 ardışık tam sayının toplamı \( A \) olduğuna göre, sayılar küçükten büyüğe sıralandığında altıncı sıradaki sayının \( A \) cinsinden değeri nedir?
Çözümü GösterBirinci sayıya \( b \) diyelim. Bu durumda ikinci sayı \( b + 1 \) olur.
Ardışık sayıların toplamını alalım.
\( b + (b + 1) + (b + 2) + \ldots + (b + 10) = A \)
\( 11b + (1 + 2 + 3 + \ldots + 10) = A \)
1'den \( n \)'ye kadar olan doğal sayıların toplamı \( \frac{n(n + 1)}{2} \) formülü ile bulunur.
\( 11b + \dfrac{10 \cdot 11}{2} = A \)
\( 11b + 55 = A \)
Altıncı sıradaki sayı \( b + 5 \) olur.
\( 11(b + 5) = A \)
\( b + 5 = \dfrac{A}{11} \) olarak bulunur.
\( 2 - 5 + 8 - 11 + \ldots + 110 - 113 + 116 \) işleminin sonucu kaçtır?
Çözümü GösterTerimleri ikişerli grupladığımızda son terim hariç her çıkarma işleminin sonucunun -3 olduğunu görürüz.
\( (2 - 5) + (8 - 11) + \ldots + (110 - 113) + 116 \)
\( = (-3) + (-3) + \ldots + (-3) + 116 \)
Parantez içindeki sayı ikililerinin her iki terimi de 6'şar artmaktadır.
2'den 110'a kadar 6'şar 6'şar saydığımızda kaç \( a - b \) şeklinde sayı ikilisi olduğunu bulalım.
İkili sayısı \( = \dfrac{110 - 2}{6} + 1 = 19 \)
Buna göre verilen sayı dizisinde son terim hariç toplamları -3 olan 19 tane sayı ikilisi vardır.
\( = 19 \cdot (-3) + 116 \)
\( = -57 + 116 = 59 \) bulunur.
\( 1 + 2 + 3 + \ldots + n \lt 10000 \)
eşitsizliğini sağlayan en büyük \( n \) tam sayı değeri nedir?
Çözümü Göster1'den \( n \)'ye kadar olan tam sayıların toplamı \( \frac{n(n + 1)}{2} \) formülü ile bulunur.
Verilen eşitsizlikte bu formülü kullanalım.
\( \dfrac{n(n + 1)}{2} \lt 10000 \)
\( n(n + 1) \lt 20000 \)
Çarpımları 20000'den küçük olan en büyük iki ardışık sayıyı bulmalıyız.
\( 140^2 = 19600 \)
\( 141^2 = 19881 \)
\( 142^2 = 20164 \)
\( 141 \cdot 142 = 20022 \)
Buna göre çarpımları 20000'den küçük olan en büyük iki ardışık sayı 140 ve 141 olur.
\( 140 \cdot 141 = 19740 \lt 20000 \)
\( n = 140 \) olarak bulunur.
İlk \( 2n \) pozitif tam sayının toplamı, ilk \( n \) pozitif tam sayının toplamından 155 fazla olduğuna göre, ilk \( 4n \) pozitif tam sayının toplamı kaçtır?
Çözümü GösterArdışık sayılarda terimler toplamı formülü kullanalım.
\( \text{Terimler toplamı} = \dfrac{\text{İlk terim} + \text{Son terim}}{2} \cdot \text{Terim sayısı} \)
1 ve \( n \) arasındaki ardışık tam sayıların toplamını bulalım.
\( S_n = \dfrac{1 + n}{2} \cdot n \)
\( = \dfrac{n(n + 1)}{2} \)
1 ve \( 2n \) arasındaki ardışık tam sayıların toplamını bulalım.
\( S_{2n} = \dfrac{1 + 2n}{2} \cdot 2n \)
\( = \dfrac{2n(2n + 1)}{2} = n(2n + 1) \)
İlk \( 2n \) pozitif tam sayının toplamı, ilk \( n \) pozitif tam sayının toplamından 155 fazladır.
\( S_{2n} = S_n + 155 \)
\( n(2n + 1) = \dfrac{n(n + 1)}{2} + 155 \)
\( 4n^2 + 2n = n^2 + n + 310 \)
\( 3n^2 + n - 310 = 0 \)
\( (n - 10)(3n + 31) = 0 \)
\( n \) pozitif olduğu için \( n = 10 \) olur.
1 ve \( 4n \) arasındaki ardışık tam sayıların toplamını bulalım.
\( S_{4n} = \dfrac{1 + 4n}{2} \cdot 4n \)
\( = 2n(1 + 4n) \)
\( n = 10 \) yazalım.
\( = 20(1 + 40) = 820 \) bulunur.
\( A = 1 \cdot 3 + 3 \cdot 5 + 5 \cdot 7 + ... + 17 \cdot 19 \) olduğuna göre,
\( B = 2 \cdot 3 + 4 \cdot 5 + 6 \cdot 7 + ... + 18 \cdot 19 \) toplamı \( A \) cinsinden kaçtır?
Çözümü Göster\( A = 1 \cdot 3 + 3 \cdot 5 + 5 \cdot 7 + ... + 17 \cdot 19 \)
\( B = 2 \cdot 3 + 4 \cdot 5 + 6 \cdot 7 + ... + 18 \cdot 19 \)
İkinci ifadeden birinci ifadeyi çıkardığımızda ardışık tek sayı dizisi elde ederiz.
\( B - A = 3 + 5 + 7 + ... + 19 \)
Eşitliğin sağ tarafındaki ardışık sayıların toplamını bulalım.
Bu sayı dizisinde ilk terim 3, son terim 19, artış miktarı 2'dir.
Bir ardışık sayı dizisindeki terim sayısı aşağıdaki formülle bulunur.
\( \text{Terim sayısı} = \dfrac{\text{Son terim} - \text{İlk terim}}{\text{Artış miktarı}} + 1 \)
\( = \dfrac{19 - 3}{2} + 1 = 9 \)
Bir ardışık sayı dizisindeki terimler toplamı aşağıdaki formülle bulunur.
\( \text{Terimler toplamı} = \dfrac{\text{İlk terim} + \text{Son terim}}{2} \cdot \text{Terim sayısı} \)
\( B - A = \dfrac{3 + 19}{2} \cdot 9 \)
\( = 11 \cdot 9 = 99 \)
Buna göre \( B \) sayısı \( A \) cinsinden aşağıdaki gibi bulunur.
\( B = A + 99 \)
132 tane ardışık tam sayının toplamı \( 12! \) olduğuna göre, bu sayıların medyanı kaçtır?
Çözümü GösterElemanları küçükten büyüğe sıralanmış bir sayı kümesi tek sayıda eleman içeriyorsa sayıların medyanı ortadaki terimdir, çift sayıda eleman içeriyorsa ortadaki iki terimin ortalamasına eşittir.
Sayı kümesi ardışık sayılardan oluşuyorsa her iki durumda da medyan tüm sayıların ortalamasına eşittir.
Ortalama \( = \dfrac{12!}{132} \)
\( = \dfrac{12 \cdot 11 \cdot 10!}{12 \cdot 11} \)
\( = 10! \) bulunur.
\( a, b, c \) ortak farkı 10 olan ardışık sayılardır.
\( \left( 1 + \dfrac{10}{a} \right)\left( 1 + \dfrac{10}{b} \right)\left( 1 + \dfrac{10}{c} \right) = 6 \)
olduğuna göre, bu sayılardan en büyüğü kaçtır?
Çözümü Göster\( a \lt b \lt c \) olarak kabul edelim.
Verilen ardışık sayıları ortak bir \( k \) değişkeni cinsinden aşağıdaki şekilde yazabiliriz.
\( a = k \)
\( b = k + 10 \)
\( c = k + 20 \)
Bu değerleri verilen eşitlikte yerine yazalım.
\( \left( 1 + \dfrac{10}{k} \right)\left( 1 + \dfrac{10}{k + 10} \right)\left( 1 + \dfrac{10}{k + 20} \right) = 6 \)
\( \dfrac{k + 10}{k} \cdot \dfrac{k + 20}{k + 10} \cdot \dfrac{k + 30}{k + 20} = 6 \)
Pay ve paydadaki ifadeleri sadeleştirelim.
\( \dfrac{k + 30}{k} = 6 \)
\( k + 30 = 6k \)
\( k = 6 \)
Sayılardan en büyüğünü bulalım.
\( c = k + 20 = 26 \) bulunur.
Ceyda sınava hazırlanmak için ilk gün 10 soru çözmüştür, sonraki günlerde her gün soru sayısını birer artırarak devam etmiştir.
Buna göre Ceyda 200. sorusunu kaçıncı günde çözer?
Çözümü GösterCeyda'nın çözdüğü soru sayısı 1. gün 10, 2. gün 11, 3. gün 12, \( n \). gün \( n + 9 \) olur.
Ceyda'nın \( n \) gün sonunda çözmüş olacağı toplam soru sayısını bulalım.
\( \text{Terimler toplamı} = \dfrac{\text{İlk terim} + \text{Son terim}}{2} \cdot \text{Terim sayısı} \)
\( = \dfrac{10 + n + 9}{2} \cdot n \)
\( = \dfrac{n(n + 19)}{2} \)
Ceyda'nın hangi gün 200. soruyu çözdüğünü bulmak için \( n \)'ye değer verelim.
\( n = 10 \Longrightarrow \dfrac{10(10 + 19)}{2} = 145 \)
\( n = 11 \Longrightarrow \dfrac{11(11 + 19)}{2} = 165 \)
\( n = 12 \Longrightarrow \dfrac{12(12 + 19)}{2} = 186 \)
\( n = 13 \Longrightarrow \dfrac{13(13 + 19)}{2} = 208 \)
Buna göre Ceyda 200. sorusunu 13. günde çözer.
Ders sırasında sıkılan Yusuf, kareli defterinin bir sayfasının 1. satırında 1 kare, 2. satırında 2 kare olacak şekilde her satırında satır numarası kadar kareyi boyuyor.
Buna göre Yusuf 100. kareyi kaçıncı satırda boyar?
Çözümü Göster1. satırda 1, 2. satırda 2, \( n \). satırda \( n \) kare boyanıyor.
Buna göre \( n \). satır tamamlandığında boyanan toplam kare sayısı \( \frac{n(n + 1)}{2} \) formülü ile bulunur.
Bu sayının en az 100 olacağı \( n \) değerini bulalım.
\( \dfrac{n(n + 1)}{2} \ge 100 \)
\( n(n + 1) \ge 200 \)
\( n = 10 \Longrightarrow 10(10 + 1) = 110 \not\ge 200 \)
\( n = 11 \Longrightarrow 11(11 + 1) = 132 \not\ge 200 \)
\( n = 12 \Longrightarrow 12(12 + 1) = 156 \not\ge 200 \)
\( n = 13 \Longrightarrow 13(13 + 1) = 182 \not\ge 200 \)
\( n = 14 \Longrightarrow 14(14 + 1) = 210 \ge 200 \)
Buna göre 100. kare 14. satırda boyanır.
Aşağıdaki kümelerden hangisinin elemanlarının ortalaması en küçüktür?
(a) 1 ile 86 arasında 5'in katları
(b) 1 ile 86 arasında 7'nin katları
(c) 1 ile 86 arasında 9'un katları
(d) 1 ile 86 arasında 11'in katları
(e) 1 ile 86 arasında 13'ün katları
Çözümü GösterBir ardışık sayı dizisindeki terimler toplamı aşağıdaki formülle bulunur.
\( \text{Terimler toplamı} = \dfrac{\text{İlk terim} + \text{Son terim}}{2} \cdot \text{Terim sayısı} \)
Buna göre terimlerin ortalaması aşağıdaki gibi olur.
\( \dfrac{\text{Terimler toplamı}}{\text{Terim sayısı}} = \dfrac{\text{İlk terim} + \text{Son terim}}{2} \)
Dolayısıyla ardışık sayıların ortalaması terim sayısına değil, ilk ve son terime bağlı olarak değişir.
Verilen kümelere bu formülü uygulayalım.
(a) seçeneğindeki kümenin ilk terimi 5, son terimi 85'tir.
Ortalama \( = \dfrac{5 + 85}{2} = 45 \)
(b) seçeneğindeki kümenin ilk terimi 7, son terimi 84'tür.
Ortalama \( = \dfrac{7 + 84}{2} = 45,5 \)
(c) seçeneğindeki kümenin ilk terimi 9, son terimi 81'dir.
Ortalama \( = \dfrac{9 + 81}{2} = 45 \)
(d) seçeneğindeki kümenin ilk terimi 11, son terimi 77'dir.
Ortalama \( = \dfrac{11 + 77}{2} = \dfrac{88}{2} = 44 \)
(e) seçeneğindeki kümenin ilk terimi 13, son terimi 78'dir.
Ortalama \( = \dfrac{13 + 78}{2} = 45,5 \)
(d) seçeneğindeki kümenin elemanlarının ortalaması en küçüktür.
Ardışık beş pozitif tam sayının çarpımı, birden büyük rakamlardan hangilerine her zaman tam bölünmez?
Çözümü GösterBu sayıların farklı seçimlerine birkaç örnek verelim.
\( 1 \cdot 2 \cdot 3 \cdot 4 \cdot 5 \)
\( 2 \cdot 3 \cdot 4 \cdot 5 \cdot 6 \)
\( 3 \cdot 4 \cdot 5 \cdot 6 \cdot 7 \)
\( 4 \cdot 5 \cdot 6 \cdot 7 \cdot 8 \)
\( 5 \cdot 6 \cdot 7 \cdot 8 \cdot 9 \)
Ardışık beş pozitif tam sayı 1 ya da 2 tane 4'e bölünen sayı, ek olarak 1 ya da 2 tane 2'ye bölünen sayı, 1 ya da 2 tane 3'e bölünen sayı ve 1 tane 5'e bölünen sayı içerir.
Dolayısıyla ardışık beş tam sayı içinde her zaman en az üç tane 2, en az bir tane 3 ve bir tane 5 çarpanı bulunur ve bu sayıların çarpımı 1, 2, 3, 4, 5, 6 ve 8 rakamlarına her zaman tam bölünür.
Buna göre bu sayıların çarpımı 7 ve 9 rakamlarına her zaman bölünmez.
Ardışık üç tam sayının toplamı bu sayıların çarpımına eşit olduğuna göre, bu sayılardan en büyüğü en çok kaç olabilir?
Çözümü GösterArdışık sayılara \( n - 1, n, n + 1 \) diyelim.
Ardışık sayıların toplamı çarpımlarına eşittir.
\( (n - 1) + n + (n + 1) = (n - 1)n(n + 1) \)
\( 3n = n(n^2 - 1) \)
\( n^3 - n - 3n = 0 \)
\( n(n^2 - 4) = 0 \)
\( n(n - 2)(n + 2) = 0 \)
Bu denklemin çözüm kümesi her bir çarpanı sıfır yapan değerlerden oluşur.
\( n \in \{ -2, 0, 2 \} \)
Bu sayılardan en büyüğü \( n = 2 \) olduğunda oluşan en büyük terim olan \( n + 1 = 3 \) olur.
Bir yönetici ofisindeki çalışanlara 1. çalışana 2 adet, 2. çalışana 4 adet, 3. çalışana 6 adet ve \( n \). çalışana \( 2n \) adet olacak şekilde kalem dağıtıyor. Bu işlem sonucunda tüm kalemler dağıtılmış oluyor.
Yönetici daha sonra tüm kalemleri topluyor ve bu sefer herkese eşit sayıda olacak şekilde dağıtıyor. Bu durumda \( n \). çalışanın aldığı kalem sayısı ilk durumdan 10 eksik olduğuna göre, toplam dağıtılan kalem sayısı kaçtır?
Çözümü Gösterİlk seferde dağıtılan kalem sayısını ardışık sayıların toplam formülü ile aşağıdaki şekilde hesaplayabiliriz.
\( \text{Terimler toplamı} = \dfrac{\text{İlk terim} + \text{Son terim}}{2} \cdot \text{Terim sayısı} \)
\( = \dfrac{2 + 2n}{2} \cdot n = n(n + 1) \)
Kalem sayısını toplam kişi sayısına bölelim.
\( \dfrac{n(n + 1)}{n} = n + 1 \)
Bu sayı aynı zamanda ilk durumda \( n \). kişinin aldığı kalem sayısının 10 eksiğine eşittir.
\( n + 1 = 2n - 10 \)
\( n = 11 \)
Buna göre toplam kalem sayısı \( 11 \cdot 12 = 132 \) olarak bulunur.
\( A = 2 \cdot 5 + 3 \cdot 6 + 4 \cdot 7 + \ldots + 16 \cdot 19 \)
toplamında her terimin ilk çarpanı 3 artırılıp ikinci çarpanı 2 azaltılırsa toplam nasıl değişir?
Çözümü GösterYeni oluşan sayıya \( B \) diyelim.
\( B = 5 \cdot 3 + 6 \cdot 4 + 7 \cdot 5 + \ldots + 19 \cdot 17 \)
\( A \) ve \( B \) ifadelerinin terimlerini birebir karşılaştıralım.
\( A \) sayısında birinci terimde 2 tane 5 varken \( B \) sayısında 3 tane 5 vardır. \( A \) sayısında ikinci terimde 3 tane 6 varken \( B \) sayısında 4 tane 6 vardır.
Buna göre iki ifadenin farkını aldığımızda ardışık sayıların toplamını elde ederiz.
\( B - A = 5 + 6 + 7 + \ldots + 19 \)
Bu ardışık sayı dizisinde \( 19 - 5 + 1 = 15 \) terim vardır.
Bir ardışık sayı dizisindeki terimler toplamı aşağıdaki formülle bulunur.
\( \text{Terimler toplamı} = \dfrac{\text{İlk terim} + \text{Son terim}}{2} \cdot \text{Terim sayısı} \)
\( B - A = \dfrac{5 + 19}{2} \cdot 15 \)
\( = 12 \cdot 15 = 180 \)
Buna göre toplam 180 artar.
5 tane iki basamaklı ardışık doğal sayının toplamı bir sayma sayısının küpüne eşittir.
Buna göre bu ardışık sayıların en büyüğü kaçtır?
Çözümü GösterArdışık sayıları yazalım.
\( (ab), (ab) + 1, \ldots, (ab) + 4 \)
Bu sayıların toplamı bir \( x \) sayma sayısının küpüne eşittir.
\( 5(ab) + 10 = x^3 \)
\( 5(ab) = x^3 - 10 \)
Bir sayma sayısının küpü (\( x^3 \)) aşağıdakilerden biri olabilir. \( (ab) \) sayısı iki basamaklı olduğu için ardışık sayıların toplamı daha büyük bir tam küp sayı olamaz.
1, 8, 27, 64, 125, 216, 343, 512
Bu sayıların 10 eksiği (\( x^3 - 10 \)) aşağıdakilerden biri olabilir.
-9, -2, 17, 54, 115, 206, 333, 502...
Bu ifade \( 5(ab) \) ifadesine eşittir, dolayısıyla 5'in bir tam sayı katı olmalıdır.
Yukarıdaki listede bu koşulu sağlayan sayı sadece 115'tir.
\( 5(ab) = x^3 - 10 = 115 \)
\( (ab) = 23 \)
Sayıların en büyüğü \( (ab) + 4 = 27 \) olur.
Kayra'nın oturduğu binada zemin katta 3 daire, sonraki her katta 4'er daire vardır. Daire numaraları zeminden itibaren 1 ile başlayan ardışık sayılardır ve daire numaralarının aritmetik ortalaması 38'dir.
Buna göre, Kayra zemin kat dahil olmak üzere kaç katlı bir binada oturmaktadır?
Çözümü GösterBinadaki zemin kat dahil kat sayısına \( k \) dersek toplam daire sayısı \( 3 + 4(k - 1) = 4k - 1 \) olur.
Daire numaralarının toplamını ardışık sayıların toplam formülü ile bulalım.
\( \text{Terimler toplamı} = \dfrac{\text{İlk terim} + \text{Son terim}}{2} \cdot \text{Terim sayısı} \)
\( = \dfrac{1 + 4k - 1}{2} \cdot (4k - 1) \)
\( = 2k(4k - 1) \)
Bu toplamın daire sayısına bölümü aritmetik ortalamayı verir.
\( \dfrac{2k(4k - 1)}{4k - 1} = 38 \)
\( k = 19 \) bulunur.
Sevda bir sayıdan başlayarak ileriye dörder, Orkun da aynı sayıdan başlayarak ileriye sekizer ritmik sayıyor. Sevda 20 sayı saydıktan sonra saymayı bırakıyor, Orkun ise 40 sayı sayana kadar devam ediyor.
Sevda'nın saydığı sayıların toplamı \( a \) olduğuna göre, Orkun'un saydığı sayıların toplamı \( a \) cinsinden kaçtır?
Çözümü GösterSevda ve Orkun'ın saymaya başladıkları sayıya \( x \) diyelim.
Sevda'nın saydığı ilk sayı \( x \), son sayı \( x + 4(20 - 1) = x + 76 \) olur.
Sevda'nın saydığı sayıların toplamını bulalım. Bu toplam \( a \)'ya eşittir.
\( \text{Terimler toplamı} = \dfrac{\text{İlk terim} + \text{Son terim}}{2} \cdot \text{Terim sayısı} \)
\( = \dfrac{x + (x + 76)}{2} \cdot 20 \)
\( = 20x + 760 = a \)
Orkun'un saydığı ilk sayı \( x \), son sayı \( x + 8(40 - 1) = x + 312 \) olur.
Orkun'un saydığı sayıların toplamını bulalım.
\( = \dfrac{x + (x + 312)}{2} \cdot 40 \)
\( = 40x + 6240 \)
Orkun'un saydığı sayıların toplamını \( a \) cinsinden yazalım.
\( 40x + 6240 = 2(20x + 760) + 4720 \)
\( = 2a + 4720 \) bulunur.
Başlangıçta 123 sayfa olan bir kitabın herhangi bir bölümünden ardışık 4 yaprak koparılıyor.
Geriye kalan yapraklardaki sayfa numaralarının toplamı \( 117 \cdot 62 \) olduğuna göre, koparılan yapraklardaki sayfa numaralarının en küçüğü kaçtır?
Çözümü GösterKitaptaki sayfa sayısına \( n \) diyelim.
İlk durumdaki sayfa numaralarının toplamını bulalım.
Sayfa numaralarının toplamı \( = \dfrac{n(n + 1)}{2} \)
\( = \dfrac{123 \cdot 124}{2} = 123 \cdot 62 \)
Koparılan yapraklardaki sayfa numaralarının toplamını bulalım.
\( 123 \cdot 62 - 117 \cdot 62 = (123 - 117) \cdot 62 \)
\( = 62 \cdot 6 = 372 \)
Koparılan 4 yapraktaki 8 sayfanın numaraları \( a, a + 1, a + 2 , a + 3, a + 4, a + 5, a + 6, a + 7 \) şeklindedir.
Bu sayıların toplamı 372'dir.
\( \text{Terimler toplamı} = \dfrac{\text{İlk terim} + \text{Son terim}}{2} \cdot \text{Terim sayısı} \)
\( 372 = \dfrac{a + (a + 7)}{2} \cdot 8 \)
\( 2a + 7 = 93 \)
\( a = 43 \) bulunur.