Basamak Kavramı

0-9 arası sayıları sadece rakamları kullanarak ifade edebiliriz, ancak daha büyük sayıları ifade etmek için bu rakamları belirli kurallar dahilinde bir araya getirebileceğimiz bir basamak sistemine ihtiyaç duyarız. Bir basamak sisteminde her rakam bulunduğu basamakla birlikte bir büyüklük ifade eder. Örneğin, 143 ve 341 sayıları aynı rakamlardan oluşsa da, her rakamın sayı içindeki konumu farklı olduğu için iki sayı farklı büyüklükler ifade etmektedir.

Geçmişte kullanılmış ve günümüzde kullanılmakta olan pek çok basamak sistemi vardır. Özellikle bilgisayar yazılımları ikili, sekizli ve onaltılı sistemleri yoğunlukla kullanmaktadır. Bununla birlikte, matematikte ve günlük hayatta en yaygın şekilde kullandığımız basamak sistemi 0-9 arası rakamları kullanan onlu basamak sistemidir.

Basamak sistemi bilgisi, sayı kavramının iyi anlaşılması dışında dört işlem ve sayıları karşılaştırma, sıralama ve yuvarlama işlemleri açısından da son derece önemlidir.

Tam sayılarda onlu basamak sisteminin işleyişi kısaca aşağıdaki gibidir:

• Her sayı isimleri ve birim değerleri farklı basamaklardan oluşur. Bir sayı kaç basamaktan oluşuyorsa, o kadar basamaklı bir sayı olduğunu söyleriz.
• Her basamak 0-9 arası rakamlardan birini içerir.
• En sağdaki basamak en küçük değere sahip basamaktır ve birim değeri \( 10^0 = 1 \)'dir. Sağdan ikinci basamağın birim değeri \( 10^1 = 10 \), sağdan üçüncü basamağın birim değeri \( 10^2 = 100 \)'dür. Basamakların birim değerleri sola doğru 10'un kuvvetleri şeklinde artar.
• Her basamağın basamak değeri, o basamaktaki rakam ile basamağın birim değerinin çarpımına eşittir.
• Bir sayının değeri, tüm basamakların basamak değerlerinin toplamına eşittir.

Aşağıdaki şekilde 9 basamaklı \( 123.456.789 \) sayısının basamak isimleri ve basamakların birim değerleri gösterilmiştir:

Aşağıda \( 456.789 \) sayısı için gösterildiği gibi, her basamaktaki rakam aslında kendisinden sonraki basamaklarda sıfır olan, ama bu sıfırların gösterilmediği daha büyük bir sayının değerini taşımaktadır.

Yukarıda şekildeki \( 456.789 \) sayısının basamaklarının basamak değerlerinin hesaplaması aşağıdaki tabloda verilmiştir:

Basamak Adı	Hesaplama	Basamak Değeri
Yüz binler basamağı	\( 4 \times 100.000 \)	\( 400.000 \)
On binler basamağı	\( 5 \times 10.000 \)	\( 50.000 \)
Binler basamağı	\( 6 \times 1.000 \)	\( 6.000 \)
Yüzler basamağı	\( 7 \times 100 \)	\( 700 \)
Onlar basamağı	\( 8 \times 10 \)	\( 80 \)
Birler basamağı	\( 9 \times 1 \)	\( 9 \)

Bu basamak değerlerini topladığımızda aşağıdaki gibi sayının gerçek sayısal değerine ulaşırız:

İlkokulda onlu basamak sisteminin ilk öğretim yöntemlerinden olan onlu sistem blokları ile 245 sayısının modellenmiş şekli aşağıdaki gibidir. Burada da her basamakta kullanılan farklı bloklardan, her basamağın birim değerinin sola doğru 10'un kuvvetleri şeklinde büyüdüğünü görebiliriz.

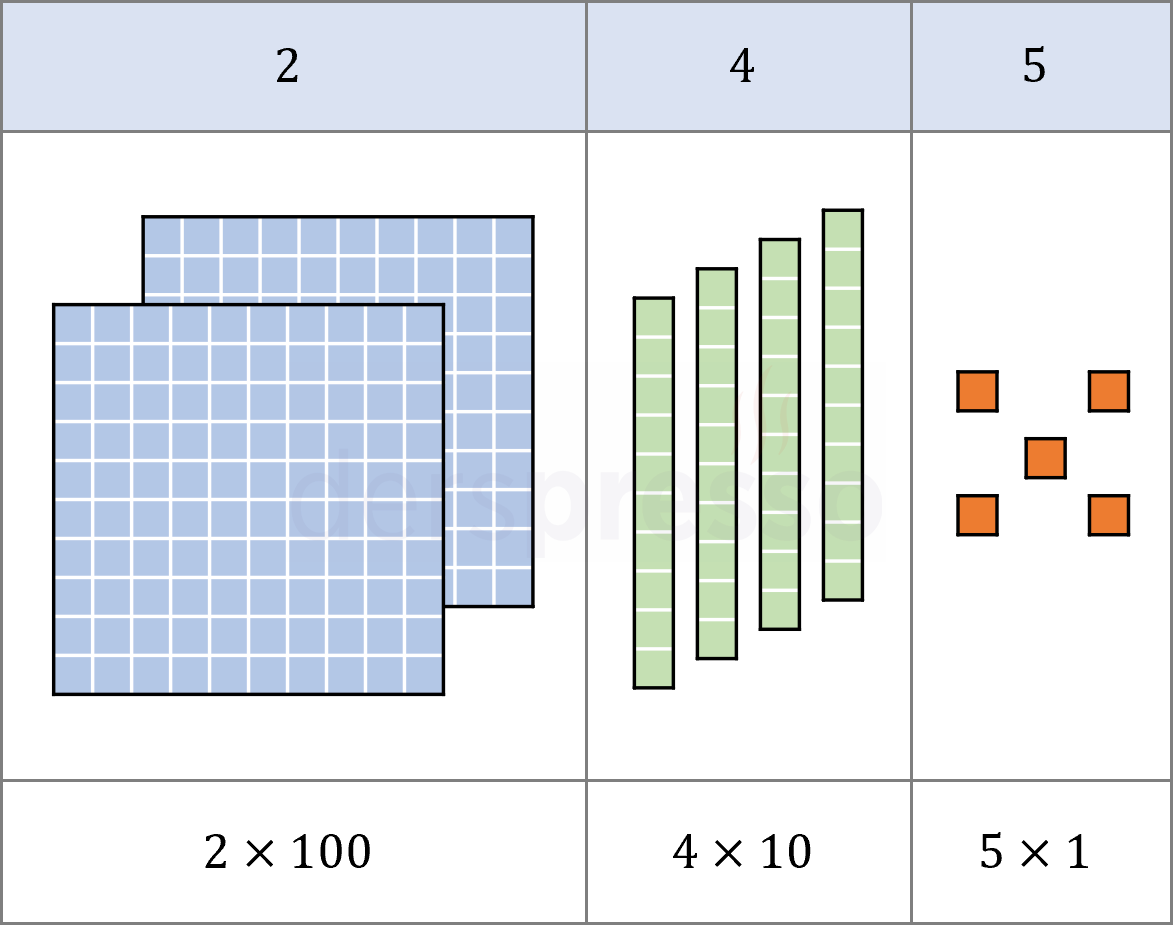
Bir Sayının Çözümlenmesi

Bir sayının basamaklarının basamak değerlerinin toplamı şeklinde yazılışına o sayının çözümlenmesi denir.

Aşağıda iki ve üç basamaklı birer sayının çözümlenmesi gösterilmiştir.

Aşağıda altı basamaklı bir sayının çözümlenmesi gösterilmiştir.

Aşağıdaki çözümlemeye göre, iki basamaklı bir sayı ve rakamları yer değiştirmiş halinin toplamı, sayının rakamları toplamının 11 katına eşittir.

Aşağıdaki çözümlemeye göre, iki basamaklı bir sayı ve rakamları yer değiştirmiş halinin farkı, sayının rakamları farkının 9 katına eşittir.

Bir sayının aşağıdaki şekilde basamaklarını ayırarak farklı sayıların toplamı şeklinde yazabiliriz.

Bir Sayının Basamaklarında Yapılan Değişiklikler

Bir tam sayının sonuna eklenen bir sıfır, sayının değerini \( 10^1 = 10 \) katına, iki sıfır \( 10^2 = 100 \) katına, \( n \) sıfır ise \( 10^n \) katına çıkarır.

Bir tam sayının başına eklenen bir ya da birden fazla sıfır, sayının değerini değiştirmez.

Bir sayının belirli bir basamağındaki rakam bir arttırılırsa ya da azaltılırsa, sayının değeri basamağın birim değeri kadar artar ya da azalır.

Bir sayının belirli bir basamağındaki rakam \( n \) arttırılırsa ya da azaltılırsa, sayının değeri \( n \) çarpı basamağın birim değeri kadar artar ya da azalır.

En Küçük/En Büyük Sayılar

Basamak değerleri bilgisini kullanarak belirli koşulları sağlayan en küçük ve en büyük sayıları kolaylıkla bulabiliriz.

İki basamaklı en küçük ve en büyük bazı sayılar aşağıdaki gibidir.

Üç basamaklı en küçük ve en büyük bazı sayılar aşağıdaki gibidir.

Dört basamaklı en küçük ve en büyük bazı sayılar aşağıdaki gibidir.