Pozitif ve Negatif Sayılar

Sıfırdan büyük sayılara pozitif sayılar, sıfırdan küçük sayılara negatif sayılar denir.

Pozitif sayılar sayı doğrusunda sıfırın sağındaki, negatif sayılar da solundaki sayılardır.

Sayı doğrusu
Sayı doğrusu

Bir sayının önünde bulunan ve sayının pozitif ya da negatif olduğunu gösteren sembole o sayının işareti denir. Pozitif sayılar sayının önüne konan "\( + \)" işareti ile, negatif sayılar da "\( - \)" işareti ile gösterilir. Sayının önünde bir işaret olmadığı durumda sayının pozitif olduğu anlaşılmalıdır.

Pozitif ve negatif işaretleri
Pozitif ve negatif işaretleri

Sıfır sayısı ne pozitif ne de negatiftir, bu yüzden işaretsizdir. Önüne gelecek pozitif ya da negatif işareti sıfır sayısının değerini değiştirmez.

İki pozitif sayıdan mutlak değerce daha büyük olan sayı doğrusunda daha sağda olduğu için daha büyüktür. İki negatif sayıdan mutlak değerce daha büyük olan sayı doğrusunda daha solda olduğu için daha küçüktür.

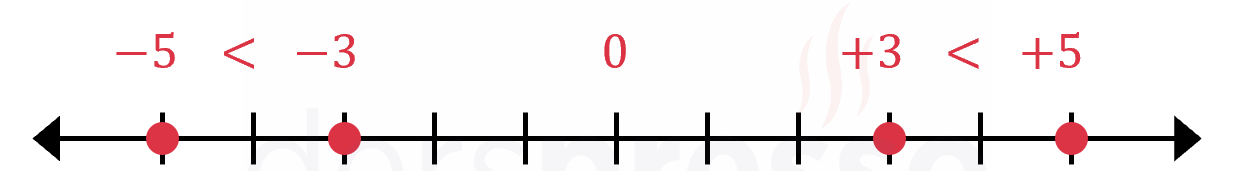
Pozitif ve negatif sayıların karşılaştırması
Pozitif ve negatif sayıların karşılaştırması

Pozitif ve negatif reel sayılar kümelerinin ve sıfır sayısının birleşim kümesi reel sayılar kümesine eşittir. Benzer şekilde, pozitif ve negatif tam sayılar kümelerinin ve sıfır sayısının birleşim kümesi tam sayılar kümesine eşittir.

Bir Sayının Toplamaya Göre Tersi

Bir sayının toplamaya göre tersi, o sayı ile toplandığında sıfır sonucunu veren sayıdır. Bir sayının toplamaya göre tersi o sayının ters işaretlisidir. Sıfırın toplamaya göre tersi sıfırdır.

Bir sayının toplamaya göre tersinin tersi kendisine eşittir.

Pozitif ve Negatif Sayılarla İşlemler

Bu bölümde pozitif ve negatif sayılarla işlemlere dair bazı kurallardan bahsedeceğiz.

Pozitif Sayıyla Toplama

Bir sayı pozitif bir sayı ile toplandığında sayının değeri artmış ve sayı sayı doğrusu üzerinde sağa taşınmış olur.

Pozitif sayı ile toplama
Pozitif sayı ile toplama

Negatif Sayıyla Toplama

Bir sayı negatif bir sayı ile toplandığında sayının değeri azalmış ve sayı sayı doğrusu üzerinde sola taşınmış olur. Dolayısıyla negatif bir sayı ile toplama işlemi bir çıkarma işlemi olarak da düşünülebilir.

Negatif sayı ile toplama
Negatif sayı ile toplama

Pozitif Sayı Çıkarma

Bir sayıdan pozitif bir sayı çıkarıldığında sayının değeri azalmış ve sayı sayı doğrusu üzerinde sola taşınmış olur.

Pozitif sayı çıkarma
Pozitif sayı çıkarma

Negatif Sayı Çıkarma

Bir sayıdan negatif bir sayı çıkarıldığında sayının değeri artmış ve sayı sayı doğrusu üzerinde sağa taşınmış olur. Dolayısıyla negatif bir sayı çıkarma işlemi bir toplama işlemi olarak da düşünülebilir.

Negatif sayı çıkarma
Negatif sayı çıkarma

Kısaca özetlersek, bir sayıyı negatif bir sayı ile toplamakla aynı sayının pozitifini çıkarmak aynı işlemdir.

Benzer şekilde, bir sayıdan negatif bir sayı çıkarmakla aynı sayının pozitifi ile toplamak aynı işlemdir.

Pozitif sayıların toplamı her zaman pozitif, negatif sayıların toplamı her zaman negatiftir.

Zıt işaretli iki sayı toplandığında sonuç mutlak değer olarak büyük olan sayının işaretini alır. Mutlak değerleri eşit ve zıt işaretli iki sayının toplamı sıfır olur.

Toplamlarının işareti bilinen sayıların pozitif/negatif olma durumları hakkında aşağıdaki çıkarımlar yapılabilir.

Pozitif/Negatif Sayılarla Çarpma

Pozitif ve negatif sayıların birbiriyle çarpımının pozitif/negatif olma durumları aşağıdaki gibidir. Buna göre, sayıların işaretleri aynı ise sonuç pozitif, sayılar ters işaretli ise sonuç negatiftir.

İşlem Örnek
\( (+) \cdot (+) = (+) \) \( 3 \cdot 2 = 6 \)
\( (+) \cdot (-) = (-) \) \( 3 \cdot (-2) = -6 \)
\( (-) \cdot (+) = (-) \) \( (-3) \cdot 2 = -6 \)
\( (-) \cdot (-) = (+) \) \( (-3) \cdot (-2) = 6 \)

Pek çok çarpandan oluşan çarpma işleminde negatif çarpanların sayısı çift ise sonuç pozitif, tek ise sonuç negatiftir. Pozitif çarpanların sayısının sonucun işaretine etkisi yoktur.

Pozitif/Negatif Sayılarla Bölme

Pozitif ve negatif sayıların birbirine bölümünün pozitif/negatif olma durumları çarpmadaki ile aynıdır. Buna göre, sayıların işaretleri aynı ise sonuç pozitif, sayılar ters işaretli ise sonuç negatiftir.

İşlem Örnek
\( (+) \div (+) = (+) \) \( 8 \div 2 = 4 \)
\( (+) \div (-) = (-) \) \( 8 \div (-2) = -4 \)
\( (-) \div (+) = (-) \) \( (-8) \div 2 = -4 \)
\( (-) \div (-) = (+) \) \( (-8) \div (-2) = 4 \)

Pozitif/Negatif Sayıların Tek/Çift Sayı Üsleri

Pozitif/negatif sayıların pozitif tek/çift sayı üslerinin pozitif/negatif olma durumları aşağıdaki gibidir.

İşlem Örnek
\( (+)^\text{Çift} = (+) \) \( 3^2 = 9 \)
\( (+)^\text{Tek} = (+) \) \( 3^3 = 27 \)
\( (-)^\text{Çift} = (+) \) \( (-3)^2 = 9 \)
\( (-)^\text{Tek} = (-) \) \( (-3)^3 = -27 \)

Bu tabloya göre, üs (sıfırdan farklı olmak üzere) çift sayı ise sonuç tabanın işaretinden bağımsız her zaman pozitiftir, tek sayı ise tabanın işareti ile aynıdır.

Üs işlemi tekrarlı çarpma olduğu için, bu sonucu yukarıdaki çarpma kuralından da türetebiliriz. Buna göre, pozitif sayıların çarpımı çarpan sayısından bağımsız her zaman pozitiftir. Negatif sayıların çarpımında çarpan sayısı çift ise sonuç pozitif, tek ise sonuç negatiftir.

NOT: Yukarıdaki tablo negatif sayıların çift dereceli köklerinin reel sayılar kümesinde tanımlı olmamasını da açıklamaktadır. Buna göre, bir sayının çift sayıda üssü hiçbir zaman negatif olamaz, dolayısıyla negatif bir sayının çift dereceli kökünün de reel sayılarda çözümü yoktur.

Üs işleminin işlem önceliği diğer işlemlerden yüksektir, dolayısıyla üssü alınan sayının önündeki negatif işaretine dikkat edilmelidir. Aşağıdaki işlemlerin tümünde üs işleminin tabanı \( -2 \) değil \( 2 \)'dir ve negatif işareti üs işleminin sonucuna uygulanmaktadır.

Negatif bir sayının üssü alınmak istendiğinde parantez negatif işaretini de içine alacak ve üs işlemi tüm paranteze uygulanacak şekilde yerleştirilmelidir.

SORU 1 :

\( a, b \in \mathbb{R} \) olmak üzere,

\( a \cdot b^2 \lt 0 \)

\( a^2 \cdot b \gt 0 \)

olduğuna göre, \( a \) ve \( b \)'nin işaretleri nedir?

Verilen eşitsizliklere göre \( a \) ve \( b \) sıfırdan farklı reel sayılardır.

Birinci eşitsizlik: Sıfırdan farklı bir sayının çift kuvveti her zaman pozitif olduğu için \( b^2 \) pozitiftir. \( a \cdot b^2 \) ifadesi negatif olduğuna göre \( a \) negatiftir.

İkinci eşitsizlik: \( a^2 \) çift kuvvetten dolayı pozitiftir. \( a^2 \cdot b \) ifadesi pozitif olduğuna göre \( b \) pozitiftir.

Buna göre \( a \) negatif, \( b \) pozitiftir.

SORU 2 :

\( x, y, z \in \mathbb{R} \) olmak üzere,

\( x^2 \cdot y \lt 0 \)

\( y \cdot z \gt 0 \)

\( x \cdot z \lt 0 \)

olduğuna göre, \( x \), \( y \) ve \( z \)'nin işaretleri nedir?

Verilen eşitsizliklere göre \( x \), \( y \) ve \( z \) sıfırdan farklı reel sayılardır.

Birinci eşitsizlik: Sıfırdan farklı bir sayının çift kuvveti her zaman pozitif olduğu için \( x^2 \) pozitiftir. \( x^2 \cdot y \) ifadesi negatif olduğuna göre \( y \) negatiftir.

İkinci eşitsizlik: \( y \cdot z \) ifadesinin pozitif olması için \( y \) ve \( z \) aynı işaretli olmalıdır. Birinci eşitsizlikte \( y \)'yi negatif olarak bulmuştuk, dolayısıyla \( z \) de negatiftir.

Üçüncü eşitsizlik: \( x \cdot z \) ifadesinin negatif olması için \( x \) ve \( z \) ters işaretli olmalıdır. İkinci eşitsizlikte \( z \)'yi negatif olarak bulmuştuk, dolayısıyla \( x \) pozitiftir.

Buna göre \( x \) pozitif, \( y \) ve \( z \) negatiftir.

SORU 3 :

\( x, y, z \in \mathbb{R} \) olmak üzere,

\( x \cdot y \lt 0 \)

\( y \cdot z \gt 0 \)

\( \dfrac{x \cdot y}{z} \lt 0 \)

olduğuna göre, \( x \), \( y \) ve \( z \)'nin işaretleri nedir?

Verilen eşitsizliklere göre \( x \), \( y \) ve \( z \) sıfırdan farklı reel sayılardır.

Birinci eşitsizlik: \( x \cdot y \) ifadesinin negatif olması için \( x \) ve \( y \) ters işaretli olmalıdır.

İkinci eşitsizlik: \( y \cdot z \) ifadesinin pozitif olması için \( y \) ve \( z \) aynı işaretli olmalıdır.

Üçüncü eşitsizlik: Birinci eşitsizlikten paydaki \( x \cdot y \) ifadesinin negatif olduğunu biliyoruz. Bu durumda tüm ifadenin negatif olması için \( z \) pozitif olmalıdır.

İkinci eşitsizlikte \( y \) ve \( z \)'nin aynı işaretli olduğunu bulmuştuk. \( z \) pozitif olduğu için \( y \) de pozitiftir.

Birinci eşitsizlikte \( x \) ve \( y \)'nin ters işaretli olduğunu bulmuştuk. \( y \) pozitif olduğu için \( x \) negatiftir.

Buna göre \( x \) negatif, \( y \) ve \( z \) pozitiftir.

SORU 4 :

\( y \lt z \lt x \) olmak üzere,

\( x^5 \cdot y^6 \cdot z^7 \) çarpımının sonucu negatif olduğuna göre, \( x \), \( y \) ve \( z \) sayılarının işaretleri nedir?

Verilen ifade negatif olduğu için sayılardan hiçbiri sıfır olamaz.

\( x^5 \cdot y^6 \cdot z^7 \) çarpımında \( y^6 \) çift kuvvetli olduğu için sonucu pozitiftir. Buna göre \( x \) ve \( z \)'den biri pozitif diğeri negatif olmalıdır.

Sayılar arasındaki sıralamada \( z \) sayısı \( x \)'ten küçük olduğu için \( z \) negatif \( x \) pozitif olmalıdır. \( y \) sayısı \( z \)'den küçük olduğu için \( y \) de negatif olmalıdır.

Buna göre \( x \) pozitif, \( y \) ve \( z \) negatiftir.

SORU 5 :

\( a, b, c, d, e, f \) reel sayı dizisinde birbirini takip eden üç sayının çarpımı pozitiftir.

Bu sayılardan \( c \) negatif ve \( e \) pozitif olduğuna göre, \( a, b, d, f \) sayılarının işaretleri nedir?

Verilen sayı dizisinde birbirini takip eden üç sayının çarpımı pozitiftir.

\( c \cdot d \cdot e = (+) \)

\( (-) \cdot d \cdot (+) = (+) \)

Buna göre \( d \) sayısı negatiftir.

\( b \cdot c \cdot d = (+) \)

\( b \cdot (-) \cdot (-) = (+) \)

Buna göre \( b \) sayısı pozitiftir.

\( a \cdot b \cdot c = (+) \)

\( a \cdot (+) \cdot (-) = (+) \)

Buna göre \( a \) sayısı negatiftir.

\( d \cdot e \cdot f = (+) \)

\( (-) \cdot (+) \cdot f = (+) \)

Buna göre \( f \) sayısı negatiftir.

\( a, b, d, f \) sayılarının işaretleri sırasıyla \( -, +, -, - \) olarak bulunur.

SORU 6 :
Soru

Yukarıda verilen sayı doğrusuna göre aşağıdakilerden hangileri her zaman pozitiftir?

I. \( a + c \)

II. \( b - c \)

III. \( a - b \)

IV. \( c - a \)

V. \( b \cdot c \)

I. öncül: Sayı doğrusuna göre \( a \) negatif \( c \) pozitiftir, ancak mutlak değer olarak büyüklüklerini bilmediğimiz için toplamlarının pozitif/negatif olma durumunu kesin bilemeyiz.

II. öncül: Daha küçük bir sayıdan daha büyük bir sayıyı çıkardığımızda sonuç negatif olur.

III. öncül: Daha küçük bir sayıdan daha büyük bir sayıyı çıkardığımızda sonuç negatif olur.

IV. öncül: Daha büyük bir sayıdan daha küçük bir sayıyı çıkardığımızda sonuç pozitif olur.

V. öncül: \( b \) negatif ve \( c \) pozitif olduğu için çarpımları negatif olur.

Buna göre sadece IV. maddedeki ifade her zaman pozitiftir.

SORU 7 :

\( \abs{a} \gt a \)

\( a \cdot b \cdot c \lt 0 \)

\( b + c \lt 0 \)

olduğuna göre, \( a \), \( b \) ve \( c \) sayılarının işaretleri nedir?

Bir sayının mutlak değeri kendisinden büyükse o sayı negatiftir. Buna göre \( a \) negatiftir.

\( a \cdot b \cdot c \lt 0 \) eşitsizliğinde \( a \) negatif olduğu için \( b \cdot c \gt 0 \) olmalıdır, dolayısıyla \( b \) ve \( c \) aynı işaretlidir.

\( b + c \) toplamı negatif olduğuna göre, işaretleri aynı olan \( b \) ve \( c \) negatif olmalıdır.

Buna göre \( a \), \( b \) ve \( c \) sayılarının üçü de negatiftir.

SORU 8 :

\( \{-19, -17, -1, 1, 2, 3, 6\} \) kümesinden seçilen 3 sayının çarpımının alabileceği en küçük değer kaçtır?

Küme pozitif ve negatif sayılar içerdiği için seçilecek sayıların çarpımının en küçük değeri negatif olmalıdır.

Çarpımın negatif olması için seçilecek sayıların ya üçü de negatif olmalıdır ya da biri negatif ikisi pozitif olmalıdır.

Durum 1: 3 sayı da negatif

\( -19 \cdot (-17) \cdot (-1) = -19 \cdot 17 \)

Durum 2: 1 sayı negatif, 2 sayı pozitif

Sayıları hem pozitif hem de negatif tarafta mutlak değerce en büyük seçmeliyiz.

\( -19 \cdot 6 \cdot 3 = -19 \cdot 18 \)

2. durumda bulduğumuz değer daha küçüktür.

\( -19 \cdot 18 = -342 \) bulunur.

SORU 9 :

\( x \lt 0 \lt y \) olmak üzere,

I. \( -x^2 \)

II. \( x - y \)

III. \( x + y \)

IV. \( x^2 + y^2 \)

ifadelerinden hangileri kesinlikle pozitiftir?

I. öncül: \( x^2 \) ifadesi her zaman pozitif olduğu için \( -x^2 \) negatif olur.

II. öncül: Daha küçük \( x \) sayısından daha büyük \( y \) sayısını çıkardığımızda sonuç her zaman negatif olur.

III. öncül: \( x + y \) toplamı \( \abs{x} \lt \abs{y} \) ise pozitif, \( \abs{x} \gt \abs{y} \) ise negatif, \( \abs{x} = \abs{y} \) ise sıfırdır. Bu işlemin sonucunun işareti hakkında kesin bir şey söyleyemeyiz.

IV. öncül: Sıfırdan farklı bir sayının karesi her zaman pozitif olduğu için \( x^2 + y^2 \) toplamı her zaman pozitiftir.

Buna göre sadece IV. öncüldeki ifade her zaman pozitiftir.

SORU 10 :

\( a, b \in \mathbb{R} \) olmak üzere,

\( b - a \lt 0 \lt a \cdot b \lt a + b \)

olduğuna göre, \( a \), \( b \) ve \( 0 \) sayılarını küçükten büyüğe doğru sıralayın.

Eşitsizlikleri parça parça inceleyelim.

\( b - a \lt 0 \) olduğuna göre \( b \lt a \) olur.

\( 0 \lt a \cdot b \) olduğuna göre \( a \) ve \( b \)'nin işaretleri aynıdır.

\( 0 \lt a + b \) olduğuna göre işaretleri aynı olan \( a \) ve \( b \)'nin ikisi de pozitiftir.

Buna göre sıralama \( 0 \lt b \lt a \) şeklinde olur.

SORU 11 :

\( x + y \lt 0 \)

\( y - z \gt 0 \)

olduğuna göre, aşağıdaki öncüllerden hangileri kesinlikle doğrudur?

I. \( y \) pozitif ise \( x \) negatiftir.

II. \( z \) negatif ise \( y \) pozitiftir.

III. \( z \) pozitif ise \( x \) de pozitiftir.

I. öncül:

\( x + y \) ifadesi negatif olduğuna göre, sayılardan en az biri negatiftir.

\( y \) pozitif ise \( x \) negatif olmak zorundadır.

I. öncül her zaman doğrudur.

II. öncül:

\( y - z \gt 0 \Longrightarrow y \gt z \)

\( z \) negatif ise daha büyük olan \( y \) sayısı pozitif ya da negatif olabilir.

II. öncül doğru ya da yanlış olabilir.

III. öncül:

\( z \) pozitif ise daha büyük olan \( y \) sayısı da pozitif olmalıdır.

\( x + y \) ifadesi negatif olduğuna göre, sayılardan en az biri negatiftir.

\( y \) pozitif ise \( x \) negatif olmak zorundadır.

III. öncül her zaman yanlıştır.

Buna göre sadece I. öncül kesinlikle doğrudur.

SORU 12 :

\( x \lt y \lt 0 \lt z \) olmak üzere,

Aşağıdaki ifadelerden hangilerinin sonucu sıfır olabilir?

I. \( x - y - z \)

II. \( x + y + z \)

III. \( x \cdot y + z \)

I. öncül: \( x \) sayısı \( y \) sayısından küçük olduğu için \( x - y \) ifadesi negatiftir. Negatif bir sayıdan pozitif \( z \) sayısını çıkardığımızda sonuç yine negatif olur. Bu ifade sıfır olamaz.

II. öncül: \( x + y \) toplamının sonucu negatiftir. Negatif bir sayı ile pozitif \( z \) sayısını topladığımızda sonuç sıfır olabilir (örnek: -3 - 2 + 5).

III. öncül: \( x \cdot y \) çarpımının sonucu pozitiftir. Pozitif bir sayı ile pozitif \( z \) sayısını topladığımızda sonuç pozitif olur. Bu ifade sıfır olamaz.

Buna göre yalnız II. öncül sıfır olabilir.

SORU 13 :

\( a \in \mathbb{Z^+} \) olmak üzere,

\( x^{4a + 3} \lt 0 \)

\( x^{6a + 9} \cdot y^{8a} \cdot z^{10a + 7} \gt 0 \)

\( y^{16a + 17} \cdot z^{4a + 13} \gt 0 \)

olduğuna göre, aşağıdakilerden hangileri sıfır olabilir?

I. \( x^{20} - y^{10} \)

II. \( (y - z)^4 + (x - z)^8 \)

III. \( x^{y - z} \)

\( x^{4a + 3} \lt 0 \) eşitsizliğini inceleyelim.

\( 4a + 3 \) ifadesi tek sayıdır. Bir sayının tek sayı üssünün işareti sayının işareti ile aynıdır.

\( x \lt 0 \)

\( x^{6a + 9} \cdot y^{8a} \cdot z^{10a + 7} \gt 0 \) eşitsizliğini inceleyelim.

\( x \) negatif ve \( 6a + 9 \) ifadesi tek sayı olduğu için \( x^{6a + 9} \) ifadesi negatiftir.

\( 8a \) çift sayı olduğu için \( y^{8a} \) ifadesi pozitiftir.

\( x^{6a + 9} \) ifadesi negatif ve \( y^{8a} \) ifadesi pozitif olduğundan \( z^{10a + 7} \) ifadesi negatiftir.

\( 10a + 7 \) tek sayı olduğu için \( z \) negatif olur.

\( z \lt 0 \)

\( y^{16a + 17} \cdot z^{4a + 13} \gt 0 \) eşitsizliğini inceleyelim.

\( z \) negatif ve \( 4a + 13 \) ifadesi tek sayı olduğu için \( z^{4a + 13} \) ifadesi negatiftir.

Buna göre \( y^{16a + 17} \) ifadesi negatiftir.

\( 16a + 17 \) ifadesi tek sayı olduğu için \( y \) negatif olmalıdır.

\( y \lt 0 \)

Buna göre \( x, y, z \) sayılarının üçü de negatiftir.

Bu bilgileri kullanarak verilen öncülleri inceleyelim.

I. öncül:

\( x^{20} - y^{10} \)

\( x \) ve \( y \) negatif sayılarının çift sayı kuvvetleri pozitiftir.

İki pozitif sayının farkı sıfır olabilir.

I. öncül sıfır olabilir.

II. öncül:

\( (y - z)^4 + (x - z)^8 \)

\( x = y = z \) olması durumunda bu ifadede parantez içleri, dolayısıyla tüm ifade sıfıra eşit olur.

II. öncül sıfır olabilir.

III. öncül:

\( x^{y - z} \)

\( y - z \) ifadesi pozitif, negatif ya da sıfır olabilir.

Negatif \( x \) sayısının tek sayı kuvvetleri negatif, çift sayı kuvvetleri pozitif olur, sonuç hiçbir durumda (\( y = z \) olduğu durum dahil) sıfır olamaz.

III. öncül sıfır olamaz.

Buna göre I. ve II. öncüller sıfıra eşit olabilir.

SORU 14 :

\( x \lt y \lt z \lt -x \) olmak üzere,

I. \( z - x \)

II. \( xy - x^2 \)

III. \( x + y \)

ifadelerinden hangileri kesinlikle negatiftir?

\( x \lt -x \) eşitsizliği sadece \( x \) negatif olduğunda sağlanır (\( -3 \lt -(-3) \)).

I. öncül: \( x \lt z \lt -x \) eşitsizliğinden \( \abs{z} \lt \abs{x} \) çıkarımını yapabiliriz. Buna göre \( z \) sayısından mutlak değerce kendisinden daha büyük olan negatif \( x \) sayısını çıkarırsak sonuç pozitif olur.

II. öncül: \( xy - x^2 = x(y - x) \) şeklinde yazalım. \( x \lt y \) olduğu için \( y - x \) farkı pozitif olur. \( x \) negatif olduğu için \( x(y - x) \) çarpımı negatif olur.

III. öncül: \( x \lt y \lt -x \) eşitsizliğinden \( \abs{y} \lt \abs{x} \) çıkarımını yapabiliriz. \( x \) mutlak değerce daha büyük olduğu için \( y \) pozitif olsa da \( x + y \) ifadesi negatif olur.

Buna göre II. ve III. öncüldeki ifadeler her zaman negatiftir.

SORU 15 :

\( a, b \in \mathbb{R} \) olmak üzere,

\( a^9 \cdot b^5 \lt 0 \) olduğuna göre, aşağıdakilerden hangileri \( \frac{6a + 2b}{a} \) ifadesinin sonucu olabilir?

I. \( \dfrac{7}{2} \)

II. \( \dfrac{33}{4} \)

III. 5

Bir sayının tek sayı üssünün işareti o sayının işareti ile aynıdır, dolayısıyla \( a^9 \cdot b^5 \lt 0 \) ise \( a \cdot b \lt 0 \) olur.

Buna göre \( a \) ve \( b \) ters işaretli sayılardır.

\( \frac{6a+2b}{a} \) ifadesini düzenleyelim.

\( \dfrac{6a}{a} + \dfrac{2b}{a} = 6 + \dfrac{2b}{a} \)

\( a \) ve \( b \) ters işaretli oldukları için \( \frac{2b}{a} \) sayısı negatif bir sayıdır.

Buna göre aşağıdaki eşitsizliği yazabiliriz.

\( \dfrac{6a + 2b}{a} \lt 6 \)

Sorudaki ifadelerden sadece I. ve III. 6'dan küçük olduğu için verilen ifadenin sonucu olabilir.

SORU 16 :

\( x, y, z \in \mathbb{R} \) olmak üzere,

\( x + y = 0 \)

\( 0 \lt x \cdot y \cdot z \)

\( y \cdot z - x \cdot y \lt 0 \)

olduğuna göre, \(x \), \( y \) ve \( z \) sayılarının işaretleri nedir?

\( x + y = 0 \Longrightarrow x = -y \)

Buna göre \( x \) ve \( y \) ya ikisi de sıfırdır ya da ters işaretli sayılardır.

\( 0 \lt x \cdot y \cdot z \) olduğuna göre sayılardan herhangi biri sıfır değildir, buna göre \( x \) ve \( y \) ters işaretli oldukları için \( z \) negatif olur.

\( y \cdot z - x \cdot y \lt 0 \Longrightarrow y \cdot z \lt x \cdot y \)

\( x \) ve \( y \) ters işaretli oldukları için çarpımları negatiftir. Buna göre \( y \cdot z \) çarpımı da negatif olur. \( z \) negatif olduğuna göre \( y \) pozitif olur.

Yukarıda \( x \) ve \( y \)'nin ters işaretli olduklarını bulduğumuz için bu durumda \( x \) negatif olur.

Buna göre \( x \) ve \( z \) negatif, \( y \) pozitiftir.

SORU 17 :

\( c - b \gt 0 \)

\( a + c \lt 0 \)

\( b - a \gt 0 \)

\( b \cdot c - a \lt 0 \)

olduğuna göre, \( a \), \( b \) ve \( c \)'nin işaretleri nedir?

\( c - b \gt 0 \Longrightarrow c \gt b \)

\( b - a \gt 0 \Longrightarrow b \gt a \)

\( b \cdot c - a \lt 0 \Longrightarrow b \cdot c \lt a \)

Bu iki eşitsizliği birlikte yazalım.

\( a \lt b \lt c \)

\( a + c \lt 0 \) olabilmesi için ya \( a \) ve \( c \) birlikte negatif ya da \( a \) negatif ve \( c \) pozitif olmalıdır.

O halde \( a \) her durumda negatiftir.

\( a \) ve \( c \) birlikte negatif ise \( a \lt b \lt c \) eşitsizliğinden \( b \) de negatif olur.

\( a \) negatif ve \( c \) pozitif ise \( b \) sıfır, pozitif ya da negatif olabilir.

\( b \cdot c \lt a \) eşitsizliğinde \( a \) negatif olduğu için \( b \) ve \( c \) zıt işaretli olmalıdır, dolayısıyla \( c \) pozitif olur.

Buna göre \( a \) ve \( b \) negatif, \( c \) pozitiftir.

SORU 18 :

\( x \) bir negatif çift sayı olduğuna göre, aşağıdakilerden hangileri negatiftir?

I. \( -x^8 \)

II. \( (-5)^x \)

III. \( \dfrac{-x}{\abs{-2x}} \)

IV. \( -3^x \)

V. \( \sqrt[9]{x} \)

VI. \( -x^{-7} \)

I. öncül:

Negatif bir sayının çift sayı kuvveti pozitif olacağından \( x^8 \) pozitiftir, dolayısıyla \( -x^8 \) negatif olur.

II. öncül:

\( (-5)^x = \dfrac{1}{(-5)^{-x}} \)

\( -x \) pozitif çift sayıdır. Negatif bir sayının pozitif çift sayı kuvveti pozitif olacağından \( (-5)^{-x} \) pozitiftir. Bu durumda \( \frac{1}{(-5)^{-x}} \) ifadesi de pozitif olur.

III. öncül:

\( -x \) ve paydadaki mutlak değer ifadesi pozitiftir.

Pozitif bir sayının pozitif bir sayıya bölümü pozitif olduğundan sonuç pozitif olur.

IV. öncül:

\( 3^x \) ifadesi \( x \)'in tüm değerleri için pozitiftir, dolayısıyla \( -3^x \) negatif olur.

V. öncül:

Derecesi tek sayı olan köklü ifadelerde ifadenin işareti kök içinin işareti ile aynıdır, dolayısıyla \( x \) negatif olduğu için \( \sqrt[9]{x} \) negatif olur.

VI. öncül:

\( -x^{-7} = -\dfrac{1}{x^7} \)

Negatif bir sayının pozitif tek sayı kuvveti negatiftir, dolayısıyla \( x^7 \) negatif olur. Bu durumda \( -\frac{1}{x^7} \) ifadesi pozitif olur.

Buna göre I., IV. ve V. öncüller negatiftir.

SORU 19 :

\( a, b, c \in \mathbb{Z^-} \) olmak üzere,

\( c \lt b \lt a \) olduğuna göre,

\( abc \) çarpımına en yakın sonuç aşağıdakilerden hangisidir?

(a) \( (a - 1)bc \)

(b) \( (b - 1)ac \)

(c) \( (c - 1)ab \)

\( c \lt b \lt a \)

\( a, b, c \) negatif sayılardır.

\( \abs{a} \lt \abs{b} \lt \abs{c} \)

Öncüllerdeki parantezleri genişletelim.

(a) \( (a - 1)bc = abc - bc \)

(b) \( (b - 1)ac = abc - ac \)

(c) \( (c - 1)ab = abc - ab \)

\( abc \) çarpımı üç negatif sayının çarpımından oluştuğu için negatiftir ve üç ifadede de ortaktır.

\( bc \), \( ac \) ve \( ab \) çarpımları iki negatif sayının çarpımı olduğu için pozitiftir.

\( a \) ve \( b \) mutlak değerce en küçük iki sayı olduğundan çarpımları \( bc \) ve \( ac \)'ye göre daha küçüktür.

Buna göre \( (c - 1)ab = abc - ab \) ifadesi \( abc \) ifadesine en yakındır.

Doğru cevap (c) seçeneğidir.

« Önceki
Sayı Doğrusu
Sonraki »
Basamak Kavramı

Faydalı buldunuz mu?   Evet   Hayır