Devirli Ondalık Sayılar
Ondalık gösterimi bir basamaktan sonra kendini tekrarlayarak sonsuza giden rasyonel sayılara devirli ondalık sayı denir. Devirli ondalık sayılarda tekrar eden basamakların üstüne yatay bir çizgi (devir çizgisi) konarak bu basamaklar bir kez yazılabilir.
\( 0,\overline{\textcolor{red}{3}} = 0,\textcolor{red}{333}... \)
\( 0,\overline{\textcolor{red}{18}} = 0,\textcolor{red}{181818}... \)
\( 2,41\overline{\textcolor{red}{6}} = 2,41\textcolor{red}{666}... \)
\( 5,3\overline{\textcolor{red}{485}} = 5,3\textcolor{red}{485485}... \)
Yukarıdaki örneklerde görebileceğimiz gibi, devirli ondalık sayıların bir ya da birden fazla basamağı tekrar edebilir. Ayrıca basamaklar virgülden sonraki herhangi bir basamaktan başlayarak tekrar edebilir.
Bir sayının ondalık kısmının sadece kendini tekrarlaması ya da sadece sonsuza gitmesi devirli olması için yeterli değildir, ondalık basamaklar kendini tekrarlayarak sonsuza gitmelidir.
\( \pi \) sayısı ondalık basamakları sonsuza gitse de bu basamaklar kendini tekrarlamadığı için devirli değildir.
\( \pi = 3,141592... \)
Aşağıdaki sayının ondalık basamakları kendini 5 kez tekrarlasa da sonsuza gitmediği için devirli değildir.
\( 0,2323232323 \)
Bir sayının sonuna sonsuza kadar giden sıfır eklenmesi o sayıyı devirli ondalık sayı yapmaz.
En sade haliyle paydası sadece 2 ve/veya 5 asal çarpanlarını içeren bir kesirli ifadenin ondalık gösterimi sonlu sayıda ondalık basamak içerir, dolayısıyla devirli değildir. Paydası 2 ve 5 dışında asal çarpan içeren kesirli ifadelerin ondalık gösterimi sonsuz sayıda ondalık basamak içerir, dolayısıyla devirlidir.
Aşağıdaki sayıların ondalık gösterimleri devirli değildir.
\( \dfrac{1}{4} = \dfrac{1}{2^2} = 0,25 \)
\( \dfrac{7}{50} = \dfrac{7}{2 \cdot 5^2} = 0,14 \)
Aşağıdaki sayıların ondalık gösterimleri devirlidir.
\( \dfrac{5}{6} = \dfrac{5}{2 \cdot 3} = 0,8\overline{3} \)
\( \dfrac{3}{14} = \dfrac{9}{2 \cdot 7} = 0,2\overline{142857} \)
Tüm devirli ondalık sayılar kesirli şekilde yazılabilirler, dolayısıyla rasyonel sayıdırlar. Ondalık kısımları tekrar etmeden sonsuza giden (\( \pi \) sayısı gibi) sayılar ise kesirli şekilde yazılamazlar, dolayısıyla irrasyonel sayıdırlar.
Devirli Ondalık Sayıların Kesirli Gösterimi
Devirli ondalık sayılar aşağıdaki formülle kesirli gösterime dönüştürülebilir.
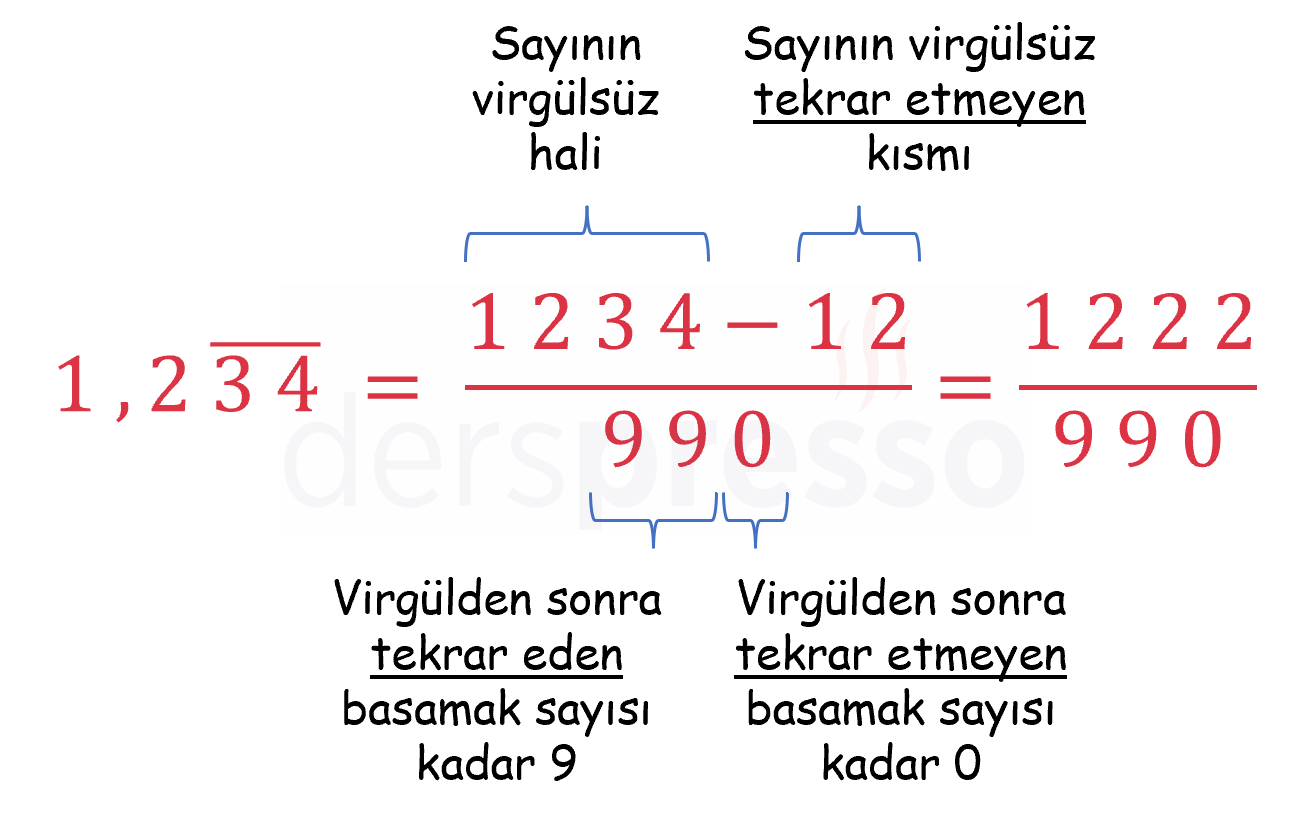
\( 0,\overline{4} = \dfrac{4 - 0}{9} = \dfrac{4}{9} \)
\( 0,\overline{36} = \dfrac{36 - 0}{99} = \dfrac{36}{99} \)
\( 1,3\overline{2} = \dfrac{132 - 13}{90} = \dfrac{119}{90} \)
\( 3,5\overline{48} = \dfrac{3548 - 35}{990} = \dfrac{3513}{990} \)
\( 12,34\overline{567} = \dfrac{1234567 - 1234}{99900} = \dfrac{1233333}{99900} \)
İSPATI GÖSTER
Bu formülü önce iki örnek üzerinden türetip sonra genel ispatını göstereceğiz.
Örnek 1:
\( x = 0,333... \)
İki tarafı 10'la çarpalım.
\( 10x = 3,333... \)
Bu eşitliği ilk eşitlikten taraf tarafa çıkaralım.
\( 9x = 3 \)
\( x = \dfrac{3}{9} = \dfrac{1}{3} \)
Örnek 2:
\( x = 0,272727... \)
İki tarafı önce 100'le çarpalım.
\( 100x = 27,272727... \)
Bu eşitliği ilk eşitlikten taraf tarafa çıkaralım.
\( 99x = 27 \)
\( x = \dfrac{27}{99} = \dfrac{3}{11} \)
Genel İspat:
\( x = a,bcdcdcd... \)
\( x \) devirli ondalık sayısında \( a \) sayının tam sayı kısmı, \( b \) devirli olmayan ondalık kısmı ve \( (cd) \) devirli ondalık kısmı olmak üzere,
Önce iki tarafı devirli olmayan tüm ondalık basamaklar virgülün solunda kalacak şekilde 10'un bir kuvveti ile çarpalım (bu durumda \( 10^1 \)).
\( 10x = ab,cdcdcd... \)
Sonra iki tarafı devirli ondalık basamakların bir tam devri de virgülün solunda kalacak şekilde 10'un bir kuvveti ile çarpalım (bu durumda \( 10^3 \)).
\( 1000x = abcd,cdcdcd... \)
Birinci eşitliği ikinci eşitlikten taraf tarafa çıkaralım. Dikkat edilirse eşitliklerin her ikisinde de sağ tarafın ondalık kısmı sadece devirli ondalık basamaklardan oluştuğu için bu ondalık kısımlar birbirini götürecektir.
\( 1000x - 10x = (abcd) - (ab) \)
\( 990x = (abcd) - (ab) \)
\( x = \dfrac{(abcd) - (ab)}{990} \)
Aşağıdaki sayılar birbirine eşittir. Bu sayılar yukarıdaki formülle kesirli gösterime dönüştürüldüğünde aynı rasyonel sayıya karşılık geldikleri görülebilir.
\( 0,\overline{\textcolor{red}{3}} = 0,\overline{\textcolor{red}{33}} = 0,\overline{\textcolor{red}{333}} \)
\( 1,0\overline{\textcolor{red}{45}} = 1,0\overline{\textcolor{red}{4545}} \)
Devirli olmayan bir ondalık sayı son basamağındaki rakam bir eksiltilerek ve sonuna devreden bir 9 eklenerek kendisine eşit devirli bir ondalık sayıya dönüştürülebilir.
\( 0,457 = 0,456\overline{9} \)
\( 3,802 = 3,801\overline{9} \)
\( 1 = 0,\overline{9} \)
Benzer şekilde devreden kısmı 9 olan bir devirli ondalık sayı devreden kısmı silinerek ve solundaki basamağa 1 eklenerek kendisine eşit devirli olmayan bir sayıya dönüştürülebilir.
\( 2,1\overline{9} = 2,2 \)
\( 99,\overline{9} = 100 \)
Aşağıdaki devirli ondalıklı sayıları kesirli sayılara çevirin.
(a) \( 5,\overline{27} \)
(b) \( 11,0\overline{11} \)
(c) \( 0,38\overline{9} \)
Çözümü Göster(a) seçeneği:
\( 5,\overline{27} = \dfrac{527 - 5}{99} \)
\( = \dfrac{522}{99} = \dfrac{58}{11} \)
(b) seçeneği:
\( 11,0\overline{11} = 11,0\overline{1} \)
\( = \dfrac{1101 - 110}{90} \)
\( = \dfrac{991}{90} \)
(c) seçeneği:
\( 0,38\overline{9} = \dfrac{389 - 38}{900} \)
\( = \dfrac{351}{900} = \dfrac{39}{100} \)
Bu sonuç aşağıdaki iki ondalık ifadenin birbirine eşit olduğunu göstermektedir.
\( 0,38\overline{9} = 0,39 \)
Aşağıdaki devirli ondalıklı sayıları kesirli sayılara çevirin.
(a) \( -2,21\overline{4} \)
(b) \( 3,01\overline{52} \)
(c) \( -0,01\overline{94} \)
Çözümü Göster(a) seçeneği:
\( -2,21\overline{4} = -\dfrac{2214 - 221}{900} \)
\( = -\dfrac{1993}{900} \)
(b) seçeneği:
\( 3,01\overline{52} = \dfrac{30152 - 301}{9900} \)
\( = \dfrac{29851}{9900} \)
(c) seçeneği:
\( -0,01\overline{94} = -\dfrac{194 - 1}{9900} \)
\( = -\dfrac{193}{9900} \)
\( \dfrac{0,1\overline{5} + 2,1\overline{7}}{3,\overline{45} - 1,\overline{21}} \) işleminin sonucu kaçtır?
Çözümü GösterDevirli ondalık sayıları kesirli sayılara çevirelim.
\( \dfrac{\frac{15 - 1}{90} + \frac{217 - 21}{90}}{\frac{345 - 3}{99} - \frac{121 - 1}{99}} \)
\( = \dfrac{\frac{14 + 196}{90}}{\frac{342 - 120}{99}} \)
\( = \dfrac{210}{90} \div \dfrac{222}{99} \)
\( = \dfrac{210}{90} \cdot \dfrac{99}{222} \)
\( = \dfrac{7}{3} \cdot \dfrac{33}{74} \)
\( = \dfrac{77}{74} \) bulunur.
\( a = 0,\overline{75} \) ve \( b = 0,\overline{25} \) olduğuna göre,
\( \dfrac{1}{a} + \dfrac{1}{b} \) toplamı kaçtır?
Çözümü GösterDevirli ondalık sayıları kesirli sayılara çevirelim.
\( a = 0,\overline{75} = \dfrac{75}{99} \)
\( b = 0,\overline{25} = \dfrac{25}{99} \)
\( \dfrac{1}{a} + \dfrac{1}{b} = \dfrac{1}{\frac{75}{99}} + \dfrac{1}{\frac{25}{99}} \)
\( = \dfrac{99}{75} + \dfrac{99}{25} \)
\( = \dfrac{99}{75} + \dfrac{297}{75} \)
\( = \dfrac{396}{75} = \dfrac{132}{25} \) bulunur.
Aşağıdaki sayıları küçükten büyüğe doğru sıralayın.
\( x = \dfrac{1}{1,\overline{81}} \)
\( y = 0,5\overline{1} \)
\( z = \dfrac{5}{9} \)
Çözümü GösterTüm sayıları kesirli şekilde yazalım.
\( x = \dfrac{1}{\frac{181 - 1}{99}} = \dfrac{99}{180} \)
\( y = \dfrac{51 - 5}{90} = \dfrac{92}{180} \)
\( z = \dfrac{5}{9} = \dfrac{100}{180} \)
Buna göre sayıların sıralaması aşağıdaki gibi olur.
\( y \lt x \lt z \)
\( \dfrac{1}{x} = 2,\overline{1} \) olduğuna göre, \( \dfrac{1}{\frac{2}{38x - 1}} \) ifadesinin eşiti nedir?
Çözümü GösterBirinci eşitlikteki devirli ondalık sayıyı kesre çevirelim.
\( \dfrac{1}{x} = \dfrac{21 - 2}{9} \)
\( \dfrac{1}{x} = \dfrac{19}{9} \)
\( x = \dfrac{9}{19} \)
Bulduğumuz değeri ikinci ifadede yerine yazalım.
\( \dfrac{1}{\frac{2}{38 \cdot \frac{9}{19} - 1}} = \dfrac{1}{\frac{2}{17}} \)
\( = \dfrac{17}{2} \) bulunur.
\( 5,\overline{9} + 6,\overline{9} + 7,\overline{9} + \ldots + 15,\overline{9} \) işleminin sonucu kaçtır?
Çözümü GösterDevirli ondalık sayıları kesirli sayılara çevirelim.
\( 5,\overline{9} = \dfrac{59 - 5}{9} = 6 \)
\( 6,\overline{9} = \dfrac{69 - 6}{9} = 7 \)
\( \vdots \)
\( 15,\overline{9} = \dfrac{159 - 15}{9} = 16 \)
Buna göre verilen ifade 6 - 16 arası tam sayıların toplamıdır.
\( 6 + 7 + 8 + \ldots + 16 \)
\( \text{Terimler toplamı} = \dfrac{\text{İlk terim} + \text{Son terim}}{2} \cdot \text{Terim sayısı} \)
\( = \dfrac{6 + 16}{2} \cdot (16 - 6 + 1) \)
\( = 121 \) bulunur.
\( 0,11\overline{3} \) devirli ondalık sayısı \( x \) pozitif tam sayısı ile çarpıldığında bir tam sayı olmaktadır.
Buna göre \( x \) en az kaçtır?
Çözümü GösterDevirli ondalık sayıyı kesirli gösterimde yazalım.
\( 0,11\overline{3} = \dfrac{113 - 11}{900} \)
\( = \dfrac{102}{900} = \dfrac{17}{150} \)
17 ve 150 aralarında asal olduğu için kesir daha fazla sadeleşmez.
Buna göre bu ifade ile çarpıldığında ifadeyi tam sayı yapacak en küçük \( x \) sayısı 150 olur.
\( 4,\overline{2} + 2,1\overline{7} \) toplamı en küçük hangi pozitif tam sayı ile çarpılırsa sonuç bir tam sayı olur?
Çözümü GösterDevirli ondalıklı sayıları kesirli sayılara çevirelim.
\( \dfrac{42 - 4}{9} + \dfrac{217 - 21}{90} = \dfrac{38}{9} + \dfrac{196}{90} \)
\( = \dfrac{380}{90} + \dfrac{196}{90} \)
\( = \dfrac{576}{90} = \dfrac{32}{5} \)
32 ve 5 aralarında asal olduğu için kesir daha fazla sadeleşmez.
Buna göre bu ifade ile çarpıldığında ifadeyi tam sayı yapacak en küçük sayı 5 olur.
\( 6,1\overline{37} - 3,41\overline{2} \) işleminin sonucu kaçtır?
Çözümü GösterSayıları normal ondalıklı sayı şeklinde yazıp birbirinden çıkaralım.
\( 6,1\overline{37} = 6,137373737... \)
\( 3,41\overline{2} = 3,41222222... \)
\( 6,1\overline{37} - 3,41\overline{2} = 2,725151515... \)
\( = 2,72\overline{51} \) bulunur.
\( a = 0,383838383838 \ldots \)
\( b = 0,020902090209 \ldots \)
\( c = 9,181818181818 \ldots \)
olduğuna göre, \( \dfrac{a}{b \cdot c} \) işleminin sonucu kaçtır?
Çözümü GösterDevirli ondalıklı sayıları kesirli sayılara çevirelim.
\( a = 0,383838383838 \ldots \)
\( = 0,\overline{38} = \dfrac{38}{99} \)
\( b = 0,020902090209 \ldots \)
\( = 0,\overline{0209} = \dfrac{209}{9999} \)
\( c = 9,181818181818 \ldots \)
\( = 9,\overline{18} = \dfrac{918 - 9}{99} = \dfrac{101}{11} \)
Bulduğumuz kesirleri verilen ifadede yerine yazalım.
\( \dfrac{a}{b \cdot c} = \dfrac{\frac{38}{99}}{\frac{209}{9999} \cdot \frac{101}{11}} \)
\( = \dfrac{38}{99} \cdot \dfrac{9999}{209} \cdot \dfrac{11}{101} \)
Pay ve paydadaki sayıları aralarında sadeleştirelim.
\( = \dfrac{2}{1} \cdot \dfrac{101}{11} \cdot \dfrac{11}{101} \)
\( = 2 \) bulunur.
Aşağıdaki kesirlerden hangilerinin ondalık gösterimi devirlidir?
\( \dfrac{29}{210}, \dfrac{91}{112}, \dfrac{393}{625}, \dfrac{288}{512}, \dfrac{93}{150} \)
Çözümü GösterEn sade haliyle paydası sadece 2 ve/veya 5 asal çarpanlarını içeren bir kesirli ifadenin ondalık gösterimi sonlu sayıda ondalık basamak içerir, dolayısıyla devirli değildir. Paydası 2 ve 5 dışında asal çarpan içeren kesirli ifadelerin ondalık gösterimi sonsuz sayıda ondalık basamak içerir, dolayısıyla devirlidir.
Verilen ifadelerin pay ve paydalarını asal çarpanlarına ayıralım ve ifadeleri en sade hallerine getirelim.
\( \dfrac{29}{210} = \dfrac{29}{2 \cdot 3 \cdot 5 \cdot 7} \)
\( \dfrac{91}{112} = \dfrac{7 \cdot 13}{7 \cdot 2^4} = \dfrac{13}{2^4} \)
\( \dfrac{393}{625} = \dfrac{3 \cdot 131}{5^4} \)
\( \dfrac{288}{512} = \dfrac{2^5 \cdot 3^2}{2^9} = \dfrac{3^2}{2^4} \)
\( \dfrac{93}{150} = \dfrac{3 \cdot 31}{2 \cdot 3 \cdot 5^2} = \dfrac{31}{2 \cdot 5^2} \)
Verilen öncüllerin en sade hallerinde sadece birinci sayının paydası 2 ve 5 dışında asal çarpan içerdiği için ondalık gösterimi devirlidir.
\( \dfrac{(0,\overline{a})}{(0,0\overline{a})} \div \dfrac{(a,a)}{(aa)} \) işleminin sonucu kaçtır?
Çözümü GösterDevirli ondalık sayıları kesirli sayılara çevirelim.
\( \dfrac{(0,\overline{a})}{(0,0\overline{a})} \div \dfrac{(a, a)}{(aa)} = \dfrac{\frac{a}{9}}{\frac{a}{90}} \div \dfrac{(a,a) \cdot 10}{(aa) \cdot 10} \)
\( = \dfrac{90}{9} \div \dfrac{(aa)}{(aa) \cdot 10} \)
\( = 10 \div \dfrac{1}{10} \)
\( = 10 \cdot 10 = 100 \) bulunur.
\( \dfrac{2}{3} + \dfrac{7}{33} = (0,\overline{ab}) \) olduğuna göre, \( 18 \cdot (b,\overline{a}) \) çarpımının sonucu kaçtır?
Çözümü Göster\( \dfrac{2}{3} + \dfrac{7}{33} = \dfrac{66}{99} + \dfrac{21}{99} \)
\( = \dfrac{87}{99} = 0,\overline{87} = (0,\overline{ab}) \)
Buna göre \( a = 8 \) ve \( b = 7 \) olur.
\( 18 \cdot (b,\overline{a}) = 18 \cdot 7,\overline{8} \)
\( = 18 \cdot \dfrac{78 - 7}{9} = 142 \) bulunur.
\( (ab) \) ve \( (ba) \) iki basamaklı pozitif tam sayılardır.
\( (a,\overline{b}) - (b,\overline{a}) = \dfrac{24}{9} \)
olduğuna göre, \( a + b \) toplamı en fazla kaçtır?
Çözümü GösterDevirli ondalıklı sayıları kesirli sayılara çevirelim.
\( \dfrac{(ab) - a}{9} - \dfrac{(ba) - b}{9} = \dfrac{24}{9} \)
\( ((ab) - a) - ((ba) - b) = 24 \)
\( (ab) \) ve \( (ba) \) sayılarının çözümlemesini yapalım.
\( (10a + b - a) - (10b + a - b) = 24 \)
\( 10a + b - a - 10b - a + b = 24 \)
\( 8a - 8b = 24 \)
\( a - b = 3 \)
\( a + b \) toplamı iki rakam da en büyük değerini aldığında en büyük olur.
\( a = 9, \quad b = 6 \)
\( a + b = 9 + 6 = 15 \) bulunur.
\( 13 \div 11 \) işleminin sonucu ondalık sayı şeklinde yazıldığında virgülden sonraki ilk 1597 basamağın toplamı kaçtır?
Çözümü GösterSoruda verilen bölme işlemini yaparak sonucu ondalık sayı şeklinde yazalım.
\( 13 \div 11 = 1\dfrac{2}{11} = 1,\overline{18} = 1,181818\dots \)
Bu devirli ondalık sayının ilk 1597 basamağının 799 tanesi 1, 798 tanesi 8'dir.
\( 799 \cdot 1 + 798 \cdot 8 = 7183 \) bulunur.
Aşağıdaki kesirlerin ondalık gösteriminde virgülden sonraki 125. basamak kaçtır?
(a) \( \dfrac{26}{27} \)
(b) \( \dfrac{19}{13} \)
(c) \( \dfrac{62}{165} \)
Çözümü Göster(a) seçeneği:
26'yı 27'ye böldüğümüzde virgülden sonra 962 rakamlarının (toplam 3 basamak) tekrar ettiğini görürüz.
\( \dfrac{26}{27} = 0,\overline{962} \)
125'i 3'e böldüğümüzde kalan 2'dir, dolayısıyla virgülden sonraki 125. basamak 2. basamak ile aynıdır.
\( 125 = 3 \cdot 41 + 2 \)
Buna göre virgülden sonraki 125. basamak 6'dır.
(b) seçeneği:
\( \dfrac{19}{13} = 1 + \dfrac{6}{13} \)
6'yı 13'e böldüğümüzde virgülden sonra 461538 rakamlarının (toplam 6 basamak) tekrar ettiğini görürüz.
\( \dfrac{6}{13} = 0,\overline{461538} \)
125'i 6'ya böldüğümüzde kalan 5'tir, dolayısıyla virgülden sonraki 125. basamak 5. basamak ile aynıdır.
\( 125 = 6 \cdot 20 + 5 \)
Buna göre virgülden sonraki 125. basamak 3'tür.
(c) seçeneği:
62'yi 165'e böldüğümüzde virgülden sonra 3 rakamının geldiğini, sonra 75 rakamlarının (toplam 2 basamak) tekrar ettiğini görürüz.
\( \dfrac{62}{165} = 0,3\overline{75} \)
Dolayısıyla virgülden sonra ilk basamaktan sonra çift basamaklar 7, tek basamaklar 5 olur.
Buna göre virgülden sonraki 125. basamak 5'tir.
\( a \) ve \( b \) birer rakam olmak üzere,
\( (0,a\overline{b}) = \dfrac{11}{18} \) olduğuna göre, \( ab \) çarpımı kaçtır?
Çözümü Göster\( (0,a\overline{b}) = \dfrac{(ab) - a}{90} = \dfrac{11}{18} = \dfrac{55}{90} \)
\( (ab) - a = 55 \)
İki basamaklı \( (ab) \) sayısını çözümlenmiş şekilde yazalım.
\( (10a + b) - a = 55 \)
\( 9a + b = 55 \)
\( a \) ve \( b \) birer rakam olmak üzere, bu eşitliğin tek çözümü vardır.
\( a = 6, \quad b = 1 \)
\( ab = 6 \cdot 1 = 6 \) bulunur.
\( x \) ve \( y \) birer rakam olmak üzere,
\( \dfrac{(x,\overline{y}) - (x,\overline{x}) + (y,\overline{x})}{(0,\overline{x})} = 4 \) olduğuna göre, \( x + y \) toplamı kaçtır?
Çözümü Göster\( \dfrac{(x,\overline{y}) - (x,\overline{x}) + (y,\overline{x})}{(0,\overline{x})} \)
Devirli ondalıklı sayıları kesirli sayılara çevirelim.
\( = \dfrac{\frac{(xy) - x}{9} - \frac{(xx) - x}{9} + \frac{(yx) - y}{9}}{\frac{x}{9}} \)
\( = \dfrac{(xy) - x - (xx) + x + (yx) - y}{x} \)
Sayıları çözümlenmiş şekilde yazalım.
\( = \dfrac{10x + y - x - 10x - x + x + 10y + x - y}{x} \)
\( = \dfrac{10y}{x} = 4 \)
\( 5y = 2x \)
\( x \) ve \( y \) birer rakam olmak üzere, bu eşitliğin tek çözümü vardır.
\( x = 5, \quad y = 2 \)
\( x + y = 5 + 2 = 7 \) bulunur.
\( x, y, z \) sıfırdan farklı rakamlardır.
\( (x,y\overline{z}) + (y,x\overline{z}) = \dfrac{12}{5} \)
olduğuna göre, \( x + y + z \) toplamı kaçtır?
Çözümü GösterDevirli ondalıklı sayıları kesirli sayılara çevirelim.
\( \dfrac{(xyz) - (xy)}{90} + \dfrac{(yxz) - (yx)}{90} = \dfrac{12}{5} \)
\( (xyz) - (xy) + (yxz) - (yx) = \dfrac{12}{5} \cdot 90 \)
\( (xyz) - (xy) + (yxz) - (yx) = 216 \)
\( (xyz) \), \( (yxz) \), \( (xy) \) ve \( (yx) \) sayılarının çözümlemesini yapalım.
\( 100x + 10y + z - (10x + y) + 100y + 10x + z - (10y + x) = 216 \)
\( 99x + 99y + 2z = 216 \)
Değişkenler sıfırdan farklı birer rakam oldukları için sadece aşağıdaki değerleri alabilirler.
\( x = 1, \quad y = 1, \quad z = 9 \)
\( x + y + z = 1 + 1 + 9 = 11 \) bulunur.
\( \dfrac{0,\overline{3} + 0,\overline{4} + \ldots + 0,\overline{9}}{2,\overline{1} + 2,\overline{2} + \ldots + 2,\overline{8}} \) işleminin sonucu kaçtır?
Çözümü GösterDevirli ondalıklı sayıları kesirli sayılara çevirelim.
\( \dfrac{\frac{3}{9} + \frac{4}{9} + \ldots + \frac{9}{9}}{\frac{21 - 2}{9} + \frac{22 - 2}{9} + \ldots + \frac{28 - 2}{9}} \)
\( = \dfrac{\frac{3}{9} + \frac{4}{9} + \ldots + \frac{9}{9}}{\frac{19}{9} + \frac{20}{9} + \ldots + \frac{26}{9}} \)
\( = \dfrac{\frac{3 + 4 + \ldots + 9}{9}}{\frac{19 + 21 + \ldots + 26}{9}} \)
Pay ve paydadaki kesirli ifadelerin paydaları sadeleşir.
\( = \dfrac{3 + 4 + \ldots + 9}{19 + 21 + \ldots + 26} \)
Pay ve paydadaki ardışık sayıların toplamını bulalım.
\( \text{Terimler toplamı} = \dfrac{\text{İlk terim} + \text{Son terim}}{2} \cdot \text{Terim sayısı} \)
\( = \dfrac{\frac{3 + 9}{2} \cdot (9 - 3 + 1)}{\frac{19 + 26}{2} \cdot (26 - 19 + 1)} \)
\( = \dfrac{6 \cdot 7}{45 \cdot 4} = \dfrac{7}{30} \) bulunur.
Özlem 165 sayısını devirli \( (1,\overline{ab}) \) sayısı ile çarpmak yerine yanlışlıkla \( (1,ab) \) ile çarpıyor ve bulduğu sonucun olması gereken sonuçtan \( 0,5 \) eksik olduğu görülüyor.
Buna göre \( (ab) \) sayısı kaçtır?
Çözümü GösterÖzlem'in yaptığı ve yapması gereken işlemlerin farkını alalım.
\( 165 \cdot (1,\overline{ab}) - 165 \cdot (1,ab) = 0,5 \)
\( 165 \cdot [(1,\overline{ab}) - (1,ab)] = 0,5 \)
\( 165 \cdot (0,00\overline{ab}) = 0,5 \)
\( (0,00\overline{ab}) = \dfrac{1}{330} \)
Devirli ondalık sayıyı kesirli gösterimde yazalım.
\( \dfrac{(ab)}{9900} = \dfrac{1}{330}\)
\( (ab) = 30 \) bulunur.
\( \dfrac{3}{10} + \dfrac{6}{100} + \dfrac{3}{1000} + \dfrac{6}{10000} + \ldots \) işleminin sonucu kaçtır?
Çözümü Gösterİşlemin terimlerini ondalık sayı olarak yazalım.
\( 0,3 + 0,06 + 0,003 + 0,0006 + \ldots \)
Bu işlemin sonucunda aşağıdaki devirli ondalık sayı elde edilir.
\( = 0,363636 \ldots = 0,\overline{36} \)
Devirlik ondalık sayıyı kesre çevirelim.
\( = \dfrac{36}{99} = \dfrac{4}{11} \) bulunur.
\( x, y, z \) sıfırdan farklı rakamlardır.
\( 3x + \dfrac{1}{2y + \frac{z}{8}} = 9,\overline{4} \) olduğuna göre, \( xyz \) çarpımı kaçtır?
Çözümü GösterDevirli ondalıklı sayıyı kesirli sayıya çevirelim.
\( 3x + \dfrac{1}{2y + \frac{z}{8}} = 9 + \dfrac{4}{9} \)
\( 3x \) bir tam sayıdır. \( \frac{1}{2y + \frac{z}{8}} \) ifadesi de paydası 1'den büyük olduğu için \( (0, 1) \) aralığında bir sayıdır. Dolayısıyla her iki terim sırasıyla eşitliğin sağ tarafındaki sayının tam sayı ve ondalık kısımlarına karşılık gelir.
\( 3x = 9 \Longrightarrow x = 3 \)
\( \dfrac{1}{2y + \frac{z}{8}} = \dfrac{4}{9} \)
Eşitliğin taraflarının çarpmaya göre tersini alalım.
\( 2y + \dfrac{z}{8} = \dfrac{9}{4} \)
\( 2y + \dfrac{z}{8} = 2 + \dfrac{1}{4} \)
\( 2y \) bir tam sayıdır. \( \frac{z}{8} \) ifadesi \( z \)'nin en büyük değerinde \( \frac{9}{8} = 1 + \frac{1}{8} \) olur. \( \frac{1}{8} \ne \frac{1}{4} \) olduğu için \( z \lt 8 \) olmalıdır ve her iki terim sırasıyla eşitliğin sağ tarafındaki sayının tam sayı ve ondalık kısımlarına karşılık gelir.
\( 2y = 2 \Longrightarrow y = 1 \)
\( \dfrac{z}{8} = \dfrac{1}{4} = \dfrac{2}{8} \)
\( z = 2 \)
\( xyz = 3 \cdot 1 \cdot 2 = 6 \) bulunur.