İşlemler
Bir ya da daha fazla sayıda terimi kullanarak bir matematiksel hesaplama sonucunda bir sonuç üreten fonksiyonlara işlem denir.
Matematiksel ya da mantıksal işlemlerde kullanılan sembollere operatör denir. Örneğin matematikte sıklıkla kullanılan \( +, -, \times, \div, !, \land, \lor, \Rightarrow, \cap, \cup \) sembolleri birer operatördür.
İşlem Tipleri
İşlemleri genel olarak iki başlık altında inceleyebiliriz.
İkili İşlemler
İki terimi olan işlemlere ikili işlem denir. İkili işlemlere aşağıdaki örnekleri verebiliriz.
- Toplama: \( a + b \)
- Çıkarma: \( a - b \)
- Çarpma: \( a \cdot b \)
- Bölme: \( a \div b \)
- Üslü İfadeler: \( a^b \)
Birli İşlemler
Tek bir terimi olan işlemlere birli işlem denir. Birli işlemlere aşağıdaki örnekleri verebiliriz.
- Negatif: \( -a \)
- Faktöriyel: \( a! \)
- Karekök: \( \sqrt{a} \)
- Mutlak değer: \( \abs{a} \)
İşlem Özellikleri
İşlemler aşağıdaki özelliklere sahip olup olmadıklarına göre değerlendirilirler.
Değişme Özelliği
Bir işlemin terimleri aralarında yer değiştirdiğinde işlem sonucu değişmiyorsa o işlemin değişme özelliği vardır.
\( A \) işlemin tanım kümesi olmak üzere, her \( a, b \in A \) için,
\( a \otimes b = b \otimes a \) ise,
\( \otimes \) işleminin \( A \) kümesinde değişme özelliği vardır.
Örnek olarak aşağıdaki işlemlerin değişme özelliği vardır.
Toplama: \( a + b = b + a \)
Çarpma: \( a \cdot b = b \cdot a \)
Kümelerde birleşim: \( A \cup B = B \cup A \)
Kümelerde kesişim: \( A \cap B = B \cap A \)
Uzaklık: \( \abs{a - b} = \abs{b - a} \)
Aşağıdaki işlemlerin değişme özelliği yoktur.
\( a \ne b \) olmak üzere,
Çıkarma: \( a - b \ne b - a \)
Bölme: \( a \div b \ne b \div a \)
Üs: \( a^b \ne b^a \)
Birleşme Özelliği
Bir işlemde işlemlerin yapılış sırası işlem sonucunu değiştirmiyorsa o işlemin birleşme özelliği vardır.
\( A \) işlemin tanım kümesi olmak üzere, her \( a, b, c \in A \) için,
\( a \otimes (b \otimes c) = (a \otimes b) \otimes c \) ise,
\( \otimes \) işleminin \( A \) kümesinde birleşme özelliği vardır.
Örnek olarak aşağıdaki işlemlerin birleşme özelliği vardır.
Toplama: \( (a + b) + c = a + (b + c) \)
Çarpma: \( (a \cdot b) \cdot c = a \cdot (b \cdot c) \)
Mantıksal "ve": \((p \land q) \land r = p \land (q \land r) \)
Mantıksal "veya": \( (p \lor q) \lor r = p \lor (q \lor r) \)
Toplama/Çıkarma Üzerinde Dağılma Özelliği
Bir terimin toplam ya da farktan oluşan diğer bir terim ile işleminin sonucu, o terimin toplanan/farkı alınan terimlerin herbiri ile işleminin sonuçlarının toplamına/farkına eşitse o işlemin toplama/çıkarma üzerinde dağılma özelliği vardır.
\( A \) işlemin tanım kümesi olmak üzere, her \( a, b, c \in A \) için,
\( a \otimes (b \pm c) = (a \otimes b) \pm (a \otimes c) \) ise,
\( \otimes \) işleminin \( A \) kümesinde toplama/çıkarma üzerinde soldan dağılma özelliği vardır.
\( (b \pm c) \otimes a = b \otimes a \pm c \otimes a \) ise
\( \otimes \) işleminin \( A \) kümesinde toplama/çıkarma üzerinde sağdan dağılma özelliği vardır.
Yukarıdaki tanım toplama/çıkarma işlemleri üzerinde dağılma özelliği için olsa da, bir işlemin herhangi bir işlem üzerinde dağılma özelliği tanımlanabilir.
Örnek olarak aşağıdaki işlemlerin belirtilen işlem üzerinde dağılma özelliği vardır.
Çarpmanın toplama/çıkarma üzerinde soldan ve sağdan:
\( a \cdot (b \pm c) = a\cdot b \pm a\cdot c \)
\( (b \pm c) \cdot a = b\cdot a \pm c\cdot a \)
Bölmenin toplama ve çıkarma üzerinde sadece sağdan:
\( a \div (b \pm c) \ne a \div b \pm a \div c \)
\( (b \pm c) \div a = b \div a \pm c \div a \)
Kümelerde kesişimin birleşim üzerinde ve birleşimin kesişim üzerinde soldan ve sağdan:
\( A \cap (B \cup C) = (A \cap B) \cup (A \cap C) \)
\( A \cup (B \cap C) = (A \cup B) \cap (A \cup C) \)
Mantıkta "ve"nin "veya" üzerinde ve "veya"nın "ve" üzerinde soldan ve sağdan:
\( p \land (q \lor r) \equiv (p \land q) \lor (p \land r) \)
\( p \lor (q \land r) \equiv (p \lor q) \land (p \lor r) \)
Kapalılık Özelliği
Bir işlemin bir kümenin tüm elemanları ile sonucu yine o kümenin bir elemanı ise o işlemin o kümede kapalılık özelliği vardır.
\( A \) işlemin tanım kümesi olmak üzere, her \( a, b \in A \) için,
\( a \otimes b = c \in A \) ise,
\( \otimes \) işleminin \( A \) kümesinde kapalılık özelliği vardır.
Kapalılık özelliğine aşağıdaki örnekleri verebiliriz.
- Tam sayılarda toplama işlemi: İki tam sayının toplamı yine bir tam sayıdır, dolayısıyla toplama işlemi tam sayılar kümesinde kapalıdır.
- Tek sayılar kümesinde çarpma işlemi: İki tek sayının çarpımı yine tek sayıdır, dolayısıyla çarpma işlemi tek sayılar kümesinde kapalıdır.
- Doğal sayılar kümesinde çıkarma işlemi: İki doğal sayının farkı bir doğal sayı olmayabilir (\( 1 - 2 = -1 \)), dolayısıyla çıkarma işlemi doğal sayılar kümesinde kapalı değildir.
- Tam sayılar kümesinde bölme işlemi: İki tam sayının bölümü bir tam sayı olmayabilir (\( 1 \div 2 \)), dolayısıyla bölme işlemi tam sayılar kümesinde kapalı değildir.
Birim (Etkisiz) Eleman Özelliği
Bir işleme girdi olan her elemanın değişmeden işlem sonucuna yansımasını sağlayan bir \( e \) elemanı varsa bu elemana o işlemin birim (etkisiz) elemanı denir.
\( A \) işlemin tanım kümesi olmak üzere, her \( a \in A \) için,
\( a \otimes e = e \otimes a = a \) ise,
\( \otimes \) işleminin birim (etkisiz) elemanı \( e \)'dir.
Bir elemanın bir işlemin birim elemanı olabilmesi için, bu özelliğinin tanım kümesindeki tüm elemanlar için geçerli olması gerekir. Aşağıdaki örnekte \( 0 \)'la girdiği işlemin sonucu yine \( 0 \) olan \( 4 \) sayısı çarpma işlemi için birim eleman değildir, çünkü \( 0 \) dışında bir sayı ile çarpıldığında aynı sonucu vermeyecektir.
\( 0 \cdot 4 = 0 \)
\( 2 \cdot 4 \ne 2 \)
Bazı işlemlerin birim elemanları aşağıdaki gibidir:
| Konu | İşlem | Birim Eleman (\( e \)) | Örnek İşlem |
|---|---|---|---|
| 4 İşlem | Toplama | \( 0 \) | \( a + 0 = 0 + a = a \) |
| 4 İşlem | Çarpma | \( 1 \) | \( a \cdot 1 = 1 \cdot a = a \) |
| Bölenler | EKOK | \( 1 \) | \( EKOK(a, 1) = EKOK(1, a) = a \) |
| Mantık | Ve | \( 1 \) | \( p \land 1 = 1 \land p = p \) |
| Mantık | Veya | \( 0 \) | \( p \lor 0 = 0 \lor p = p \) |
| Mantık | Ya Da | \( 0 \) | \( p \veebar 0 = 0 \veebar p = p \) |
| Mantık | Ancak ve Ancak | \( 1 \) | \( p \Leftrightarrow 1 = 1 \Leftrightarrow p = p \) |
| Kümeler | Birleşim | \( \emptyset \) | \( A \cup \emptyset = \emptyset \cup A = A \) |
| Kümeler | Kesişim | \( E \) | \( A \cap E = E \cap A = A \) |
Ters Eleman Özelliği
Bir işlemin tanım kümesindeki her \( a \) elemanını o işlemin birim elemanına dönüştüren bir \( a^{-1} \) elemanı varsa bu elemana \( a \) elemanının ters elemanı denir. Bir işlemde her elemanın ters elemanının tanımlı olabilmesi için o işlemin birim elemanının tanımlı olması gerekir.
\( A \) işlemin tanım kümesi olmak üzere, her \( a \in A \) için,
\( a \otimes a^{-1} = a^{-1} \otimes a = e \) ise,
\( \otimes \) işleminde \( a \) elemanının ters elemanı \( a^{-1} \)'dir.
Bazı işlemlerin ters elemanları aşağıdaki gibidir:
| Konu | İşlem | Ters Eleman | Örnek İşlem |
|---|---|---|---|
| 4 İşlem | Toplama | \( -a \) | \( a + (-a) = e = 0 \) |
| 4 İşlem | Çarpma | \( \dfrac{1}{a} \) | \( a \cdot \dfrac{1}{a} = e = 1 \) |
Pozitif/Negatif ve Artı/Eksi Farkı
Pozitif/negatif sembolleri birli işlemler olarak sayıların işaretini belirler, artı/eksi sembolleri ise ikili işlemler olarak sayılar arasında toplama/çıkarma işlemine karşılık gelir.
Aşağıdaki şekilde bu işlemler arasındaki fark gösterilmiştir.
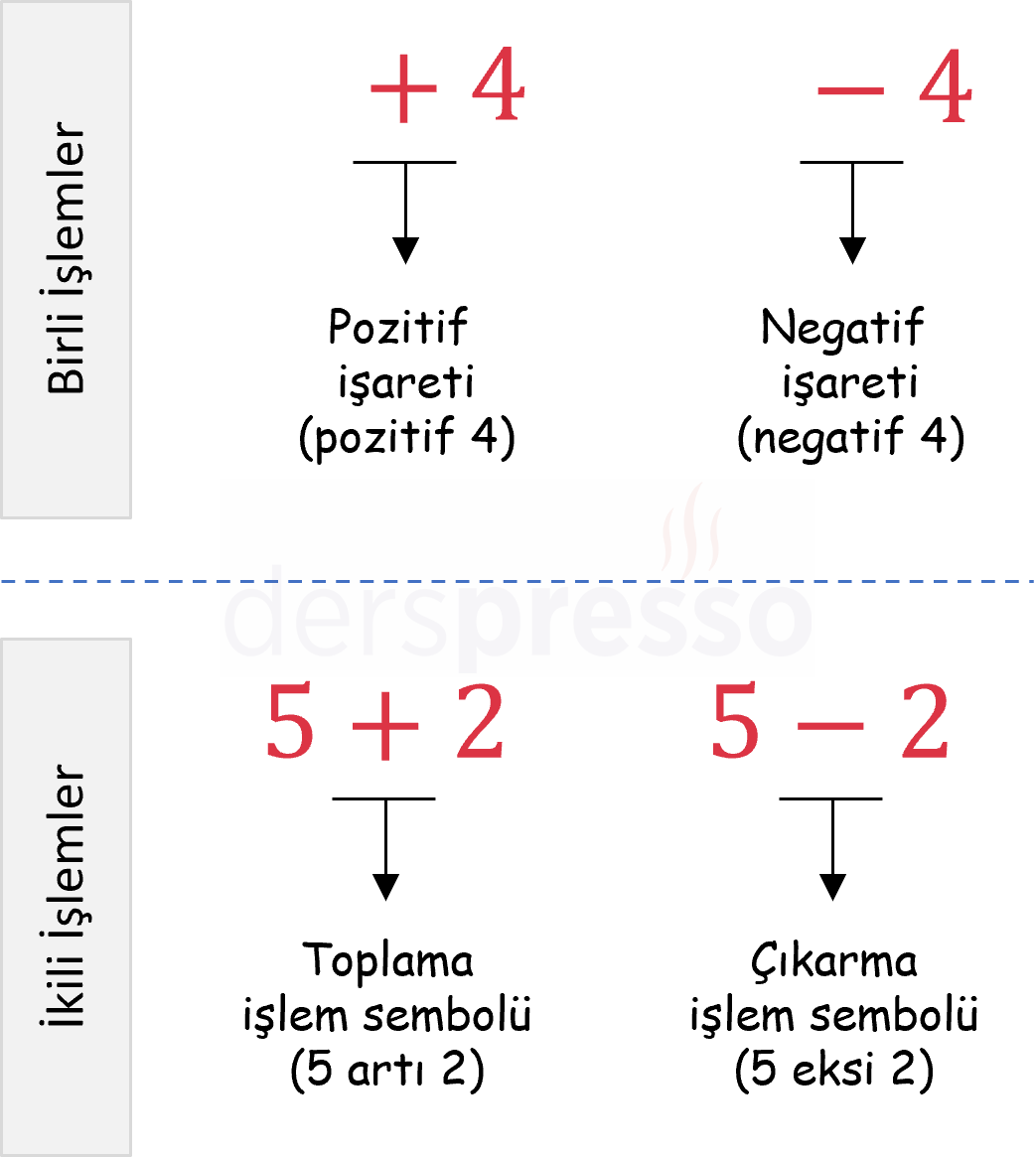
Bu işaretler arasında çoğu zaman bir ayrım yapılmasa da, aşağıdaki gibi iki işlemi de içeren ifadelerin çözümlemesinde bu ayrımın bilinmesi faydalı olacaktır.
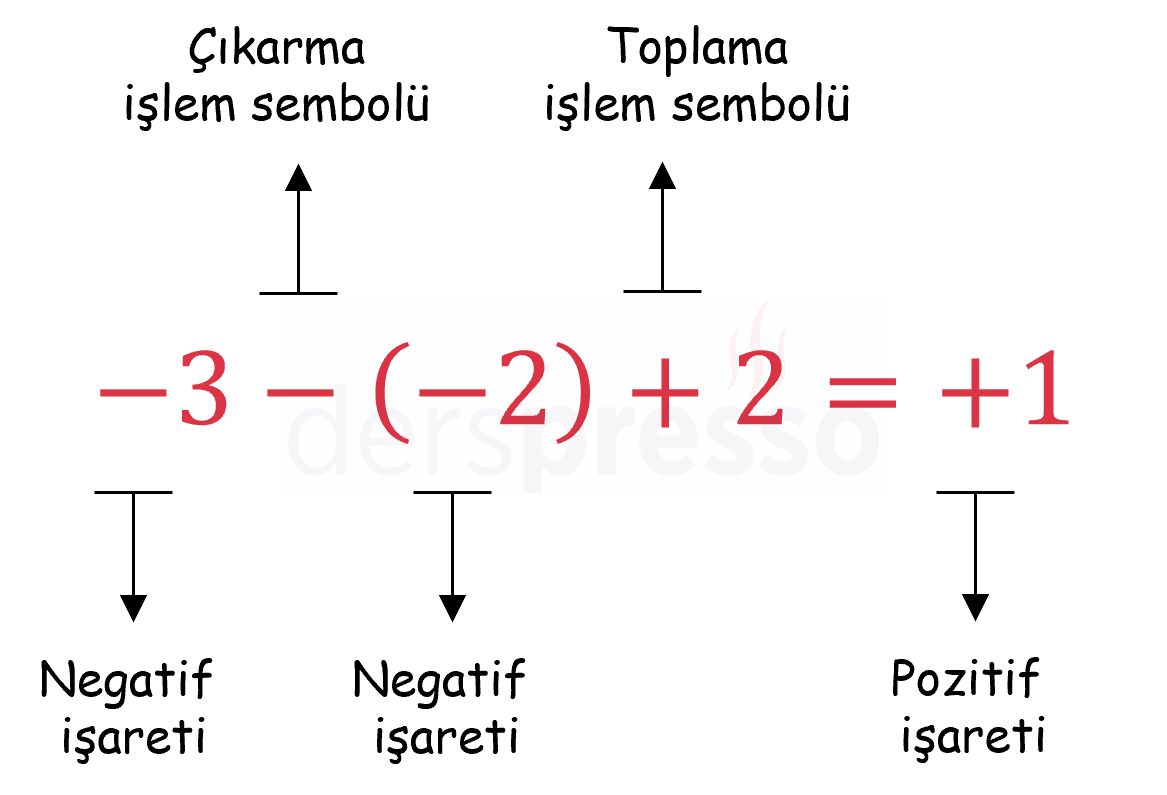
\( a$b \) işlemi \( 2a + b + ab \) şeklinde tanımlanıyor.
Buna göre \( 3$2 + 4$3 \) toplamının sonucu kaçtır?
Çözümü Göster\( *a* \) işlemi \( a \) sayısının harf ile yazılışındaki harf sayısını ifade etmektedir.
Örneğin, 5 (beş) sayısının yazılışında 3 harf vardır.
\( *5* = 3 \)
Buna göre, \( \dfrac{*7* + *11*}{*13*} - \dfrac{2 \cdot *3* + 1}{*6*} \) işleminin sonucu kaçtır?
Çözümü GösterSoldan ve sağdan okunuşları aynı olan sayılara palindromik sayı denir (örneğin 24742, 147741).
\( !a! \) işlemi, \( a \) sayısı palindromik ise sonucu \( a \) olarak, değilse 0 olarak vermektedir.
Buna göre \( !22! \cdot !5! - !111! + !123! \) ifadesinin değeri kaçtır?
Çözümü Göster\( n \in \mathbb{N} \) olmak üzere,
\( \lt n \gt \) işlemi \( n \) sayısından küçük tek sayıların toplamı olarak tanımlanıyor.
\( \lt a + 3 \gt - \lt a \gt = 47 \) olduğuna göre, \( a \) tam sayısı kaçtır?
Çözümü GösterDoğal sayılar arasındaki \( a \bowtie b \) işlemi, \( a \) sayısının en büyük rakamı ile \( b \) sayısının en küçük rakamının çarpımı şeklinde tanımlanıyor.
\( (4x3y) \) sayısı 9'a, \( (9x56) \) sayısı 11'e tam bölündüğüne göre, \( (4x3y) \bowtie (9x56) \) işleminin sonucu kaçtır?
Çözümü Göster\( \square, \triangle, \bowtie \) sembollerinin her biri \( +, -, \times \) işlemlerinden yalnız biri ile eşleştirilecektir.
Buna göre, \( (7 \triangle 4) \bowtie 5 \square 3 \) ifadesinin alabileceği en büyük değer için \( 2 \square 1 \triangle 6 \bowtie 6 \) işleminin sonucu kaçtır?
Çözümü Göster\( \dfrac{x + y}{x \otimes y} = xy - 5x - 1 \)
olduğuna göre, \( 2 \otimes 7 \) işleminin sonucu kaçtır?
Çözümü Göster\( \square a = a(a + 2) \)
\( \triangle b = (b + 1)(2b + 3) \) işlemleri tanımlanıyor.
Buna göre \( \triangle (\square 3) \) işleminin sonucu kaçtır?
Çözümü Göster\( a \square b = a^2 + ab + b \) şeklinde tanımlanıyor.
Buna göre, \( x \square 3 = (x - 1) \square 1 \) eşitliğini sağlayan \( x \) değeri nedir?
Çözümü Göster\( (xyz) \) ve \( (yxz) \) rakamları farklı üç basamaklı doğal sayılardır.
Üç basamaklı sayılar arasında aşağıdaki iki işlem tanımlanıyor.
\( \overline{(abc)} = c(ab + 1) \)
\( \underline{(abc)} = a(bc + c) \)
Buna göre, \( \overline{(xyz)} = \underline{(yxz)} \) eşitliğini sağlayan kaç tane \( (xyz) \) doğal sayısı yazılabilir?
Çözümü Göster