Sayı Doğrusu

Matematikte ilk öğrendiğimiz kavramlardan biri olan sayı doğrusu üzerinde sayıları görsel olarak gösterebiliriz, karşılaştırabiliriz ve temel işlemleri yapabiliriz.

Sayı doğrusunun bazı özellikleri şunlardır:

• Sayı doğrusu üzerindeki her bir noktayı bir reel sayı olarak ifade edebiliriz. Aynı şekilde, her bir reel sayı sayı doğrusu üzerinde farklı bir noktaya karşılık gelir. Bir diğer ifadeyle, reel sayılarla sayı doğrusu üzerindeki noktalar arasında birebir eşleme yapabiliriz.
• Sıfır sayısının sağındaki sayılar pozitif sayılar, solundaki sayılar negatif sayılardır.
• Sıfır sayısı ne pozitiftir ne de negatiftir.
• Sayı doğrusunun uçlarında bulunan oklar sayı doğrusunun sonsuza gittiğini gösterir.

Analitik geometride gördüğümüz iki boyutlu kartezyen düzlemindeki \( x \) ve \( y \) eksenlerini de birbirine dik şekilde yerleştirilmiş iki sayı doğrusu olarak düşünebiliriz. Bu açıdan baktığımızda sayı doğruları dikey de olabilir. Dikey bir sayı doğrusunda sayılar yukarıya doğru gidildikçe büyür, aşağıya doğru gidildikçe küçülür.

Sayı Doğrusu Üzerindeki Sayıların Karşılaştırması

Sayı doğrusu üzerindeki sayılar sağa doğru gidildikçe büyür, sola doğru gidildikçe küçülür. Dolayısıyla herhangi bir nokta, sayı doğrusunun pozitif ya da negatif tarafında olmasından bağımsız olarak solunda kalan tüm noktalardan daha büyük, sağında kalan tüm noktalardan daha küçük bir sayıya karşılık gelir.

Sayı Doğrusu Üzerinde Uzaklık

İki sayının farkının mutlak değeri, bu iki sayının sayı doğrusu üzerinde aralarındaki uzaklığa eşittir. Birbirinden farklı iki nokta arasındaki uzaklık, sayıların farkının mutlak değeri alındığı için her zaman pozitif bir değerdir ve hangi sayıdan hangisi çıkartılırsa çıkartılsın mutlak değer tanımı gereği aynı pozitif sonucu verecektir.

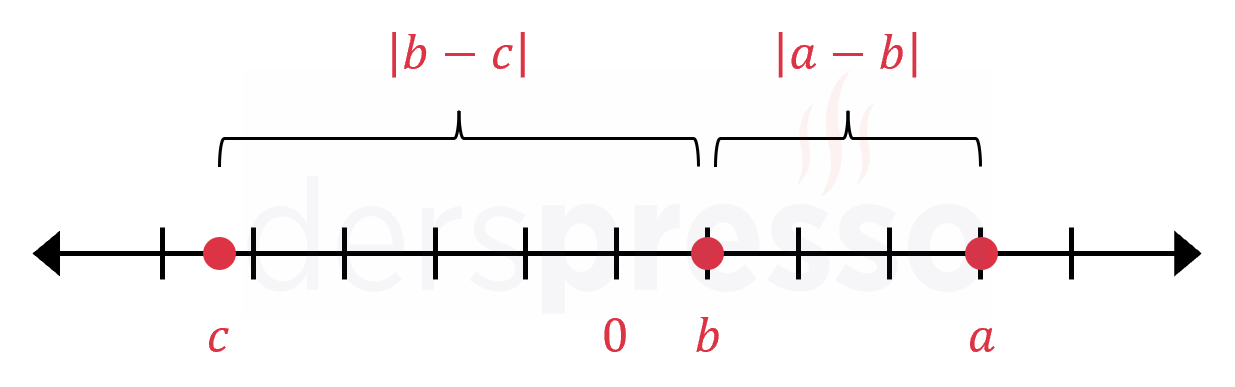
Bir sayının sadece kendisinin mutlak değeri, o sayının sayı doğrusu üzerinde orijine (sıfır noktasına) olan uzaklığını verir.

Sayı Doğrusu ve Reel Sayılar

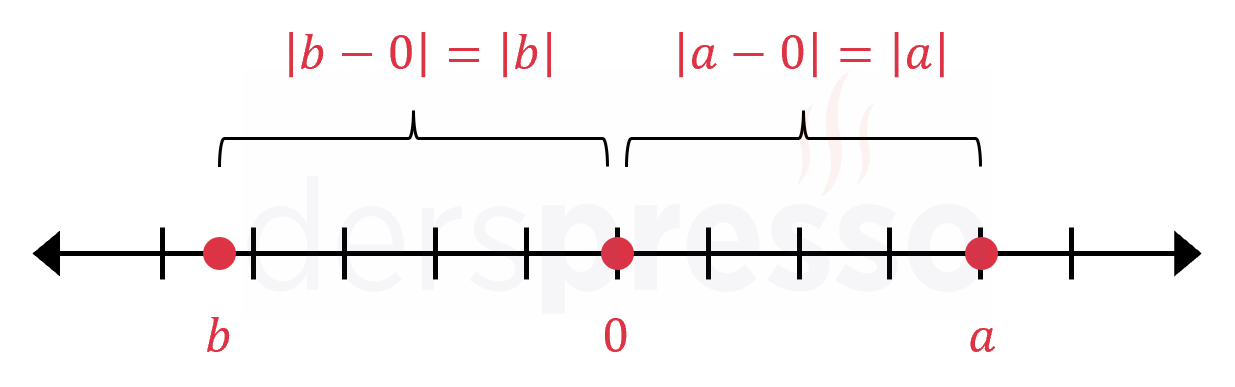
Sayı doğrusu tüm reel sayıları kapsar ve herhangi iki nokta arasınının detayına indiğimizde sonsuz sayıda reel sayıya ve bu sayıların karşılık geldiği noktaya ulaşabiliriz. Bir irrasyonel sayı olan, yani virgülden sonraki basamakları tekrarsız şekilde sonsuza giden, \( \pi \) sayısının sayı doğrusu üzerindeki yeri aşağıdaki şekilde temsili olarak gösterilmiştir.