Alt Küme
Bir \( B \) kümesinin her elemanı \( A \) kümesinin de elemanı ise \( B \) kümesi \( A \) kümesinin bir alt kümesidir.
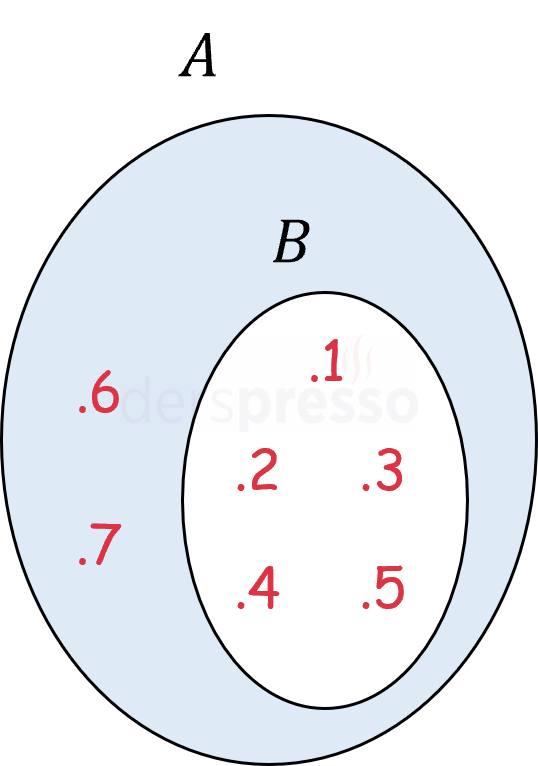
Her \( x \) için, \( x \in B \Rightarrow x \in A \) ise,
\( B \) kümesi \( A \) kümesinin bir alt kümesidir.
\( A = \{ a, b, c, d, e \} \)
\( B = \{ b, d \} \)
\( B \) kümesinin her elemanı \( A \) kümesinin de elemanı olduğu için \( B \) kümesi \( A \) kümesinin bir alt kümesidir.
\( B \) kümesi \( A \) kümesinin bir alt kümesi ise \( A \) kümesinin \( B \) kümesinin elemanları dışında başka elemanları da olabilir ya da iki küme eşit kümeler olabilir.
\( B \) kümesi \( A \) kümesinin bir alt kümesi ise aralarındaki ilişki "\( \subseteq \)" sembolü ile gösterilir. Alt küme sembolündeki eşitlik çizgisi iki kümenin eşit kümeler de olabileceğini gösterir.
\( B \subseteq A \)
\( s(B) \le s(A) \)
\( B \) kümesinin \( A \) kümesinde bulunmayan en az bir elemanı varsa \( B \) kümesi \( A \) kümesinin bir alt kümesi değildir.
En az bir \( x \) için, \( x \in B \land x \notin A \) ise,
\( B \) kümesi \( A \) kümesinin bir alt kümesi değildir.
İSPATI GÖSTER
\( B \) kümesinin \( A \) kümesinin bir alt kümesi olduğu durum için alt küme tanımını yazalım.
Her \( x \) için, \( x \in B \Rightarrow x \in A \) ise \( B \) kümesi \( A \) kümesinin bir alt kümesidir.
Bu ifadeyi sembolik şekilde yazalım.
\( \forall x, x \in B \Rightarrow x \in A \)
\( B \) kümesinin \( A \) kümesinin bir alt kümesi olmadığı durum için bu ifadenin değilini alalım.
\( (\forall x, x \in B \Rightarrow x \in A)' \)
\( \equiv \exists x, (x \in B \Rightarrow x \in A)' \)
Parantez içindeki "ise" ifadesini "veya" ifadesi şeklinde yazalım.
\( \equiv \exists x, ((x \in B)' \lor x \in A)' \)
\( \equiv \exists x, (x \notin B \lor x \in A)' \)
\( \equiv \exists x, x \in B \land x \notin A \)
Buna göre, en az bir \( x \) için, \( x \in B \Rightarrow x \in A \) ise \( B \) kümesi \( A \) kümesinin bir alt kümesi değildir.
Eleman sembolünde elemanlar küme parantezi içine alınmaz, alt küme sembolünde ise alınır. Aşağıdaki eleman ve alt küme gösterimlerindeki ayrımlara dikkat edilmelidir.
\( A = \{ 1, 2, \{ 2, 3 \} \} \) olmak üzere,
\( s(A) = 3 \)
\( 1, 2 \in A \)
\( \{ 2, 3 \} \in A \)
\( \{ 1 \} \notin A \)
\( 3 \notin A \)
\( \{ 1 \} \subseteq A \)
\( \{ 1, 2 \} \subseteq A \)
\( \{ 1, \{ 2, 3 \} \} \subseteq A \)
\( \{ 2, 3 \} \not\subseteq A \)
\( \{ \{ 2, 3 \} \} \subseteq A \)
\( \{ 3 \} \not\subseteq A \)
Öz Alt Küme
\( B \) kümesi \( A \) kümesinin bir alt kümesi iken \( A \) kümesinin \( B \) kümesinin elemanları dışında başka elemanları da varsa (yani iki küme eşit kümeler değilse) \( B \) kümesi \( A \) kümesinin bir öz alt kümesidir.
\( B \) kümesi \( A \) kümesinin bir öz alt kümesi ise aralarındaki ilişki "\( \subset \)" sembolü ile gösterilir. Alt küme sembolünde bulunan eşitlik çizgisinin öz alt küme sembolünde bulunmaması iki kümenin eşit kümeler olamayacağını gösterir.
\( B \subset A \)
\( s(B) \lt s(A) \)
NOT: Bazı kaynaklarda "\( \subset \)" sembolü iki kümenin eşitliğini de kapsayacak şekilde ve "\( \subseteq \)" sembolü ile eş anlamlı olarak kullanılmaktadır. Biz burada "\( \subset \)" sembolünü öz alt küme anlamıyla kullanıyor olacağız.
Sayı kümeleri arasındaki alt küme ilişkisi aşağıdaki şekilde ifade edilebilir.
\( \mathbb{Z^+} \subset \mathbb{N} \subset \mathbb{Z} \subset \mathbb{Q} \subset \mathbb{R} \subset \mathbb{C} \)
Kapsama
Alt küme sembolleri yönleri tersine çevrilerek de kullanılabilir. Bu durumda sembolün solundaki küme alt küme değil, kapsayan (üst) küme olmaktadır.
\( B \subseteq A \Longleftrightarrow A \supseteq B \)
\( B \subset A \Longleftrightarrow A \supset B \)
\( B \not\subseteq A \Longleftrightarrow A \not\supseteq B \)
\( B \not\subset A \Longleftrightarrow A \not\supset B \)
Alt Küme İşlem Kuralları
Boş küme tüm kümelerin bir alt kümesidir.
\( \emptyset \subseteq A \)
İSPATI GÖSTER
Boş kümenin tüm kümelerin bir alt kümesi olduğunu çelişki ile ispat yöntemiyle ispatlayalım.
Herhangi bir \( A \) kümesi tanımlayalım ve boş kümenin \( A \) kümesinin bir alt kümesi olmadığını varsayalım.
\( \emptyset \not\subseteq A \)
Alt küme tanımına göre, bu durumda boş kümenin \( A \) kümesinin elemanı olmayan en az bir elemanı bulunmalıdır.
\( \exists x \in \emptyset, x \notin A \)
Boş küme tanımına göre, boş kümenin hiçbir elemanı yoktur, dolayısıyla \( x \in \emptyset \) doğru olamaz.
Bir çelişki ile karşılaştığımız için yaptığımız \( \emptyset \not\subseteq A \) varsayımı doğru olamaz, o zaman boş küme \( A \) kümesinin bir alt kümesi olmalıdır.
\( \emptyset \subseteq A \)
Her küme kendisinin bir alt kümesidir.
\( A \subseteq A \)
İSPATI GÖSTER
\( A \subseteq A \) olduğunu gösterelim.
Alt küme tanımına göre, bir küme diğer bir kümenin alt kümesi ise birinci kümenin her elemanı ikinci kümenin de elemanıdır.
\( \forall x, x \in A \Rightarrow x \in A \)
\( p \Rightarrow p \) ifadesi bir totolojidir.
\( p \Rightarrow p \equiv 1 \)
\( A \subseteq A \) olduğunu göstermiş olduk.
Her küme evrensel kümenin bir alt kümesidir.
\( A \subseteq E \)
İki küme birbirinin alt kümesi ise bu iki küme eşittir. İki kümenin eşit olduğunu göstermek için en sık kullanılan yöntem, bu iki kümeden her birinin diğerinin alt kümesi olduğunu ayrı ayrı göstermektir.
\( A \subseteq B \) ve \( B \subseteq A \Longleftrightarrow A = B \)
\( A \) kümesi \( B \) kümesinin, \( B \) kümesi de \( C \) kümesinin birer alt kümesi ise \( A \) kümesi \( C \) kümesinin bir alt kümesidir.
\( A \subseteq B \) ve \( B \subseteq C \) ise \( A \subseteq C \)
\( A = \{ a, b, \{ a \}, \{ a, c \}, \{ b, c \} \} \) olduğuna göre, aşağıdakilerden hangileri doğrudur?
I. \( \{ a, b \} \in A \)
II. \( \{ a, c \} \subset A \)
III. \( c \in A \)
IV. \( A \in A \)
V. \( s(A) = 3 \)
Çözümü Göster\( A \) kümesinin 5 elemanı vardır ve bu elemanlar \( a \), \( b \), \( \{ a \} \), \( \{ a, c \} \) ve \( \{ b, c \} \)'dir.
\( \in \) sembolünü kullanırken elemanlar küme parantezi içine alınmaz, \( \subseteq \) ve \( \subset \) sembollerini kullanırken ise alınır.
I. öncül yanlıştır, doğrusu \( a, b \in A \) veya \( \{ a, b \} \subset A \) olmalıdır.
II. öncül yanlıştır, doğrusu \( \{ a, c \} \in A \) veya \( \{\{ a, c \}\} \subset A \) olmalıdır.
III. öncül yanlıştır, doğrusu \( c \notin A \) olmalıdır.
IV. öncül yanlıştır, doğrusu \( A \subseteq A \) olmalıdır.
V. öncül yanlıştır, doğrusu \( s(A) = 5 \) olmalıdır.
Buna göre verilen öncüllerin tümü yanlıştır.
\( A = \{ 1, 2, \{ 1 \}, \{ 2 \}, \{ 1, 2 \} \} \) olduğuna göre, aşağıdakilerden hangileri doğrudur?
I. \( s(A) = 5 \)
II. \( \{ 1, 2 \} \subset A \)
III. \( \{ 1, \{ 1 \} \} \subset A \)
IV. \( \{ 1, 2 \} \in A \)
V. \( \{ 2, \{ 2 \} \} \in A \)
Çözümü Göster\( A \) kümesinin 5 elemanı vardır ve bu elemanlar \( 1 \), \( 2 \), \( \{ 1 \} \), \( \{ 2 \} \) ve \( \{ 1, 2 \} \)'dir.
\( \in \) sembolünü kullanırken elemanlar küme parantezi içine alınmaz, \( \subseteq \) ve \( \subset \) sembollerini kullanırken ise alınır.
I. öncül doğrudur. \( \{ 1, 2 \} \) gibi parantez içindeki elemanlar tek birer elemandır.
II. öncül doğrudur. \( 1 \) ve \( 2 \) elemanlarından oluşan küme \( A \) kümesinin alt kümesidir.
III. öncül doğrudur. \( 1 \) ve \( \{ 1 \} \) elemanlarından oluşan küme \( A \) kümesinin alt kümesidir.
IV. öncül doğrudur. \( \{ 1, 2 \} \) \( A \) kümesinin bir elemanıdır.
V. öncül yanlıştır. \( A \) kümesinin \( \{ 2, \{2\} \} \) diye bir elemanı yoktur. İfadenin doğrusu \( \{ 2, \{ 2 \} \} \subset A \) veya \( 2, \{ 2 \} \in A \) olmalıdır.
Buna göre V. öncül dışındaki öncüller doğrudur.
\( A \subset \{ 2, 5 \} \) ve \( B \subset \{ 1, 4, 5, 7, 9 \} \) olduğuna göre, aşağıdakilerden hangileri doğru olabilir?
I. \( A \subset B \)
II. \( B \subset A \)
III. \( A \subseteq B \subseteq A \)
IV. \( A \subseteq \emptyset \subset B \)
Çözümü Göster\( A = \{ 5 \} \) ve \( B = \{ 5, 7 \} \) olduğunda \( A \subset B \) olacağı için I. öncül doğru olabilir.
\( A = \{ 2, 5 \} \) ve \( B = \{ 5 \} \) olduğunda \( B \subset A \) olacağı için II. öncül doğru olabilir.
\( A = B \) olduğunda \( A \subseteq B \subseteq A \) olacağı için III. öncül doğru olabilir.
\( A = \emptyset \) ve \( B = \{ 5 \} \) olduğunda \( A \subseteq \emptyset \subset B \) olacağı için IV. öncül doğru olabilir.
Buna göre 4 öncül de doğru olabilir.
\( P \subset Q \) olduğuna göre,
\( (P \cap Q') \cup [P \cup (P' \cap Q)]' \) ifadesinin en sade hali nedir?
Çözümü Göster\( Q \) kümesi \( P \) kümesini kapsayacak şekilde bir Venn şeması çizelim.
Venn şemasını kullanarak işlemleri sadeleştirelim.
\( (P \cap Q') \cup [P \cup (P' \cap Q)]' \)
\( = \emptyset \cup [P \cup (Q - P)]' \)
\( = \emptyset \cup [Q]' \)
\( = Q' \) bulunur.