Kümelerin Kesişimi
İki ya da daha fazla kümenin ortak elemanlarından oluşan kümeye bu kümelerin kesişim kümesi denir. Kümeler arasındaki kesişim işlemi için \( \cap \) sembolü kullanılır.
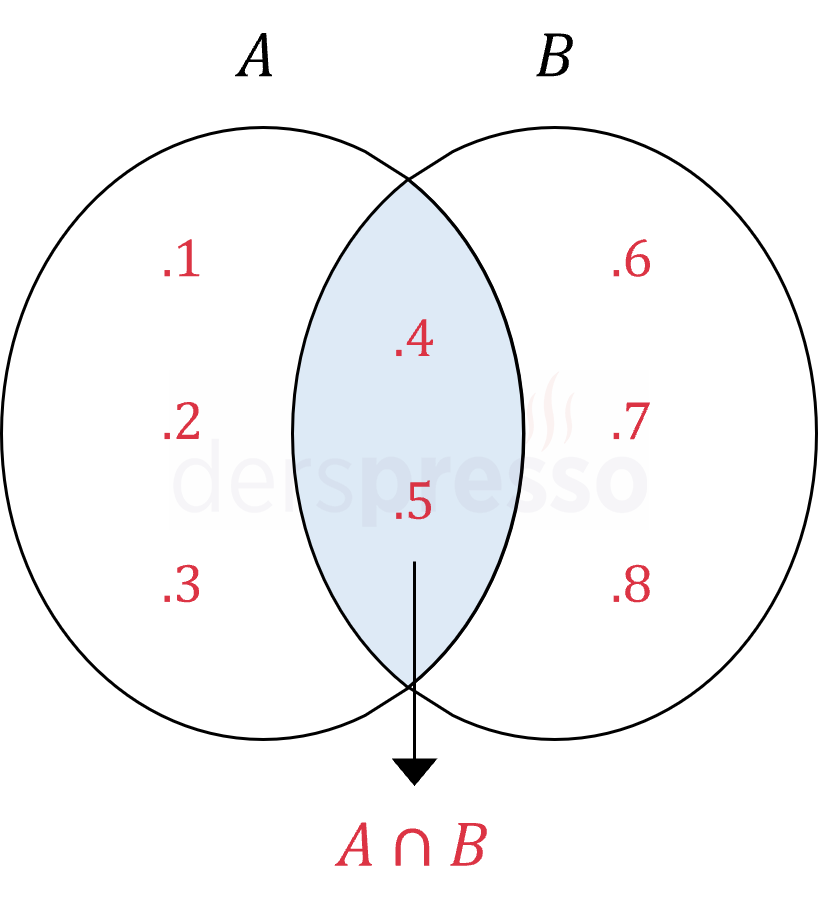
\( A \cap B = \{ x \mid x \in A \land x \in B \} \)
\( A = \{ 1, 2, 3, \textcolor{red}{4}, \textcolor{red}{5} \} \)
\( B = \{ \textcolor{red}{4}, \textcolor{red}{5}, 6, 7, 8 \} \)
\( A \cap B = \{ \textcolor{red}{4}, \textcolor{red}{5} \} \)
Bu tanıma göre, bir eleman iki (ya da daha fazla) kümeden her birinin elemanı ise kesişim kümelerinin de elemanıdır. Benzer şekilde, bir eleman iki (ya da daha fazla) kümenin kesişim kümesinin elemanı ise bu kümelerden her birinin elemanıdır.
Üç kümenin kesişim kümesinin liste ve Venn şeması gösterimleri aşağıdaki gibidir.
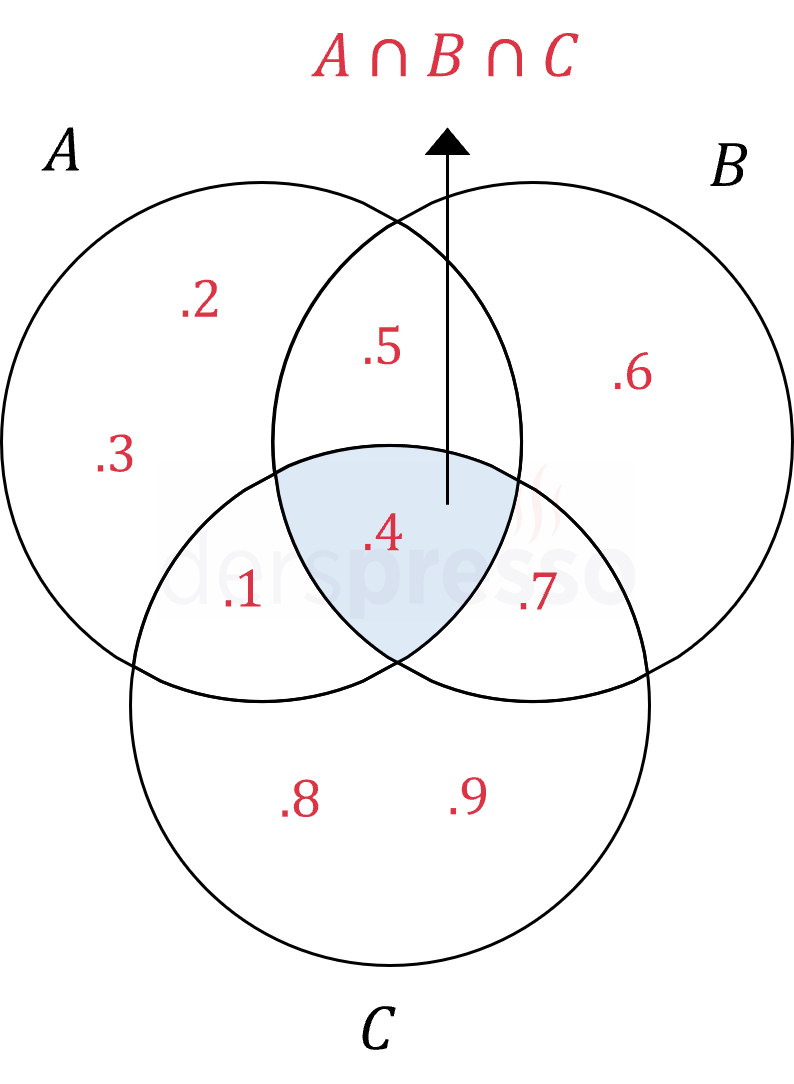
\( A = \{ 1, 2, 3, \textcolor{red}{4}, 5 \} \)
\( B = \{ \textcolor{red}{4}, 5, 6, 7 \} \)
\( C = \{ 1, \textcolor{red}{4}, 7, 8, 9 \} \)
\( A \cap B \cap C = \{ \textcolor{red}{4} \} \)
Bu üç kümenin ikili kesişim kümeleri aşağıdaki gibidir. Dikkat edilirse ikili kesişim kümeleri üçlü kesişim kümesini de kapsar.
\( A \cap B = \{ \textcolor{red}{4}, 5 \} \)
\( A \cap C = \{ 1, \textcolor{red}{4} \} \)
\( B \cap C = \{ \textcolor{red}{4}, 7 \} \)
Ayrık Küme
Ortak elemanları olmayan, bir diğer ifadeyle kesişim kümeleri boş küme olan kümelere ayrık küme denir.
\( A \cap B = \emptyset \) ise,
\( A \) ve \( B \) ayrık kümelerdir.
\( A = \{ 1, 2, 3, 4 \} \)
\( B = \{ 5, 6, 7, 8 \} \)
\( A \cap B = \emptyset \)
Bu tanıma göre boş küme dahil her küme boş küme ile ayrık kümelerdir.
\( A \cap \emptyset = \emptyset \)
\( \emptyset \cap \emptyset = \emptyset \)
İkişerli Ayrık Kümeler
İkiden fazla kümenin ayrık olması iki şekilde olabilir.
Birinci durumda kümelerin tümünde ortak olan bir eleman yoktur, ancak kümelerin ikişerli kesişim kümelerinin ortak elemanları olabilir.
\( A = \{ 1, \textcolor{red}{2} \} \)
\( B = \{ \textcolor{red}{2}, \textcolor{blue}{3} \} \)
\( C = \{ \textcolor{blue}{3}, 4 \} \)
\( A \cap B = \{ \textcolor{red}{2} \} \)
\( B \cap C = \{ \textcolor{blue}{3} \} \)
\( A \cap B \cap C = \emptyset \)
İkinci durumda ise kümelerin ikişerli de olmak üzere hiçbir ortak elemanı yoktur.
\( A = \{ 1, 2 \} \)
\( B = \{ 3, 4 \} \)
\( C = \{ 5, 6 \} \)
\( A \cap B = B \cap C \) \( = A \cap C \) \( = A \cap B \cap C = \emptyset \)
İkiden fazla kümenin ayrık olduğu belirtildiğinde kastedilen çoğu zaman bu ikinci durumdur, bunu daha net ifade etmek için kullanılabilecek ifade bu kümelerin ikişerli ayrık olmasıdır.
Kesişim İşlem Özellikleri
Kesişim işleminin değişme özelliği vardır.
\( A \cap B = B \cap A \)
\( x \) elemanı \( A \cap B \) kümesinin bir elemanı olsun.
\( x \in A \cap B \)
Kesişim kümesi tanımına göre, \( x \) hem \( A \) kümesinin hem de \( B \) kümesinin elemanıdır.
\( x \in A \land x \in B \)
"Ve" işleminin değişme özelliği vardır.
\( x \in B \land x \in A \)
Kesişim kümesi tanımına göre, \( x \) hem \( B \) kümesinin hem de \( A \) kümesinin elemanı ise kesişim kümelerinin de elemanıdır.
\( x \in B \cap A \)
Kesişim işleminin birleşme özelliği vardır.
\( A \cap (B \cap C) = (A \cap B) \cap C \)
\( A = \{ 1, 2, 3, 4, 5 \} \)
\( B = \{ 1, 2, 3, 6, 7 \} \)
\( C = \{ 1, 2, 4, 6, 8 \} \)
\( A \cap (B \cap C) = A \cap \{ 1, 2, 6 \} \) \( = \{ 1, 2 \} \)
\( (A \cap B) \cap C = \{ 1, 2, 3 \} \cap C \) \( = \{ 1, 2 \} \)
\( x \) elemanı \( A \cap (B \cap C) \) kümesinin bir elemanı olsun.
\( x \in A \cap (B \cap C) \)
Kesişim kümesi tanımına göre, \( x \) hem \( A \) kümesinin hem de \( B \cap C \) kümesinin elemanıdır.
\( x \in A \land x \in B \cap C \)
Kesişim kümesi tanımına göre, \( x \) hem \( B \) kümesinin hem de \( C \) kümesinin elemanıdır.
\( x \in A \land (x \in B \land x \in C) \)
"Ve" işleminin birleşme özelliği vardır.
\( (x \in A \land x \in B) \land x \in C \)
Kesişim kümesi tanımına göre, \( x \) hem \( A \) kümesinin hem de \( B \) kümesinin elemanı ise kesişim kümelerinin de elemanıdır.
\( x \in A \cap B \land x \in C \)
Kesişim kümesi tanımına göre, \( x \) hem \( A \cap B \) kümesinin hem de \( C \) kümesinin elemanı ise kesişim kümelerinin de elemanıdır.
\( x \in (A \cap B) \cap C \)
Kesişim işleminin değişme ve birleşme özellikleri olduğu için, sadece kesişim işleminden oluşan bir ifadede kümeler arasındaki parantezler kaydırılabilir ya da kaldırılabilir ve kümelerin sırası değiştirilebilir.
\( (A \cap B) \cap (C \cap D) \)
\( = A \cap (B \cap C) \cap D \)
\( = A \cap B \cap C \cap D \)
\( = D \cap B \cap A \cap C \)
Kesişim işleminin birleşme işlemi üzerinde soldan ve sağdan dağılma özelliği vardır.
\( A \cap (B \cup C) = (A \cap B) \cup (A \cap C) \)
\( (A \cup B) \cap C = (A \cap C) \cup (B \cap C) \)
\( A = \{ 1, 2, 3 \} \)
\( B = \{ 2, 4, 5 \} \)
\( C = \{ 3, 4, 6 \} \)
\( A \cap (B \cup C) = A \cap \{ 2, 3, 4, 5, 6 \} \) \( = \{ 2, 3 \} \)
\( (A \cap B) \cup (A \cap C) = \{ 2 \} \cup \{ 3 \} \) \( = \{ 2, 3 \} \)
\( (A \cup B) \cap C = \{ 1, 2, 3, 4, 5 \} \cap C \) \( = \{ 3, 4 \} \)
\( (A \cap C) \cup (B \cap C) = \{ 3 \} \cup \{ 4 \} \) \( = \{ 3, 4 \} \)
\( x \) elemanı \( A \cap (B \cup C) \) kümesinin bir elemanı olsun.
\( x \in A \cap (B \cup C) \)
Kesişim kümesi tanımına göre, \( x \) hem \( A \) kümesinin hem de \( B \cup C \) kümesinin elemanıdır.
\( x \in A \land x \in B \cup C \)
Birleşim kümesi tanımına göre, \( x \) \( B \) kümesinin veya \( C \) kümesinin elemanıdır.
\( x \in A \land (x \in B \lor x \in C) \)
"Ve" işleminin "veya" işlemi üzerinde dağılma özelliği vardır.
\( (x \in A \land x \in B) \lor (x \in A \land x \in C) \)
Kesişim kümesi tanımına göre, \( x \) iki kümenin birlikte elemanı ise kesişim kümelerinin de elemanıdır.
\( (x \in A \cap B) \lor (x \in A \cap C) \)
Birleşim kümesi tanımına göre, \( x \) \( A \cap B \) kümesinin veya \( A \cap C \) kümesinin elemanı ise birleşim kümelerinin elemanıdır.
\( x \in (A \cap B) \cup (A \cap C) \)
Kesişim işleminin birim (etkisiz) elemanı evrensel kümedir.
\( A \cap E = A \)
Kesişim İşlem Kuralları
Bir kümenin boş küme ile kesişimi boş kümedir.
\( A \cap \emptyset = \emptyset \)
Boş küme tüm kümelerin bir alt kümesidir.
\( \emptyset \subseteq A \cap \emptyset \)
Bir küme, kendisi ile bir diğer kümenin kesişimini kapsar.
\( A \cap \emptyset \subseteq \emptyset \)
Kümelerin eşitliği tanımına göre, iki küme birbirinin alt kümesi ise bu iki küme birbirine eşittir.
\( A \cap \emptyset = \emptyset \)
Bir kümenin kendisiyle kesişimi kendisine eşittir.
\( A \cap A = A \)
Kümelerin eşitliği tanımına göre, \( A \cap A = A \) olduğunu göstermek için \( A \cap A \subseteq A \) ve \( A \subseteq A \cap A \) olduğunu ayrı ayrı gösterelim.
(1) \( A \cap A \subseteq A \) olduğunu gösterelim.
\( x \in A \cap A \) olsun.
Kesişim kümesi tanımına göre, \( x \) iki kümenin kesişiminin elemanı ise her iki kümenin de elemanıdır.
\( x \in A \land x \in A \)
\( p \land p \equiv p \)
\( x \in A \)
\( A \cap A \subseteq A \) olduğunu göstermiş olduk.
(2) \( A \subseteq A \cap A \) olduğunu gösterelim.
\( x \in A \) olsun.
\( p \equiv p \land p \)
\( x \in A \land x \in A \)
Kesişim kümesi tanımına göre, \( x \) iki kümenin elemanı ise kümelerin kesişiminin de elemanıdır.
\( x \in A \cap A \)
\( A \subseteq A \cap A \) olduğunu göstermiş olduk.
Kümelerin eşitliği tanımına göre, bir kümenin kendisiyle kesişimi kendisine eşittir.
\( A \cap A = A \)
Bir kümenin evrensel kümeyle kesişimi kendisine eşittir.
\( A \cap E = A \)
Bir küme bir diğer kümenin alt kümesiyse kesişimleri birinci küme olur.
\( A \subseteq B \) ise,
\( A \cap B = A \)
Kümelerin eşitliği tanımına göre, \( A \cap B = A \) olduğunu göstermek için \( A \cap B \subseteq A \) ve \( A \subseteq A \cap B \) olduğunu ayrı ayrı gösterelim.
\( A \subseteq B \) olduğunu kabul edelim.
(1) \( A \cap B \subseteq A \) olduğunu gösterelim.
\( A \cap B \subseteq A \) olduğunu göstermek için, her \( x \in A \cap B \) için \( x \in A \) olduğunu gösterelim.
\( x \in A \cap B \) olsun.
Kesişim kümesi tanımına göre, \( x \) hem \( A \) kümesinin hem \( B \) kümesinin elemanıdır.
\( x \in A \land x \in B \)
\( x \) \( A \) kümesinin bir elemanıdır.
\( x \in A \)
\( A \cap B \subseteq A \) olduğunu göstermiş olduk.
(2) \( A \subseteq A \cap B \) olduğunu gösterelim.
\( A \subseteq A \cap B \) olduğunu göstermek için, her \( x \in A \) için \( x \in A \cap B \) olduğunu gösterelim.
\( x \in A \) olsun.
\( A \subseteq B \) kabulü gereği, her \( x \in A \) için \( x \in B \) olur.
Kesişim kümesi tanımına göre, \( x \) hem \( A \) kümesinin hem \( B \) kümesinin elemanı ise \( A \cap B \) kümesinin de bir elemanıdır.
\( x \in A \cap B \)
\( A \subseteq A \cap B \) olduğunu göstermiş olduk.
Kümelerin eşitliği tanımına göre, iki küme birbirinin alt kümesi ise bu iki küme birbirine eşittir.
\( A \cap B = A \)
İki kümenin kesişimi, her iki kümenin de alt kümesidir.
\( A \cap B \subseteq A \)
\( A \cap B \subseteq B \)
\( x \in A \cap B \) olsun.
Kesişim kümesi tanımına göre, \( x \) \( A \cap B \) kümesinin elemanı ise hem \( A \) kümesinin hem \( B \) kümesinin elemanıdır.
\( x \in A \land x \in B \)
Bir \( p \land q \) önermesi doğru ise \( p \) önermesi de doğrudur.
\( x \in A \)
Her \( x \in A \cap B \) için \( x \in A \) olduğuna göre, \( A \cap B \) kümesi \( A \) kümesinin bir alt kümesidir.
\( A \cap B \subseteq A \)
Bir küme ayrı ayrı iki kümenin alt kümesi ise kesişim kümelerinin de alt kümesidir.
\( A \subseteq X \land A \subseteq Y \Rightarrow A \subseteq X \cap Y \)
\( x \in A \) olsun.
Alt küme tanımına göre, \( A \subseteq X \land A \subseteq Y \) olduğu için \( x \) hem \( X \) kümesinin hem \( Y \) kümesinin elemanı olur.
\( x \in X \land x \in Y \)
Kesişim kümesi tanımına göre, \( x \) hem \( A \) kümesinin hem \( B \) kümesinin elemanı ise \( A \cap B \) kesişim kümesinin de elemanıdır.
\( x \in X \cap Y \)
Her \( x \in A \) için \( x \in X \cap Y \) olduğuna göre, \( A \) kümesi \( X \cap Y \) kümesinin bir alt kümesidir.
\( A \subseteq X \cap Y \)
Yukarıda verilen \( A, B \) ve \( C \) kümeleri için aşağıdakilerden hangileri yanlıştır?
I. \( A \cap B = \{b, d, g\} \)
II. \( A \cap C = \{c, k\} \)
III. \( B \cap C = \{d\} \)
IV. \( s(A) = 7 \)
V. \( s(C) = 2 \)
I. öncül doğrudur.
\( A \cap C = \{ c, d, k \} \) olduğu için II. öncül yanlıştır.
III. öncül doğrudur.
\( A = \{ a, b, c, d, e, g, k \} \) olduğu için IV. öncül doğrudur.
\( C = \{ c, d, f, h, k \} \) olduğu için V. öncül yanlıştır.
Buna göre II. ve V. öncüller yanlıştır.
\( A = \{ x \mid x = 3a + 2, a \in \mathbb{N} \} \)
\( B = \{ x \mid x = 5b + 2, b \in \mathbb{N} \} \) olduğuna göre,
\( A \cap B \) kümesinin en küçük üç elemanının toplamı kaçtır?
\( A \) kümesi 3'e bölününce 2 kalanını veren, \( B \) kümesi de 5'e bölününce 2 kalanını veren doğal sayılardan oluşmaktadır.
\( A = \{ 2, 5, 8, 11, 14, 17, \ldots \} \)
\( B = \{ 2, 7, 12, 17, 22, 27, \ldots \} \)
Buna göre iki kümenin kesişim kümesindeki elemanlar, 2 eksiği hem 3'e hem de 5'e, yani 15'e tam bölünen doğal sayılardır. Dolayısıyla, kesişim kümesindeki elemanlar 15'e bölününce 2 kalanını veren doğal sayılardan oluşur.
\( A \cap B = \{ 2, 17, 32, 47, 62, \ldots \} \)
Bu sayıların en küçük üçünün toplamı \( 2 + 17 + 32 = 51 \) olarak bulunur.
\( A = \{x \mid x = 3k, k \in \mathbb{Z^+}, x \lt 30\} \)
\( B = \{x \mid x = 2k, k \in \mathbb{Z^+}, x \le 10\} \)
\( C = \{x \mid x = 5k, k \in \mathbb{Z^+}, x \le 25\} \)
kümeleri veriliyor. Bu kümeleri kapsayan evrensel küme,
\( E = \{x \mid x \in \mathbb{Z^+}, x \le 30\} \)
olduğuna göre, bu kümelerin eleman sayılarını Venn şemasında gösterin.
Verilen kümelerin elemanlarını listeleyelim.
\( E = \{1, 2, 3, \ldots, 29, 30\} \)
\( A = \{3, 6, 9, 12, 15, 18, 21, 24, 27\} \)
\( B = \{2, 4, 6, 8, 10\} \)
\( C = \{5, 10, 15, 20, 25\} \)
\( A \cap B = \{6\} \)
\( A \cap C = \{15\} \)
\( B \cap C = \{10\} \)
\( A \cap B \cap C = \emptyset \)
Buna göre kümelerin eleman sayıları aşağıdaki gibi olur.
\( K \) kümesinin alt kümelerinin sayısı 32, \( L \) kümesinin alt kümelerinin sayısı 16 olduğuna göre,
\( K \cap L \) kümesinin eleman sayısı en çok kaç olabilir?
\( n \) elemanlı bir kümenin alt küme sayısı \( 2^n \) formülü ile bulunur.
\( K \) kümesinin alt kümelerinin sayısı \( 32 = 2^5 \) ise \( s(K) = 5 \) olur.
\( L \) kümesinin alt kümelerinin sayısı \( 16 = 2^4 \) ise \( s(L) = 4 \) olur.
\( K \cap L \) kümesinin eleman sayısının en çok olması için daha çok elemanlı olan \( K \) kümesi \( L \) kümesini kapsamalı, yani \( L \) kümesi iki kümenin kesişim kümesine eşit olmalıdır.
\( L \subset K \)
\( L = K \cap L \)
Buna göre \( s(K \cap L) = s(L) = 4 \) olur.
Yukarıdaki Venn şemasında,
2 ile tam bölünen sayılar kümesi \( A \),
3 ile tam bölünen sayılar kümesi \( B \),
24 ile tam bölünen sayılar kümesi \( C \)
olduğuna göre, aşağıdaki sayılardan hangileri taralı bölgenin bir elemanıdır?
0, 48, 60, 72, 84
Taralı bölgenin elemanı hem 2 hem de 3 ile (dolayısıyla 6 ile) tam bölünmeli, ancak 24 ile tam bölünmemelidir.
0, 48 ve 72 sayıları 6 ile tam bölünürler, ancak 24 ile de tam bölündüklerinden \( C \) kümesinin birer elemanıdır.
60 ve 84 sayıları 6 ile tam bölünürler, 24 ile tam bölünmedikleri için taralı bölgenin birer elemanıdır.
Yukarıdaki Venn şemasında,
\( 3 \)'e tam bölünen sayılar kümesi \( A \),
\( 5 \)'e tam bölünen sayılar kümesi \( B \),
\( 10 \)'a tam bölünen sayılar kümesi \( C \)
olduğuna göre, aşağıdaki sayılardan hangileri taralı bölgenin bir elemanıdır?
0, 5, 10, 15, 20, 30, 45, 135
Verilen şekildeki taralı bölgenin elemanları 3'e ve 5'e (yani 15'e) tam bölünen, ama 10'a tam bölünmeyen sayıları içerir.
Verilen sayılar içinde 15, 45 ve 135 sayıları bu koşulları sağlar. 0 ve 30 sayıları 15'e tam bölünseler de 10'a da tam bölündükleri için taralı bölgenin elemanı değildir.
\( k \in \mathbb{Z} \) olmak üzere,
\( A = \{ 3, 9, 27, k \} \)
kümesinin her elemanı 3 ile çarpılarak dört elemanlı yeni bir küme elde ediliyor.
Bu iki kümenin kesişim kümesi 3 elemanlı olduğuna göre, \( k \)'nın alabileceği değerler toplamı kaçtır?
Oluşturalacak yeni küme \( B \) kümesi olsun.
\( B = \{9, 27, 81, 3k\} \)
k'lı elemanlar dışında iki kümenin (9 ve 27 olmak üzere) ikişer elemanı ortaktır. Üçüncü elemanın da ortak olması iki şekilde sağlanabilir.
\( A \) kümesinin "3" elemanı \( B \) kümesinin "3k" elemanına eşit olur.
\( 3 = 3k \Longrightarrow k = 1 \)
\( A \) kümesinin "k" elemanı \( B \) kümesinin "81" elemanına eşit olur.
\( k = 81 \)
Buna göre \( k \)'nın alabileceği değerler toplamı \( 81 + 1 = 82 \) olur.