Küme Problemleri
Küme problemlerinde, küme işlem kuralları kullanılarak farklı sayıda kümenin eleman sayıları bulunmaya çalışılır. Bu tip problemlerde Venn şeması sıklıkla kullanılır.
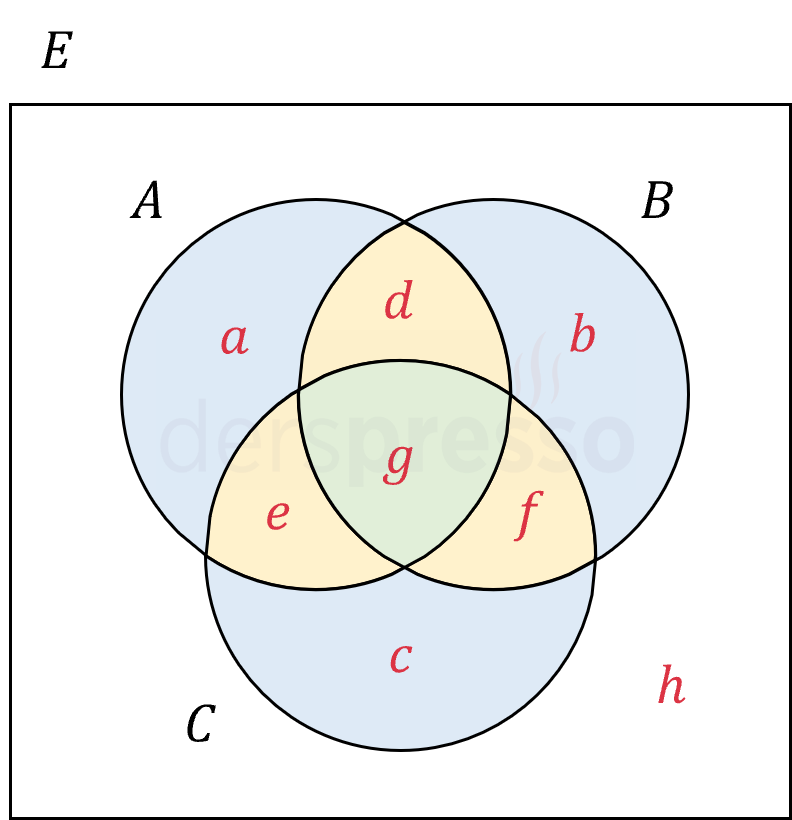
Aşağıda küme problemlerinin çözümüne temel teşkil etmesi açısından örnek bir küme seti ve farklı alt küme durumları verilmiştir. Bu örnekte bir sınıftaki öğrencilerin Almanca (\( A \)), İngilizce (\( I \)) ve Fransızca (\( F \)) konuşma dağılımları Venn şeması şeklinde verilmiştir. Şekildeki harfler ilgili bölgelerdeki kişi sayılarını göstermektedir.

| Sözel Anlatım | Sayısal Gösterim | Küme Gösterimi |
|---|---|---|
| Tüm kişiler | \( a + b + \ldots + h \) | \( E \) |
| Sadece bir dil bilenler | \( a + c + g \) | \( [A - (I \cup F)] \cup [I - (A \cup F)] \cup [F - (A \cup I)] \) |
| Sadece iki dil bilenler | \( b + d + f \) | \( [(A \cap I) \cup (A \cap F) \cup (I \cap F)] - (A \cap I \cap F) \) |
| En az bir dil bilenler | \( a + b + \ldots + g \) | \( A \cup I \cup F \) |
| En az iki dil bilenler | \( b + d + e + f \) | \( (A \cap I) \cup (A \cap F) \cup (I \cap F) \) |
| En çok bir dil bilenler | \( a + c + g + h \) | \( E - [(A \cap I) \cup (A \cap F) \cup (I \cap F)] \) |
| En çok iki dil bilenler | \( a + b + c + d + f + g + h \) | \( E - (A \cap I \cap F) \) |
| Hiçbir dil bilmeyenler | \( h \) | \( E - (A \cup I \cup F) \) |
| Almanca bilen, ama Fransızca bilmeyenler | \( a + b \) | \( A - F \) |
| İngilizce veya Fransızca bilen, ama Almanca bilmeyenler | \( c + f + g \) | \( (I \cup F) - A \) |
| İngilizce ve Fransızca bilen, ama Almanca bilmeyenler | \( f \) | \( (I \cap F) - A \) |
35 kişilik bir sınıfta kalemi veya silgisi olan 16 kişi, silgisi olmayan 22 kişi, kalemi olmayan 24 kişi vardır?
Buna göre, hem kalemi hem de silgisi olan kaç kişi vardır?
Çözümü GösterKalemi olanların kümesine \( K \), silgisi olanların kümesine \( S \), evrensel kümeye \( E \) diyelim.
Bu kümeleri Venn şeması ile gösterelim ve her bölgenin eleman sayısını bir değişken olarak işaretleyelim.

Soruda hem kalemi hem de silgisi olanların sayısı, yani \( b \) değeri isteniyor.
Sınıf mevcudu:
\( a + b + c + d = 35 \)
Kalemi veya silgisi olanların sayısı:
\( a + b + c = 16 \)
Silgisi olmayanların sayısı:
\( a + d = 22 \)
Kalemi olmayanların sayısı:
\( c + d = 24 \)
Bu denklemlerden oluşan denklem sistemini çözdüğümüzde aşağıdaki değerleri buluruz.
\( a = 3, \quad b = 8, \quad c = 5, \quad d = 19 \)
Buna göre, hem kalemi hem de silgisi olan \( b = 8 \) kişi vardır.
Almanca ve Fransızca dillerinden en az birini bilenlerin oluşturduğu 48 kişilik toplulukta, Almanca bilmeyenlerin sayısı her iki dili bilenlerin sayısının iki katı, Fransızca bilenlerin sayısı Almanca bilenlerin \( \frac{3}{2} \) katıdır.
Buna göre bu toplulukta Almanca bilen kaç kişi vardır?
Çözümü GösterAlmanca bilenlerin kümesine \( A \), Fransızca bilenlerin kümesine \( F \) diyelim.
Bu kümeleri Venn şeması ile gösterelim ve her bölgenin eleman sayısını bir değişken olarak işaretleyelim.

Soruda Almanca bilenlerin sayısı, yani \( a + c \) toplamı isteniyor.
Soruda verilen bilgileri değişkenler cinsinden ifade edelim.
İki dilden en az birini bilenlerin sayısı:
\( a + b + c = 48 \)
Almanca bilmeyenlerin sayısı her iki dili bilenlerin sayısının iki katıdır.
\( b = 2c \)
Fransızca bilenlerin sayısı Almanca bilenlerin \( \frac{3}{2} \) katıdır.
\( b + c = \frac{3}{2}(a + c) \)
\( 2b + 2c = 3a + 3c \)
\( 2b = 3a + c \)
Birinci denklemde \( b = 2c \) koyalım.
\( a + 2c + c = 48 \)
\( a + 3c = 48 \)
Üçüncü denklemde \( b = 2c \) koyalım.
\( 2(2c) = 3a + c \)
\( a = c \)
Bu iki denklemi ortak çözelim.
\( a + 3a = 48 \)
\( a = c = 12 \)
\( a + c = 24 \)
Buna göre, toplulukta Almanca bilen 24 kişi vardır.
Bir sınıfta İngilizce ve Almanca dillerinden en az birini bilen 32, en çok birini bilen 28 öğrenci vardır.
Bu sınıfta Almanca bilmeyen 15 öğrenci bulunduğuna göre, İngilizce bilen kaç öğrenci vardır?
Çözümü Gösterİngilizce bilen öğrenciler kümesine \( I \), Almanca bilen öğrenciler kümesine \( A \) diyelim.
Bu kümeleri Venn şeması ile gösterelim ve her bölgenin eleman sayısını bir değişken olarak işaretleyelim.

Soruda İngilizce bilen öğrenci sayısı, yani \( a + b \) toplamı isteniyor.
Soruda verilen bilgileri değişkenler cinsinden ifade edelim.
En az bir dil bilenlerin sayısı:
\( a + b + c = 32 \)
En çok bir dil bilenlerin sayısı:
\( a + c + d = 28 \)
Almanca bilmeyenlerin sayısı:
\( a + d = 15 \)
Yukarıdaki ikinci eşitlikten üçüncü eşitliği taraf tarafa çıkaralım.
\( a + c + d - (a + d)= 28 - 15 \)
\( c = 13 \)
Bu değeri birinci eşitlikte yerine koyalım.
\( a + b + 13 = 32 \)
\( a + b = 19 \)
Buna göre, sınıfta İngilizce bilen 19 öğrenci vardır.
40 kişilik bir sınıfta matematik dersinde 21 öğrenci, kimya dersinde 24 öğrenci başarılı olmuştur.
Her iki derste başarısız olan 6 öğrenci olduğuna göre, sadece kimya dersinde başarılı olan kaç öğrenci vardır?
Çözümü GösterMatematik dersinde başarılı olan öğrencilerin kümesine \( M \), kimya dersinde başarılı olan öğrencilerin kümesine \( K \) diyelim.
Bu kümeleri Venn şeması ile gösterelim ve her bölgenin eleman sayısını bir değişken olarak işaretleyelim.

Soruda sadece kimya dersinde başarılı olan öğrenci sayısı, yani \( c \) değeri isteniyor.
Soruda verilen bilgileri değişkenler cinsinden ifade edelim.
Matematik dersinde başarılı olanlar:
\( a + b = 21 \)
Kimya dersinde başarılı olanlar:
\( b + c = 24 \)
Her iki derste de başarısız olanlar:
\( d = 6 \)
Sınıf mevcudu:
\( a + b + c + d = 40 \)
Yukarıdaki ilk 3 eşitliği taraf tarafa toplayalım.
\( (a + b) + (b + c) + d = 21 + 24 + 6 \)
\( a + 2b + c + d = 51 \)
Bu eşitlikten sınıf mevcudu eşitliğini taraf tarafa çıkaralım.
\( b = 51 - 40 = 11 \)
\( b \) değerini kimya dersi eşitliğinde yerine koyalım.
\( b + c = 11 + c = 24 \)
\( c = 13 \)
Buna göre, sınıfta sadece kimya dersinde başarılı olan 13 öğrenci vardır.
Bir turist kafilesi İngilizce, Almanca ve Fransızca dillerinden en az birini bilenlerden oluşmaktadır. İngilizce bilenler, diğer iki dili de bilmemektedir.
Grupta İngilizce bilen 5 kişi, sadece Fransızca bilen 2 kişi, Fransızca bilen 6 kişi olduğuna ve Almanca bilenlerin sayısı Fransızca bilenlerin sayısının 2 katı olduğuna göre, sadece Almanca bilen kaç kişi vardır?
Çözümü Gösterİngilizce bilenlerin kümesine \( I \), Almanca bilenlerin kümesine \( A \), Fransızca bilenlerin kümesine \( F \) diyelim.
Bu kümeleri Venn şeması ile gösterelim ve her bölgenin eleman sayısını bir değişken olarak işaretleyelim.
İngilizce bilenler diğer iki dili bilmediği için, \( I \) kümesi diğer iki kümeden ayrıktır.

Soruda sadece Almanca bilen kişi sayısı, yani \( y \) değeri isteniyor.
İngilizce bilen kişi sayısı:
\( x = 5 \)
Sadece Fransızca bilen kişi sayısı:
\( m = 2 \)
Fransızca bilen kişi sayısı:
\( z + m = 6 \)
\( z = 4 \)
Almanca bilenler Fransızca bilenlerin sayısının 2 katıdır.
\( y + z = 2(z + m) \)
\( y + 4 = 2(6) \)
\( y = 8 \)
Buna göre, grupta sadece Almanca bilen 8 kişi vardır.
36 kişilik bir spor kulübünde herkes futbol oynarken 10 kişi basketbol ve voleybol da oynamaktadır.
Sadece futbol oynayanların sayısı 12 kişi olduğuna göre, bu sporlardan yalnız ikisini yapanların sayısı kaçtır?
Çözümü GösterFutbol oynayanların kümesine \( F \), basketbol oynayanların kümesine \( B \), voleybol oynayanların kümesine \( V \) diyelim.
Bu kümeleri Venn şeması ile gösterelim ve her bölgenin eleman sayısını bir değişken olarak işaretleyelim.
Tüm oyuncular futbol oynadığı için \( F \) kümesi diğer iki kümeyi kapsar.

Soruda sporlardan yalnız ikisini yapanların sayısı, yani \( a + c \) toplamı isteniyor.
Soruda verilen bilgileri değişkenler cinsinden ifade edelim.
Kulüpteki toplam kişi sayısı 36'dır.
\( a + b + c + d = 36 \)
Üç sporu da yapanların sayısı 10'dur.
\( b = 10 \)
Sadece futbol oynayanların sayısı 12'dir.
\( d = 12 \)
\( b \) ve \( d \) değerlerini toplam kişi sayısı eşitliğinde yerine koyalım.
\( a + b + c + d = 36 \)
\( a + 10 + c + 12 = 36 \)
\( a + c = 14 \)
Buna göre, kulüpte yalnız iki sporu yapan 14 kişi vardır.
Bir grup öğrencinin \( \frac{4}{7} \)'si biyoloji dersi, \( \frac{3}{5} \)'i kimya dersi alıyor. Bu grupta her iki dersi de alan öğrenci sayısı en az kaç olabilir?
Çözümü GösterBiyoloji alan öğrencilerin kümesine \( B \), kimya alan öğrencilerin kümesine \( K \) diyelim.
Biyoloji, kimya ve her iki dersi alan öğrenci sayıları tam sayı olmalıdır. Bunun sağlanması için gruptaki toplam öğrenci sayısı verilen kesirlerdeki paydaların, yani 7'nin ve 5'in bir ortak katı olmalıdır.
7'nin ve 5'in en küçük ortak katı 35'tir.
\( EKOK(7, 5) = 35 \)
Her iki dersi de alan öğrenci sayısının en küçük değeri istendiği için gruptaki öğrenci sayısını 35 olarak almalıyız.
Bu durumda biyoloji alan öğrenci sayısı \( 35 \cdot \frac{4}{7} = 20 \), kimya alan öğrenci sayısı \( 35 \cdot \frac{3}{5} = 21 \) olur.
İki kümenin birleşim kümesinin eleman sayısı formülünü yazalım.
Tüm öğrencilerin kümesi \( B \cup K \), iki dersi de alan öğrencilerin kümesi \( B \cap K \) olur.
\( s(B \cup K) = s(B) + s(K) - s(B \cap K) \)
\( 35 = 20 + 21 - s(B \cap K) \)
\( s(B \cap K) = 20 + 21 - 35 = 6 \)
Buna göre, her iki dersi de alan öğrenci sayısı en az 6 olabilir.
Herkesin Türkçe bildiği 32 kişilik bir kafilede, İngilizce bilenler Almanca bilmemektedir. Bu kafilede bu üç dilden yanlız birini bilen 10 kişi vardır.
Türkçe ve Almanca bilen 8 kişi olduğuna göre, Türkçe ve İngilizce bilen kaç kişi vardır?
Çözümü GösterTürkçe bilenlerin kümesine \( T \), İngilizce bilenlerin kümesine \( I \), Almanca bilenlerin kümesine \( A \) diyelim.
Bu kümeleri Venn şeması ile gösterelim ve her bölgenin eleman sayısını bir değişken olarak işaretleyelim.
Herkes Türkçe bildiği için \( T \) kümesi evrensel kümeyi temsil eder ve diğer iki kümeyi kapsar.
İngilizce bilenler Almanca bilmedikleri için bu iki küme ayrık kümelerdir.

Soruda Türkçe ve İngilizce bilen kişi sayısı, yani \( a \) değeri isteniyor.
Soruda verilen bilgileri değişkenler cinsinden ifade edelim.
Kafiledeki kişi sayısı:
\( a + b + c = 32 \)
Yalnız bir dil bilen kişi sayısı:
\( c = 10 \)
Türkçe ve Almanca bilen kişi sayısı:
\( b = 8 \)
Bu değerleri toplam kişi sayısı formülünde yerine koyalım.
\( a + 8 + 10 = 32 \)
\( a = 14 \)
Buna göre, kafilede Türkçe ve İngilizce bilen 14 kişi vardır.
\( A \) kümesinin elemanlarının %60'ı \( B \) kümesinin elemanı değildir, \( B \) kümesinin elemanlarının ise %50'si \( A \) kümesinin elemanı değildir.
\( s(A \cup B) = 56 \) olduğuna göre, \( s(B \cap A') \) kaçtır?
Çözümü Göster\( A \) kümesinin eleman sayısına \( 10a \) diyelim.
\( A \) kümesinin elemanlarının %60'ı \( B \) kümesinin elemanı değilse \( s(A - B) = 6a \) ve \( s(A \cap B) = 4a \) olur.
\( B \) kümesinin elemanlarının ise %50'si \( A \) kümesinin elemanı değilse \( s(B - A) = s(A \cap B) = 4a \) olur.
Verileri Venn şeması ile gösterelim.

\( s(A \cup B) = 14a = 56 \)
\( a = 4 \)
Aşağıdaki küme özdeşliğini kullanalım.
\( B \cap A' = B - A \)
\( s(B \cap A') = s(B - A) \)
\( = 4a = 16 \) bulunur.
\( A = \{ x \mid x \lt 80, x = 4k, k \in \mathbb{N} \} \)
\( B = \{ x \mid x \le 60, x = 3k, k \in \mathbb{N} \} \)
olduğuna göre, \( A \cap B \) kümesinin eleman sayısı kaçtır?
Çözümü Göster\( A \) kümesi 80'den küçük olan ve 4'e tam bölünen doğal sayılardan oluşur.
\( B \) kümesi 60'tan küçük ya da eşit olan ve 3'e tam bölünen doğal sayılardan oluşur.
İki kümenin kesişimi ise 60'tan küçük ya da eşit olan ve hem 3'e hem de 4'e, yani 12'ye tam bölünen doğal sayılardan oluşur.
\( A \cap B = \{ x \mid x = 12k, x \le 60, k \in \mathbb{N} \} \)
\( = \{0, 12, 24, 36, 48, 60\} \)
\( s(A \cap B) = 6 \) bulunur.
\( A = \{ x \mid x \lt 100, x = 2n, n \in \mathbb{Z^+} \} \)
\( B = \{ x \mid x \le 150, x = 3n, n \in \mathbb{Z^+} \} \)
olduğuna göre, \( s(A \cup B) \) kaçtır?
Çözümü Göster\( A \) kümesi 100'den küçük olan ve 2'ye tam bölünen pozitif tam sayılardan oluşur.
\( [1, 100) \) aralığındaki 99 tam sayının 49'u 2'ye tam bölünür.
\( A = \{ 2, 4, 6, 8, \ldots 98 \} \)
\( s(A) = 49 \)
\( B \) kümesi 150'den küçük ya da eşit olan ve 3'e tam bölünen pozitif tam sayılardan oluşur.
\( [1, 150] \) aralığındaki 150 tam sayının 50'si 3'e tam bölünür.
\( B = \{ 3, 6, 9, 12, \ldots 150 \} \)
\( s(B) = 50 \)
Bu iki kümenin kesişimi \( [1, 100) \) aralığındaki hem 2'ye hem de 3'e, yani 6'ya tam bölünen sayılardan oluşur.
\( [1, 100) \) aralığındaki 99 tam sayının 16'sı 6'ya tam bölünür.
\( A \cap B = \{ 6, 12, 18, 24, \ldots, 96 \} \)
\( s(A \cap B) = 16 \)
İki kümenin birleşiminin eleman sayısı formülünü kullanalım.
\( s(A \cup B) = s(A) + s(B) - s(A \cap B) \)
\( = 49 + 50 - 16 = 83 \) bulunur.
Bir sınıfta tarih ve coğrafya derslerinin en az birinden geçen 36, en çok birinden geçen 21, yalnız birinden geçen 13 kişi vardır.
Buna göre bu sınıfta kaç kişi vardır?
Çözümü GösterTarih dersinden geçenlerin kümesine \( T \), coğrafya dersinden geçenlerin kümesine \( C \), evrensel kümeye \( E \) diyelim.
Bu kümeleri Venn şeması ile gösterelim ve her bölgenin eleman sayısını bir değişken olarak işaretleyelim.

Soruda sınıftaki toplam kişi sayısı, yani \( a + b + c + d \) toplamı isteniyor.
En az bir dersten geçenlerin sayısı:
\( b + c + d = 36 \)
En çok bir dersten geçenlerin sayısı:
\( a + b + d = 21 \)
Yalnız bir dersten geçenlerin sayısı:
\( b + d = 13 \)
Bu denklemlerden oluşan denklem sistemini çözdüğümüzde aşağıdaki değerleri buluruz.
\( a = 8, \quad c = 23 \)
Bu değerleri kullanarak sınıf mevcudunu bulalım.
\( a + c + \underbrace{b + d}_\text{13} = 8 + 23 + 13 \)
\( = 44 \) bulunur.
Ayşe Hanım evine misafirliğe gelecek 30 kişi için 30'ar kişilik kola, portakal suyu ve elma suyu hazırlamıştır. Gelen misafirlerin tümü bir ya da üç çeşit içecekten birer bardak içmiştir.
Misafirler gittiğinde 8 kişilik kola, 10 kişilik portakal suyu ve 14 kişilik elma suyu arttığına göre, üç çeşit içecek içen kaç misafir vardır?
Çözümü GösterKola içenlerin kümesine \( K \), portakal suyu içenlerin kümesine \( P \), elma suyu içenlerin kümesine \( E \) diyelim.
Misafirler \( 30 - 8 = 22 \) bardak kola, \( 30 - 10 = 20 \) bardak portakal suyu, \( 30 - 14 = 16 \) bardak elma suyu içmiştir.
\( K \), \( P \) ve \( E \) kümelerini Venn şeması ile gösterelim ve her üç içecekten de içenlerin sayısına \( x \) diyelim.
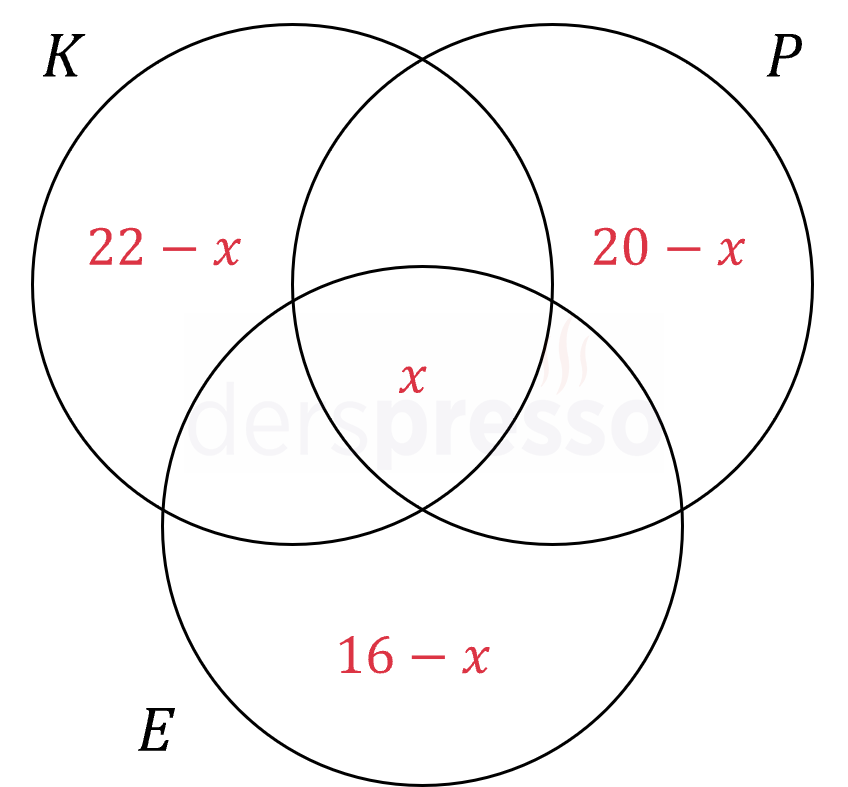
Buna göre sadece kola içenlerin sayısı \( 22 - x \), sadece portakal suyu içenlerin sayısı \( 20 - x \), sadece elma suyu içenlerin sayısı ise \( 16 - x \) olur.
Misafirlerin tamamı bir ya da üç içecek içtiğine göre, kümelerin ikili kesişimleri boş küme olur.
Venn şemasındaki sayıların toplamı toplamı misafir sayısını verir.
\( (22 - x) + (20 - x) + (16 - x) + x = 30 \)
\( 58 - 2x = 30 \)
\( x = 14 \) bulunur.
Masa tenisi, basketbol ve yüzme kurslarından en az birine katılanlardan oluşan 50 kişilik bir toplulukta yüzme kursuna katılanların başka kurslara katılmadığı biliniyor.
Bu toplulukta masa tenisi kursuna katılmayan 21 kişi, basketbol kursuna katılmayan 23 kişi ve yalnız bir kursa katılan 30 kişi olduğuna göre, basketbol kursuna katılanların sayısı yüzme kursuna katılanların sayısından kaç fazladır?
Çözümü GösterMasa tenisi kursuna katılanların kümesine \( M \), basketbol kursuna katılanların kümesine \( B \), yüzme kursuna katılanların kümesine \( Y \) diyelim.
Bu kümeleri Venn şeması ile gösterelim ve her bölgenin eleman sayısını bir değişken olarak işaretleyelim.
Yüzme kursuna katılanlar başka kursa katılmadıkları için \( Y \) kümesi diğer iki kümeden ayrık bir kümedir.

Soruda basketbol kursuna katılanların sayısının yüzme kursuna katılanların sayısından kaç fazla olduğu, yani \( (c + d) - a \) farkı isteniyor.
Soruda verilen bilgileri değişkenler cinsinden ifade edelim.
Topluluk mevcudu:
\( a + b + c + d = 50 \)
Masa tenisi kursuna katılmayan kişi sayısı:
\( a + d = 21 \)
Basketbol kursuna katılmayan kişi sayısı:
\( a + b = 23 \)
Yalnız bir kursa katılan kişi sayısı:
\( a + b + d = 30 \)
Bu denklemlerden oluşan denklem sistemini çözdüğümüzde aşağıdaki değerleri buluruz.
\( a = 14, \quad b = 9, \quad c = 20, \quad d = 7 \)
Buna göre, basketbol kursuna katılanların sayısı yüzme kursuna katılanların sayısından \( (c + d) - a = (20 + 7) - 14 = 13 \) fazladır.
Bir müzik topluluğunda üyelerin yüzde 55'i klasik müzik çalmakta, diğerleri çalmamaktadır. Klasik müzik çalanların yüzde 20'si, çalmayanların yüzde 60'ı klasik müzik sevmediğini söylemektedir.
Klasik müzik sevenler içinde klasik müzik çalmayanların oranı kaçtır?
Çözümü GösterMüzik topluluğundaki toplam üye sayısına 100 kişi diyelim.
Bu durumda klasik müzik çalan 55, çalmayan 45 üye bulunur.
Klasik müzik çalan 55 üye içinde \( 55 \cdot \frac{20}{100} = 11 \) üye klasik müzik sevmemekte, kalan 44 üye sevmektedir.
Klasik müzik çalmayan 45 üye içinde \( 45 \cdot \frac{60}{100} = 27 \) üye klasik müzik sevmemekte, kalan 18 üye sevmektedir.
Buna göre klasik müzik seven toplam \( 44 + 18 = 62 \) üye vardır.
Klasik müzik sevenler içinde klasik müzik çalmayanların oranı:
\( \dfrac{\text{Sevip çalmayanlar}}{\text{Toplam sevenler}} = \dfrac{18}{62} = \dfrac{9}{31} \) bulunur.
Eyüp pencereden okul bahçesinde oynayan çocukları seyrederken çocukların yarısının atkı taktığına, atkı takmayanların sayısının bere takmayanların sayısının iki katı olduğuna, çocukların taktığı atkı ve berelerin toplamının 45 adet olduğuna dikkat ediyor.
Buna göre bahçede oynayan çocuk sayısı kaçtır?
Çözümü GösterAtkı takan çocukların kümesine \( A \), bere takan çocukların kümesine \( B \) diyelim.

Çocukların yarısı atkı takıyor.
\( a + b = \dfrac{a + b + c + d}{2} \)
\( a + b = c + d \)
Atkı takmayanların sayısı bere takmayanların sayısının iki katıdır.
\( c + d = 2(a + d) \)
\( 2a - c + d = 0 \)
Çocukların taktığı atkı ve berelerin toplamı 45 adettir.
\( a + b \) çocuk atkı, \( b + c \) çocuk bere takıyor.
\( a + b + b + c = 45 \)
\( a + 2b + c = 45 \)
Üçüncü denklemin taraflarını iki ile çarpalım.
\( 2a + 4b + 2c = 90 \)
Bu denklemi ikinci denklem ile taraf tarafa toplayalım.
\( (2a - c + d) + (2a + 4b + 2c) = 0 + 90 \)
\( 4a + 4b + c + d = 90 \)
\( a + b = c + d \) eşitliğini kullanalım.
\( 4a + 4b + a + b = 90 \)
\( 5a + 5b = 90 \)
\( a + b = 18 \)
\( a + b = c + d \) eşitliğini kullanalım.
\( a + b = c + d = 18 \)
Tüm çocukların sayısı \( a + b + c + d \) olur.
\( a + b + c + d = 18 + 18 = 36 \) bulunur.
Bir üniversitedeki fotoğrafçılık ve dağcılık kulüpleriyle ilgili aşağıdakiler bilinmektedir.
- Fotoğrafçılık kulübüne üye olmayan kişiler, dağcılık kulübüne üye olmayan kişilerin bir alt kümesidir.
- Fotoğrafçılık kulübüne üye olmayan kişi sayısı 28'dir.
- Dağcılık kulübüne üye olmayan kişi sayısı 42'dir.
- Her iki kulübe de üye olmayan kişiler dışındakilerin sayısı 23'tür.
Buna göre fotoğrafçılık kulübüne üye olan kişi sayısı ile dağcılık kulübüne üye olan kişi sayısı toplamı kaçtır?
Çözümü GösterFotoğrafçılık kulübüne üye olan kişilerin kümesine \( A \), dağcılık kulübüne üye olan kişilerin kümesine \( B \) diyelim.
Fotoğrafçılık kulübüne üye olmayan kişiler, dağcılık kulübüne üye olmayan kişilerin bir alt kümesidir.
\( A' \subseteq B' \)
\( B \) kümesinin tümleyeni \( A \) kümesinin tümleyenini kapsıyorsa \( A \) kümesi \( B \) kümesini kapsar.
\( B \subseteq A \)
Bu kümeleri bir Venn şemasında gösterelim.

Fotoğrafçılık kulübüne üye olmayan kişi sayısı 28'dir.
\( s(A') = z = 28 \)
Dağcılık kulübüne üye olmayan kişi sayısı 42'dir.
\( s(B') = y + z = 42 \)
\( y = 14 \)
\( s[(A' \cap B')'] = 23 \)
De Morgan kuralını uygulayalım.
\( s(A \cup B) = x + y = 23 \)
\( x = 9 \)
Her iki kulübün üye sayılarının toplamını bulalım.
\( s(A) + s(B) = (9 + 14) + 9 = 32 \) bulunur.
Aslı ve Timur, dokuz rakamdan oluşan öğrenci numaralarının bazı basamaklarını hatırlamıyorlar.
Aslı: 0*12*9*32
Timur: 26**1*715
Aslı'nın öğrenci numarasındaki rakamlar \( A \) kümesinin elemanlarını, Timur'un öğrenci numarasındaki rakamlar \( T \) kümesinin elemanlarını oluşturmaktadır.
\( s(A) = 8, \quad s(T) = 6 \)
\( A \cap T = \{ 1, 2, 5, 8 \} \) olduğuna göre, Aslı'nın öğrenci numarasında bulunmayan rakamların toplamı kaçtır?
Çözümü Göster\( A \) ve \( T \) kümelerinin bilinen elemanlarını yazalım.
\( A = \{ 0, 1, 2, 3, 9, \ldots \} \)
\( T = \{ 1, 2, 5, 6, 7, \ldots \} \)
\( A \cap T = \{ 1, 2, 5, 8 \} \) olarak veriliyor. Buna göre \( A \) kümesi \( \{ 5, 8 \} \), \( T \) kümesi \( \{ 8 \} \) elemanını da içerir.
\( A = \{ 0, 1, 2, 3, 5, 8, 9, \ldots \} \)
\( T = \{ 1, 2, 5, 6, 7, 8, \ldots \} \)
\( s(T) = 6 \) olduğu için \( T \) kümesinin tüm elemanları biliniyor.
\( T = \{ 1, 2, 5, 6, 7, 8 \} \)
\( s(A) = 8 \) olduğu için \( A \) kümesinin bilinmeyen bir elemanı daha vardır.
Öğrenci numaraları rakamlardan oluştuğu için \( A \) kümesinde eksik olan üç rakam 4, 6 ve 7'dir.
6 ve 7 elemanları \( B \) kümesinde bulunduğu için \( A \) kümesinde bulunamaz, aksi takdirde bu elemanlar \( A \cap T \) kümesinin de elemanı olurdu.
Buna göre \( A \) kümesinin eksik olan elemanı 4'tür.
\( A = \{ 0, 1, 2, 3, 4, 5, 8, 9 \} \)
Aslı'nın öğrenci numarasında bulunmayan rakamların toplamı \( 6 + 7 = 13 \) olarak bulunur.
Bir film yapım ekibindeki çalışanlar ihtiyaca göre kamera önünde veya kamera arkasında görev alabilmektedir.
Kamera önünde çalışanların yüzdesi %48 ile %53 arasında, kamera arkasında çalışanların yüzdesi %65 ile %68 arasında, bu iki grupta da çalışmayan ve setteki diğer işlerde görev alanların yüzdesi ise %1 ile %3 arasında değişmektedir.
Buna göre hem kamera önünde hem de kamera arkasında görev alanların yüzdesi hangi aralıkta olabilir?
Çözümü GösterKamera önünde çalışanların kümesine \( A \), kamera arkasında çalışanların kümesine \( B \) diyelim.
Her iki grupta da görev alanların yüzdesine \( x \) diyelim.
Ekipteki toplam kişi sayısı evrensel kümeyi temsil ettiği için %100 değerine karşılık gelir.
Bu kümeleri bir Venn şemasında gösterelim ve \( x \) değerini kullanarak her bölgenin en küçük ve en büyük değerlerini ayrı ayrı gösterelim.
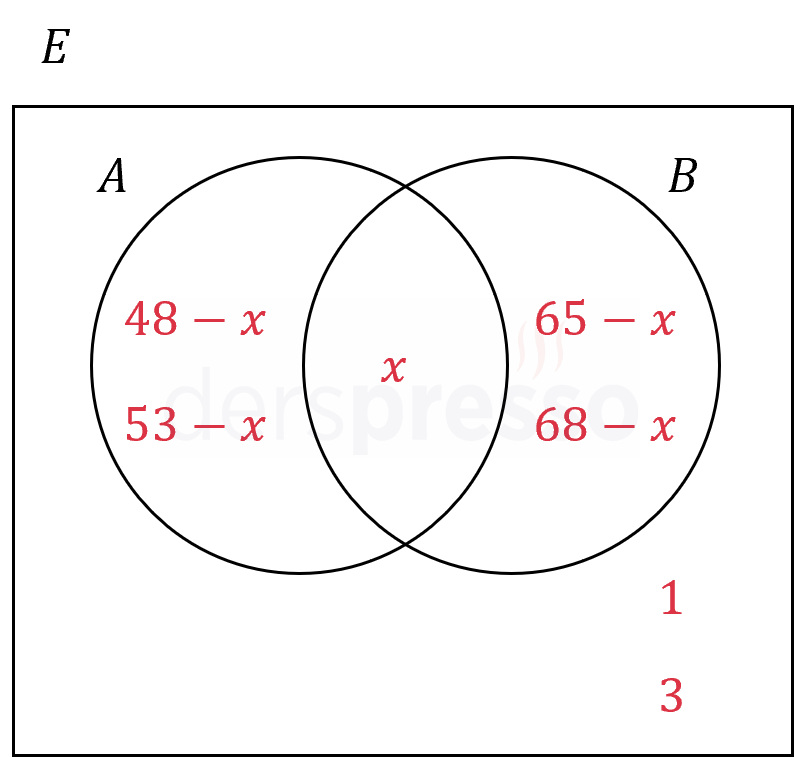
\( x \) değer aralığını, her bir bölge için verilen aralığın en küçük ve en büyük değerini ayrı ayrı kullanarak bulmalıyız.
Önce her grup için alt sınır değerlerini (%48, %65, %1) dikkate alalım.
\( (48 - x) + x + (65 - x) + 1 = 100 \)
\( x = 14 \)
Şimdi her grup için üst sınır değerlerini (%53, %68, %3) dikkate alalım.
\( (53 - x) + x + (68 - x) + 3 = 100 \)
\( x = 24 \)
Buna göre her iki grupta da görev alanların yüzdesi için aralık aşağıdaki gibi olur.
\( \%14 \le x \le \%24 \)
Bir okuldaki kimya laboratuvarında deney yapan iki ayrı gruptan birincisinde 25, ikincinde 23 öğrenci vardır.
Kimya öğretmeni birinci gruptaki kız öğrencilerinin tamamını ikinci gruba, ikinci gruptaki erkek öğrencilerin yarısını birinci gruba alıyor. Bu değişiklik ile toplam 23 öğrenci grup değiştiriyor ve ikinci gruptaki öğrenci sayısı birinci gruptaki öğrenci sayısının iki katı oluyor.
Buna göre değişiklikten önce birinci gruptaki kız öğrenci sayısı kaçtır?
Çözümü GösterDeğişiklik öncesinde her iki gruptaki kız ve erkek öğrenci sayılarını gösteren bir tablo oluşturalım.
Birinci gruptaki erkek öğrencilerin sayısına \( x \) diyelim. Bu durumda birinci gruptaki kız öğrencilerin sayısı \( 25 - x \) olur.
İkinci gruptaki erkek öğrencilerin sayısına \( 2y \) diyelim. Bu durumda ikinci gruptaki kız öğrencilerin sayısı \( 23 - 2y \) olur.

Değişiklik sonrasında her iki gruptaki kız ve erkek öğrenci sayılarını gösteren bir tablo oluşturalım.
Birinci grupta kız öğrenci kalmamıştır.
İkinci gruptaki erkek öğrencilerin yarısı (\( y \)) birinci gruba geçmiştür.
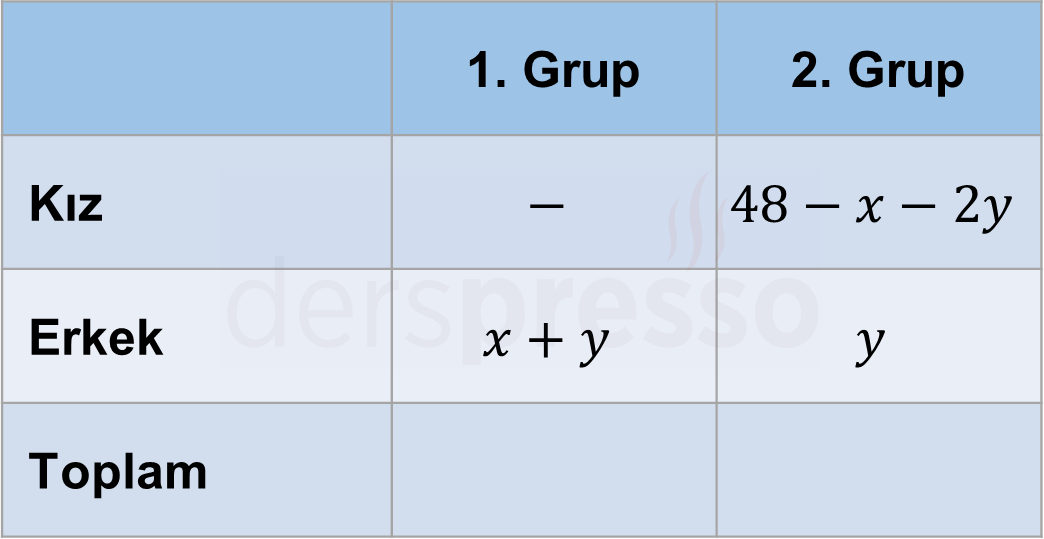
Bu değişiklik sonucunda toplam 23 öğrenci grup değiştirmiştir.
\( 25 - x + y = 23 \)
Bu değişiklik sonucunda ikinci gruptaki öğrenci sayısı birinci gruptaki öğrenci sayısının 2 katı oluyor.
\( 48 - x - 2y + y = 2(x + y) \)
\( 48 - x - y = 2x + 2y \)
\( x + y = 16 \)
İki denklemi taraf tarafa toplayalım.
\( 25 + 2y = 23 + 16 \)
\( y = 7 \)
\( x = 9 \)
Buna göre değişiklikten önce birinci gruptaki kız öğrenci sayısı \( 25 - x = 16 \) olarak bulunur.
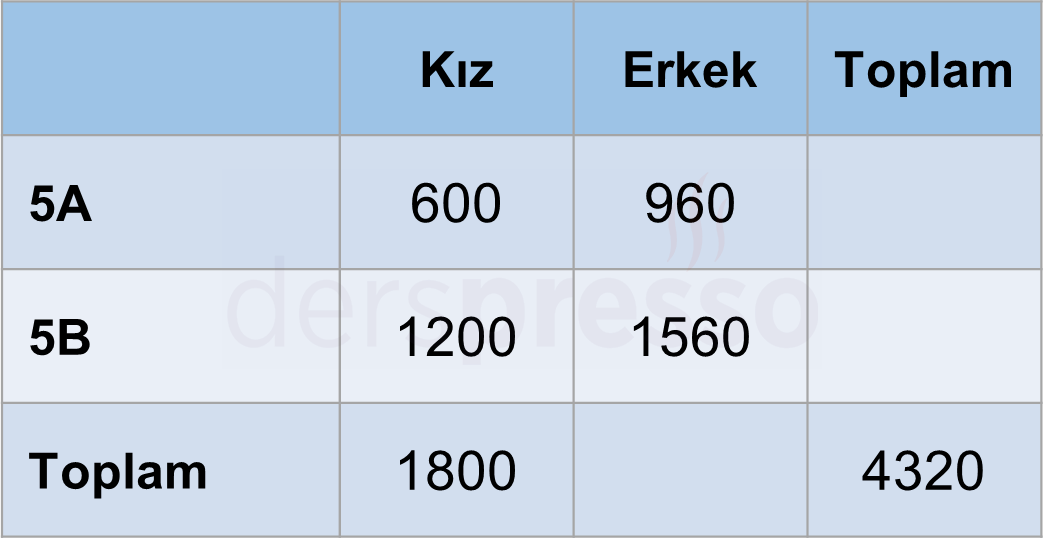
Bir okulda iki şubenin katıldığı bir sınavla ilgili aşağıdakiler biliniyor.
- İki şubeden sınava 45'er öğrenci katılmıştır.
- İki şubenin sınavdaki not ortalaması 48'dir.
- 5A şubesindeki kızların not ortalaması 40'tır.
- Tüm kızların not ortalaması 45'tir.
- 5A şubesindeki erkeklerin not ortalaması, 5B şubesindeki kızların not ortalamasının \( \frac{2}{3} \) katıdır.
- 5A şubesinde 15 kız, 5B şubesinde 20 erkek vardır.
Buna göre 5B şubesindeki erkeklerin not ortalaması kaçtır?
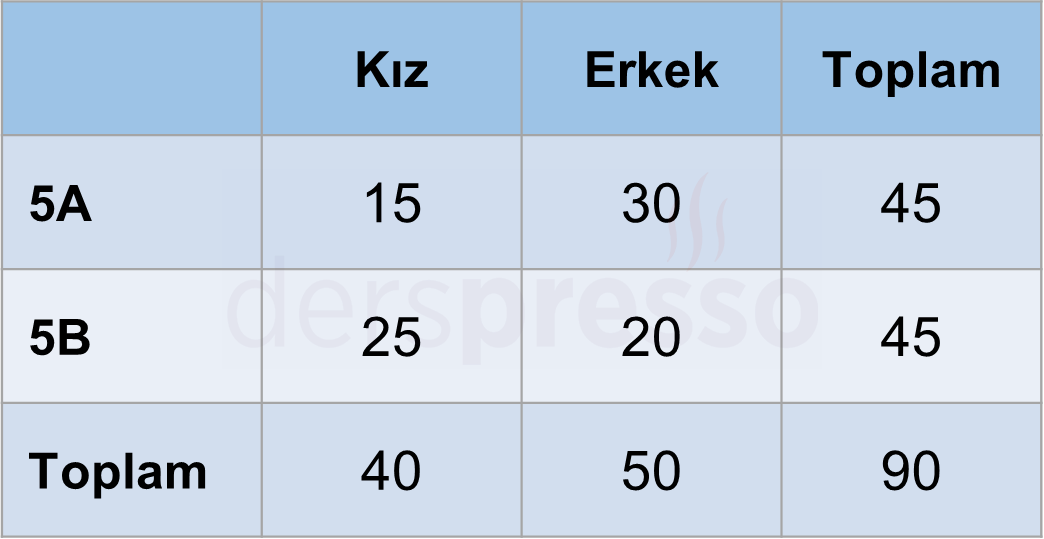
Çözümü Göster5A şubesinde 15 kız öğrenci olduğuna göre 30 erkek öğrenci vardır.
5B şubesinde 20 erkek öğrenci olduğuna göre 25 kız öğrenci vardır.
Buna göre şubelerdeki kız/erkek öğrenci sayıları aşağıdaki gibi olur.
5A şubesindeki kızların not ortalaması 40 ise toplam notu \( 40 \times 15 = 600 \) olur.
Tüm kızların not ortalaması 45 ise tüm kızların toplam notu \( 45(15 + 25) = 1800 \) olur.
5B şubesindeki kızların toplam notu \( 1800 - 600 = 1200 \) olur.
5B şubesindeki kızların not ortalamasını hesaplayalım.
\( \dfrac{1200}{25} = 48 \)
5A şubesindeki erkeklerin not ortalaması, 5B şubesindeki kızların not ortalamasının \( \frac{2}{3} \) katıdır.
\( 48 \times \dfrac{2}{3} = 32 \)
5A şubesindeki erkeklerin toplam notunu hesaplayalım.
\( 32 \times 30 = 960 \)
Tüm okulun toplam notunu hesaplayalım.
\( 48 \times 90 = 4320 \)
5B şubesindeki erkeklerin toplam notunu hesaplayalım.
\( 4320 - 1800 - 960 = 1560 \)
5B şubesindeki erkeklerin not ortalamasını hesaplayalım.
\( \dfrac{1560}{20} = 78 \) bulunur.
Özet olarak şubelerdeki kız/erkek öğrencilerinin toplam notları aşağıdaki gibi olur.
A ve B şubelerinde okuyan öğrencilerin bulunduğu bir grupta, kız öğrencilerin toplam sayısı A sınıfında okuyan erkek öğrencilerin sayısına, B sınıfında okuyan erkek öğrenci sayısı A sınıfındaki toplam öğrenci sayısına eşittir.
B sınıfında okuyan 30 öğrenci olduğuna göre, A sınıfında okuyan erkek öğrenci sayısı kaçtır?
Çözümü GösterA sınıfında okuyan erkek öğrencilerin sayısına \( a \), B sınıfında okuyan erkek öğrencilerin sayısına \( b \) diyelim.
Verilen bilgileri bir tabloya yerleştirelim.
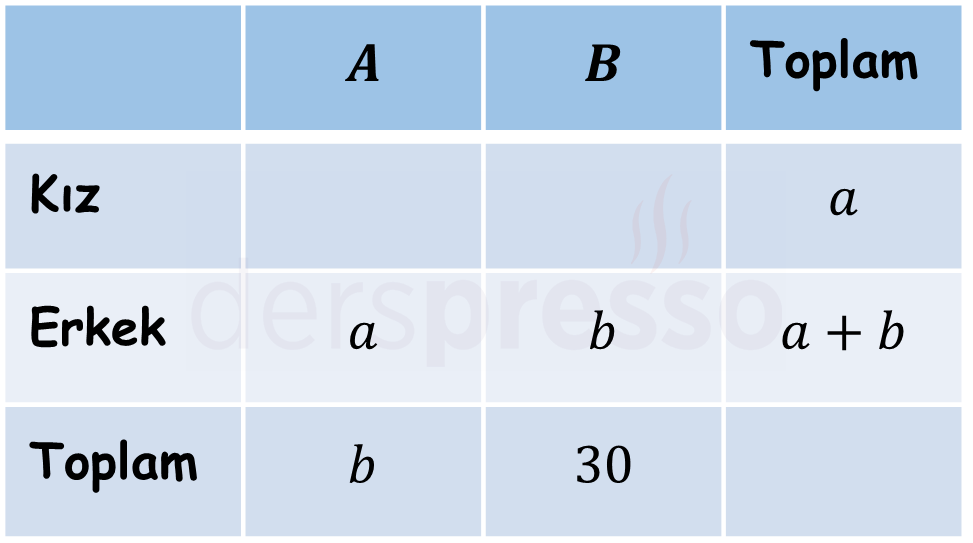
Soruda A sınıfında okuyan erkek öğrenci sayısı, yani \( a \) değeri isteniyor.
Sütun ve satırdaki toplamlar birbirlerine eşit olmalıdır.
\( b + 30 = a + (a + b) \)
\( a = 15 \)
Buna göre, A sınıfında okuyan 15 erkek öğrenci vardır.
62 kişilik bir sınıfta öğrencilerin 40'ı erkek, 24'ü gözlüklüdür.
Gözlüksüz kızların sayısı gözlüklü erkeklerin sayısının yarısı ise sınıfta kaç gözlüklü kız vardır?
Çözümü GösterGözlüksüz kızların sayısına \( x \) diyelim.
Verilen bilgileri aşağıdaki tabloya siyah renk ile yerleştirelim ve boş hücreleri kırmızı renk ile dolduralım.
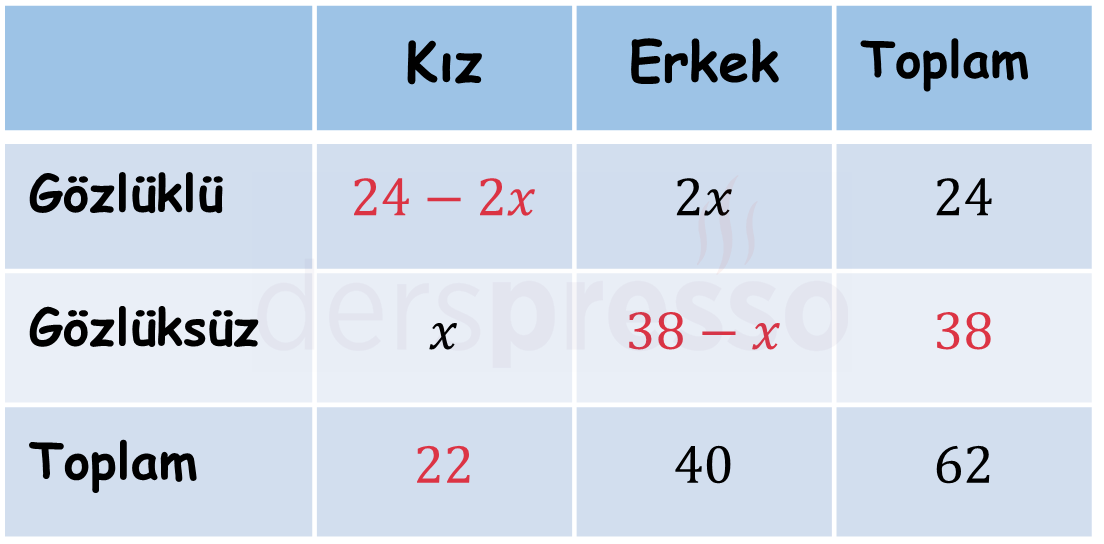
Erkek öğrenciler sütununu kullanarak \( x \)'i bulalım.
\( 2x + (38 - x) = 40 \)
\( x + 38 = 40 \)
\( x = 2 \)
Buna göre gözlüklü kız öğrencilerin sayısı \( 24 - 2x = 24 - 2(2) = 20 \) bulunur.
58 kişilik bir turist grubunda,
- Alman kadınlar ingiliz erkeklerin iki katıdır.
- İngiliz kadınlar ingiliz erkeklerden 5 fazladır.
- Alman erkekler alman kadınlardan 1 eksiktir.
Buna göre bu grupta kaç kadın vardır?
Çözümü Gösterİngiliz erkeklerin sayısına \( x \) diyelim.
Verilen bilgileri aşağıdaki tabloya siyah renk ile yerleştirelim ve boş hücreleri kırmızı renk ile dolduralım.
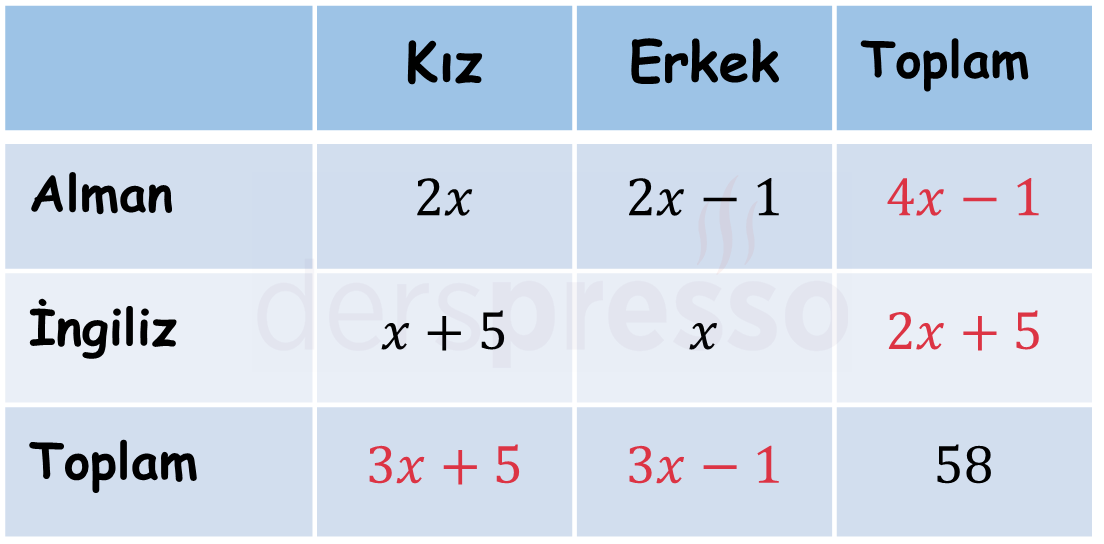
Satır ve sütun toplamlarının toplamı birbirine eşit ve 58 olmalıdır.
Sütun toplamlarının toplamını alalım.
\( (3x + 5) + (3x - 1) = 58 \)
\( 6x + 4 = 58 \)
\( x = 9 \)
Buna göre turist grubundaki kadınların sayısı \( 3x + 5 = 3(9) + 5 = 32 \) olarak bulunur.
Bir spor kulübünde oyuncular futbol ve basketboldan sadece birini oynamaktadır. Bu kulüpte 16 erkek 20 kadın oyuncu vardır, 19 oyuncu basketbol oynamaktadır ve futbol oynayan erkeklerle basketbol oynayan kadınların toplamı 13'tür.
Buna göre bu kulüpte futbol oynayan kaç kadın vardır?
Çözümü GösterFutbol oynayan erkeklerin sayısına \( x \) diyelim.
Verilen bilgileri aşağıdaki tabloya siyah renk ile yerleştirelim ve boş hücreleri kırmızı renk ile dolduralım.
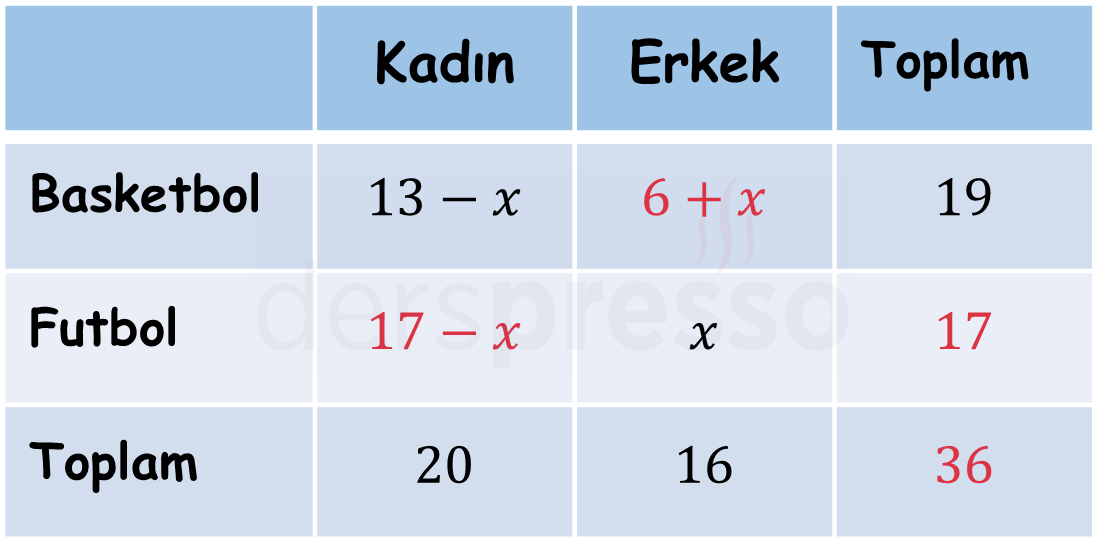
Erkekler sütununu kullanarak \( x \)'i bulalım.
\( (6 + x) + x = 16 \)
\( x = 5 \)
Futbol oynayan kadın sayısını bulalım.
\( 17 - x = 17 - 5 = 12 \) bulunur.
Bir kasabada kadınların sayısının erkeklerin sayısına oranı \( \frac{7}{6} \)'dır. Ehliyeti olan kadınların sayısının ehliyeti olan erkeklerin sayısına oranı \( \frac{5}{4} \)'tür. Ehliyeti olmayan kadınların sayısının ehliyeti olmayan erkeklerin sayısına oranı ise \( \frac{2}{3} \)'tür.
Bu kasabada ehliyeti olan 12960 erkek olduğuna göre, ehliyeti olmayan kadınların sayısı kaçtır?
Çözümü GösterKasabadaki toplam kadın sayısına \( 7k \), toplam erkek sayısına \( 6k \) diyelim.
Ehliyeti olan erkeklerin sayısını kullanarak ehliyeti olan kadınların sayısını bulalım.
Ehliyeti olan kadınların sayısına \( x \) diyelim.
\( \dfrac{x}{12960} = \dfrac{5}{4} \)
\( x = \dfrac{12960 \cdot 5}{4} = 16200 \)
Toplam kadın ve erkek sayılarından ehliyeti olan kadın ve erkek sayılarını çıkarırsak ehliyeti olmayan kadın ve erkek sayılarını buluruz.
Tüm bilgileri kullanarak bir tablo oluşturalım.
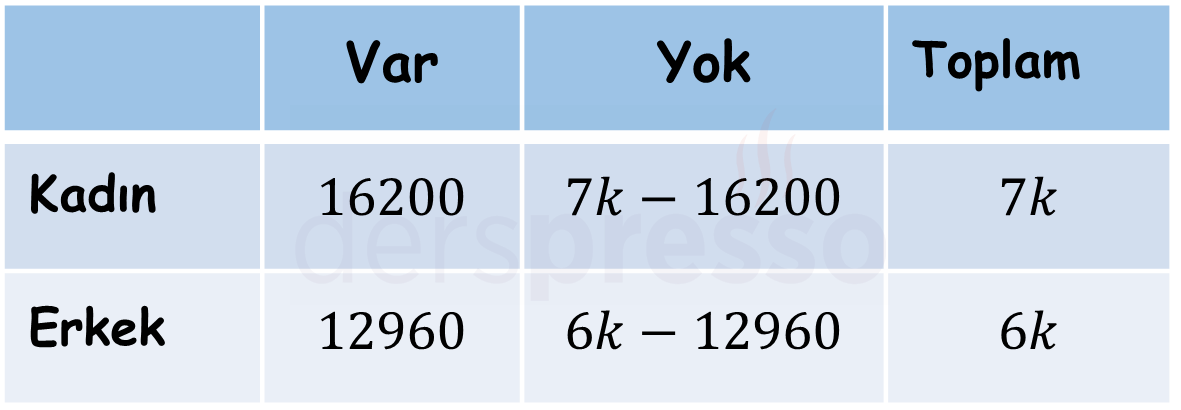
Ehliyeti olmayan kadınların sayısının ehliyeti olmayan erkeklerin sayısına oranı \( \frac{2}{3} \)'tür.
\( \dfrac{7k - 16200}{6k - 12960} = \dfrac{2}{3} \)
\( 21k - 48600 = 12k - 25920 \)
\( 9k = 22680 \)
\( k = 2520 \)
Ehliyeti olmayan kadınların sayısını bulalım.
\( 7k - 16200 = 17640 - 16200 \)
\( = 1440 \) bulunur.
30 tercümanın bulunduğu bir tercüme bürosunda İngilizce konuşan 21 kişi, Almanca konuşan 23 kişi, İspanyolca konuşan 25 kişi, Fransızca konuşan 26 kişi vardır.
Bu tercüme bürosunda bu dört dili de konuşan tercüman sayısı en az kaç olabilir?
Çözümü GösterTercüme bürosunda 9 kişi İngilizce, 7 kişi Almanca, 5 kişi İspanyolca, 4 kişi Fransızca konuşmamaktadır.
Bu kişilerin farklı kişiler olduklarını varsayarsak en az bir dil konuşmayan tercüman sayısı en fazla \( 9 + 7 + 5 + 4 = 25 \) olabilir.
Buna göre dört dili de konuşan tercüman sayısı en az \( 30 - 25 = 5 \) olabilir.
Üç basamaklı sayılardan kaç tanesi 5 ile bölündüğü halde 4 ile bölünmez?
Çözümü Göster\( 999 - 99 = 900 \) tane üç basamaklı sayı vardır.
Üç basamaklı 900 sayının dörtte biri 4'e tam bölünür.
\( \dfrac{900}{4} = 225 \)
Üç basamaklı 900 sayının beşte biri 5'e tam bölünür.
\( \dfrac{900}{5} = 180 \)
Bu iki kümenin kesişimi, hem 4'e hem 5'e, yani 20'ye tam bölünen 3 basamaklı sayılardır.
Üç basamaklı 900 sayının yirmide biri 20'ye tam bölünür.
\( \dfrac{900}{20} = 45 \)
5 ile bölünen sayılardan 20 ile bölünen sayıları çıkarırsak 5 ile bölündüğü halde 4 ile bölünmeyen sayıları buluruz.
\( 180 - 45 = 135 \) bulunur.
Bir okuldaki 160 öğrenciden 152'si futbol, 98'i basketbol oynuyor.
Buna göre, sadece futbol oynayan öğrencilerin sayısı aşağıdakilerden hangisi olabilir?
(a) \( 52 \quad \) (b) \( 55 \quad \) (c) \( 63 \quad \) (d) \( 68 \)
Çözümü GösterSadece futbol oynayan öğrenci sayısına \( a \), sadece basketbol oynayan öğrenci sayısına \( c \), ikisini de oynayan öğrenci sayısına \( b \), ikisini de oynamayan öğrenci sayısına \( d \) diyelim.

Soruda verilen bilgileri birer eşitlik olarak yazalım.
\( a + b + c + d = 160 \)
\( a + b = 152 \)
\( b + c = 98 \)
İkinci ve üçüncü eşitlikleri taraf tarafa toplayalım.
\( a + 2b + c = 250 \)
Sadece futbolu seven öğrenci sayısının aralığını bulmak için alabileceği en küçük ve en büyük değerleri bulmamız gerekir.
Yukarıdaki birinci eşitliği dördüncüden taraf tarafa çıkaralım.
\( (a + 2b + c) - (a + b + c + d) = 250 - 160 \)
\( b - d = 90 \)
\( a \)'nın en büyük değerini bulmak için \( d \)'nin en küçük değerini kullanalım.
\( d = 0 \)
\( b - d = b - 0 = 90 \)
\( b = 90 \)
\( a + b = 152 \)
\( a = 62 \)
\( a \)'nın en küçük değerini bulmak için \( d \)'nin en büyük değerini kullanalım.
Yukarıdaki ikinci eşitliği birinciden taraf tarafa çıkaralım.
\( (a + b + c + d) - (a + b) = 160 - 152 \)
\( c + d = 8 \)
\( c = 0 \) olursa \( d \) en büyük değerini alır.
\( d = 8 \)
\( b - d = b - 8 = 90 \)
\( b = 98 \)
\( a + b = 152 \)
\( a = 54 \)
\( a \)'nın değer aralığı aşağıdaki gibi bulunur.
\( a \in [54, 62] \)
Buna göre cevap (b) seçeneğidir.
Bir sınıftaki 25 öğrencinin kalemkutusunda siyah, mavi ve kırmızı renkteki tükenmez kalemlerden en az biri vardır.
Siyah kaleme sahip öğrenci sayısı, mavi kaleme sahip öğrenci sayısı ve kırmızı kaleme sahip öğrenci sayısının toplamı 34'tür. 7 öğrencide ise bu kalemlerin en az iki farklı rengi vardır.
Buna göre kaç öğrencide sadece iki farklı renkte kalem vardır?
Çözümü GösterSiyah, mavi ve kırmızı renkte kaleme sahip öğrencilerin kümesine sırasıyla \( A, B, C \) diyelim.
Bir Venn şeması çizelim ve kesişim kümelerinin eleman sayılarına \( x, y, z, t \) diyelim.

Üç kümenin birleşiminin eleman sayısı aşağıdaki formülle hesaplanır.
\( s(A \cup B \cup C) = s(A) + s(B) + s(C) - s(A \cap B) - s(B \cap C) - s(A \cap C) + s(A \cap B \cap C) \)
Grupta toplam 25 öğrenci vardır.
\( s(A \cup B \cup C) = 25 \)
Siyah kaleme sahip öğrenci sayısı, mavi kaleme sahip öğrenci sayısı ve kırmızı kaleme sahip öğrenci sayısının toplamı 34'tür.
\( s(A) + s(B) + s(C) = 34 \)
Bu değerleri birleşim kümesi formülünde yerine koyalım.
\( 25 = 34 - (x + t) - (y + t) - (z + t) + t \)
\( x + y + z + 2t = 9 \)
7 öğrencide kalemlerin en az iki farklı rengi vardır.
\( x + y + z + t = 7 \)
İki denklemi taraf tarafa çıkaralım.
\( t = 9 - 7 = 2 \)
Sadece iki farklı renkte kaleme sahip öğrenci sayısı \( x + y + z \) olur.
\( x + y + z + 2 = 7 \)
\( x + y + z = 5 \) bulunur.
Bir çikolata firmasının iki yeni ürünü hakkında yaptığı bir araştırmada ürünler 250 katılımcıya tattırılıyor ve her bir ürünü beğenip beğenmedikleri sorusuna ayrı ayrı "Evet" ya da "Hayır" cevabı vermeleri isteniyor.
Araştırma sonuçlarında "Evet" cevaplarının sayısının "Hayır" cevaplarının sayısından 240 fazla olduğu, ayrıca en az bir ürünü beğendiğini söyleyen katılımcıların sayısının en fazla bir ürünü beğendiğini söyleyen katılımcıların sayısının iki katı olduğu görülüyor.
Buna göre sadece bir ürünü beğenen katılımcıların sayısı kaçtır?
Çözümü GösterBirinci ürünü beğenen katılımcıların kümesine \( A \), ikinci ürünü beğenen katılımcıların kümesine \( B \) diyelim.
Bu kümeleri bir Venn şemasında gösterelim.
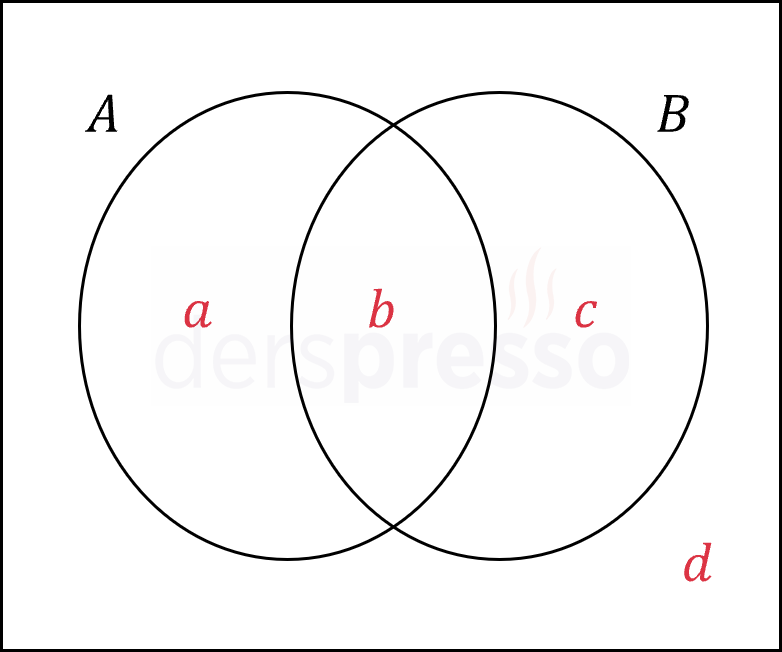
Katılımcıların toplam sayısı 250'dir.
\( a + b + c + d = 250 \)
Birinci ürünü beğenen \( a + b \) kişi, ikinci ürünün beğenen \( b + c \) kişi olduğuna göre, anket sonuçlarındaki "Evet" cevaplarının sayısı \( a + 2b + c \) olur.
Birinci ürünü beğenmeyen \( c + d \) kişi, ikinci ürünü beğenmeyen \( a + d \) kişi olduğuna göre, anket sonuçlarındaki "Hayır" cevaplarının sayısı \( a + c + 2d \) olur.
"Evet" cevaplarının sayısı "Hayır" cevaplarının sayısından 240 fazladır.
\( a + 2b + c = a + c + 2d + 240 \)
\( b = d + 120 \)
En az bir ürünü beğendiğini söyleyen katılımcıların sayısı, en fazla bir ürünü beğendiğini söyleyen katılımcıların sayısının iki katıdır.
\( a + b + c = 2(a + c + d) \)
\( a + b + c = 2a + 2c + 2d \)
\( b = a + c + 2d \)
Eşitliğin taraflarına \( b \) ekleyelim.
\( 2b = a + b + c + 2d \)
\( 2b = (a + b + c + d) + d \)
Katılımcıların toplam sayısı 250'dir.
\( 2b = 250 + d \)
Yukarıda bulduğumuz \( b = d + 120 \) değerini yerine koyalım.
\( 2(d + 120) = 250 + d \)
\( d = 10 \)
\( b = 10 + 120 = 130 \)
Sadece bir ürünü beğenen katılımcıların sayısı \( a + c \) olur.
\( a + b + c + d = 250 \)
\( a + c = 250 - b - d \)
\( = 250 - 130 - 10 = 110 \) bulunur.
Bir öğretmen kümeler konusunu anlatırken elemanları harflerden oluşan ve eleman sayıları sırasıyla 9 ve 11 olan \( X \) ve \( Y \) kümelerini tanımlıyor.
Öğretmen daha sonra \( X \) kümesinin elemanlarıyla yazılabilecek kelimelere "kitap" ve "kerpiç" kelimelerini, \( Y \) kümesinin elemanlarıyla yazılabilecek kelimelere "öğrenci" ve "centilmen" kelimelerini örnek olarak veriyor.
Buna göre \( X \cap Y \) kümesinin elemanlarıyla aşağıdaki kelimelerden hangisi kesinlikle yazılamaz?
(a) Terlik, (b) Kiremit, (c) Retina, (d) Tekerlek, (e) Terazi
Çözümü Göster\( X \) ve \( Y \) kümelerinin bilinen elemanlarını yazalım.
\( X = \{ k, i, t, a, p, e, r, ç, \ldots \} \)
\( Y = \{ ö, ğ, r, e, n, c, i, t, l, m, \ldots \} \)
\( X \) kümesi 9, \( Y \) kümesi 11 elemanlı olduğuna göre, her iki kümede bilinmeyen birer eleman vardır.
\( X \cap Y \) kümesinin bilinen elemanlarını bulalım.
\( X \cap Y = \{ e, i, r, t, \ldots \} \)
Verilen seçenekleri sırayla inceleyelim.
"Terlik" kelimesinden \( X \cap Y \) kümesinin elemanlarını elediğimizde geriye "l" ve "k" harfleri kalır.
\( X \) kümesindeki eksik elemanı "l" harfi, \( Y \) kümesindeki eksik elemanı "k" harfi olarak seçtiğimiz durumda bu kelime yazılabilir.
"Kiremit" kelimesinden \( X \cap Y \) kümesinin elemanlarını elediğimizde geriye "k" ve "m" harfleri kalır.
\( X \) kümesindeki eksik elemanı "m" harfi, \( Y \) kümesindeki eksik elemanı "k" harfi olarak seçtiğimiz durumda bu kelime yazılabilir.
"Retina" kelimesinden \( X \cap Y \) kümesinin elemanlarını elediğimizde geriye "n" ve "a" harfleri kalır.
\( X \) kümesindeki eksik elemanı "n" harfi, \( Y \) kümesindeki eksik elemanı "a" harfi olarak seçtiğimiz durumda bu kelime yazılabilir.
"Tekerlek" kelimesinden \( X \cap Y \) kümesinin elemanlarını elediğimizde geriye "k" ve "l" harfleri kalır.
(a) seçeneği için yazdıklarımız bu seçenek için de geçerlidir. Bu kelime de yazılabilir.
"Terazi" kelimesinden \( X \cap Y \) kümesinin elemanlarını elediğimizde geriye "a" ve "z" harfleri kalır.
\( X \) kümesindeki eksik elemanı "z" harfi olarak seçebiliriz, ancak \( Y \) kümesinde "a" ve "z" harflerinin ikisi de bulunmadığından tek bir elemanı eksik olan \( Y \) kümesine bu iki elemanı birden ekleyemeyiz.
Kesinlikle yazılamayacak seçenek (e) seçeneğidir.
Bir arkadaş grubundaki kişilerin %70'i Wordle, %50'si Sudoku oynamaktadır.
Bu grupta 14 kişi hem Wordle hem Sudoku oynadığına göre, grupta en çok kaç kişi oyunların ikisini de oynamamaktadır?
Çözümü GösterWordle oynayanların kümesine \( W \), Sudoku oynayanların kümesine \( S \) diyelim.
Bu kümeleri bir Venn şemasında gösterelim.
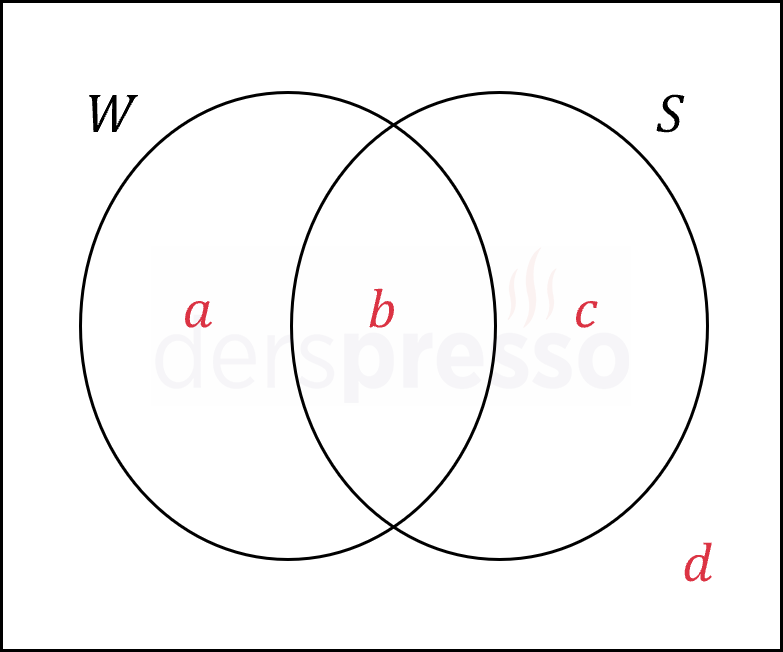
Gruptaki toplam kişi sayısına \( x \) diyelim.
Verilen bilgileri denklem haline getirelim.
\( a + b + c + d = x \)
\( a + b = \dfrac{70x}{100} = \dfrac{7x}{10} \)
\( b + c = \dfrac{50x}{100} = \dfrac{x}{2} \)
\( b = 14 \) olarak veriliyor.
\( a + 14 = \dfrac{7x}{10} \)
\( a = \dfrac{7x}{10} - 14 \)
\( 14 + c = \dfrac{x}{2} \)
\( c = \dfrac{x}{2} - 14 \)
\( a, b, c \) değerlerini ilk denklemde yerine koyalım.
\( a + b + c + d = x \)
\( \dfrac{7x}{10} - 14 + 14 + \dfrac{x}{2} - 14 + d = x \)
\( d = 14 - \dfrac{x}{5} \)
Soruda \( d \)'nin en büyük değeri istenmektedir.
\( d \) değerinin en büyük çıkması için \( x \) değeri en küçük olmalıdır. Ayrıca \( x \)'e bağlı \( a, b, c \) değerleri tam sayı olmalı ve negatif olmamalıdır.
\( x \)'e bağlı \( \frac{7x}{10} \), \( \frac{x}{2} \) ve \( \frac{x}{5} \) ifadelerinin tümünü tam sayı yapacak şekilde \( x = 10k \) diyelim.
\( a = \dfrac{7x}{10} - 14 = 7k - 14 \)
\( c = \dfrac{x}{2} - 14 = 5k - 14 \)
\( d = 14 - \dfrac{x}{5} = 14 - 2k \)
\( a \) ve \( c \)'yi negatif yapmayan değerler içinde \( k \)'nın en küçük değeri \( k = 3 \) olur.
\( d = 14 - 2k \)
\( = 14 - 2(3) = 8 \) bulunur.
Glütensiz ve vegan yemekler yapan bir restoran eve servis hizmeti de sunmaktadır. Bazı müşteriler sadece glütensiz ya da sadece vegan yemek sipariş ederken, bazıları her ikisini de sipariş etmektedir. Müşterilerin belirli bir günde verdiği siparişlerle ilgili aşağıdakiler bilinmektedir.
- Glütensiz yemek sipariş edip eve servis isteyen, vegan yemek sipariş edip restoranda yiyen ve sadece vegan yemek sipariş edip eve servis isteyen müşteri sayıları birbirine eşittir.
- Restoranda yiyen müşteri sayısı, eve servis isteyen müşteri sayısının iki katıdır.
- Glütensiz yemek sipariş eden müşteri sayısının üç katı, vegan yemek sipariş eden müşteri sayısının beş katından 18 fazladır.
- İki yemekten de sipariş eden müşteri sayısı 10'dur.
- Glütensiz yemek sipariş edip restoranda yiyen müşteri sayısı 36'dır.
Buna göre bu günde sipariş edilen toplam yemek sayısı kaçtır?
Çözümü GösterGlütensiz yemek sipariş eden müşterilerin kümesine \( G \), vegan yemek sipariş eden müşterilerin kümesine \( V \) diyelim.
Eve servis isteyen müşterilerin kümesine \( E \), restoranda yiyen müşterilerin kümesine \( R \) diyelim.
Bu kümeleri bir Venn şemasında gösterelim.
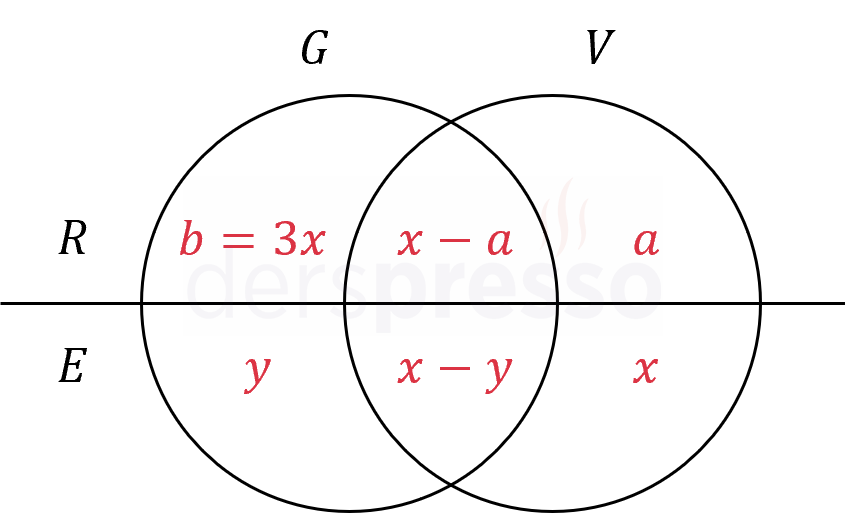
Sadece vegan yemek sipariş edip eve servis isteyen müşteri sayısına \( x \), sadece glütensiz yemek sipariş edip eve servis isteyen müşteri sayısına \( y \), sadece vegan yemek sipariş edip restoranda yiyen müşteri sayısına \( a \) diyelim.
Vegan yemek sipariş edip restoranda yiyen ve sadece vegan yemek sipariş edip eve servis isteyen müşteri sayıları birbirine eşittir.
Buna göre iki yemekten de sipariş edip restoranda yiyen müşteri sayısı \( x - a \) olur.
Glütensiz yemek sipariş edip eve servis isteyen ve sadece vegan yemek sipariş edip eve servis isteyen müşteri sayıları birbirine eşittir.
Buna göre iki yemekten de sipariş edip eve servis isteyen müşteri sayısı \( x - y \) olur.
Sadece glütensiz yemek sipariş edip restoranda yiyen müşteri sayısına \( b \) diyelim.
Restoranda yiyen müşteri sayısı, eve servis isteyen müşteri sayısının iki katıdır.
\( b + x - a + a = 2(y + x - y + x) \)
\( b + x = 4x \)
\( b = 3x \)
Soruda verilen diğer bilgileri sırasıyla denklem halinde yazalım.
Glütensiz yemek sipariş eden müşteri sayısının üç katı, vegan yemek sipariş eden müşteri sayısının beş katından 18 fazladır.
\( 3(5x - a) = 5(3x - y) + 18 \)
\( 15x - 3a = 15x - 5y + 18 \)
\( 5y = 3a + 18 \)
İki yemekten de sipariş eden müşteri sayısı 10'dur.
\( (x - a) + (x - y) = 10 \)
\( 2x - a - y = 10 \)
Glütensiz yemek sipariş edip restoranda yiyen müşteri sayısı 36'dır.
\( 4x - a = 36 \)
\( a = 4x - 36 \)
Son denklemde bulduğumuz \( a \) değerini birinci denklemde yerine yazalım.
\( 5y = 3a + 18 \)
\( 5y = 3(4x - 36) + 18 \)
\( 5y = 12x - 108 + 18 \)
\( 12x - 5y = 90 \)
Aynı \( a \) değerini ikinci denklemde yerine yazalım.
\( 2x - a - y = 10 \)
\( 2x - (4x - 36) - y = 10 \)
\( 2x + y = 26 \)
İki denklemi ortak çözdüğümüzde aşağıdaki değerleri buluruz.
\( x = 10, \quad y = 6 \)
Bulduğumuz \( x \) değerini kullanarak \( a \) değerini bulalım.
\( a = 4x - 36 \)
\( = 4(10) - 36 = 4 \)
Bulduğumuz değerleri Venn şemasında yerlerine yerleştirelim.

Sipariş edilen glutensiz yemeklerin sayısını bulalım.
\( 30 + 6 + 6 + 4 = 46 \)
Sipariş edilen vegan yemeklerin sayısını bulalım.
\( 4 + 10 + 6 + 4 = 24 \)
Sipariş edilen toplam yemek sayısını bulalım.
\( 46 + 24 = 70 \) bulunur.
Bir yemek yarışmasına katılan 50 yarışmacıya yapmaları için üç farklı yemek verilmiştir.
İlk yemeği yapabilen 42, ikinci yemeği yapabilen 38, üçüncü yemeği yapabilen 33 yarışmacı olduğuna göre, tüm yemekleri yapmayı başaran yarışmacı sayısı en az kaçtır?
Çözümü Göster1. Yöntem:
Tüm yemekleri yapmayı başaran yarışmacı sayısının en az olduğu durum, her bir yemeği yapamayan yarışmacıların tümünün farklı kişiler olduğu durumdur.
İlk yemeği yapamayan 8, ikinci yemeği yapamayan 12, üçüncü yemeği yapamayan 17 yarışmacı vardır.
Bu durumda en az bir yemeği yapamayan yarışmacı sayısı en fazla \( 8 + 12 + 17 = 37 \) olabilir.
Buna göre tüm yemekleri yapmayı başaran yarışmacı sayısı en az \( 50 - 37 = 13 \) olabilir.
2. Yöntem:
Yukarıdaki çözümü cebirsel olarak gösterelim.
Her bir yemeği yapabilen yarışmacıların kümesine sırasıyla \( A, B, C \) diyelim.
Bu kümeleri bir Venn şemasında gösterelim.
Buna göre mavi renkteki bölgeler sadece bir yemeği yapabilen yarışmacılara, turuncu renkteki bölgeler sadece iki yemeği yapabilen yarışmacılara, yeşil renkteki bölge ise üç yemeği de yapabilen yarışmacılara karşılık gelir.
Toplam 50 yarışmacı vardır.
\( a + b + c + d + e + f + g + h = 50 \)
İlk yemeği yapabilen 42 yarışmacı vardır.
\( a + d + e + g = 42 \)
İkinci yemeği yapabilen 38 yarışmacı vardır.
\( b + d + f + g = 38 \)
Üçüncü yemeği yapabilen 33 yarışmacı vardır.
\( c + e + f + g = 33 \)
Üç denklemi taraf tarafa toplayalım.
\( a + b + c + 2d + 2e + 2f + 3g = 113 \)
Toplam yarışmacı sayısı eşitliğini 2 ile çarpıp bu denklemden çıkaralım.
\( 2a + 2b + 2c + 2d + 2e + 2f + 2g + 2h = 100 \)
\( -a - b - c + g - 2h = 113 - 100 \)
\( g = 13 + (a + b + c + 2h) \)
Tüm yemekleri yapmayı başaran yarışmacı sayısı (\( g \)), en küçük değerini \( a, b, c, h \) değerleri sıfır olduğunda alır.
\( g = 13 \) bulunur.