Birinci Dereceden Denklem Sistemleri
Aynı bilinmeyenleri içeren, iki ya da daha fazla denklemden oluşan ve tüm denklemleri birlikte sağlayan bir çözümü bulunmaya çalışılan denklem grubuna denklem sistemi denir.
İki bilinmeyen ve iki denklemden oluşan aşağıdaki denklem sistemini birinci dereceden denklem sistemlerine örnek olarak verebiliriz.
\( \begin{cases} 3x + 2y - 24 = 0 \\ x - y + 7 = 0 \end{cases} \)
\( (x, y) = (4, 6) \) ikilisinin bu denklem sisteminin bir çözümü olabilmesi için sistemdeki iki denklemi de sağlaması gerekir. Bu değerleri denklemlerde yerine koyarak eşitliklerin sağlanıp sağlanmadığını kontrol edelim.
\( x = 4 \) ve \( y = 6 \) için:
\( 3 \cdot 4 + 2 \cdot 6 - 24 = 0 \)
\( 4 - 6 + 7 = 5 \ne 0 \)
Buna göre \( (4, 6) \) ikilisi birinci denklemin bir çözümüdür, ama ikinci denklemin bir çözümü değildir. Her iki denklem birlikte sağlanmadığı için \( (4, 6) \) ikilisi bu denklem sisteminin bir çözümü değildir.
Şimdi de \( (x, y) = (2, 9) \) sıralı ikilisinin bu denklem sisteminin bir çözümü olup olmadığına bakalım.
\( x = 2 \) ve \( y = 9 \) için:
\( 3 \cdot 2 + 2 \cdot 9 - 24 = 0 \)
\( 2 - 9 + 7 = 0 \)
Her iki denklem birlikte sağlandığı için \( (2, 9) \) ikilisi bu denklem sisteminin bir çözümüdür.
Buna göre \( n \) denklemden oluşan bir denklem sisteminin çözüm kümesi sistemdeki denklemlerin ayrı ayrı çözüm kümelerinin kesişim kümesine eşittir.
\( \text{ÇK} = \text{ÇK}_1 \cap \text{ÇK}_2 \cap \ldots \cap \text{ÇK}_n \)
Birinci Dereceden Denklem Sistemlerinin Çözümü
Birinci dereceden denklem sistemlerinin çözümünde kullanabileceğimiz bazı yöntemler aşağıdaki gibidir.
Yerine Koyma Yöntemi
Bu yöntemde bilinmeyenlerden biri herhangi bir denklemde yalnız bırakılır, sonra eşit olduğu ifade ikinci denklemde yerine konur ve ikinci denklem bir bilinmeyenli denklem şeklinde çözülür.
Yerine koyma yönteminin adımlarını yukarıda kullandığımız örnek üzerinden gösterelim.
\( \begin{cases} 3x + 2y - 24 = 0 \\ x - y + 7 = 0 \end{cases} \)
Adım 1: Bilinmeyenlerden biri herhangi bir denklemde yalnız bırakılarak diğer bilinmeyen cinsinden yazılır.
İkinci denklemde \( y \) bilinmeyenini yalnız bırakalım.
\( x - y + 7 = 0 \)
\( y = x + 7 \)
Adım 2: Elde edilen eşitlik diğer denklemde yerine konur ve bu denklem bir bilinmeyenli denklem şeklinde çözülür.
Elde ettiğimiz eşitliği birinci denklemde \( y \) yerine koyalım.
\( 3x + 2y - 24 = 0 \)
\( 3x + 2(x + 7) - 24 = 0 \)
\( 3x + 2x + 14 - 24 = 0 \)
\( 5x = 10 \)
\( x = 2 \)
Adım 3: Bulunan değer orijinal denklemlerden birinde yerine konur ve diğer bilinmeyenin değeri bulunur.
İkinci denklemde \( x = 2 \) koyarak \( y \) değerini bulalım.
\( x - y + 7 = 0 \)
\( 2 - y + 7 = 0 \)
\( y = 9 \)
Denklem sisteminin çözümünü yukarıda sağlamasını yapmış olduğumuz gibi \( (x, y) = (2, 9) \) olarak bulmuş olduk.
\( x = 2 \) değerini birinci denklemde yerine koymuş olsaydık da aynı \( y \) değerini elde edeceğimizi teyit edelim.
\( 3x + 2y - 24 = 0 \)
\( 3 \cdot 2 + 2y - 24 = 0 \)
\( 2y = 18 \)
\( y = 9 \)
Bu yöntemde ilk adımda hangi denklemdeki hangi bilinmeyeni yalnız bırakırsak bırakalım aynı sonucu elde ederiz.
Bir denklem sistemindeki denklemlerden biri \( y = ax + b \) formunda ise yerine koyma yöntemi daha hızlı sonuç verecektir.
Yok Etme (Eliminasyon) Yöntemi
Bu yöntemde denklemler bilinmeyenlerden birinin katsayıları birbirini götürecek ve bir bilinmeyenli bir denklem elde edilecek şekilde düzenlenir ve taraf tarafa toplanır.
Yok etme yönteminin adımlarını aynı örnek üzerinden gösterelim.
\( \begin{cases} 3x + 2y - 24 = 0 \\ x - y + 7 = 0 \end{cases} \)
Adım 1: Yok edilecek bilinmeyen seçilir.
Bu örnekte \( x \) bilinmeyenini yok edelim.
Adım 2: Her iki denklemde seçilen bilinmeyenin katsayıları birbirinin toplamaya göre tersi olacak şekilde denklemlerden birinin ya da ikisinin tarafları sabit sayılarla çarpılır.
\( x \) bilinmeyeninin birinci denklemde katsayısı 3, ikinci denklemde 1'dir.
Bu katsayıları birbirinin toplamaya göre tersi yapmak için ikinci denklemin taraflarını \( -3 \) ile çarpalım.
\( -3(x - y + 7) = -3 \cdot 0 \)
\( -3x + 3y - 21 = 0 \)
Adım 3: Denklemler taraf tarafa toplanır ve seçilen bilinmeyenin toplam satırında birbirini götürmesi sağlanır.
İki denklemi taraf tarafa toplayalım.
\( 3x + 2y - 24 = 0 \)
\( -3x + 3y - 21 = 0 \)
==================
\( 0x + 5y - 45 = 0 \)
\( 5y - 45 = 0 \)
Adım 4: Elde edilen tek bilinmeyenli denklem çözülür.
\( y \) bilinmeyenini yalnız bırakalım.
\( 5y - 45 = 0 \)
\( 5y = 45 \)
\( y = 9 \)
Adım 5: Bulunan değer orijinal denklemlerden birinde yerine konur ve diğer bilinmeyenin değeri bulunur.
Bulduğumuz \( y \) değerini ikinci denklemde yerine koyalım.
\( x - y + 7 = 0 \)
\( x - 9 + 7 = 0 \)
\( x = 2 \)
Denklem sisteminin çözümünü diğer yöntemde olduğu gibi \( (x, y) = (2, 9) \) olarak bulmuş olduk.
Bir denklem sistemindeki denklemlerin tümü \( ax + by + c = 0 \) formunda ise yok etme yöntemi daha hızlı sonuç verecektir.
Eşitleme Yöntemi
Bu yöntemde her iki denklemde aynı bilinmeyen yalnız bırakılır ve bu bilinmeyenin eşit olduğu ifadeler birbirine eşitlenir.
Eşitleme yönteminin adımlarını aynı örnek üzerinden gösterelim.
\( \begin{cases} 3x + 2y - 24 = 0 \\ x - y + 7 = 0 \end{cases} \)
Adım 1: Yalnız bırakılacak bilinmeyen seçilir.
Bu örnekte \( x \) bilinmeyenini yalnız bırakalım.
Adım 2: Her iki denklemde bu bilinmeyen yalnız bırakılır.
Birinci denklemde \( x \)'i yalnız bırakalım.
\( x = -\dfrac{2}{3}y + 8 \)
İkinci denklemde \( x \)'i yalnız bırakalım.
\( x = y - 7 \)
Adım 3: Yalnız bırakılan bilinmeyenin eşit olduğu iki ifade birbirine eşitlenir.
İki denklemde \( x \)'in eşit olduğu ifadeleri eşitleyelim.
\( x = x \)
\( -\dfrac{2}{3}y + 8 = y - 7 \)
Adım 4: Elde edilen bir bilinmeyenli denklem çözülür.
\( y \)'li terimleri eşitliğin sol tarafında, sabit terimleri sağ tarafında toplayalım.
\( -\dfrac{5}{3}y = -15 \)
\( y = 9 \)
Adım 5: Bulunan değer orijinal denklemlerden birinde yerine konur ve diğer bilinmeyenin değeri bulunur.
Bulduğumuz \( y \) değerini ikinci denklemde yerine koyalım.
\( x - y + 7 = 0 \)
\( x - 9 + 7 = 0 \)
\( x = 2 \)
Bir denklem sistemindeki denklemlerin tümü \( y = ax + b \) formunda ise eşitleme yöntemi daha hızlı sonuç verecektir.
Grafik Yöntemi
Önceki bölümde gördüğümüz üzere, birinci dereceden iki bilinmeyenli bir denklemin grafiği bir doğrudur ve bu doğrunun üzerindeki tüm noktalar denklemin birer çözümüdür. Bir denklem sisteminde ise sistemdeki tüm denklemlerin grafiklerinin (varsa) kesişim noktası denklem sisteminin çözümünü verir. Buna göre doğrular tek bir noktada kesişiyorsa denklem sisteminin tek bir çözümü vardır, doğrular paralel ise (kesişmiyor ise) denklem sisteminin bir çözümü yoktur, doğrular çakışık ise denklem sisteminin sonsuz çözümü vardır.
Yukarıda kullandığımız denklem sistemindeki iki denklemin grafiklerini çizelim.
\( \begin{cases} 3x + 2y - 24 = 0 \\ x - y + 7 = 0 \end{cases} \)
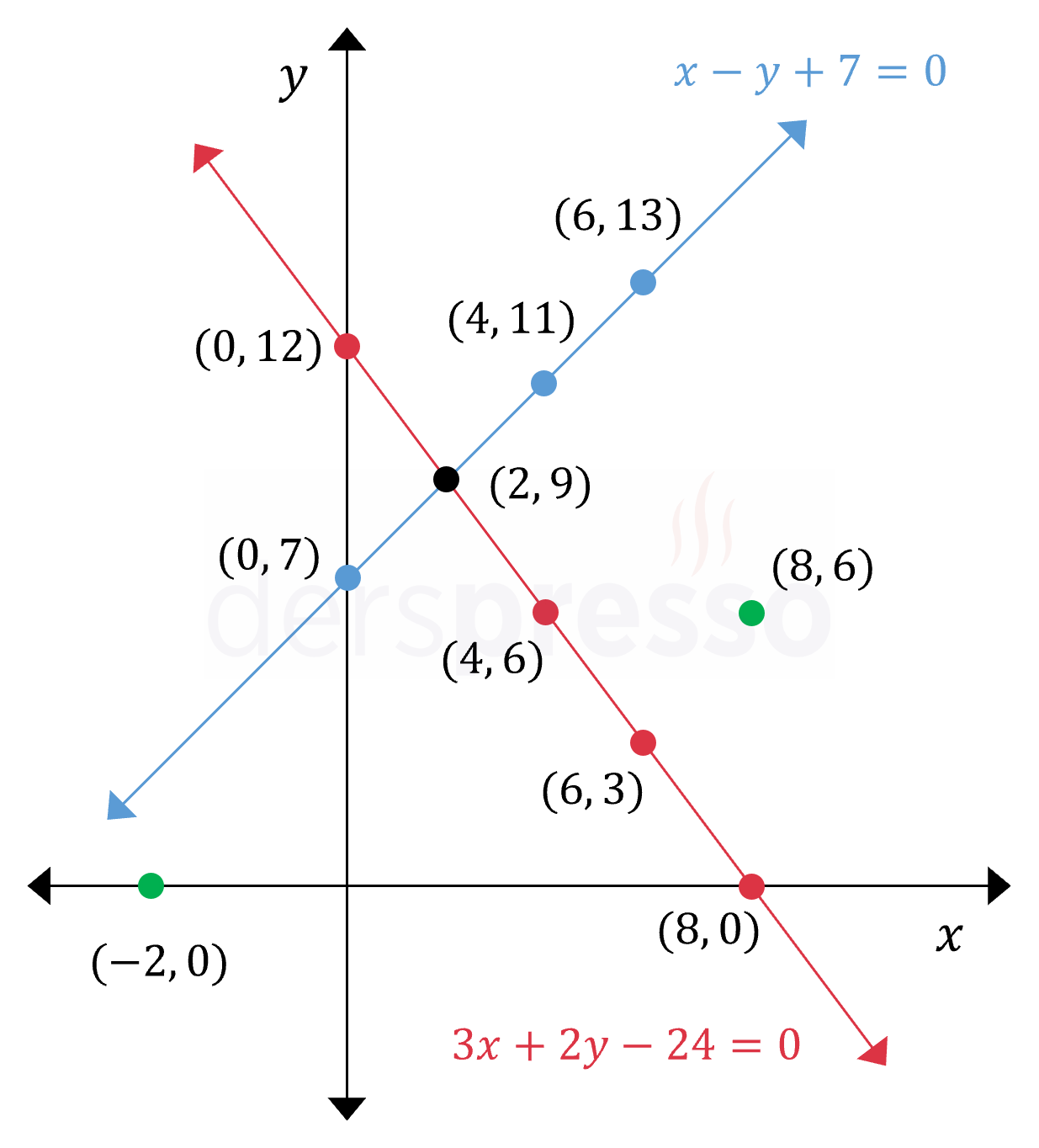
Denklem grafiklerinde işaretli bazı noktaların iki denklemi sağlama durumları aşağıdaki gibidir.
| Nokta | \( 3x + 2y - 24 = 0 \) | \( x - y + 7 = 0 \) |
|---|---|---|
| \( (-2, 0) \) | \( 3 \cdot (-2) + 2 \cdot 0 - 24 = -30 \ne 0 \) | \( -2 - 0 + 7 = 5 \ne 0 \) |
| \( (8, 6) \) | \( 3 \cdot 8 + 2 \cdot 6 - 24 = 12 \ne 0 \) | \( 8 - 6 + 7 = 9 \ne 0 \) |
| \( (0, 12) \) | \( 3 \cdot 0 + 2 \cdot 12 - 24 = 0 \) | \( 0 - 12 + 7 = -5 \ne 0 \) |
| \( (2, 9) \) | \( 3 \cdot 2 + 2 \cdot 9 - 24 = 0 \) | \( 2 - 9 + 7 = 0 \) |
| \( (4, 6) \) | \( 3 \cdot 4 + 2 \cdot 6 - 24 = 0 \) | \( 4 - 6 + 7 = 5 \ne 0 \) |
| \( (6, 3) \) | \( 3 \cdot 6 + 2 \cdot 3 - 24 = 0 \) | \( 6 - 3 + 7 = 10 \ne 0 \) |
| \( (8, 0) \) | \( 3 \cdot 8 + 2 \cdot 0 - 24 = 0 \) | \( 8 - 0 + 7 = 15 \ne 0 \) |
| \( (0, 7) \) | \( 3 \cdot 0 + 2 \cdot 7 - 24 = -10 \ne 0 \) | \( 0 - 7 + 7 = 0 \) |
| \( (4, 11) \) | \( 3 \cdot 4 + 2 \cdot 11 - 24 = 10 \ne 0 \) | \( 4 - 11 + 7 = 0 \) |
| \( (6, 13) \) | \( 3 \cdot 6 + 2 \cdot 13 - 24 = 20 \ne 0 \) | \( 6 - 13 + 7 = 0 \) |
Bu grafiği ve tabloyu aşağıdaki şekilde yorumlayabiliriz.
- Her noktanın ilgili denklemi sağladığı durumlar yeşil, sağlamadığı durumlar pembe ile tabloda işaretlenmiştir.
- Bir nokta bir denklemin grafiği üzerindeyse o denklemi sağlamakta, değilse sağlamamaktadır.
- Her iki doğrunun da üzerinde olmayan iki nokta (\( (-2, 0) \) ve \( (8, 6) \)) iki denklemi de sağlamamaktadır.
- Her iki doğrunun kesişimi olan nokta (\( (2, 9) \)) her iki denklemi de sağlamaktadır.
Özetlemek gerekirse, bir denklemin çözüm kümesi o denklemin grafiği üzerindeki tüm noktalardır. Bir denklem sisteminin çözüm kümesi ise denklem sistemindeki denklemlerin grafiklerinin (varsa) kesişim noktası ya da noktalarıdır.
Matris Yöntemi
Lineer denklem sistemleri matrisler yardımıyla da çözülebilir. Bu yöntemlerden Gauss eliminasyon yöntemini, Cramer kuralını ve ters matris yöntemini ilgili bölümlerde inceleyeceğiz.
\( m - k = 5 \) ve \( 6m + 3k = 39 \) olduğuna göre, \( m^k \) kaça eşittir?
Çözümü GösterBirinci denklemde \( k \)'yı yalnız bırakalım.
\( m - k = 5 \)
\( k = m - 5 \)
Bulduğumuz \( k \) değerini ikinci denklemde yerine koyalım.
\( 6m + 3k = 39 \)
\( 6m + 3(m - 5) = 39 \)
\( 6m + 3m - 15 = 39 \)
\( 9m - 15 = 39 \)
Sabit terimi eşitliğin sağ tarafına atarak \( m \)'li terimi yalnız bırakalım.
\( 9m = 54 \)
Eşitliğin iki tarafını 9'a bölelim.
\( m = 6 \)
Bu değeri kullanarak \( k \) değerini bulalım.
\( k = m - 5 = 1 \)
Buna göre \( m^k = 6^1 = 6 \) bulunur.
\( x, y \in\mathbb{R} \) olmak üzere,
\( \dfrac{x}{y} = \dfrac{7}{8} \)
\( 3x - 4y = 55 \)
eşitlikleri veriliyor. Buna göre \( y - x \) farkı kaçtır?
Çözümü GösterBirinci eşitlikte içler - dışlar çarpımı yapalım.
\( 8x = 7y \)
\( 8x - 7y = 0 \)
İki denklemden oluşan denklem sistemini çözmek için birinci denklemi 4, ikinci denklemi -7 ile çarpalım.
\( 32x - 28y = 0 \)
\( -21x + 28y = -385 \)
Eşitlikleri taraf tarafa toplayalım.
\( 32x + (-21x) - 28y + 28y = 0 + (-385) \)
\( 11x = -385 \)
\( x = -35 \)
\( y \) değerini bulmak için bu değeri denklemlerden birinde yerine koyalım.
\( 8x = 7y \)
\( 8(-35) = 7y \)
\( y = -40 \)
Buna göre \( y - x = -40 - (-35) = -5 \) olarak bulunur.
\( 4mx - 10 = y \)
\( (n - m)x + 2m = 2y \)
denklem sisteminin çözüm kümesi \( (x, y) = (1, 6) \) olduğuna göre, \( n \) kaçtır?
Çözümü GösterBir denklem sisteminin çözüm kümesi sistemdeki tüm denklemleri sağlamalıdır.
Buna göre \( (x, y) = (1, 6) \) sıralı ikilisini önce birinci denklemde yerine koyalım.
\( 4m(1) - 10 = 6 \)
\( 4m = 16 \)
\( m = 4 \)
\( (x, y) = (1, 6) \) sıralı ikilisini ikinci denklemde yerine koyalım.
\( (n - m)1 + 2m = 2(6) \)
\( m = 4 \) değerini kullanalım.
\( n - 4 + 2(4) = 12 \)
\( n = 8 \) bulunur.
Bir kitaplıktaki kitaplar hakkında aşağıdaki bilgiler veriliyor.
- Bu kitaplıkta 3 tür kitap bulunmaktadır.
- Şiir türünde olmayan kitap sayısı 22'dir.
- Deneme türünde olmayan kitap sayısı 19'dur.
- Roman türünde olmayan kitap sayısı 5'tir.
Buna göre bu kitaplıktaki roman sayısı kaçtır?
Çözümü GösterKitaplıktaki şiir türündeki kitap sayısına \( s \), deneme türündeki kitap sayısına \( d \), roman türündeki kitap sayısına \( r \) diyelim.
Verilen bilgilere göre denklemler kuralım.
Şiir türünde olmayan kitap sayısı 22'dir.
\( d + r = 22 \)
Deneme türünde olmayan kitap sayısı 19'dur.
\( s + r = 19 \)
Roman türünde olmayan kitap sayısı 5'tir.
\( s + d = 5 \)
Üç denklemi taraf tarafa toplayalım.
\( 2s + 2d + 2r = 22 + 19 + 5 \)
Eşitliğin sol tarafını 2 parantezine alalım.
\( 2(s + d + r) = 46 \)
\( s + d + r = 23 \)
Roman sayısını bulmak için toplam kitap sayısından roman olmayan kitapların sayısını, yani \( s + d \) toplamını çıkaralım.
\( r = s + d + r - (s + d) \)
\( = 23 - 5 = 18 \) bulunur.
\( x, y \in \mathbb{Z^-} \) olmak üzere,
\( 9x^2 = 53 + y^2 \) denklemi veriliyor.
Buna göre \( y \) kaçtır?
Çözümü GösterBilinmeyenleri eşitliğin solunda toplayalım.
\( 9x^2 - y^2 = 53 \)
Kare farkı özdeşliğini kullanarak ifadeyi çarpanlarına ayıralım.
\( (3x)^2 - y^2 = 53 \)
\( (3x - y)(3x + y) = 53 \)
53 asal sayı olduğuna göre çarpanları sırasıyla \( \pm 1 \) ve \( \pm 53 \) olabilir.
\( x \) ve \( y \) negatif oldukları için \( 3x + y \) toplamı negatiftir, dolayısıyla \( 3x - y \) de negatif olmalıdır.
\( 3x - y = -1 \)
\( 3x + y = -53 \)
Bu denklemleri taraf tarafa toplayarak \( y \)'yi yok edelim.
\( 6x = -54 \)
\( x = -9 \)
\( x \) değerini iki denklemden birinde yerine koyarak \( y \) değerini bulalım.
\( 3(-9) - y = -1 \)
\( -27 - y = -1 \)
\( y = -26 \) bulunur.
\( 4x - y = 9 \)
\( 12x - 18 = 3y \)
denklemlerinin ortak çözüm kümesini bulunuz.
Çözümü Göster1. yöntem:
İki bilinmeyenli iki denklemden oluşan bu denklem sistemini çözmek için yerine koyma yöntemini kullanalım.
İlk denklemde \( y \)'yi yalnız bırakalım.
\( y = 4x - 9 \)
Bulduğumuz \( y \) değerini ikinci denklemde yerine koyalım.
\( 12x - 18 = 3(4x - 9) \)
\( 12x - 18 = 12x - 27 \)
\( -18 = -27 \)
Bu eşitlik hiçbir \( x \) değeri için sağlanmayacağı için çözüm kümesi boş kümedir.
Çözüm kümesi: \( x \in \emptyset \)
2. yöntem:
İki denklem de birinci dereceden ve iki bilinmeyenli olduğu için birer doğru ifade ederler.
İki denklemde de \( y \)'yi yalnız bırakalım.
\( y = 4x - 9 \)
\( y = 4x - 6 \)
İki denklemde de \( x \) katsayıları (eğimler) birbirine eşit, sabit terimler farklı olduğu için denklemlerin karşılık geldiği doğrular birbirine paraleldir.
Paralel doğrular hiçbir noktada kesişmedikleri için denklemlerin çözüm kümeleri boş küme olur.
\( (m - 2)x + 3y = 5 \)
\( 6x + (n + 4)y = -10 \)
denklem sisteminin çözüm kümesi sonsuz sayıda eleman içerdiğine göre, \( m + n \) kaçtır?
Çözümü Gösterİki denklem de birinci dereceden olduğu için birer doğru ifade ederler.
İki denklemin çözüm kümesi sonsuz sayıda eleman içeriyorsa bu doğrular çakışık olmalıdır.
İki doğrunun çakışık olması için denklemlerinin katsayılarının ve sabit terimlerinin oranları birbirine eşit olmalıdır.
Doğruların kapalı denklemlerini yazalım.
\( (m - 2)x + 3y - 5 = 0 \)
\( 6x + (n + 4)y + 10 = 0 \)
\( \dfrac{m - 2}{6} = \dfrac{3}{n + 4} = \dfrac{-5}{10} \)
\( \dfrac{m - 2}{6} = \dfrac{3}{n + 4} = \dfrac{-1}{2} \)
Sabit terimlerin oranı \( \frac{-1}{2} \) olduğu için diğer terimler arasında da aynı oran bulunmalıdır.
\( \dfrac{m - 2}{6} = \dfrac{-1}{2} \)
İçler - dışlar çarpımı yapalım.
\( 2(m - 2) = -1(6) \)
\( 2m - 4 = -6 \)
\( m = -1 \)
\( y \)'nin katayıları arasındaki oranı inceleyelim.
\( \dfrac{3}{n + 4} = \dfrac{-1}{2} \)
İçler - dışlar çarpımı yapalım.
\( 2(3) = -1(n + 4) \)
\( 6 = -n - 4 \)
\( n = -10 \)
\( m + n = -1 + (-10) = -11 \) olarak bulunur.
\( \dfrac{x + y}{8} - \dfrac{x - y}{5} = -1 \)
\( \dfrac{x + y}{4} - \dfrac{x - y}{9} = 24 \)
eşitlikleri veriliyor. Buna göre, \( y \) kaçtır?
Çözümü GösterDenklemleri \( x \) ve \( y \) için çözmek daha uzun zaman alacağı için \( x + y \) ve \( x - y \) için çözelim. Bunun için aşağıdaki gibi değişken değiştirme uygulayalım.
\( x + y = a \)
\( x - y = b \)
Buna göre denklemler aşağıdaki gibi olur.
\( \dfrac{a}{8} - \dfrac{b}{5} = -1 \)
\( \dfrac{a}{4} - \dfrac{b}{9} = 24 \)
İki bilinmeyenli iki denklemden oluşan sistemi çözmek için yok etme yöntemini kullanalım.
İkinci denklemi \( -\frac{1}{2} \) ile çarpalım.
\( -\dfrac{a}{8} + \dfrac{b}{18} = -12 \)
Denklemleri taraf tarafa toplayalım.
\( -\dfrac{b}{5} + \dfrac{b}{18} = -1 + (-12) \)
\( -\dfrac{18b}{90} + \dfrac{5b}{90} = -13 \)
\( -\dfrac{13b}{90} = -13 \)
\( 13b = 13 \cdot 90 \)
\( b = 90 \)
Bu değeri denklemlerden birinde yerine koyarak \( a \) değerini bulalım.
\( \dfrac{a}{4} - \dfrac{90}{9} = 24 \)
\( \dfrac{a}{4} - 10 = 24 \)
\( \dfrac{a}{4} = 34 \)
\( a = 136 \)
Bulduğumuz \( a \) ve \( b \) değerlerini değişken değiştirmek için kullandığımız denklemlerde yerine koyalım.
\( x + y = a = 136 \)
\( x - y = b = 90 \)
İki bilinmeyenli iki denklemden oluşan bu sistemi çözmek için yok etme yöntemini kullanalım.
Denklemleri taraf tarafa toplayalım.
\( x + x + y + (-y) = 136 + 90 \)
\( 2x = 226 \)
\( x = 113 \)
Bu değeri denklemlerden birinde yerine koyarak \( y \) değerini bulalım.
\( x + y = 136 \)
\( 113 + y = 136 \)
\( y = 136 - 113 = 23 \) bulunur.
\( (a + b)x + 3y - 6 = 0 \)
\( 2x + (4a - 3b)y - 12 = 0 \)
doğruları \( A(\frac{9}{2}, -1) \) noktasında kesiştiğine göre, \( \frac{a}{b} \) oranı kaçtır?
Çözümü GösterBu iki doğru \( A \) noktasında kesişiyorlarsa bu noktanın koordinatları iki doğrunun denklemini de sağlamalıdır.
\( A \) noktasının koordinatlarını iki denklemde de yerine koyalım.
Denklem 1:
\( (a + b)x + 3y - 6 = 0 \)
\( (a + b)\dfrac{9}{2} + 3(-1) - 6 = 0 \)
\( \dfrac{9(a + b)}{2} - 9 = 0 \)
\( a + b \) ifadesini eşitlikte yalnız bırakalım.
\( \dfrac{9(a + b)}{2} = 9 \)
\( 9(a + b) = 2 \cdot 9 \)
\( a + b = 2 \)
Denklem 2:
\( 2x + (4a - 3b)y - 12 = 0 \)
\( 2 \cdot \dfrac{9}{2} + (4a - 3b)(-1) - 12 = 0 \)
\( 9 + 3b - 4a - 12 = 0 \)
\( 3b - 4a \) ifadesini eşitlikte yalnız bırakalım.
\( 3b - 4a = 12 - 9 = 3 \)
Elde ettiğimiz iki bilinmeyenli iki denklemi eşitleme yöntemi ile çözelim.
İki denklemde de \( a \)'yı yalnız bırakalım.
\( a = 2 - b \)
\( 4a = 3b - 3 \Longrightarrow a = \dfrac{3b - 3}{4} \)
Bulduğumuz ifadeleri birbirine eşitleyelim.
\( a = 2 - b = \dfrac{3b - 3}{4} \)
İçler - dışlar çarpımı yapalım.
\( 4(2 - b) = 3b - 3 \)
\( 8 - 4b = 3b - 3 \)
Sabit terimleri eşitliğin sol tarafında, bilinmeyenleri sağ tarafında toplayalım.
\( 11 = 7b \)
Eşitliğin taraflarını 7'ye bölelim.
\( b = \dfrac{11}{7} \)
\( b \) değerini eşitliklerden birinde yerine koyarak \( a \) değerini bulalım.
\( a = 2 - \dfrac{11}{7} = \dfrac{3}{7} \)
\( \frac{a}{b} \) oranını bulalım.
\( \dfrac{a}{b} = \dfrac{\frac{3}{7}}{\frac{11}{7}} = \dfrac{3}{11} \) olarak bulunur.
\( 3x - 4y + 11z = 28 \)
\( 9x + 7y + 33z = 198 \)
denklemleri veriliyor. Buna göre \( y \) kaçtır?
Çözümü GösterDenklemleri incelediğimizde \( x \) ve \( z \) değişkenlerinin katsayılarının oranının sabit olduğunu görüyoruz, bu da iki değişkeni tek seferde yok edebileceğimizi göstermektedir.
Birinci denklemin taraflarını -3 ile çarpalım.
\( -9x + 12y - 33z = -84 \)
\( 9x + 7y + 33z = 198 \)
Denklemleri taraf tarafa toplayalım.
\( 12y + 7y = -84 + 198 \)
\( 19y = 114 \)
\( y = 6 \) bulunur.
\( a, b, c, d \) sayılarının üçerli toplamı alındığında 121, 159, 172, 193 sayıları elde ediliyor.
Buna göre bu sayılardan en küçüğü kaçtır?
Çözümü GösterSayıların üçerli toplamını alalım.
\( a + b + c = 121 \)
\( a + b + d = 159 \)
\( a + c + d = 172 \)
\( b + c + d = 193 \)
4 eşitliği taraf tarafa toplayalım.
\( 3a + 3b + 3c + 3d = 645 \)
\( a + b + c + d = 215 \)
4 tam sayı arasından en küçüğünü bulmak için, bu denklemden yukarıdaki 4 eşitlik içinde sonucu en büyük olanı çıkaralım.
\( a + b + c + d - (b + c + d) = 215 - 193 \)
\( a = 22 \) bulunur.
\( 2a + b + 4c = 150 \)
\( 4a + 7b + c = 220 \)
\( 3a + 5b + 2c = 190 \)
eşitliklerine göre, \( a, b, c \) bilinmeyenlerinin ortalaması kaçtır?
Çözümü GösterÜç bilinmeyenin ortalamasını bulmak için bilinmeyenlerin değerlerini ayrı ayrı bulabiliriz, alternatif olarak bilinmeyenlerin toplamını bulmak için katsayıları aynı olan yeni bir eşitlik elde etmeye çalışabiliriz.
İlk iki eşitliği taraf tarafa toplayalım.
\( (2a + b + 4c) + (4a + 7b + c) = 150 + 220 \)
\( 6a + 8b + 5c = 370 \)
Bu eşitlikten sorudaki üçüncü eşitliği çıkaralım.
\( (6a + 8b + 5c) - (3a + 5b + 2c) = 370 - 190 \)
\( 3a + 3b + 3c = 180 \)
\( a + b + c = 60 \)
Bilinmeyenlerin ortalamasını bulmak için toplamlarını üçe bölelim.
\( \dfrac{a + b + c}{3} = \dfrac{60}{3} \)
\( = 20 \) bulunur.
\( \dfrac{xy}{x + y} = \dfrac{2}{7} \)
\( \dfrac{yz}{y + z} = \dfrac{2}{5} \)
\( \dfrac{xz}{x + z} = \dfrac{2}{3} \)
olduğuna göre, \( x \) kaçtır?
Çözümü GösterBirinci denklemde eşitliğin her iki tarafının çarpmaya göre tersini alalım.
\( \dfrac{x + y}{xy} = \dfrac{7}{2} \)
\( \dfrac{x}{xy} + \dfrac{y}{xy} = \dfrac{7}{2} \)
\( \dfrac{1}{y} + \dfrac{1}{x} = \dfrac{7}{2} \)
Aynı işlemleri ikinci denkleme uygulayalım.
\( \dfrac{y + z}{yz} = \dfrac{5}{2} \)
\( \dfrac{y}{yz} + \dfrac{z}{yz} = \dfrac{5}{2} \)
\( \dfrac{1}{z} + \dfrac{1}{y} = \dfrac{5}{2} \)
Aynı işlemleri üçüncü denkleme uygulayalım.
\( \dfrac{x + z}{xz} = \dfrac{3}{2} \)
\( \dfrac{x}{xz} + \dfrac{z}{xz} = \dfrac{3}{2} \)
\( \dfrac{1}{z} + \dfrac{1}{x} = \dfrac{3}{2} \)
İkinci denklemi \( -1 \) ile çarpalım ve bulduğumuz üç denklemi yazalım.
\( \dfrac{1}{y} + \dfrac{1}{x} = \dfrac{7}{2} \)
\( -\dfrac{1}{z} - \dfrac{1}{y} = -\dfrac{5}{2} \)
\( \dfrac{1}{z} + \dfrac{1}{x} = \dfrac{3}{2} \)
Denklemleri taraf tarafa toplayalım.
\( \dfrac{2}{x} = \dfrac{5}{2} \)
İçler - dışlar çarpımı yapalım.
\( 5x = 4 \)
\( x = \dfrac{4}{5} \) bulunur.
\( 2x = -5y + 9 \)
\( x + 2y = 6 \)
eşitliklerine göre, \( x + y \) toplamı kaçtır?
Çözümü Gösterİki bilinmeyenli iki denklemden oluşan bu denklem sistemini çözmek için yerine koyma yöntemini kullanalım.
İkinci denklemde \( x \)'i yalnız bırakalım.
\( x = 6 - 2y \)
Bulduğumuz \( x \) değerini birinci denklemde yerine koyalım.
\( 2(6 - 2y) = -5y + 9 \)
Parantezi genişletelim.
\( 12 - 4y = -5y + 9 \)
\( y = -3 \)
Bu değeri denklemlerden birinde yerine koyarak \( x \) değerini bulalım.
\( x + 2(-3) = 6 \)
\( x - 6 = 6 \)
\( x = 12 \)
\( x + y = 12 + (-3) = 9 \) bulunur.
\( x^2 - 2x + 3y^2 = 12 \)
\( 2y + x + 2 = 0 \)
eşitlikleri veriliyor. Bu denklem sisteminin çözümü olan \( (x, y) \) ikililerini bulunuz.
Çözümü Gösterİki bilinmeyenli iki denklemden oluşan bu denklem sistemini çözmek için yerine koyma yöntemini kullanalım.
İkinci denklemde \( x \)'i yalnız bırakalım.
\( x = -2y - 2 \)
Bulduğumuz \( x \) değerini birinci denklemde yerine koyalım.
\( (-2y - 2)^2 - 2(-2y - 2) + 3y^2 = 12 \)
Parantezleri genişletelim.
\( 4y^2 + 8y + 4 + 4y + 4 + 3y^2 = 12 \)
Benzer terimleri kendi aralarında toplayalım.
\( 7y^2 + 12y + 8 = 12 \)
Tüm terimleri eşitliğin sol tarafında toplayalım.
\( 7y^2 + 12y - 4 = 0 \)
İfadeyi çarpanlarına ayıralım.
\( (7y - 2)(y + 2) = 0 \)
\( y = \frac{2}{7} \) ya da \( y = -2 \)
Bu değerleri denklemlerden birinde yerine koyarak \( x \) değerlerini bulalım.
\( y = \frac{2}{7} \) için:
\( 2(\dfrac{2}{7}) + x + 2 = 0 \)
\( x = -\dfrac{18}{7} \)
Buna göre \( (x, y) = (-\frac{18}{7}, \frac{2}{7}) \) denklemin bir çözümüdür.
\( y = -2 \) için:
\( 2(-2) + x + 2 = 0 \)
\( x = 2 \)
Buna göre \( (x, y) = (2, -2) \) denklemin bir çözümüdür.
Çözüm kümesi: \( (x, y) \in \{(-\frac{18}{7}, \frac{2}{7}), (2, -2)\} \)