Birinci Dereceden Bir Bilinmeyenli Denklemler
Birinci dereceden bir bilinmeyenli denklemler, derecesi bir olan tek bir bilinmeyenden oluşan denklemlerdir.
\( a, b \in \mathbb{R}, \quad a \ne 0 \) olmak üzere,
\( ax + b = 0 \)
Bu denklemde \( x \) denklemin bilinmeyeni, \( a \) ve \( b \) denklemin katsayılarıdır. \( b \) katsayısı aynı zamanda denklemin sabit terimidir.
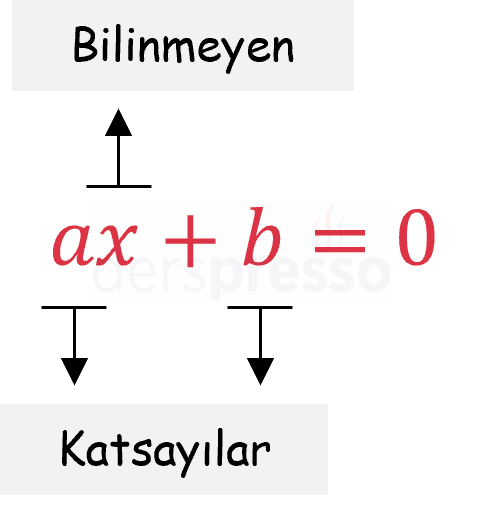
Birinci dereceden bir bilinmeyenli denklemler farklı formlarda olabilir. Aşağıdaki denklemlerin tümünde terimler düzenlendiğinde ilk satırdaki \( ax + b = 0 \) formundaki \( 2x - 4 = 0 \) denklemi elde edilebilir.
\( 2x - 4 = 0 \)
\( 2x = 4 \)
\( 4(x - 1) = 2x \)
\( \dfrac{4x + 2}{2} = x + 3 \)
\( ax + b = 0 \) Denkleminin Çözüm Kümesi
\( ax + b = 0 \) formundaki denklemlerin çözüm kümesi üç farklı şekilde olabilir.
Tek Çözüm
\( a \) katsayısının sıfırdan farklı olduğu durumda denklemin tek çözümü olur.
\( a \ne 0 \) ise,
\( ax + b = 0 \)
\( x = -\dfrac{b}{a} \)
Çözüm kümesi: \( x = -\dfrac{b}{a} \)
\( 3x - 15 = 0 \)
\( 3x = 15 \)
\( x = 5 \)
Çözüm kümesi: \( x = 5 \)
Tüm Reel Sayılar
\( a \) ve \( b \) katsayılarının ikisinin de sıfır olduğu durumda denklemin tüm reel sayılar olmak üzere sonsuz çözümü olur. \( a = 0 \) olduğu durumda bu denklemin bir lineer denklem olmayacağını vurgulayalım.
\( a = b = 0 \) ise,
\( ax + b = 0 \)
\( 0x + 0 = 0 \)
\( 0 = 0 \)
Çözüm kümesi: \( x \in \mathbb{R} \)
\( (m - 3n)x + 2m - 5n - 2 = 0 \)
Yukarıdaki denklemin sonsuz çözümünün olması için \( m \) ve \( n \) değerleri ne olmalıdır?
Denklemin sonsuz çözümünün olması için \( x \) katsayısı ve sabit terim sıfır olmalıdır.
\( m - 3n = 0 \)
\( \Longrightarrow m = 3n \)
\( 2m - 5n - 2 = 0 \)
\( \Longrightarrow 6n - 5n - 2 = 0 \)
\( \Longrightarrow n = 2 \)
\( m = 3n = 6 \)
\( (m, n) = (6, 2) \) bulunur.
Bu değerleri denklemde yerine koyalım.
\( (6 - 3 \cdot 2)x + 2 \cdot 6 - 5 \cdot 2 - 2 = 0 \)
\( 0x + 0 = 0 \)
\( a \) ve \( b \) katsayılarının ikisi de sıfır olduğunda oluşan \( 0 = 0 \) eşitliği, \( x \) bilinmeyeninin alabileceği tüm değerler için, yani \( x \)'in değerinden bağımsız olarak eşitliğin sağlanacağını gösterir, dolayısıyla çözüm kümesi tüm reel sayılar olur.
Boş Küme
\( a \) katsayısı sıfır, \( b \) katsayısı sıfırdan farklı olduğu durumda denklemin çözüm kümesi boş küme olur. Yukarıdaki duruma benzer şekilde, \( a = 0 \) olduğu durumda bu denklemin bir lineer denklem olmayacağını vurgulayalım.
\( a = 0, \quad b \ne 0 \) ise,
\( ax + b = 0 \)
\( 0x + b = 0 \)
\( b = 0 \)
\( b \ne 0 \) varsaydığımız için eşitlik hiçbir \( x \) değeri için sağlanmaz.
Çözüm kümesi: \( x \in \{\} \)
\( (3m + 9)x - m - 2n - 7 = 0 \)
Yukarıdaki denklemin çözüm kümesinin boş küme olması için \( n \) hangi değeri alamaz?
Denklemin çözüm kümesinin boş küme olması için \( x \) katsayısı sıfır olmalı ve sabit terim sıfırdan farklı olmalıdır.
\( 3m + 9 = 0 \)
\( \Longrightarrow m = -3 \)
\( -m - 2n - 7 \ne 0 \)
\( \Longrightarrow 3 - 2n - 7 \ne 0 \)
\( \Longrightarrow n \ne -2 \)
Buna göre denklemin çözüm kümesinin boş küme olması için \( n = -2 \) değerini alamaz.
\( b \)'nin değerini sıfırdan farklı aldığımız için, yukarıda oluşan \( b = 0 \) eşitliği \( x \)'in hiçbir değeri için eşitliğin sağlanmayacağını gösterir, dolayısıyla çözüm kümesi boş küme olur.
Birinci Dereceden Bir Bilinmeyenli Denklemlerin Çözümü
Birinci dereceden bir bilinmeyenli denklemlerin çözümünde bilinmeyen eşitliğin bir tarafında yalnız ve katsayısız bir şekilde bırakılır ve eşitliği sağlayan bilinmeyen değeri bulunur. Bunu sağlarken önceki bölümde gördüğümüz denklem özellikleri kullanılır.
Birinci dereceden bir bilinmeyenli denklemlerin çözüm adımlarını bir örnek üzerinden gösterelim.
Aşağıdaki denklemi sağlayan \( x \) değerini bulalım.
\( 3(x + 4) - 2x + 6 = \dfrac{-2(x + 8)}{3} \)
Adım 1: Taraflardan biri kesirli ifade şeklindeyse her iki tarafa aynı çarpma işlemi uygulanarak paydadan kurtulunur. Her iki taraf da kesirli ifade şeklindeyse içler - dışlar çarpımı yapılır.
Denklemin sağ tarafındaki paydadan kurtulmak için her iki tarafı 3 ile çarpalım.
\( (3(x + 4) - 2x + 6) \cdot 3 = \dfrac{-2(x + 8)}{3} \cdot 3 \)
\( 3(3(x + 4) - 2x + 6) = -2(x + 8) \)
Adım 2: Eşitliğin her iki tarafındaki parantezli terimler dağıtılır.
Denklemin iki tarafındaki parantezleri dağıtalım.
\( 9(x + 4) - 6x + 18 = -2x - 16 \)
\( 9x + 36 - 6x + 18 = -2x - 16 \)
Adım 3: Her iki taraftaki benzer terimler kendi aralarında toplanır.
Denklemin sol tarafındaki benzer terimleri toplayalım.
\( 3x + 54 = -2x - 16 \)
Adım 4: Her iki tarafa aynı toplama ve çıkarma işlemleri uygulanarak bilinmeyenli terimler eşitliğin bir tarafında, sabit terimler eşitliğin diğer tarafında toplanır. İşlem kolaylığı açısından bilinmeyenlerin bilinmeyen katsayısının daha büyük olduğu tarafta toplanması tercih edilebilir.
Eşitliğin sağ tarafındaki \( x \)'li terimi eşitliğin sol tarafına almak için her iki tarafa \( 2x \) ekleyelim.
\( 3x + 54 + 2x = -2x - 16 + 2x \)
\( 5x + 54 = -16 \)
Eşitliğin sol tarafındaki sabit terimi eşitliğin sağ tarafına almak için her iki taraftan \( 54 \) çıkaralım.
\( 5x + 54 - 54 = -16 - 54 \)
\( 5x = -70 \)
Adım 5: Her iki tarafa aynı çarpma ve bölme işlemleri uygulanarak bilinmeyenin katsayısı 1'e getirilir. Bu adım sonucunda bulunan değer denklemin olası bir çözümüdür.
\( x \)'in katsayısını 1'e getirmek için her iki tarafı 5'e bölelim.
\( \dfrac{5x}{5} = \dfrac{-70}{5} \)
\( x = -14 \)
Adım 6: Bulunan değer orijinal denklemde yerine konarak eşitliğin sağlanıp sağlanmadığı kontrol edilir.
\( x = -14 \) değerini orijinal denklemde yerine koyalım.
\( 3(x + 4) - 2x + 6 = \dfrac{-2(x + 8)}{3} \)
\( 3(-14 + 4) - 2(-14) + 6 \stackrel{?}{=} \dfrac{-2(-14 + 8)}{3} \)
\( -30 + 28 + 6 \stackrel{?}{=} \dfrac{12}{3} \)
\( 4 = 4 \)
Eşitlik sağlandığı için \( x = -14 \) değeri denklemin çözümüdür.
Çözüm kümesi: \( x = -14 \)
Bir miktar paranın 30 TL eksiğinin üçte ikisi, paranın üç katının 20 TL fazlasının beşte birine eşitse bu para kaç TL'dir?
Sorudaki bilinmeyeni tanımlayalım ve verilen bilgileri cebirsel ifadelere dönüştürerek denklemi kuralım.
\( x \): Para miktarı
\( (x - 30) \cdot \dfrac{2}{3} = (3x + 20) \cdot \dfrac{1}{5} \)
Denklemi düzenleyelim.
\( \dfrac{2(x - 30)}{3} = \dfrac{3x + 20}{5} \)
Denklemin iki tarafındaki paydalardan kurtulmak için içler - dışlar çarpımı yapalım.
\( 2(x - 30) \cdot 5 = (3x + 20) \cdot 3 \)
\( 10(x - 30) = 3(3x + 20) \)
Denklemin iki tarafındaki parantezleri dağıtalım.
\( 10x - 300 = 9x + 60 \)
\( x \)'li terimleri eşitliğin sol tarafına almak için her iki taraftan \( 9x \) çıkaralım.
\( 10x - 300 - 9x = 9x + 60 - 9x \)
\( x - 300 = 60 \)
Sabit terimleri eşitliğin sağ tarafına almak için her iki tarafa \( 300 \) ekleyelim.
\( x - 300 + 300 = 60 + 300 \)
\( x = 360 \)
Bulduğumuz değeri orijinal denklemde yerine koyarak eşitliği sağlayıp sağlamadığını kontrol edelim.
\( (x - 30) \cdot \dfrac{2}{3} = (3x + 20) \cdot \dfrac{1}{5} \)
\( (360 - 30) \cdot \dfrac{2}{3} = (3(360) + 20) \cdot \dfrac{1}{5} \)
\( 330 \cdot \dfrac{2}{3} = 1100 \cdot \dfrac{1}{5} \)
\( 220 = 220 \)
Eşitlik sağlandığı için verilen koşulları sağlayan para miktarı 220 TL'dir.
Çözüm kümesi: \( x = 220 \)
Aşağıdaki denklemleri sağlayan \( x \) değerlerini bulunuz.
(a) \( 25 - (6 - 2x) = 35 - 3(2x + 8) \)
(b) \( 6x - 1 - 3(x + 12) - 8x = 4(5 - 2x) \)
(c) \( 45x - 9(3x - 7) - 80 = 30(x - 2) - 6x - 17 \)
Çözümü Göster(a) seçeneği:
\( 25 - (6 - 2x) = 35 - 3(2x + 8) \)
Verilen eşitlikteki parantezleri genişletelim.
\( 25 - 6 + 2x = 35 - 6x - 24 \)
Benzer terimleri kendi aralarında toplayalım.
\( 19 + 2x = 11 - 6x \)
\( x \)'li terimleri eşitliğin sol tarafına, sabit terimleri sağ tarafına atarak \( x \)'i yalnız bırakalım.
\( 8x = -8 \)
Eşitliğin taraflarını 8'e bölelim.
\( x = -1 \)
(b) seçeneği:
\( 6x - 1 - 3(x + 12) - 8x = 4(5 - 2x) \)
Verilen eşitlikteki parantezleri genişletelim.
\( 6x - 1 - 3x - 36 - 8x = 20 - 8x \)
Benzer terimleri kendi aralarında toplayalım.
\( -5x - 37 = 20 - 8x \)
\( x \)'li terimleri eşitliğin sol tarafına, sabit terimleri sağ tarafına atarak \( x \)'i yalnız bırakalım.
\( 3x = 57 \)
Eşitliğin taraflarını 3'e bölelim.
\( x = 19 \)
(c) seçeneği:
\( 45x - 9(3x - 7) - 80 = 30(x - 2) - 6x - 17 \)
Verilen eşitlikteki parantezleri genişletelim.
\( 45x - 27x + 63 - 80 = 30x - 60 - 6x - 17 \)
Benzer terimleri kendi aralarında toplayalım.
\( 18x - 17 = 24x - 77 \)
\( x \)'li terimleri eşitliğin sol tarafına, sabit terimleri sağ tarafına atarak \( x \)'i yalnız bırakalım.
\( -6x = -60 \)
Eşitliğin taraflarını -6'ya bölelim.
\( x = 10 \)
Aşağıdaki denklemlerin çözüm kümelerini bulunuz.
(a) \( 18x - 2(3x - 1) = 86 \)
(b) \( 2(3x - 5) + 3 = 4x - 15 \)
(c) \( 3(2x - 1) + 6(-x - 1) = 5(4x + 5) - 2(10x - 4) \)
Çözümü Göster(a) seçeneği:
\( 18x - 2(3x - 1) = 86 \)
Verilen eşitlikteki parantezi genişletelim.
\( 18x - 6x + 2 = 86 \)
Benzer terimleri kendi aralarında toplayalım.
\( 12x + 2 = 86 \)
Sabit terimi eşitliğin sağ tarafına atarak \( x \)'li terimi yalnız bırakalım.
\( 12x = 84 \)
Eşitliğin iki tarafını 12'ye bölelim.
\( x = 7 \)
(b) seçeneği:
\( 2(3x - 5) + 3 = 4x - 15 \)
Verilen eşitlikteki parantezi genişletelim.
\( 6x - 10 + 3 = 4x - 15 \)
Benzer terimleri kendi aralarında toplayalım.
\( 6x - 7 = 4x - 15 \)
Sabit terimleri eşitliğin sağ tarafında, \( x \)'li terimleri eşitliğin sol tarafında toplayalım.
\( 6x - 4x = -15 + 7 \)
Benzer terimleri kendi aralarında toplayalım.
\( 2x = -8 \)
Eşitliğin iki tarafını 2'ye bölelim.
\( x = -4 \)
(c) seçeneği:
\( 3(2x - 1) + 6(-x - 1) = 5(4x + 5) - 2(10x - 4) \)
Verilen eşitlikteki parantezleri genişletelim.
\( 6x - 3 - 6x - 6 = 20x + 25 - 20x + 8 \)
Benzer terimleri kendi aralarında toplayalım.
\( -9 = 33 \)
Bu eşitlik hiçbir \( x \) değeri için sağlanmayacağı için çözüm kümesi boş kümedir.
Çözüm kümesi: \( x \in \emptyset \)
Aşağıdaki denklemleri sağlayan \( x \) değerlerini bulunuz.
(a) \( \dfrac{3x}{4} + \dfrac{x}{6} = 66 \)
(b) \( \dfrac{x - 2}{2} - 3x = -\dfrac{5x}{2} - 1 \)
(c) \( \dfrac{\frac{15x}{2} - 4}{5} - \dfrac{1 + 3x}{2} = 0 \)
Çözümü Göster(a) seçeneği:
\( \dfrac{3x}{4} + \dfrac{x}{6} = 66 \)
Eşitliğin sol tarafındaki rasyonel ifadelerin paydalarını eşitleyelim.
\( \dfrac{9x}{12} + \dfrac{2x}{12} = 66 \)
Paydaki \( x \)'li ifadeleri toplayalım.
\( \dfrac{11x}{12} = 66 \)
İçler - dışlar çarpımı yapalım.
\( 11x = 66 \cdot 12 \)
Eşitliğin her iki tarafını 11'e bölelim.
\( x = \dfrac{66 \cdot 12}{11} \)
\( x = 72 \)
(b) seçeneği:
\( \dfrac{x - 2}{2} - 3x = -\dfrac{5x}{2} - 1 \)
Eşitlikteki tüm terimlerin paydalarını eşitleyelim.
\( \dfrac{x - 2}{2} - \dfrac{6x}{2} = -\dfrac{5x}{2} - \dfrac{2}{2} \)
\( \dfrac{x - 2 - 6x}{2} = \dfrac{-5x - 2}{2} \)
Eşitliğin taraflarını 2 ile çarpalım.
\( x - 2 - 6x = -5x - 2 \)
Benzer terimleri kendi aralarında toplayalım.
\( -5x - 2 = -5x - 2 \)
\( 0 = 0 \)
Bu eşitlik tüm \( x \) değerleri için sağlanacağı için çözüm kümesi tüm reel sayılardır.
Çözüm kümesi: \( x \in \mathbb{R} \)
(c) seçeneği:
\( \dfrac{\frac{15x}{2} - 4}{5} - \dfrac{1 + 3x}{2} = 0 \)
Eşitlikteki tüm terimlerin paydalarını eşitleyelim.
\( \dfrac{2(\frac{15x}{2} - 4)}{10} - \dfrac{5(1 + 3x)}{10} = 0 \)
\( \dfrac{2(\frac{15x}{2} - 4) - 5(1 + 3x)}{10} = 0 \)
Eşitliğin taraflarını 10 ile çarpalım.
\( 2(\dfrac{15x}{2} - 4) - 5(1 + 3x) = 0 \)
Verilen eşitlikteki parantezleri genişletelim.
\( 15x - 8 - 5 - 15x = 0 \)
Benzer terimleri kendi aralarında toplayalım.
\( -13 = 0 \)
Bu eşitlik hiçbir \( x \) değeri için sağlanmayacağı için çözüm kümesi boş kümedir.
Çözüm kümesi: \( x \in \emptyset \)
Aşağıdaki denklemleri sağlayan \( x \) değerlerini bulunuz.
(a) \( \dfrac{x}{3} - \dfrac{2x}{9} - 13 = \dfrac{1}{3} + x \)
(b) \( \dfrac{2}{2 - x} = \dfrac{4}{3 - x} \)
(c) \( \dfrac{2x - 3}{4x + 1} = \dfrac{-x - 1}{5 - 2x} \)
Çözümü Göster(a) seçeneği:
\( \dfrac{x}{3} - \dfrac{2x}{9} - 13 = \dfrac{1}{3} + x \)
Eşitlikteki tüm terimlerin paydalarını eşitleyelim.
\( \dfrac{3x}{9} - \dfrac{2x}{9} - \dfrac{117}{9} = \dfrac{3}{9} + \dfrac{9x}{9} \)
\( \dfrac{3x - 2x - 117}{9} = \dfrac{3 + 9x}{9} \)
Eşitliğin taraflarını 9 ile çarpalım.
\( 3x - 2x - 117 = 3 + 9x \)
Benzer terimleri kendi aralarında toplayalım.
\( x - 117 = 3 + 9x \)
\( x \)'li terimleri eşitliğin sol tarafına, sabit terimleri sağ tarafına atarak \( x \)'i yalnız bırakalım.
\( -8x = 120 \)
Eşitliğin taraflarını -8'e bölelim.
\( x = -15 \)
(b) seçeneği:
\( \dfrac{2}{2 - x} = \dfrac{4}{3 - x} \)
İçler - dışlar çarpımı yapalım.
Bu işlemi yaparken paydaları sıfır yapan \( x = 2 \) ve \( x = 3 \) değerlerinin denklemin geçerli birer çözümü olamayacağını not edelim.
\( 2(3 - x) = 4(2 - x) \)
\( 6 - 2x = 8 - 4x \)
\( x \)'li terimleri eşitliğin sol tarafına, sabit terimleri sağ tarafına atarak \( x \)'i yalnız bırakalım.
\( 2x = 2 \)
Eşitliğin taraflarını 2'ye bölelim.
\( x = 1 \)
(c) seçeneği:
\( \dfrac{2x - 3}{4x + 1} = \dfrac{-x - 1}{5 - 2x} \)
İçler - dışlar çarpımı yapalım.
Bu işlemi yaparken paydaları sıfır yapan \( x = -\frac{1}{4} \) ve \( x = \frac{5}{2} \) değerlerinin denklemin geçerli birer çözümü olamayacağını not edelim.
\( (2x - 3)(5 - 2x) = (4x + 1)(-x - 1) \)
\( 10x - 4x^2 - 15 + 6x = -4x^2 - 4x - x - 1 \)
Benzer terimleri kendi aralarında toplayalım.
\( 16x - 4x^2 - 15 = -4x^2 - 5x - 1 \)
\( x \)'li terimleri eşitliğin sol tarafına, sabit terimleri sağ tarafına atarak \( x \)'i yalnız bırakalım.
\( 21x = 14 \)
Eşitliğin taraflarını 21'e bölelim.
\( x = \dfrac{14}{21} = \dfrac{2}{3} \)
Aşağıdaki denklemleri sağlayan \( x \) değerlerini bulunuz.
(a) \( \dfrac{x}{3} + 8x - 5 = \dfrac{5(x - 7)}{6} \)
(b) \( \dfrac{3x - 8}{2} - \dfrac{12 - 2x}{3} = \dfrac{11x}{6} \)
(c) \( \dfrac{1}{3}(2x + 14) - \dfrac{1}{5}(-2x - 3) =\dfrac{1}{6}(x + 10) \)
Çözümü Göster(a) seçeneği:
\( \dfrac{x}{3} + 8x - 5 = \dfrac{5(x - 7)}{6} \)
Eşitlikteki tüm terimlerin paydalarını eşitleyelim.
\( \dfrac{2x}{6} + \dfrac{6(8x - 5)}{6} = \dfrac{5(x - 7)}{6} \)
\( \dfrac{2x + 6(8x - 5)}{6} = \dfrac{5(x - 7)}{6} \)
Eşitliğin taraflarını 6 ile çarpalım.
\( 2x + 6(8x - 5) = 5(x - 7) \)
Verilen eşitlikteki parantezleri genişletelim.
\( 2x + 48x - 30 = 5x - 35 \)
Benzer terimleri kendi aralarında toplayalım.
\( 50x - 30 = 5x - 35 \)
\( x \)'li terimleri eşitliğin sol tarafına, sabit terimleri sağ tarafına atarak \( x \)'i yalnız bırakalım.
\( 45x = -5 \)
Eşitliğin taraflarını 45'e bölelim.
\( x = -\dfrac{5}{45} = -\dfrac{1}{9} \)
(b) seçeneği:
\( \dfrac{3x - 8}{2} - \dfrac{12 - 2x}{3} = \dfrac{11x}{6} \)
Eşitlikteki tüm terimlerin paydalarını eşitleyelim.
\( \dfrac{3(3x - 8)}{6} - \dfrac{2(12 - 2x)}{6} = \dfrac{11x}{6} \)
\( \dfrac{3(3x - 8) - 2(12 - 2x)}{6} = \dfrac{11x}{6} \)
Eşitliğin taraflarını 6 ile çarpalım.
\( 3(3x - 8) - 2(12 - 2x) = 11x \)
Verilen eşitlikteki parantezleri genişletelim.
\( 9x - 24 - 24 + 4x = 11x \)
Benzer terimleri kendi aralarında toplayalım.
\( 13x - 48 = 11x \)
\( x \)'li terimleri eşitliğin sol tarafına, sabit terimleri sağ tarafına atarak \( x \)'i yalnız bırakalım.
\( 2x = 48 \)
Eşitliğin taraflarını 2'ye bölelim.
\( x = 24 \)
(c) seçeneği:
\( \dfrac{1}{3}(2x + 14) - \dfrac{1}{5}(-2x - 3) =\dfrac{1}{6}(x + 10) \)
Eşitlikteki tüm terimlerin paydalarını eşitleyelim.
\( \dfrac{10}{30}(2x + 14) - \dfrac{6}{30}(-2x - 3) = \dfrac{5}{30}(x + 10) \)
\( \dfrac{10(2x + 14) - 6(-2x - 3)}{30} = \dfrac{5(x + 10)}{30} \)
Eşitliğin taraflarını 30 ile çarpalım.
\( 10(2x + 14) - 6(-2x - 3) = 5(x + 10) \)
Verilen eşitlikteki parantezleri genişletelim.
\( 20x + 140 + 12x + 18 = 5x + 50 \)
Benzer terimleri kendi aralarında toplayalım.
\( 32x + 158 = 5x + 50 \)
\( x \)'li terimleri eşitliğin sol tarafına, sabit terimleri sağ tarafına atarak \( x \)'i yalnız bırakalım.
\( 27x = -108 \)
Eşitliğin taraflarını 27'ye bölelim.
\( x = -4 \)
\( -(3x + 6) - 2x - [-4x + (6 + x)] = -8x + (14x - 100) \)
olduğuna göre, \( x \) kaçtır?
Çözümü GösterEşitliğin iki tarafındaki parantezleri açarak benzer terimleri toplayalım.
\( -3x - 6 - 2x + 4x - (6 + x) = -8x + 14x - 100 \)
\( -3x - 6 - 2x + 4x - 6 - x = -8x + 14x - 100 \)
\( -2x - 12 = 6x - 100 \)
\( x \)'i yalnız bırakalım.
\( 8x = 88 \)
\( x = 11 \) bulunur.
\( (k - 7)x^4 + 5x^{n - 1} - 3kn = 8 \) ifadesi \( x \) değişkenine bağlı birinci dereceden bir bilinmeyenli bir denklemdir.
Buna göre \( x \) kaçtır?
Çözümü GösterDenklemin birinci dereceden olması için \( x^4 \)'lü terimin katsayısı sıfır olmalıdır.
\( k - 7 = 0 \Longrightarrow k = 7 \)
Denklemin birinci dereceden olması için ikinci terimin kuvveti 1 olmalıdır.
\( n - 1 = 1 \Longrightarrow n = 2 \)
Bulduğumuz \( k \) ve \( n \) değerlerini kullanarak denklemi yazalım.
\( 5x - 3 \cdot 7 \cdot 2 = 8 \)
\( 5x - 42 = 8 \)
Sabit terimi eşitliğin sağ tarafına atarak \( x \)'li terimi yalnız bırakalım.
\( 5x = 50 \)
Eşitliğin iki tarafını 5'e bölelim.
\( x = 10 \) bulunur.
\( \dfrac{t - 4}{5} - \dfrac{2t - 6}{3} = 4 \)
olduğuna göre, \( t \) kaçtır?
Çözümü GösterKesirlerin paydalarını eşitleyelim.
\( EKOK(5, 3) = 15 \)
Birinci kesri 3 ile, ikinci kesri 5 ile genişletelim.
\( \dfrac{3(t - 4)}{5 \cdot 3} - \dfrac{5(2t - 6)}{3 \cdot 5} = 4 \)
\( \dfrac{3t - 12}{15} - \dfrac{10t - 30}{15} = 4 \)
Elde ettiğimiz kesirleri tek paydada birleştirelim.
\( \dfrac{3t - 12 - 10t + 30}{15} = 4 \)
Paydaki benzer terimleri toplayalım.
\( \dfrac{-7t + 18}{15} = 4 \)
Eşitliğin iki tarafını 15 ile çarparak kesirli ifadeden kurtulalım.
\( \dfrac{15(-7t + 18)}{15} = 15 \cdot 4 \)
\( -7t + 18 = 60 \)
Sabit terimi eşitliğin sağ tarafına atarak \( t \)'li terimi yalnız bırakalım.
\( -7t + 18 - 18 = 60 - 18 \)
\( -7t = 42 \)
Eşitliğin iki tarafını -7'ye bölelim.
\( t = -6 \) bulunur.
\( \dfrac{k(3k - 2x)}{2x - 3k} + 4 = 0 \)
denkleminin çözüm kümesini bulunuz.
Çözümü GösterPaydaki parantez ifadesinin içini ve dışını \( -1 \) ile çarpalım.
\( \dfrac{-k(2x - 3k)}{2x - 3k} + 4 = 0 \)
Çözüm kümesinin paydadaki \( 2x - 3k \) ifadesini sıfır yapan \( x \) değerini içeremeyeceğini not ederek pay ve paydadaki bu çarpanı sadeleştirelim.
\( -k + 4 = 0 \)
\( k = 4 \)
Buna göre \( k = 4 \) değeri için eşitlik \( x \) değerinden bağımsız olarak sağlanır.
\( \dfrac{4(12 - 2x)}{2x - 12} + 4 = 0 \)
\( 2x - 12 \) ifadesini sıfır yapan \( x \) değerini bulalım.
\( 2x - 12 = 0 \)
\( x = 6 \)
Buna göre denklemin çözüm kümesi \( x = 6 \) hariç tüm reel sayılardır.
Çözüm kümesi: \( x \in \mathbb{R} - \{6\} \)
\( k \) sıfırdan farklı bir reel sayıdır.
\( (k - 5)x + 2k - 12 = 10 \)
denkleminin kökü 2 olduğuna göre, \( 2kx + 3k + 12 = 5x - k \) denkleminin çözüm kümesini bulunuz.
Çözümü Gösterİlk denklemin kökü 2 olduğuna göre \( x = 2 \) değeri eşitliği sağlar.
\( (k - 5) \cdot 2 + 2k - 12 = 10 \)
\( 2k - 10 + 2k - 12 = 10 \)
\( 4k - 22 = 10 \)
Sabit terimi eşitliğin sağ tarafına alarak \( k \)'lı ifadeyi yalnız bırakalım.
\( 4k = 32 \)
Eşitliğin taraflarını 4'e bölelim.
\( k = 8 \)
\( k \) değerini ikinci denklemde yerine koyalım.
\( 2 \cdot 8x + 3 \cdot 8 + 12 = 5x - 8 \)
\( 16x + 24 + 12 = 5x - 8 \)
\( 16x + 36 = 5x - 8 \)
Elde ettiğimiz bu denklemi çözelim.
Sabit terimleri eşitliğin sağ tarafında, \( x \)'li terimleri sol tarafında toplayalım.
\( 16x - 5x = -8 - 36 \)
\( 11x = -44 \)
Eşitliğin taraflarını 11'e bölelim.
\( x = -4 \)
Çözüm kümesi: \( x \in \{-4\} \)
\( \dfrac{36}{2 + \dfrac{4}{\frac{x - 2}{x + 7}}} + 3 = 15 \)
denklemini sağlayan \( x \) değeri nedir?
Çözümü Göster\( x \) bilinmeyenini adım adım işlemlerle yalnız bırakalım.
3'ü eşitliğin sağ tarafına atalım.
\( \dfrac{36}{2 + \dfrac{4}{\frac{x - 2}{x + 7}}} = 12 \)
12 elde etmek için 36 3'e bölünmelidir, dolayısıyla kesrin paydası 3 olmalıdır.
\( 2 + \dfrac{4}{\frac{x - 2}{x + 7}} = 3 \)
2'yi eşitliğin sağ tarafına atalım.
\( \dfrac{4}{\frac{x - 2}{x + 7}} = 1 \)
1 elde etmek için 4 4'e bölünmelidir, dolayısıyla kesrin paydası 4 olmalıdır.
\( \dfrac{x - 2}{x + 7} = 4 \)
İçler - dışlar çarpımı yapalım.
\( x - 2 = 4(x + 7) \)
Parantezi genişletelim.
\( x - 2 = 4x + 28 \)
Sabit terimleri eşitliğin sağ tarafında, bilinmeyenli terimleri eşitliğin sol tarafında toplayalım.
\( -3x = 30 \)
Eşitliğin her iki tarafını -3'e bölelim.
\( x = -10 \) bulunur.
\( (2a - 3b)x - 3ab = (x - 4b)a + ab \)
denklemi her \( x \) reel sayısı için sağlandığına göre, \( a \) ve \( b \) arasındaki bağıntı nedir?
Çözümü GösterParantezleri genişleterek denklemi düzenleyelim.
\( 2ax - 3bx - 3ab = ax - 4ab + ab \)
Sabit terimleri eşitliğin sağ tarafında, bilinmeyenli terimleri eşitliğin sol tarafında toplayalım.
\( 2ax - 3bx - ax = -4ab + ab + 3ab \)
\( ax - 3bx = 0 \)
Eşitliğin sol tarafını \( x \) parantezine alalım.
\( (a - 3b)x = 0 \)
Bu eşitlik her \( x \) reel sayıları için sağlanıyorsa \( a - 3b = 0 \) olmalıdır. Bu sayede eşitlik \( x \) değerinden bağımsız olarak her durumda sağlanacaktır.
\( a - 3b = 0 \Longrightarrow a = 3b \) bulunur.
\( *(x)* = 7 - 4x \) işlemi veriliyor.
\( *(12 + *(2 - k)*)* = 59 \)
olduğuna göre, \( k \) kaçtır?
Çözümü Göster\( *()* \) işlemi içindeki ifadeyi -4 ile çarpıp 7 eklemektedir.
Bu işlemi içteki işlemden başlayarak verilen denkleme uygulayarak \( k \)'yı bulalım.
\( *(12 + [7 - 4(2 - k)])* = 59 \)
Parantezi genişletelim.
\( *(12 + 7 - 8 + 4k)* = 59 \)
\( *(4k + 11)* = 59 \)
İşlemi tekrar uygulayalım.
\( 7 - 4(4k + 11) = 59 \)
Parantezi genişletelim.
\( 7 - 16k - 44 = 59 \)
Sabit terimleri eşitliğin sağ tarafında toplayalım.
\( -16k = 96 \)
Eşitliğin her iki tarafını -16'ya bölelim.
\( k = -6 \) bulunur.
\( \dfrac{8a^3 + 1}{4a^2 - 1} = 7 + 2a \)
eşitliğini sağlayan \( a \) değeri kaçtır?
Çözümü GösterTüm terimleri eşitliğin sol tarafında toplayalım.
\( \dfrac{8a^3 + 1}{4a^2 - 1} - 7 - 2a = 0 \)
\( \dfrac{8a^3 + 1 - 28a^2 + 7 - 8a^3 + 2a}{4a^2 - 1} = 0 \)
\( \dfrac{-28a^2 + 2a + 8}{4a^2 - 1} = 0 \)
Paydaki tüm terimleri \( -2 \)'ye bölelim.
\( \dfrac{14^2 - a - 4}{4a^2 - 1} = 0 \)
Pay ve paydadaki ifadeleri çarpanlarına ayıralım.
\( \dfrac{(7a - 4)(2a + 1)}{(2a - 1)(2a + 1)} = 0 \)
Eşitliğin çözümünün \( a = -\frac{1}{2} \) olamayacağını not ederek \( 2a + 1 \) çarpanlarını sadeleştirelim.
\( \dfrac{7a - 4}{2a - 1} = 0 \)
Paydayı sıfır yapmamak koşuluyla (\( a \ne \frac{1}{2} \)), payı sıfır yapan \( a \) değeri denklemin çözümüdür.
\( 7a - 4 = 0 \)
\( a = \dfrac{4}{7} \) bulunur.
\( \dfrac{4}{x + 3} - \dfrac{3}{x - 3} = \dfrac{-18}{x^2 - 9} \)
denkleminin çözüm kümesini bulunuz.
Çözümü GösterRasyonel ifadelerin paydalarını eşitleyelim.
\( \dfrac{4(x - 3)}{(x + 3)(x - 3)} - \dfrac{3(x + 3)}{(x - 3)(x + 3)} = \dfrac{-18}{(x - 3)(x + 3)} \)
Çözüm kümesinin paydaları sıfır yapan \( x = 3 \) ve \( x = -3 \) değerlerini içeremeyeceğini not ederek eşitliğin taraflarını \( (x - 3)(x + 3) \) ile çarpalım.
\( 4(x - 3) - 3(x + 3) = -18 \)
\( 4x - 12 - 3x - 9 = -18 \)
\( x = 3 \)
\( x = 3 \) değeri verilen eşitlikte tanımsızlığa yol açtığı için çözüm kümesi bu değeri içeremez.
Çözüm kümesi: \( x \in \emptyset \)