Gauss Eliminasyon Yöntemi
Gauss eliminasyon yöntemi, bir lineer denklem sistemini kolay çözülebilir bir forma getirmek için temel satır işlemlerinin hangi kurallar dahilinde uygulanması gerektiğini belirten bir yöntemdir. Bu "kolay çözülebilir formu" aşağıda satır eşelon formu olarak tanımlayacağız.
Gauss eliminasyon yöntemi lineer denklem sistemlerinin çözümü dışında matrislerin determinantının ve rankının hesaplanması ve bir matrisin tersinin bulunmasında da kullanılır.
Satır Eşelon Formu
Gauss eliminasyon yönteminin temel amacı, bir lineer denklem sistemine ait artırılmış matrisi satır işlemleri kullanarak satır eşelon formuna getirmek ve bu sadeleştirilmiş formu kullanarak denklem sistemini daha kolay bir şekilde çözmektir.
Ön bir bilgi olarak aşağıdaki iki tanımlamayı yapalım.
- Bir matriste tüm elemanları sıfır olan satıra sıfır satırı denir.
- Satır eşelon formundaki bir matriste bir satırın sıfırdan farklı soldan ilk elemanına o satırın pivotu denir.
Satır eşelon formundaki bir matris aşağıdaki koşulları sağlar.
- Sıfır satırları matrisin en altında yer alır.
- Sıfır satırı olmayan bir satırın pivotu bir önceki satırın pivotunun sağındaki bir sütunda bulunur.
- Bunun bir sonucu olarak, bir pivotun aynı sütunda ve altında bulunan elemanlar sıfırdır.
Aşağıda satır eşelon formunda olan üç matris verilmiştir: İkinci ve üçüncü matrislerde sıfır satırları matrisin en altındadır. Her satırın turuncu ile işaretli pivotu bir önceki satırın pivotunun sağındaki bir sütundadır. Ayrıca tüm pivotların aynı sütunda ve altında bulunan elemanlar sıfırdır.
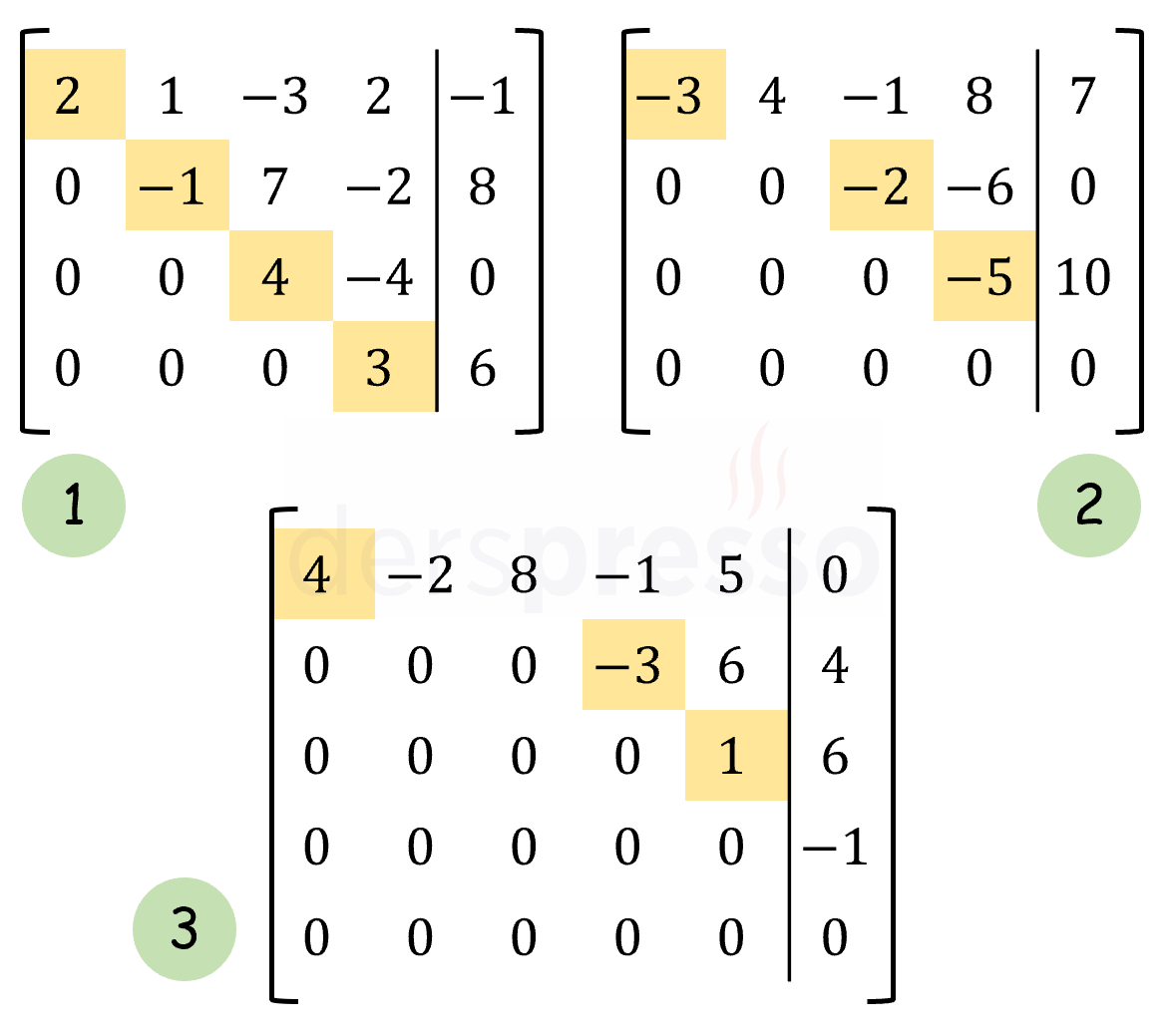
Aşağıda satır eşelon formunda olmayan üç matris verilmiştir: Birinci matriste sıfır satırı matrisin en altında değil 3. satırdadır. İkinci ve üçüncü matrislerde 3. satırın pivotları bir önceki satırın pivotunun sağındaki bir sütunda değildir. Ayrıca üçüncü matriste 2. satırın pivotunun aynı sütunda ve altında bulunan elemanların tümü sıfır değildir (\( a_{43} = 1 \)).
Gauss eliminasyon yöntemi, "matrisi satır eşelon formuna getirme" ve "geriye doğru yerine koyma" olmak üzere iki adımdan oluşur.
Matrisi Satır Eşelon Formuna Getirme
Gauss eliminasyon yönteminin birinci adımında, lineer denklem sistemine ait artırılmış matris aşağıdaki adımlar takip edilerek satır eşelon formuna getirilir.
- Tüm elemanları sıfır olmayan soldan ilk sütun bulunur. Bu sütundaki sıfırdan farklı elemanlardan biri pivot olarak seçilir. Pivot seçiminde aşağıdaki iki kriter dikkate alınabilir.
- İlgili sütunda en üstteki eleman sıfırdan farklı ise yer değiştirme satır işlemine gerek bırakmamak için bu ilk eleman seçilebilir.
- İşlem kolaylığı açısından 1 ya da -1 değerine sahip bir eleman tercih edilebilir.
- Belirlenen pivot ilk satırda değilse bulunduğu satır yer değiştirme satır işlemi ile ilk satıra alınır.
- Belirlenen pivotla aynı sütunda ve altında bulunan sıfırdan farklı elemanlar toplama satır işlemleri ile sıfıra eşitlenir.
- Yukarıdaki adımlar sıfır satırı olmayan her satırın pivotu belirlenene kadar ve pivotu belirlenen satırların hariç tutulduğu alt matris için tekrarlanır.
Şimdi bu yöntemi kullanarak aşağıdaki lineer denklem sistemini satır eşelon formuna getirelim.
\( \begin{array}{rrrrcl} -x_1 & -2x_2 & −4x_3 & +2x_4 & = & 29 \\ 2x_1 & +4x_2 & +5x_3 & -3x_4 & = & -35 \\ -4x_1 & & +2x_3 & -3x_4 & = & 0 \\ 3x_1 & +2x_2 & -3x_3 & +6x_4 & = & 26 \end{array} \)
| İşlem | Denklem Sistemi |
|---|---|
|
Verilen denklem sistemini artırılmış matris formunda yazalım. |
\( \left[ \begin{array}{cccc|c} -1 & -2 & -4 & 2 & 29 \\ 2 & 4 & 5 & -3 & -35 \\ -4 & 0 & 2 & -3 & 0 \\ 3 & 2 & -3 & 6 & 26 \end{array} \right] \) |
|
Tüm elemanları sıfır olmayan soldan ilk sütun birinci sütundur. Bu sütundaki sıfırdan farklı elemanlar içinde \( a_{11} = -1 \) elemanını pivot olarak seçelim. |
\( \left[ \begin{array}{cccc|c} \color{red}{-1} & -2 & -4 & 2 & 29 \\ 2 & 4 & 5 & -3 & -35 \\ -4 & 0 & 2 & -3 & 0 \\ 3 & 2 & -3 & 6 & 26 \end{array} \right] \) |
|
Belirlediğimiz pivotla aynı sütunda ve altında bulunan sıfırdan farklı elemanları toplama satır işlemleri ile sıfıra eşitleyelim. \( 2R_1 + R_2 \rightarrow R_2 \) \( -4R_1 + R_3 \rightarrow R_3 \) \( 3R_1 + R_4 \rightarrow R_4 \) Bu işlemler sonucunda birinci sütun istediğimiz forma gelmiş oldu. İşleme pivotunu belirlediğimiz ilk satırın hariç tutulduğu alt matris ile devam edelim. |
\( \left[ \begin{array}{cccc|c} \color{red}{-1} & -2 & -4 & 2 & 29 \\ 0 & 0 & -3 & 1 & 23 \\ 0 & 8 & 18 & -11 & -116 \\ 0 & -4 & -15 & 12 & 113 \end{array} \right] \) |
|
Tüm elemanları sıfır olmayan soldan ilk sütun ikinci sütundur. Bu sütundaki sıfırdan farklı elemanlar içinde \( a_{32} = 8 \) elemanını pivot olarak seçelim. |
\( \left[ \begin{array}{cccc|c} \color{red}{-1} & -2 & -4 & 2 & 29 \\ 0 & 0 & -3 & 1 & 23 \\ 0 & \color{red}{8} & 18 & -11 & -116 \\ 0 & -4 & -15 & 12 & 113 \end{array} \right] \) |
|
Belirlediğimiz pivot üçüncü satırda bulunduğu için yer değiştirme satır işlemi ile ikinci satıra alalım. \( R_2 \leftrightarrow R_3 \) |
\( \left[ \begin{array}{cccc|c} \color{red}{-1} & -2 & -4 & 2 & 29 \\ 0 & \color{red}{8} & 18 & -11 & -116 \\ 0 & 0 & -3 & 1 & 23 \\ 0 & -4 & -15 & 12 & 113 \end{array} \right] \) |
|
Belirlediğimiz pivotla aynı sütunda ve altında bulunan sıfırdan farklı elemanları toplama satır işlemleri ile sıfıra eşitleyelim. \( \dfrac{1}{2}R_2 + R_4 \rightarrow R_4 \) Bu işlemler sonucunda ikinci sütun istediğimiz forma gelmiş oldu. İşleme pivotunu belirlediğimiz ilk iki satırın hariç tutulduğu alt matris ile devam edelim. |
\( \left[ \begin{array}{cccc|c} \color{red}{-1} & -2 & -4 & 2 & 29 \\ 0 & \color{red}{8} & 18 & -11 & -116 \\ 0 & 0 & -3 & 1 & 23 \\ 0 & 0 & -6 & \frac{13}{2} & 55 \end{array} \right] \) |
|
Tüm elemanları sıfır olmayan soldan ilk sütun üçüncü sütundur. Bu sütundaki sıfırdan farklı elemanlar içinde \( a_{33} = -3 \) elemanını pivot olarak seçelim. |
\( \left[ \begin{array}{cccc|c} \color{red}{-1} & -2 & -4 & 2 & 29 \\ 0 & \color{red}{8} & 18 & -11 & -116 \\ 0 & 0 & \color{red}{-3} & 1 & 23 \\ 0 & 0 & -6 & \frac{13}{2} & 55 \end{array} \right] \) |
|
Belirlediğimiz pivotla aynı sütunda ve altında bulunan sıfırdan farklı elemanları toplama satır işlemleri ile sıfıra eşitleyelim. \( -2R_3 + R_4 \rightarrow R_4 \) Bu işlemler sonucunda üçüncü sütun istediğimiz forma gelmiş oldu. İşleme pivotunu belirlediğimiz ilk üç satırın hariç tutulduğu alt matris ile devam edelim. |
\( \left[ \begin{array}{cccc|c} \color{red}{-1} & -2 & -4 & 2 & 29 \\ 0 & \color{red}{8} & 18 & -11 & -116 \\ 0 & 0 & \color{red}{-3} & 1 & 23 \\ 0 & 0 & 0 & \frac{9}{2} & 9 \end{array} \right] \) |
|
Sıfır olmayan soldan ilk sütun dördüncü sütundur. Bu sütundaki tek eleman olan \( a_{44} = \frac{9}{2} \) elemanını pivot olarak seçelim. Sıfır satırı olmayan her satırın pivotunu belirlediğimiz için işlem tamamlanmıştır. Elde ettiğimiz matris satır eşelon formundadır. |
\( \left[ \begin{array}{cccc|c} \color{red}{-1} & -2 & -4 & 2 & 29 \\ 0 & \color{red}{8} & 18 & -11 & -116 \\ 0 & 0 & \color{red}{-3} & 1 & 23 \\ 0 & 0 & 0 & \color{red}{\frac{9}{2}} & 9 \end{array} \right] \) |
Yukarıda her adımda elde ettiğimiz matrislerin karşılık geldiği denklem sistemlerinin denk olduğunu, dolayısıyla tümünün çözüm kümelerinin aynı olduğunu tekrar hatırlatalım.
Geriye Doğru Yerine Koyma
Gauss eliminasyon yönteminin ikinci adımında, elde edilen satır eşelon formundaki matris kullanılarak denklem sistemi çözülür.
Satır eşelon formu, basamaklı yapısı sebebiyle lineer denklem sistemindeki en son denklemden geriye doğru giderek her adımda bir değişkenin değerini bulmamıza ve denklem sistemini kolay bir şekilde çözmemize imkan sağlar.
Elde ettiğimiz satır eşelon formundaki matrisi denklem sistemi şeklinde yazalım.
\( \begin{array}{rrrrcl} -x_1 & -2x_2 & −4x_3 & +2x_4 & = & 29 \\ & 8x_2 & +18x_3 & -11x_4 & = & -116 \\ & & -3x_3 & +x_4 & = & 23 \\ & & & \frac{9}{2}x_4 & = & 9 \end{array} \)
Denklem sistemini son denklemden başlayarak geriye doğru çözelim.
Dördüncü denklemi kullanarak \( x_4 \) değerini bulalım.
\( \dfrac{9}{2}x_4 = 9 \)
\( x_4 = 2 \)
Üçüncü denklemi ve \( x_4 \) değerini kullanarak \( x_3 \) değerini bulalım.
\( -3x_3 + x_4 = 23 \)
\( -3x_3 + 2 = 23 \)
\( x_3 = -7 \)
İkinci denklemi ve \( x_3, x_4 \) değerlerini kullanarak \( x_2 \) değerini bulalım.
\( 8x_2 + 18x_3 - 11x_4 = -116 \)
\( 8x_2 + 18(-7) - 11(2) = -116 \)
\( x_2 = 4 \)
Birinci denklemi ve \( x_2, x_3, x_4 \) değerlerini kullanarak \( x_1 \) değerini bulalım.
\( -x_1 - 2x_2 - 4x_3 + 2x_4 = 29 \)
\( -x_1 - 2(4) - 4(-7) + 2(2) = 29 \)
\( x_1 = -5 \)
Buna göre lineer denklem sisteminin tek çözümü \( (x_1, x_2, x_3, x_4) = (-5, 4, -7, 2) \) olarak bulunur.
Bu çözümü verilen orijinal denklem sisteminde yerine koyarak sağlamasını yapalım.
\( \begin{array}{rrrrcl} -x_1 & -2x_2 & −4x_3 & +2x_4 & = & 29 \\ 2x_1 & +4x_2 & +5x_3 & -3x_4 & = & -35 \\ -4x_1 & & +2x_3 & -3x_4 & = & 0 \\ 3x_1 & +2x_2 & -3x_3 & +6x_4 & = & 26 \end{array} \)
\( \begin{array}{rrrrcl} -(-5) & -2(4) & −4(-7) & +2(2) & = & 29 \\ 2(-5) & +4(4) & +5(-7) & -3(2) & = & -35 \\ -4(-5) & & +2(-7) & -3(2) & = & 0 \\ 3(-5) & +2(4) & -3(-7) & +6(2) & = & 26 \end{array} \)
Tüm denklemler sağlandığı için bulduğumuz çözümün geçerli olduğunu teyit etmiş olduk.
Bir lineer denklem sisteminin sonsuz sayıda satır eşelon formu vardır, örneğin yukarıdaki örnekte son adımda elde edilen matrisin herhangi bir satırının tüm elemanları 2 ile çarpılırsa yine orijinal denklem sistemi ile aynı çözüm kümesine sahip bir denklem sistemi elde edilir.
Ayrıca bir matris farklı satır işlemleri takip edilerek geçerli bir satır eşelon formuna getirilebilir.
Bu bölümde öğrendiklerimizi aşağıdaki şekilde özetleyebiliriz.
- Bir matris, temsil ettiği lineer denklem sisteminin çözüm kümesinde değişik yapmadan temel satır işlemleri kullanılarak sadeleştirilebilir.
- Satır eşelon formu bir denklem sisteminin kolay şekilde çözülebileceği bir form tanımlar.
- Gauss eliminasyon yöntemi, bir matrisi satır eşelon formuna en pratik şekilde getirmek için bir yöntem sunar.
Önümüzdeki bölümde bu yöntemin geriye doğru yerine koyma adımına alternatif olarak kullanılabilecek Gauss - Jordan eliminasyon yönteminden bahsedeceğiz.