Rasyonel Fonksiyonların Tanımsız Olduğu Noktalar

Rasyonel fonksiyonların pay ve paydasını oluşturan polinom fonksiyonları tüm reel sayılar kümesinde tanımlı fonksiyonlardır. Rasyonel fonksiyonlar ise iki farklı sebeple bazı \( x \) değerleri için tanımsız olabilmektedir.

1. Payı sıfır yapmadan paydayı sıfır yapan \( x \) değerleri: Rasyonel fonksiyonlar bu \( x \) değerlerinde tanımsız olur ve önceki bölümde gördüğümüz gibi bu \( x \) değerlerinde fonksiyon grafiğinde dikey asimptotlar oluşur.
2. Hem payı hem de paydayı aynı anda sıfır yapan \( x \) değerleri: Rasyonel fonksiyonlar bu \( x \) değerlerinde de tanımsız olur ve bu \( x \) değerlerinde fonksiyon grafiğinde birer "boşluk" oluşur. Bu bölümde bu ikinci durumu inceleyeceğiz.

İlk önce aşağıdaki gibi bir ikinci dereceden polinom fonksiyonu (parabol) tanımlayalım.

Bu fonksiyonun grafiği aşağıdaki gibidir.

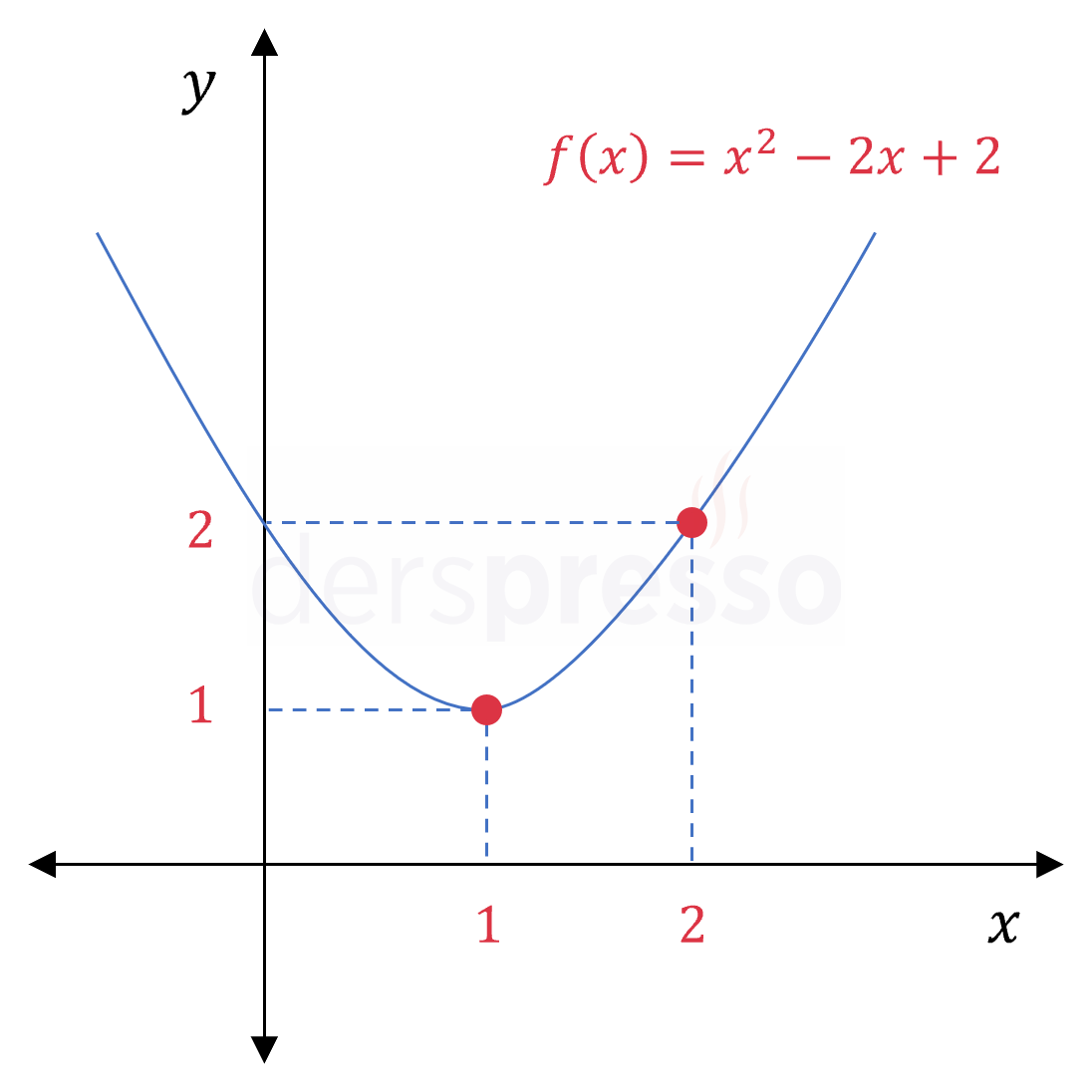
Şimdi de aşağıdaki gibi bir rasyonel fonksiyon tanımlayalım.

\( x = 2 \) değerinin paydadaki birinci derece ifadeyi sıfır yaptığını zaten görebiliyoruz, bu fonksiyondaki diğer bir özel durum, \( x = 2 \) değerinin payı da sıfır yapıyor olmasıdır, bu da \( (x - 2) \)'nin bu polinomun çarpanlarından biri olduğunu gösterir. Nitekim paydaki polinomu \( (x - 2) \)'ye polinom bölmesi ile bölersek, ifadenin aşağıdaki gibi çarpanlarına ayrıldığını görebiliriz.

Pay ve paydaki ortak \( (x - 2) \) çarpanlarını sadeleştirdiğimizde geriye bir önceki örnekteki \( f(x) \) fonksiyonunun kaldığını görürüz.

\( g(x) \)'in bu sadeleşmiş haline \( g_1(x) \) dedik, bunun sebebi pay ve paydadaki çarpanları sadeleştirdiğimizde elde edeceğimiz fonksiyonun tam olarak orijinal fonksiyonla özdeş olmamasıdır, bunu aşağıda açıklamaya çalışacağız.

Bir grafik programı kullanarak \( g(x) \) fonksiyonunun grafiğini çizersek aşağıdaki grafiği elde ederiz.

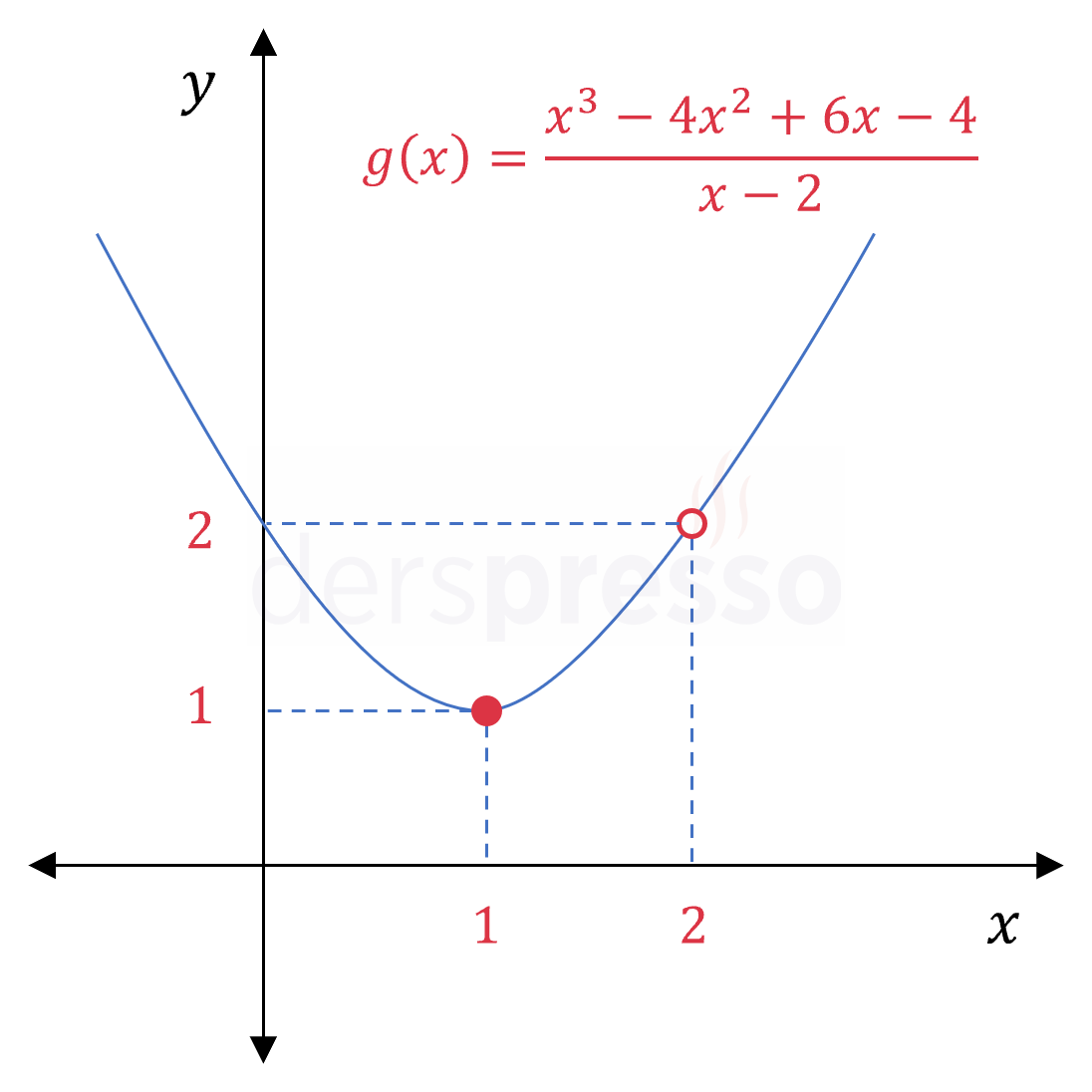
Görebileceğimiz gibi, \( f(x) \) fonksiyonu ve \( g(x) \)'in sadeleşmiş hali aynı fonksiyonlar olsa da, \( f(x) \) ve \( g(x) \) fonksiyon grafikleri arasında önemli bir fark vardır, o da \( g(x) \) grafiğinin \( x = 2 \) noktasında tanımsız olması ve bu tanımsızlıktan dolayı bu noktada bir boşluk oluşmasıdır.

Bu durumu şu şekilde de açıklayabiliriz: Eğer bir rasyonel fonksiyonun pay ve paydasında ortak bir çarpan varsa, fonksiyonun grafiği pay ve paydadaki bu çarpanın sadeleşmiş haliyle oluşmaktadır, ancak bu çarpan orijinal fonksiyonda paydada bulunduğu için fonksiyon yine de bu değeri alamamaktadır ve dolayısıyla fonksiyon bu noktada tanımsız olmaktadır.

Özetle, eğer bir fonksiyonun pay ve paydasındaki bazı çarpanlar sadeleşiyorsa, fonksiyonun sadeleştirmiş hali ile orijinal halinin özdeş fonksiyonlar olduğunu söyleyemeyiz. Orijinal fonksiyondaki bu çarpanlar ve tanımsız noktalar fonksiyonun tanımının ve tanım kümesinin ayrılmaz bir parçasıdır ve her ne kadar sadeleştirme sonrasında cebirsel ve grafiksel açıdan çok benzer bir fonksiyon ortaya çıksa da tanım kümesi farklı bir fonksiyon oluşmaktadır.