Köklü İfade Grafikleri
Köklü ifadelerin tanım ve görüntü kümeleri ifadenin derecesinin tek ya da çift olmasına göre farklılık gösterdiği için, köklü ifadelerin grafiklerini de ifadenin derecesine göre ayrı ayrı incelememiz gerekir.
Tek Dereceli Köklü İfadelerin Grafiği
Önceki bölümde gördüğümüz gibi, tek dereceli köklü ifadelerin tanım ve görüntü kümeleri tüm reel sayılardır.
| Kökün Derecesi | Tanım Kümesi | Görüntü Kümesi |
|---|---|---|
| Tek Dereceli (\( \sqrt[2n + 1]{x} \)) | \( \mathbb{R} \) | \( \mathbb{R} \) |
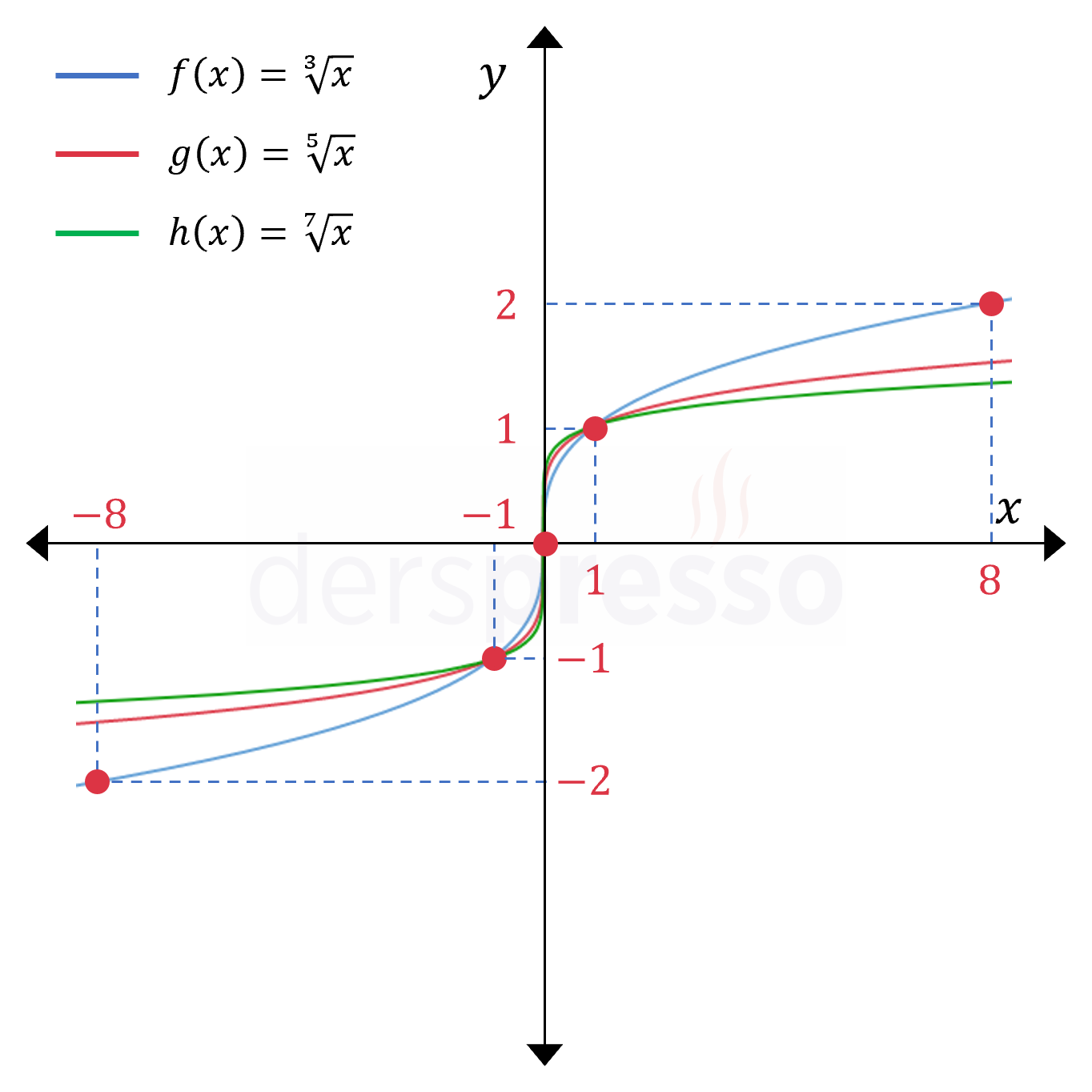
Bu grafikler doğrultusunda tek dereceli köklü ifadelerin grafikleri ile ilgili şu yorumları yapabiliriz.
- Tek dereceli bir köklü ifadenin içi ve sonucu hem pozitif hem de negatif olabildiği için, ifadenin grafiği tüm reel sayılarda tanımlıdır.
- \( x = 0 \) olduğunda kök içinin her dereceden kökü sıfır olduğu için, grafik her zaman orijinden geçer.
- \( x = 1 \) olduğunda kök içinin her dereceden kökü \( 1 \) olduğu için, grafik her zaman \( (1, 1) \) noktasından geçer.
- \( x = -1 \) olduğunda kök içinin her dereceden kökü \( -1 \) olduğu için, grafik her zaman \( (-1, -1) \) noktasından geçer.
- \( 0 \lt x \lt 1 \) olduğunda daha yüksek dereceli köklü ifadenin sonucu daha büyüktür, dolayısıyla grafiği de daha yukarıdan geçer.
- \( 1 \lt x \) olduğunda daha yüksek dereceli köklü ifadenin sonucu daha küçüktür, dolayısıyla grafiği de daha aşağıdan geçer.
- Tek dereceli köklü ifadelerin grafikleri orijine göre simetriktir.
Çift Dereceli Köklü İfadelerin Grafiği
Önceki bölümde gördüğümüz gibi, çift dereceli köklü ifadelerin tanım ve görüntü kümesi sadece sıfır ve pozitif reel sayılardır.
| Kökün Derecesi | Tanım Kümesi | Görüntü Kümesi |
|---|---|---|
| Çift Dereceli (\( \sqrt[2n]{x} \)) | \( \mathbb{R^+} \cup \{ 0 \} \) | \( \mathbb{R^+} \cup \{ 0 \} \) |
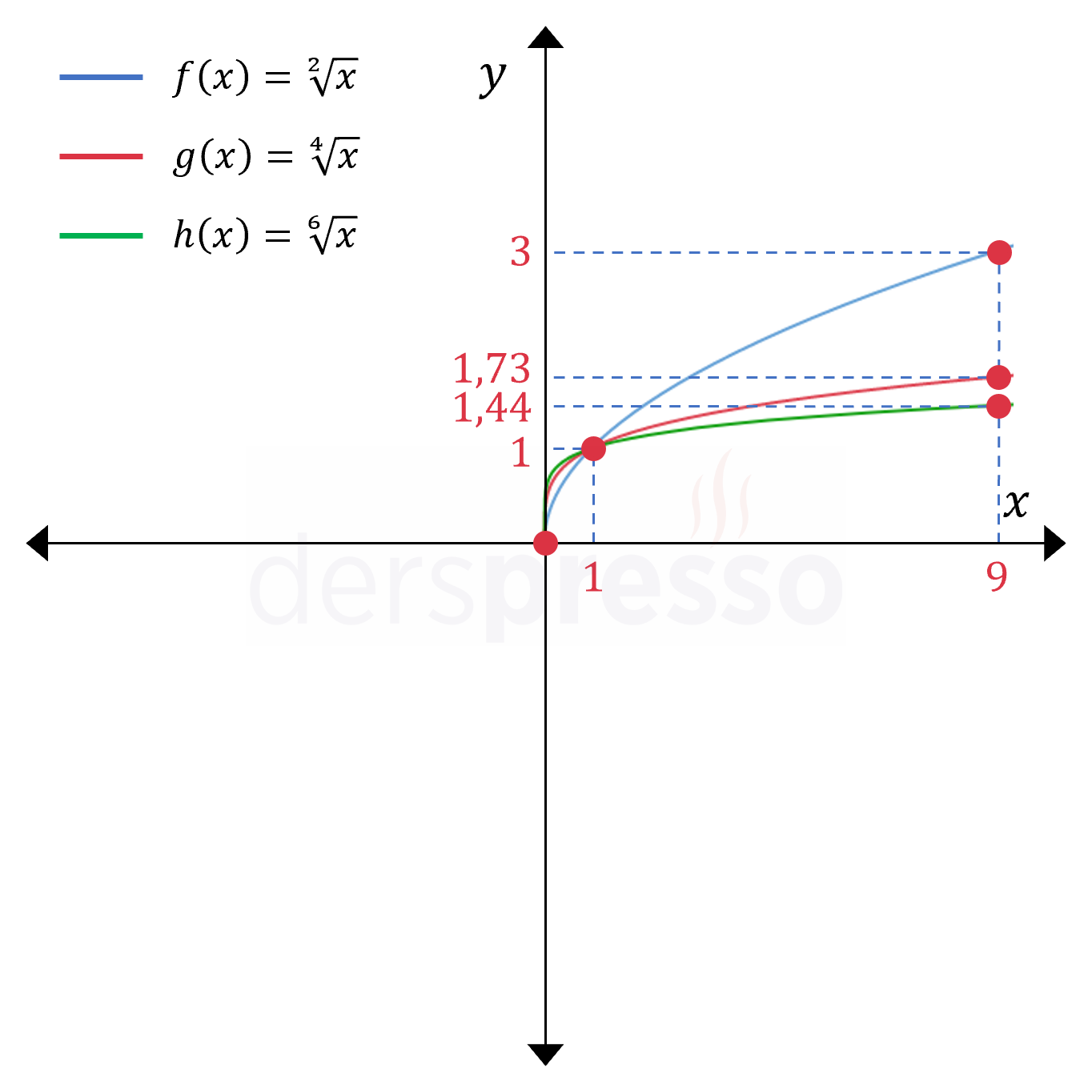
Bu fonksiyon grafikleri doğrultusunda çift dereceli köklü fonksiyonlarla ilgili şu yorumları yapabiliriz.
- Çift dereceli bir köklü ifadenin kök içi ve sonucu negatif olamayacağı için, ifadenin grafiği \( [0, \infty) \) arasında tanımlıdır.
- \( x = 0 \) olduğunda kök içinin her dereceden kökü sıfır olduğu için, grafik her zaman orijinden geçer.
- \( x = 1 \) olduğunda kök içinin her dereceden kökü bir olduğu için, grafik her zaman \( (1, 1) \) noktasından geçer.
- \( 0 \lt x \lt 1 \) olduğunda daha yüksek dereceli köklü ifadenin sonucu daha büyüktür, dolayısıyla grafiği de daha yukarıdan geçer.
- \( 1 \lt x \) olduğunda daha yüksek dereceli köklü ifadenin sonucu daha küçüktür, dolayısıyla grafiği de daha aşağıdan geçer.