Üçgenin Çevresi ve Alanı
Üçgenin Çevresi
Üçgenin çevresi üçgenin üç kenar uzunluğunun toplamına eşittir.
\( \text{Ç}(ABC) = a + b + c \)
Benzer Üçgenlerin Çevresi
Benzer iki üçgenin çevrelerinin oranı üçgenlerin benzerlik oranına eşittir.

\( ABC \) ve \( KLM \) üçgenlerinin benzerlik oranı \( k \) ise,
\( \dfrac{\text{Ç}(ABC)}{\text{Ç}(KLM)} = k \)
Üçgenin Alanı
Tabanı ve Yüksekliği Bilinen Üçgenin Alanı
Üçgenin alanı bir kenar uzunluğu ile o kenara ait yüksekliğin çarpımının yarısına eşittir.
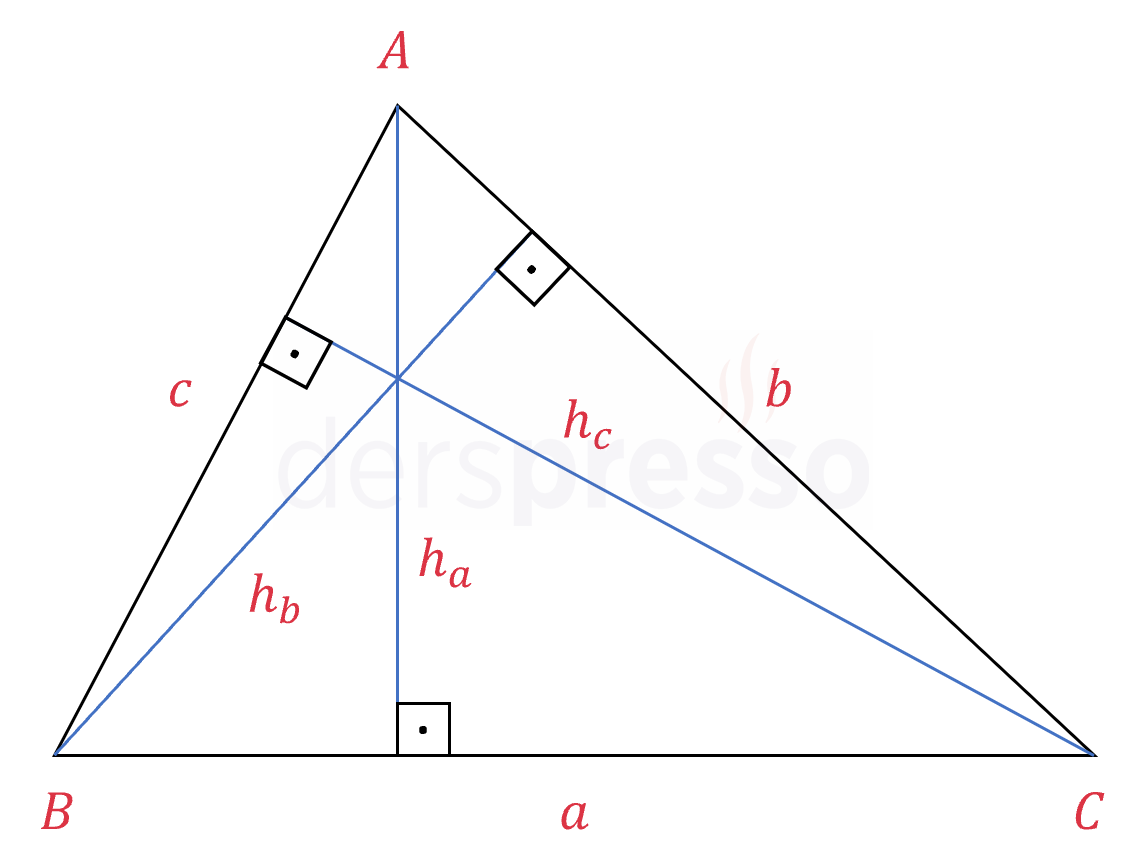
\( A(ABC) = \dfrac{a \cdot h_a}{2} = \dfrac{b \cdot h_b}{2} = \dfrac{c \cdot h_c}{2} \)
İSPATI GÖSTER
DİK ÜÇGENİN ALANI:

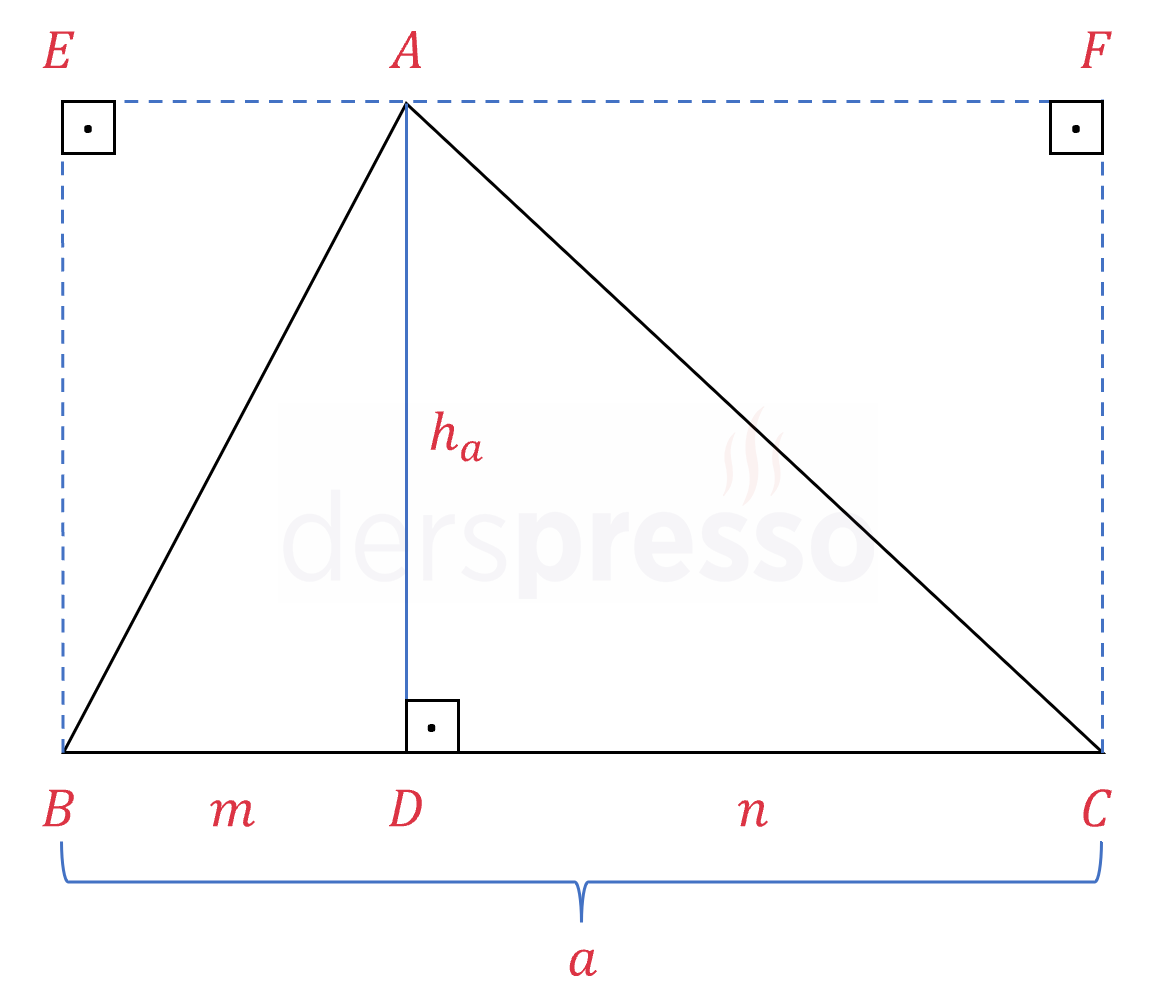
\( ABC \) üçgeninin dik kenarlarına paralel doğrular çizdiğimizde yukarıdaki gibi bir dikdörtgen elde ederiz.
Dikdörtgenin alan formülünü yazalım.
\( A(ABCD) = a \cdot h_a \)
Üçgenin \( [AC] \) kenarı \( ABCD \) dikdörtgenin köşegenidir ve dikdörtgenin alanını iki eşit parçaya böler.
Buna göre \( ABC \) üçgeninin alanı aşağıdaki gibi olur.
\( A(\overset{\triangle}{ABC}) = \dfrac{A(ABCD)}{2} \)
\( = \dfrac{a \cdot h_a}{2} \)
DAR AÇILI ÜÇGENİN ALANI:
\( ABC \) üçgeninin yüksekliği üçgeni \( ABD \) ve \( ADC \) üçgenleri olmak üzere iki dik üçgene ayırır.
\( ABC \) üçgeninin alanı \( ABD \) ve \( ADC \) üçgenlerinin alanları toplamına eşittir.
\( A(ABC) = A(ABD) + A(ADC) \)
Dik üçgenlerin alanlarını yukarıda bulduğumuz dik üçgen alan formülünü kullanarak yazalım.
\( A(ABD) = \dfrac{m \cdot h_a}{2} \)
\( A(ADC) = \dfrac{n \cdot h_a}{2} \)
\( A(ABC) = \dfrac{m \cdot h_a}{2} + \dfrac{n \cdot h_a}{2} \)
\( = \dfrac{(m + n) \cdot h_a}{2} \)
\( = \dfrac{a \cdot h_a}{2} \)
GENİŞ AÇILI ÜÇGENİN ALANI:

Geniş açılı köşenin iki kenarını uzatarak üçgeni bir dik üçgene tamamlayalım.
\( ABC \) üçgeninin alanı \( ADC \) ve \( ADB \) dik üçgenlerinin alanları farkına eşittir.
\( A(ABC) = A(ADC) - A(ADB) \)
Dik üçgenlerin alanlarını yukarıda bulduğumuz dik üçgen alan formülünü kullanarak yazalım.
\( A(ADC) = \dfrac{(d + a) \cdot h_a}{2} \)
\( A(ADB) = \dfrac{d \cdot h_a}{2} \)
\( A(ABC) = \dfrac{(d + a) \cdot h_a}{2} - \dfrac{d \cdot h_a}{2} \)
\( = \dfrac{(d + a - d) \cdot h_a}{2} \)
\( = \dfrac{a \cdot h_a}{2} \)
İki Kenar ve Arasındaki Açı Bilinen Üçgenin Alanı
İki kenar uzunluğu ve bu kenarlar arasındaki açı bilinen üçgenin alanı sinüs alan formülü ile hesaplanabilir.

\( A(ABC) = \dfrac{1}{2} \cdot b \cdot c \cdot \sin{\widehat{A}} \)
\( A(ABC) = \dfrac{1}{2} \cdot a \cdot c \cdot \sin{\widehat{B}} \)
\( A(ABC) = \dfrac{1}{2} \cdot a \cdot b \cdot \sin{\widehat{C}} \)
İSPATI GÖSTER
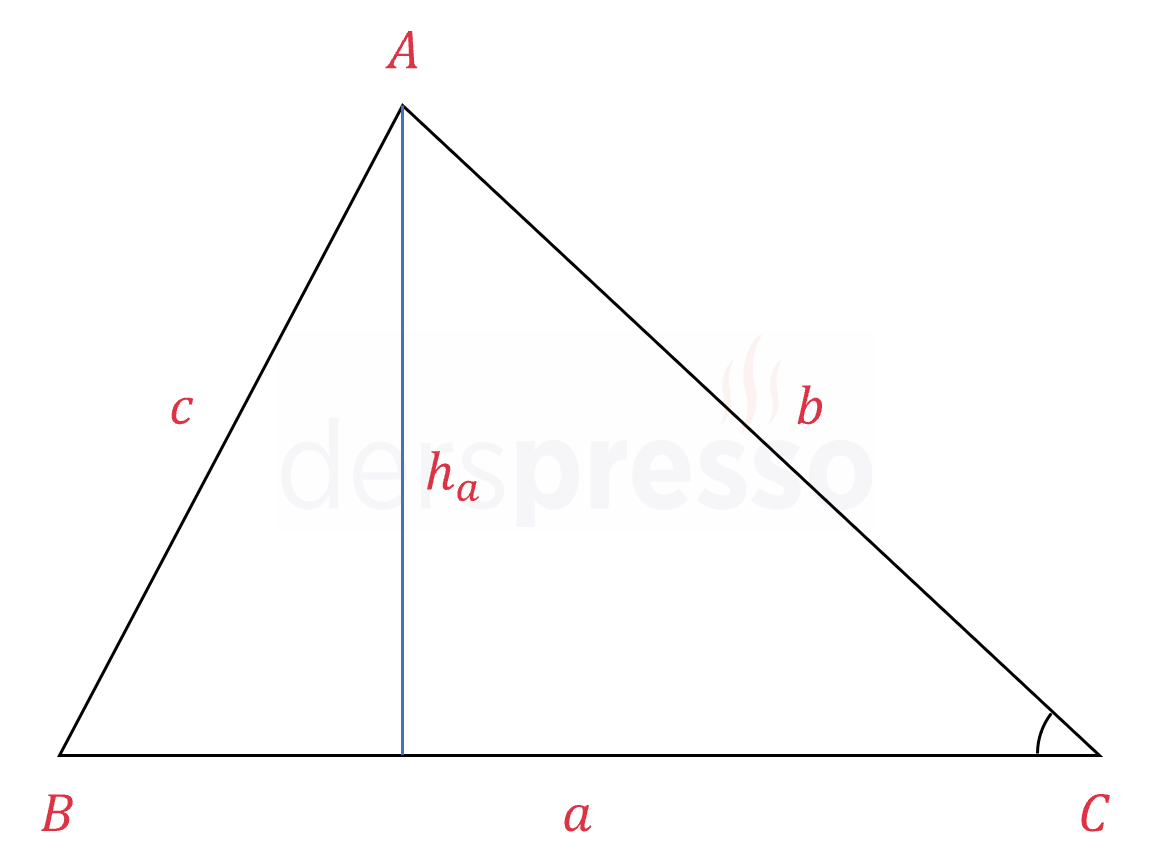
\( ABC \) üçgeninin alanını yazalım.
\( A(\overset{\triangle}{ABC}) = \dfrac{a \cdot h_a}{2} \)
\( h_a \) yüksekliğini \( C \) açısının sinüsü cinsinden yazalım.
\( \sin{\widehat{C}} = \dfrac{h_a}{b} \)
\( h_a = b \cdot \sin{\widehat{C}} \)
\( h_a \) yüksekliğini alan formülünde yerine koyalım.
\( A(\overset{\triangle}{ABC}) = \dfrac{a \cdot b \cdot \sin{\widehat{C}}}{2} \)
\( = \dfrac{1}{2} \cdot a \cdot b \cdot \sin{\widehat{C}} \)
Benzer formülleri diğer köşeler için de yazabiliriz.
Üç Kenarı Bilinen Üçgenin Alanı
Üç kenarının uzunluğu bilinen üçgenin alanı, Heron formülü olarak da bilinen aşağıdaki formülle hesaplanabilir.
\( u \) üçgenin yarı çevresi olmak üzere,
\( u = \dfrac{1}{2}(a + b + c) \)
\( A(ABC) = \sqrt{u(u - a)(u - b)(u - c)} \)
Kenar uzunlukları 5, 6 ve 7 br olan üçgenin alanı:
\( u = \dfrac{1}{2}(5 + 6 + 7) = 9 \)
\( A = \sqrt{9(9 - 5)(9 - 6)(9 - 7)} = 6\sqrt{6} \)
Üç Kenarı ve İç Teğet Çemberinin Yarıçapı Bilinen Üçgenin Alanı

Üç kenar uzunluğu ve iç teğet çemberinin yarıçapı (\( r \)) bilinen üçgenin alanı aşağıdaki formülle hesaplanır. Hatırlatma olarak, bir üçgende iç teğet çemberin merkezi iç açıortayların kesişim noktasıdır.
\( u \) üçgenin yarı çevresi olmak üzere,
\( u = \dfrac{1}{2}(a + b + c) \)
\( A(ABC) = u \cdot r \)
İSPATI GÖSTER
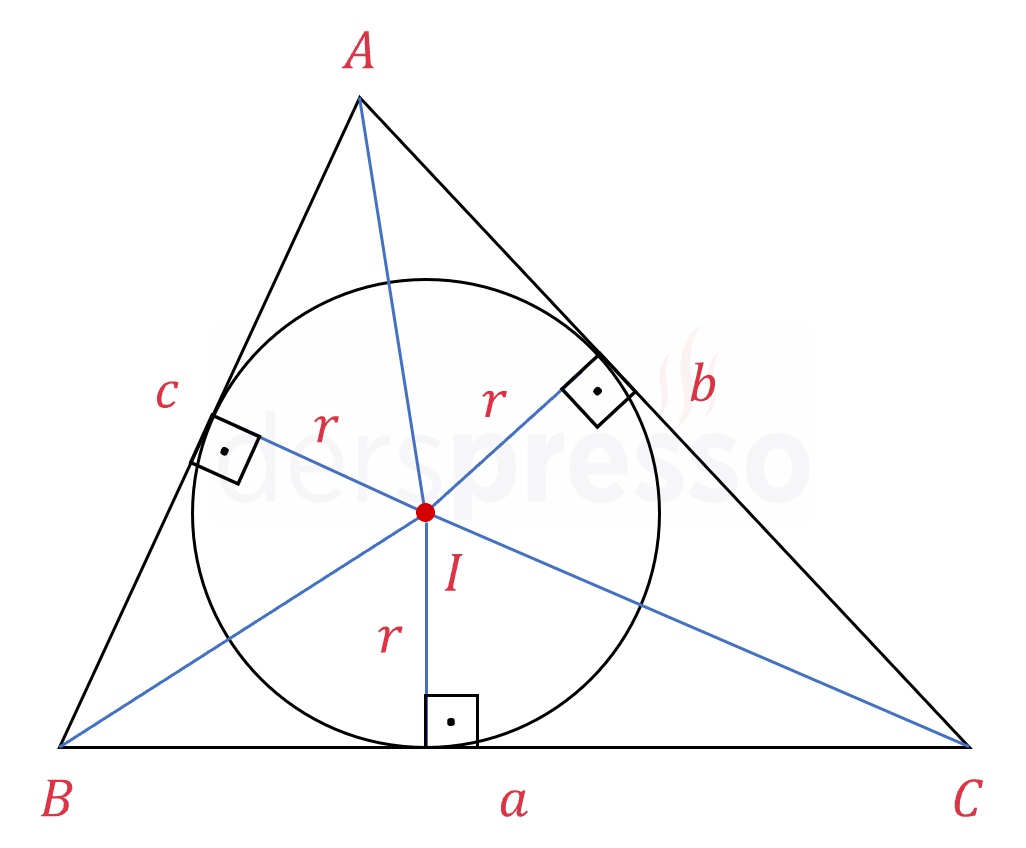
İç teğet çemberin merkezi olan \( I \) noktasından üçgenin köşelerine birer doğru çizelim.
\( ABC \) üçgeninin alanı oluşan \( ABI \), \( BCI \) ve \( CAI \) üçgenlerinin alanları toplamına eşittir.
\( A(ABC) = A(ABI) + A(BCI) + A(CAI) \)
İç teğet çember \( ABC \) üçgeninin kenarlarına teğet olduğu için yarıçap üç kenarı da dik keser, dolayısıyla aynı zamanda üç üçgenin de yüksekliğidir.
Buna göre üçgenlerin alanlarını aşağıdaki gibi yazabiliriz.
\( A(\overset{\triangle}{ABI}) = \dfrac{c \cdot r}{2} \)
\( A(\overset{\triangle}{BCI}) = \dfrac{a \cdot r}{2} \)
\( A(\overset{\triangle}{CAI}) = \dfrac{b \cdot r}{2} \)
\( A(ABC) = \dfrac{c \cdot r}{2} + \dfrac{a \cdot r}{2} + \dfrac{b \cdot r}{2} \)
\( = \dfrac{(a + b + c) \cdot r}{2} \)
\( ABC \) üçgeninin çevresinin yarısına \( u \) dersek yukarıdaki alan formülünü \( u \) cinsinden aşağıdaki gibi yazabiliriz.
\( u = \dfrac{a + b + c}{2} \)
\( A(\overset{\triangle}{ABC}) = u \cdot r \)
Üç Kenarı ve Çevrel Çemberinin Yarıçapı Bilinen Üçgenin Alanı
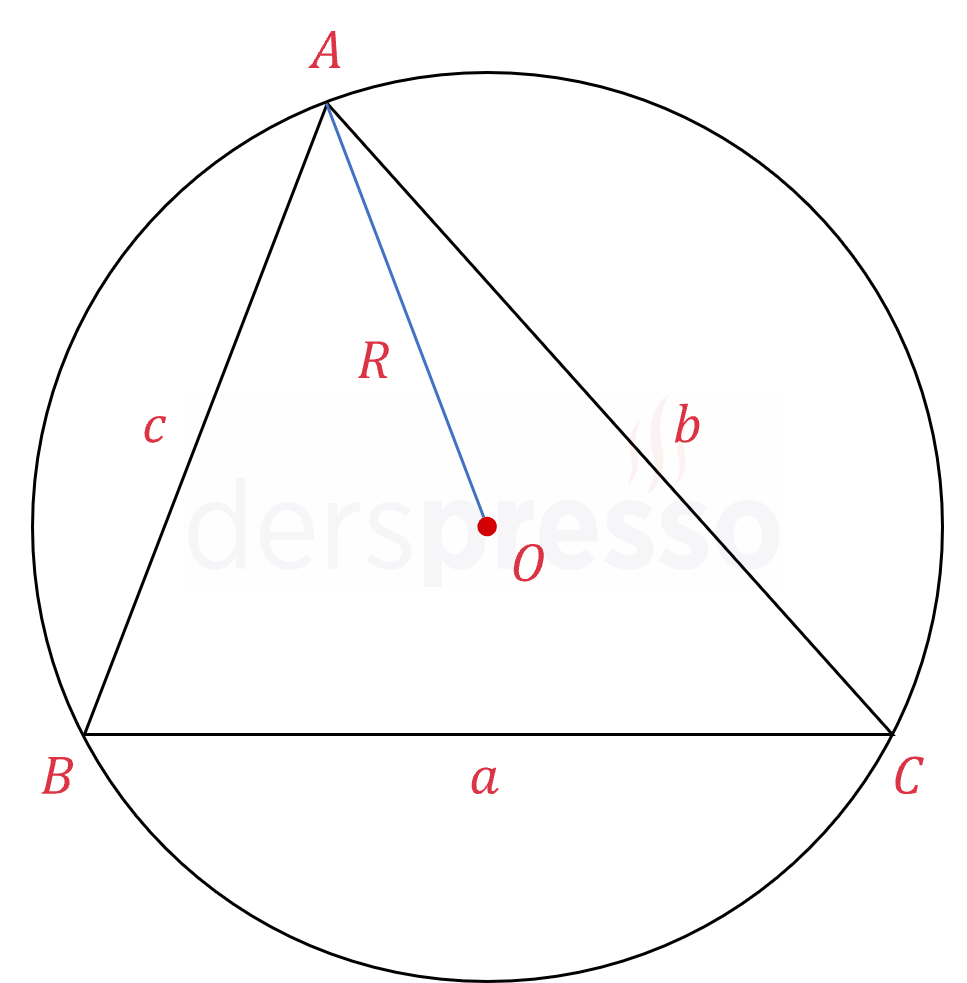
Üç kenarı ve çevrel çemberinin yarıçapı (\( R \)) bilinen üçgenin alanı aşağıdaki formülle hesaplanır. Hatırlatma olarak, bir üçgende çevrel çemberin merkezi orta dikmelerin kesişim noktasıdır.
\( A(ABC) = \dfrac{a \cdot b \cdot c}{4R} \)
İSPATI GÖSTER
Bu formülün ispatı için trigonometri teoremlerinde ispatını verdiğimiz aşağıdaki formülü kullanalım.
\( \dfrac{a}{\sin(\hat{A})} = \dfrac{b}{\sin(\hat{B})} = \dfrac{c}{\sin(\hat{C})} = 2R \)
\( \sin(\hat{C}) = \dfrac{c}{2R} \)
İki kenar uzunluğu ve bu kenarlar arasındaki açı bilinen üçgenin alan formülünde bu değeri yerine koyalım.
\( A(\overset{\triangle}{ABC}) = \dfrac{1}{2} \cdot a \cdot b \cdot \sin{\widehat{C}} \)
\( = \dfrac{1}{2} \cdot a \cdot b \cdot \dfrac{c}{2R} \)
\( = \dfrac{a \cdot b \cdot c}{4R} \)
Analitik Düzlemde Üçgenin Alanı
Analitik düzlemde doğrusal olmayan üç noktanın oluşturduğu üçgenin alanı aşağıdaki formülle hesaplanır.
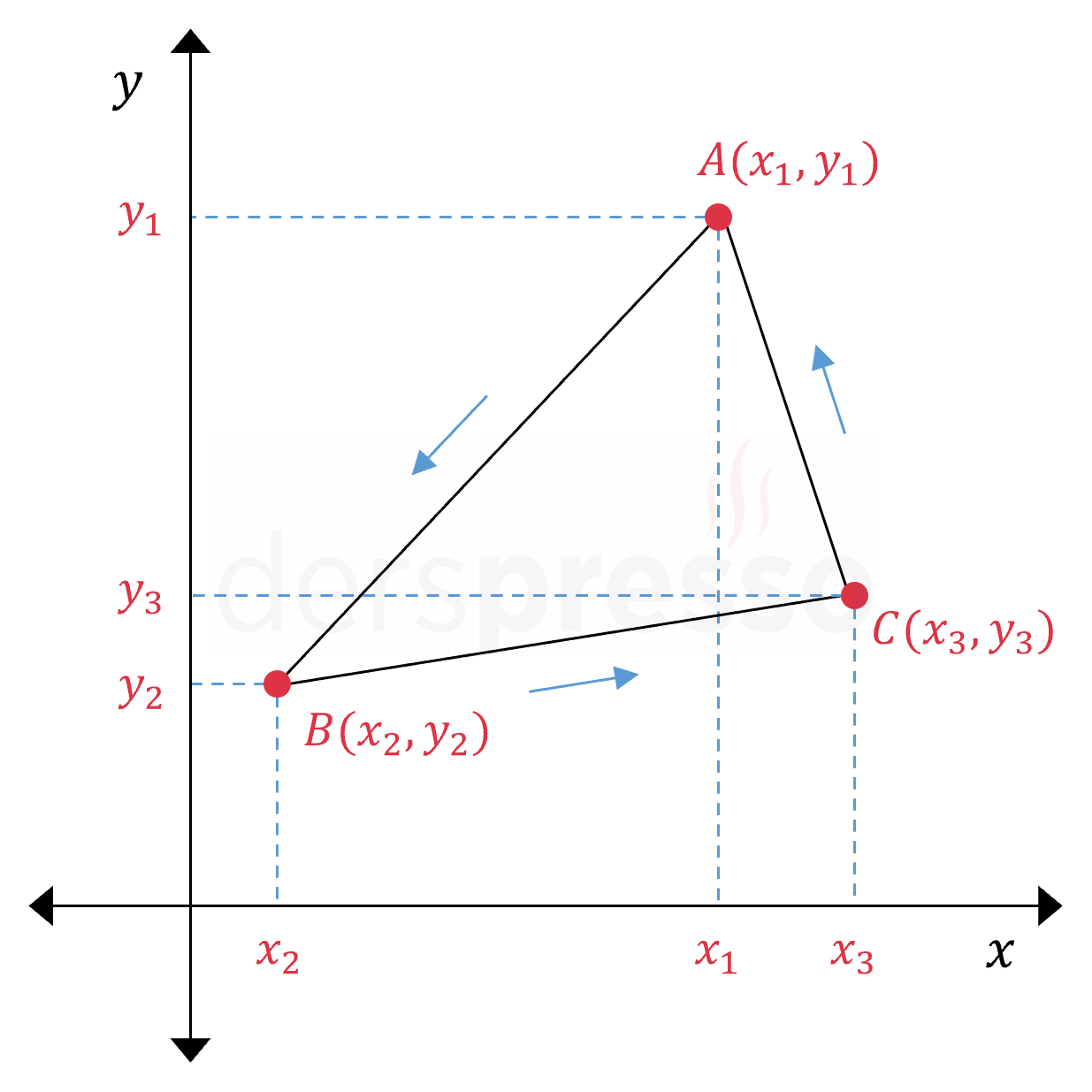
\( A(x_1, y_1) \), \( B(x_2, y_2) \) ve \( C(x_3, y_3) \) noktalarının oluşturduğu üçgenin alanı:
\( A(ABC) = \begin{bmatrix} x_1 & y_1 \\ x_2 & y_2 \\ x_3 & y_3 \\ x_1 & y_1 \end{bmatrix} \)
\( = \dfrac{1}{2} \abs{(x_1y_2 + x_2y_3 + x_3y_1) - (x_2y_1 + x_3y_2 + x_1y_3)} \)
İSPATI GÖSTER
Pozitif alan değeri elde etmek için \( A \), \( B \) ve \( C \) noktalarını üçgenin köşelerine saatin tersi yönünde yerleştirelim.
Üçgeni içine alan aşağıdaki gibi bir \( BDEF \) dikdörtgeni çizelim.
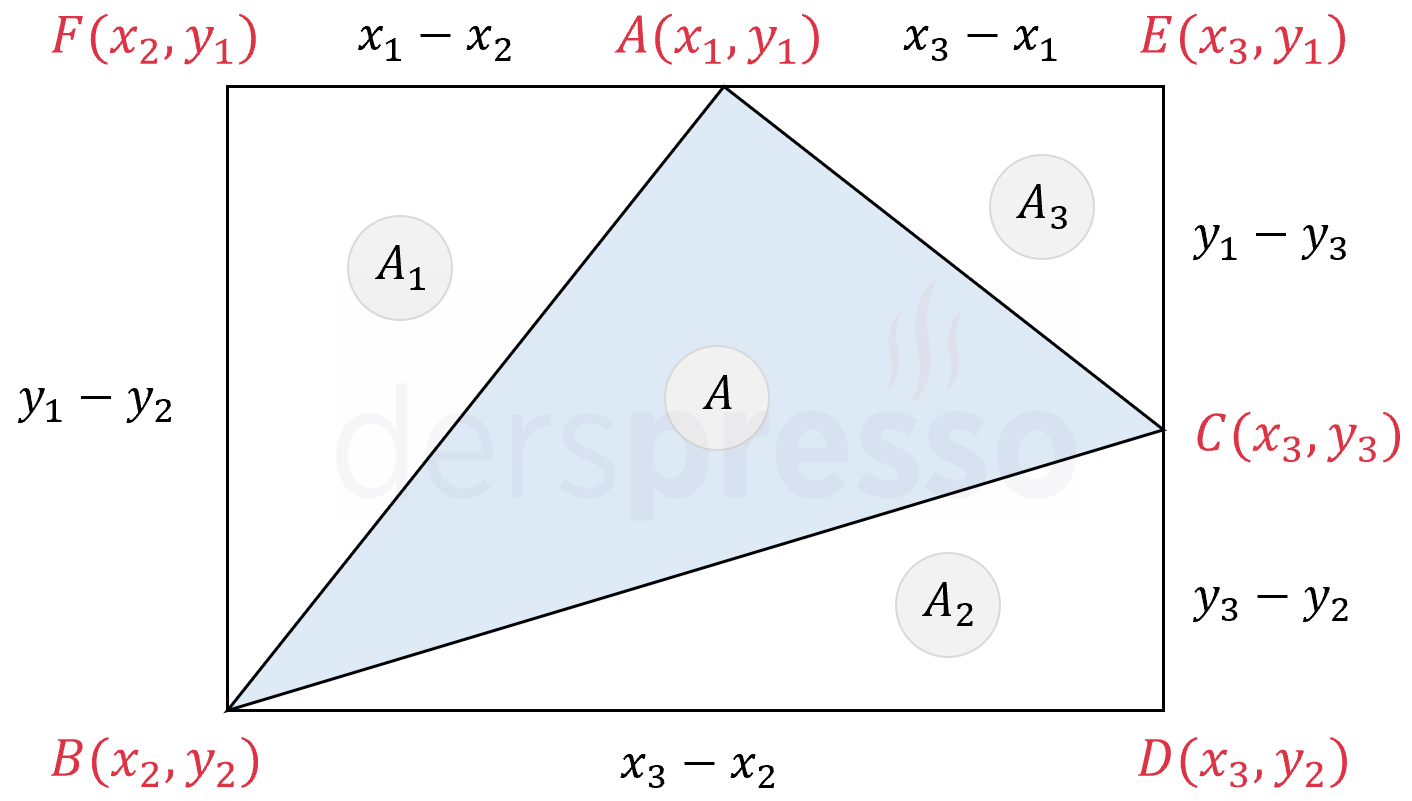
Üçgenin ve dikdörtgenin köşelerinin koordinatları ve köşe noktaları arası uzaklıklar şekilde belirtildiği gibi olur.
Dikdörtgenin içinde oluşan dört üçgenin alanlarına \( A \), \( A_1 \), \( A_2 \) ve \( A_3 \) diyelim.
Alanını bulmak istediğimiz üçgenin alanını dikdörtgenin alanından diğer üç üçgenin alanını çıkarak bulabiliriz.
\( A(ABC) = A(BDEF) - A(AFB) - A(BDC) - A(CEA) \)
\( A = A(BDEF) - A_1 - A_2 - A_3 \)
Dikdörtgenin alanını hesaplayalım.
\( A(BDEF) = (x_3 - x_2)(y_1 - y_2) \)
\( = x_3y_1 - x_3y_2 - x_2y_1 + x_2y_2 \)
Üçgenlerin alanlarını hesaplayalım.
\( A_1 = \dfrac{1}{2}(x_1 - x_2)(y_1 - y_2) \)
\( = \dfrac{1}{2}(x_1y_1 - x_1y_2 - x_2y_1 + x_2y_2) \)
\( A_2 = \dfrac{1}{2}(x_3 - x_2)(y_3 - y_2) \)
\( = \dfrac{1}{2}(x_3y_3 - x_3y_2 - x_2y_3 + x_2y_2) \)
\( A_3 = \dfrac{1}{2}(x_3 - x_1)(y_1 - y_3) \)
\( = \dfrac{1}{2}(x_3y_1 - x_3y_3 - x_1y_1 + x_1y_3) \)
Bu ifadeleri yukarıdaki üçgen alan formülünde yerlerine yazalım.
\( A = A(BDEF) - A_1 - A_2 - A_3 \)
\( = (x_3y_1 - x_3y_2 - x_2y_1 + x_2y_2) - \dfrac{1}{2}(x_1y_1 - x_1y_2 - x_2y_1 + x_2y_2) - \dfrac{1}{2}(x_3y_3 - x_3y_2 - x_2y_3 + x_2y_2) - \dfrac{1}{2}(x_3y_1 - x_3y_3 - x_1y_1 + x_1y_3) \)
Bu işlemdeki sadeleştirmeleri yaptığımızda aşağıdaki formülü elde ederiz.
\( = \dfrac{1}{2} [(x_1y_2 + x_2y_3 + x_3y_1) - (x_2y_1 + x_3y_2 + x_1y_3)] \)
Benzer Üçgenlerin Alanı
Benzer iki üçgenin alanlarının oranı üçgenlerin benzerlik oranının karesine eşittir.

\( ABC \) ve \( KLM \) üçgenlerinin benzerlik oranı \( k \) ise,
\( \dfrac{A(ABC)}{A(KLM)} = k^2 \)
Üçgenlerin Alanları Arasındaki İlişkiler
Yükseklikleri eşit olan üçgenlerin alanları bu yüksekliklerin ait olduğu kenarların uzunluklarıyla doğru orantılıdır.

Birer kenarı eşit olan üçgenlerin alanları bu kenara ait yüksekliklerle doğru orantılıdır.
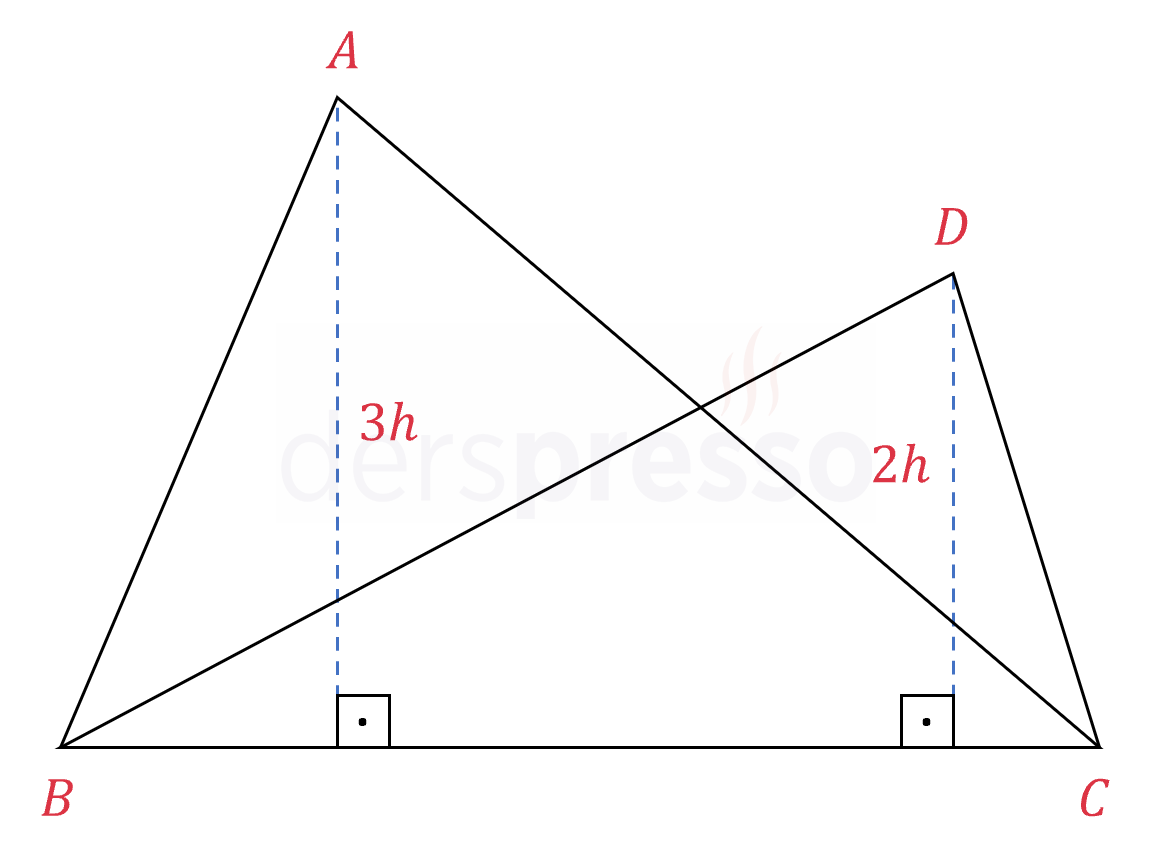
\( \dfrac{A(ABC)}{A(DBC)} = \dfrac{3}{2} \)
Sinüs alan formülünün bir uygulaması olarak; bir üçgenin iki kenarı eşit parçalara bölündüğünde, tepe noktaları aynı olacak şekilde oluşan üçgenlerin alanları yan kenar uzunluk oranlarının çarpımı ile doğru orantılıdır.
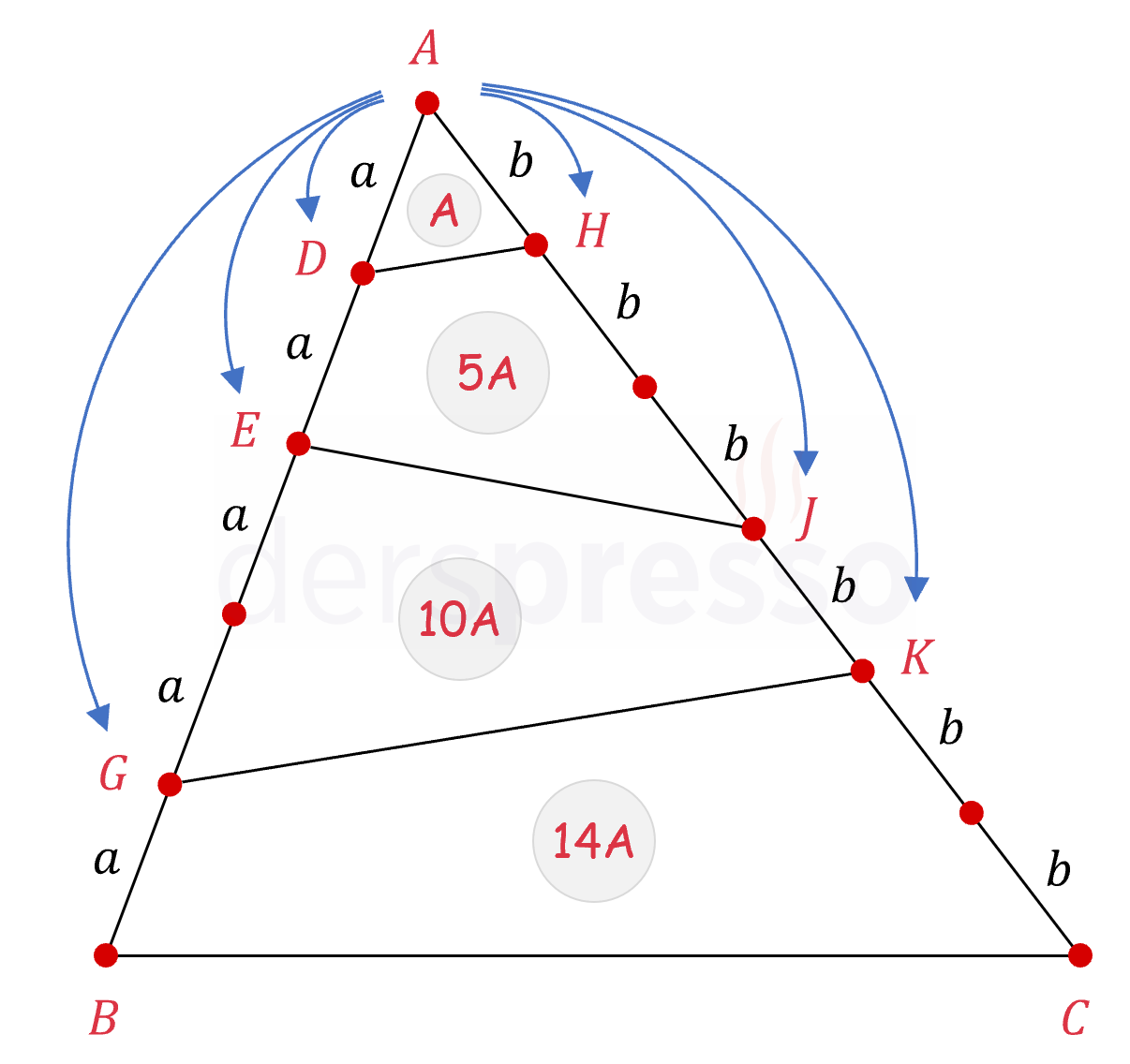
\( ADH \) üçgeninin alanı:
\( a \cdot b \Longrightarrow A \) ise,
\( AEJ \) üçgeninin alanı:
\( 2a \cdot 3b \Longrightarrow 6A \)
\( AGK \) üçgeninin alanı:
\( 4a \cdot 4b \Longrightarrow 16A \)
\( ABC \) üçgeninin alanı:
\( 5a \cdot 6b \Longrightarrow 30A \)
Bu doğrultuda oluşan dörtgenlerin alanları aşağıdaki gibi bulunur.
\( DHJE \) dörtgeninin alanı:
\( 6A - A = 5A \)
\( EJKG \) dörtgeninin alanı:
\( 16A - 6A = 10A \)
\( GKCB \) dörtgeninin alanı:
\( 30A - 16A = 14A \)
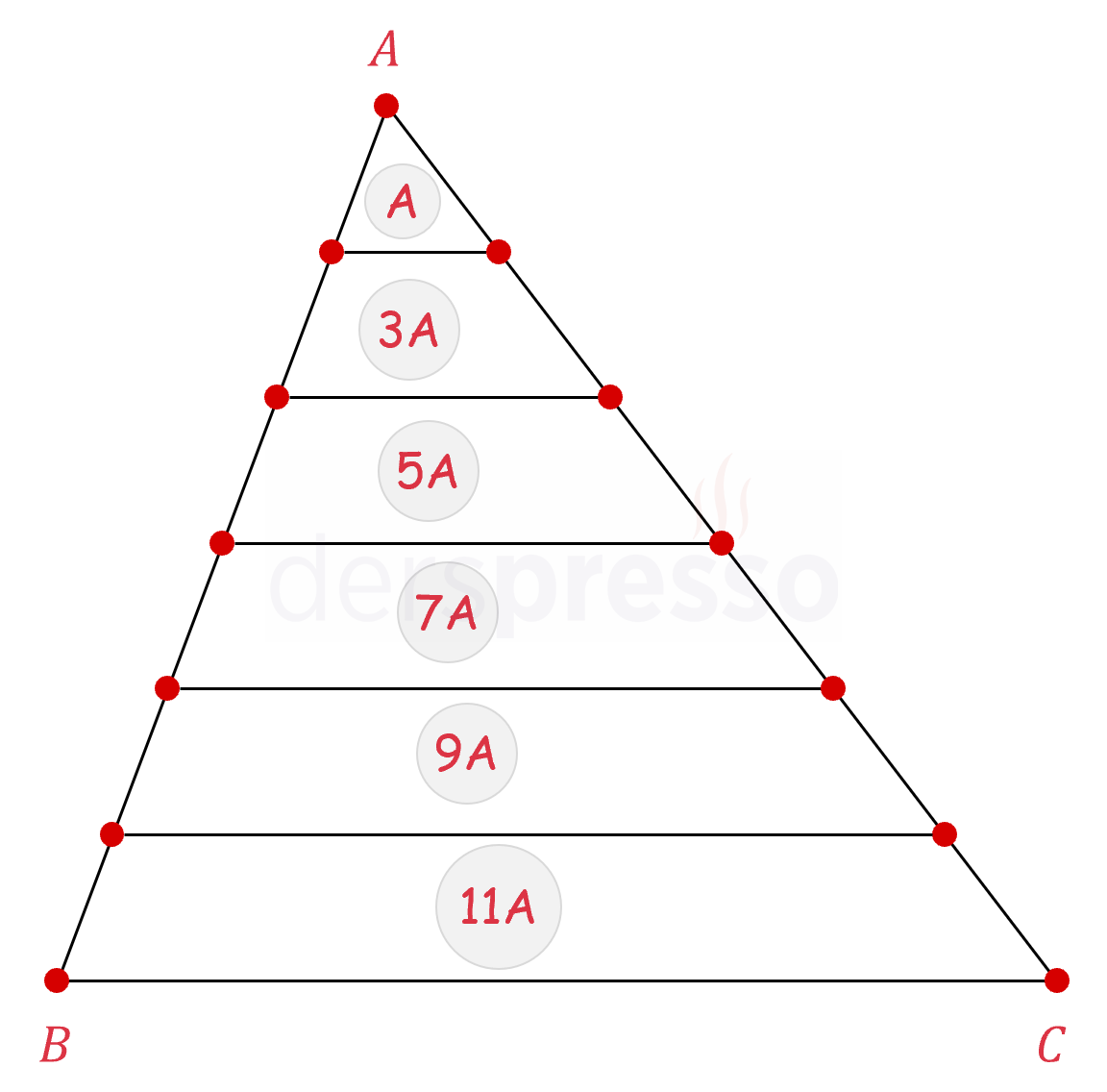
Yukarıdaki kuralın özel bir durumu olarak; bir üçgenin iki kenarı da eşit sayıda parçalara bölündüğünde, tepe noktaları aynı olacak şekilde oluşan üçgen ve dörtgenlerin alanlarının oranı ardışık tek sayılarla orantılı olur.
Birbirine paralel iki doğrudan birinde tabanı, diğerinde tepe noktası bulunan üçgenlerin alanı, taban sabit kaldığı sürece birbirine eşittir. Bunun sebebi oluşan tüm üçgenlerin taban ve yükseklik uzunluklarının eşit olmasıdır.
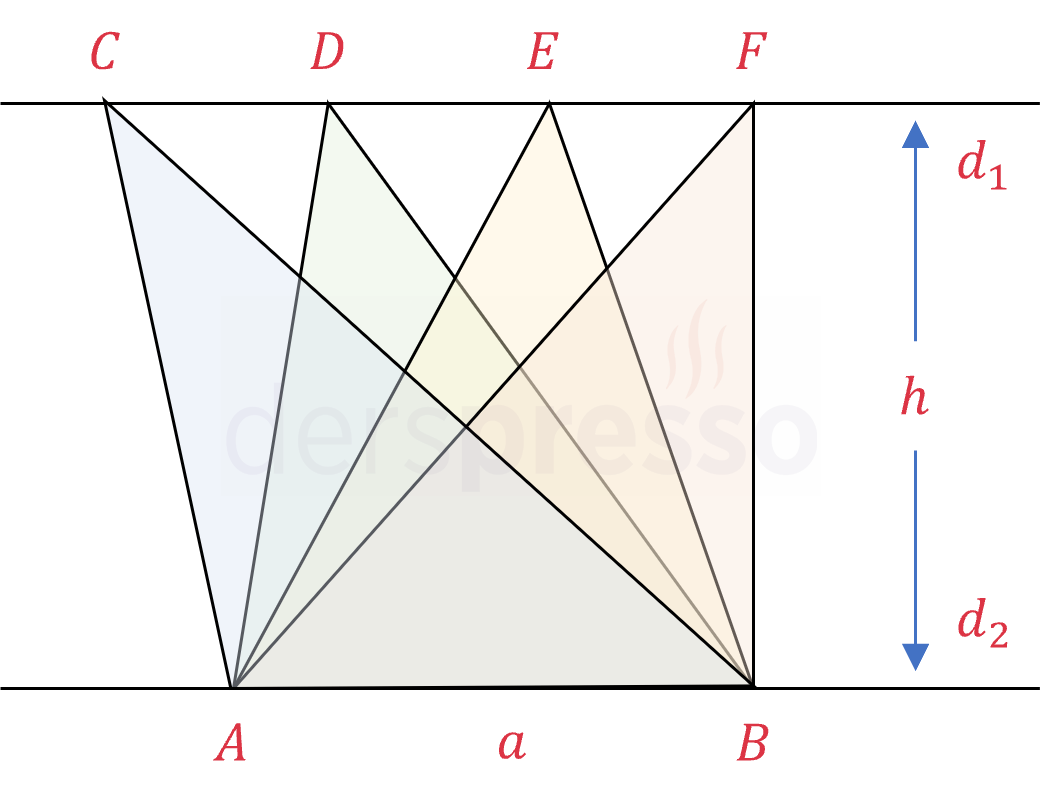
\( d_1 \parallel d_2 \) olmak üzere,
\( A(ABC) = A(ABD) = A(ABE) = A(ABF) = \dfrac{a \cdot h}{2} \)

Şekilde verilenlere göre \( ABCD \) dik yamuğunun alanı kaç \( \text{ br}^2 \) olur?
Çözümü Göster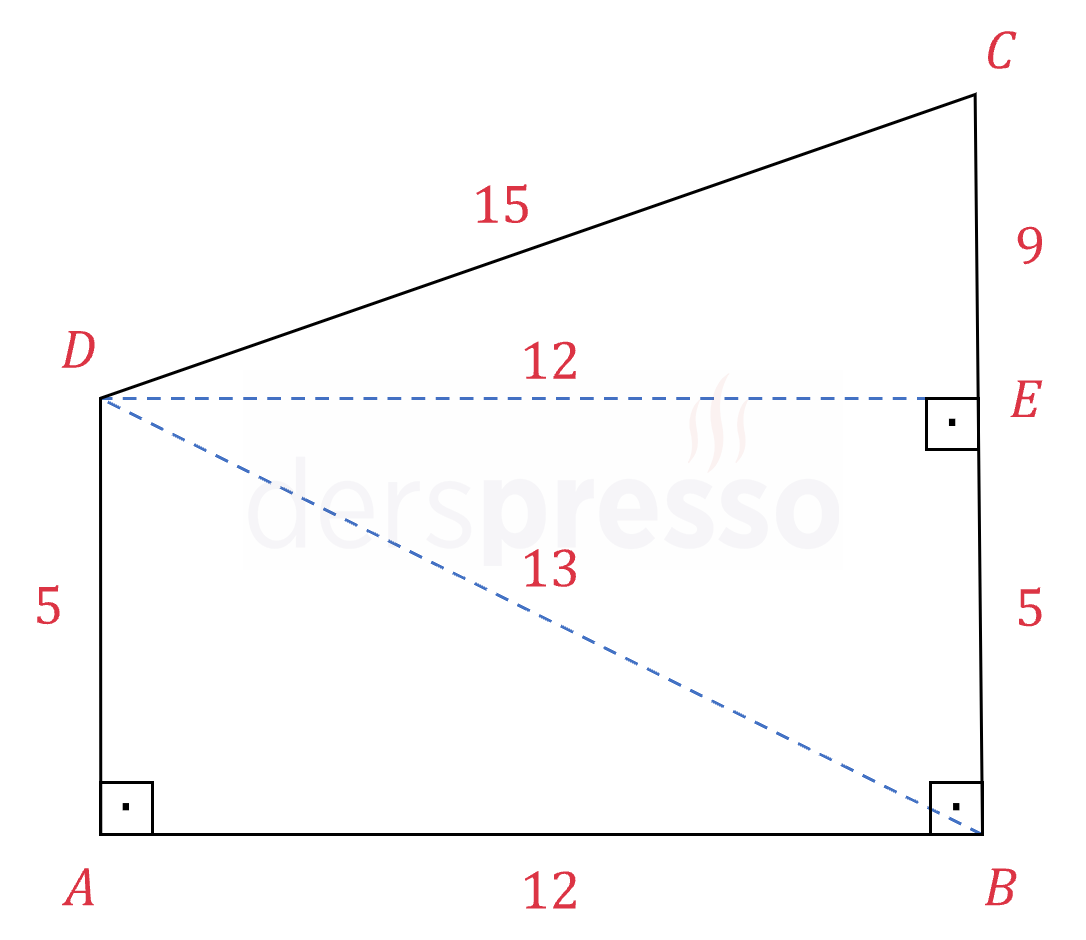
Dik yamuğun \( B \) ve \( D \) köşelerini birleştirelim ve \( D \) köşesinden \( [BC] \) kenarına bir dik indirelim (mavi kesikli çizgiler).
Pisagor teoremini kullanarak \( \abs{BD} \) uzunluğunu bulalım.
\( \abs{BD}^2 = 5^2 + 12^2 \)
\( \abs{BD} = 13 \) br
\( ABED \) bir dikdörtgen olduğu için karşılıklı kenar uzunlukları birbirine eşittir.
\( \abs{DE} = \abs{AB} = 12 \) br
\( \abs{BE} = \abs{AD} = 5 \) br
Pisagor teoremini kullanarak \( \abs{EC} \) uzunluğunu bulalım.
\(15^2 = 12^2 + \abs{EC}^2 \)
\( \abs{EC} = 9 \) br
Bu noktada dik yamuğun alanını \( [BD] \) doğru parçasının oluşturduğu iki üçgenin alanlarını toplayarak bulabiliriz.
\( A(ABCD) = A(\overset{\triangle}{ABD}) + A(\overset{\triangle}{BCD}) \)
\( = \dfrac{5 \cdot 12}{2} + \dfrac{(9 + 5) \cdot 12}{2} \)
\( = 30 + 84 = 114 \text{ br}^2 \) bulunur.
Alternatif olarak alanı yamuk alan formülü ile de bulabiliriz.
\( A(ABCD) = \dfrac{(5 + 5 + 9) \cdot 12}{2} \)
\( = 114 \text{ br}^2 \) bulunur.