Dik Üçgen
Bir açısı \( 90° \) olan üçgene dik üçgen denir.

Dik üçgenin bazı özellikleri aşağıdaki gibidir.
- Dik üçgenin diklik merkezi (yüksekliklerin kesişim noktası) dik kenarların kesiştiği köşededir (\( A \) noktası).
- Dik üçgenin orta dikmelerinin kesişim noktası hipotenüsün orta noktasıdır.
- Dik üçgenler çeşitkenar ya da ikizkenar olabilir ancak eşkenar olamaz.
- Dik üçgenin dik olmayan iki açısı dar ve tümler açılardır.
- Dik üçgende dik açının gördüğü kenara (\( [CB] \) kenarı) hipotenüs adı verilir ve dik üçgenin en uzun kenarıdır.
Pisagor Teoremi
Pisagor teoremine göre, dik üçgende hipotenüs uzunluğunun karesi diğer iki kenar uzunluklarının kareleri toplamına eşittir.
\( a^2 = b^2 + c^2 \)
Hipotenüs uzunluğu 102 br, bir dik kenar uzunluğu 98 br olan üçgenin diğer dik kenar uzunluğunu bulalım.
\( 102^2 = 98^2 + c^2 \)
\( c^2 = 102^2 - 98^2 = (102 - 98)(102 + 98) \)
\( c = \sqrt{4 \cdot 200} = 20\sqrt{2} \) br
İSPATI GÖSTER
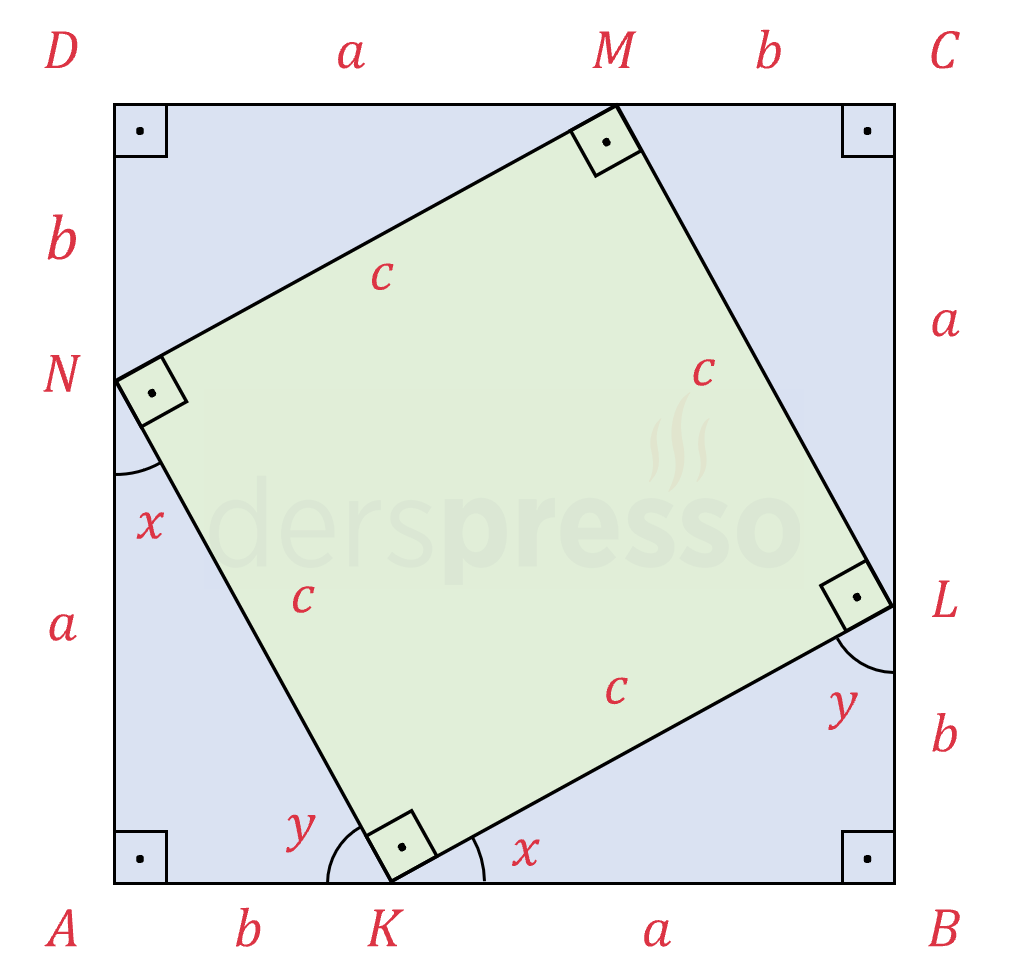
Yukarıdaki \( ABCD \) karesinin kenarları üzerinde her kenar uzunluğunu \( a \) ve \( b \) birim olmak üzere iki parçaya bölecek şekilde \( K \), \( L \), \( M \) ve \( N \) noktalarını işaretleyelim ve bu noktaları birleştirelim.
Mavi dik üçgenlerin ikişer kenar uzunlukları ve bu kenarların arasındaki dik açılar eşit olduğu için kosinüs teoreminden karşı kenar (hipotenüs) uzunlukları da eşittir. Bu kenar uzunluklarına \( c \) diyelim.
Dik üçgenlerin dik olmayan açıları tümler açılardır.
\( x + y = 90° \)
Bu eşitliği \( KLMN \) dörtgeninin tüm köşelerindeki \( x \) ve \( y \) açılarına uygularsak \( KLMN \) eşkenar dörtgeninin köşe açılarının dik olduğunu ve şeklin bir kare olduğunu buluruz.
Şimdi \( ABCD \) karesinin alanını yazalım.
\( A(ABCD) = (a + b)^2 = a^2 + 2ab + b^2 \)
İçteki \( KLMN \) karesinin alanını yazalım.
\( A(KLMN) = c^2 \)
Bir yeşil dik üçgenin alanını yazalım.
\( A(AKN) = \dfrac{ab}{2} \)
\( ABCD \) karesinin alanı \( KLMN \) karesinin alanı ve dört dik üçgenin alanları toplamına eşittir.
\( A(ABCD) = A(KLMN) + 4 \cdot A(AKN) \)
\( a^2 + 2ab + b^2 = c^2 + 4 \cdot \dfrac{ab}{2} \)
Eşitliğin iki tarafındaki ortak terimleri sadeleştirirsek Pisagor teoremini elde ederiz.
\( a^2 + b^2 = c^2 \)
Bu teoremin karşıtı da doğrudur. Buna göre, bir dik üçgende yukarıdaki eşitlik sağlanıyorsa eşitliğin solundaki kenarı gören açı dik açıdır.
Bir dik üçgende hipotenüse çizilen kenarortay iki ikizkenar üçgen oluşturur. "Muhteşem Üçlü" olarak da adlandırılan bu kurala göre; hipotenüse çizilen kenarortay, hipotenüste böldüğü iki parça ile eşit uzunluktadır. Tüm kenarortaylarda olduğu gibi, bu kenarortay üçgenin alanını iki eşit parçaya böler.

\( \abs{AD} = \abs{BD} = \abs{DC} \)
\( m(\widehat{ABD}) = m(\widehat{BAD}) \)
\( m(\widehat{ACD}) = m(\widehat{CAD}) \)
İSPATI GÖSTER
\( D \) noktasından \( [AB] \) kenarına paralel bir doğru çizelim ve \( [AC] \) kenarını kestiği noktaya \( E \) diyelim.

\( \abs{BD} = \abs{DC} \) ve \( [ED] \parallel [AB] \) olduğu için \( [ED] \) üçgenin bir orta tabanıdır, dolayısıyla \( [AC] \) kenarını ortalar.
\( \abs{AE} = \abs{EC} \)
\( [ED] \parallel [AB] \) olduğu için \( \widehat{DEC} \) açısı \( \widehat{BAC} \) ile eş açılardır.
\( m(\widehat{DEC}) = m(\widehat{BAC}) = 90° \)
\( ADC \) üçgeninde \( [AC] \) kenarına ait \( [ED] \) yüksekliği \( [AC] \) kenarını ortaladığı için \( ADC \) üçgeni ikizkenar olmak zorundadır.
\( m(\widehat{DAE}) = m(\widehat{DCE}) \)
\( \abs{AD} = \abs{DC} \)
Buna göre, dik üçgende hipotenüse çizilen kenarortay hipotenüste böldüğü iki parça ile eşit uzunluktadır.
Bir dik üçgende \( \abs{AD} = \abs{BD} \) ya da \( \abs{AD} = \abs{DC} \) eşitlikleri verilirse \( [AD] \) hipotenüsün kenarortayıdır ve \( \abs{BD} = \abs{DC} \) olur.
Dik Üçgen Bağıntıları
Dik üçgenlerle ilgili aşağıdaki bağıntıları yazabiliriz.

Öklid'in yükseklik bağıntısına göre; bir dik üçgende hipotenüse ait yüksekliğin karesi, hipotenüs üzerinde oluşan iki parçanın uzunluklarının çarpımına eşittir.
\( h^2 = m \cdot n \)
İSPATI GÖSTER

\( m(\hat{ACD}) = m(\hat{BAD}) = x \)
Her iki açının tanjant oranını yazalım.
\( \tan{x} = \dfrac{h}{n} = \dfrac{m}{h} \)
İçler dışlar çarpımı yapalım.
\( h^2 = m \cdot n \)
Öklid'in dik kenar bağıntılarına göre; bir dik üçgende dik kenar uzunluğunun karesi, hipotenüs ile hipotenüsün bu dik kenar tarafındaki parçasının uzunluklarının çarpımına eşittir
\( b^2 = n \cdot a \)
\( c^2 = m \cdot a \)
İSPATI GÖSTER

\( \overset{\triangle}{ADC} \) üçgeni için Pisagor teoremi formülünü yazalım.
\( b^2 = h^2 + n^2 \)
\( h^2 \) yerine yukarıdaki yükseklik bağıntısındaki eşitini yazalım.
\( b^2 = m \cdot n + n^2 \)
\( b^2 = n \cdot (m + n) \)
\( b^2 = n \cdot a \)
Benzer bir gösterimi diğer kenar için de yapabiliriz.
Alan bağıntısı:
\( b \cdot c = a \cdot h \)
İSPATI GÖSTER

Dik üçgenin alanını, hipotenüsü ve bir dik kenarı taban alarak iki farklı şekilde yazabiliriz.
\( A(\overset{\triangle}{ABC}) = \dfrac{b \cdot c}{2} = \dfrac{a \cdot h}{2} \)
\( b \cdot c = a \cdot h \)
Ters Pisagor teoremi olarak da adlandırılan kurala göre, dik üçgenin yükseklikleri arasında aşağıdaki bağıntı vardır.
\( \dfrac{1}{b^2} + \dfrac{1}{c^2} = \dfrac{1}{h^2} \)
İSPATI GÖSTER

Dik üçgenin alanını hem dik kenarlar hem de hipotenüs üzerinden yazalım.
\( \dfrac{b \cdot c}{2} = \dfrac{a \cdot h}{2} \)
\( b \cdot c = a \cdot h \)
Eşitliğin taraflarının karesini alalım.
\( b^2 \cdot c^2 = a^2 \cdot h^2 \)
\( \dfrac{1}{h^2} = \dfrac{a^2}{b^2 \cdot c^2} \)
Pisagor teoremini kullanalım.
\( \dfrac{1}{h^2} = \dfrac{b^2 + c^2}{b^2 \cdot c^2} \)
\( \dfrac{1}{h^2} = \dfrac{c^2}{b^2 \cdot c^2} + \dfrac{b^2}{b^2 \cdot c^2} \)
\( \dfrac{1}{h^2} = \dfrac{1}{b^2} + \dfrac{1}{c^2} \)
Özel Dik Üçgenler
Bazı dik üçgenlerin kenar uzunlukları daha kolay akılda tutulabilir değerlere sahiptir ve sağladıkları işlem kolaylığı açısından da sorularda daha sık karşımıza çıkmaktadır.
Açılarına Göre Özel Üçgenler
Açıları itibariyle en sık karşımıza çıkan dik üçgenler 45-45-90° ve 30-60-90° üçgenleridir.
| Şekil | Açılar | Kenarlar |
|---|---|---|

|
45-45-90° üçgeni | Bu üçgende kenar uzunlukları arasında \( 1:1:\sqrt{2} \) orantısı vardır. |

|
30-60-90° üçgeni | Bu üçgende kenar uzunlukları arasında \( 1:\sqrt{3}:2 \) orantısı vardır. |

|
15-75-90° üçgeni | Bu üçgende hipotenüs uzunluğu hipotenüse ait yüksekliğin 4 katıdır. |
Pisagor Üçgenleri
Kenar uzunlukları birer tam sayı olan dik üçgenler Pisagor üçgeni olarak adlandırılırlar. Kenar uzunlukları bir Pisagor üçgeninin tam sayı katı olan üçgenler de birer Pisagor üçgenidir.
Aşağıda bazı Pisagor üçgenlerinin kenar uzunlukları verilmiştir.
| Şekil | Pisagor Üçgeni | Benzer Üçgenler |
|---|---|---|

|
3-4-5 üçgeni | 6-8-10, 9-12-15, 12-16-20, 15-20-25 ... |

|
5-12-13 üçgeni | 10-24-26, 15-36-39, 20-48-52 ... |

|
7-24-25 üçgeni | 14-28-50, 21-72-75, 28-96-100 |

|
8-15-17 üçgeni | 16-30-34, 24-45-51, 32-60-68 |
Aşağıdaki formüller kullanılarak herhangi \( m \) ve \( n \) tam sayı ikilisi ile Pisagor üçgenleri türetilebilir.
\( m, n \in \mathbb{Z^+} \) olmak üzere,
Aşağıdaki formüllerle hesaplayacağımız \( a \), \( b \) ve \( c \) değerleri bir Pisagor üçgeninin kenar uzunluklarını verir.
\( a = m^2 - n^2 \)
\( b = 2mn \)
\( c = m^2 + n^2 \)
\( m = 10 \) ve \( n = 3 \) için Pisagor üçgeni:
\( a = 10^2 - 3^2 = 91 \)
\( b = 2(10)(3) = 60 \)
\( c = 10^2 + 3^2 = 109 \)
\( a^2 + b^2 = c^2 \)
\( 91^2 + 60^2 = 109^2 \)
\( 8281 + 3600 = 11881 \)
İSPATI GÖSTER
\( a = m^2 - n^2 \)
\( b = 2mn \)
\( c = m^2 + n^2 \)
Yukarıdaki formülleri Pisagor teoremi formülünde yerine koyalım.
\( a^2 + b^2 = c^2 \)
\( (m^2 - n^2)^2 + (2mn)^2 = (m^2 + n^2)^2 \)
\( m^4 - 2m^2n^2 + n^4 + 4m^2n^2 = m^4 + 2m^2n^2 + n^4 \)
\( m^4 + 2m^2n^2 + n^4 = m^4 + 2m^2n^2 + n^4 \)
Bu değerleri yerine koyduğumuzda eşitliğin sağlandığını görüyoruz, dolayısıyla herhangi \( (m, n) \) ikilisini ve bu formülleri kullanarak hesaplayacağımız kenar uzunluklarının Pisagor teoremini sağlayacağını, dolayısıyla bir dik üçgenin kenar uzunluklarına karşılık geleceğini söyleyebiliriz.
Bazı \( m \) ve \( n \) değerleri için oluşan Pisagor üçgenleri aşağıdaki tabloda gösterilmiştir.
| \( m \) | \( n \) | \( a = m^2 - n^2 \) | \( b = 2mn \) | \( c = m^2 + n^2 \) |
|---|---|---|---|---|
| 2 | 1 | 3 | 4 | 5 |
| 3 | 2 | 5 | 12 | 13 |
| 4 | 1 | 15 | 8 | 17 |
| 4 | 3 | 7 | 24 | 25 |
| 5 | 2 | 21 | 20 | 29 |
| 5 | 4 | 9 | 40 | 41 |
Dik Üçgenin Diğer Özellikleri
Dik üçgenin iç teğet çemberinin yarıçapı aşağıdaki formülle hesaplanır.
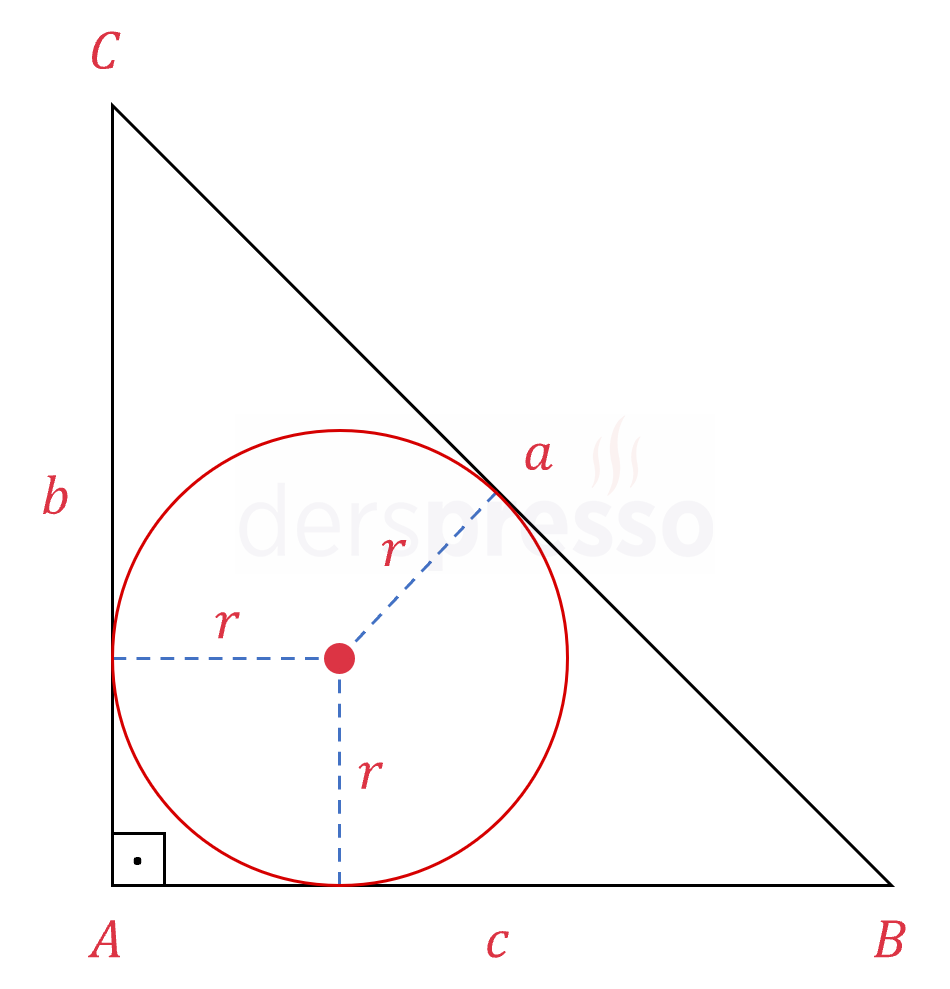
\( r = \dfrac{b + c - a}{2} \)
İSPATI GÖSTER
Aşağıda verilen dik üçgenin kenar uzunlukları \( a \), \( b \) ve \( c \)'dir.
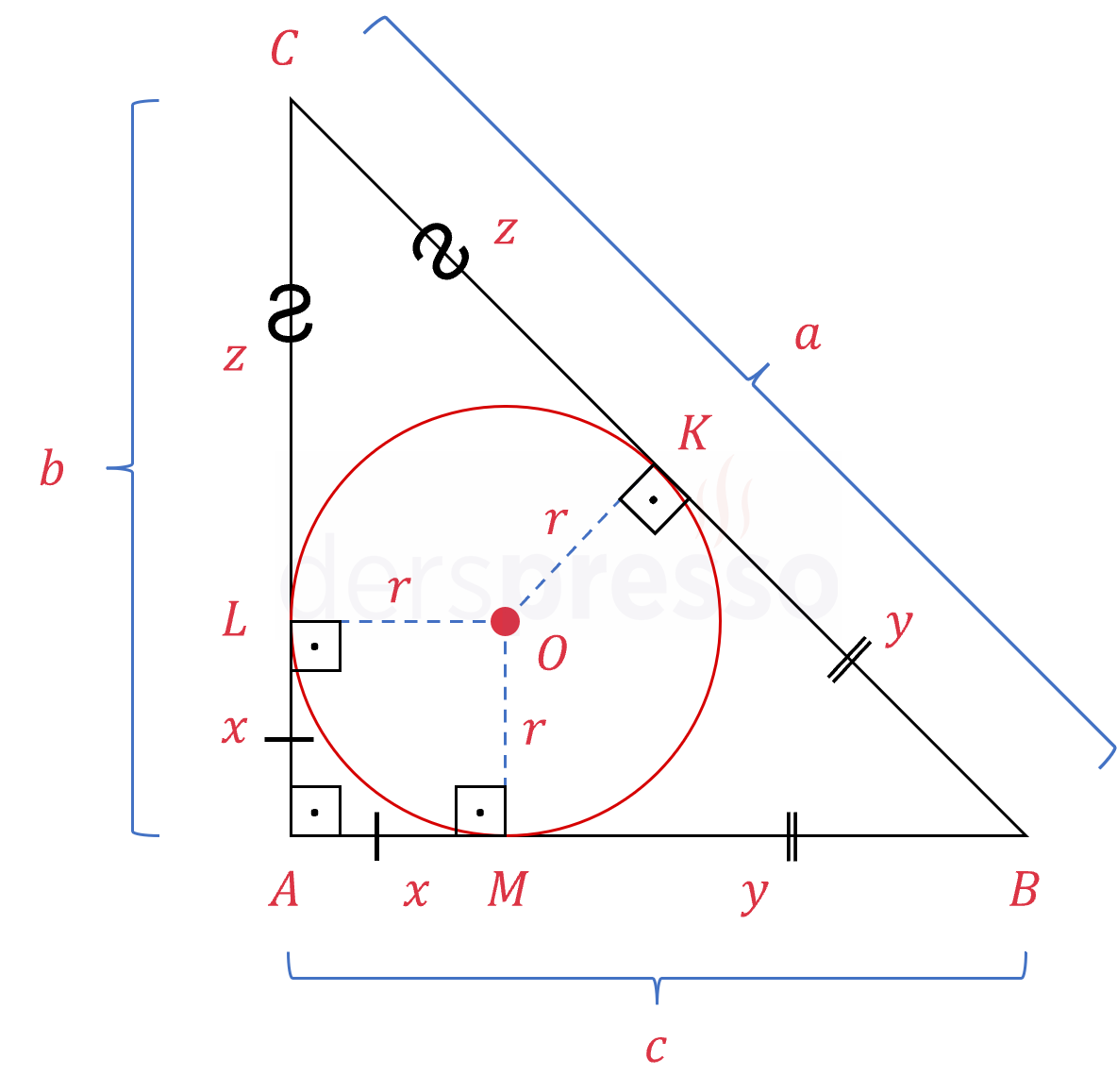
Bir çemberin dışındaki bir noktadan çembere çizilen teğetlerin uzunlukları birbirine eşittir.
\( \abs{AM} = \abs{AL} = x \)
\( \abs{BM} = \abs{BK} = y \)
\( \abs{CK} = \abs{CL} = z \)
Bu teğetlerin uzunlukları toplamı üçgenin kenar uzunlukları toplamına eşittir.
\( 2x + 2y + 2z = a + b + c \)
\( y + z = a \) olduğu için,
\( 2x + 2a = a + b + c \)
\( 2x = b + c - a \)
\( x = \dfrac{b + c - a}{2} \)
\( [AL] \) ve \( [AM] \) çemberin teğetleri olduğu için çemberi dik keserler. \( \widehat{LAM} \) açısı da üçgenin dik açısı olduğu için \( AMOL \) dörtgeni bir dikdörtgendir ve karşılıklı kenar uzunlukları birbirine eşittir, dolayısıyla \( x \) uzunlukları çemberin yarıçapına eşittir.
\( x = r = \dfrac{b + c - a}{2} \)
Dik üçgenin alanı dik kenarların çarpımının yarısıdır.
\( A = \dfrac{b \cdot c}{2} \)

Şekilde \( ABC \) dik üçgeni verilmiştir.
\( \abs{AB} = 12, \quad \abs{AC} = 16 \)
\( \abs{BD} = \abs{DC} \)
olduğuna göre, \( \abs{AD} = x \) kaçtır?
Çözümü Göster\( ABC \) üçgeni 3-4-5 özel üçgeni ile \( k = 4 \) benzerlik oranına sahip 12-16-20 üçgenidir.
\( \abs{BC} = 20 \)
\( \abs{BD} = \abs{DC} = 10 \)
\( [AD] \) hipotenüsü ortaladığı için muhteşem üçlünün üçüncü kenarıdır.
\( \abs{BD} = \abs{DC} = \abs{AD} \)
\( \abs{AD} = 10 \) olarak bulunur.

Şekilde \( ABC \) dik üçgeni verilmiştir.
\( \abs{AB} = x - 2, \quad \abs{BC} = x \)
\( \abs{AC} = 2\sqrt{5} \)
olduğuna göre, \( x \) kaçtır?
Çözümü Göster\( ABC \) dik üçgeninde Pisagor teoremini kullanalım.
\( \abs{AB}^2 + \abs{BC}^2 = \abs{AC}^2 \)
\( (x - 2)^2 + x^2 = (2\sqrt{5})^2 \)
\( x^2 - 4x + 4 + x^2 = 20 \)
\( 2x^2 - 4x - 16 = 0 \)
\( 2(x - 4)(x + 2) = 0 \)
\( x = -2 \) ya da \( x = 4 \)
Kenar uzunluğu negatif olamayacağı için \( x = -2 \) geçerli bir çözüm değildir.
\( x = 4 \) bulunur.

Şekilde \( ABC \) dik üçgeni verilmiştir.
\( \abs{AB} = 15, \quad \abs{AD} = 17 \)
\( \abs{DC} = 12 \)
olduğuna göre, \( \abs{AC} = x \) kaçtır?
Çözümü Göster\( ABD \) üçgeni 8-15-17 özel üçgenidir.
\( \abs{BD} = 8 \)
\( \abs{BC} = 8 + 12 = 20 \)
\( ABC \) üçgeni 3-4-5 özel üçgeni ile \( k = 5 \) benzerlik oranına sahip 15-20-25 üçgenidir.
\( \abs{AC} = x = 25 \) bulunur.

Şekilde \( ABC \) ve \( BDC \) dik üçgenleri verilmiştir.
\( \abs{BD} = 5, \quad \abs{DC} = 6 \)
\( \abs{AC} = \sqrt{41} \)
olduğuna göre, \( \abs{AB} = x \) kaçtır?
Çözümü Göster\( BDC \) üçgeninde Pisagor teoremini kullanalım.
\( \abs{BC}^2 = \abs{BD}^2 + \abs{DC}^2 \)
\( = 5^2 + 6^2 \)
\( \abs{BC} = \sqrt{61} \)
\( ABC \) üçgeninde Pisagor teoremini kullanalım.
\( \abs{BC}^2 = \abs{AB}^2 + \abs{AC}^2 \)
\( (\sqrt{61})^2 = x^2 + (\sqrt{41})^2 \)
\( x^2 = 20 \)
\( x = 2\sqrt{5} \) bulunur.

Şekilde \( ABC \) dik üçgeni verilmiştir.
\( \abs{DC} = 2\abs{BD} \)
\( \abs{AD} = 8, \quad \abs{AC} = 12 \)
olduğuna göre, \( \abs{BC} \) kaçtır?
Çözümü Göster\( \abs{AB} = x \)
\( \abs{BD} = y, \abs{DC} = 2y \) diyelim.

\( ABD \) ve \( ABC \) üçgenlerinde Pisagor teoremini kullanalım.
\( \abs{AB}^2 + \abs{BD}^2 = \abs{AD}^2 \)
\( x^2 + y^2 = 8^2 = 64 \)
\( \abs{AB}^2 + \abs{BC}^2 = \abs{AC}^2 \)
\( x^2 + (3y)^2 = 12^2 = 144 \)
1. denklemi 2. denklemden taraf tarafa çıkaralım.
\( 9y^2 - y^2 = 144 - 64 \)
\( y^2 = 10 \)
Uzunluk değeri negatif olamaz.
\( y = \sqrt{10} \)
\( \abs{BC} = 3y = 3\sqrt{10} \) bulunur.

Şekilde \( ABC \) üçgeni verilmiştir.
\( \abs{AC} = 10 \)
\( m(\widehat{ABC}) = 45°, \quad m(\widehat{ACB}) = 30° \)
olduğuna göre, \( \abs{AB} = x \) kaçtır?
Çözümü Göster\( A \) köşesinden \( [BC] \) kenarına bir dikme indirelim.
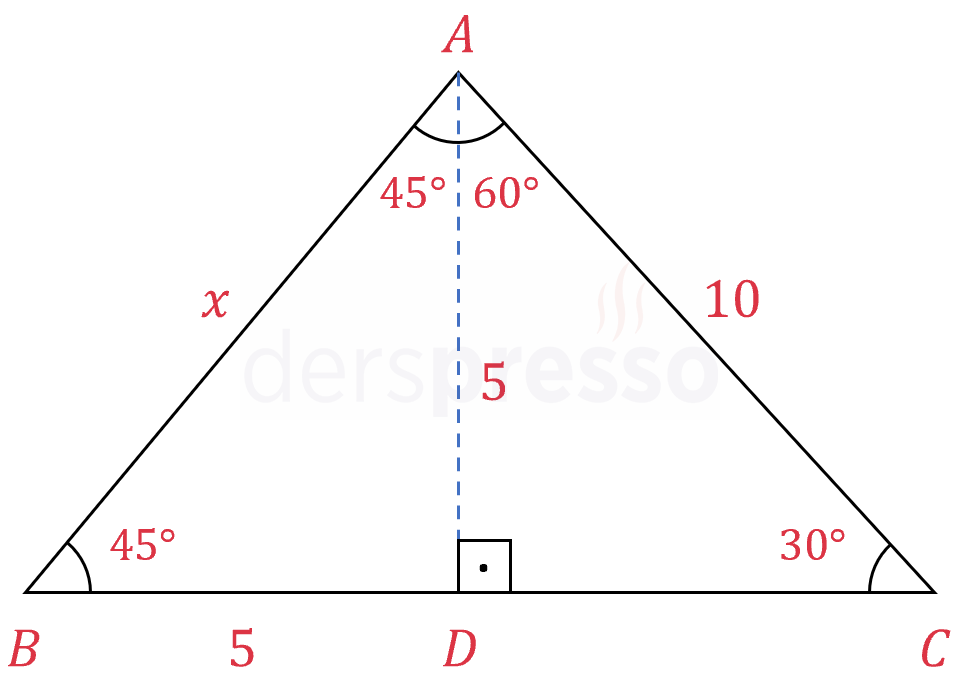
\( ADC \) üçgeni 30-60-90° üçgeni olur. 30-60-90° üçgeninde kenar uzunlukları arasındaki orantı sırasıyla \( 1:\sqrt{3}:2 \) şeklinde olur.
\( \abs{AD} = 5 \)
\( ABD \) üçgeni 45-45-90° üçgeni olur. 45-45-90° üçgeninde kenar uzunlukları arasındaki orantı sırasıyla \( 1:1:\sqrt{2} \) şeklinde olur.
\( \abs{AB} = x = 5\sqrt{2} \) bulunur.

Şekilde \( ABC \) dik üçgeni verilmiştir.
\( \abs{AC} = 6, \quad \abs{BC} = 10 \)
\( \abs{BD} = \abs{DA} \)
olduğuna göre, \( \abs{DC} = x \) kaçtır?
Çözümü Göster\( ABC \) üçgeni 3-4-5 özel üçgeni ile \( k = 2 \) benzerlik oranına sahip 6-8-10 üçgenidir.
\( \abs{AB} = 8 \)
\( \abs{BD} = \abs{DA} = 4 \)
\( ADC \) üçgeninde Pisagor teoremini kullanalım.
\( \abs{DC}^2 = \abs{DA}^2 + \abs{AC}^2 \)
\( x^2 = 4^2 + 6^2 \)
\( x = 2\sqrt{13} \) bulunur.

Şekilde \( ABC \) üçgeni verilmiştir.
\( m(\widehat{ABC}) = 45° \)
\( \abs{AB} = 5\sqrt{2}, \quad \abs{BC} = 17 \)
olduğuna göre, \( \abs{AC} = x \) kaçtır?
Çözümü Göster\( A \) köşesinden \( [BC] \) kenarına dikme indirelim.
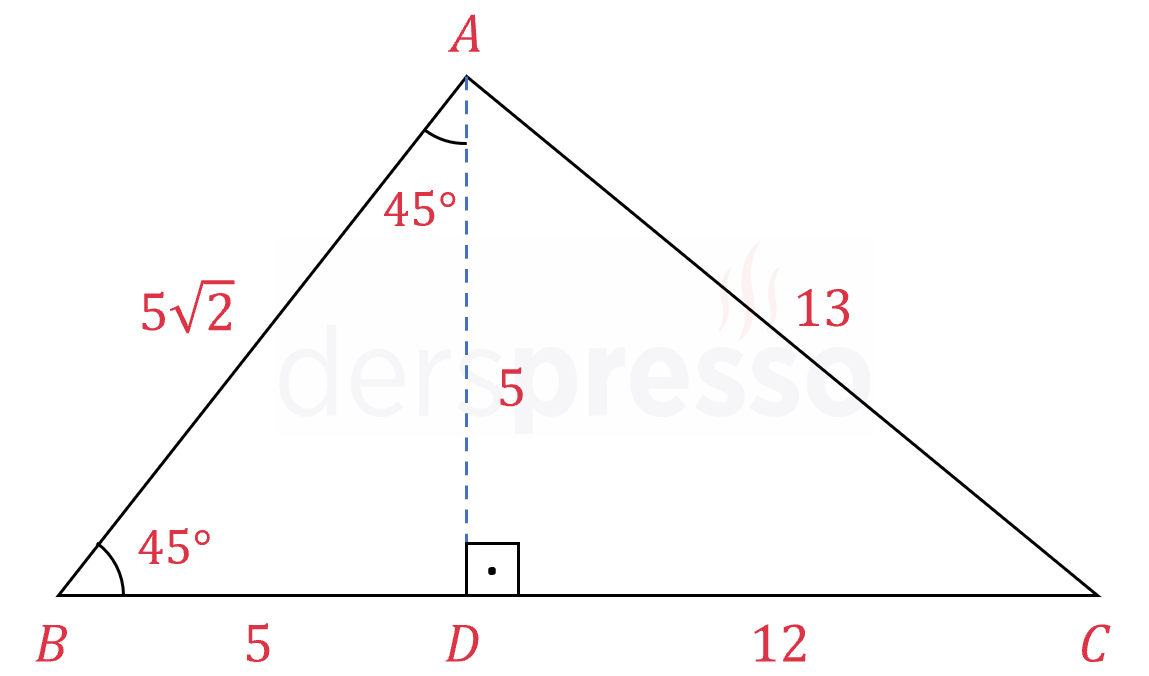
\( ABD \) üçgeni 45-45-90° üçgeni olur. 45-45-90° üçgeninde kenar uzunlukları arasındaki orantı sırasıyla \( 1:1:\sqrt{2} \) şeklinde olur.
\( \abs{AD} = \abs{BD} = 5 \)
\( \abs{DC} = \abs{BC} - \abs{BD} \)
\( = 17 - 5 = 12 \)
\( ADC \) üçgeni 5-12-13 özel üçgenidir.
\( \abs{AC} = 13 \) olarak bulunur.

\( [AD] \perp [CD], \quad m(\widehat{BCD}) = 30° \)
\( \abs{AB} = 17, \quad \abs{BC} = 10 \)
\( \abs{AD} = 20 \)
olduğuna göre, \( \abs{CD} = x \) değeri kaçtır
Çözümü Göster\( B \) noktasından \( [AD] \) ve \( [CD] \) kenarlarına dikmeler çizerek \( BEDF \) dikdörtgeni oluşturalım.
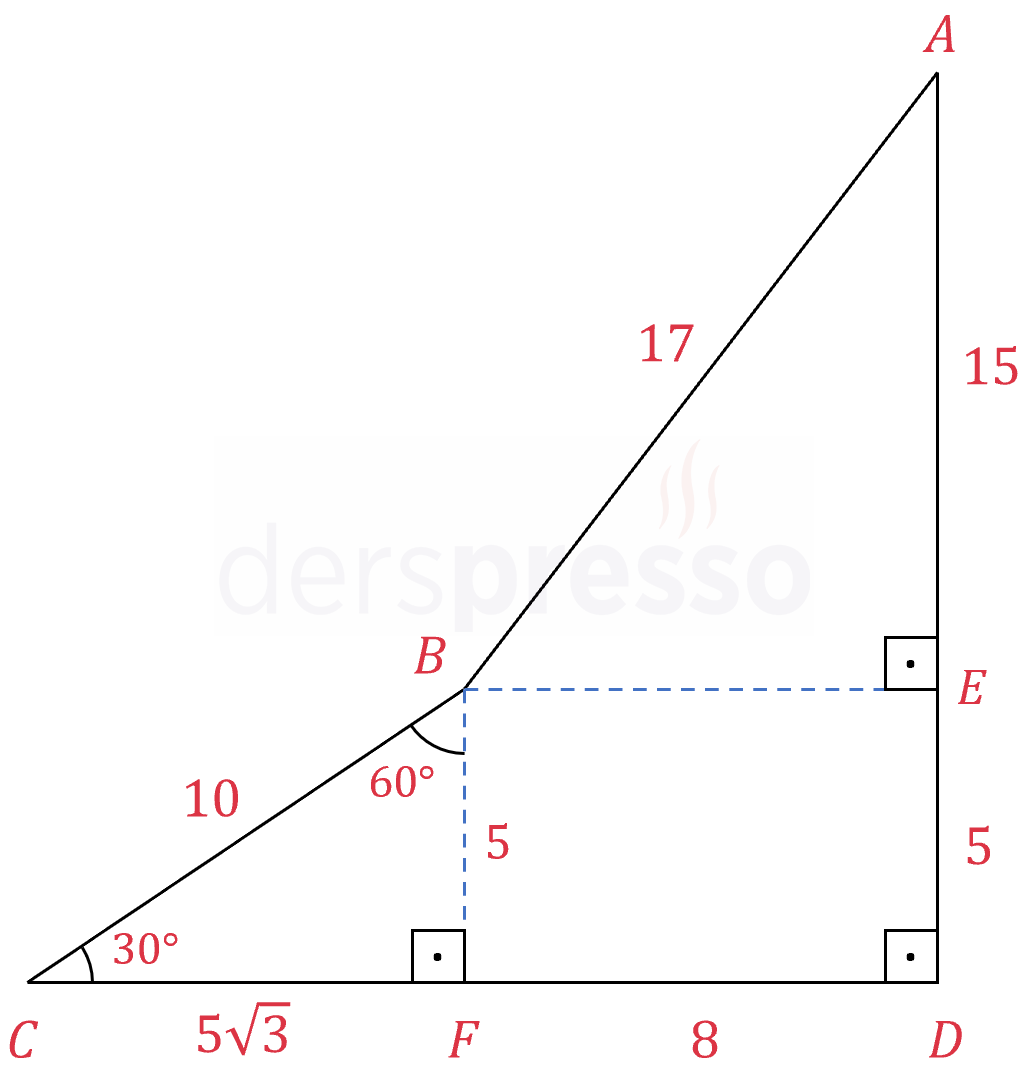
\( BCF \) üçgeni 30-60-90° üçgeni olur. 30-60-90° üçgeninde kenar uzunlukları arasındaki orantı sırasıyla \( 1:\sqrt{3}:2 \) şeklinde olur.
\( \abs{BF} = 5, \quad \abs{CF} = 5\sqrt{3} \)
Dikdörtgende karşılıklı kenar uzunlukları eşittir.
\( \abs{ED} = \abs{BF} = 5 \)
\( \abs{AE} = 20 - 5 = 15 \)
\( ABE \) dik üçgeni 8-15-17 özel üçgenidir.
\( \abs{BE} = \abs{FD} = 8 \)
\( \abs{CD} = \abs{CF} + \abs{FD} \)
\( x = 5\sqrt{3} + 8 \) olarak bulunur.
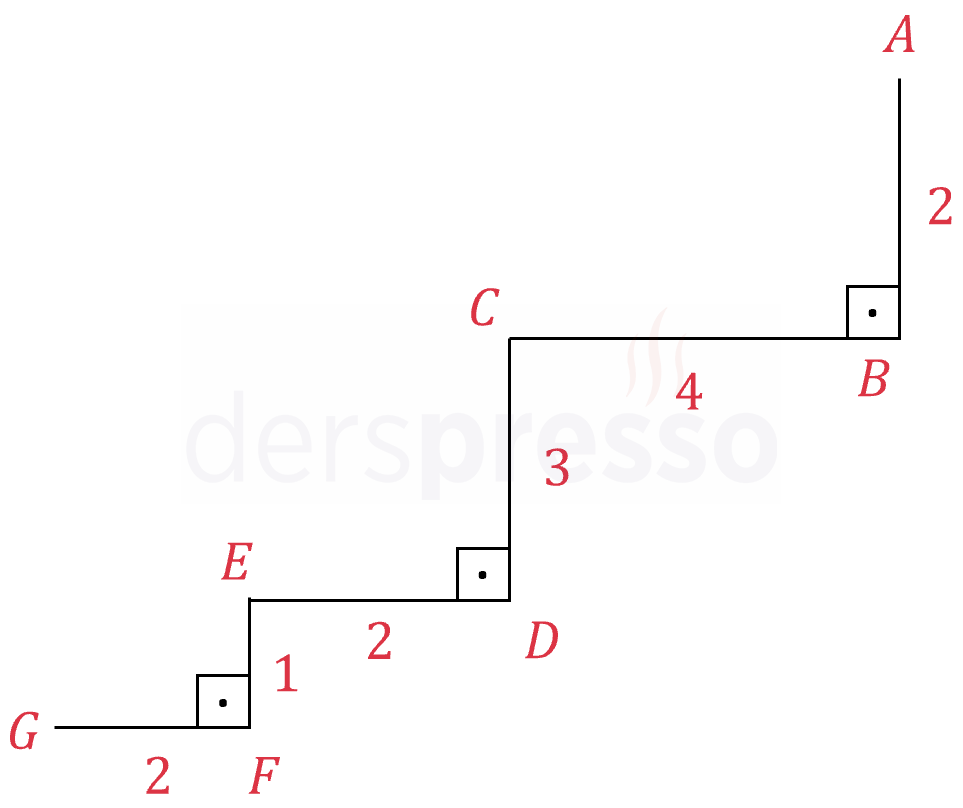
Yukardaki şekildeki kenar uzunlukları aşağıdaki gibidir.
\( \abs{AB} = 2, \quad \abs{CB} = 4 \)
\( \abs{CD} = 3, \quad \abs{ED} = 2 \)
\( \abs{EF} = 1, \quad \abs{GF} = 2 \)
olduğuna göre, \( A \) ve \( G \) noktaları arasındaki uzaklık en az kaçtır?
Çözümü Göster\( A \) ve \( G \) noktaları arasındaki uzaklığın en küçük değeri iki nokta arasında çizilen doğrunun uzunluğuna eşittir.
Bu iki noktayı birleştirelim. Bu doğru aynı zamanda oluşan \( GHA \) dik üçgeninin hipotenüsüdür.
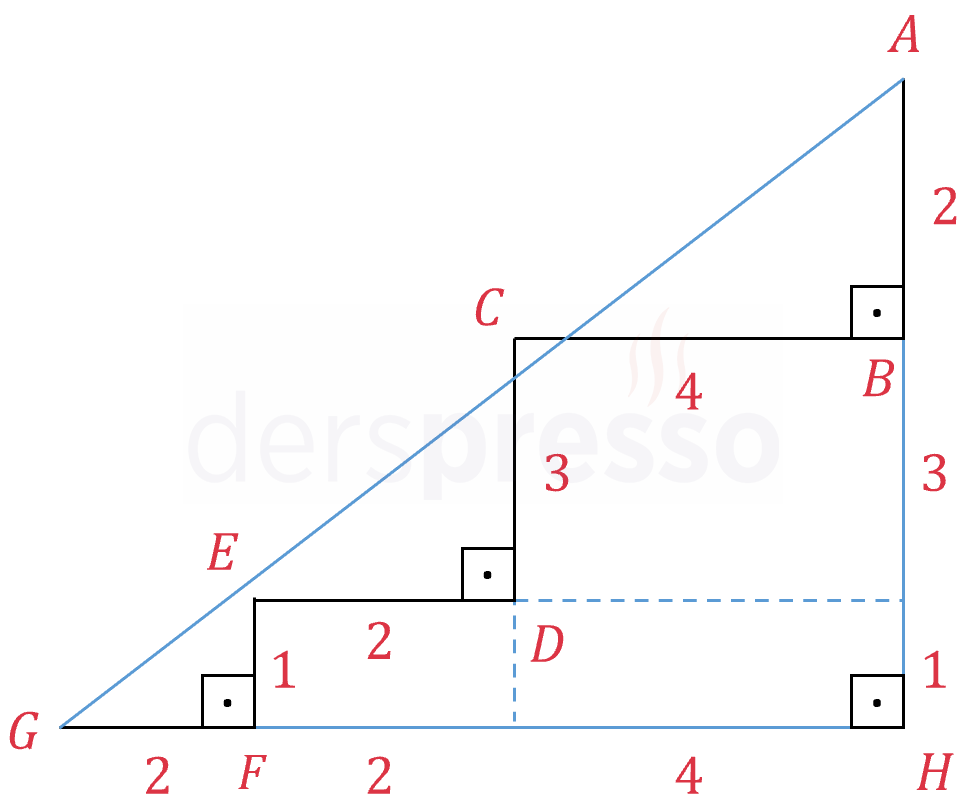
Dik üçgenin dik kenar uzunluklarını bulmak için verilen şekildeki yatay ve dikey uzunlukların toplamını alalım.
Yatay uzunlukların toplamı \( = \abs{GF} + \abs{ED} + \abs{CB} = 8 \)
Dikey uzunlukların toplamı \( = \abs{AB} + \abs{CD} + \abs{EF} = 6 \)
Pisagor teoremini kullanarak \( \abs{AG} \) uzunluğunu bulalım.
\( \abs{AG}^2 = 8^2 + 6^2 = 10^2 \)
\( \abs{AG} = 10 \) bulunur.

Şekilde \( ABC \) dik üçgeni verilmiştir.
\( \abs{AD} = \abs{DC} = \abs{DE} \)
\( \abs{BE} = 9, \quad \abs{EC} = 4 \)
olduğuna göre, \( [AC] \) doğru parçasının uzunluğu nedir?
Çözümü Göster\( [AD] \), \( [DC] \) ve \( [DE] \) doğru parçalarının uzunlukları eşit olduğu için \( [ED] \) doğru parçasının bir dik köşeden çizildiğini söyleyebiliriz.
Buna göre \( A \) köşesinden \( E \) noktasına çizilen doğru parçası \( [BC] \) kenarını dik keser.
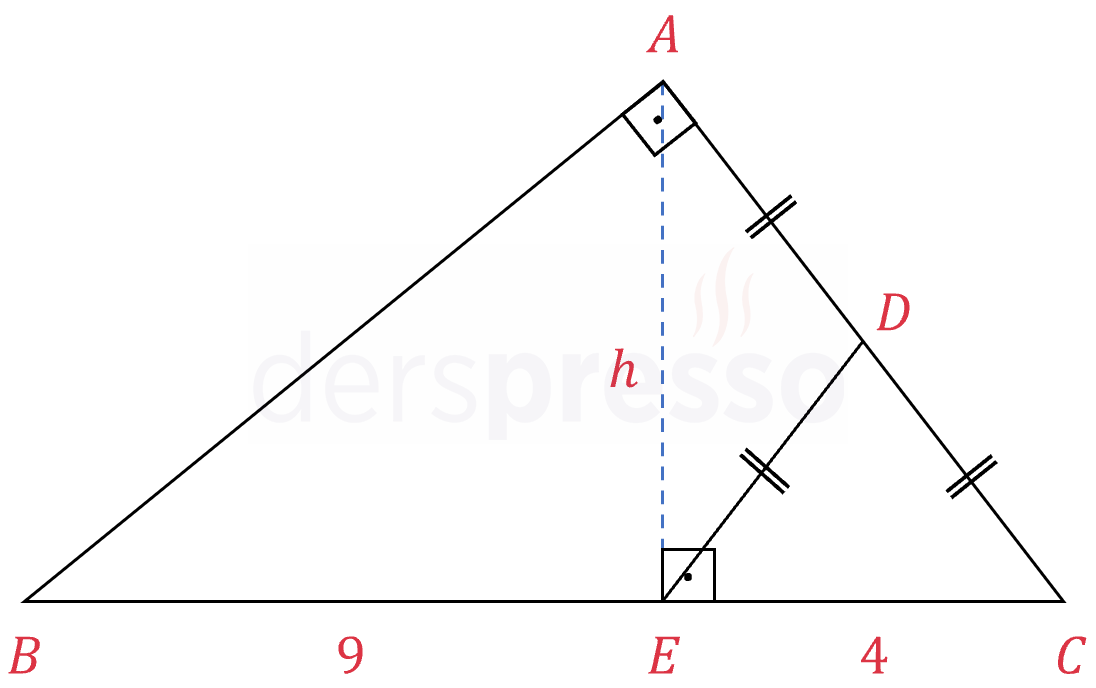
\( [AE] \perp [BC] \)
\( \abs{AE} = h \) diyelim.
\( h \) uzunluğunu Öklid bağlantısını kullanarak bulalım.
\( h^2 = 9 \cdot 4 \)
\( h = 6 \)
\( \abs{AC} \) değeri için \( AEC \) üçgeninde Pisagor teoremini kullanalım.
\( \abs{AC}^2 = \abs{AE}^2 + \abs{EC}^2 \)
\( = 6^2 + 4^2 \)
\( \abs{AC} = 2\sqrt{13} \) bulunur.

Şekilde \( ABC \) ve \( EDC \) dik üçgenleri verilmiştir.
\( [AB] \parallel [DE] \)
\( \abs{AB} = 4, \abs{DE} = 5, \abs{BD} = 12 \)
olduğuna göre, \( \abs{AE} \) kaçtır?
Çözümü Göster\( [AB] \) doğru parçasını aşağı doğru uzatalım ve \( E \) noktasından bu doğru parçasına bir dikme çizelim.
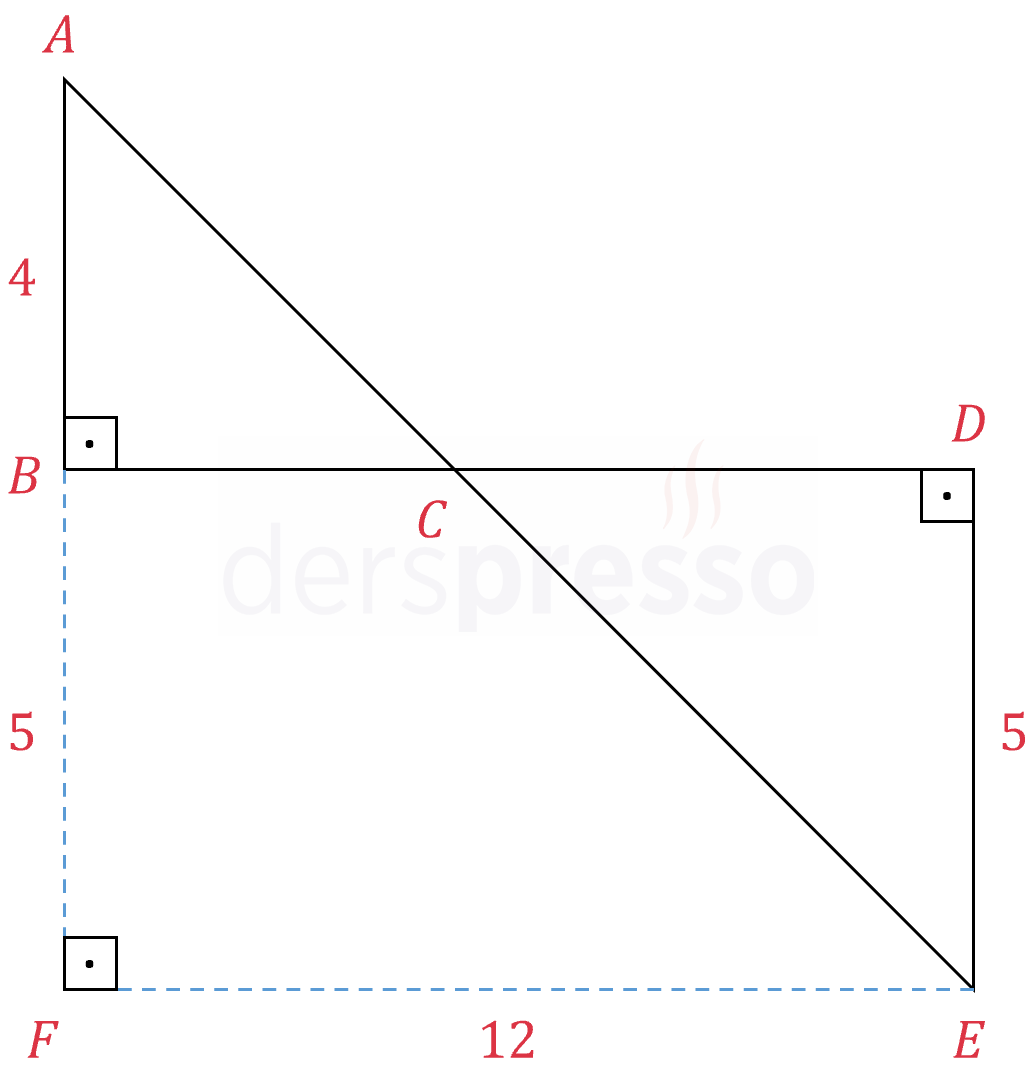
İki doğru parçasının kesiştiği noktaya \( F \) diyelim.
\( [AF] \perp [FE] \)
Oluşan \( BDEF \) dörtgeni bir dikdörtgendir.
Dikdörtgende karşılıklı kenar uzunlukları eşittir.
\( \abs{BF} = \abs{DE} = 5 \)
\( \abs{FE} = \abs{BD} = 12 \)
\( \abs{AF} = 4 + 5 = 9 \)
Bu uzunlukları kullanarak \( \abs{AE} \) uzunluğunu bulalım.
\( AFE \) üçgeni 3-4-5 özel üçgeni ile \( k = 3 \) benzerlik oranına sahip 9-12-15 üçgenidir.
Bu durumda hipetenüs uzunluğu \( \abs{AE} = 15 \) olarak bulunur.

Şekilde \( ABC \) üçgeni verilmiştir.
\( \abs{AC} = 6\sqrt{2} \)
\( m(\widehat{ABC}) = 30°, \quad m(\widehat{BAC}) = 15° \)
olduğuna göre, \( \abs{AB} = x \) kaçtır?
Çözümü Göster\( [BC] \) doğru parçasını sağa doğru uzatalım ve \( A \) noktasından bu doğru parçasına bir dikme indirelim.
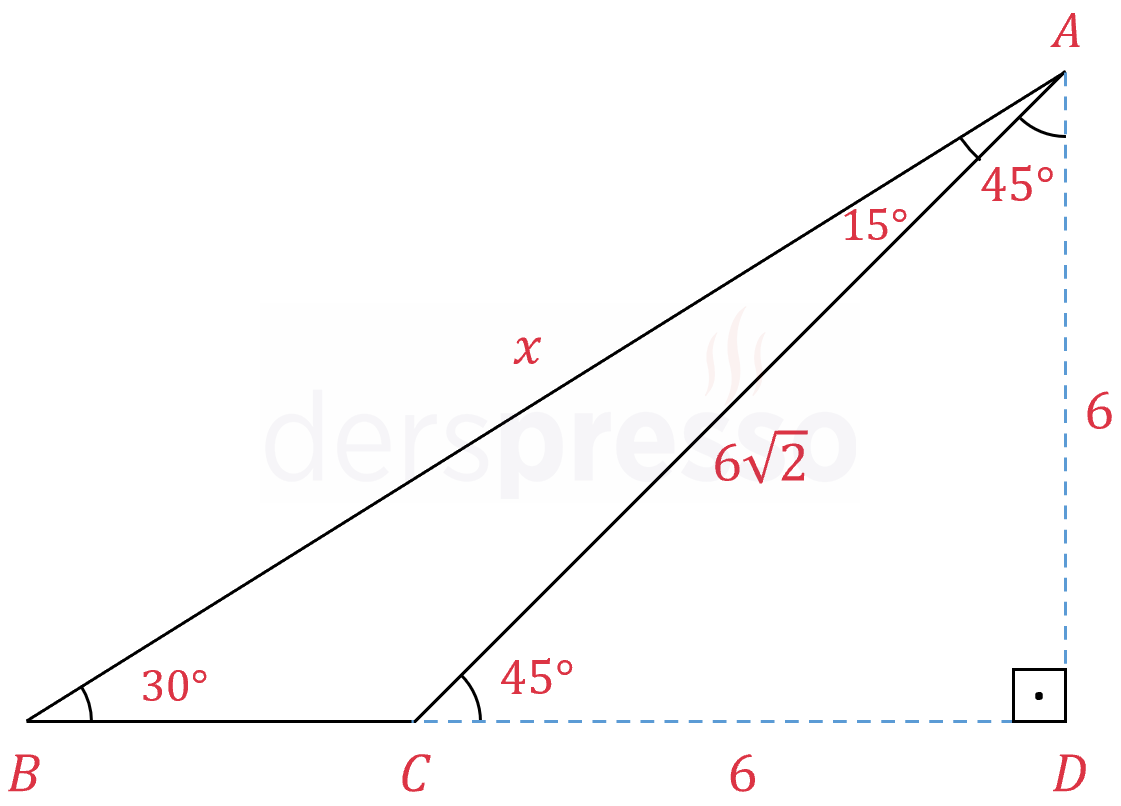
\( [AD] \perp [BD] \)
Oluşan üçgenlerden \( ACD \) üçgeni de 45-45-90° özel üçgeni olur. 45-45-90° üçgeninde kenar uzunlukları arasındaki orantı sırasıyla \( 1:1:\sqrt{2} \) şeklinde olur.
\( \abs{AD} = \abs{CD} = 6 \)
Oluşan üçgenlerden \( ABD \) üçgeni 30-60-90° özel üçgeni olur. 30-60-90° üçgeninde kenar uzunlukları arasındaki orantı sırasıyla \( 1:\sqrt{3}:2 \) şeklinde olur.
\( \abs{AB} = 2 \cdot \abs{AD} = 12 \) bulunur.

Şekilde \( ABD \) üçgeni verilmiştir.
\( \abs{AC} = \abs{AD} = 13 \)
\( \abs{BC} = 7, \quad \abs{CD} = 10 \)
olduğuna göre, \( \abs{AB} = x \) kaçtır?
Çözümü Göster\( \abs{AC} = \abs{AD} \) olduğuna göre \( ACD \) ikizkenar üçgendir.
\( ACD \) üçgeninde \( [CD] \) kenarına ait yüksekliği çizelim.
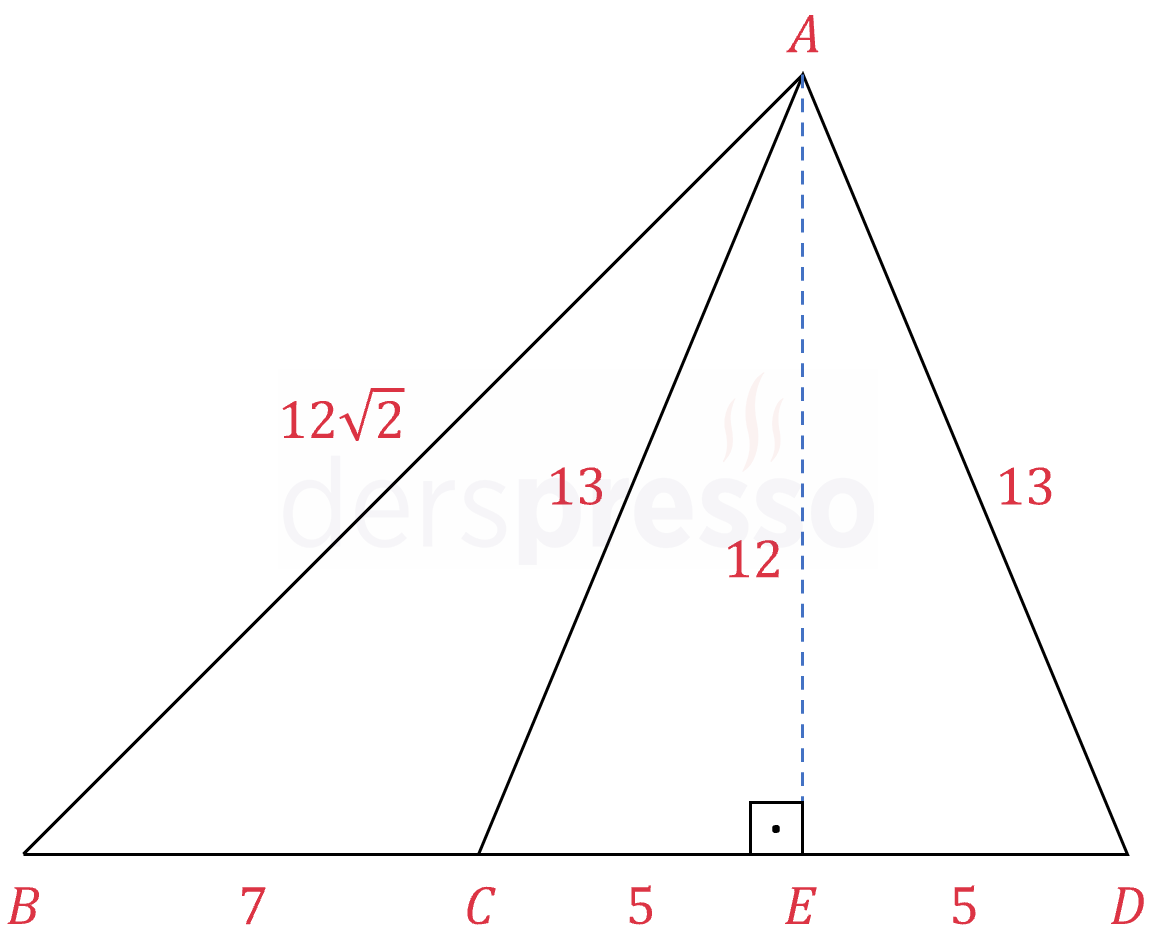
İkizkenar üçgende tabana ait yükseklik aynı zamanda kenarortaydır.
\( \abs{CE} = \abs{ED} = 5 \)
\( ACE \) dik üçgeni 5-12-13 özel üçgeni olur.
\( \abs{AE} = 12 \)
\( \abs{AB} \) uzunluğunu bulmak için \( ABE \) dik üçgenini kullanalım.
\( \abs{BE} = 7 + 5 = 12 \)
\( \abs{BE} = \abs{AE} = 12 \) olduğu için \( ABE \) üçgeni bir 45-45-90° özel üçgenidir. 45-45-90° üçgeninde kenar uzunlukları arasındaki orantı sırasıyla \( 1:1:\sqrt{2} \) şeklinde olur.
\( x = \abs{AB} = 12\sqrt{2} \) olarak bulunur.

Şekilde \( BCD \) ve \( BAD \) dik üçgenleri verilmiştir.
\( \abs{CD} = 6, \quad \abs{AD} = 4 \)
\( \abs{AB} + \abs{BC} = 10 \)
olduğuna göre, \( \abs{BD} \) kaçtır?
Çözümü Göster\( \abs{AB} = a \) ve \( \abs{BC} = b \) diyelim.
\( BAD \) üçgeninde Pisagor teoremini kullanalım.
\( \abs{AB}^2 + \abs{AD}^2 = \abs{BD}^2 \)
\( a^2 + 4^2 = \abs{BD}^2 \)
\( BCD \) üçgeninde Pisagor teoremini kullanalım.
\( \abs{BC}^2 + \abs{CD}^2 = \abs{BD}^2 \)
\( b^2 + 6^2 = \abs{BD}^2 \)
İki denklem \( \abs{BD}^2 \) değerine eşit olduğu için birbirine eşitleyebiliriz.
\( a^2 + 4^2 = b^2 + 6^2 = \abs{BD}^2 \)
Denklemi düzenleyelim.
\( a^2 - b^2 = 6^2 - 4^2 \)
\( (a - b)(a + b) = 20 \)
\( \abs{AB} + \abs{BC} = a + b = 10 \) olarak veriliyor.
\( 20 = (a - b)(10) \)
\( a - b = 2 \)
Bu denklemi \( a + b = 10 \) denklemi ile taraf tarafa toplayalım.
\( a = 6, \quad b = 4 \)
İki üçgenden birinde Pisagor teoremi ile hipotenüs uzunluğunu bulalım.
\( \abs{BD}^2 = \abs{AB}^2 + \abs{AD}^2 \)
\( = 6^2 + 4^2 \)
\( \abs{BD} = 2\sqrt{13} \) bulunur.

Şekilde \( ABC \) ve \( EDG \) dik üçgenleri verilmiştir.
\( \abs{FG} = 2, \quad \abs{GC} = 1 \)
\( \abs{AF} = \sqrt{30}, \quad \abs{DG} = 2\sqrt{5} \)
olduğuna göre, \( \abs{BE} = x \) kaçtır?
Çözümü Göster\( EDG \) dik üçgeninde Öklid bağıntısını kullanalım.
\( \abs{DG}^2 = \abs{GF} \cdot \abs{GE} \)
\( (2\sqrt{5})^2 = 2 \cdot (2 + \abs{EF}) \)
\( \abs{EF} = 8 \)
Şimdi \( ABC \) üçgeninde Öklid bağıntısını kullanalım.
\( \abs{AF}^2 = \abs{BF} \cdot \abs{FC} \)
\( \sqrt{30}^2 = (x + 8) \cdot (2 + 1) \)
\( x = 2 \) bulunur.

\( [BA] \perp [AC], [ED] \perp [BC] \)
\( \abs{BE} = 6, \quad \abs{EA} = 2 \)
\( \abs{BD} = \abs{DC} \)
olduğuna göre, \( \abs{AC} = x \) kaçtır?
Çözümü Göster\( C \) köşesinden \( E \) noktasına bir doğru parçası çizelim.
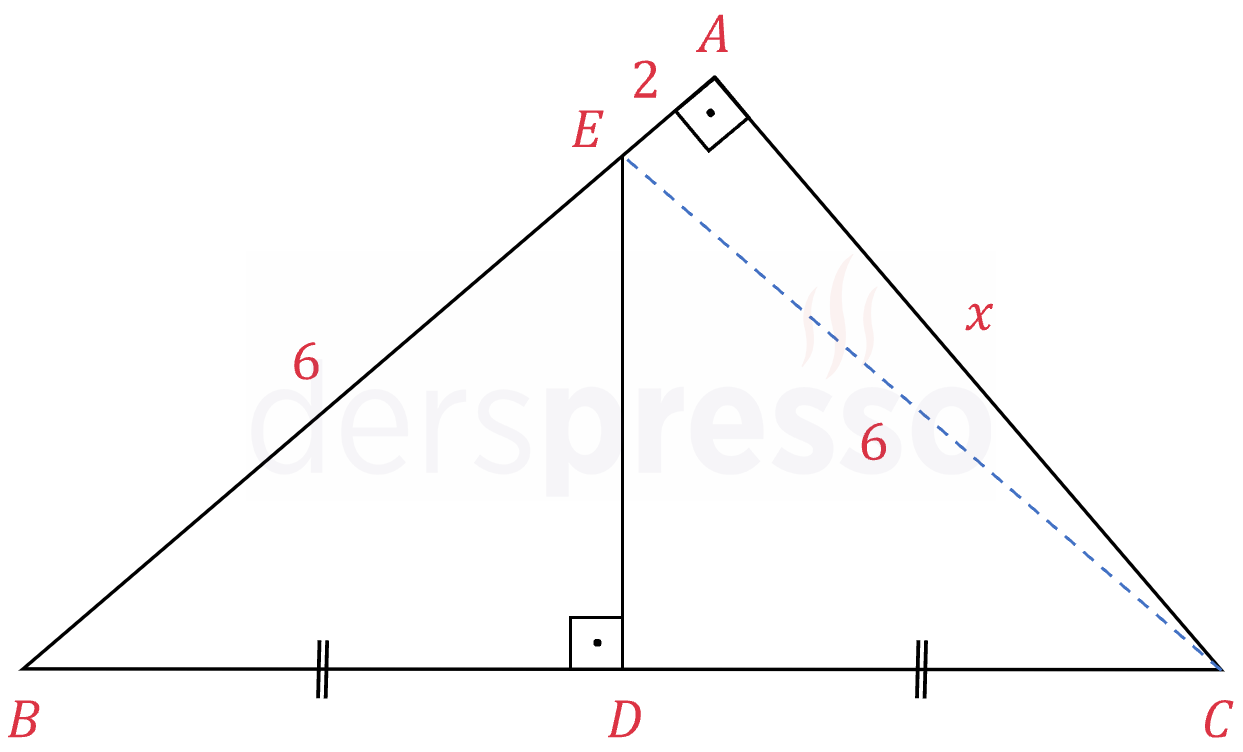
\( EBC \) üçgeninde \( [BC] \) kenarına ait yükseklik \( [BC] \) kenarını ortaladığı için \( EBC \) üçgeni ikizkenardır.
\( \abs{EB} = \abs{EC} = 6 \)
\( AEC \) üçgeninde Pisagor teoremini kullanarak \( x \) uzunluğunu bulalım.
\( \abs{AE}^2 + \abs{AC}^2 = \abs{EC}^2 \)
\( 2^2 + x^2 = 6^2 \)
\( 4 + x^2 = 36 \)
\( x = 4\sqrt{2} \) bulunur.

Şekilde \( ABC \) üçgeni verilmiştir.
\( [DE] \perp [BC] \)
\( \abs{AD} = \abs{DC} \)
\( \abs{BE} = 8, \quad \abs{EC} = 2 \)
olduğuna göre, \( \abs{DE} = x \) kaçtır?
Çözümü Göster\( A \) köşesinden \( [BC] \) kenarına bir dikme indirelim.
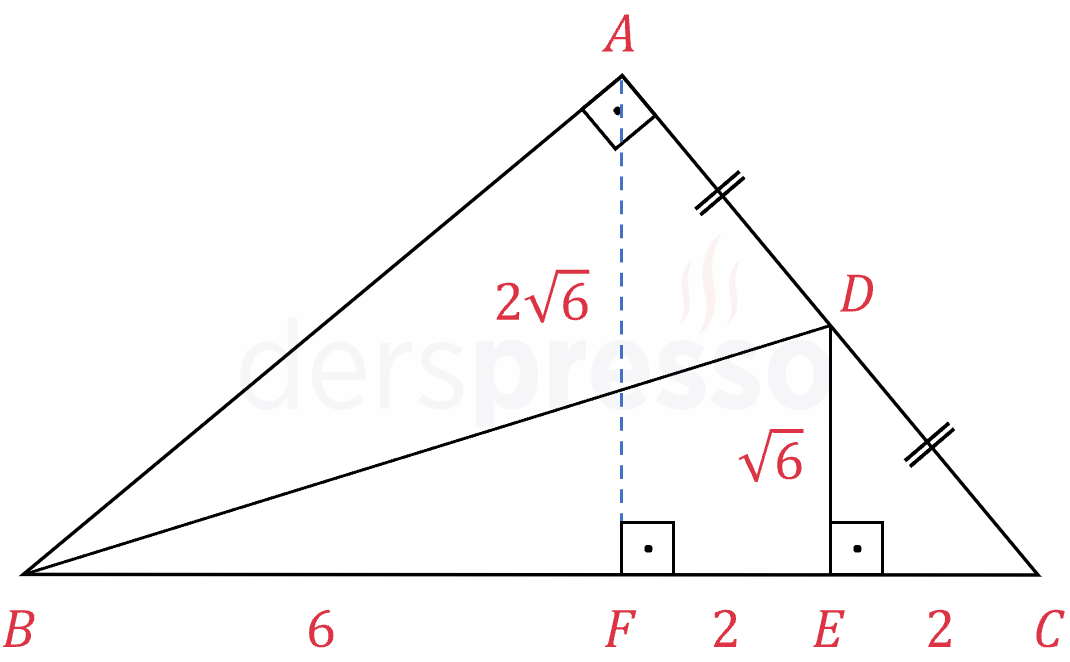
\( [DE] \parallel [AF] \) ve \( \abs{AD} = \abs{DC} \) olduğu için \( [DE] \) doğru parçası \( AFC \) üçgeninin orta tabanı olur.
\( \abs{FE} = \abs{EC} = 2 \)
\( ABC \) üçgeninde Öklid bağıntısını kullanalım.
\( \abs{AF}^2 = \abs{BF} \cdot \abs{FC} \)
\( = 6 \cdot 4 \)
\( \abs{AF} = 2\sqrt{6} \)
Bir üçgende orta taban uzunluğu taban uzunluğunun yarısıdır.
\( 2\abs{DE} = \abs{AF} \)
\( \abs{DE} = x = \sqrt{6} \) bulunur.
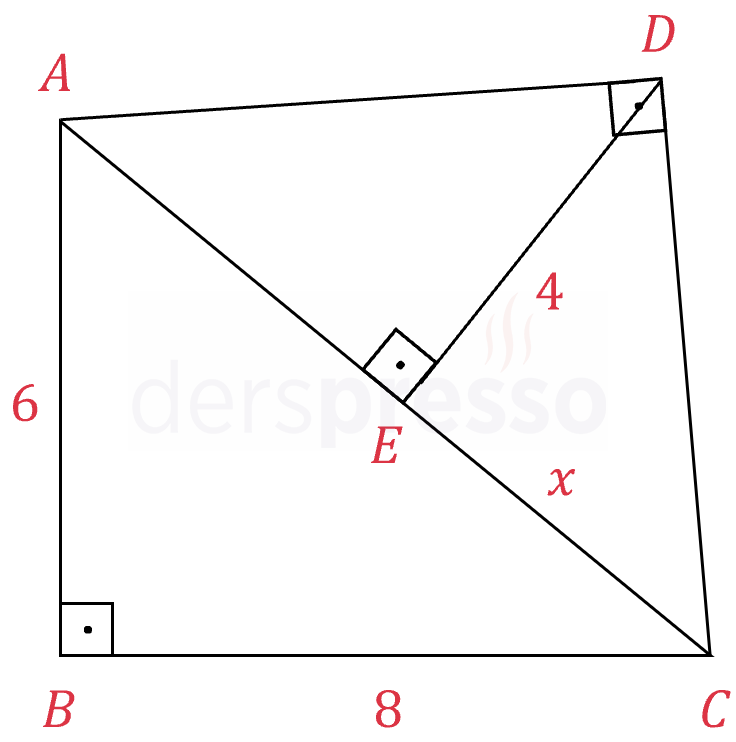
Şekilde \( ABC \) ve \( ADC \) dik üçgenleri verilmiştir.
\( \abs{AB} = 6, \quad \abs{BC} = 8 \)
\( \abs{DE} = 4, \quad \abs{AE} \gt \abs{EC} \)
olduğuna göre, \( \abs{EC} = x \) kaçtır?
Çözümü Göster\( ABC \) üçgeni 3-4-5 özel üçgeni ile \( k = 2 \) benzerlik oranına sahip 6-8-10 üçgenidir.
\( \abs{AC} = 10 \)
\( \abs{EC} = x \) ise \( \abs{AE} = 10 - x \) olur.
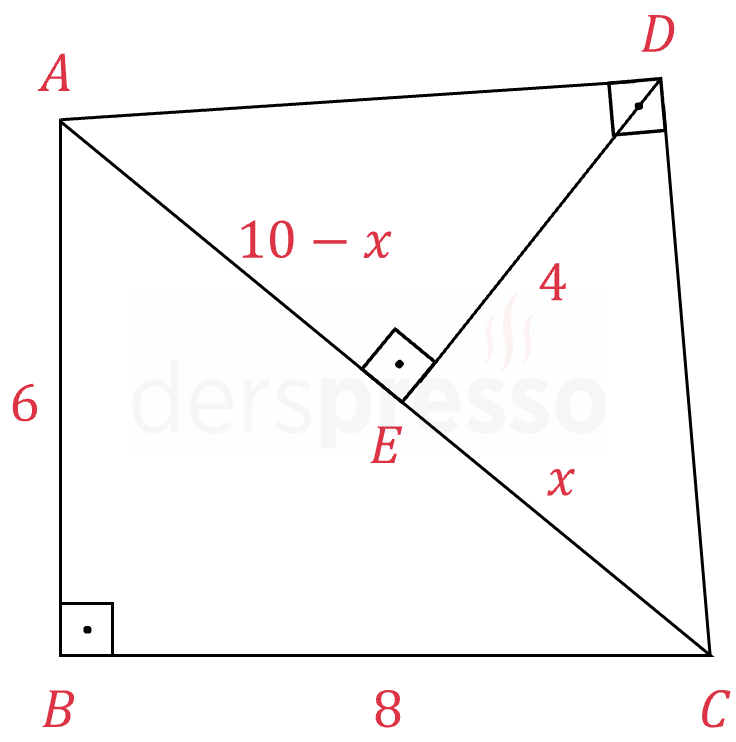
\( ADC \) üçgeninde Öklid bağıntısını kullanalım.
\( \abs{DE}^2 = \abs{AE} \cdot \abs{EC} \)
\( 4^2 = (10 - x) \cdot x \)
\( x^2 - 10x + 16 = 0 \)
\( (x - 2)(x - 8) = 0 \)
\( x = 2 \) ya da \( x = 8 \)
\( \abs{AE} \gt \abs{EC} \) olduğu için \( x = 2 \) olur.

\( [AB] \perp [BC] \)
\( m(\widehat{BAD}) = 45°, \quad m(\widehat{BCD}) = 60° \)
\( \abs{AD} = 5\sqrt{2}, \quad \abs{DC} = 6\sqrt{3} \)
olduğuna göre, \( \abs{AB} = x \) kaçtır?
Çözümü Göster\( D \) noktasından \( [AB] \) ve \( [BC] \) kenarlarına birer dikme çizelim.
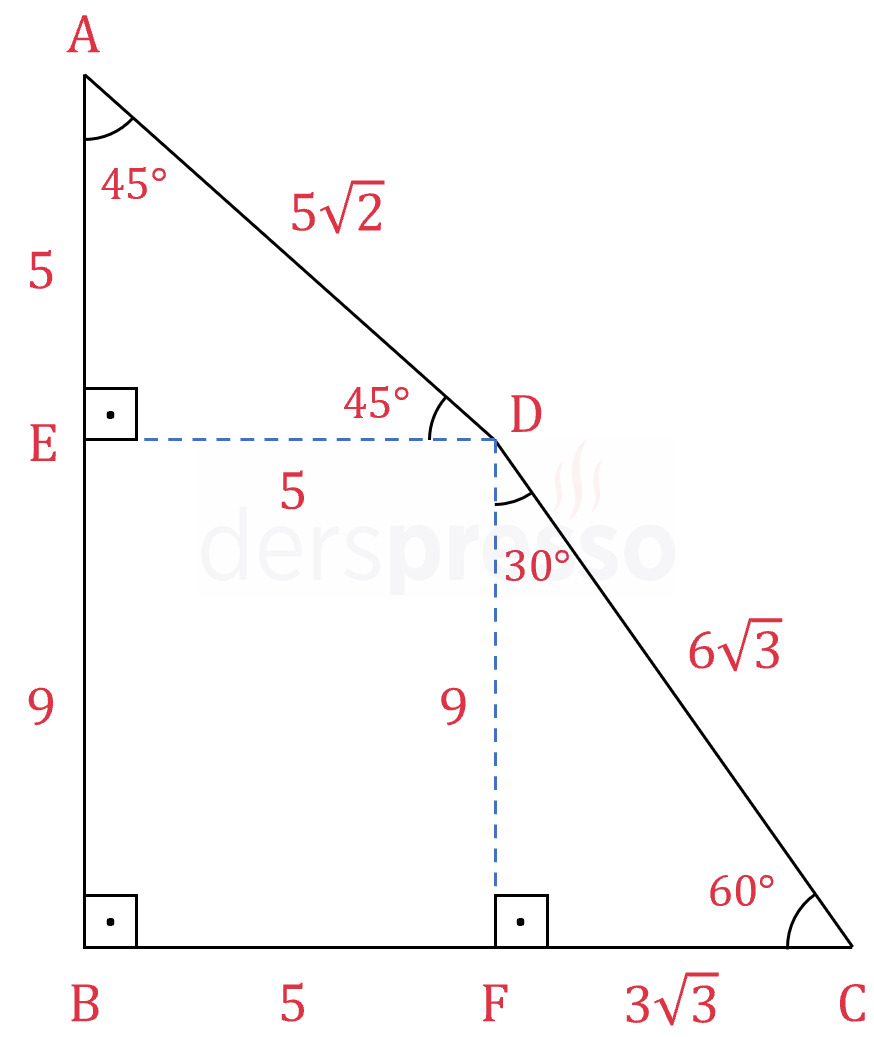
\( [DF] \perp [BC] \)
\( m(\widehat{FDC}) = 30° \)
\( DFC \) üçgeni 30-60-90° üçgeni olur. 30-60-90° üçgeninde kenar uzunlukları arasındaki orantı sırasıyla \( 1:\sqrt{3}:2 \) şeklinde olur.
\( \abs{FC} = 3\sqrt{3}, \abs{DF} = 9 \)
\( [DE] \perp [AB] \)
\( m(\widehat{ADE}) = 45° \)
\( AED \) üçgeni 45-45-90° üçgeni olur. 45-45-90° üçgeninde kenar uzunlukları arasındaki orantı sırasıyla \( 1:1:\sqrt{2} \) şeklinde olur.
\( \abs{ED} = \abs{AE} = 5 \)
\( EBFD \) bir dikdörtgendir.
Dikdörtgende karşılıklı kenar uzunlukları eşittir.
\( \abs{EB} = \abs{DF} = 9 \)
\( \abs{AB} = x = 9 + 5 = 14 \) bulunur.

Şekilde \( ABC \) üçgeni verilmiştir.
\( \abs{AB} = 4\sqrt{2}, \quad \abs{DC} = 4 \)
\( \abs{BD} = a, \quad \abs{AD} = b \)
olduğuna göre, \( \dfrac{a}{b} \) kaçtır?
Çözümü GösterÖnce \( ABD \) üçgeninde Pisagor teoremini kullanalım.
\( \abs{BD}^2 + \abs{AD}^2 = \abs{AB}^2 \)
\( a^2 + b^2 = (4\sqrt{2})^2 = 32 \)
Şimdi \( ABC \) üçgeninde Öklid bağıntısını kullanalım.
\( \abs{AD}^2 = \abs{BD} \cdot \abs{DC} \)
\( b^2 = a \cdot 4 = 4a \)
İkinci denklemdeki \( b^2 \) değerini ilk denklemde yerine koyalım.
\( a^2 + 4a = 32 \)
\( (a + 8)(a - 4) = 0 \)
Uzunluk değeri negatif olamayacağı için \( a = 4 \) olur.
Bulduğumuz değeri ikinci denklemde yerine koyarak \( b \) değerini bulalım
\( b^2 = 4 \cdot 4 \)
\( b = \pm 4 \)
Uzunluk değeri negatif olamayacağı için \( b = 4 \) olur.
\( \dfrac{a}{b} = \dfrac{4}{4} = 1 \) bulunur.
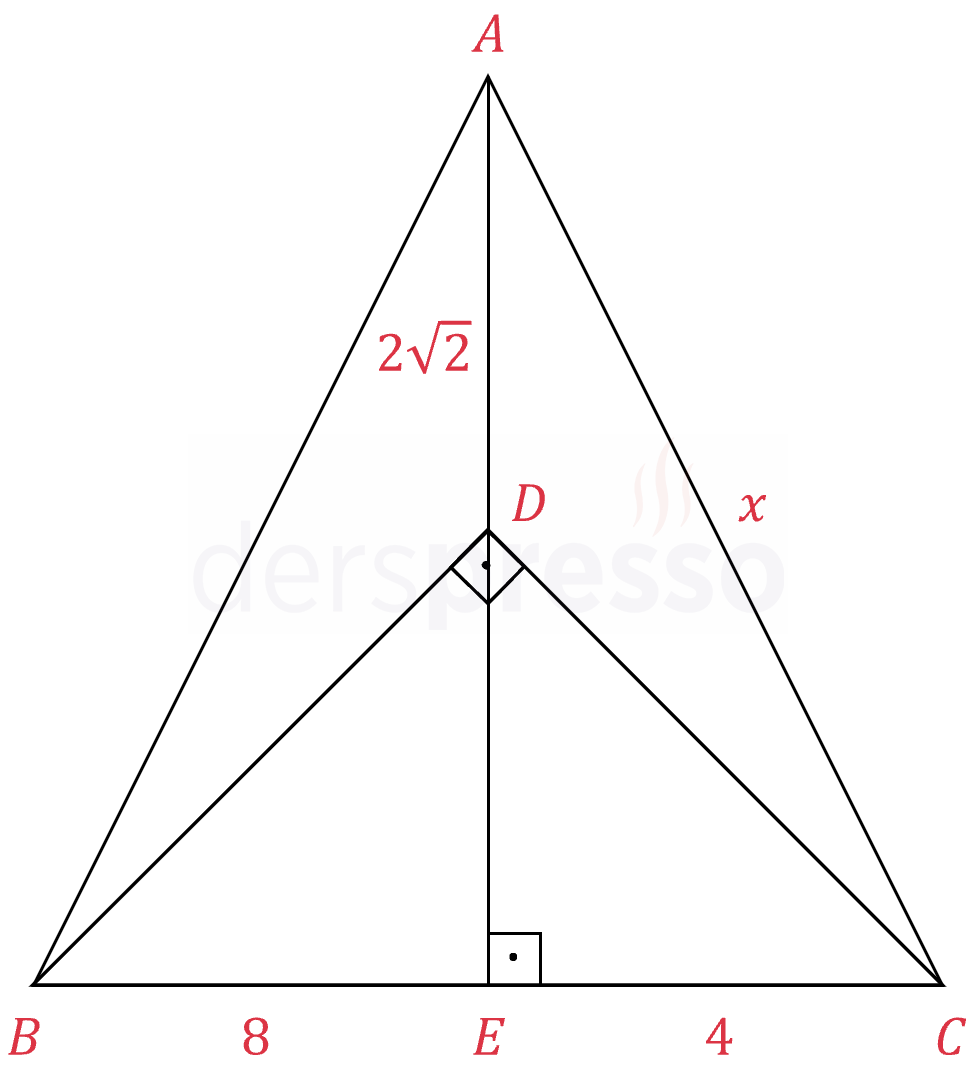
\( [AE] \perp [BC], [BD] \perp [DC] \)
\( \abs{BE} = 8, \quad \abs{EC} = 4 \)
\( \abs{AD} = 2\sqrt{2} \)
olduğuna göre, \( \abs{AC} = x \) kaçtır?
Çözümü Göster\( BDC \) üçgeninde Öklid bağıntısını kullanalım.
\( \abs{DE}^2 = \abs{BE} \cdot \abs{EC} \)
\( = 8 \cdot 4 = 32 \)
\( \abs{DE} = 4\sqrt{2} \)
\( AEC \) üçgeninde Pisagor teoremini kullanarak \( \abs{AC} = x \) değerini bulalım.
\( \abs{AE}^2 + \abs{EC}^2 = \abs{AC}^2 \)
\( (4\sqrt{2} + 2\sqrt{2})^2 + 4^2 = \abs{AC}^2 \)
\( 72 + 16 = \abs{AC}^2 \)
\( \abs{AC} = x = 2\sqrt{22} \) bulunur.