Kenarortay
Üçgenin bir köşesini karşısındaki kenarın orta noktası ile birleştiren doğru parçasına o kenara ait kenarortay denir. \( A \), \( B \) ve \( C \) köşelerine ait kenarortaylar sırasıyla \( V_a \), \( V_b \) ve \( V_c \) ile gösterilir.
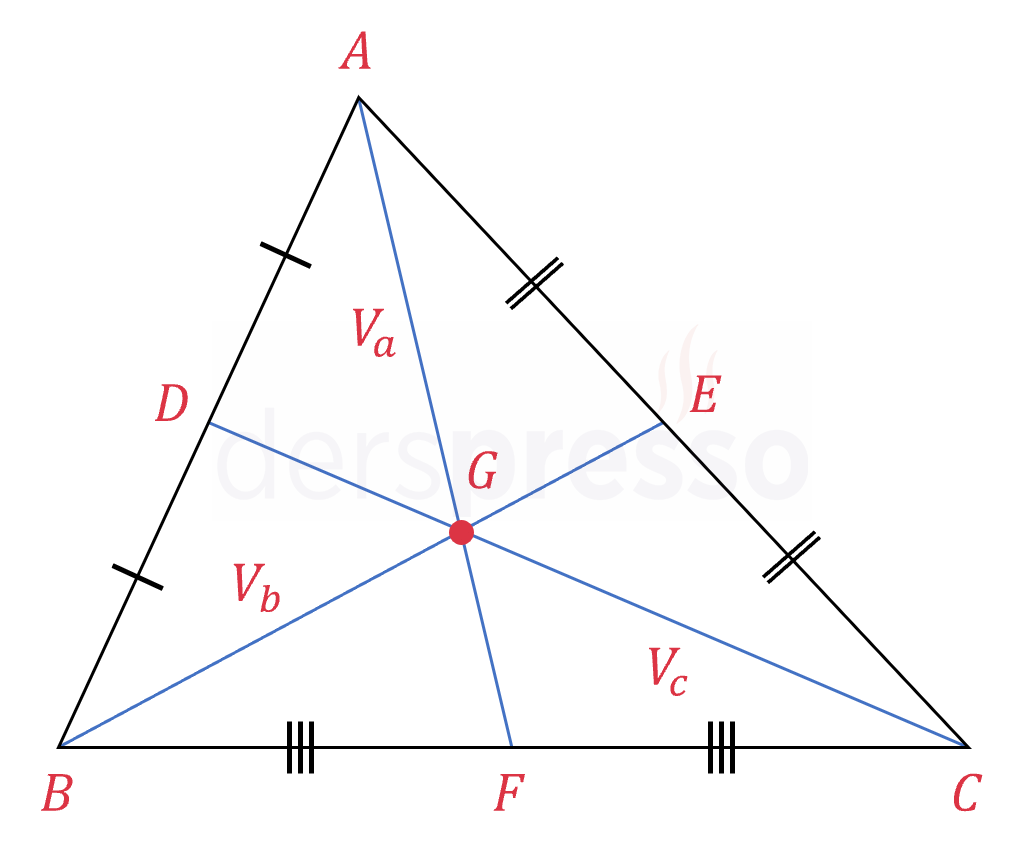
Bir üçgenin kenarortayları her zaman tek bir noktada ve üçgenin içinde kesişir. Bu nokta üçgenin ağırlık merkezidir ve \( G \) ile gösterilir.
Üçgenin ağırlık merkezi kenarortayları 2'ye 1 oranında böler.
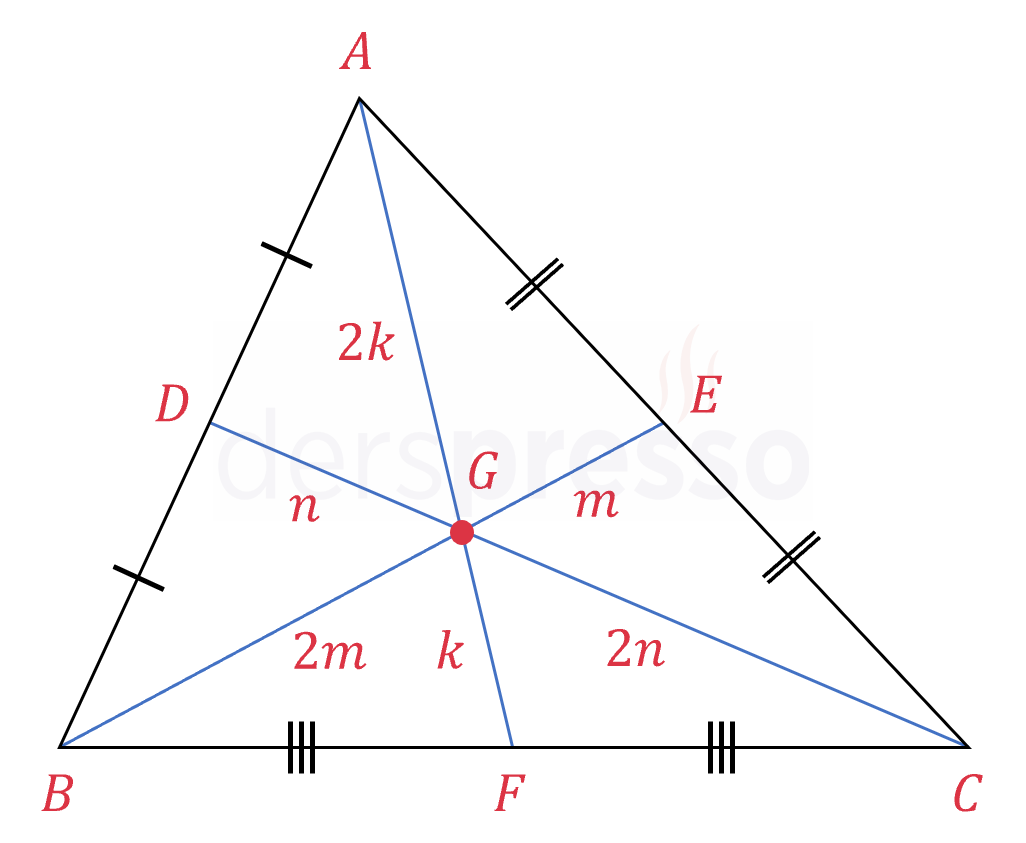
\( \abs{AG} = 2\abs{GF} \)
\( \abs{BG} = 2\abs{GE} \)
\( \abs{CG} = 2\abs{GD} \)
İSPATI GÖSTER
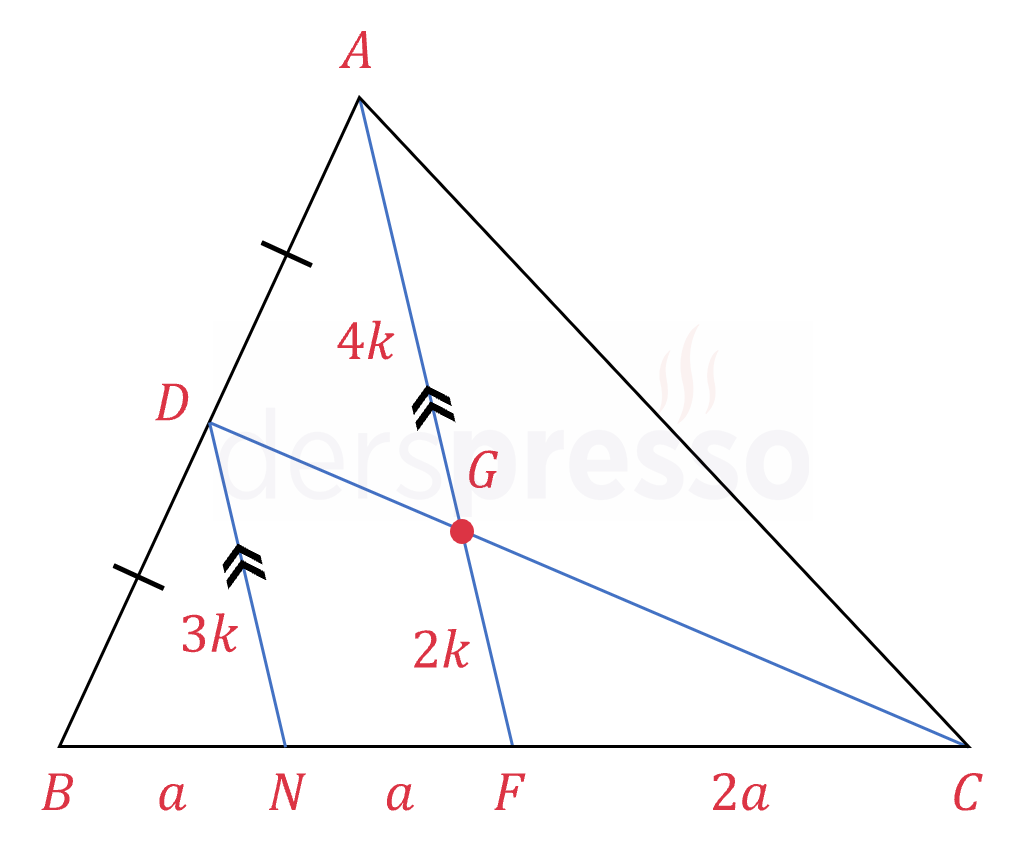
\( G \) üçgenin ağırlık merkezi olmak üzere, kenar uzunluklarına aşağıdaki değerleri verelim.
\( \abs{AF} = 6k \)
\( \abs{BC} = 4a \)
\( [AF] \) kenarortay olduğu için, karşı kenarı ikiye böler.
\( \abs{BF} = \abs{FC} = 2a \)
\( D \) noktasından geçen ve \( [AF] \) kenarortayına paralel \( [DN] \) doğru parçasını çizelim. \( [CD] \) de kenarortay olduğu için, \( D \) noktası \( [AB] \) kenarının orta noktasıdır.
\( \abs{BD} = \abs{DA} \)
\( [DN] \) \( [AF] \)'ye paralel ve \( \abs{BD} = \abs{DA} \) olduğu için, \( [DN] \) \( \overset{\triangle}{BAF} \) üçgeninin orta tabanıdır ve uzunluğu \( [AF] \)'nin yarısına eşittir.
\( \abs{DN} = \dfrac{\abs{AF}}{2} = 3k \)
\( [DN] \) \( \overset{\triangle}{BAF} \) üçgeninin orta tabanı olduğu için \( [BF] \) kenarını da ikiye böler.
\( \abs{BN} = \abs{NF} = a \)
\( \overset{\triangle}{DNC} \) üçgenine temel orantı teoremini uygulayalım.
\( \dfrac{\abs{CF}}{\abs{CN}} = \dfrac{\abs{FG}}{\abs{ND}} \)
\( \dfrac{2a}{3a} = \dfrac{\abs{FG}}{3k} \)
\( \abs{FG} = 2k \)
Buna göre, \( \abs{AF} = 6k \) dediğimiz için, \( \abs{AG} = 4k \) olarak bulmuş ve üçgenin ağırlık merkezinin kenarortayı \( 4k:2k = 2:1 \) oranında böldüğünü göstermiş olduk.
Bir üçgende aşağıdakilerden biri verildiyse oluşan nokta üçgenin ağırlık merkezidir ve tüm kenarortaylar bu noktadan geçer.
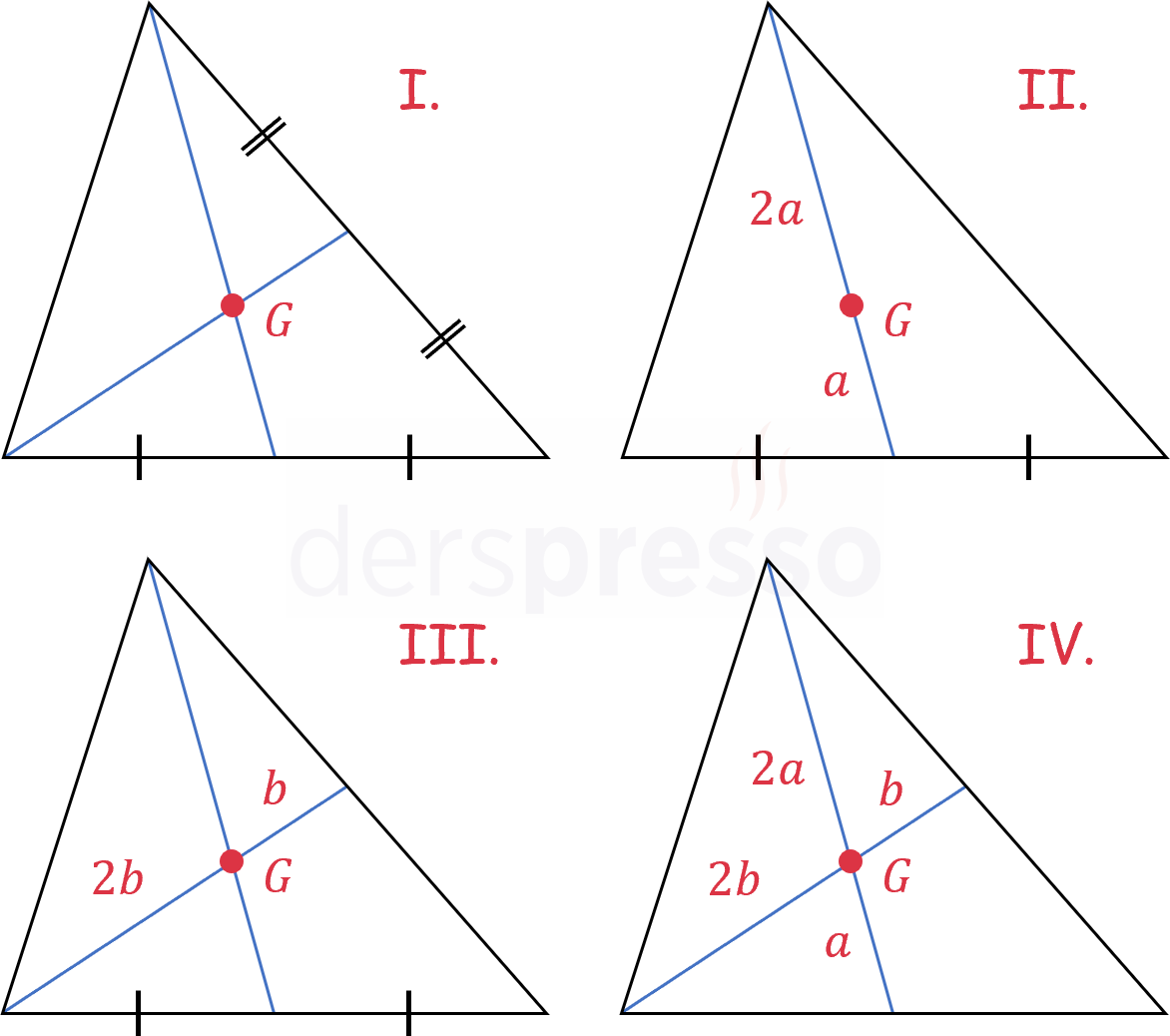
- İki kenarortay
- Bir kenarortay ve bu kenarortayı 2:1 oranında bölen nokta
- Bir kenarortay ve bu kenarortayın 2:1 oranında böldüğü ikinci bir doğru parçası
- Birbirini 2:1 oranında bölen iki doğru parçası
Kenarortaylar üçgenin alanını 6 eşit parçaya böler.
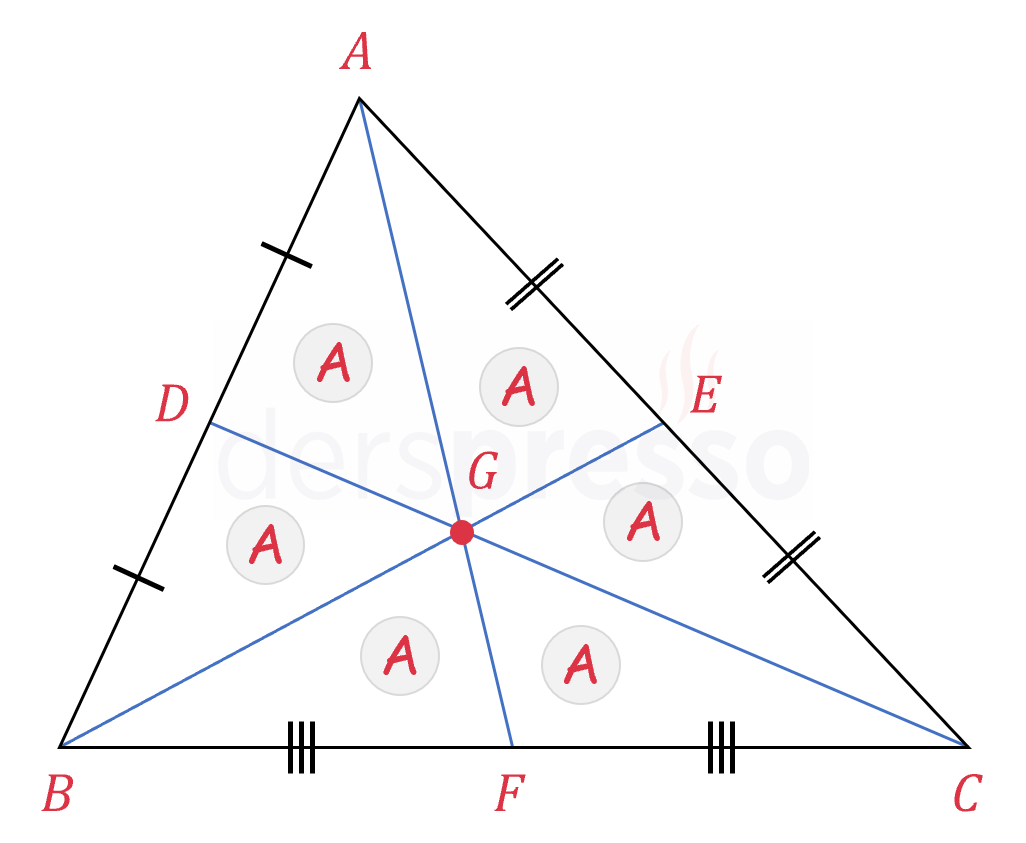
\( A(\overset{\triangle}{ABC}) = 6A \) diyelim.
\( [AF] \) kenarortayı tabanı iki eşit parçaya böldüğü için, alanı da iki eşit parçaya böler:
\( A(\overset{\triangle}{ABF}) = 3A \)
\( A(\overset{\triangle}{AFC}) = 3A \)
\( G \) ağırlık merkezi \( [AF] \) kenarortayını 2:1 oranında böler. Bu kenarortayı \( ABF \) üçgeninin tabanı olarak düşünürsek, bu üçgenin alanı da 2:1 oranında bölünür:
\( A(\overset{\triangle}{ABG}) = 2A \)
\( A(\overset{\triangle}{GBF}) = A \)
\( [CD] \) kenarortayı \( [AB] \) kenarını iki eşit parçaya böldüğü için, \( ABG \) üçgeninin alanını da iki eşit parçaya böler:
\( A(\overset{\triangle}{GDA}) = A \)
\( A(\overset{\triangle}{GDB}) = A \)
Aşağıdaki şekildeki gibi kenarortayların kenarları kestikleri noktalar birleştirildiğinde elde edilen üçgenle ilgili şunlar söylenebilir.
- \( DEF \) üçgeninin her bir kenarı \( ABC \) üçgeninin iki kenarını ortaladığı için aynı zamanda \( ABC \) üçgeninin birer orta tabanıdır.
- Her bir orta taban \( ABC \) üçgeninin kenarlarını olduğu gibi kenarortayı da eşit iki parçaya böldüğü için, oluşan şekilde kenarortayın parçalarının uzunluklarının oranı 3:1:2 olur (buna 3-1-2 kuralı da denir).
- \( ABC \) üçgeninin ağırlık merkezi olan \( G \) noktası \( DEF \) üçgeninin de kenarortaylarını 2:1 oranında böldüğü için, \( DEF \) üçgeninin de ağırlık merkezidir.
- \( DEF \) üçgeni \( ABC \) üçgeninin alanını 4 eşit parçaya böler.
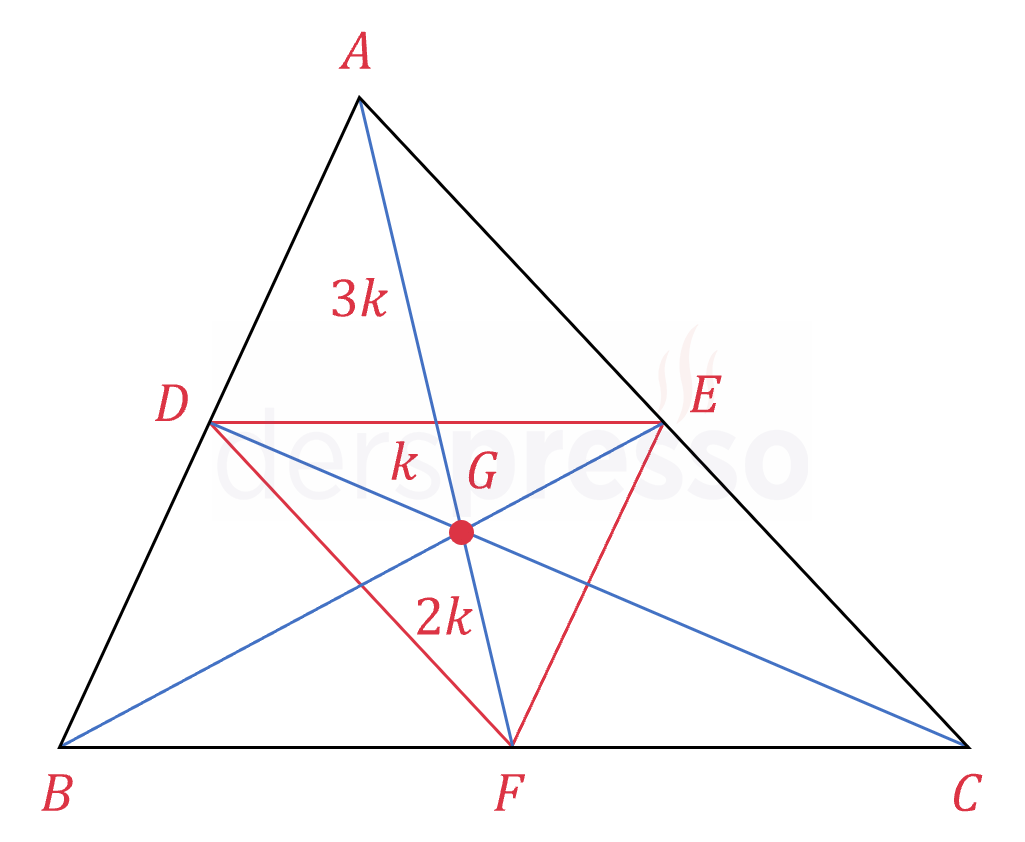
\( A(ADE) = A(BDF) = A(FEC) = A(DEF) \)
İSPATI GÖSTER
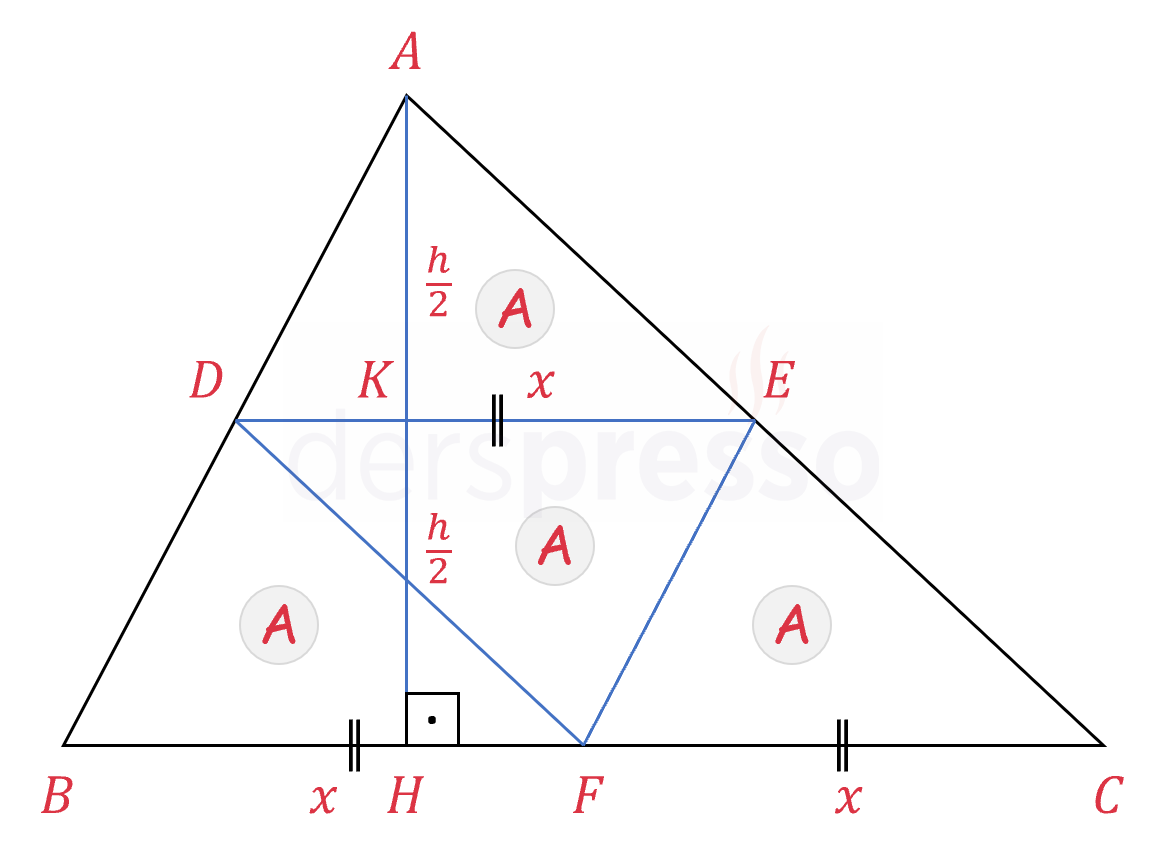
\( [EF] \) doğru parçası \( ABC \) üçgeninin orta tabanı ise \( [BC] \) kenarını ortalar.
\( \abs{BF} = \abs{FC} = x \)
\( [DE] \) doğru parçası \( ABC \) üçgeninin orta tabanı ise uzunluğu \( [BC] \) kenarının yarısına eşittir.
\( \abs{DE} = \abs{BF} = \abs{FC} = x \)
Yukarıda ispatını gösterdiğimiz üzere, \( [DE] \) doğru parçası tabana ait yüksekliği ortalar.
\( \abs{AK} = \abs{KH} = \dfrac{h}{2} \)
Buna göre \( ADE \), \( DBF \), \( DEF \) ve \( EFC \) üçgenlerinin tümünün tabanını \( x \) ve yüksekliğini \( \frac{h}{2} \) şeklinde ifade edebiliriz.
\( A = \dfrac{x \cdot \frac{h}{2}}{2} \)
Ağırlık merkezinden geçen ve tabana (ya da herhangi bir kenara) paralel olan doğrunun uzunluğu üçgen benzerliğinden dolayı taban uzunluğunun \( \frac{2}{3} \)'üdür. Kenarortay, tabanı olduğu gibi bu paralel doğruyu da iki eşit parçaya böler. Ayrıca bu paralel doğru üçgenin yan kenarlarını da 2:1 oranında böler.
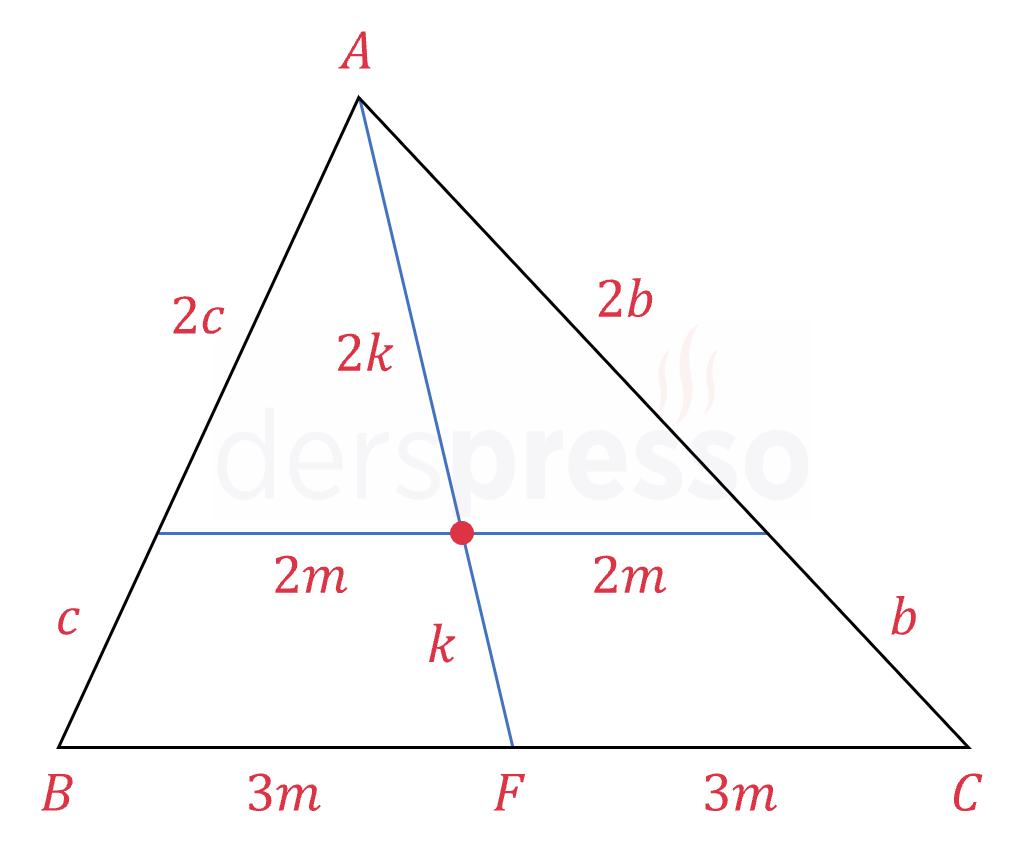
Bir üçgenin en uzun kenarortayı üçgenin en kısa kenarına aittir.
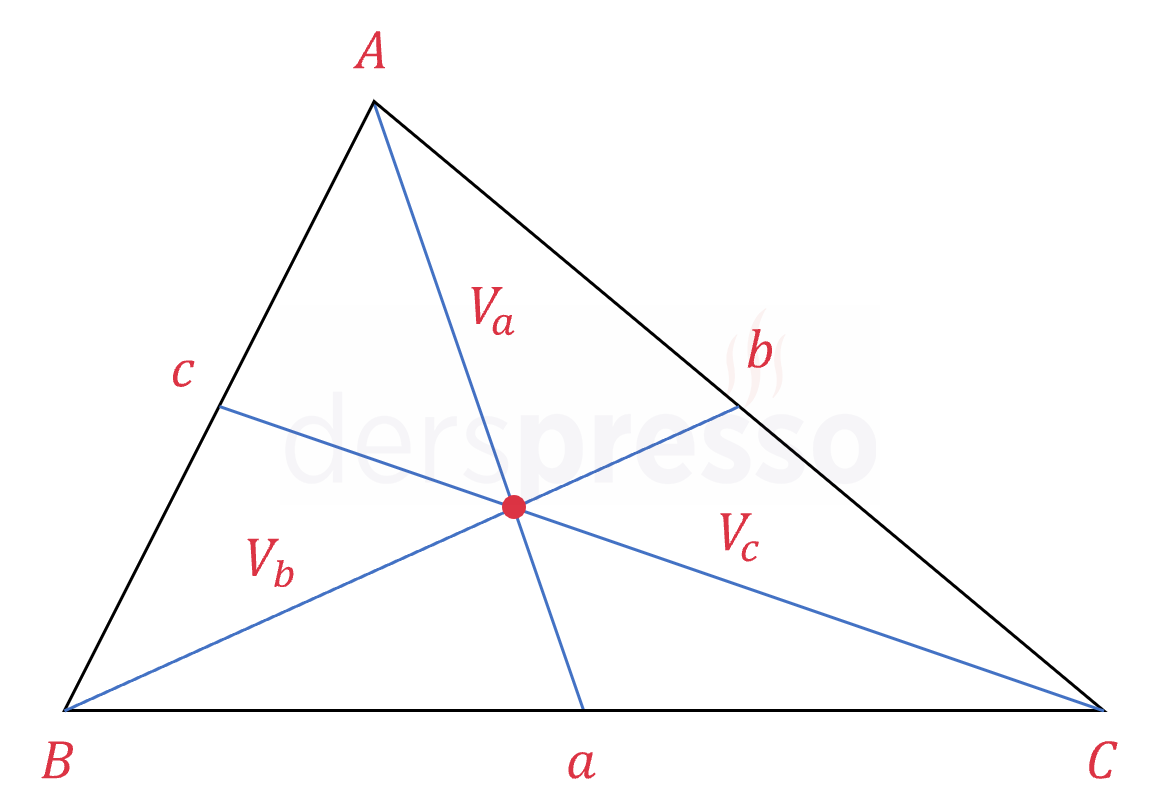
\( a \ge b \ge c \) ise,
\( V_a \le V_b \le V_c \)
Kenarortay Teoremi
Bir üçgende kenarortay uzunluğu üçgenin kenar uzunlukları cinsinden aşağıdaki şekilde ifade edilebilir.

\( 2 V_a^2 = b^2 + c^2 - \dfrac{a^2}{2} \)
İSPATI GÖSTER

Üçgenin kenarortayı \( [AF] \) ve yüksekliği \( [AN] \) olmak üzere,
\( \abs{AF} = V_a \)
\( \abs{AN} = h_a \)
\( \abs{BC} = a \)
\( \abs{BF} = \abs{FC} = \dfrac{a}{2} \)
\( \abs{NF} = x \) diyelim.
\( \abs{BN} = \dfrac{a}{2} - x \)
\( \abs{CN} = \dfrac{a}{2} + x \)
\( \overset{\triangle}{ANB} \) üçgeninde Pisagor teoremini uygulayalım.
\( c^2 = \left( \dfrac{a}{2} - x \right)^2 + {h_a}^2 \)
\( c^2 = \dfrac{a^2}{4} - ax + x^2 + {h_a}^2 \)
\( \overset{\triangle}{ANC} \) üçgeninde Pisagor teoremini uygulayalım.
\( b^2 = \left( \dfrac{a}{2} + x \right)^2 + {h_a}^2 \)
\( b^2 = \dfrac{a^2}{4} + ax + x^2 + {h_a}^2 \)
İki eşitliği taraf tarafa toplayalım.
\( b^2 + c^2 = \dfrac{a^2}{2} + 2x^2 + 2{h_a}^2 \)
Şimdi de \( \overset{\triangle}{ANF} \) üçgeninde Pisagor teoremini uygulayalım.
\( {V_a}^2 = x^2 + {h_a}^2 \)
\( {h_a}^2 = {V_a}^2 - x^2 \)
Yukarıda elde ettiğimiz eşitlikteki \( {h_a}^2 \) yerine bu değeri yazalım.
\( b^2 + c^2 = \dfrac{a^2}{2} + 2x^2 + 2({V_a}^2 - x^2) \)
\( b^2 + c^2 = \dfrac{a^2}{2} + 2{V_a}^2 \)
\( V_a \)'yı yalnız bırakırsak kenarortay teoremi formülünü elde ederiz.
\( 2{V_a}^2 = b^2 + c^2 - \dfrac{a^2}{2} \)
Tüm kenarortaylar için bu eşitlik yazılıp taraf tarafa toplandığında aşağıdaki formül elde edilir.
\( V_a^2 + V_b^2 + V_c^2 = \dfrac{3}{4} \cdot (a^2 + b^2 + c^2) \)
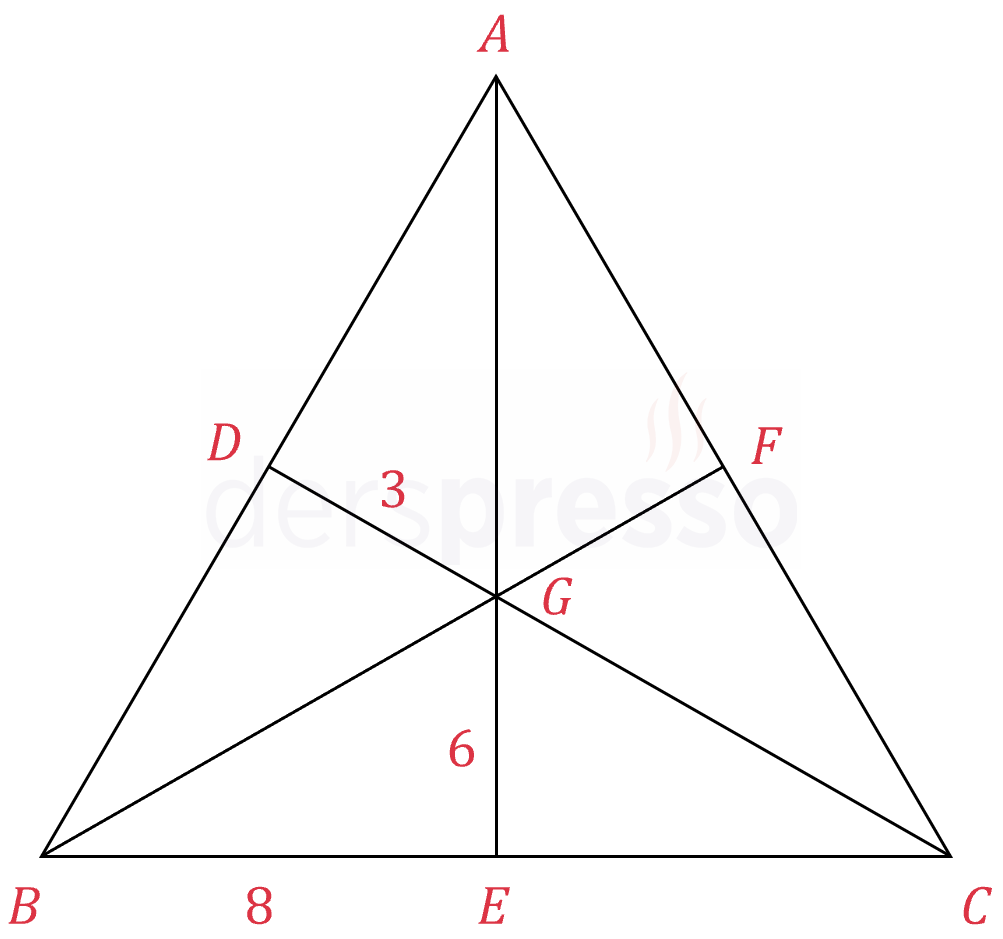
\( G \) noktası \( ABC \) üçgeninin ağırlık merkezidir.
\( \abs{BE} = 8, \abs{GE} = 6, \abs{DG} = 3 \)
olduğuna göre, \( \abs{GC} + \abs{EC} + \abs{AG} \) toplamının sonucu kaçtır?
Çözümü Göster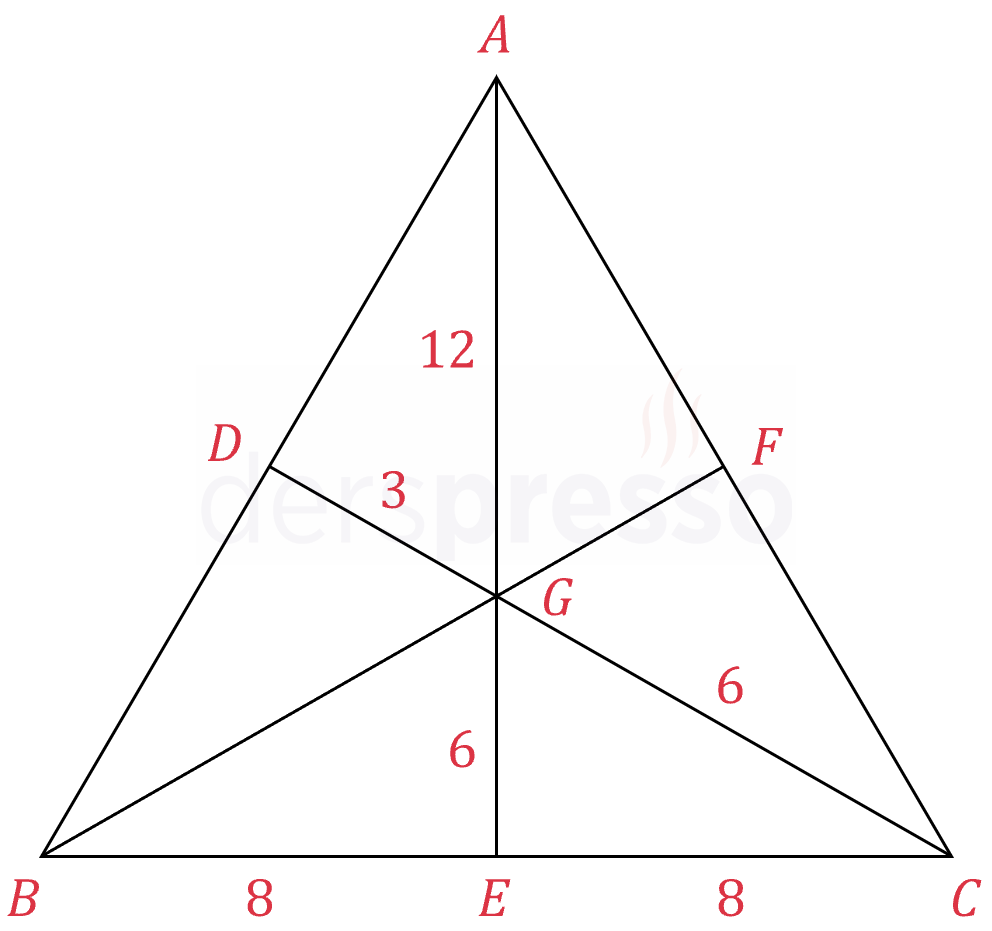
Bir üçgenin köşesinden karşı kenarına çizilen bir doğru üçgenin ağırlık merkezinden geçiyorsa doğru üçgenin bir kenarortayıdır.
Buna göre \( [AE] \), \( [BF] \) ve \( [CD] \) doğru parçaları üçgenin kenarortaylarıdır.
Kenarortaylar kestikleri kenarları iki eş parçaya bölerler.
\( \abs{EC} = \abs{BE} = 8 \)
Bir üçgenin ağırlık merkezi kenarortayları 2:1 oranında böler.
\( 2\abs{DG} = \abs{GC} = 6 \)
\( 2\abs{GE} = \abs{AG} = 12 \)
\( \abs{GC} + \abs{EC} + \abs{AG} = 6 + 8 + 12 = 26 \) olarak bulunur.

\( ABC \) üçgeninin ağırlık merkezi \( G \), \( ADC \) üçgeninin ağırlık merkezi \( G' \) noktasıdır.
\( \abs{GG'} = 8 \) olduğuna göre, \( \abs{BD} \) kaçtır?
Çözümü Göster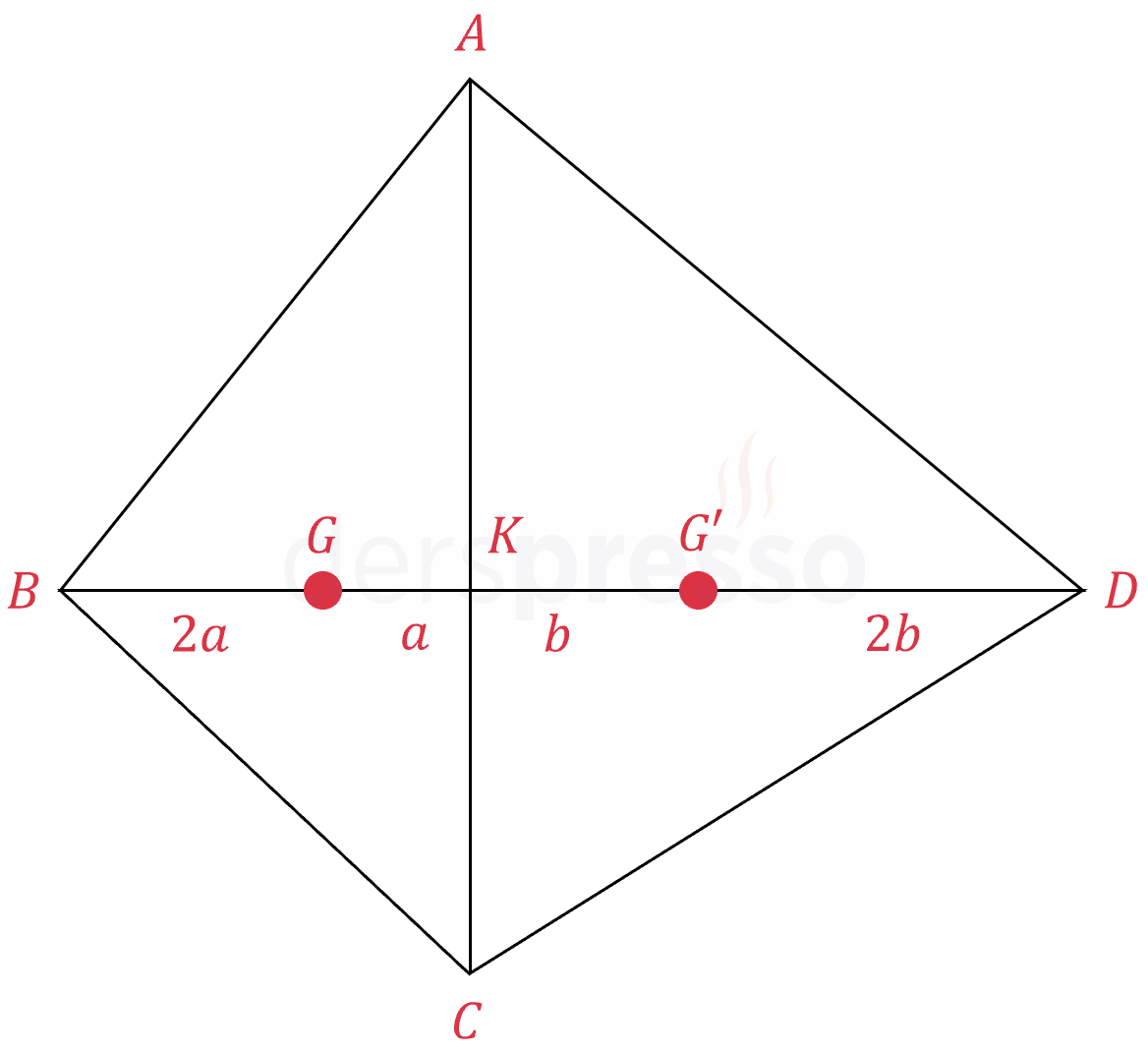
Bir üçgenin ağırlık merkezi kenarortayların kesişim noktasıdır ve kenarortayları 2:1 oranında böler.
\( \abs{GK} = a \Longrightarrow \abs{GB} = 2a \)
\( \abs{G'K} = b \Longrightarrow \abs{G'D} = 2b \)
Soruda istenen \( \abs{BD} = 3a + 3b \) uzunluğudur.
\( \abs{GG'} = a + b = 8 \)
\( \abs{BD} = 3(a + b) = 24 \) olarak bulunur.

\( ABC \) üçgeninin ağırlık merkezi \( G \) noktasıdır.
\( \abs{GE} = \dfrac{25}{2}, \abs{AG} = 48 \)
\( \abs{AB} = \abs{AC} \)
olduğuna göre, \( \abs{BD} = x \) kaçtır?
Çözümü Göster
Bir üçgenin ağırlık merkezi kenarortayların kesişim noktasıdır ve kenarortayları 2:1 oranında böler.
\( \abs{AG} = 48 \Longrightarrow \abs{GD} = 24 \)
\( \abs{GE} = \dfrac{25}{2}\Longrightarrow \abs{BG} = 25 \)
\( [AD] \) doğrusu ağırlık merkezinden geçip ikizkenar üçgenin tabanına indiği için \( [BC] \) kenarının hem kenarortayı hem de yüksekliğidir.
\( [AD] \perp [BC] \)
Buna göre \( BDG \) üçgeni 7-24-25 özel dik üçgenidir.
\( \abs{BD} = x = 7 \) olarak bulunur.

\( G \) noktası \( ABC \) üçgeninin ağırlık merkezidir.
\( [FE] \parallel [BC] \)
\( \abs{FG} = 2, \abs{AE} = 8, \abs{AB} = 12 \)
olduğuna göre, \( \abs{FE} \) kaçtır?
Çözümü Göster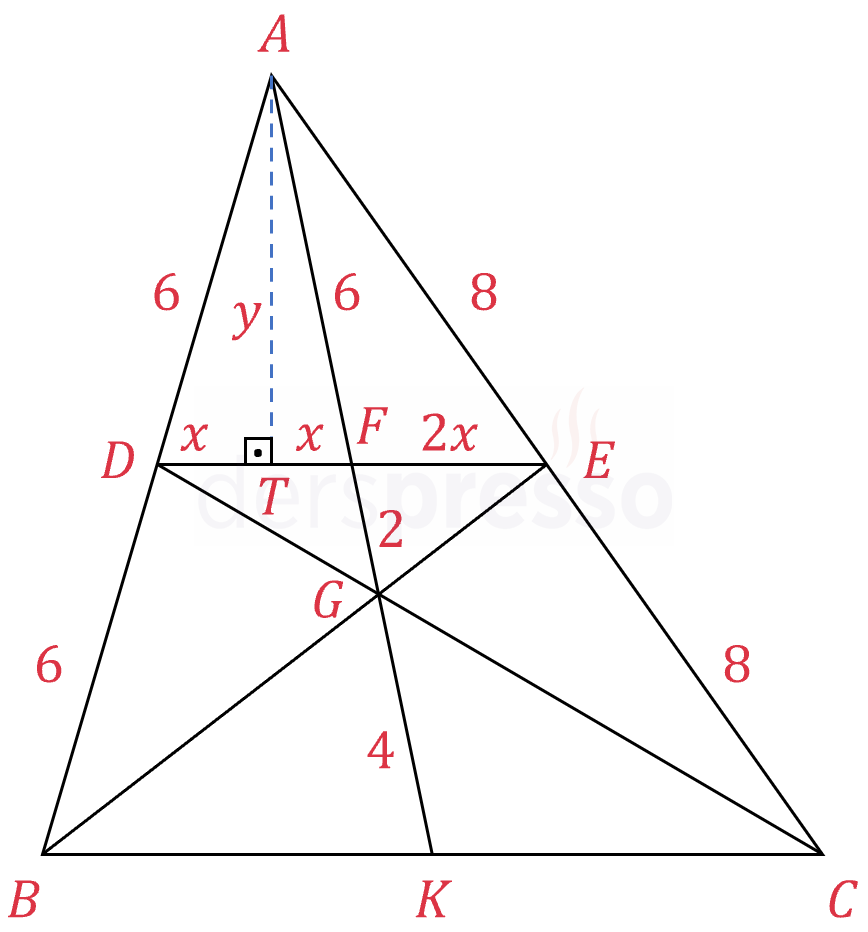
\( [AK] \), \( [BE] \) ve \( [CD] \) üçgenin ağırlık merkezinden geçtikleri için üçgenin birer kenarortayıdır ve sırasıyla \( [BC] \), \( [AC] \) ve \( [AB] \) kenarlarını iki eşit parçaya bölerler.
\( \abs{AD} = \abs{DB} = 6 \)
\( [FE] \) doğrusunu \( [AB] \) doğrusuna kadar uzatalım. Bu doğru üçgenin yan kenarlarının orta noktalarını birleştirdiği için \( ABC \) üçgeninin orta tabanıdır.
\( [AK] \) kenarortayı ve \( [DE] \) orta tabanını ikiye böler.
\( \abs{DF} = \abs{FE} \)
Orta taban ve ağırlık merkezi bir kenarortayı 3:1:2 oranında böler.
\( \abs{AF} = 6, \abs{FG} = 2, \abs{GK} = 4 \)
\( ADF \) üçgeninin ikizkenar olduğunu görmüş olduk.
\( A \) köşesinden \( [DF] \) kenarına bir dik indirelim.
İkizkenar üçgende tabana indirilen yükseklik aynı zamanda kenarortaydır.
\( \abs{DT} = \abs{TF} = x \)
\( \abs{FE} = 2x \)
\( ATF \) ve \( ATE \) üçgenleri birer dik üçgendir.
Bu iki üçgene Pisagor teoremini uygulayabilmek için \( \abs{AT} = y \) diyelim.
\( ATF \) üçgeni için:
\( y^2 + x^2 = 6^2 \)
\( ATE \) üçgeni için:
\( y^2 + (3x)^2 = 8^2 \)
İkinci denklemden birinci denklemi taraf tarafa çıkaralım.
\( 9x^2 - x^2 = 8^2 - 6^2 \)
\( x^2 = \dfrac{7}{2} \)
\( x = \dfrac{\sqrt{14}}{2} \)
\( \abs{FE} = 2x = \sqrt{14} \) bulunur.

\( G \) noktası \( ABC \) üçgeninin ağırlık merkezidir.
\( \abs{AG} = 6, \abs{BG} = 4, \abs{CG} = 5 \)
olduğuna göre \( \abs{BC} = x \) kaçtır?
Çözümü Göster
\( [AG] \) doğrusunu \( [BC] \) kenarına kadar uzatalım.
Bu doğru üçgenin ağırlık merkezinden geçtiği için üçgenin bir kenarortayıdır.
Ağırlık merkezi kenarortayları 2:1 oranında böler.
\( \abs{AG} = 6 \Longrightarrow \abs{GD} = 3 \)
\( \abs{BC} \) uzunluğunu bulmak için kenarortay teoremini kullanalım.
\( 2\abs{GD}^2 = \abs{BG}^2 + \abs{GC}^2 - \dfrac{\abs{BC}^2}{2} \)
\( 2 \cdot 3^2 = 4^2 + 5^2 - \dfrac{x^2}{2} \)
\( \abs{BC} = x = \sqrt{46} \) olarak bulunur.

\( ABC \) bir dik üçgendir.
\( \abs{AD} = \abs{DB} \)
\( \abs{DE} = 12, \abs{EC} = 3\abs{AE} \)
olduğuna göre, \( \abs{AC} \) kaçtır?
Çözümü Göster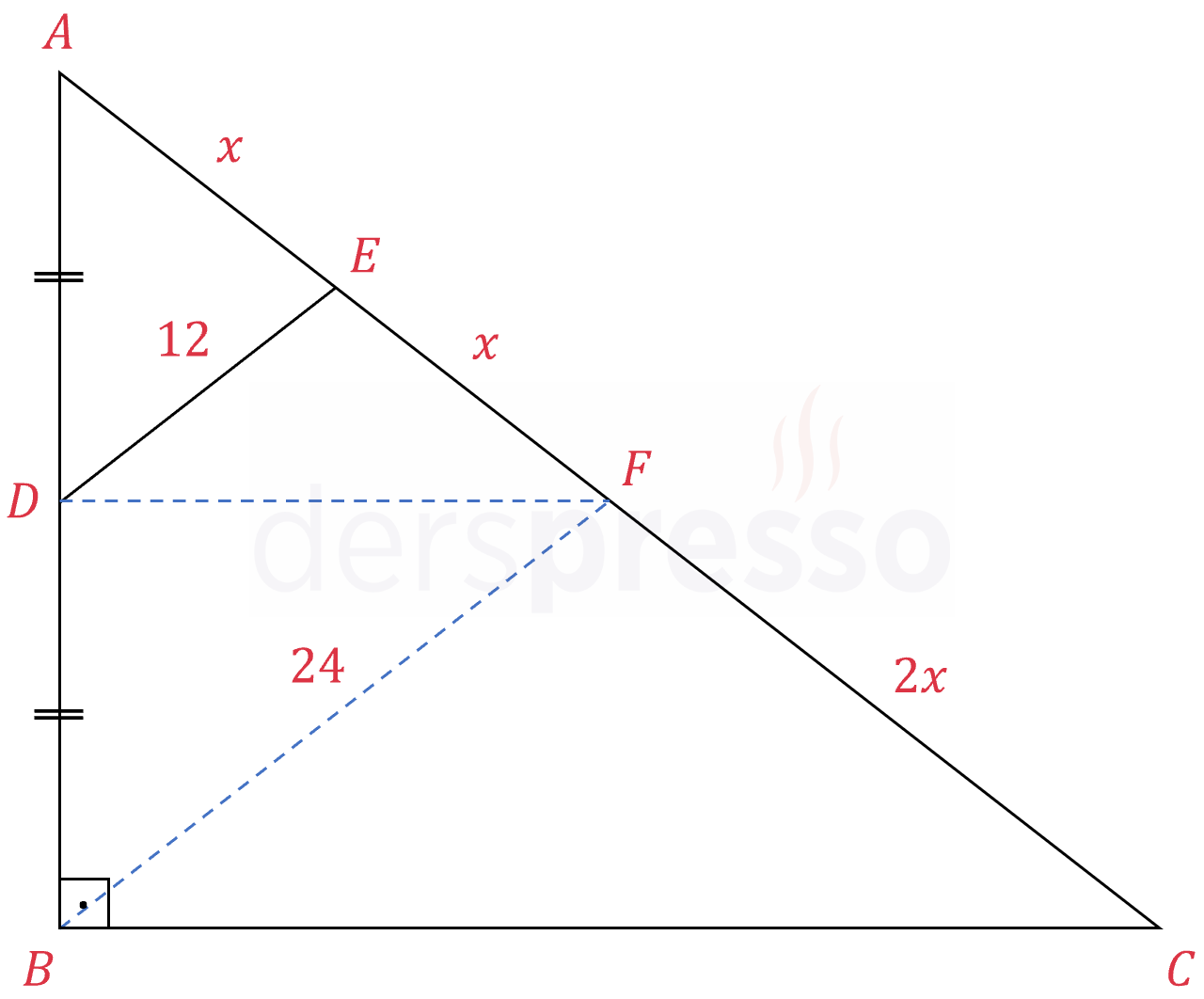
\( \abs{AE} = x \) diyelim.
\( B \) köşesinden \( [AC] \) kenarına bir kenarortay çizelim.
\( \abs{AE} = \abs{EF} = x \)
\( \abs{FC} = 2x \)
\( [DE] \) doğrusu \( ABF \) üçgeninin kenar orta noktalarını birleştirdiği için üçgenin orta tabanıdır.
\( \abs{BF} = 2 \cdot \abs{DE} = 24 \)
\( [BF] \), \( [AF] \) ve \( [FC] \) muhteşem üçlü oluştururlar.
\( \abs{AF} = \abs{FC} = 2x = 24 \)
\( \abs{AC} = 4x = 48 \) olarak bulunur.

\( G \) noktası \( ABC \) dik üçgeninin ağırlık merkezidir.
\( \abs{GE} = \abs{EC}, \abs{AC} = 18 \)
olduğuna göre, \( \abs{DE} = x \) kaçtır?
Çözümü Göster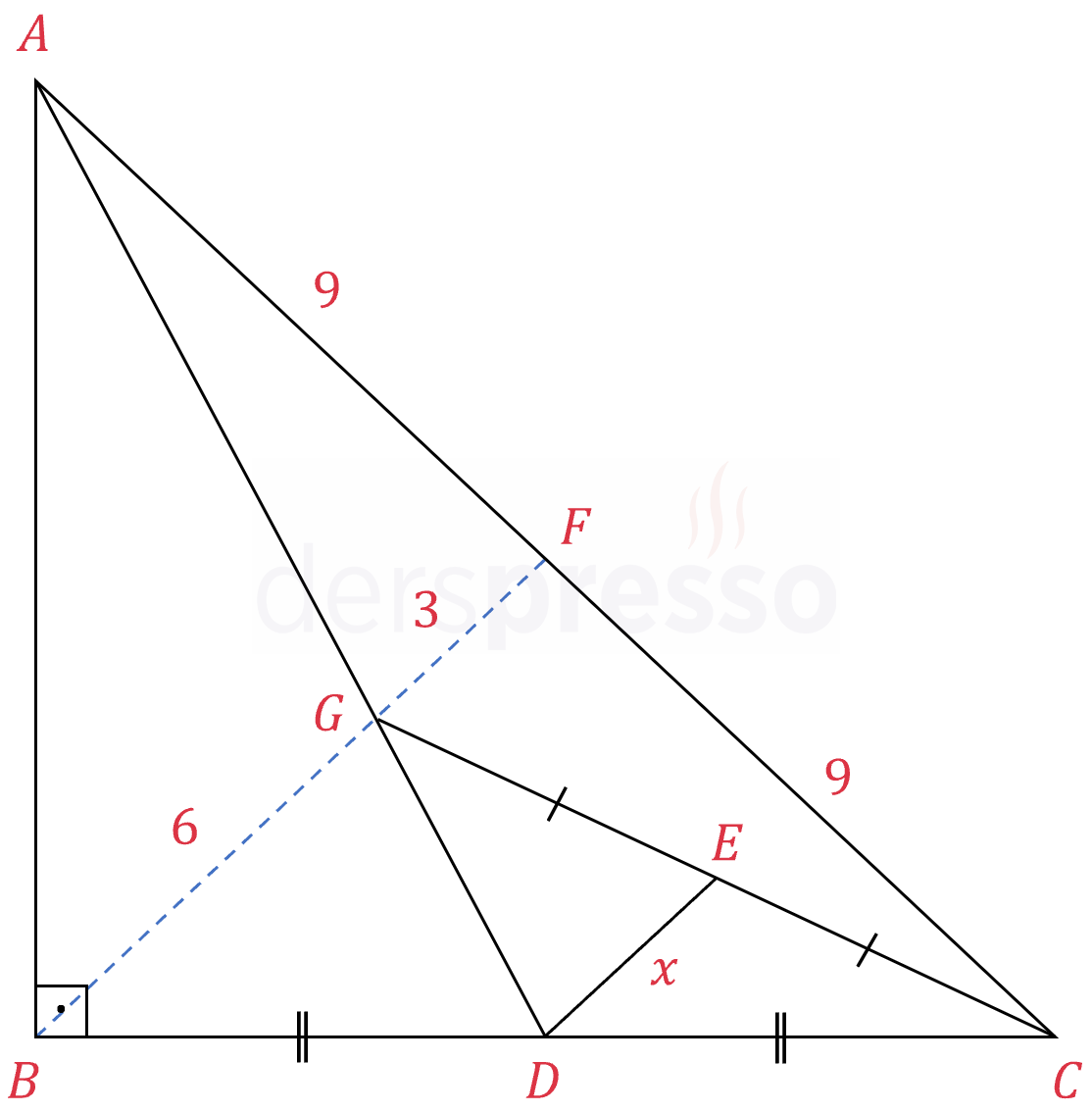
\( B \) köşesinden \( [AC] \) kenarına \( G \) noktasından geçen bir doğru çizelim. Bu doğru ağırlık merkezinden geçtiği için bir kenarortaydır.
Bu doğru ile \( ABC \) üçgeninde muhteşem üçlü oluşur.
\( \abs{AF} = \abs{FC} = \abs{BF} = 9 \)
Bir üçgenin ağırlık merkezi kenarortayları 2:1 oranında böler.
\( \abs{BG} = 6, \abs{GF} = 3 \)
\( [AD] \) doğru parçası ağırlık merkezinden geçtiği için kenarortaydır.
\( \abs{BD} = \abs{DC} \)
\( [DE] \) doğru parçası \( BGC \) üçgeninin iki kenarının orta noktalarını birleştirdiği için üçgenin orta tabanıdır.
Orta tabanın uzun tabana oranı 1:2'dir.
\( \abs{DE} = x = 3 \) bulunur.

Şekilde \( ABD \) ve \( EBC \) üçgenleri verilmiştir.
\( \abs{AE} = \abs{EB} = 18, \abs{BD} = \abs{DC} = 24 \)
olduğuna göre, \( \abs{BG} = x \) kaçtır?
Çözümü Göster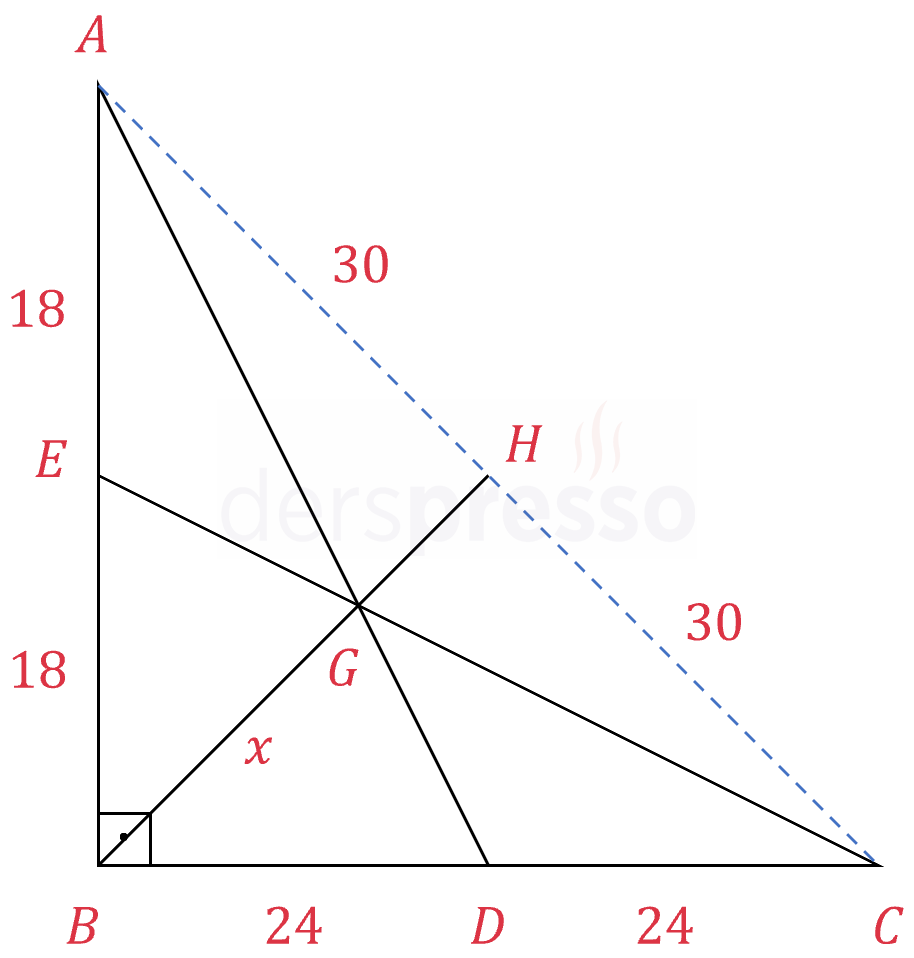
\( A \) ve \( C \) noktalarını birleştirerek \( ABC \) üçgeni oluşturalım.
\( ABC \) dik üçgeni 3-4-5 özel dik üçgeninin 12 katıdır.
\( \abs{AC} = 5 \cdot 12 = 60 \)
\( [CE] \) doğrusu \( [AB] \) kenarını, \( [AD] \) doğrusu da \( [BC] \) kenarını iki eşit parçaya böldüğü için \( [AD] \) ve \( [EC] \) doğruları kenarortaylardır.
\( B \) köşesinden \( [AC] \) kenarına kenarortay doğrusu çizelim. Bir üçgenin tüm kenarortayları ağırlık merkezinden geçtiği için bu kenarortay da \( G \) noktasında geçer.
Bunun sonucunda \( ABC \) üçgeninde muhteşem üçlü oluşur.
\( \abs{AH} = \abs{HC} = \abs{BH} = 30 \)
Bir üçgende ağırlık merkezi kenarortayları 2:1 oranında böler.
\( \abs{BG} = x = 20 \) bulunur.

Şekilde \( ABC \) ikizkenar üçgeni verilmiştir.
\( \abs{AB} = \abs{AC} \)
\( [BE] \perp [CD] \)
\( \abs{BE} = \abs{CD} = 21 \)
olduğuna göre, \( ABC \) üçgeninin alanı kaç birimkaredir?
Çözümü Göster\( A \) köşesinden tabana ait yüksekliği çizelim.
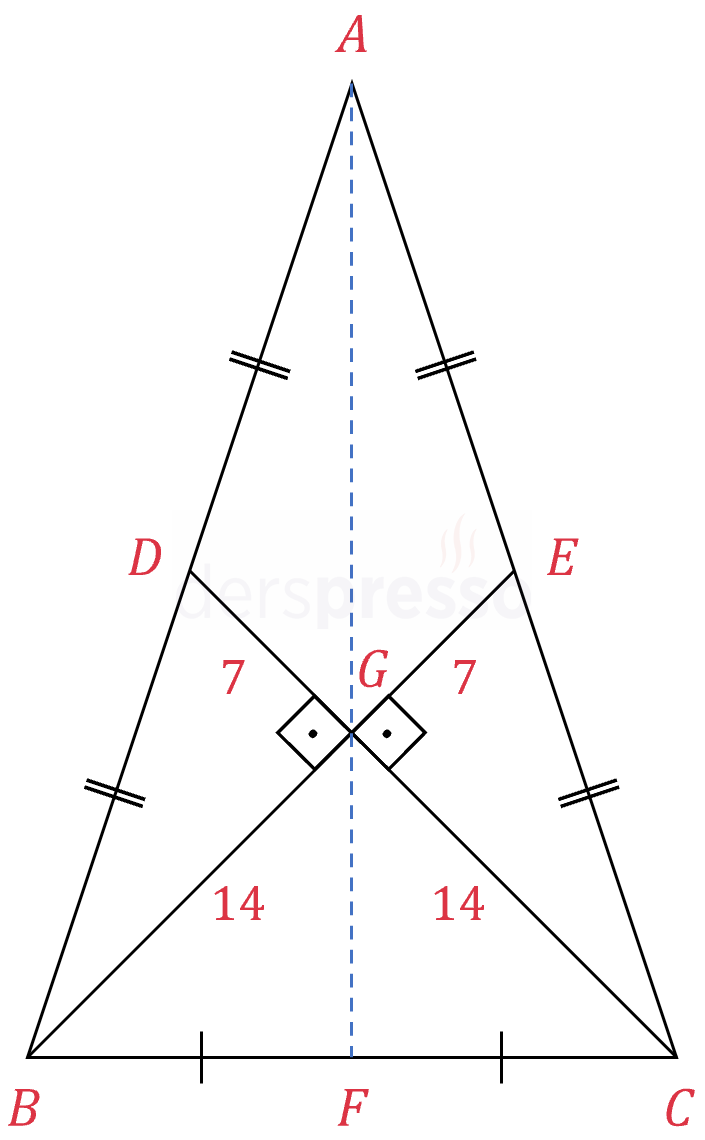
İkizkenar üçgende tabana ait yükseklik tabanı ortalar, dolayısıyla \( [AF] \) tabana ait kenarortaydır.
\( \abs{BF} = \abs{FC} \)
Bir üçgende kenarortaylar tek bir noktada kesişir ve bu nokta kenarortayları 2:1 oranında böler.
\( \abs{BE} = \abs{CD} = 21 \) olduğuna göre,
\( \abs{BG} = \abs{CG} = 14 \)
\( \abs{GE} = \abs{GD} = 7 \)
Tabanı ve yüksekliği bilinen \( BGD \) üçgeninin alanını bulalım.
\( A(BGD) = \dfrac{14 \cdot 7}{2} = 49 \)
Kenarortaylar üçgenin alanını 6 eşit parçaya böler.
\( A(ABC) = 49 \cdot 6 = 294 \) birimkare olarak bulunur.

\( ABC \) bir dik üçgendir.
\( \abs{AE} = \abs{EC}, \abs{AD} = \abs{BD} \)
\( \abs{BC} = 18, \abs{DF} = 2\abs{FC} \)
olduğuna göre, \( \abs{EF} = x \) kaçtır?
Çözümü Göster
\( \abs{FC} = y \) diyelim. Bu durumda \( \abs{DF} = 2y \) olur.
\( A \) köşesinden \( [BC] \) kenarına bir kenarortay çizelim. Bu kenarortay \( [DC] \) doğru parçasını üçgenin ağırlık merkezi olan \( G \) noktasında keser.
\( ABC \) üçgeninde muhteşem üçlü oluşur.
\( \abs{AH} = \abs{BH} = \abs{HC} = 9 \)
\( G \) ağırlık merkezi kenarortayları 2:1 oranında böler.
\( \abs{DG} = \abs{GF} = \abs{FC} = y \)
Bu durumda \( [EF] \) doğrusu \( AGC \) üçgeninin iki kenarının orta noktalarını birleştirdiği için üçgenin orta tabanıdır.
\( \abs{AG} = 2x \)
\( G \) ağırlık merkezi kenarortayları 2:1 oranında böler.
\( \abs{GH} = x \)
\( \abs{AH} = 9 = 3x \)
\( \abs{EF} = x = 3 \) olarak bulunur.