Polinomların Çarpanları ve Sıfırları
Konu tekrarı için: Özdeşlikler | Çarpanlara Ayırma
Çarpımları \( P(x) \) polinomunu veren polinomlara \( P(x) \) polinomunun çarpanları denir.
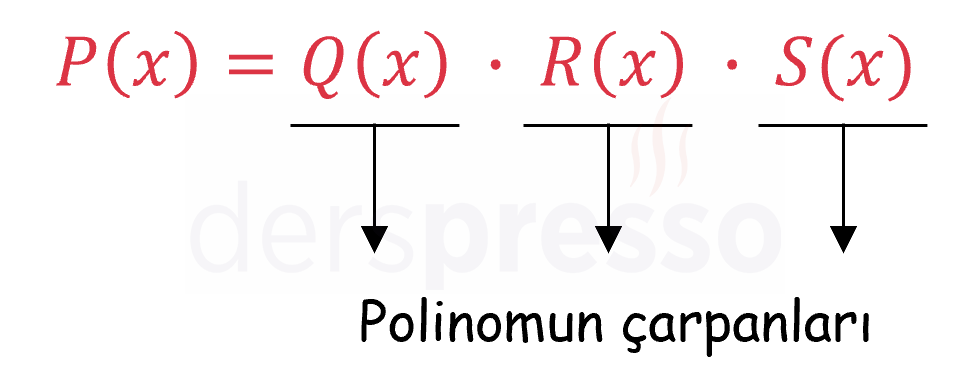
\( 3x^2 + 8x - 3 = (3x - 1)(x + 3) \)
\( 2x^5 + x^4 - 2x - 1 = (2x + 1)(x^2 + 1)(x + 1)(x - 1) \)
Bir polinom ve çarpanlarına ayrılmış hali birbirine eşit polinomlardır. Bir polinomun çarpanları arasında çarpma işlemi yapıldığında yine orijinal polinom elde edilir.
Bir polinomun çarpanlarına ayrılmış hali çarpanlar dışında ek bir terim içeremez. Aşağıdaki polinom çarpanlarına ayrılmış bir polinom değildir.
\( 2(x + 1)(x - 2)(x + 3) \textcolor{red}{+ 1} \)
Polinomun Sıfırları
Bir polinomda \( x \) yerine konduğunda polinom değerini sıfır yapan değerlere polinomun sıfırları denir.
\( P(x) = x^3 - 5x^2 + 3x + 6 \)
\( P(2) = 2^3 - 5(2)^2 + 3(2) + 6 = 0 \)
\( x = 2 \) polinom değerini sıfır yaptığı için polinomun bir sıfırıdır.
Polinom Denklemi ve Kökleri
Bir polinomun sıfıra eşitlenmiş denklem haline polinom denklemi denir.
\( P(x) = 0 \)
Çarpanlarına ayrılmış bir polinom denkleminin her bir çarpanını sıfır yapan değerlere o polinom denkleminin kökleri denir.
Bir \( P(x) \) polinomunun sıfırları aynı zamanda \( P(x) = 0 \) polinom denkleminin kökleridir, bir diğer ifadeyle polinom denklemini sağlar.
\( P(x) = (x + 1)(x - 2) \)
\( x \in \{-1, 2\} \) değerleri \( P(x) \) polinomunun sıfırları ve \( P(x) = 0 \) polinom denkleminin kökleridir.
\( P(-1) = 0, \quad P(2) = 0 \)
Çarpan Teoremi
Çarpan teoremi önceki bölümde gördüğümüz kalan teoreminin bir uzantısıdır ve bir polinomun sıfırları ve çarpanları arasındaki ilişkiyi tanımlar.
Çarpan teoremine göre, bir \( a \) sayısı bir polinomun sıfırı ise \( x - a \) bu polinomun bir çarpanıdır. Bunun karşıtı da doğrudur, yani \( x - a \) bir polinomun çarpanı ise \( a \) sayısı bu polinomun bir sıfırıdır.
\( P(x) \) bir polinom ve \( a \in \mathbb{R} \) olmak üzere,
(1) \( P(a) = 0 \) ise \( (x - a) \) \( P(x) \) polinomunun bir çarpanıdır.
(2) \( (x - a) \) \( P(x) \) polinomunun bir çarpanı ise \( P(a) = 0 \) olur.
\( P(x) = x^3 - 2x^2 + 1 \)
\( P(1) = 1^3 - 2(1)^2 + 1 = 0 \)
\( x = 1 \) verdiğimizde polinom değeri 0 olduğu için \( (x - 1) \) polinomun bir çarpanıdır.
\( P(x) = (x - 1) \cdot Q(x) \)
Polinom bölmesi ile polinomun diğer çarpanını bulabiliriz.
\( P(x) = (x - 1)(x^2 - x - 1) \)
\( R(x) = x(x + 5)(x - 2) \)
Çarpan teoremine göre her bir çarpanı sıfır yapan \( \{ -5, 0, 2 \} \) değerleri polinomun sıfırlarıdır.
İSPATI GÖSTER
Aşağıdaki gibi bir polinom bölme işlemi tanımlayalım.
\( B(x) \ne 0 \) olmak üzere,
\( P(x) = B(x) \cdot Q(x) + K(x) \)
Çarpan teoreminin iki kısmının ispatını sırayla yapalım.
(1) \( P(a) = 0 \) ise \( (x - a) \) \( P(x) \) polinomunun bir çarpanıdır.
Daha önce ispatını yaptığımız kalan teoremine göre, \( P(x) \) polinomunun birinci dereceden bir \( x - a \) polinomuna bölümünden kalan \( P(a) \) olur.
\( P(x) = (x - a) \cdot Q(x) + P(a) \)
\( P(a) = 0 \) ise bu bölme işlemi aşağıdaki şekilde olur.
\( P(x) = (x - a) \cdot Q(x) \)
Bu durumda \( (x - a) \) polinomun bir çarpanı olmuş olur.
(2) \( (x - a) \) \( P(x) \) polinomunun bir çarpanı ise \( P(a) = 0 \) olur.
Kalan teoremine göre, \( P(x) \) polinomunun birinci dereceden bir \( x - a \) polinomuna bölümünden kalan \( P(a) \) olur.
\( P(x) = (x - a) \cdot Q(x) + P(a) \)
\( (x - a) \) polinomu \( P(x) \) polinomunun bir çarpanı ise \( P(x) \) polinomunu tam bölüyor demektir, dolayısıyla bölme işleminde kalan sıfır olur.
\( P(a) = 0 \)
\( P(x) = (x - a) \cdot Q(x) \)
Bir \( P(x) \) polinomunun çarpanı olan polinomların sıfırları/çarpanları, \( P(x) \) polinomunun da birer sıfırıdır/çarpanıdır.
\( P(x) = Q_1(x) \cdot Q_2(x) \) ise,
\( Q_1(x) \) ve \( Q_2(x) \) polinomlarının çarpanları/sıfırları, \( P(x) \) polinomunun da çarpanları/sıfırlarıdır.
\( P(x) = Q_1(x) \cdot Q_2(x) \) olmak üzere,
\( Q_1(3) = 0 \) veya \( Q_2(3) = 0 \) ise \( P(3) = 0 \) olur.
Cebirin Temel Teoremi
Cebirin temel teoremine göre, reel katsayılı ve \( n \). dereceden (\( n \ge 1 \)) bir polinom denkleminin, tekrar eden kökler katları adedince sayılmak koşuluyla, reel ya da karmaşık sayı toplam \( n \) kökü vardır.
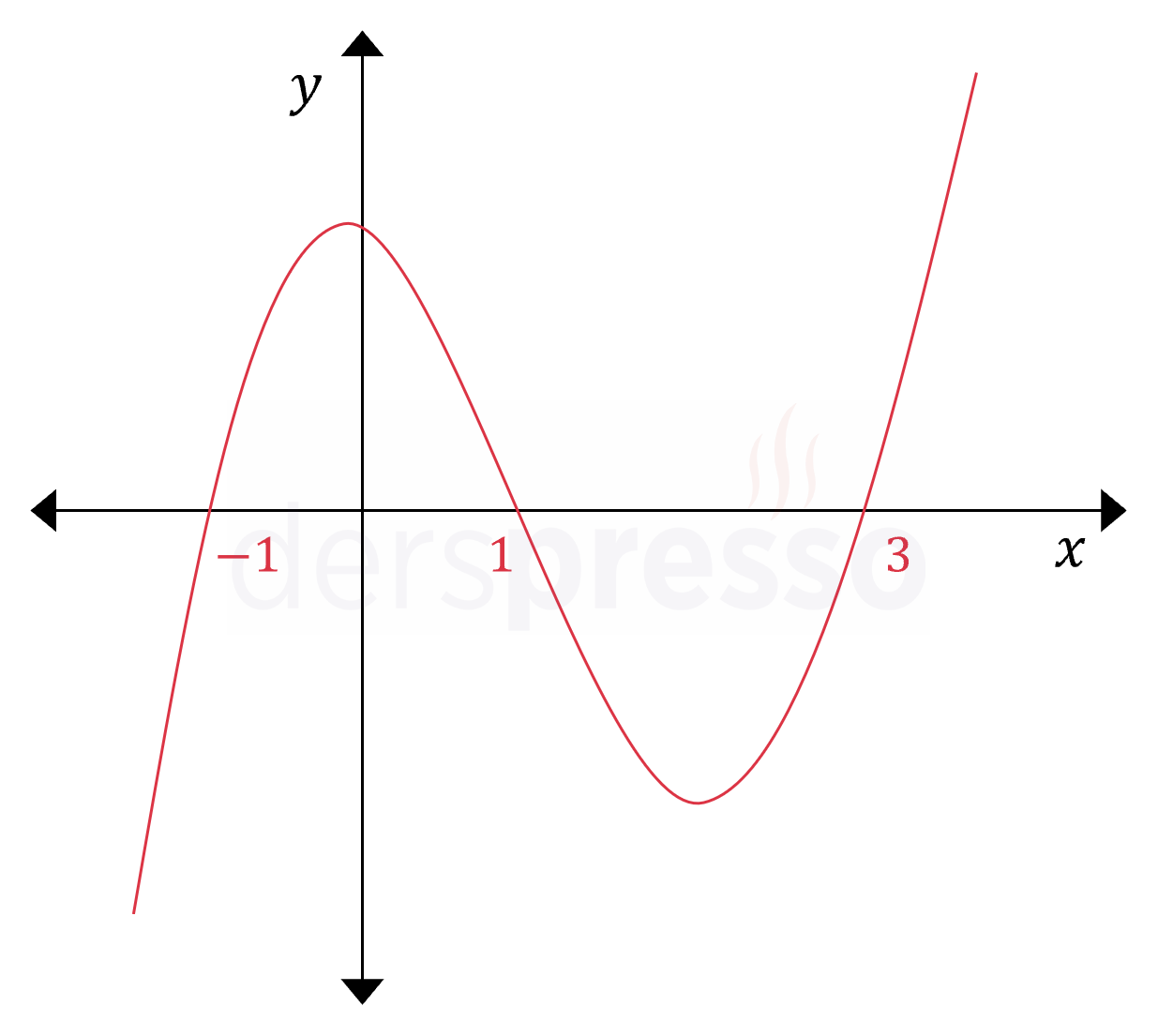
Bir polinom denkleminin reel kökleri aynı zamanda o polinomun grafiğinin \( x \) eksenini kestiği noktaların apsis değerlerini verir. Buna göre, bir polinom denkleminin reel köklerinin sayısı o polinom grafiğinin \( x \) eksenini kaç noktada kestiğini gösterir.
Reel katsayılı bir polinom denkleminin karmaşık sayı kökleri varsa bu kökler mutlaka birbirinin eşleniği şeklinde olur, dolayısıyla karmaşık sayı köklerin sayısı sadece ikinin katları şeklinde olabilir.
Reel katsayılı bir \( P(x) \) polinomu ve \( a \) reel sayısı için aşağıdaki ifadelerden herhangi birinin doğru olması diğerlerinin de doğru olmasını gerektirir.
- \( x = a \) değeri polinomu sıfır yapar (\( P(a) = 0 \)).
- \( x - a \) ifadesi \( P(x) \) polinomunun bir çarpanıdır (\( P(x) = (x - a) \cdot Q(x) \)).
- \( x = a \) değeri \( P(x) = 0 \) polinom denkleminin bir köküdür.
- Polinom fonksiyonunun grafiği \( x \) eksenini \( a \) noktasında keser.
Polinom grafiklerini polinom fonksiyonları konusunda daha detaylı ele alacağız.
Polinomun Sıfırlarının Bulunması
Bir polinomun sıfırlarını bulmak için kullanılabilecek yöntemlerden bazıları aşağıdaki gibidir.
Çarpanlara Ayırma
Tüm çarpanlarına ayrılmış bir polinomda herhangi bir çarpanı sıfır yapan \( x \) değeri polinomun bir sıfırıdır.
\( P(x) = x^3 - 3x^2 - x + 3 \)
\( = (x + 1)(x - 1)(x - 3) \)
Polinomun sıfırları: \( x \in \{-1, 1, 3\} \)
Farklı çarpanlara ayırma yöntemleri çarpanlara ayırma bölümünde detaylandırılmıştır.
Polinom Grafiği
Bir polinom fonksiyonunun grafiğinin \( x \) eksenini kestiği noktaların apsis değerleri polinomun birer sıfırıdır.
Yukarıdaki \( P(x) \) polinomunu bir fonksiyon olarak tanımladığımızda grafiği aşağıdaki gibi olur.
Rasyonel Kök Teoremi
Bir polinomun rasyonel kökleri önümüzdeki bölümde inceleyeceğimiz rasyonel kök teoremi ile de bulunabilir.
Deneme Yanılma Yöntemi
Bazı durumlarda \( 0, \pm 1, \pm 2 \) gibi denemesi kolay değerler polinomda yerine konarak da polinomun sıfırları bulunabilir.
\( P(x) = x^{32} + x^{11} - 2 \)
\( P(1) = 1^{32} + 1^{11} - 2 = 0 \)
Buna göre \( x = 1 \) polinomun bir sıfırıdır.
\( P(x) = (x - 1) \cdot Q(x) \)
2. Dereceden Polinomlar
İkinci dereceden bir polinomun sıfırları ikinci dereceden denklemler konusunda gördüğümüz kök bulma formülü ile de bulunabilir.
\( P(x) = ax^2 + bx + c \) olmak üzere,
\( x_{1, 2} = \dfrac{-b \pm \sqrt{b^2 - 4ac}}{2a} \)
\( P(x) = x^2 - 6x + 7 \)
\( x_{1, 2} = \dfrac{-(-6) \pm \sqrt{(-6)^2 - 4(1)(7)}}{2(1)} \)
Polinomun sıfırları: \( x \in \{3 - \sqrt{2}, 3 + \sqrt{2}\} \)
\( P(x) = (x - 3 + \sqrt{2})(x - 3 - \sqrt{2}) \)
Polinom Bölmesi
Bir \( a \) değerinin bir polinomu sıfır yaptığı ya da \( x - a \) ifadesinin polinomun bir çarpanı olduğu biliniyorsa polinom bölmesi yöntemiyle polinom \( (x - a) \) polinomuna bölünerek daha sade bir polinom elde edilebilir ve bu daha düşük dereceli polinom yukarıdaki yöntemler kullanılarak çarpanlarına ayrılabilir.
\( P(x) = 6x^3 - 5x^2 - 3x + 2 \)
Diğer yöntemlerle polinomu çarpanlarına ayıramadığımızı varsayalım.
\( P(1) = 6(1)^3 - 5(1)^2 - 3(1) + 2 = 0 \)
\( x = 1 \) polinomu sıfır yaptığı için \( (x - 1) \) polinomun bir çarpanıdır.
\( P(x) = (x - 1) \cdot Q(x) \)
Polinom bölmesi ile polinomun diğer çarpanını bulalım.
\( P(x) = (x - 1)(6x^2 + x - 2) \)
2. dereceden ifadeyi kolaylıkla çarpanlarına ayırabiliriz.
\( P(x) = (x - 1)(2x - 1)(3x + 2) \)
\( P(x) = x^4 - 2x^3 + 7x + 1 \) polinomu veriliyor.
\( x - 2 \) ifadesinin \( P(x) \) polinomunun bir çarpanı olmadığını gösterin.
Çözümü GösterÇarpan teoremine göre, \( x - 2 \) ifadesi \( P(x) \) polinomunun bir çarpanı ise bu çarpanı sıfır yapan \( x = 2 \) değeri polinomu da sıfır yapar, yani \( P(2) = 0 \) olur. Eğer \( P(2) = 0 \) değilse \( x - 2 \) ifadesi \( P(x) \) polinomunun bir çarpanı değildir.
\( P(2) \) değerini bulalım.
\( P(2) = 2^4 - 2(2)^3 + 7(2) + 1 \)
\( = 16 - 16 + 14 + 1 = 15 \neq 0 \)
Sonuç sıfır olmadığı için \( x - 2 \) ifadesi \( P(x) \) polinomunun bir çarpanı değildir.
\( P(x) = 2x^3 - 5x^2 - x + 6 \) polinomu veriliyor.
\( x + 1 \) ifadesinin \( P(x) \) polinomunun bir çarpanı olduğu gösteriniz ve \( P(x) = 0 \) denkleminin köklerini bulunuz.
Çözümü GösterÇarpan teoremine göre, \( x + 1 \) ifadesi \( P(x) \) polinomunun bir çarpanı ise bu çarpanı sıfır yapan \( x = -1 \) değeri polinomu da sıfır yapar, yani \( P(-1) = 0 \) olur. Eğer \( P(-1) = 0 \) değilse \( x + 1 \) ifadesi \( P(x) \) polinomunun bir çarpanı değildir.
\( P(-1) \) değerini bulalım.
\( P(-1) = 2(-1)^3 - 5(-1)^2 - (-1) + 6 \)
\( = -2 - 5 + 1 + 6 = 0 \)
\( P(-1) = 0 \) olduğu için \( x + 1 \) ifadesi \( P(x) \) polinomunun bir çarpanıdır.
Diğer kökleri bulmak için polinomu çarpanlarına ayıralım.
\( P(x) \) polinomunu polinom bölmesi ile \( x + 1 \)'e böldüğümüzde bölüm polinomu olarak \( 2x^2 - 7x + 6 \) bulunur.
\( P(x) = (x + 1)(2x^2 - 7x + 6) \)
Bulduğumuz ikinci dereceden polinomu çarpanlarına ayıralım.
\( P(x) = (x + 1)(2x - 3)(x - 2) \)
\( P(x) = 0 \) denkleminin kökleri yukarıdaki çarpanları sıfır yapan değerlerdir.
Çözüm kümesi: \( x \in \{-1, \frac{3}{2}, 2\} \)
\( k \in \mathbb{R} \) olmak üzere,
\( P(x) = x^3 - 4x^2 - x + 4k^2 \)
\( x - k \) ifadesi \( P(x) \) polinomunun bir çarpanı olduğuna göre, \( k \)'nın alabileceği değerleri bulunuz.
Çözümü GösterÇarpan teoremine göre, \( x - k \) ifadesi \( P(x) \) polinomunun bir çarpanı ise bu çarpanı sıfır yapan \( x = k \) değeri polinomu da sıfır yapar, yani \( P(k) = 0 \) olur. Eğer \( P(k) = 0 \) değilse \( x - k \) ifadesi \( P(x) \) polinomunun bir çarpanı değildir.
\( P(k) = k^3 - 4k^2 - k + 4k^2 = 0 \)
\( k^3 - k = 0 \)
\( k(k^2 - 1) = 0 \)
\( k(k - 1)(k + 1) = 0 \)
Buna göre \( k \)'nın alabileceği değerler aşağıdaki gibidir.
\( k \in \{-1, 0, 1\} \)
\( P(x) = 2x^4 - 5x^3 - 11x^2 + 20x + 12 \) polinomunun çarpanlarından ikisi \( 2x + 1 \) ve \( x - 3 \) olduğuna göre, polinomun sıfırlarını bulunuz.
Çözümü Göster\( P(x) = (2x + 1)(x - 3)Q(x) \)
\( P(x) = (2x^2 - 5x - 3)Q(x) \)
\( P(x) \) polinomunu \( 2x^2 - 5x - 3 \) polinomuna polinom bölmesi ile bölerek diğer çarpanı bulalım.
\( P(x) = (2x + 1)(x - 3)(x^2 - 4) \)
\( P(x) = (2x + 1)(x - 3)(x - 2)(x + 2) \)
Polinomun sıfırları her bir çarpanı sıfır yapan değerlerden oluşur.
\( x \in \{-2, -\frac{1}{2}, 2, 3\} \)
\( P(x) \) ikinci dereceden bir polinomdur.
\( P(4) = P(6) = 0 \) olduğuna göre, \( \frac{P(3)}{P(5)} \) kaçtır?
Çözümü Göster\( P(x) \) ikinci bir polinom olduğuna ve sıfırları bilindiğine göre polinomu aşağıdaki gibi yazabiliriz.
\( P(x) = a(x - 4)(x - 6) \)
\( P(3) \) ve \( P(5) \) değerlerini \( a \) cinsinden bulalım.
\( P(3) = a(3 - 4)(3 - 6) = 3a \)
\( P(5) = a(5 - 4)(5 - 6) = -a \)
\( \dfrac{P(3)}{P(5)} = \dfrac{3a}{-a} = -3 \) bulunur.
\( P(x) = 3x^3 - (a + 3)x^2 + (b - 2)x + 2a + 2 \) polinomunun çarpanlarından biri \( x^2 - 2x \) olduğuna göre, \( a \cdot b \) kaçtır?
Çözümü Göster\( x^2 - 2x = x(x - 2) \)
\( P(x) \) polinomunun çarpanlarından ikisi \( x \) ve \( x - 2 \) olduğuna göre, \( x = 0 \) ve \( x = 2 \) değerleri polinomu sıfır yapar.
\( x = 0 \) için:
\( P(0) = 3(0)^3 - (a + 3)(0)^2 + (b - 2)(0) + 2a + 2 = 0 \)
\( a = -1 \)
\( x = 2 \) için:
\( P(2) = 3(2)^3 - (-1 + 3)(2)^2 + (b - 2)(2) + 2(-1) + 2 = 0 \)
\( 24 - 8 + 2b - 4 - 2 + 2 = 0 \)
\( b = -6 \)
Buna göre \( a \cdot b = (-1) \cdot (-6) = 6 \) bulunur.
\( a \) ve \( b \) asal sayılardır.
Başkatsayısı 1 olan 3. dereceden \( P(x) \) polinomunun kökleri \( 5 \), \( a \) ve \( b \) olarak veriliyor.
\( P(0) = -175 \) olduğuna göre, \( P(8) \) kaçtır?
Çözümü GösterVerilen bilgiler doğrultusunda polinom tanımını aşağıdaki şekilde yazabiliriz.
\( P(x) = (x - 5)(x - a)(x - b) \)
\( P(0) \) değerini bulmak için \( x = 0 \) yazalım.
\( P(0) = (0 - 5)(0 - a)(0 - b) = -175 \)
\( (-5)(-a)(-b) = -175 \)
\( a \cdot b = 35 \)
\( a \) ve \( b \) asal sayılar oldukları için, iki sayı \( 5 \) ve \( 7 \) olur.
\( P(x) = (x - 5)(x - 5)(x - 7) \)
\( = (x - 5)^2(x - 7) \)
\( P(8) \) değerini bulmak için \( x = 8 \) yazalım.
\( P(8) = (8 - 5)^2(8 - 7) = 9 \) bulunur.
\( P(x) = x^4 - 3x^3 + (3m + 2)x^2 - (m - 1)^2x - 1 \) polinomunun çarpanlarından biri \( x - 1 \) olduğuna göre,
\( m \)'nin alabileceği değerler çarpımı nedir?
Çözümü Göster\( x - 1 \) polinomun bir çarpanı olduğuna göre, bu çarpanı sıfır yapan \( x \) değeri polinomu da sıfır yapar.
\( x - 1 = 0 \Longrightarrow x = 1 \)
\( P(1) = 1^4 - 3(1)^3 + (3m + 2)(1)^2 - (m - 1)^2(1) - 1 = 0 \)
\( 1 - 3 + (3m + 2) - (m - 1)^2 - 1 = 0 \)
\( -2 + 3m + 2 - m^2 + 2m - 1 - 1 = 0 \)
\( m^2 - 5m + 2 = 0 \)
Bu ikinci dereceden denklemin deltası sıfırdan büyük olduğu için birbirinden farklı iki reel sayı kökü vardır.
\( m \)'nin alabileceği değerler çarpımı için ikinci dereceden denklemin kökler çarpımı formülünü kullanalım.
Kökler çarpımı \( = \dfrac{c}{a} = \dfrac{2}{1} = 2 \) bulunur.
\( a \gt 0 \) olmak üzere,
\( P(x) = 2x^3 - (2a + 4)x^2 + 14x + 2b \) polinomunun çarpanlarından ikisi \( x - a \) ve \( x + 1 \) olduğuna göre,
\( P(x) = 0 \) denkleminin kökleri nelerdir?
Çözümü GösterÇarpan teoremine göre \( x - a \) ifadesi \( P(x) \) polinomunun bir çarpanı ise \( P(a) = 0 \) olur.
\( P(a) = 2a^3 - (2a + 4)a^2 + 14a + 2b = 0 \)
\( 2a^3 - 2a^3 - 4a^2 + 14a + 2b = 0 \)
\( 4a^2 - 14a = 2b \)
\( 2a^2 - 7a = b \)
Benzer şekilde, \( x + 1 \) polinomun bir çarpanı ise \( P(-1) = 0 \) olur.
\( P(-1) = 2(-1)^3 - (2a + 4)(-1)^2 + 14(-1) + 2b = 0 \)
\( -2 - 2a - 4 - 14 + 2b = 0 \)
\( -20 - 2a + 2b = 0 \)
\( 10 + a = b \)
Değeri \( b \) olan iki ifadeyi birbirine eşitleyelim.
\( 2a^2 - 7a = 10 + a \)
\( 2a^2 - 8a - 10 = 0 \)
\( 2(a + 1)(a - 5) = 0 \)
\( a = -1 \) ya da \( a = 5 \)
\( a \gt 0 \) olarak verildiği için \( a = 5 \) olur.
\( a \) değerini yukarıdaki denklemlerden birinde yerine koyarak \( b \) değerini bulalım.
\( 10 + a = b \Longrightarrow b = 15 \)
\( a \) ve \( b \) değerlerini polinomda yerine koyalım.
\( P(x) = 2x^3 - 14x^2 + 14x + 30 \)
Polinomun iki çarpanının \( x - 5 \) ve \( x + 1 \) olduğunu biliyoruz.
\( P(x) = (x - 5)(x + 1)Q(x) \)
\( P(x) = (x^2 - 4x - 5)Q(x) \)
Polinom bölmesi ile diğer çarpanı bulalım.
\( P(x) = (x^2 - 4x - 5)(2x - 6) \)
Polinomun çarpanlarına ayrılmış şekilde yazılışı aşağıdaki gibi olur.
\( P(x) = 2(x - 5)(x + 1)(x - 3) \)
\( P(x) = 0 \) denkleminin çözüm kümesi yukarıdaki her bir çarpanı sıfır yapan değerlerden oluşur.
Çözüm kümesi: \( x \in \{-1, 3, 5\} \)
\( x^3 + \dfrac{k - 1}{5}x^2 - 5kx - 5k - 1 = 0 \) polinom denkleminin bir kökü \( x = -1 \) olarak veriliyor.
Buna göre, \( k \) reel sayısını ve denklemin çözüm kümesini bulunuz.
Çözümü Göster\( x = -1 \) denklemin bir kökü ise eşitliği sağlamalıdır.
Denklemde \( x = -1 \) yazarak \( k \) sabit sayısını bulalım.
\( (-1)^3 + \dfrac{k - 1}{5}(-1)^2 - 5k(-1) - 5k - 1 = 0 \)
\( -1 + \dfrac{k - 1}{5} + 5k - 5k - 1 = 0 \)
\( \dfrac{k - 1}{5} = 2 \)
\( k = 11 \)
\( k \) değerini denklemde yerine yazalım.
\( x^3 + 2x^2 - 55x - 56 = 0 \)
Çarpan teoremine göre, \( x = -1 \) değeri \( P(x) = 0 \) denkleminin bir kökü ise \( x + 1 \) ifadesi \( P(x) \) polinomun bir çarpanıdır.
\( x^3 + 2x^2 - 55x - 56 \) ifadesini \( x + 1 \) ifadesine polinom bölmesi ile bölerek diğer çarpanı bulalım.
\( (x + 1)(x^2 + x - 56) = 0 \)
İkinci dereceden ikinci çarpanı kolaylıkla çarpanlarına ayırabiliriz.
\( (x + 1)(x + 8)(x - 7) = 0 \)
Denklemin çözüm kümesi her bir çarpanı sıfır yapan değerlerden oluşur.
Çözüm kümesi: \( x \in \{-8, -1, 7\} \)
\( P(x) \) bir polinom ve \( x \cdot P(x) = x^2 + 3x + a - 4 \) olduğuna göre \( P(a) \) kaçtır?
Çözümü Göster\( P(x) \) ifadesini yalnız bırakalım.
\( P(x) = \dfrac{x^2 + 3x + a - 4}{x} \)
\( P(x) \)'in polinom olabilmesi için, \( x \) ifadesi \( x^2 + 3x + a - 4 \) polinomunu tam bölmelidir.
Paydaki ifade \( x \)'e tam bölünebiliyorsa \( x \) paydaki ifadenin bir çarpanıdır, bir diğer ifadeyle \( x = 0 \) değeri payı sıfır yapar.
Paydaki polinomda \( x = 0 \) koyarak ifadeyi sıfıra eşitleyelim.
\( 0^2 + 3(0) + a - 4 = 0 \)
\( a = 4 \)
\( P(x) = \dfrac{x^2 + 3x}{x} = x + 3 \)
\( P(a) = P(4) = 4 + 3 = 7 \) bulunur.
\( a \in \mathbb{R} \) olmak üzere,
\( (x + 1) \cdot P(x) = x^4 - ax^3 - x + a + 4 \)
\( P(x) \) bir polinom olduğuna göre, \( a \) kaçtır?
Çözümü Göster\( P(x) \) ifadesini yalnız bırakalım.
\( P(x) = \dfrac{x^4 - ax^3 - x + a + 4}{x + 1} \)
\( P(x) \)'in polinom olabilmesi için, \( x + 1 \) ifadesi \( x^4 - ax^3 - x + a + 4 \) polinomunu tam bölmelidir.
Paydaki ifade \( x + 1 \)'e tam bölünebiliyorsa \( x + 1 \) paydaki ifadenin bir çarpanıdır, bir diğer ifadeyle \( x + 1 \)'i sıfır yapan \( x = -1 \) değeri payı da sıfır yapar.
Paydaki polinomda \( x = -1 \) koyarak ifadeyi sıfıra eşitleyelim.
\( x^4 - ax^3 - x + a + 4 = 0 \)
\( (-1)^4 - a(-1)^3 - (-1) + a + 4 = 0 \)
\( 1 + a + 1 + a + 4 = 0 \)
\( a = -3 \)
Buna göre \( a = -3 \) olması durumunda paydaki ifade \( x + 1 \)'e tam bölünür.
\( P(x) = \dfrac{x^4 + 3x^3 - x + 1}{x + 1} \)
Pay ve payda arasında polinom bölmesi yaparsak payın paydaya kalansız bölündüğünü görürüz.
\( P(x) = x^3 + 2x^2 - 2x + 1 \)
\( m \in \mathbb{R} \) olmak üzere,
\( (x - 2) \cdot P(x) = x^3 - x - m \) olduğuna göre, \( P(x - 3) \) polinomunun \( 2x \) ile bölümünden kalan kaçtır?
Çözümü Göster\( P(x) \) ifadesini yalnız bırakalım.
\( P(x) = \dfrac{x^3 - x - m}{x - 2} \)
\( P(x) \)'in polinom olabilmesi için, \( x - 2 \) ifadesi \( x^3 - x - m \) polinomunu tam bölmelidir.
Paydaki ifade \( x - 2 \)'ye tam bölünebiliyorsa \( x - 2 \) paydaki ifadenin bir çarpanıdır, bir diğer ifadeyle \( x - 2 \)'yi sıfır yapan \( x = 2 \) değeri payı da sıfır yapar.
Paydaki polinomda \( x = 2 \) koyarak ifadeyi sıfıra eşitleyelim.
\( 2^3 - 2 - m = 0 \Longrightarrow m = 6 \)
\( P(x) = \dfrac{x^3 - x - 6}{x - 2} \)
\( x^3 - x - 6 \) polinomunu \( x - 2 \) polinomuna bölersek bölüm \( x^2 + 2x + 3 \) olur.
\( P(x) = x^2 + 2x + 3 \)
Kalan teoremine göre, \( P(x - 3) \) polinomunun \( 2x \) ile bölümünden kalan \( x = 0 \) koyduğumuzda elde ettiğimiz \( P(0 - 3) = P(-3) \) olur.
\( P(-3) = (-3)^2 + 2(-3) + 3 = 6 \) bulunur.
Başkatsayısı 2 olan üçüncü dereceden bir \( P(x) \) polinomunda,
\( P(-2) = P(1) = P(5) = 0 \) eşitliği veriliyor.
\( P(x) \)'in \( x - 3 \) ile bölümünden kalan kaçtır?
Çözümü Göster\( P(-2) = P(1) = P(5) = 0 \) ise bu üç değer \( P(x) \) polinomunun birer sıfırıdır ve \( x + 2 \), \( x - 1 \) ve \( x - 5 \) polinomun çarpanlarıdır.
Polinom üçüncü dereceden olduğu için sabit bir sayı hariç başka bir çarpanı yoktur.
\( P(x) = a(x + 2)(x - 1)(x - 5) \)
Polinomun başkatsayısı 2 olarak veriliyor.
\( P(x) = 2(x + 2)(x - 1)(x - 5) \)
Kalan teoremine göre, \( P(x) \) polinomunun \( x - 3 \) polinomuna bölümünden kalan, bölen polinomunu sıfır yapan \( x = 3 \) değeri için bölünen polinomunun değeri, yani \( P(3) \) olur.
\( P(3) = 2(3 + 2)(3 - 1)(3 - 5) \)
\( = -40 \) bulunur.
\( P(x) \) üçüncü dereceden bir polinomdur.
\( P(-1) = P(1) = P(3) = 5 \) ve
\( P(2) = 11 \) eşitlikleri veriliyor.
Buna göre \( P(x) \) polinomunun sabit terimi kaçtır?
Çözümü GösterÜçüncü dereceden polinomun değeri üç farklı \( x \) değeri için birbirine eşit ve 5'tir.
Buna göre bu üç değer \( P(x) - 5 \) polinomunu sıfır yapar, dolayısıyla polinomun çarpanlarını aşağıdaki şekilde yazabiliriz.
\( P(x) - 5 = a(x + 1)(x - 1)(x - 3) \)
\( P(x) = a(x + 1)(x - 1)(x - 3) + 5 \)
\( a \) katsayısını bulmak için \( P(2) \) değerini kullanalım.
\( P(2) = 11 = a(2 + 1)(2 - 1)(2 - 3) + 5 \)
\( a = \dfrac{6}{-3} = -2 \)
Buna göre polinom tanımı aşağıdaki gibi olur.
\( P(x) = 2(x + 1)(x - 1)(x - 3) + 5 \)
Polinomun sabit terimini bulmak için \( x = 0 \) yazalım.
\( P(0) = -2(0 + 1)(0 - 1)(0 - 3) + 5 \)
\( = -1 \) bulunur.
Başkatsayısı 1 olan 3. dereceden \( P(x) \) polinomunun çarpanlarından biri \( x^2 - 5 \)'dir.
\( P(x) \) polinomunun \( x \) ile bölümünden kalan -5 olduğuna göre \( P(x + 1) \) polinomunun \( x - 2 \) ile bölümünden kalan kaçtır?
Çözümü Göster3. dereceden \( P(x) \) polinomunun 2. dereceden bir çarpanı verildiğine göre diğer çarpanı 1. dereceden olur.
\( P(x) = a(x - b)(x^2 - 5) \)
Polinomun başkatsayısı 1 olarak veriliyor.
\( P(x) = (x - b)(x^2 - 5) \)
Kalan teoremine göre, \( P(x) \) polinomunun \( x \) ile bölümünden kalan -5 ise \( P(0) = -5 \) olur.
\( P(0) = (0 - b)(0^2 - 5) = -5 \)
\( (-b)(-5) = -5 \)
\( b = -1 \)
Buna göre \( P(x) \) tanımı aşağıdaki gibi olur.
\( P(x) = (x + 1)(x^2 - 5) \)
Kalan teoremine göre, \( P(x + 1) \) polinomunun \( x - 2 \) polinomuna bölümünden kalan, bölen polinomunu sıfır yapan \( x = 2 \) değeri için bölünen polinomunun değeri, yani \( P(2 + 1) = P(3) \) olur.
\( P(3) = (3 + 1)(3^2 - 5) = 16 \) bulunur.
Başkatsayısı 1 olan 2. dereceden \( P(x) \) polinomunun sıfırdan ve birbirinden farklı sıfırları \( P(0) \) ve \( m \)'dir.
Buna göre \( m \) kaçtır?
Çözümü GösterSıfırları bilinen ikinci dereceden polinomu aşağıdaki gibi yazabiliriz.
\( P(x) = a(x - P(0))(x - m) \)
Polinomun başkatsayısı 1 olarak veriliyor.
\( P(x) = (x - P(0))(x - m) \)
\( x = 0 \) yazalım.
\( P(0) = (0 - P(0))(0 - m) \)
\( P(0) = -P(0)(-m) \)
\( m = 1 \) bulunur.
\( P(x) = ax^2 + 3ax - a - 9 \) polinomu veriliyor.
\( P(3x - 1) \) polinomunun çarpanlarından biri \( x \) olduğuna göre, \( a \) kaçtır?
Çözümü Göster\( P(3x - 1) \) polinomunun çarpanlarından biri \( x \) olduğuna göre, \( x = 0 \) değeri polinomu sıfır yapar.
\( P(3(0) - 1) = P(-1) = 0 \)
Polinom tanımında \( x = -1 \) yazalım.
\( P(-1) = a(-1)^2 + 3a(-1) - a - 9 \)
\( 0 = a - 3a - a - 9 \)
\( a = -3 \) bulunur.
2. dereceden \( P(x) \) polinomunun başkatsayısı 5'tir.
\( P(-4) \cdot P(1) = 0 \)
\( P(-2) \cdot P(4) = 0 \)
\( P(1) \cdot P(4) \ne 0 \)
olduğuna göre, polinomun sabit terimi kaçtır?
Çözümü Göster\( P(1) \cdot P(4) \ne 0 \) olduğundan \( P(1) \ne 0 \) ve \( P(4) \ne 0 \) olur.
Dolayısıyla \( P(-4) = 0 \) ve \( P(-2) = 0 \) olmalıdır.
Buna göre \( P(x) \) polinomunun sıfırları \( -4 \) ve \( -2 \) olur.
Başkatsayısı 5 ve sıfırları \( -4 \) ve \( -2 \) olan \( P(x) \) polinomunu yazalım.
\( P(x) = 5(x + 4)(x + 2) \)
\( = 5x^2 + 30x + 40 \)
\( P(x) \) polinomunun sabit terimi 40'tır.
\( a, b \in \mathbb{Z} \) olmak üzere,
\( P(x) = x^3 - ax^2 - (b + 2)x + 4b \)
\( Q(x) = x^2 - 2ax + b \)
\( P(-4) = 0, \quad Q(-4) \ne 0 \) veriliyor.
\( Q(x) \) polinomunun sıfırları aynı zamanda \( P(x) \) polinomunun da sıfırları olduğuna göre, \( a + b \) kaçtır?
Çözümü Göster\( P(-4) = 0 \) ve \( Q(-4) \ne 0 \) olduğuna göre, \( x = -4 \) \( P(x) \) polinomunun bir sıfırıdır, ancak \( Q(x) \) polinomunun bir sıfırı değildir.
Buna göre, \( x + 4 \) \( P(x) \) polinomunun bir çarpanıdır, ancak \( Q(x) \) polinomunun bir çarpanı değildir.
\( Q(x) \) polinomunun sıfırları aynı zamanda \( P(x) \) polinomunun da sıfırları olduğuna göre, \( P(x) \) polinomunu aşağıdaki şekilde yazabiliriz.
\( P(x) = Q(x) \cdot (x + 4) \)
\( x^3 - ax^2 - (b + 2)x + 4b = (x^2 - 2ax + b)(x + 4) \)
\( x^3 - ax^2 - (b + 2)x + 4b = x^3 + 4x^2 - 2ax^2 - 8ax + bx + 4b \)
\( x^3 - ax^2 - (b + 2)x + 4b = x^3 + (4 - 2a)x^2 + (b - 8a)x + 4b \)
İki polinomun eşitliğinde dereceleri aynı terimlerin katsayıları birbirine eşittir.
\( -a = 4 - 2a \Longrightarrow a = 4 \)
\( -(b + 2) = b - 8a \Longrightarrow b = 15 \)
\( a + b = 4 + 15 = 19 \) bulunur.
Başkatsayısı 4 olan 6. dereceden \( P(x) \) polinomunun köklerinden üçü \( -i \), \( 2i \) ve \( -3i \) karmaşık sayılarıdır.
Buna göre \( P(1) \) kaçtır?
Çözümü GösterReel katsayılı polinomların karmaşık sayı kökleri varsa bu kökler ikişerli olarak birbirinin eşleniği şeklinde bulunurlar.
Soruda verilen kökler birbirinin eşleniği olmadığı için polinomun 6 kökü aşağıdaki gibi olur.
\( x \in \{i, -i, 2i, -2i, 3i, -3i\} \)
Buna göre polinomu aşağıdaki gibi yazabiliriz.
\( P(x) = 4(x - i)(x + i)(x - 2i)(x + 2i)(x - 3i)(x + 3i) \)
\( (x - ai)(x + ai) = x^2 + a^2 \) özdeşliğini kullanalım.
\( P(x) = 4(x^2 + 1)(x^2 + 4)(x^2 + 9) \)
\( P(1) \) değerini bulmak için \( x = 1 \) yazalım.
\( P(1) = 4(1^2 + 1)(1^2 + 4)(1^2 + 9) \)
\( = 4(2)(5)(10) = 400 \) bulunur.
\( x^3 + ax^2 + bx - c = 0 \) denkleminin kökleri arasında \( 2 : 3 : 11 \) şeklinde bir orantı vardır.
\( c = 4224 \) olduğuna göre, \( a + b \) toplamı kaçtır?
Çözümü GösterDenklemin köklerine \( 2k \), \( 3k \) ve \( 11k \) diyelim.
Denklemi bu kök değerlerini kullanarak çarpanlarına ayrılmış şekilde yazalım.
\( (x - 2k)(x - 3k)(x - 11k) = 0 \)
\( (x^2 - 5kx + 6k^2)(x - 11k) = 0 \)
\( x^3 - 16kx^2 + 61k^2x - 66k^3 = 0 \)
Bu polinomun katsayılarını verilen polinom ile karşılaştıralım.
\( a = -16k, b = 61k^2, c = 66k^3 \)
\( c = 4224 \) olarak veriliyor.
\( c = 66k^3 = 4224 \)
\( k = 4 \)
\( a \) ve \( b \) değerlerini bulalım.
\( a = -16k = -64 \)
\( b = 61k^2 = 976 \)
\( a + b = 912 \) bulunur.
\( a, b \in \mathbb{Z} \) olmak üzere,
\( P(x) = (x - a)x^2 + b(12 - x) \)
\( Q(x) = x^3 + b(6 - x^2) - (a - 6)x \)
\( x - 4 \) ifadesi \( P(x) \) ve \( Q(x) \) polinomlarının ortak çarpanı olduğuna göre, \( a \cdot b \) çarpımı kaçtır?
Çözümü GösterÇarpan teoremine göre \( x - 4 \) iki polinomun ortak bir çarpanı ise \( P(4) = Q(4) = 0 \) olur.
\( P(4) = (4 - a)4^2 + b(12 - 4) = 0 \)
\( 64 - 16a + 8b = 0 \)
\( 16a - 8b = 64 \)
\( Q(4) = 4^3 + b(6 - 4^2) - (a - 6)4 = 0 \)
\( 64 - 10b - 4a + 24 = 0 \)
\( 4a + 10b = 88 \)
İlk denklemi -4'e bölelim ve denklemleri taraf tarafa toplayalım.
\( (-4a + 2b) + (4a + 10b) = -16 + 88 \)
\( 12b = 72 \Longrightarrow b = 6 \)
2. denklemde \( b = 6 \) yazalım.
\( 4a + 10(6) = 88 \)
\( a = 7 \)
Buna göre \( a \cdot b = 7 \cdot 6 = 42 \) bulunur.
\( (x + 2)(2x - 3)(x - 1) = 5(1 - x^2) - x + 1 \) denkleminin çözüm kümesini bulunuz.
Çözümü GösterParantezleri genişletelim.
\( (2x^2 + x - 6)(x - 1) = -5x^2 - x + 6 \)
\( 2x^3 - 2x^2 + x^2 - x - 6x + 6 = -5x^2 - x + 6 \)
\( 2x^3 - x^2 - 7x + 6 = -5x^2 - x + 6 \)
Tüm terimleri eşitliğin sol tarafında toplayalım.
\( 2x^3 + 4x^2 - 6x = 0 \)
Eşitliğin sol tarafını çarpanlarına ayıralım.
\( 2x(x^2 + 2x - 3) = 0 \)
\( 2x(x + 3)(x - 1) = 0 \)
Denklemin çözüm kümesi yukarıdaki çarpanları sıfır yapan değerlerdir.
Çözüm kümesi: \( x \in \{-3, 0, 1\} \)
\( a, b, c \in \mathbb{R} \) olmak üzere,
\( x^4 - ax^3 + bx^2 - 108x + c = 0 \) denklemi dört katlı köke sahip olduğuna göre, \( c \) kaçtır?
Çözümü GösterDenklemin dört katlı köküne \( r \) diyelim.
\( (x - r)^4 = x^4 - 4rx^3 + 6r^2x^2 - 4r^3x + r^4 \)
Bu denklemi soruda verilen denkleme eşitleyelim.
\( x^4 - 4rx^3 + 6r^2x^2 - 4r^3x + r^4 = x^4 - ax^3 + bx^2 - 108x + c \)
İki polinomun eşitliğinde dereceleri aynı olan terimlerin katsayıları birbirine eşittir.
\( x \)'li terimlerin katsayılarını eşitleyelim.
\( -4r^3 = -108 \)
\( r = 3 \)
Sabit terimleri eşitleyelim.
\( c = r^4 \)
\( = 3^4 = 81 \) bulunur.
\( \dfrac{P(x + 1) + x - 2}{x^2 - 1} \) ifadesi bir polinom olduğuna göre, \( P(x) \) polinomunun \( x^2 - 2x \) ile bölümünden kalan kaçtır?
Çözümü GösterVerilen ifade bir polinom olduğuna göre, paydaki ifade \( x^2 - 1 = (x - 1)(x + 1) \) polinomuna kalansız bölünmelidir, dolayısıyla \( x - 1 \) ve \( x + 1 \) çarpanlarını içermeli ve \( x = 1 \) ve \( x = -1 \) değerleri paydaki polinomu sıfır yapmalıdır.
\( x = 1 \) için:
\( P(1 + 1) + 1 - 2 = 0 \)
\( P(2) = 1 \)
\( x = -1 \) için:
\( P(-1 + 1) + (-1) - 2 = 0 \)
\( P(0) = 3 \)
Sorudaki bölme işlemini yazalım. Bölen polinomu ikinci dereceden bir polinom olduğu için kalan polinomu birinci dereceden bir polinom olmalıdır.
\( x^2 - 2x = x(x - 2) \)
\( P(x) = x(x - 2) \cdot Q(x) + ax + b \)
Dikkat edilirse polinom değerlerini bulduğumuz \( x = 0 \) ve \( x = 2 \) değerleri, bu bölme işleminde bölen polinomunu sıfır yapan değerlerdir.
\( x = 0 \) yazalım.
\( P(0) = 0(0 - 2) \cdot Q(0) + a(0) + b = 3 \)
\( b = 3 \)
\( x = 2 \) yazalım.
\( P(2) = 2(2 - 2) \cdot Q(2) + a(2) + b = 1 \)
\( 2a + 3 = 1 \)
\( a = -1 \)
Kalan polinomu \( ax + b = -x + 3 \) olarak bulunur.
Katsayılar toplamı 60 ve sabit terimi 18 olan dördüncü dereceden ve reel katsayılı bir polinom \( x + 1 \), \( x + 2 \) ve \( x - 3 \) ile tam bölünebilmektedir.
Buna göre, bu polinom \( x - 2 \) ile bölündüğünde kalan kaçtır?
Çözümü Göster\( P(x) \) polinomunun sabit terimi \( P(0) \) değerine eşittir.
\( P(0) = 18 \)
\( P(x) \) polinomunun katsayılar toplamı \( P(1) \) değerine eşittir.
\( P(1) = 60 \)
Reel katsayılı bir polinomun karmaşık sayı sıfırları varsa bu sıfırlar birbirinin eşleniği olacak şekilde ikinin katları adedince bulunabilir.
Polinomun sıfırlarından üçü reel sayı olarak verildiği için, dördüncü sıfır da reel sayı olmalıdır.
Buna göre polinomu aşağıdaki şekilde yazabiliriz.
\( P(x) = (x + 1)(x + 2)(x - 3)(ax + b) \)
\( a \) ve \( b \) değerlerini bulmak için \( P(0) \) ve \( P(1) \) değerlerini kullanalım.
\( P(0) = 18 = (0 + 1)(0 + 2)(0 - 3)(a(0) + b) \)
\( -6b = 18 \)
\( b = -3 \)
\( P(1) = 60 = (1 + 1)(1 + 2)(1 - 3)(a(1) + b) \)
\( -12(a - 3) = 60 \)
\( a = -2 \)
Buna göre \( P(x) \) polinomu aşağıdaki gibidir.
\( P(x) = (x + 1)(x + 2)(x - 3)(-2x - 3) \)
Kalan teoremine göre, \( P(x) \) polinomunun \( x - 2 \) polinomuna bölümünden kalan, bölen polinomunu sıfır yapan \( x = 2 \) değeri için bölünen polinomunun değeri, yani \( P(2) \) olur.
\( P(2) = (2 + 1)(2 + 2)(2 - 3)(-2(2) - 3) \)
\( = 84 \) bulunur.
Üçüncü dereceden bir \( P(x) \) polinom fonksiyonunun grafiği orijine göre simetriktir.
\( P(-1) = -5 \)
\( P(2) = 22 \)
olduğuna göre, \( P(3) \) kaçtır?
Çözümü GösterOrijine göre simetrik fonksiyonlar tek fonksiyondur ve tüm terimlerinin derecesi tek sayıdır.
Buna göre \( P(x) \) polinomu \( x^2 \) ve \( x^0 \) terimlerini içermez.
\( P(x) = ax^3 + bx \)
\( P(x) \) polinomunda \( x = -1 \) ve \( x = 2 \) yazalım.
\( P(-1) = a(-1)^3 + b(-1) = -5 \)
\( -a - b = -5 \)
\( P(2) = a(2)^3 + b(2) = 22 \)
\( 8a + 2b = 22 \)
Bu iki denklemi ortak çözdüğümüzde aşağıdaki değerleri buluruz.
\( a = 2, \quad b = 3 \)
Buna göre \( P(x) \) polinomu aşağıdaki gibi olur
\( P(x) = 2x^3 + 3x \)
\( P(3) \) değerini bulmak için \( x = 3 \) yazalım.
\( P(3) = 2(3)^3 + 3(3) = 63 \) bulunur.
6. dereceden bir \( P(x) \) polinomu ile ilgili aşağıdakiler biliniyor.
\( P(-1) = P(0) = P(4) = 5 \)
\( P(x) = 5 \) polinomun en küçük değeri ve \( P(1) = 41 \) olduğuna göre, \( P(3) \) kaça eşittir?
Çözümü Göster\( P(x) \) polinomu verilen üç noktada en küçük değerine ulaşıyorsa \( P(x) - 5 \) polinomunun bu üç noktada çift katlı kökleri vardır (bu noktalarda \( x \) eksenine teğettir).
Buna göre \( P(x) - 5 \) polinomunu aşağıdaki şekilde yazabiliriz.
\( P(x) - 5 = a(x + 1)^2x^2(x - 4)^2 \)
\( P(x) = a(x + 1)^2x^2(x - 4)^2 + 5 \)
\( a \) değerini bulmak için \( x = 1 \) koyalım.
\( P(1) = a(1 + 1)^2(1)^2(1 - 4)^2 + 5 \)
\( 41 = a(4)(1)(9) + 5 \)
\( a = 1 \)
Buna göre \( P(x) \) polinomunun tanımı aşağıdaki gibidir.
\( P(x) = (x + 1)^2x^2(x - 4)^2 + 5 \)
\( P(3) \) değerini bulmak için \( x = 3 \) koyalım.
\( P(3) = (3 + 1)^2(3)^2(3 - 4)^2 + 5 \)
\( = 16 \cdot 9 \cdot 1 + 5 \)
\( = 144 + 5 = 149 \) bulunur.
\( P(x) \) üçüncü dereceden bir polinomdur.
\( P(x) \)'in \( x^2 - 2x - 3 \) ile bölümünden kalan 4'tür.
\( P(x) \)'in \( x^2 - 4x + 3 \) ile bölümünden kalan 4'tür.
\( P(0) = 13 \) olduğuna göre, \( P(4) \) kaçtır?
Çözümü GösterVerilen bölme işlemlerindeki bölenleri çarpanlarına ayıralım.
\( x^2 - 2x - 3 = (x + 1)(x - 3) \)
\( x^2 - 4x + 3 = (x - 1)(x - 3) \)
Verilen bölme işlemlerini yazalım.
\( P(x) = (x + 1)(x - 3) \cdot Q_1(x) + 4 \)
\( P(x) = (x - 1)(x - 3) \cdot Q_2(x) + 4 \)
Bu iki eşitliğe göre, \( P(x) \) polinomu \( x + 1 \), \( x - 1 \) ve \( x - 3 \) ile bölündüğünde aynı 4 kalanını verir.
Buna göre \( x \in \{-1, 1, 3\} \) değerleri \( P(x) - 4 \) polinomunu sıfır yapar, dolayısıyla polinomun çarpanlarını aşağıdaki şekilde yazabiliriz.
\( P(x) - 4 = a(x + 1)(x - 1)(x - 3) \)
\( P(x) = a(x + 1)(x - 1)(x - 3) + 4 \)
\( a \) katsayısını bulmak için \( P(0) = 13 \) değerini kullanalım.
\( P(0) = a(0 + 1)(0 - 1)(0 - 3) + 4 = 13 \)
\( 3a + 4 = 13 \)
\( a = 3 \)
\( P(4) \) değerini bulmak için \( x = 4 \) yazalım.
\( P(4) = 3(4 + 1)(4 - 1)(4 - 3) + 4 \)
\( = 3(5)(3)(1) + 4 = 49 \) bulunur.
\( s, t \in \mathbb{R^+} \) olmak üzere,
\( P(x) = (x - \frac{s}{t})^2 + s + 3t \) polinomu \( x \) eksenine teğettir.
Buna göre \( 2P(x + 7) \cdot [P(x - 4) - 1] \) polinomunun sıfırlarının çarpımı kaçtır?
Çözümü Gösterİkinci dereceden polinomu tepe noktası bilinen parabol denklemi biçiminde aşağıdaki gibi yazabiliriz.
Parabolün tepe noktası \( T(r, k) \) olmak üzere,
\( P(x) = a(x - r)^2 + k \)
Buradan \( r = \frac{s}{t} \) ve \( k = s + 3t \) olarak bulunur.
Polinom grafiği \( x \) eksenine teğet olduğu için tepe noktasının ordinat değeri sıfırdır
\( s + 3t = 0 \Longrightarrow s = -3t \)
\( P(x) = (x - \frac{-3t}{t})^2 + (-3t) + 3t \)
\( = (x + 3)^2 \)
Sorudaki ifadeyi yazalım.
\( 2P(x + 7) \cdot [P(x - 4) - 1] \)
\( = 2(x + 7 + 3)^2 \cdot [(x - 4 + 3 )^2 - 1] \)
\( = 2(x + 10)^2 \cdot [(x - 1)^2 - 1] \)
\( = 2(x + 10)^2 \cdot (x - 1 - 1)(x - 1 + 1) \)
\( = 2(x + 10)^2 \cdot (x - 2)x \)
Bu ifadeyi sıfır yapan değerler \( x \in \{-10, 2, 0\} \) olup çarpımları 0'dır.
Katsayıları birer rakam olan ve sıfırlarından biri \( -\frac{1}{2} \) olan ikinci dereceden kaç farklı polinom yazılabilir?
Çözümü GösterSıfırlarından biri \( -\frac{1}{2} \) olan ikinci dereceden polinomu aşağıdaki şekilde yazabiliriz.
\( P(x) = (2x + 1)(ax + b) \)
\( P(x) = 2ax^2 + (a + 2b)x + b \)
Sabit terimin tam sayı olması için \( b \) tam sayı olmalıdır.
\( a + 2b \) katsayısının tam sayı olması için \( b \) ile birlikte \( a \) da tam sayı olmalıdır.
Buna göre polinomun katsayılarını birer rakam yapan tam sayı \( a \) ve \( b \) değerlerini bulalım.
\( a = 0 \) olması durumunda polinom birinci dereceden olur.
\( a = 1 \) için:
\( P(x) = 2x^2 + (1 + 2b)x + b \)
Tüm katsayıları rakam yapan \( b \) değerleri:
\( b \in \{0, 1, 2, 3, 4\} \)
\( a = 2 \) için:
\( P(x) = 4x^2 + (2 + 2b)x + b \)
Tüm katsayıları rakam yapan \( b \) değerleri:
\( b \in \{0, 1, 2, 3\} \)
\( a = 3 \) için:
\( P(x) = 6x^2 + (3 + 2b)x + b \)
Tüm katsayıları rakam yapan \( b \) değerleri:
\( b \in \{0, 1, 2, 3\} \)
\( a = 4 \) için:
\( P(x) = 8x^2 + (4 + 2b)x + b \)
Tüm katsayıları rakam yapan \( b \) değerleri:
\( b \in \{0, 1, 2\} \)
\( a \gt 4 \) olması durumunda başkatsayı rakam olmaz.
Buna göre istenen koşulları sağlayan \( 5 + 4 + 4 + 3 = 16 \) farklı polinom yazılabilir.
\( P(x) + P(2) = P(1) + x^2 + x - 2 \) eşitliğine göre aşağıdakilerden hangileri doğrudur?
I. \( P(x) \) polinomunun \( x \) ile bölümünden kalan -6'dır.
II. \( P(x) \) polinomunun bir çarpanı \( x + 3 \)'tür.
III. \( P(x + 1) \) polinomu \( x + 1 \) ile tam bölünür.
Çözümü Göster\( x = 1 \) yazalım.
\( P(1) + P(2) = P(1) + 1^2 + 1 - 2 \)
\( P(2) = 0 \)
\( x = 2 \) yazalım.
\( P(2) + P(2) = P(1) + 2^2 + 2 - 2 \)
\( P(1) = -4 \)
\( P(x) \) ikinci dereceden bir polinom olduğuna göre tanımını aşağıdaki şekilde yazabiliriz.
\( P(x) = a(x - x_1)(x - x_2) \)
\( P(1) \) ve \( P(2) \) sabit sayılar oldukları için polinomların eşitliğinden \( P(x) \) polinomunun başkatsayısı 1 olmalıdır.
\( P(x) = (x - x_1)(x - x_2) \)
\( P(2) = 0 \) olduğu için köklerden biri \( x = 2 \) olur.
\( P(x) = (x - 2)(x - x_2) \)
\( P(1) \) değerini bildiğimiz için \( x = 1 \) yazalım.
\( P(1) = (1 - 2)(1 - x_2) = -4 \)
\( x_2 = -3 \)
Buna göre \( P(x) \) polinomunun tanımı aşağıdaki gibi olur.
\( P(x) = (x - 2)(x + 3) \)
I. öncül: \( P(x) \) polinomunun \( x \) ile bölümünden kalanı bulmak için \( x = 0 \) yazdığımızda -6 buluruz. Bu öncül doğrudur.
II. öncül: \( x + 3 \) polinomun bir çarpanı olduğu için bu öncül doğrudur.
III. öncül: \( P(x + 1) \) polinomunun \( x + 1 \) ile bölümünden kalan \( x = -1 \) yazdığımızda elde ettiğimiz \( P(-1 + 1) = P(0) \) değeridir. \( P(0) = -6 \) olduğu için bu bölüm kalansız olmaz. Bu öncül yanlıştır.
Buna göre I. ve II. öncüller doğrudur.
\( P(x) \) ikinci dereceden bir polinomdur.
\( P(x) \) ve \( P(x - 2) \) polinomlarının ortak kökü 1'dir.
\( P(0) = -4 \) olduğuna göre, \( P(2) \) kaçtır?
Çözümü Göster\( P(x - 2) \) polinomunun grafiği \( P(x) \) polinomunun grafiğinin iki birim sağa ötelenmiş halidir.
Bu iki polinomun birer kökü ortak ve 1 ise \( P(x) \) polinomunun büyük kökü \( 1 \), küçük kökü \( 1 - 2 = -1 \) olmalıdır.
Buna göre \( P(x) \) polinomunu aşağıdaki gibi yazabiliriz.
\( P(x) = a(x - 1)(x + 1) \)
Polinomun başkatsayısını bulmak için \( P(0) = -4 \) değerini kullanalım.
\( P(0) = a(0 - 1)(0 + 1) = -4 \)
\( a = 4 \)
\( P(x) = 4(x - 1)(x + 1) \)
\( P(2) \) değerini bulmak için \( x = 2 \) yazalım.
\( P(2) = 4(2 - 1)(2 + 1) = 12 \) bulunur.
\( P(x) \) başkatsayısı 1 olan 3. dereceden bir polinomdur.
\( P(1) = 3, \quad P(2) = 6, \quad P(3) = 9 \) veriliyor.
Buna göre \( P(5) \) kaçtır?
Çözümü Göster3. dereceden polinomun 3 farklı noktası arasındaki ilişkiyi inceleyelim.
\( x \)'in her 1 birim artışında polinom değeri 3 birim arttığına göre, bu üç değer \( P(x) - 3x \) polinomunun sıfırlarıdır.
Buna göre \( P(x) \) polinomunu aşağıdaki gibi yazabiliriz.
\( P(x) - 3x = a(x - 1)(x - 2)(x - 3) \)
\( P(x) = a(x - 1)(x - 2)(x - 3) + 3x \)
Polinomun başkatsayısı 1 olarak veriliyor.
\( P(x) = (x - 1)(x - 2)(x - 3) + 3x \)
\( P(5) \) değerini bulmak için \( x = 5 \) yazalım.
\( P(5) = (5 - 1)(5 - 2)(5 - 3) + 3(5) = 39 \) bulunur.
\( P(x) = x^4 + 8x^3 + 24x^2 + 32x - 65 \) polinomunu sıfır yapan reel sayı \( x \) değerlerinin çarpımı kaçtır?
Çözümü GösterPolinomu sıfıra eşitleyelim.
\( x^4 + 8x^3 + 24x^2 + 32x - 65 = 0 \)
Eşitliğin sol tarafını düzenleyelim.
\( x^4 + 8x^3 + 24x^2 + 32x + 16 - 81 = 0 \)
\( x^4 + 4x^3(2) + 6x^2(2)^2 + 4x(2)^3 + 2^4 - 81 = 0 \)
Eşitliğin sol tarafı son terim hariç \( (x + 2)^4 \) ifadesinin açılımıdır.
\( (x + 2)^4 - 3^4 = 0 \)
\( ((x + 2)^2 - 3^2)((x + 2)^2 - 4 + 3^2) = 0 \)
\( ((x + 2) - 3)((x + 2) + 3)((x + 2)^2 - 4 + 9) = 0 \)
\( (x - 1)(x + 5)(x^2 + 4x + 9) = 0 \)
İlk iki çarpanı sıfır yapan yapan değerler polinomun reel birer sıfırıdır. Üçüncü çarpanın deltası sıfırdan küçük olduğu için bu çarpanı sıfır yapan reel sayı değer yoktur.
Buna göre polinomu sıfır yapan reel sayı değerlerin çarpımı \( 1 \cdot (-5) = -5 \) bulunur.
Katsayıları tam sayı olan 4. dereceden \( P(x) \) polinomu ile ilgili aşağıdakiler bilinmektedir.
\( P(x + 3) \) polinomunun bir çarpanı \( x - 2 \)'dir.
\( P(0) = -6 \)
\( \dfrac{P(x + 7)}{x + 4}, \dfrac{P(x - 5)}{x - 3} \) ve \( \dfrac{P(x)}{x - 1} \) ifadeleri birer polinomdur.
Buna göre, \( P(8) \) kaçtır?
Çözümü Göster\( P(x + 7) \) polinomunun \( x + 4 \) ile bölümü yine bir polinom ise bu ifadeye kalansız bölünür.
\( P(x + 7) = (x + 4) \cdot Q_1(x) \)
\( x = -4 \) verelim.
\( P(-4 + 7) = (-4 + 4) \cdot Q_1(-4) \)
\( P(3) = 0 \)
Benzer şekilde \( P(x - 5) \) polinomunun \( x - 3 \) ile bölümü bir polinom ise bu ifadeye kalansız bölünür.
\( x = 3 \Longrightarrow P(-2) = 0 \)
Benzer şekilde \( P(x) \) polinomunun \( x - 1 \) ile bölümü bir polinom ise bu ifadeye kalansız bölünür.
\( x = 1 \Longrightarrow P(1) = 0 \)
\( P(x + 3) \) polinomunun çarpanlarından biri \( x - 2 \) ise \( x = 2 \) polinomun sıfırlarından biridir.
\( x = 2 \Longrightarrow P(5) = 0 \)
Buna göre 4. dereceden \( P(x) \) polinomunun dört sıfırını da biliyor oluruz.
\( P(-2) = P(1) = P(3) = P(5) = 0 \)
Polinomun denklemini aşağıdaki şekilde yazabiliriz.
\( P(x) = a(x - 3)(x + 2)(x - 1)(x - 5) \)
Polinomun başkatsayısını bulmak için \( P(0) = -6 \) değerini kullanalım.
\( P(0) = a(0 - 3)(0 + 2)(0 - 1)(0 - 5) \)
\( -6 = a(-3)(2)(-1)(-5) \)
\( a = \dfrac{1}{5} \)
\( P(x) = \dfrac{1}{5}(x - 3)(x + 2)(x - 1)(x - 5) \)
\( P(x) \) değerini bulmak için \( x = 8 \) yazalım.
\( P(8) = \dfrac{1}{5}(8 - 3)(8 + 2)(8 - 1)(8 - 5) \)
\( = 210 \) bulunur.
\( P(x) = x^5 + ax^2 + bx + c \)
\( P(x) \) polinomu \( (x - 1)^3 \) ile tam bölündüğüne göre, \( a \cdot b \cdot c \) çarpımı kaçtır?
Çözümü GösterBu soruyu türev alarak çözelim.
Bir \( P(x) \) polinomu \( (x - a)^n \) ile tam bölünüyorsa \( x - a \) polinomun \( n \) katlı bir çarpanıdır ve \( x = a \) hem \( P(x) \) polinomunun hem de \( n - 1 \) sayıda türevinin birer köküdür.
\( P(a) = P'(a) = P''(a) = \ldots = P^{n - 1}(a) = 0 \)
Buna göre verilen polinomda \( P(1) = 0 \) eşitliği sağlanır.
\( P(1) = 1 + a + b + c = 0 \)
\( a + b + c = -1 \)
Ayrıca \( P'(1) = 0 \) eşitliği de sağlanır.
\( P'(x) = 5x^4 + 2ax + b = 0 \)
\( P'(1) = 5 + 2a + b = 0 \)
\( 2a + b = -5 \)
Ayrıca \( P''(1) = 0 \) eşitliği de sağlanır.
\( P''(x) = 20x^3 + 2a = 0 \)
\( P''(1) = 20 + 2a = 0 \)
\( a = -10 \)
\( a \) değerini kullanarak diğer bilinmeyen değerlerini bulalım.
\( 2a + b = -5 \Longrightarrow b = 15 \)
\( a + b + c = -1 \Longrightarrow c = -6 \)
\( a \cdot b \cdot c = (-10) \cdot 15 \cdot (-6) = 900 \) bulunur.