Katsayılar Toplamı ve Sabit Terim Bulma
Polinomların katsayılar toplamını ve sabit terimini aşağıdaki yöntemlerle bulabiliriz.
Katsayılar Toplamı
Bir polinomun katsayılar toplamını bulmak için tüm değişkenlere 1 değeri verilir ve bu şekilde değişkenlerin yok olması ve sadece terimlerin katsayılarının kalması sağlanır.
\( P(x) = (3x - 4)^3 \) polinomunun katsayılar toplamını bulalım.
\( x = 1 \) verelim.
\( P(1) = (3(1) - 4)^3 = -1 \)
Buna göre, \( P(x) \) polinomunun katsayılar toplamı \( P(1) = -1 \)'dir.
Polinomun açılımını yazalım ve bulduğumuz sonucu kontrol edelim.
\( P(x) = 27x^3 - 108x^2 + 144x - 64 \)
Katsayıların toplamını alalım.
\( 27 + (-108) + 144 + (-64) = -1 \)
Polinomun katsayılar toplamı her zaman \( P(1) \) değerine karşılık gelmeyebilir, dolayısıyla katsayılar toplamı \( P(1) \) değerini bularak değil, tüm değişkenlere 1 değeri vererek hesaplanmalıdır.
\( P(2x + 3) = (2x^2 + 1)^3 \) polinomunun katsayılar toplamını bulalım.
\( x = 1 \) verelim.
\( P(2(1) + 3) = (2(1)^2 + 1)^3 \)
\( P(5) = 27 \)
Buna göre, \( P(2x + 3) \) polinomunun katsayılar toplamı \( P(5) = 27 \)'dir.
Polinomun açılımını yazalım ve bulduğumuz sonucu kontrol edelim.
\( P(2x + 3) = 8x^6 + 12x^4 + 6x^2 + 1 \)
Katsayıların toplamını alalım.
\( 8 + 12 + 6 + 1 = 27 \)
Çift ve Tek Dereceli Terimlerin Katsayılar Toplamı
Bir \( P(x) \) polinomunun çift ve tek dereceli terimlerinin katsayılar toplamı formülleri aşağıdaki gibidir.
Çift dereceli terimlerin katsayılar toplamı \( = \dfrac{P(1) + P(-1)}{2} \)
Tek dereceli terimlerin katsayılar toplamı \( = \dfrac{P(1) - P(-1)}{2} \)
\( P(x) = 4x^4 + 6x^3 - 10x^2 + 12x - 36 \)
\( P(1) = 4(1)^4 + 6(1)^3 - 10(1)^2 + 12(1) - 36 = -24 \)
\( P(-1) = 4(-1)^4 + 6(-1)^3 - 10(-1)^2 + 12(-1) - 36 = -60 \)
Çift dereceli terimlerin katsayılar toplamı \( = \dfrac{-24 + (-60)}{2} = \textcolor{red}{-42} \)
Çift dereceli terimlerin katsayılarının toplamını alarak bulduğumuz sonucu kontrol edelim.
\( 4 + (-10) + (-36) = \textcolor{red}{-42} \)
Tek dereceli terimlerin katsayılar toplamı \( = \dfrac{-24 - (-60)}{2} = \textcolor{blue}{18} \)
Tek dereceli terimlerin katsayılarının toplamını alarak bulduğumuz sonucu kontrol edelim.
\( 6 + 12 = \textcolor{blue}{18} \)
İSPATI GÖSTER
Bir \( P(x) \) polinomunu aşağıdaki gibi tanımlayalım.
\( P(x) = a_{2n}x^{2n} + a_{2n - 1}x^{2n - 1} + \ldots + a_3x^3 + a_2x^2 + a_1x + a_0 \)
Bu polinomda çift ve tek dereceli terimler aşağıdaki gibi olmaktadır.
Çift dereceli terimler: \( a_{2n}x^{2n}, a_{2n - 2}x^{2n - 2}, \ldots, a_2x^2, a_0 \)
Tek dereceli terimler: \( a_{2n - 1}x^{2n - 1}, a_{2n - 3}x^{2n - 3}, \ldots, a_3x^3, a_1x \)
\( P(1) \) ve \( P(-1) \) değerlerini hesaplayalım.
\( P(1) = a_{2n}(1)^{2n} + a_{2n - 1}(1)^{2n - 1} + \ldots + a_3(1)^3 + a_2(1)^2 + a_1(1) + a_0 \)
\( P(-1) = a_{2n}(-1)^{2n} + a_{2n - 1}(-1)^{2n - 1} + \ldots + a_3(-1)^3 + a_2(-1)^2 + a_1(-1) + a_0 \)
İfadeleri sadeleştirdiğimizde aşağıdaki değerleri elde ederiz. \( P(-1) \) ifadesinde çift dereceli terimlerin işaretinin pozitif kaldığına, tek dereceli terimlerin işaretinin ise negatife döndüğüne dikkat edelim.
\( P(1) = a_{2n} + a_{2n - 1} + \ldots + a_3 + a_2 + a_1 + a_0 \)
\( P(-1) = a_{2n} - a_{2n - 1} + \ldots - a_3 + a_2 - a_1 + a_0 \)
\( P(1) \) ve \( P(-1) \) toplamını aldığımızda çift dereceli terimlerden ikişer tane kaldığını, tek dereceli terimlerin ise birbirlerini götürdüğünü görürüz.
\( P(1) + P(-1) = 2a_{2n} + 2a_{2n - 2} + \ldots + 2a_2 + 2a_0 \)
Bu ifadeyi ikiye böldüğümüzde yukarıdaki çift dereceli terimlerin katsayılar toplam formülünü elde ederiz.
\( \dfrac{P(1) + P(-1)}{2} = a_{2n} + a_{2n - 2} + \ldots + a_2 + a_0 \)
\( P(1) \) ve \( P(-1) \) farkını aldığımızda da çift dereceli terimlerin birbirlerini götürdüğünü, tek dereceli terimlerin ise ikişer tane kaldığını görürüz.
\( P(1) - P(-1) = 2a_{2n - 1} + 2a_{2n - 3} + \ldots + 2a_3 + 2a_1 \)
Bu ifadeyi ikiye böldüğümüzde yukarıdaki tek dereceli terimlerin katsayılar toplam formülünü elde ederiz.
\( \dfrac{P(1) - P(-1)}{2} = a_{2n - 1} + a_{2n - 3} + \ldots + a_3 + a_1 \)
Sabit Terim
Bir polinomun sabit terimini bulmak için tüm değişkenlere 0 değeri verilir ve bu şekilde değişken içeren terimlerin yok olması ve sadece sabit terimin kalması sağlanır.
\( P(x) = (4x - 3)^3 \) polinomunun sabit terimini bulalım.
\( x = 0 \) verelim.
\( P(0) = (4(0) - 3)^3 = -27 \)
Buna göre, \( P(x) \) polinomunun sabit terimi \( P(0) = -27 \)'dir.
Polinomun açılımını yazalım ve bulduğumuz sonucu kontrol edelim.
\( P(x) = 64x^3 - 144x^2 + 108x - 27 \)
Açılımda görebileceğimiz gibi polinomun sabit terimi \( -27 \)'dir.
Polinomun sabit terimi her zaman \( P(0) \) değerine karşılık gelmeyebilir, dolayısıyla sabit terim \( P(0) \) değerini bularak değil, tüm değişkenlere 0 değeri vererek hesaplanmalıdır.
\( P(2x + 3) = (3x^2 - 2)^3 \) polinomunun sabit terimini bulalım.
\( x = 0 \) verelim.
\( P(2(0) + 3) = (3(0)^2 - 2)^3 \)
\( P(3) = -8 \)
Buna göre, \( P(2x + 3) \) polinomunun sabit terimi \( P(3) = -8 \)'dir.
Polinomun açılımını yazalım ve bulduğumuz sonucu kontrol edelim.
\( P(2x + 3) = 27x^6 - 54x^4 + 36x^2 - 8 \)
Açılımda görebileceğimiz gibi polinomun sabit terimi \( -8 \)'dir.
\( P(4x - 7) = x^3 - 6x^2 + 3x - 1 \) polinomu veriliyor.
Buna göre, \( P(x) \) polinomunun katsayılar toplamı kaçtır?
Çözümü Göster\( P(x) \) polinomunun katsayılar toplamı \( x = 1 \) yazdığımızda elde ettiğimiz \( P(1) \) değeridir.
\( P(1) \) değerini bulmak için \( P(4x - 7) \) polinomunda \( x \) yerine yazmamız gereken değeri bulalım.
\( 4x - 7 = 1 \Longrightarrow x = 2 \)
\( P(4x - 7) \) polinomunda \( x = 2 \) yazalım.
\( P(4(2) - 7) = 2^3 - 6(2)^2 + 3(2) - 1 \)
\( P(1) = -11 \) bulunur.
\( P(x) = (x^3 - 3x + 1)^2 - 2 \) polinomunun tek ve çift dereceli terimlerinin katsayılar toplamını bulunuz.
Çözümü GösterPolinomun tek ve çift dereceli terimlerinin katsayılar toplamını bulmak için \( P(1) \) ve \( P(-1) \) değerlerini bulalım.
\( P(1) = (1^3 - 3(1) + 1)^2 - 2 = -1 \)
\( P(-1) = ((-1)^3 - 3(-1) + 1)^2 - 2 = 7 \)
Çift dereceli terimlerin katsayılar toplamı:
\( \dfrac{P(1) + P(-1)}{2} = \dfrac{-1 + 7}{2} = 3 \)
Tek dereceli terimlerin katsayılar toplamı:
\( \dfrac{P(1) - P(-1)}{2} = \dfrac{-1 - 7}{2} = -4 \)
\( P(x) = (1 + x + x^2)^5 \) polinomunun çift dereceli terimlerinin katsayılarının toplamı kaçtır?
Çözümü GösterBir polinomun çift dereceli terimlerinin katsayılar toplamı formülü:
\( = \dfrac{P(1) + P(-1)}{2} \)
\( P(1) = (1 + 1 + 1^2)^5 = 3^5 = 243 \)
\( P(-1) = (1 + (-1) + (-1)^2)^5 = 1 \)
Buna göre çift dereceli terimlerin katsayıları toplamı \( \frac{243 + 1}{2} = 122 \) olarak bulunur.
\( P(x - 2) - P(x - 3) = 6x^2 - 4 \) eşitliği veriliyor.
\( P(x) \) polinomunun katsayılar toplamı 10 olduğuna göre, \( P(x) \) polinomunun sabit terimi kaçtır?
Çözümü Göster\( P(x) \) polinomunun katsayılar toplamı 10 ise \( P(1) = 10 \) demektir.
\( P(x) \) polinomunun sabit terimi \( x = 0 \) yazdığımızda elde ettiğimiz \( P(0) \) değeridir.
Verilen eşitlikte \( P(1) \) değerini kullanarak \( P(0) \) değerini bulmak için \( x = 3 \) yazalım.
\( P(3 - 2) - P(3 - 3)= 6(3)^2 - 4 \)
\( P(1) - P(0) = 54 - 4 \)
\( 10 - P(0) = 50 \)
\( P(0) = -40 \)
Buna göre \( P(x) \) polinomunun sabit terimi \( P(0) = -40 \) olarak bulunur.
\( P(x) = x^5 - 3x^3 - ax + 3 \)
\( P(2x + 1) \) polinomunun sabit terimi \( P(3x - 1) \) polinomunun katsayılar toplamına eşit olduğuna göre, \( a \) kaçtır?
Çözümü GösterBir polinomun sabit terimini bulmak için tüm değişkenlere 0 değeri verilir, dolayısıyla \( P(2x + 1) \) polinomunun sabit terimi \( P(2(0) + 1) = P(1) \) değerine eşittir.
\( P(1) \) değerini bulmak için \( P(x) \) polinomunda \( x = 1 \) yazalım.
\( P(1) = 1^5 - 3(1)^3 - a(1) + 3 \)
\( = 1 - a \)
Bir polinomun katsayılar toplamını bulmak için tüm değişkenlere 1 değeri verilir, dolayısıyla \( P(3x - 1) \) polinomunun katsayılar toplamı \( P(3(1) - 1) = P(2) \) değerine eşittir.
\( P(2) \) değerini bulmak için \( P(x) \) polinomunda \( x = 2 \) yazalım.
\( P(2) = 2^5 - 3(2)^3 - a(2) + 3 \)
\( = 11 - 2a \)
Bu iki değerin birbirine eşit olduğu bilgisi veriliyor.
\( 1 - a = 11 - 2a \)
\( a = 10 \) bulunur.
\( P(x) = (2x^4 + 2x^2 - 3)^3(3x^2 + 5)^2 \)
polinomu için aşağıda verilen öncüllerden hangileri doğrudur?
I. Sabit terimi 675'tir.
II. Katsayılar toplamı 64'tür.
III. Derecesi 16'dır.
IV. Başkatsayısı 96'dır.
Çözümü GösterI. öncül:
Bir polinomda sabit terimi bulmak için tüm değişkenlere 0 değeri verilir.
\( P(0) = (2(0)^4 + 2(0)^2 - 3)^3(3(0)^2 + 5)^2 \)
\( = (-3)^3(5)^2 = -675 \)
I. öncül yanlıştır.
II. öncül:
Bir polinomda katsayılar toplamını bulmak için tüm değişkenlere 1 değeri verilir.
\( P(1) = (2(1)^4 + 2(1)^2 - 3)^3(3(1)^2 + 5)^2 \)
\( = (2 + 2 - 3)^3(3 + 5)^2 = 64 \)
II. öncül doğrudur.
III. öncül:
Polinomun en yüksek dereceli terimini bulmak için her çarpanın en yüksek dereceli terimini alalım.
\( (2x^4)^3(3x^2)^2 = 8x^{12} \cdot 9x^4 \)
\( = 72x^{16} \)
Buna göre polinomun derecesi 16'dır.
III. öncül doğrudur.
IV. öncül:
III. öncülde bulduğumuz en yüksek dereceli terime göre, polinomun başkatsayısı 72'dir.
IV. öncül yanlıştır.
Buna göre II. ve III. öncüller doğrudur.
\( P(x) \) bir polinomdur.
\( P(x^2) = ax^7 - bx^4 + cx^3 - dx^2 + b + d - 3 \) olduğuna göre,
\( P(x) \) polinomunun katsayılar toplamı kaçtır?
Çözümü GösterPolinomlarda tanım gereği değişkenleri üssü sadece doğal sayı olabilir.
Verilen polinom \( P(x^2) \) formunda olduğu için \( P(x) \) ifadesinin bir polinom olabilmesi için \( P(x^2) \) tanımında derecesi tek sayı olan terim bulunmaması gerekir.
Buna göre \( P(x^2) \) tanımındaki \( a \) ve \( c \) katsayıları sıfır olmalıdır.
\( P(x^2) = - bx^4 - dx^2 + b + d - 3 \)
\( P(x) \) polinomunun katsayılar toplamı \( x = 1 \) yazdığımızda elde ettiğimiz \( P(1) \) değeridir.
\( P(1) \) değerini bulmak için \( x = 1 \) yazalım.
\( P(1^2) = -b(1)^4 - d(1)^2 + b + d - 3 \)
\( = -b - d + b + d - 3 = -3 \) bulunur.
\( P(x) = (x - 1)^2 + (x - 2)^2 + \ldots + (x - n)^2 \)
polinomunun sabit terimi katsayılar toplamından 25 fazla olduğuna göre, \( n \) kaçtır?
Çözümü Göster\( P(x) \) polinomunda katsayılar toplamı için \( x = 1 \), sabit terim için \( x = 0 \) yazılır.
\( P(1) = (1 - 1)^2 + (1 - 2)^2 + \ldots + (1 - n)^2 \)
\( = (0)^2 + (-1)^2 + \ldots + (1 - n)^2 \)
\( P(0) = (0 - 1)^2 + (0 - 2)^2 + \ldots + (0 - n)^2 \)
\( = (-1)^2 + (-2)^2 + \ldots + (-n)^2 \)
Polinomun sabit terimi katsayılar toplamından 25 fazladır.
Birinci eşitliği ikinci eşitlikten taraf tarafa çıkaralım.
\( 25 = (-n)^2 - 0^2 = n^2 \)
\( n = 5 \) ya da \( n = -5 \) olabilir.
Polinom tanımında \( n \) sayısı \( (1, 2, 3, \ldots) \) şeklindeki bir dizinin son terimi olduğu için değeri pozitiftir.
Buna göre \( n = 5 \) olur.
\( P(x) = 2002x^{2 - a} - 1001x^{a - 2} - 1000 \) polinomu için aşağıdakilerden hangileri doğrudur?
I. Katsayılar toplamı 1'dir.
II. Sabit terimi 1'dir.
III. Sabit bir polinomdur.
Çözümü GösterTanım gereği bir polinomda değişkenler sadece doğal sayı kuvvetleri ile bulunabilir.
\( 2 - a \ge 0 \Longrightarrow a \le 2 \)
\( a - 2 \ge 0 \Longrightarrow a \ge 2 \)
Bu iki eşitsizlik sadece \( a = 2 \) olduğunda sağlanır.
\( P(x) = 2002x^{2 - 2} - 1001x^{2 - 2} - 1000 \)
\( = 2002 - 1001 - 1000 = 1 \)
Buna göre \( P(x) \) sabit polinomdur ve üç öncül de doğrudur.
\( P(x) \), \( Q(x) \) ve \( R(x) \) birer polinom olmak üzere,
\( P(x) = Q(x) \cdot R(x + 1) \) eşitliği veriliyor.
\( P(x) \) polinomunun sabit terimi \( Q(x) \) polinomunun sabit teriminin iki katı olduğuna göre, \( R(x) \) polinomunun katsayılar toplamı kaçtır?
Çözümü GösterBir \( P(x) \) polinomunun sabit terimi \( x = 0 \) yazdığımızda elde ettiğimiz \( P(0) \) değeridir.
\( P(x) \) polinomunun sabit terimi \( Q(x) \) polinomunun sabit teriminin iki katı ise aşağıdaki eşitliği yazabiliriz.
\( P(0) = 2Q(0) \)
\( R(x) \) polinomunun katsayılar toplamı \( x = 1 \) yazdığımızda elde ettiğimiz \( R(1) \) değeridir.
Soruda verilen eşitlikte \( x = 0 \) yazalım.
\( P(0) = Q(0) \cdot R(1) \)
Bu eşitlikte \( P(0) = 2Q(0) \) yazalım.
\( 2Q(0) = Q(0) \cdot R(1) \)
\( R(1) = 2 \) bulunur.
\( P(4x + 3) \) polinomunun sabit terimi \( P(P(2)) \)'dir.
\( P(2x + 5) \) polinomunun katsayılar toplamı \( P(P(3)) \)'tür.
\( P(7) = 4 \) olduğuna göre, \( P(P(P(2))) \) kaçtır?
Çözümü Göster\( P(4x + 3) \) polinomunun sabit terimini bulmak için \( x = 0 \) yazalım.
\( P(4(0) + 3) = P(3) = P(P(2)) \)
\( P(2x + 5) \) polinomunun katsayılar toplamını bulmak için \( x = 1 \) yazalım.
\( P(2(1) + 5) = P(7) = P(P(3)) \)
Sorulan ifadeyi bulalım ve yukarıda bulduğumuz değerleri yerine koyalım.
\( P(P(P(2))) = P(P(3)) = P(7) \)
\( P(7) = 4 \) olarak verildiği için \( P(P(P(2))) = 4 \) olarak bulunur.
Başkatsayısı 1, diğer katsayıları birer doğal sayı olan 4. dereceden bir \( P(x) \) polinomunun sabit terimi 2, katsayılar toplamı 8'dir.
Bu koşullara uyan kaç farklı \( P(x) \) polinomu yazılabilir?
Çözümü Göster\( P(x) = x^4 + bx^3 + cx^2 + dx + e \)
\( P(x) \) polinomunun sabit terimi \( x = 0 \) yazdığımızda elde ettiğimiz \( P(0) \) değeridir.
\( P(0) = 0^4 + b(0)^3 + c(0)^2 + d(0) + e = 2 \)
\( P(x) = x^4 + bx^3 + cx^2 + dx + 2 \)
\( P(x) \) polinomunun katsayılar toplamı \( x = 1 \) yazdığımızda elde ettiğimiz \( P(1) \) değeridir.
\( P(1) = 1^4 + b(1)^3 + c(1)^2 + d(1) + 2 = 8 \)
\( b + c + d = 5 \)
Katsayılar doğal sayı olduğu için, problemi 5 adet özdeş 1 sayısının birbirinden farklı 3 \( b \), \( c \) ve \( d \) kutusuna farklı dağıtım sayısı şeklinde kurgulayabiliriz.
Katsayılardan bazıları sıfır olabilir, dolayısıyla özdeş \( n \) nesnenin \( k \) farklı kutuya her kutuda herhangi bir sayıda nesne olacak şekilde dağıtımı için ayraç yöntemi kullanılır.
Farklı dağıtım sayısı \( = C(n + k - 1, k - 1) \)
\( = C(5 + 3 - 1, 3 - 1) = C(7, 2) \)
\( = \dfrac{7!}{5! \cdot 2!} = 21 \) bulunur.
\( a, b, c \in \mathbb{Z^+} \) olmak üzere,
\( P(x) = (x + a)(4x + b)(7x + c) \)
polinomunun katsayılarının toplamı 165 olduğuna göre, \( abc \) çarpımı kaçtır?
Çözümü Göster\( P(x) \) polinomunun katsayılar toplamı \( x = 1 \) yazdığımızda elde ettiğimiz \( P(1) \) değeridir.
\( P(1) = (1 + a)(4(1) + b)(7(1) + c) \)
\( 165 = (1 + a)(4 + b)(7 + c) \)
\( 165 = 3 \cdot 5 \cdot 11 \)
Bu eşitliği sağlayan pozitif tam sayı \( a, b, c \) değerlerini bulalım.
\( 1 + a = 3 \Longrightarrow a = 2 \)
\( 4 + b = 5 \Longrightarrow b = 1 \)
\( 7 + c = 11 \Longrightarrow c = 4 \)
\( abc = 2 \cdot 1 \cdot 4 = 8 \) bulunur.
\( P(x) \) bir sabit polinomdur.
\( P(x) = (a + P(4)) \cdot x + 9 + 2a \) olduğuna göre, \( P(0) \) kaçtır?
Çözümü GösterSabit polinomlarda sadece sabit terim bulunur.
Buna göre \( P(x) \) tanımında \( x \) değişkeninin katsayısı \( a + P(4) = 0 \) olmalıdır.
\( a + P(4) = 0 \)
\( P(4) = -a \)
\( P(x) = 9 + 2a \)
\( P(4) \) değerini bulmak için \( x = 4 \) yazalım.
\( P(4) = 9 + 2a = -a \)
\( a = -3 \)
Buna göre \( P(x) \) tanımı aşağıdaki gibi olur.
\( P(x) = 9 + 2(-3) = 3 \)
\( P(0) = 3 \) bulunur.
\( P(x) = (9 - 3x)^5 \) polinomunun açılımındaki katsayıların mutlak değerlerinin toplamı kaçtır?
Çözümü Göster\( P(x) = (9 - 3x)^5 \) polinomunun açılımındaki katsayıların mutlak değerlerinin toplamı, \( Q(x) = (9 + 3x)^5 \) polinomunun açılımındaki katsayıların toplamına eşittir.
\( Q(x) \) polinomunda \( x = 1 \) yazarak katsayılar toplamını bulalım.
\( Q(1) = (9 + 3(1))^5 = 12^5 \) bulunur.
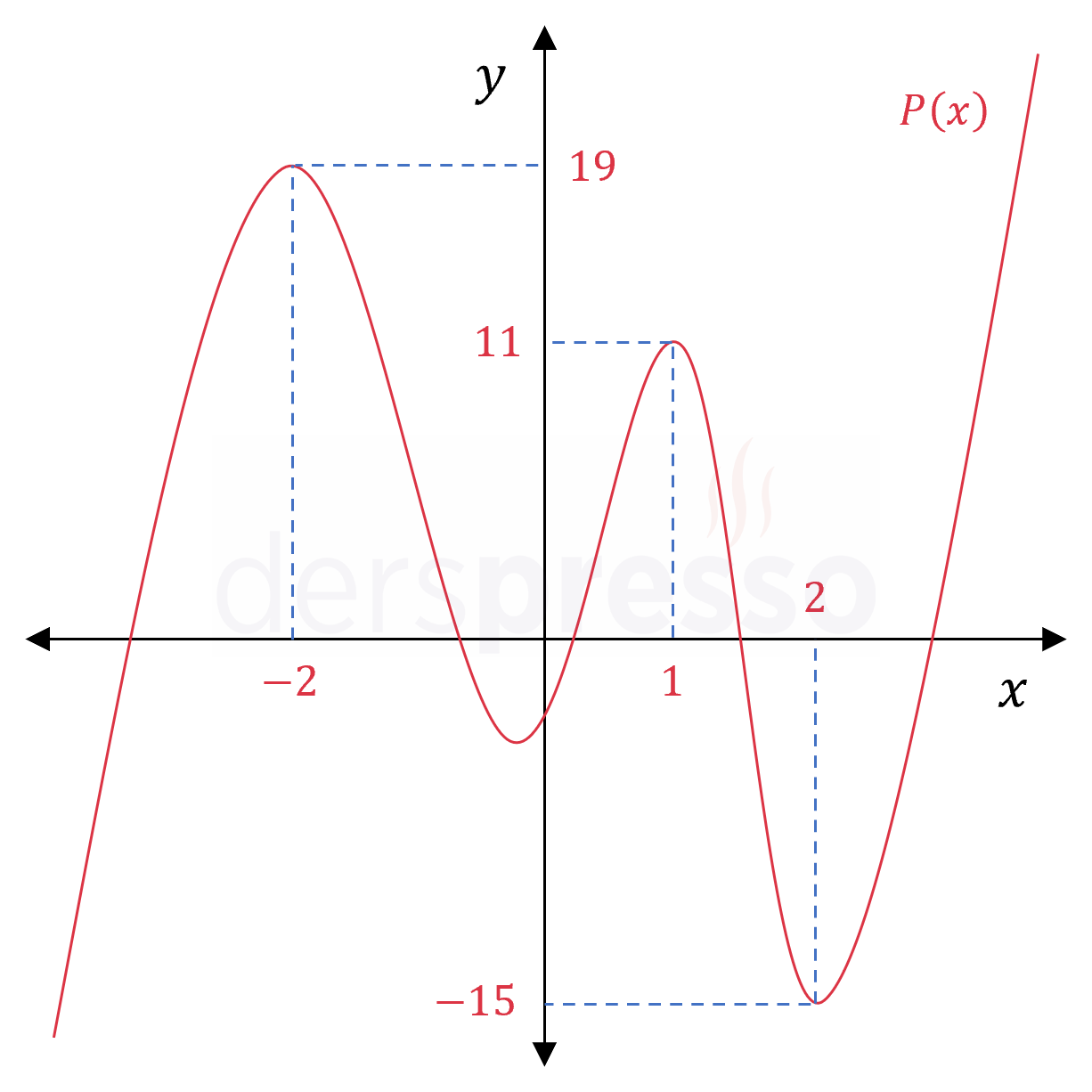
Şekilde \( P(x) \) polinomunun grafiği verilmiştir.
\( P(x) = 2x^5 + ax^4 + bx^3 + cx^2 + dx + e \)
Buna göre \( a + b + c + d + e \) toplamı kaçtır?
Çözümü Göster\( P(x) \) polinomunun katsayılar toplamı \( x = 1 \) yazdığımızda elde ettiğimiz \( P(1) \) değeridir.
\( P(1) = 2(1)^5 + a(1)^4 + b(1)^3 + c(1)^2 + d(1) + e \)
Verilen grafiği incelediğimizde \( P(1) = 11 \) olduğu görülür.
\( 2 + a + b + c + d + e = 11 \)
\( a + b + c + d + e = 9 \) olarak bulunur.