Polinomlarda Bölme İşlemi
Polinomlar arasında toplama, çıkarma ve çarpma işlemi yapabildiğimiz gibi bölme işlemi de yapabiliriz. Sayılar arasındaki bölme işlemine benzer şekilde, polinom bölme işleminde de bölünen ve bölen, işlemin sonucu olan bölüm ve bölme işlemi kalansız olmuyorsa kalan vardır. Polinom bölme işleminde bu dört terim de birer polinomdur.
Sayılar arasındaki bölme işleminde olduğu gibi, bölünen polinom bölen ve bölüm polinomlarının çarpımı ile kalan polinomunun toplamına eşittir.
\( B(x) \ne 0 \) olmak üzere,
\( P(x) = B(x) \cdot Q(x) + K(x) \)
\( 2x^2 + 5x - 6 = (x - 3) \cdot (2x + 11) + 27 \)
Yukarıdaki eşitlikte tüm terimleri \( B(x) \) polinomuna bölersek aşağıdaki eşitliği elde ederiz. Buna göre \( P(x) \) polinomunu \( B(x) \) polinomuna böldüğümüzde bölüm \( Q(x) \) olur ve tam bölünemeyen (kalan) kısım \( K(x) \) olur.
\( \dfrac{P(x)}{B(x)} = Q(x) + \dfrac{K(x)}{B(x)} \)
\( \dfrac{2x^2 + 5x - 6}{x - 3} = 2x + 11 + \dfrac{27}{x - 3} \)
Bu dört polinomun dereceleri arasında aşağıdaki iki ilişki vardır.
\( der[Q(x)] = der[P(x)] - der[B(x)] \)
\( der[K(x)] \lt der[B(x)] \)
Buna göre, 5. dereceden bir polinomu 3. dereceden bir polinoma böldüğümüzde sonuç 2. dereceden bir polinom olur. İşlem kalanlı bir bölme ise kalan polinomunun derecesi 3. dereceden küçük olmak zorundadır, çünkü kalanın üçüncü ya da daha büyük dereceden olması kalan polinomunun bölen polinomuna bir kez daha bölünebilmesi anlamına gelecektir.
Kalan polinomunun derecesi bölüm polinomunun derecesinden de küçükse işlemde \( B(x) \) ile \( Q(x) \)'in yer değiştirmesi kalanı değiştirmez.
\( \dfrac{2x^2 + 5x - 6}{\textcolor{red}{x - 3}} = \textcolor{blue}{2x + 11} + \dfrac{27}{\textcolor{red}{x - 3}} \)
\( \dfrac{2x^2 + 5x - 6}{\textcolor{blue}{2x + 11}} = \textcolor{red}{x - 3} + \dfrac{27}{\textcolor{blue}{2x + 11}} \)
\( K(x) = 0 \) ise \( P(x) \) polinomu \( B(x) \) polinomuna tam bölünüyor demektir, bu da \( B(x) \) ve \( Q(x) \) polinomlarının \( P(x) \) polinomunun birer çarpanı olduğu anlamına gelir.
\( K(x) = 0 \) ise,
\( P(x) = B(x)\cdot Q(x) \)
Bir \( P(x) \) polinomu \( x^2 - 3 \) ile bölündüğünde bölüm \(x^3 + 1 \) ve kalan \( 3x + 2 \) ise \( P(x) \) polinomunu bulunuz.
Çözümü GösterPolinom bölme işleminde bölünen polinom, bölen ve bölüm polinomlarının çarpımı ile kalan polinomunun toplamına eşittir.
\( P(x) = B(x) \cdot Q(x) + K(x) \)
\( P(x) = (x^2 - 3)(x^3 + 1) + (3x + 2) \)
Parantez içindeki ifadeleri genişletelim.
\( = x^5 + x^2 - 3x^3 - 3 + 3x + 2 \)
\( = x^5 - 3x^3 + x^2 + 3x - 1 \) bulunur.
\( P(x) \) polinomu \( 2x + 5 \) ile bölündüğünde bölüm \( 2x^3 - 2 \) ve kalan \( x - 2 \) ise \( P(x) \) polinomunu bulunuz.
Çözümü GösterPolinom bölme işleminde bölünen polinom, bölen ve bölüm polinomlarının çarpımı ile kalan polinomunun toplamına eşittir.
\( P(x) = B(x) \cdot Q(x) + K(x) \)
\( P(x) = (2x + 5)(2x^3 - 2) + (x - 2) \)
Parantez içindeki ifadeleri genişletelim.
\( = 4x^4 - 4x + 10x^3 - 10 + x - 2 \)
\( = 4x^4 + 10x^3 - 3x - 12 \) bulunur.
Polinom Bölme Yöntemleri
Polinomlar arası bölme işleminde aşağıdaki yöntemler kullanılır.
Çarpanlara Ayırma ve Sadeleştirme
Bölünen ve bölen polinomlarını çarpanlarına ayırdığımızda paydadaki bölen polinomunun çarpanlarının tümü paydaki bölünen polinomu içinde mevcutsa bu çarpanları sadeleştirerek kalansız bir şekilde işlem sonucunu bulabiliriz.
Polinom Bölmesi
Eğer bölünen ve bölen polinomları tüm çarpanlarına ayrılmıyorsa ya da ayrıldığında bölen polinomunun tüm çarpanları sadeleşmiyorsa bölme işlemi polinom bölmesi adı verilen yöntemle gerçekleştirilebilir. Bu işlem sayılarla bölme işlemine benzemekte olup, örnek bir bölme işlemi üzerinden anlatacağımız aşağıdaki adımlardan oluşur.
\( P(x) \) polinomunu \( B(x) \) polinomuna bölelim.
\( P(x) = 2x^4 + x^3 - x^2 + 12x - 5 \)
\( B(x) = x^2 + 2x \)
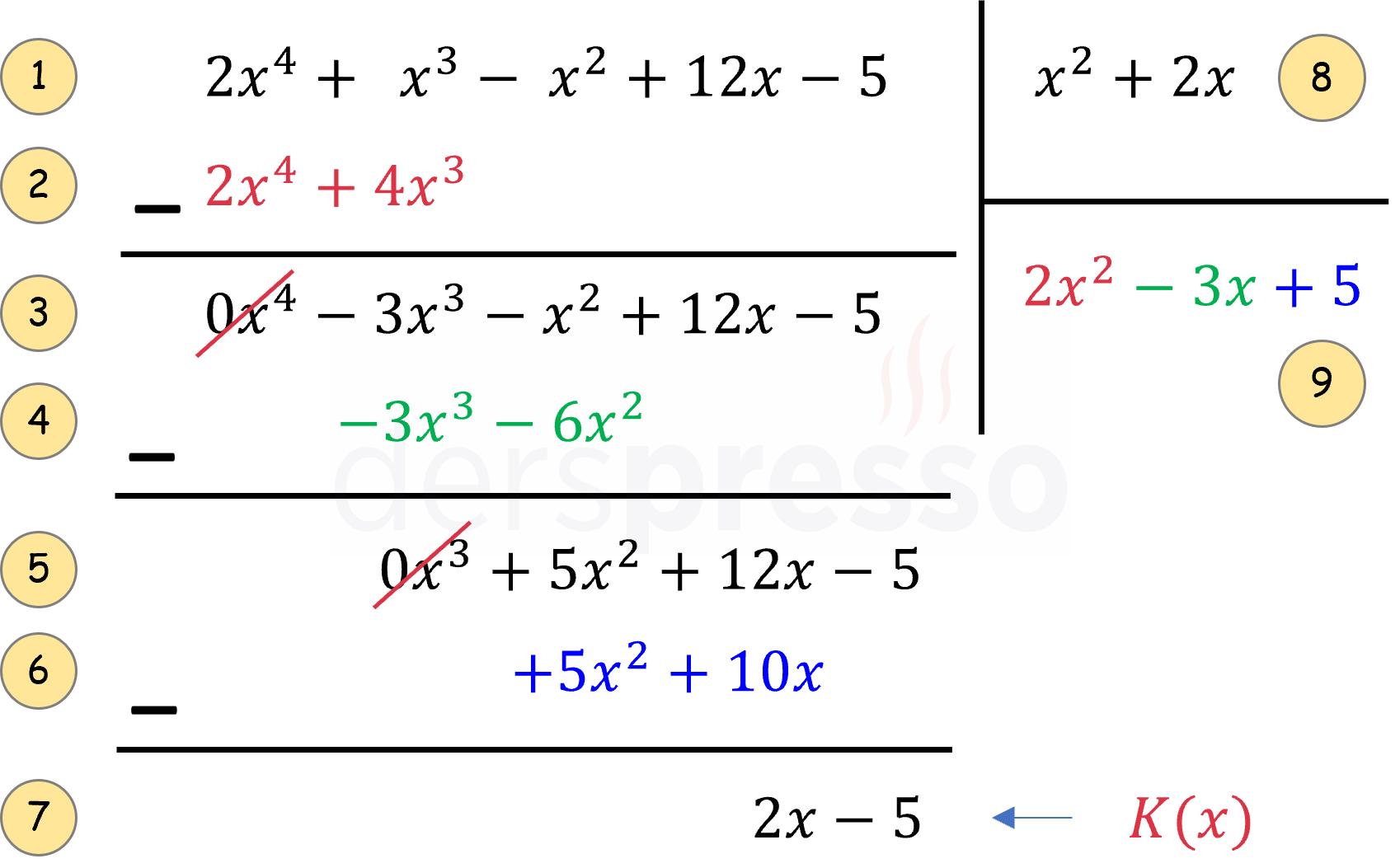
Adım 1:
Önce bölme çizgilerini çizerek bölünen (1) ve bölen (8) polinomlarını yerlerine yazarız. Bu noktada polinomların terimlerinin en yüksekten en düşük dereceye doğru sıralandığından emin olmalıyız.
Adım 2:
- Bölünen polinomunun (1) ilk terimini (\( 2x^4 \)) bölen polinomunun (8) ilk terimine (\( x^2 \)) böler ve sonucu bölüm (9) kısmına yazarız (\( 2x^2 \)).
- Bulduğumuz sonucu (\( 2x^2 \)) bölen polinomu (8) ile çarparak sonucu 2. satıra, her terim aynı dereceli terimin altına gelecek şekilde yazarız (\( 2x^4 + 4x^3 \)). Belirli bir derecede terim bölünen polinomunda yoksa o terimi bölünen polinomundaki farklı derecede bir terimle karıştırmamaya dikkat etmeliyiz.
- 2. satırdaki polinomu 1. satırdaki polinomdan benzer terimlerin katsayılarının farkını alarak çıkarır, sonucu 3. satıra yazarız (\( -3x^3 - x^2 + 12x - 5 \)).
Çıkarma işlemi sonucunda elde ettiğimiz polinomun (3) derecesi bölen polinomunun (8) derecesinden küçük olmadığı için bölme işlemine devam ederiz.
Adım 3:
Bu adımda 2. adımdaki işlemleri 1. satır yerine 3. satırı baz alarak tekrarlarız.
- 3. satırdaki polinomun ilk terimini (\( -3x^3 \)) bölen polinomunun (8) ilk terimine (\( x^2 \)) böler ve sonucu bölüm (9) kısmına yeni bir terim olarak yazarız (\( -3x \)).
- Bulduğumuz sonucu (\( -3x \)) bölen polinomu (8) ile çarparak sonucu 4. satıra yazarız (\( -3x^3 - 6x^2 \)).
- 4. satırdaki polinomu 3. satırdaki polinomdan çıkarır, sonucu 5. satıra yazarız (\( 5x^2 + 12x - 5 \)).
Çıkarma işlemi sonucunda elde ettiğimiz polinomun (5) derecesi bölen polinomunun (8) derecesinden küçük olmadığı için bölme işlemine devam ederiz.
Adım 4:
Bu adımda 2. adımdaki işlemleri 1. satır yerine 5. satırı baz alarak tekrarlarız.
- 5. satırdaki polinomun ilk terimini (\( 5x^2 \)) bölen polinomunun (8) ilk terimine (\( x^2 \)) böler ve sonucu bölüm (9) kısmına yeni bir terim olarak yazarız (\( +5 \)).
- Bulduğumuz sonucu (\( +5 \)) bölen polinomu (8) ile çarparak sonucu 6. satıra yazarız (\( 5x^2 + 10x \)).
- 6. satırdaki polinomu 5. satırdaki polinomdan çıkarır, sonucu 7. satıra yazarız (\( 2x - 5 \)).
Çıkarma işlemi sonucunda elde ettiğimiz polinomun (7) derecesi bölen polinomunun (8) derecesinden küçük olduğu için bölme işlemi tamamlanmıştır. Bölüm kısmındaki polinom (9) işlemin bölümü, kalan kısmındaki polinom (7) da kalanıdır. Kalan polinomu sıfırdan farklı olduğu için bölme işlemi kalanlı bir bölmedir.
Bu işlemin sonucunda bölüm ve kalan polinomları aşağıdaki gibi elde edilir.
\( Q(x) = 2x^2 - 3x + 5 \)
\( K(x) = 2x - 5 \)
Bu işlemin sonucunu aşağıdaki şekilde yazabiliriz.
\( P(x) = B(x) \cdot Q(x) + K(x) \)
\( \underbrace{2x^4 + x^3 - x^2 + 12x - 5}_{P(x)} = \underbrace{(x^2 + 2x)}_{B(x)} \cdot \underbrace{(2x^2 - 3x + 5)}_{Q(x)} + \underbrace{2x - 5}_{K(x)} \)
Polinomların derecelerinin yukarıda paylaştığımız kurallarla tutarlı olduğunu kontrol edebiliriz.
- Bölüm polinomunun derecesi bölünen ve bölen polinomlarının dereceleri farkına eşittir.
- Kalan polinomunun derecesi bölen polinomunun derecesinden küçüktür.
Polinomlarda EBOB ve EKOK
İki ya da daha fazla sayıda polinomun EBOB'u (en büyük ortak böleni) her bir polinomu ayrı ayrı tam bölen en yüksek dereceli polinomdur. İki ya da daha fazla sayıda polinomun EBOB'unu bulmak için polinomlar tüm çarpanlarına ayrılır ve polinomlarda ortak olan çarpanların en düşük dereceli olanları alınır.
\( P(x) = x^3(x + 3)^2(x - 1)^5 \)
\( Q(x) = x^4(x + 5)(x - 1)^2 \)
İki polinomda da ortak olan çarpanların en düşük dereceli olanları \( x^3 \) ve \( (x - 1)^2 \) olduğu için polinomların EBOB'u \( x^3(x - 1)^2 \) olur.
\( EBOB(P(x), Q(x)) = x^3(x - 1)^2 \)
İki ya da daha fazla sayıda polinomun EKOK'u (en küçük ortak katı) her bir polinomun ayrı ayrı tam böldüğü en düşük dereceli polinomdur. İki ya da daha fazla sayıda polinomun EKOK'unu bulmak için polinomlar tüm çarpanlarına ayrılır ve polinomların çarpanlarından ortak olanların en yüksek dereceli olanları, ortak olmayanların tümü alınır.
\( P(x) = x^2(x + 3)^2(x - 1)^5 \)
\( Q(x) = x(x + 5)(x - 1)^2 \)
\( EKOK(P(x), Q(x)) = x^2(x + 3)^2(x + 5)(x - 1)^5 \)
Tek bir polinomun terimlerinin EBOB'u polinomun tüm terimlerini tam bölen, bir diğer ifadeyle terimleri ortak paranteze alabileceğimiz en yüksek dereceli monom ifadedir. Bir polinomun EBOB'unu bulmak için polinomun tüm terimleri asal çarpanlarına ayrılır ve her terimde ortak olan çarpanların en düşük dereceli olanları alınır.
\( P(x) = 24x^3 - 180x^2 \)
\( 24x^3 = 2^3 \cdot 3^1 \cdot x^3 \)
\( 180x^2 = 2^2 \cdot 3^2 \cdot 5^1 \cdot x^2 \)
İki terimde de ortak olan çarpanların en düşük dereceli olanları \( 2^2 \), \( 3^1 \) ve \( x^2 \) olduğu için polinomun EBOB'u \( 12x^2 \) olur.
\( P(x) = 12x^2(2x - 15) \)
\( Q(x) = 3x^2 + 9x - 6 \)
Üç terimde de ortak olan çarpan \( 3 \) olduğu için polinomun EBOB'u \( 3 \) olur.
\( Q(x) = 3(x^2 + 3x - 2) \)
\( R(x) = 45x^5y^3 - 54x^2y^4 \)
\( 45x^5y^3 = 3^2 \cdot 5^1 \cdot x^5 \cdot y^3 \)
\( 54x^2y^4 = 2^1 \cdot 3^3 \cdot x^2 \cdot y^4 \)
İki terimde de ortak olan çarpanların en düşük dereceli olanları \( 3^2 \), \( x^2 \) ve \( y^3 \) olduğu için polinomun EBOB'u \( 9x^2y^3 \) olur.
\( R(x) = 9x^2y^3(5x^3 - 6y) \)
Aşağıdaki polinom bölme işlemlerinde bölüm ve kalan polinomlarını bulunuz.
(a) \( 2x^3 - x + 1 \) polinomunun \( x^2 + x + 1 \) ile bölümü
(b) \( 2x^4 + 3x^3 + 3x^2 - 5x - 3 \) polinomunun \( 2x^2 - x - 5 \) ile bölümü
(c) \( 9x^3 + 5 \) polinomunun \( 2x^3 - 3 \) ile bölümü
Çözümü Göster(a) seçeneği:
\( 2x^3 - x + 1 \) polinomunun \( x^2 + x + 1 \) ile bölümünde bölüm polinomu \( 2x - 2 \), kalan polinomu \( 3 - x \) olarak bulunur.
\( 2x^3 - x + 1 = (x^2 + x + 1)(2x - 2) + 3 - x \)
Bölme işleminin adımları aşağıda gösterilmiştir.
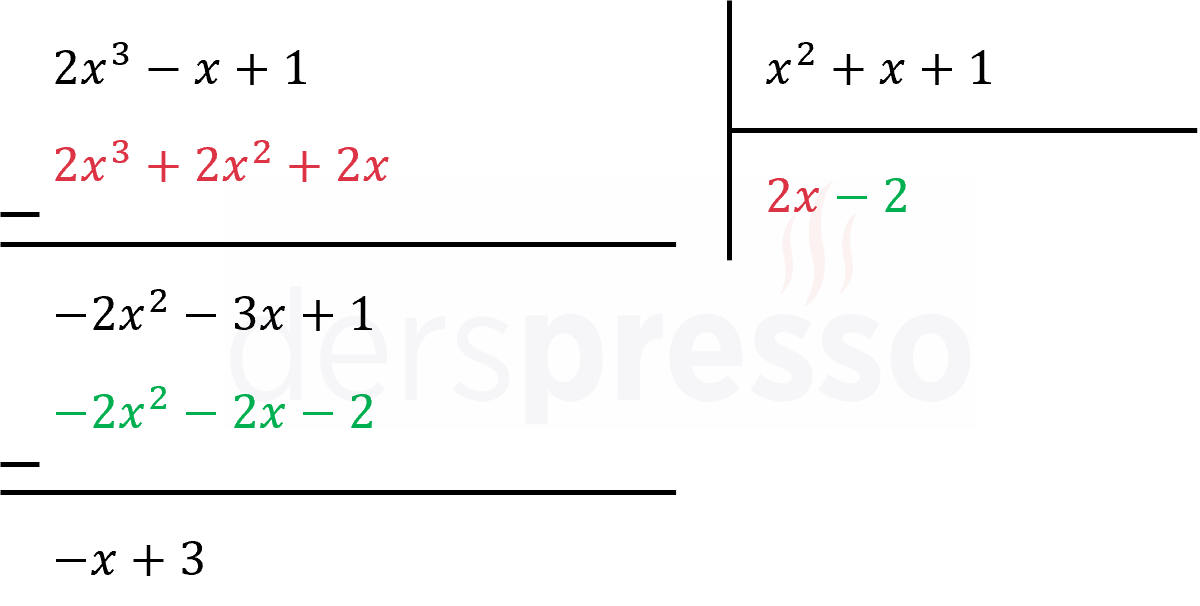
(b) seçeneği:
\( 2x^4 + 3x^3 + 3x^2 - 5x - 3 \) polinomunun \( 2x^2 - x - 5 \) ile bölümünde bölüm polinomu \( x^2 + 2x + 5 \), kalan polinomu \( 10x + 22 \) olarak bulunur.
\( 2x^4 + 3x^3 + 3x^2 - 5x - 3 = (2x^2 - x - 5)(x^2 + 2x + 5) + 10x + 22 \)
Bölme işleminin adımları aşağıda gösterilmiştir.
(c) seçeneği:
\( 9x^3 + 5 \) polinomunun \( 2x^3 - 3 \) ile bölümünde bölüm polinomu \( \frac{9}{2} \), kalan polinomu \( \frac{37}{2} \) olarak bulunur.
\( 9x^3 + 5 = (2x^3 - 3) \cdot \dfrac{9}{2} + \dfrac{37}{2} \)
Bölme işleminin adımları aşağıda gösterilmiştir.
Aşağıdaki polinom bölme işlemlerinde bölüm ve kalan polinomlarını bulunuz.
(a) \( -6x^4 + x^3 + 10x^2 + 18x + 3 \) polinomunun \( 3x + 1 \) ile bölümü
(b) \( 7x^5 + 9x^4 - 5x^3 + 3x - 8 \) polinomunun \( x^2 + 1 \) ile bölümü
(c) \( -10x^6 + 6x^5 + 2x^3 + 5x - 3 \) polinomunun \( -x^3 + x^2 - 3 \) ile bölümü
Çözümü Göster(a) seçeneği:
\( -6x^4 + x^3 + 10x^2 + 18x + 3 \) polinomunun \( 3x + 1 \) ile bölümünde bölüm polinomu \( -2x^3 + x^2 + 3x + 5 \), kalan polinomu \( -2 \) olarak bulunur.
\( -6x^4 + x^3 + 10x^2 + 18x + 3 = (3x + 1)(-2x^3 + x^2 + 3x + 5) - 2 \)
Bölme işleminin adımları aşağıda gösterilmiştir.
(b) seçeneği:
\( 7x^5 + 9x^4 - 5x^3 + 3x - 8 \) polinomunun \( x^2 + 1 \) ile bölümünde bölüm polinomu \( 7x^3 + 9x^2 - 12x - 9 \), kalan polinomu \( 15x + 1 \) olarak bulunur.
\( 7x^5 + 9x^4 - 5x^3 + 3x - 8 = (x^2 + 1)(7x^3 + 9x^2 - 12x - 9) + 15x + 1 \)
Bölme işleminin adımları aşağıda gösterilmiştir.
(c) seçeneği:
\( -10x^6 + 6x^5 + 2x^3 + 5x - 3 \) polinomunun \( -x^3 + x^2 - 3 \) ile bölümünde bölüm polinomu \( 10x^3 + 4x^2 + 4x - 28 \), kalan polinomu \( 40x^2 + 17x - 87 \) olarak bulunur.
\( -10x^6 + 6x^5 + 2x^3 + 5x - 3 = (-x^3 + x^2 - 3)(10x^3 + 4x^2 + 4x - 28) + 40x^2 + 17x - 87 \)
Bölme işleminin adımları aşağıda gösterilmiştir.
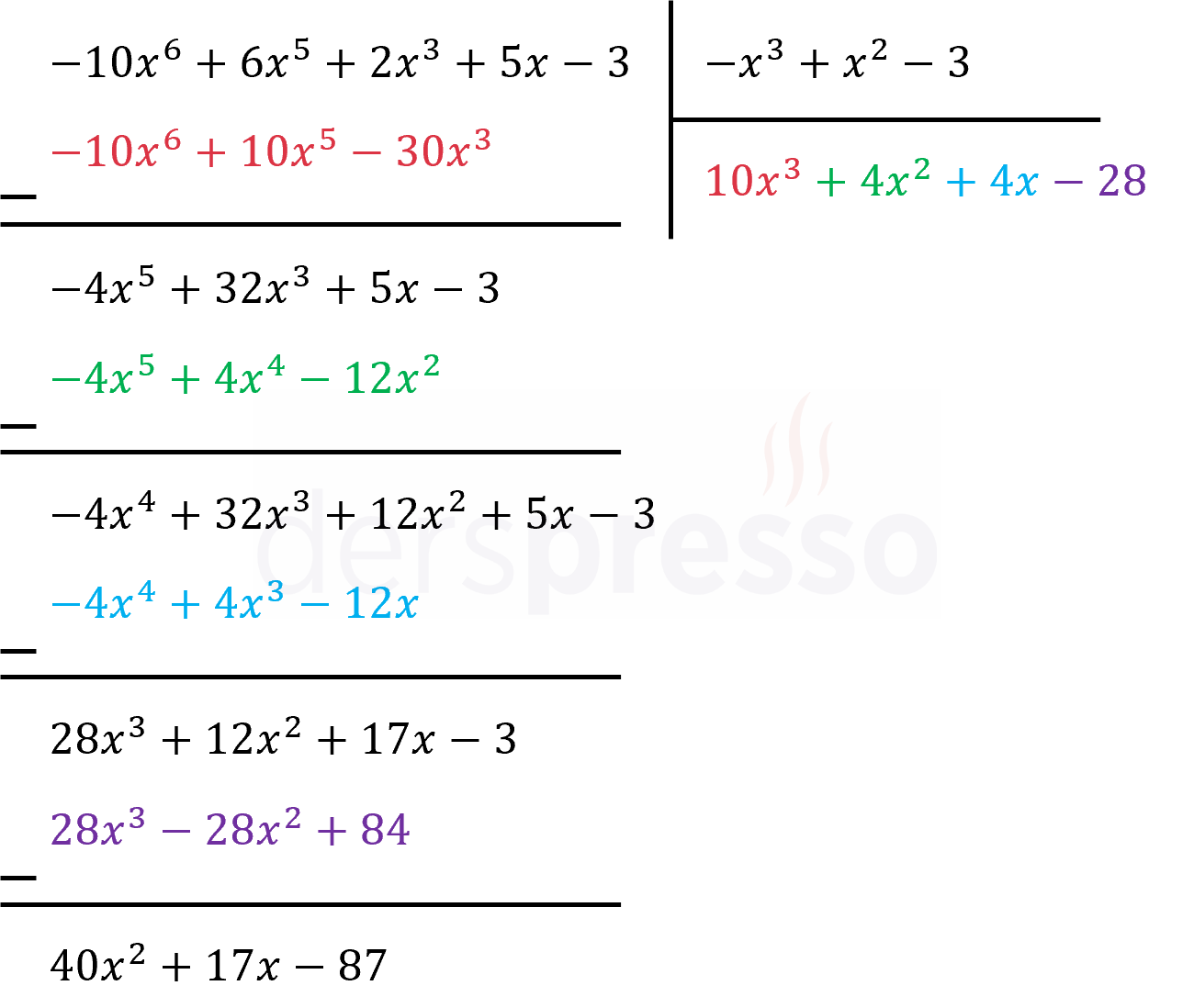
\( n \in \mathbb{Z^+} \) olmak üzere,
\( (n + 6)^2 \) ifadesi \( n + 3 \) ifadesine kalansız bölünmektedir.
Buna göre, \( n \) sayısı kaça eşittir?
Çözümü Gösterİki ifade arasında polinom bölmesi yapalım.
\( (n + 6)^2 = (n + 3)(n + 9) + 9 \)
\( \dfrac{(n + 6)^2}{n + 3} = (n + 9) + \dfrac{9}{n + 3} \)
Buna göre \( n + 3 \) ifadesi 9'u kalansız bölmelidir.
9'un pozitif bölenleri \( \{1, 3, 9\} \) sayılarıdır.
\( n \in \mathbb{Z^+} \) olduğu için \( n = 6 \) olarak bulunur.
\( P(x) = (x + 1) + (x + 2) + \ldots + (x + 20) \) polinomunun \( Q(x) = (x + 1) + (x + 2) + \ldots + (x + 10) \) polinomuna bölümünden kalan kaçtır?
Çözümü Göster\( P(x) = 20x + (1 + 2 + \ldots + 20) = 20x + \dfrac{20 \cdot 21}{2} \)
\( = 20x + 210 \)
\( Q(x) = 10x + (1 + 2 + \ldots + 10) = 10x + \dfrac{10 \cdot 11}{2} \)
\( = 10x + 55 \)
\( \dfrac{P(x)}{Q(x)} = \dfrac{20x + 210}{10x + 55} \)
\( = \dfrac{2(10x + 55) + 100}{10x + 55} \)
\( = 2 + \dfrac{100}{10x + 55} \)
Buna göre bölme işleminde kalan polinomu \( 100 \) olur.
\( f(x) = x^4 - x^3 - 7x^2 + 13x + c \) fonksiyonu \( (x - 1)^2 \) ifadesine kalansız bölünebiliyorsa \( f(c) \) kaça eşittir?
Çözümü GösterPolinom bölmesi yaptığımızda aşağıdaki sonucu elde ederiz.
\( x^4 - x^3 - 7x^2 + 13x + c = (x - 1)^2(x^2 + x - 6) \)
\( = (x^2 - 2x + 1)(x^2 + x - 6) \)
İki çarpanın sabit terimlerinin çarpımı, \( f(x) \) tanımındaki \( c \) sabit terimini verir.
\( c = 1 \cdot (-6) = -6 \)
\( f(c) = f(-6) \) değerini bulmak için \( x = -6 \) yazalım.
\( f(x) = (x^2 - 2x + 1)(x^2 + x - 6) \)
\( f(-6) = ((-6)^2 - 2(-6) + 1)((-6)^2 + (-6) - 6) \)
\( = (36 + 12 + 1)(36 - 6 - 6) \)
\( = 49 \cdot 24 = 1176 \) bulunur.
\( P(x) \) polinomu \( x^2 + x - 12 \) ile bölündüğünde bölüm \( Q(x) \) ve kalan \( 2x + 1 \) olduğuna göre,
\( P(x) \) polinomunun \( x - 3 \) ile bölümünde bölüm ve kalan polinomlarının toplamı nedir?
Çözümü GösterSoruda verilen bölme işlemini yazalım.
\( P(x) = (x^2 + x - 12)Q(x) + 2x + 1 \)
Bölen polinomunu çarpanlarına ayıralım.
\( P(x) = (x - 3)(x + 4)Q(x) + 2x + 1 \)
Eşitliğin taraflarını \( x - 3 \)'e bölelim.
\( \dfrac{P(x)}{x - 3} = (x + 4)Q(x) + \dfrac{2x + 1}{x - 3} \)
Kalan polinomu içinde \( x - 3 \) polinomu iki kez vardır.
\( = (x + 4)Q(x) + \dfrac{2(x - 3)}{x - 3} + \dfrac{7}{x - 3} \)
\( = [(x + 4)Q(x) + 2] + \dfrac{7}{x - 3} \)
Buna göre \( P(x) \) polinomunun \( x - 3 \) polinomuna bölme işleminin bölümü \( (x + 4)Q(x) + 2 \) ve kalanı \( 7 \) olur.
Bölüm ve kalan polinomlarının toplamı \( (x + 4)Q(x) + 2 + 7 = (x + 4)Q(x) + 9 \) olarak bulunur.
\( P(x) = (x^4 - x^2)(x + 1)^2 \)
\( Q(x) = x(x^2 + x - 2)^2 \)
polinomlarının EBOB ve EKOK'larını bulunuz.
Çözümü GösterVerilen polinomları çarpanlarına ayıralım.
\( P(x) = (x^4 - x^2)(x + 1)^2 \)
\( = x^2(x^2 - 1)(x + 1)^2 \)
\( = x^2(x - 1)(x + 1)(x + 1)^2 \)
\( = x^2(x - 1)(x + 1)^3 \)
\( Q(x) = x(x^2 + x - 2)^2 \)
\( = x((x - 1)(x + 2))^2 \)
\( = x(x - 1)^2(x + 2)^2 \)
Polinomların EBOB'unu bulmak için polinomlarda ortak olan çarpanların en düşük dereceli olanları alınır.
\( EBOB = x(x - 1) \)
Polinomların EKOK'unu bulmak için polinomların çarpanlarından ortak olanların en yüksek dereceli olanları, ortak olmayanların tümü alınır.
\( EKOK = x^2(x - 1)^2(x + 1)^3(x + 2)^2 \)
\( P(x) \) birinci dereceden bir polinomdur.
\( P(2x + 3) \) polinomunun \( P(x) \) polinomu ile bölümünden elde edilen bölüm ve kalanın çarpımı 12'dir.
\( P(-1) = 4 \) olduğuna göre, \( P(5) \) kaçtır?
Çözümü GösterDerece işlem kurallarına göre \( P(x) \) ve \( P(2x + 3) \) polinomlarının dereceleri aynıdır.
\( P(x) = ax + b \)
\( P(2x + 3) = a(2x + 3) + b = 2ax + 3a + b \)
\( P(2x + 3) \) polinomunu \( P(x) \) cinsinden yazalım.
\( P(2x + 3) = 2(ax + b) + 3a - b \)
\( P(2x + 3) = P(x) \cdot 2 + 3a - b \)
Buna göre \( P(2x + 3) \) polinomunun \( P(x) \) polinomuna bölümünde bölüm 2, kalan \( 3a - b \) olur.
Bu işlemde bölüm ve kalanın çarpımı 12 olarak veriliyor.
\( 2 \cdot (3a - b) = 12 \)
\( 3a - b = 6 \)
\( P(-1) \) değerini bulalım.
\( P(-1) = a(-1) + b = 4 \)
\( b - a = 4 \)
İki denklemi ortak çözdüğümüzde aşağıdaki değerleri buluruz.
\( a = 5, \quad b = 9 \)
\( P(x) \) polinom tanımı aşağıdaki gibi olur.
\( P(x) = 5x + 9 \)
\( P(5) = 5(5) + 9 = 34 \) bulunur.
\( P(x) \) polinomunun \( x^2 - 6x + 9 \) ile bölümünde bölüm \( Q(x) \), kalan \( x - 10 \) dur.
\( Q(x) \) polinomunun \( x + 6 \) ile bölümünden kalan 3, \( P(x) \) polinomunun \( x^3 - 27x + 54 \) ile bölümünden kalan \( K(x) \) olduğuna göre, \( K(-2) \) kaçtır?
Çözümü GösterVerilen birinci bölme işlemini yazalım.
\( P(x) = (x^2 - 6x + 9) \cdot Q(x) + x - 10 \)
Verilen ikinci bölme işlemini yazalım.
\( Q(x) = (x + 6) \cdot S(x) + 3 \)
\( Q(x) \) polinomunu birinci bölme işleminde yerine yazalım.
\( P(x) = (x^2 - 6x + 9) \cdot [(x + 6) \cdot S(x) + 3] + x - 10 \)
\( = (x^2 - 6x + 9) \cdot (x + 6) \cdot S(x) + (x^2 - 6x + 9) \cdot 3 + x - 10 \)
\( = (x^3 - 27x + 54 ) \cdot S(x) + 3x^2 - 17x + 17 \)
Kalan polinomunun derecesi (\( 3x^2 - 17x + 17 \)) bölen polinomunun derecesinden (\( x^3 - 27x + 54 \)) küçük olduğu için, Elde ettiğimiz bu işlem \( P(x) \) polinomunun \( x^3 - 27x + 54 \) ile bölme işlemidir, dolayısıyla bölme işleminin kalanı aşağıdaki gibi olur.
\( K(x) = 3x^2 - 17x + 17 \)
\( K(-2) = 3(-2)^2 - 17(-2) + 17 = 63 \) bulunur.
\( 5^{62} + 17 \) ifadesinin \( 5^{41} + 5^{21} + 5 \) ifadesine bölümünden kalan kaçtır?
Çözümü Göster\( x = 5^{20} \) diyelim.
Verilen ifadeleri \( x \) cinsinden yazalım.
\( 5^{62} + 17 = 5^{60}5^2 + 17 \)
\( = 25(5^{20})^3 + 17 = 25x^3 + 17 \)
\( 5^{41} + 5^{21} + 5 = 5^{40}5^1 + 5^{20}5^1 + 5 \)
\( = 5(5^{20})^2 + 5(5^{20}) + 5 = 5x^2 + 5x + 5 \)
Kalanı istenen bölme işlemini \( x \) cinsinden yazalım.
\( \dfrac{25x^3 + 17}{5x^2 + 5x + 5} \)
İki ifade arasında polinom bölme işlemi yaptığımızda aşağıdaki sonucu elde ederiz.
\( 25x^3 + 17 = (5x^2 + 5x + 5)(5x - 5) + 42 \)
Buna göre kalan 42 olarak bulunur.